2. 弗吉尼亚大学 工程与应用科学学院, 美国 夏洛茨维尔 22904-4743
2. School of Engineering and Applied Science, University of Virginia, Charlottesville 22904-4743, USA
近空间飞行器具有飞行速度快、突防能力强、隐蔽性高等特点,近空间飞行器技术的进展,将成为人类航空航天科学技术史上又一个跨时代的里程碑,潜在着巨大的经济、政治、军事价值[1]。但近空间飞行器也存在前所未有的研发技术挑战,在飞控系统设计的过程中要全面地考虑多个方面的影响[2-3]。近空间可变翼飞行器可以通过改变小翼的伸缩状态来提高飞行效率,是一种具有全新概念的飞行器,可变小翼结构增强了飞行器对环境的适应能力[4]。近年来,近空间可变翼飞行器控制技术研究取得了丰硕的研究成果,研究集中于近空间可变翼飞行器的非线性控制方法[5-9]。焦鑫等[5]针对近空间可变翼飞行器参数不确定性等动态特性,提出自适应鲁棒控制的方法,控制效果良好。鲁棒控制是一种解决不确定性问题的有效方法,且目前研究较多的非线性鲁棒控制方法具有一定抗不确定性能力[6]。Jie等[7]针对近空间可变翼飞行器爬升、巡航段控制具有气动参数不确定性的特点,提出了一种快速双幂次滑模控制,且具有全局鲁棒性的控制方法。反馈线性化的基本思想是使原来的非线性系统完全或不完全地变为线性系统,然后用线性系统的设计思想来进行控制系统设计,以满足控制要求[8]。动态逆是一种典型的利用反馈线性化思想设计的非线性控制方法,针对参数不确定性问题,吴雨珊等[9]提出一种动态逆-PID结合的控制方法。然而,文献[5-9]所提到的控制方法需要精确的飞行器模型,飞行器模型可通过机理建模或系统辨识得到,实际应用时有一定复杂度。
模型参考自适应控制方法是一种无模型控制方法,它包括反馈控制结构和自适应律部分,能有效解决参数和结构不确定问题,该方法在稳定跟踪参考信号的同时能确保闭环系统的稳定性[10]。本文将研究自适应控制方法在近空间可变翼飞行器上的应用,设计了基于LDS矩阵分解的自适应控制方法,达到小翼伸缩平滑切换的控制效果。
1 近空间可变翼飞行器模型力和力矩模型中,飞行器受到的升力和阻力为:
| $ \left\{\begin{array}{l}{L=\frac{1}{2} \rho V^{2} S_{\mathrm{w}} C_{\mathrm{L}}} \\ {D=\frac{1}{2} \rho V^{2} S_{\mathrm{w}} C_{\mathrm{D}}} \\ {M_{y}=\frac{1}{2} \rho V^{2} S_{\mathrm{w}} c_{\mathrm{A}} C_{\mathrm{m}}}\end{array}\right. $ | (1) |
式中:s表示机翼面积;ρ表示大气密度;CL表示升力系数;CD表示阻力系数;cA为机翼弦长;Cm为俯仰力矩系数。
推力模型中,用二阶系统近似表示飞行器的发动机模型[11]:
| $ \ddot{\beta}=-2 \zeta \omega \dot{\beta}-\omega^{2} \beta+\omega^{2} \beta_{\mathrm{c}} $ | (2) |
式中:βc为发动机百分比;ζ为最佳阻尼比;ω为最佳频率。
飞行器推力计算公式为:
| $ C_{\mathrm{T}}=\left\{\begin{array}{ll}{0.02576 \beta, } ~~~ {\beta<1} \\ {0.0224+0.00336 \beta, } ~~~ {\beta \geqslant 1}\end{array}\right. $ | (3) |
| $ T=\frac{1}{2} \rho V^{2} S_{w} C_{\mathrm{T}} $ | (4) |
式中:CT表示与节流阀调定值有关的推力系数;T为发动机推力。
本文研究的可变小翼面积为20 m2,小翼伸缩过程迅速,但不是突变过程,是指数变化过程。建立小翼收回过程的数学模型如下[12]:
| $ \begin{array}{C} {S_{\rm{w}}} = \\ \left\{\begin{array}{ll}{389, } & {t \leqslant T_{1}} \\ {389 \mathrm{e}^{-a\left(t-T_{1}\right)}+369\left(1-\mathrm{e}^{-a\left(t-T_{1}\right)}\right), } & {T_{1}<t \leqslant T_{2}} \\ {369, } & {T_{2}<t \leqslant T_{3}} \\ {369 \mathrm{e}^{-a\left(t-T_{3}\right)}+389\left(1-\mathrm{e}^{-a\left(t-T_{3}\right)}\right), } & {T_{3}<t \leqslant T_{4}} \\ {389, } & {t>T_{4}}\end{array}\right. \end{array} $ | (5) |
式中:Sw表示机翼面积;t为仿真试验中的仿真时间,假设小翼从伸出到完全收回模态切换所需要的时间是T2~T1,从收回到完全伸出模态切换所需要的时间是T4~T3;小翼面积为20 m2,规定第T1小翼开始收回,到T2小翼完全收回,第T3小翼开始伸出,到T4小翼完全伸出小翼收回过程中气动参数会随之发生变化;系数a和小翼伸缩速率有关。
| $ \left[ \begin{array}{l}{\dot{V}=\frac{T \cos \alpha-D}{m}-\frac{\mu}{r^{2}} \sin \gamma} \\ {\dot{\gamma}=\frac{L+T \sin \alpha}{m V}-\frac{\left(\mu-V^{2} r\right) \cos \gamma}{V_{r^{2}}}} \\ {q=\frac{M_{y}}{I_{y}}} \\ {\dot{\alpha}=q-\dot{\gamma}} \\ {\dot{h}=V \sin \gamma}\end{array}\right. $ | (6) |
式中:r为地球半径;m为飞行器的质量;μ为地球引力常量;My为俯仰力矩;Iy为转动惯量。
2 自适应控制系统设计 2.1 控制问题描述小翼的变化将改变飞行器纵向模型的升力L、阻力D、推力T以及俯仰力矩My,可表示为L+ΔL, D+ΔD, T+ΔT, M+ΔM, Δ表示小翼伸出前后气动参数影响作用下的变化量。
将纵向模型进行线性化,状态方程表达式为:
| $ \left\{\begin{array}{l}{\dot{\boldsymbol{x}}(t)=A \boldsymbol{x}(t)+B \boldsymbol{u}(t)+f} \\ {\boldsymbol{y}(t)=C \boldsymbol{x}(t)}\end{array}\right. $ | (7) |
式中:x=[V, γ, q, α, h]T,y=[V, h]T,u=[βc, δe],f=f(x0, u0)为小翼伸缩带来的不确定项。
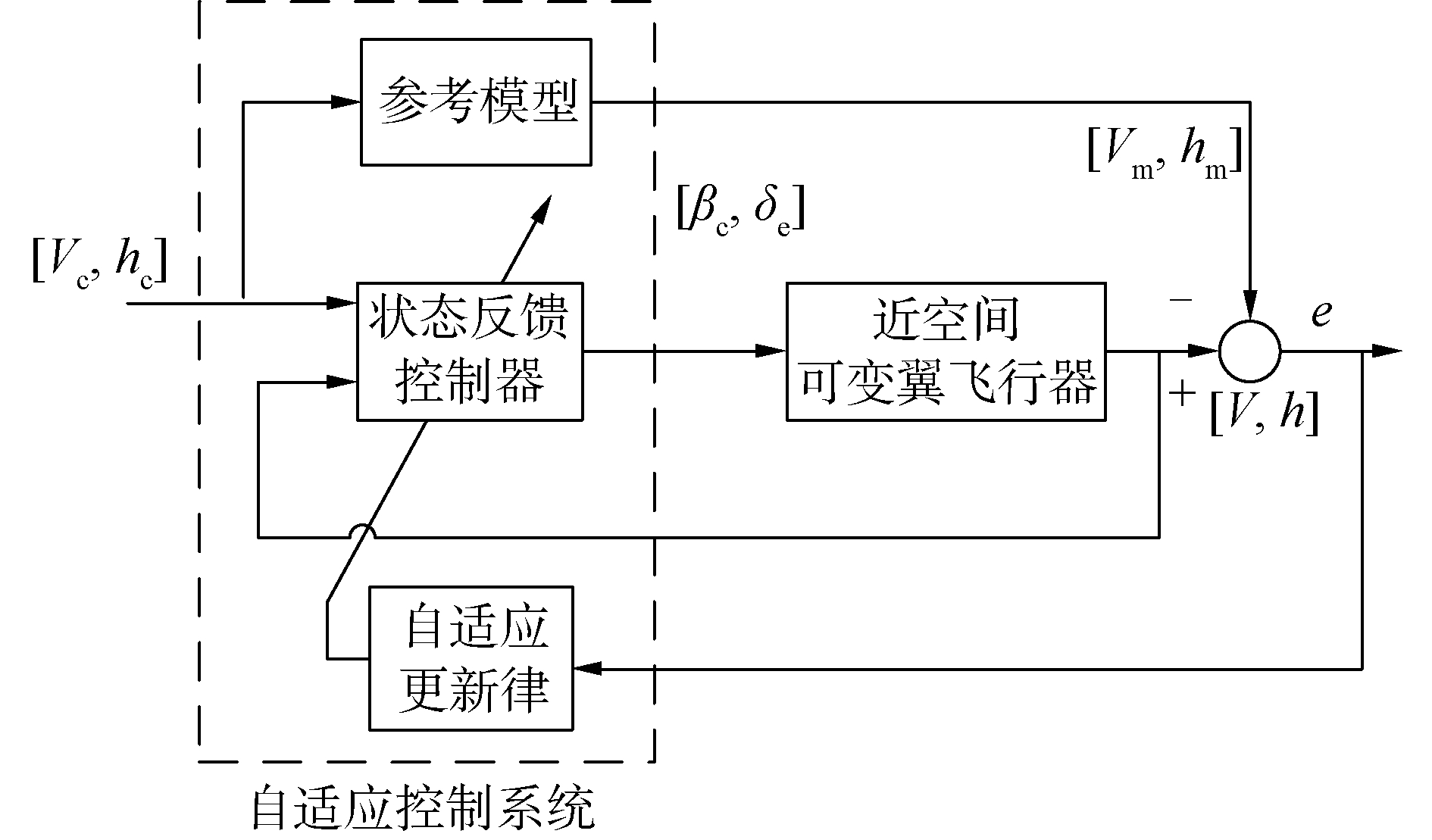
建立近空间可变翼飞行器输出反馈自适应控制系统结构如图 1所示。
|
Download:
|
| 图 1 近空间可变翼飞行器MRAC结构图 Fig. 1 Near space morphing vehicle MRAC structure | |
在控制器设计之前,先作出一些假设条件,假设条件是参考模型和自适应律设计,且能保证跟踪控制问题有解。当系统不满足严苛的假设条件时,可放宽假设条件,以满足控制器设计要求[15]。
2.2.1 参考模型设计计算得到
| $ \left\{\begin{array}{l}{\boldsymbol{y}_{m}(t)=\boldsymbol{W}_{m}(s) \boldsymbol{r}(t)} \\ {\boldsymbol{W}_{m}(s)=\boldsymbol{\xi}_{m}^{-1}(s)}\end{array}\right. $ | (8) |
式中:r(t)=Wm-1(s)[Vc(t), hc(t)]T表示参考模型输入,其中Vc(t)、hc(t)分别为速度和高度的指令信号输入。因此,根据假设条件,设计参考模型如下:
| $ \boldsymbol{y}_{m}(t)=\left[ \begin{array}{cc}{\frac{1}{\left(s+p_{1}\right)}} & {0} \\ {0} & {\frac{1}{\left(s+p_{2}\right)\left(s+p_{3}\right)}}\end{array}\right] \boldsymbol{r}(t) $ | (9) |
式中p1、p2、p3是参考模型的极点。
2.2.2 状态反馈控制器设计根据控制系统要求,设计状态反馈控制律为:
| $ \boldsymbol{u}(t)=\boldsymbol{K}_{1}^{* \mathrm{T}} x(t)+\boldsymbol{K}_{2}^{*} \boldsymbol{r}(t)+\boldsymbol{K}_{3}^{*} $ | (10) |
式中:
| $ \boldsymbol{C}\left(s \boldsymbol{I}-\boldsymbol{A}-\boldsymbol{B} \boldsymbol{K}_{1}^{* \mathrm{T}}\right)^{-1} \boldsymbol{B} \boldsymbol{K}_{2}^{*}=\boldsymbol{W}_{m}(s), \boldsymbol{W}_{m}(s)=\boldsymbol{\xi}_{m}^{-1}(s) $ | (11) |
将控制器应用到系统(7),闭环系统的输出的频域表达式为:
| $ \boldsymbol{y}(s)=\boldsymbol{C}\left(s \boldsymbol{I}-\boldsymbol{A}-\boldsymbol{B} \boldsymbol{K}_{1}^{* \mathrm{T}}\right)^{-1} \boldsymbol{B} \boldsymbol{K}_{2}^{*} r(s)+\Delta(s) $ | (12) |
式中:
根据参考模型(9)和匹配条件(11),则输出跟踪误差的频域表达式为:
| $ \boldsymbol{e}(s)=\boldsymbol{y}(s)-\boldsymbol{y}_{m}(s) $ | (13) |
将上式作拉普拉斯变换,有
| $ \lim\limits_{t \rightarrow \infty} e(t)=\lim _{s \rightarrow 0} s e(s)=\boldsymbol{D} \boldsymbol{K}_{3}^{*}+d $ | (14) |
式中:D=-C(A+BK1*)-1 B,d=-C(A+BK1*)-1f。为了消除误差,K3*表示为:
| $ \boldsymbol{K}_{3}^{*}=-\boldsymbol{D}^{-1} d $ | (15) |
结合式(14)、(15)和δ(t)=L-1[Δ(s)],可得
| $ \lim\limits_{t \rightarrow \infty}\left(\boldsymbol{y}(t)-\boldsymbol{y}_{m}(t)\right)=\lim\limits_{t \rightarrow \infty} \boldsymbol{\delta}(t)=0。$ |
通过上述分析,选择合适的参数K3*可使跟踪误差趋于零。K1*, K2*参数是平衡点出理想控制参数,通过平衡点初模型参数计算得到,而系统存在参数不确定,因此需要设计自适应律,实时更新控制律参数,来解决小翼切换时不确定性问题。
2.2.3 自适应律设计当系统参数均未知时,设计自适应状态反馈控制器为:
| $ \boldsymbol{u}(t)=\boldsymbol{K}_{1}^{\mathrm{T}} x(t)+\boldsymbol{K}_{2} r(t)+\boldsymbol{K}_{3}(t) $ | (16) |
式中:K1T(t)、K2(t)、K3(t)为未知参数K1*T、K2*、K3*的估计值。
将系统(7)重新描述为:
| $ \left\{\begin{aligned} \dot{\boldsymbol{x}}(t)=&\left(\boldsymbol{A}+\boldsymbol{B} \boldsymbol{K}_{1}^{* \mathrm{T}}\right) x(t)+\boldsymbol{B} \boldsymbol{K}_{2}^{*} \boldsymbol{r}(t)+\boldsymbol{B K}_{3}^{*}+f+\\ & \boldsymbol{B}\left(\tilde{\boldsymbol{K}}_{1}^{\mathrm{T}}(t) x(t)+\tilde{\boldsymbol{K}}_{2}(t) \boldsymbol{r}(t)+\tilde{\boldsymbol{K}}_{3}(t)\right) \\ \boldsymbol{y}(t) &=\boldsymbol{C x}(t) \end{aligned}\right. $ | (17) |
式中:
写出输出跟踪误差方程为:
| $ \mathit{\boldsymbol{e}}(t) = \mathit{\boldsymbol{y}}(t) - {\mathit{\boldsymbol{y}}_m}(t) = {\mathit{\boldsymbol{W}}_m}(s){\mathit{\boldsymbol{K}}_p}\left[ {{{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}^{\rm{T}}}\mathit{\boldsymbol{\omega }}} \right](t) + \mathit{\boldsymbol{\delta }}(t) $ | (18) |
式中:ω(t)=[xT(t), rT(t), 1]T,Θ*=[K1*T, K2*, K3*]T,
| $ \tilde{\mathit{\boldsymbol{ \boldsymbol{\varTheta}}}}(t)=\mathit{\boldsymbol{ \boldsymbol{\varTheta}}}(t)-\mathit{\boldsymbol{ \boldsymbol{\varTheta}}}^{*}, \mathit{\boldsymbol{ \boldsymbol{\varTheta}}}(t)=\left[\boldsymbol{K}_{1}^{\mathrm{T}}(t), \boldsymbol{K}_{2}(t), \boldsymbol{K}_{3}(t)\right]^{\mathrm{T}}。$ |
为了解决KP的不确定性,利用矩阵的LDS分解,即Kp=LsDsS。Ls是下三角单位矩阵,Ds为
| $ \begin{array}{l}{\boldsymbol{D}_{s}=\operatorname{diag}\left(s_{1}^{*}, s_{2}^{*}\right)=} \\ {\operatorname{diag}\left(\operatorname{sign}\left[\Delta_{1}\right] \gamma_{1}, \operatorname{sign}\left[\Delta_{2} / \Delta_{1}\right] \gamma_{2}\right)}\end{array} $ | (19) |
式中:Δ1、Δ2为矩阵Kp-1的前主子式。
将Kp代入式(18),且忽略指数衰减项δ(t),得:
| $ \boldsymbol{L}_{s}^{-1} \boldsymbol{\xi}_{m}(s) \boldsymbol{e}(t)=\boldsymbol{D}_{s} \boldsymbol{S} \mathit{\boldsymbol{\tilde { \boldsymbol{\varTheta} }}}^{\mathrm{T}}(t) \boldsymbol{\omega}(t) $ | (20) |
为了参数化矩阵Ls,引入矩阵Θ0*=(Ls-1-I),其具有如下特殊形式:
| $ \mathit{\boldsymbol{ \boldsymbol{\varTheta}}}_{0}^{*}=\left[ \begin{array}{cc}{0} & {0} \\ {\theta_{21}^{*}} & {0}\end{array}\right] $ | (21) |
可将式(20)转化为
| $ \boldsymbol{\xi}_{m}(s) \boldsymbol{e}(t)+\mathit{\boldsymbol{ \boldsymbol{\varTheta}}}_{0}^{*} \boldsymbol{\xi}_{m}(s) e(t)=\boldsymbol{D}_{s} \boldsymbol{S} \tilde{\mathit{\boldsymbol{ \boldsymbol{\varTheta}}}}^{\mathrm{T}}(t) \boldsymbol{\omega}(t) $ | (22) |
对于矩阵Θ0*,定义参数向量:θ2*=θ21*∈R,其参数向量估计值为θ2(t)=θ21(t)∈R,引入滤波器h(s)=1/f(s),f(s)=(s+p2)(s+p3)为稳定多项式,其阶数为改进的关联矩阵ξm(s)的最大阶数。将式(22)两边同乘h(s)IM可得:
| $ \overline{\boldsymbol{e}}(t)+\left[0, \boldsymbol{\theta}_{2}^{* \mathrm{T}} \eta_{2}(t)\right]^{\mathrm{T}}=\boldsymbol{D}_{s} \boldsymbol{S}h(s) \tilde{\mathit{\boldsymbol{ \boldsymbol{\varTheta}}}}^{\mathrm{T}}(t) \boldsymbol{\omega}(t) $ | (23) |
其中,e(t)=ξm(s)h(s)e(t)=[e1(t), e2(t)]T, η2(t)=e2(t)。
基于参数化的误差方程(23),引入一个估计误差信号:
| $ \boldsymbol{\varepsilon}(t)=\overline{\boldsymbol{e}}(t)+\left[0, \boldsymbol{\theta}_{2}^{\mathrm{T}}(t) \boldsymbol{\eta}_{2}(t)\right]^{\mathrm{T}}+\mathit{\boldsymbol{ \boldsymbol{\varPsi}}}(t) \boldsymbol{\xi}(t) \in \bf{R}^{2} $ | (24) |
式中:Ψ(t)是Ψ*=DsS的估计值,且
| $ \begin{array}{l}{\boldsymbol{\xi}(t)=\mathit{\boldsymbol{ \boldsymbol{\varTheta}}}^{\mathrm{T}}(t) \boldsymbol{\zeta}(t)-\boldsymbol{h}(s) \mathit{\boldsymbol{ \boldsymbol{\varTheta}}}^{\mathrm{T}}(t) \boldsymbol{\omega}(t)} \\ {\boldsymbol{\zeta}(t)=\boldsymbol{h}(s) \boldsymbol{\omega}(t)}\end{array} $ | (25) |
由式(23)~(25)可得:
| $ \begin{aligned} \boldsymbol{\varepsilon}(t)=&\left[0, \tilde{\boldsymbol{\theta}}_{2}^{\mathrm{T}}(t) \boldsymbol{\eta}_{2}(t)\right]^{\mathrm{T}}+\boldsymbol{D}_{s} \boldsymbol{S} \tilde{\mathit{\boldsymbol{ \boldsymbol{\varTheta}}}}^{\mathrm{T}}(t) \boldsymbol{\zeta}(t)+\\ & \tilde{\Psi}(t) \xi(t) \end{aligned} $ | (26) |
式中:
基于误差模型式(26),设计以下自适应律来估计控制器参数:
| $ {\dot \theta _2}(t) = \frac{{ - {\mathit{\Gamma }_{{\theta _2}}}{\varepsilon _2}(t){\eta _2}(t)}}{{{m^2}(t)}} $ | (27) |
| $ {\mathit{\boldsymbol{ \boldsymbol{\dot \varTheta} }}^{\rm{T}}}(t) = \frac{{ - {D_s}\varepsilon (t){\mathit{\boldsymbol{\zeta }}^{\rm{T}}}(t)}}{{{m^2}(t)}} $ | (28) |
| $ \mathit{\boldsymbol{ \boldsymbol{\dot \varPsi} }}(t) = \frac{{ - \mathit{\Gamma }\varepsilon (t){\mathit{\boldsymbol{\xi }}^{\rm{T}}}(t)}}{{{m^2}(t)}} $ | (29) |
式中:
| $ \mathit{\boldsymbol{m}}(t) = \sqrt {1 + {\mathit{\boldsymbol{\zeta }}^{\rm{T}}}(t)\mathit{\boldsymbol{\zeta }}(t) + {\mathit{\boldsymbol{\xi }}^{\rm{T}}}(t)\mathit{\boldsymbol{\xi }}(t) + \mathit{\boldsymbol{\eta }}_2^{\rm{T}}(t){\mathit{\boldsymbol{\eta }}_2}(t)} $ | (30) |
将自适应控制器(16)和自适应律式(27)~(29)应用于近空间可变翼飞行器,可保证小翼切换过程的稳定性及良好的跟踪性能。
定理:上述设计的自适应控制器能保证输出跟踪误差e(t)=y(t)-ym(t)满足
因篇幅限制,证明参见文献[15]。
3 仿真验证 3.1 小翼切换控制为了验证所设计的控制器的有效性,下面对小翼在伸出到收回、收回到伸出2个阶段进行仿真验证。
飞行器的初始仿参数为V0为4 590 m/s,h0为33 528 m。
指令信号设计为:
| $ V_{c}=\left\{\begin{array}{ll}{\frac{1}{6.25 s^{2}+4 s+1} \times 40+4590, } & {0<t \leqslant 50 ~\mathrm{s}} \\ {\frac{1}{6.25 s^{2}+4 s+1} \times 40+4630, } & {50 ~\mathrm{s}<t \leqslant 80 ~\mathrm{s}}\end{array}\right. $ | (31) |
| $ \begin{array}{l} {h_c} = \\ \left\{ {\begin{array}{*{20}{c}} {\frac{1}{{6.25{s^2} + 4\;s + 1}} \times 60 + 33528, \quad 0 < t \le 50\;{\rm{s}}}\\ {\frac{1}{{6.25\;{s^2} + 4\;s + 1}} \times 60 + 33588, \quad 50\;{\rm{s}} < t \le 80\;{\rm{s}}} \end{array}} \right. \end{array} $ | (32) |
仿真中,小翼先由伸出到收回,再从收回到伸出。在0~10 s,小翼处于伸出状态;在10~15 s,小翼由伸出状态切换到收回状态;在15~50 s,小翼处于收回状态;在50~55 s小翼由收回状态切换到伸出状态;在55~80 s,小翼处于伸出状态。
自适应参数设置为Γ=diag(10, 5),Ds=diag(10, 0.001),
为了验证本文设计的小翼切换自适应控制器的有效性,仿真实验以不加小翼增量线性模型的常规自适应控制器和本章设计的考虑小翼伸缩切换控制器作对比。近空间可变翼飞行器指令跟踪仿真结果如图 2~6。
|
Download:
|
| 图 2 小翼切换时油门、升降舵角度响应曲线 Fig. 2 Response curves of throttle and elevator for winglet switching | |

|
Download:
|
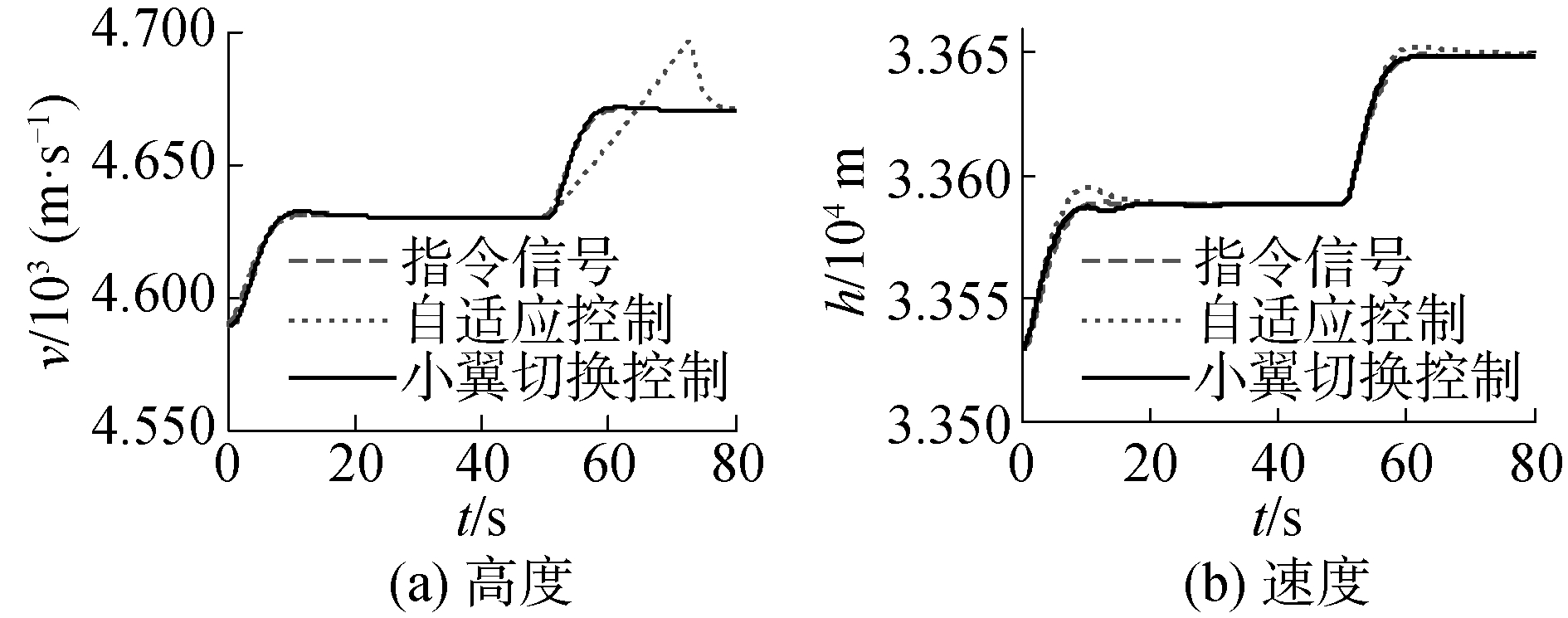
| 图 3 小翼切换时速度、高度跟踪曲线 Fig. 3 Response curve of velocity and height for winglet switching | |
|
Download:
|
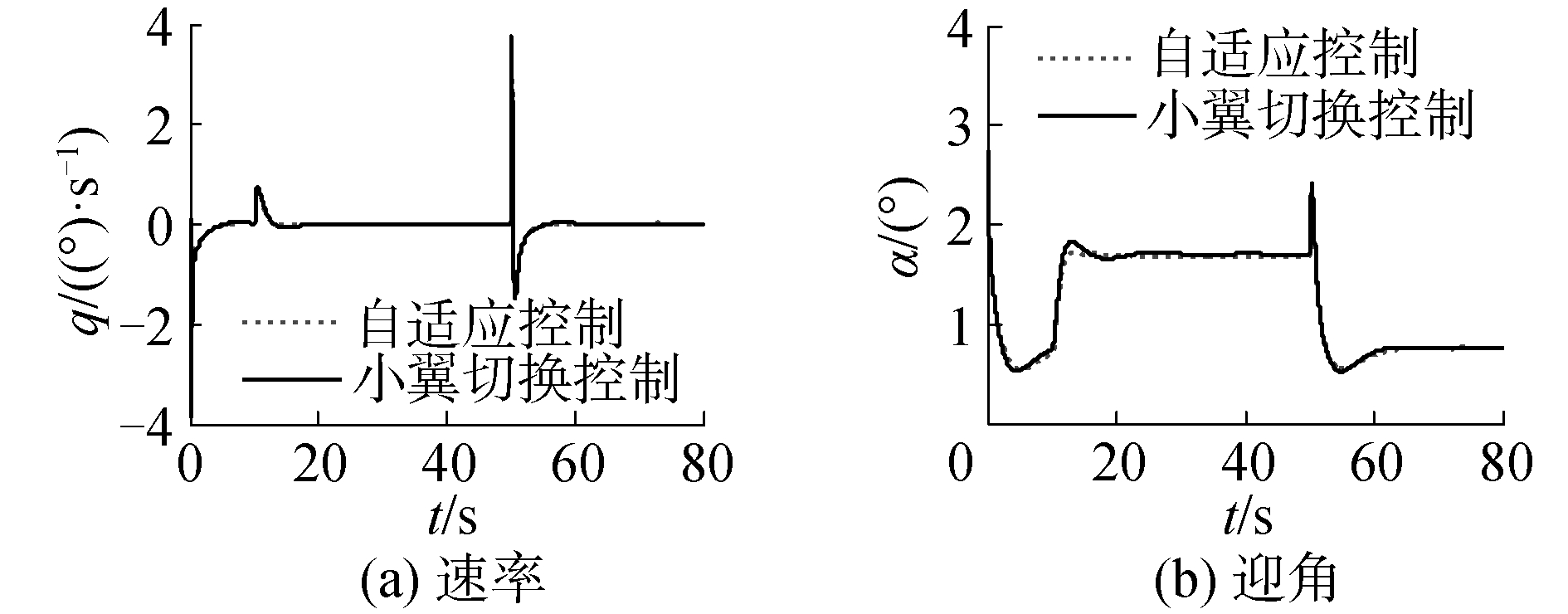
| 图 4 俯仰角速率、迎角响应曲线 Fig. 4 Response curves of pitch angle rate and angle of attack | |

|
Download:
|
| 图 5 速度、高度跟踪曲线 Fig. 5 Response curves of velocity and height with parameter perturbation | |
|
Download:
|
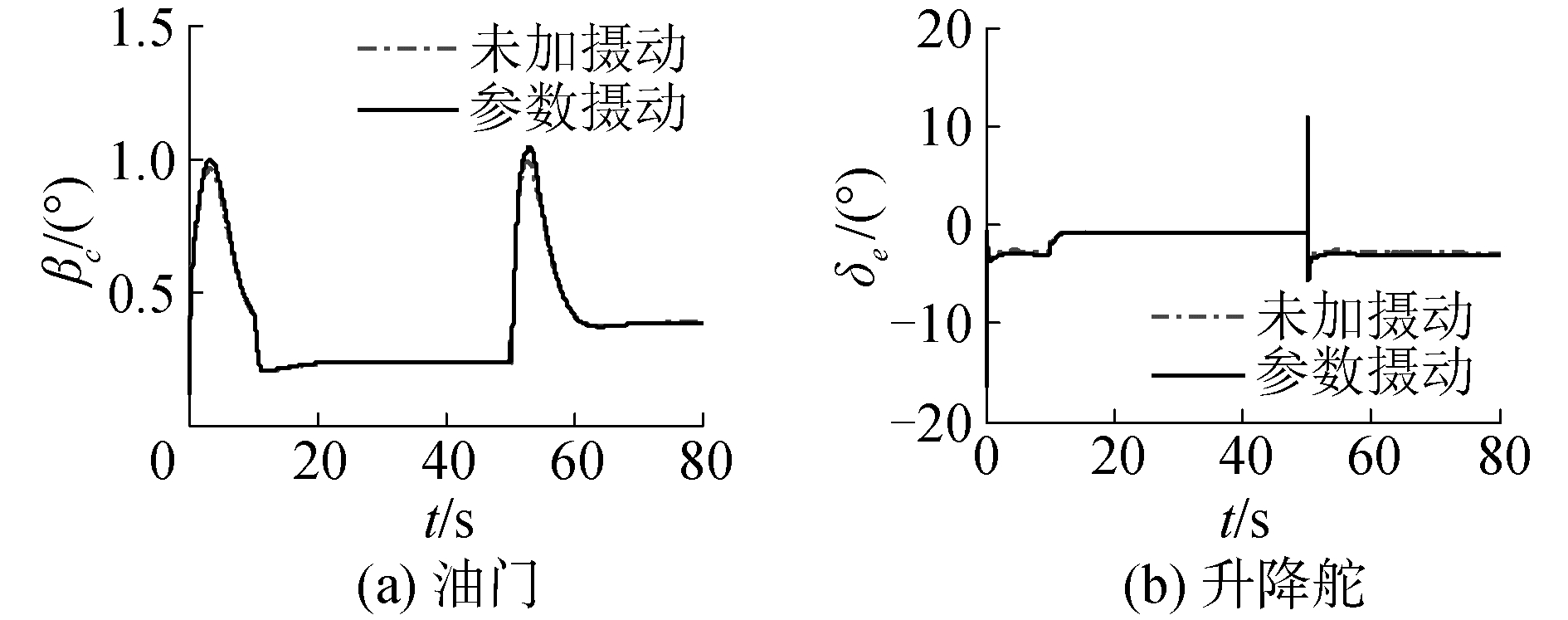
| 图 6 参数摄动时油门、升降舵响应曲线 Fig. 6 Response curves of throttle and elevator with parameted pertubation | |
从图 2~4可以看出,基于小翼伸缩不确定模型设计的自适应小翼切换控制器有良好的控制效果。常规自适应控制方法在50 s小翼伸出后不能准确跟踪速度信号,飞行器的油门在小翼切换时处于满油门状态,且抖动明显。然而本文设计的小翼切换控制器能有效跟踪飞行速度与高度,飞行器很快能跟踪指令信号,说明控制器对小翼伸缩时参数不确定有很好的抑制作用,油门和升降舵变化在合理范围,且无抖动。飞行器的其余状态量都在合理变化范围内,迎角和俯仰角速率变化平稳,整个过程平滑稳定。从整个过程可以看出,小翼由伸出到收回切换过程比小翼由收回到伸出切换过程的抖动小,这是因为小翼伸出时,飞行器处于加速爬升状态,需要能量更大,变化相对明显。
仿真结果表明:采用基于矩阵分解的自适应小翼切换控制器相比于常规自适应控制器,控制效果有明显的改善,该方法可以使小翼伸缩模态切换过程平稳过渡,具有良好的控制效果。
3.2 参数摄动下小翼切换控制近空间可变翼飞行器在小翼切换过程中具有参数不确定性,为了验证自适应控制器的鲁棒性,可表示为:
| $ \left\{\begin{array}{l}{\rho=\rho_{0}(1+\Delta \rho)} \\ {I_{y y}=I_{y 0}\left(1+\Delta I_{y y}\right)} \\ {c_{e}=c_{e 0}\left(1+\Delta c_{e}\right)} \\ {c_{a}=c_{a 0}\left(1+\Delta c_{A}\right)}\end{array}\right. $ | (33) |
式中:仿真时设定参数摄动为10%,即Δ=10%;ρ为大气密度;Iyy为俯仰力矩惯积;ce为俯仰力矩系数中的参数;ca为翼弦长。
近空间可变翼飞行器在小翼伸出爬升段飞行控制仿真曲线如图 5、图 6,仿真中考虑了飞行器在有无参数摄动2种情况。
从图 5、图 6可以看出,加入参数摄动与未加参数摄动相比,飞行器的飞行速度和飞行高度的变化曲线基本一致,控制器能很好的抑制参数摄动,切换过程存在较小差异。飞行器的输入量升降舵和油门在合理变化范围内,抖动较小,曲线基本一致。
4 结论1) 本文设计的自适应小翼切换控制器,对参数存在摄动的情况有良好的控制效果,具有良好的稳定性和较强的鲁棒性。
2) 将小翼伸缩的不确定性引入飞行器状态方程表达式,考虑了小翼伸缩的不同过程,针对新的含有不确定值的状态方程表达式设计基于矩阵分解思想的自适应控制系统。
3) 从理论上证明在小翼切换过程中控制系统的稳定性及自适应律的有界性,实验结果证明了理论推导的正确性。
| [1] |
HU Xiaoxiang, WU Ligang, HU Changhua, et al. Adaptive fuzzy integral sliding mode control for flexible air-breathing hypersonic vehicles subject to input nonlinearity[J]. Journal of aerospace engineering, 2013, 26(4): 721-734. DOI:10.1061/(ASCE)AS.1943-5525.0000193 (  0) 0)
|
| [2] |
吴宏鑫, 孟斌. 高超声速飞行器控制研究综述[J]. 力学进展, 2009, 39(6): 756-765. WU Hongxin, MENG Bin. Review on the control of hypersonic flight vehicles[J]. Advances in mechanics, 2009, 39(6): 756-765. DOI:10.3321/j.issn:1000-0992.2009.06.013 (  0) 0)
|
| [3] |
方存光, 孙勇, 王伟. 高超声速飞行器及其飞行状态控制[J]. 控制工程, 2008, 15(S1): 21-23. FANG Cunguang, SUN Yong, WANG Wei. Hypersonic aircraft and its flying status control[J]. Control engineering of China, 2008, 15(S1): 21-23. (  0) 0)
|
| [4] |
郭淑娟.可变体飞行器的飞行协调控制问题研究[D].南京: 南京航空航天大学, 2012. GUO Shujuan. Research on cooperative control of the morphing aircraft[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10287-1012041566.htm (  0) 0)
|
| [5] |
焦鑫, 江驹. 非线性系统自适应鲁棒控制器设计[J]. 哈尔滨工程大学学报, 2016, 37(3): 402-407. JIAO Xin, JIANG Ju. Design of an adaptive robust controller for nonlinear system[J]. Journal of Harbin Engineering University, 2016, 37(3): 402-407. (  0) 0)
|
| [6] |
WANG Qian, STENGEL R F. Robust nonlinear control of a hypersonic aircraft[J]. Journal of guidance, control, and dynamics, 2000, 23(4): 577-585. DOI:10.2514/2.4580 (  0) 0)
|
| [7] |
WANG J, ZONG Q, SU R, et al. Continuous high order sliding mode controller design for a flexible air-breathing hypersonic vehicle[J]. ISA transactions, 2014, 53(3): 690-698. DOI:10.1016/j.isatra.2014.01.002 (  0) 0)
|
| [8] |
顾臣风, 江驹, 吴雨珊. 近空间飞行器爬升段跟踪控制[J]. 哈尔滨工程大学学报, 2016, 37(11): 1526-1531. GU Chenfeng, JIANG Ju, WU Yushan. Tracking control for a near-space vehicle in the ascent phase[J]. Journal of Harbin Engineering University, 2016, 37(11): 1526-1531. (  0) 0)
|
| [9] |
吴雨珊, 江驹, 甄子洋, 等. 基于动态逆-PID的高超声速飞行器巡航姿态控制[J]. 飞行力学, 2015, 33(2): 145-149. WU Yushan, JIANG Ju, ZHEN Ziyang, et al. Dynamic inversion-PID based cruising attitude control of hypersonic vehicle[J]. Flight dynamics, 2015, 33(2): 145-149. (  0) 0)
|
| [10] |
TAO Gang. Adaptive control design and analysis[M]. Hoboken, NJ: Wiley-Interscience, 2003.
(  0) 0)
|
| [11] |
焦鑫, 江驹, 孟宏鹏. 基于灰色预测滑模控制的鲁棒飞行控制器设计[J]. 飞行力学, 2015, 33(6): 542-546, 550. JIAO Xin, JIANG Ju, MENG Hongpeng. Design of flight controller based on grey-prediction sliding mode control[J]. Flight dynamics, 2015, 33(6): 542-546, 550. (  0) 0)
|
| [12] |
吴雨珊, 江驹, 甄子洋, 等. 基于回馈递推的可变翼高超声速飞行器智能非线性控制[J]. 哈尔滨工程大学学报, 2016, 37(7): 963-968. WU Yushan, JIANG Ju, ZHEN Ziyang, et al. Intelligent nonlinear control for the hypersonic morphing vehicle based on the backstepping method[J]. Journal of Harbin Engineering University, 2016, 37(7): 963-968. (  0) 0)
|
| [13] |
XU Haojian, MIRMIRANI M D, IOANNOU P A. Adaptive sliding mode control design for a hypersonic flight vehicle[J]. Journal of guidance, control, and dynamics, 2004, 27(5): 829-838. DOI:10.2514/1.12596 (  0) 0)
|
| [14] |
SUN Haibin, LI Shihua, SUN Changyin. Finite time integral sliding mode control of hypersonic vehicles[J]. Nonlinear dynamics, 2013, 73(1/2): 229-244. (  0) 0)
|
| [15] |
GUO Jiaxiang, LIU Yu, TAO Gang. Multivariable MRAC with state feedback for output tracking[C]//Proceedings of 2009 American Control Conference. St. Louis, MO, USA, 2009: 592-597. https://www.researchgate.net/publication/224561185_Multivariable_MRAC_with_State_Feedback_for_Output_Tracking
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


