2. 海洋信息获取与安全工信部重点实验室(哈尔滨工程大学), 工业和信息化部, 哈尔滨 150001;
3. 哈尔滨工程大学 水声工程学院, 哈尔滨 150001
2. Key Laboratory of Marine Information Acquisition and Security(Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China;
3. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
通信是海洋环境监测及海洋信息获取的重要信息交互手段。部分典型的水声信道表现出时变稀疏多途扩展特性,会导致严重的码间干扰(inter-symbol interference,ISI),进而导致通信性能的恶化。判决反馈均衡(decision feedback equalizer,DFE)利用自适应算法迭代的更新均衡器系数[1-3],使其跟踪信道的变化,以获得更为准确的滤波结果。传统的自适应DFE采用递归最小二乘(recursive least squares, RLS)或最小均方(least mean square,LMS)算法。由于后者计算量小,结构简单,应用的更为广泛[4]。然而,普适的LMS算法的计算过程中没有考虑任何信道特性,导致了处理性能损失。为了弥补LMS算法在这方面的缺陷,学者针对水声通信信道,进行了深入研究[5-9]。PNLMS、PNLMS++、IPNLMS、VSSLMS等变步长算法,具有比固定步长的同类算法更快的收敛速度和更小的稳态误差,同时还能跟踪信道的变化[5]。为了利用水声信道的稀疏性,ZA-LMS、RZA-LMS、lp-LMS等一系列加入稀疏约束的算法,也被深入研究[9-14]。此类算法大多是在代价函数中加入各种稀疏惩罚项用以约束迭代的梯度增量[11-12],能够有效提升自适应算法的性能[14]。提高自适应算法性能还需要考虑通信信号的特性。通常认为通信信号都是圆信号,而忽略接收信号在复平面上的二阶统计特性。然而近年来研究表明部分应用广泛的信号,如BPSK和OQPSK信号,在复平面上都不具有旋转不变性,即其虚部和实部是具有相关性的[15-19]。宽线性(widely linear,WL)处理可以充分利用接收信号统计特性,从而进一步提升DFE接收机中自适应均衡算法的性能[16]。
为了提高自适应DFE对稀疏时变水声信道接收信号的处理能力,本文利用信道和信号特性改进了DFE中的自适应算法。提出的改进算法(l0-norm penalized shrinkage widely linear LMS, l0-SH-WL-LMS)具有处理稀疏时变水声信道接收信号的能力。考虑到AP算法相对于LMS算法具有的收敛快,误差小,复杂度也适中,应用范围更广泛的特点[4, 20],本文将上述改进方式应用到AP算法中,并采用对分坐标下降(dichotomous coordinate descent,DCD)处理降低其计算复杂度,得到了简化版的改进算法(dichotomous coordinate descent based l0-norm penalized shrinkage widely linear AP, l0-SH-WL-DCD-AP)。
1 均衡器系统模型水声接收机系统中常用的判决反馈均衡器基本模型如图 1所示,其输出可以表示为:

|
Download:
|
| 图 1 水声通信判决反馈均衡系统模型 Fig. 1 Block diagram of DFE receiver for underwater acoustic communication | |
| $ \hat{\boldsymbol{d}}_{s}(n)=\boldsymbol{f}^{\mathrm{H}}(n) \boldsymbol{u}(n)+\boldsymbol{g}^{\mathrm{H}}(n) \boldsymbol{d}_{\mathrm{fb}}(n), n=1, 2, \cdots, N $ | (1) |
式中:f(n)=[f0(n), f1(n), …, fNff-1(n)]是前馈滤波器的系数;Nff是前馈滤波器的长度(本文中,选取符号间隔均衡器,因此Nff约为信道有效多途扩展的长度)。g(n)=[g0(n), g1(n), …, gNfb-1(n)]是反馈滤波器的系数,Nfb是其长度。
| $ \boldsymbol{u}(n)=\boldsymbol{h}^{\mathrm{H}}(n) \boldsymbol{s}(n)+\boldsymbol{\upsilon }(n) $ | (2) |
式中:h(n)为信道冲击响应;s(n)为输入信号;υ(n)为n时刻独立均匀分布的均值为零,方差为σv2的高斯白噪声。
前馈滤波器作为均衡器的主要部分,主要作用是消除大部分信道h(n)引入的ISI,而反馈滤波器主要利用非线性特性去掉剩余干扰[4]。滤波器的收敛性能和稳态误差分别决定着通信信号中训练序列长度的选取和均衡误差。因此选取高效的自适应算法是重中之重。本节针对水声信道的稀疏时变特性和通信信号的非圆特性,设计适合水声接收机的自适应算法,应用于自适应DFE中。
1.1 l0-SH-WL-LMS算法对于LMS算法,其系数迭代公式为:
| $ \boldsymbol{f}(n+1)=\boldsymbol{f}(n)-\mu \nabla_{\mathrm{f}} \xi $ | (3) |
式中:μ为步长参数;∇F为对f取梯度操作;ξ(n)=
| $ \boldsymbol{e}(n)=\boldsymbol{u}^{\mathrm{H}}(n) \boldsymbol{f}(n)-\boldsymbol{s}(n) $ | (4) |
根据误差生成方式将其改写为:
| $ \boldsymbol{e}(n)=\boldsymbol{e}_{f}(n)+\boldsymbol{\upsilon }(n)=\boldsymbol{u}^{\mathrm{H}}(n)\left(\boldsymbol{f}_{0}-\boldsymbol{f}(n)\right)+\boldsymbol{\upsilon }(n) $ | (5) |
式中:ef(n)为无噪声先验误差;f0为最优滤波器系数。类似的,还可以得到后验误差:
| $ \varepsilon(n)=\varepsilon_{\mathrm{f}}(n)+\boldsymbol{\upsilon }(n)=\boldsymbol{u}^{\mathrm{H}}(n)\left(\boldsymbol{f}_{0}-\boldsymbol{f}(n+1)\right)+\boldsymbol{\upsilon }(n) $ | (6) |
将式(3)、(5)代入式(6),并对结果两侧同时取均方值,可得:
| $ \begin{array}{c}{\mathrm{E}\left[\left(\varepsilon_{\mathrm{f}}(n)\right)^{2}\right]=\mathrm{E}\left[\left(1-\mu \boldsymbol{u}^{\mathrm{H}}(n) \boldsymbol{u}(n)\right)^{2}\right]} \cdot\\ {\mathrm{E}\left[\left(e_{\mathrm{f}}(n)\right)^{2}\right]+\mu^{2} \mathrm{E}\left[\left(\boldsymbol{u}^{\mathrm{H}}(n) \boldsymbol{u}(n)\right)^{2}\right] \mathrm{E}\left[\boldsymbol{\upsilon }^{2}(n)\right]}\end{array} $ | (7) |
为了使后验误差最小,取式(7)对于步长μ的导数为0,并用μ(n)替换μ,得到步长的迭代方程:
| $ \mu(n)=\frac{1}{\mathrm{E}\left[\|\boldsymbol{u}(n)\|^{2}\right]} \frac{\mathrm{E}\left[\left(e_{\mathrm{f}}(n)\right)^{2}\right]}{\mathrm{E}\left[\left(e_{\mathrm{f}}(n)\right)^{2}\right]+\sigma_{v}^{2}} $ | (8) |
从式(8)可以看出此时步长取决于每一次迭代时输入的E[‖u(n)‖2]和噪声方差σv2以及上一次迭代得到的E[(ef(n))2]。通常情况下,前2项可以通过接收信号的统计特性获得。而最后一项,可以利用其时间均值迭代来代替他的统计均值降低计算难度[9]:
| $ \mathrm{E}\left[\left(e_{\mathrm{f}}(n)\right)^{2}\right]=\gamma \mathrm{E}\left[\left(e_{\mathrm{f}}(n-1)\right)^{2}\right]+(1-\gamma) e_{\mathrm{f}}^{2}(n) $ | (9) |
式中:γ为遗忘因子,通常取γ < 1,且γ≈1。
为了从先验误差e(n)中获得每一时刻的无噪声先验误差ef(n),利用压缩感知(compressing sense, CS)中的收缩降噪准则[16],得到:
| $ e_{\mathrm{f}}(n)=\operatorname{sign}(e(n)) \max (|e(n)|-Q, 0) $ | (10) |
| $ Q=\sqrt{T \sigma_{v}^{2}}, \quad 1 \leqslant T<4 $ | (11) |
基于以上推导过程,可以利用信号统计特性和先验误差,获得随系统变化的步长参数,以跟踪系统的时变特性。
为了充分利用水声信道的稀疏性,在算法代价函数中增加一种刻画系统稀疏特性的约束l0范数,得到新的代价函数:
| $ \xi=\frac{1}{2}\left|e^{2}(n)\right|+\delta\|f(n)\|_{0} $ | (12) |
式中δ为代价调节参数。可以利用范数的近似公式降低式(12)计算准度,公式为:
| $ {\left\| {\mathit{\boldsymbol{f}}(n)} \right\|_0} \approx \sum\limits_{i = 0}^{{N_{{\rm{ff}}}} - 1} {\left( {1 - {{\rm{e}}^{ - \beta \left| {{f_i}(n)} \right|}}} \right)} $ | (13) |
式中:β为近似拟合因子。代入式(12)并计算得到式(3)的改进形式:
| $ \begin{aligned} \boldsymbol{f}(n+1)=& \boldsymbol{f}(n)+\mu(n) e^{*}(n) u(n)-\\ & \kappa \operatorname{sign}(\boldsymbol{f}(n)) \mathrm{e}^{-\beta|f(n)|} \end{aligned} $ | (14) |
式中:μ、λ、β为常数,乘积可由κ代替。在迭代过程中,根据式(8)选择μ(n),则利用式(14)得到的滤波器即为适用稀疏时变水声信道的自适应滤波器。
接收信号的非圆特性使得其实部和虚部都含有重要信息,常规处理方式往往忽略了信号的复数部分,这将导致对接收信号的处理性能下降[15]。为了进一步考虑接收信号的非圆特性,在接收端,采取宽线性的处理方式,即将[uT(n), uH(n)]T作为输入信号。此时,接收系统充分利用了接收信号的二阶统计特性,可以提高处理增益。此结论将在仿真部分进一步验证。
1.2 l0-SH-WL-DCD-AP算法AP算法可以看作NLMS算法的扩展。由于它的收敛和稳态性能比NLMS算法好而需要的计算量又比RLS算法少,因此近年来的应用越来越广泛。
此时,滤波器的输入变为信号矩阵U(n)=[u(n), u(n-1), …, u(n-L+1)],其中L为投影阶数。它的系数迭代方程是在最小后验误差的约束下通过最小化系数迭代误差的二阶范数得到的,代价函数可利用多约束拉格朗日乘数法得到:
| $ \xi(n)=\|\boldsymbol{\eta}(n)\|^{2}+\left(\boldsymbol{d}_{\mathrm{fb}}(n)-\boldsymbol{u}^{\mathrm{H}}(n) \boldsymbol{f}^{\mathrm{H}}(n+1)\right) \boldsymbol{\lambda} $ | (15) |
式中:η(n)=f(n+1)-f(n)为系数迭代误差;λ是拉格朗日乘子。求解时,分别使代价函数对f和λ的偏导为0,可得AP算法的系数迭代方程:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{f}}(n + 1) = \mathit{\boldsymbol{f}}(n) + \mu \mathit{\boldsymbol{U}}(n)\left( {{\mathit{\boldsymbol{U}}^{\rm{H}}}(n)\mathit{\boldsymbol{U}}(n) + } \right.}\\ {\psi \mathit{\boldsymbol{I}}{)^{ - 1}}\mathit{\boldsymbol{e}}(n)} \end{array} $ | (16) |
类似与式(5)和式(6)的误差分类方式,可以得到AP算法无噪声先验误差与后验误差之间的关系:
| $ {\mathit{\boldsymbol{\varepsilon }}_{\rm{f}}}(n) = (1 - \mu ){\mathit{\boldsymbol{e}}_{\rm{f}}}(n) - \mu \mathit{\boldsymbol{\upsilon }}(n) $ | (17) |
对式(17)两端同时取均方值,在此基础上根据无噪声后验误差均方最小化准则得到AP算法的步长因子迭代公式:
| $ \mu(n)=\frac{\mathrm{E}\left[\left\|\boldsymbol{e}_{\mathrm{r}}(n)\right\|^{2}\right]}{\mathrm{E}\left[\left\|\boldsymbol{e}_{\mathrm{f}}(n)\right\|^{2}\right]+\mathrm{E}\left[\|\mathit{\boldsymbol{\upsilon }}(n)\|^{2}\right]} $ | (18) |
对比式(8)和(18)发现,AP算法的步长形式比LMS算法简单,这是因为在滤波器系数迭代时,AP算法已经利用了输入信号的相关特性,调整迭代速度的步长参数就不需重复考虑信号特性。
根据收缩降噪准则,对应式(10),得到AP算法的无噪声后验误差向量[17]:
| $ \boldsymbol{e}_{\mathrm{f}}(n)=\boldsymbol{D} \operatorname{sign}\left(\boldsymbol{D}^{\mathrm{T}} \boldsymbol{e}(n)\right) . * \boldsymbol{a}(n) $ | (19) |
式中:D∈RL×L是一个正交参数矩阵,通常可取离散余弦矩阵;a(n)是由ai(n)=max(‖(DTe(n))i-Q‖, 0)组成的向量;(DTe(n))i是DTe(n)中第i个元素;Q=
在代价函数式(15)中加入式(12)中相同的稀疏约束,代入式(13),可得适合时变稀疏水声信道的改进AP算法迭代方程:
| $ \begin{aligned} \boldsymbol{f}(n+1)=& \boldsymbol{f}(n)+\mu(n) \boldsymbol{U}(n) \boldsymbol{R}(n) \boldsymbol{e}(n)+\\ & \boldsymbol{\kappa} \boldsymbol{A}(n) \mathit{\boldsymbol{ \boldsymbol{\varGamma}}}(n) \end{aligned} $ | (20) |
其中,
为了利用接受通信信号的非圆特性,将滤波器的输入信号矩阵扩展为K(n)=[k(n), k(n-1), …, k(n-L+1)],其中k(n)=[uT(n), uH(n)]T。这种增广形式了提高了滤波器对信号携带信息的利用程度,使得算法的性能也有所改善。
本文发现在上述计算过程中需要进行大量的矩阵求逆运算,这将引入很高的计算复杂度。改进的l0-SH-WL-AP算法将产生Ο(L3)次加法和乘法运算,其中大部分的计算量来自于对R(n)和Α(n)的求解。这些计算量是l0-SH-WL-AP算法应用到实际的重要阻碍。为了解决这个问题,可以采用DCD法来降低改进算法所需的计算量。
DCD算法利用对分迭代法,可以在不需要乘除法的情况下求解正则方程
DCD算法利用比特翻转替代乘法操作,提升了算法的计算速度,每一次迭代使结果逐渐向预先设定的精度靠拢。在Nu次成功迭代后,得到方程最优解,此时只需进行(2 L+1)Nu+Mb次加法运算。在改进的AP算法中,共运用了DCD算法2次:利用Ζ(n)Ψ=μ(n)e(n)计算μR(n)e(n); 利用Ζ(n)Ψ=κΚH(n)Γ(n)计算κA(n)Γ(n)中的κR(n)UH(n)Γ(n),其中Ζ(n)=ΚH(n)Κ(n)+ψI。式(2)中缺少的Κ(n)在每次DCD迭代中补足。经过这样简化处理,l0-SH-WL-DCD-AP算法在一次迭代过程中只需要进行Ο(L2)次乘法运算,计算量降低了一个数量级。
2 仿真与试验数据分析本节将在时变稀疏信道条件下仿真验证l0-SH-WL-LMS算法和l0-SH-WL-DCD-AP算法的有效性及其应用改进算法的DFE接收机的性能,并利用2015-11在南海进行的单载波水声通信试验数据验证应用改进算法的DFE接收机结构。
2.1 改进算法性能仿真比较LMS、l0-SH-WL-LMS、AP、l0-SH-WL-AP和l0-SH-WL-DCD-AP算法的性能。信道冲击响应的长度为64;信号序列采用BPSK的调制方式,传输码元长度为5 000;噪声为零均值方差为1的加性高斯白噪声,信噪比为SNR=10 dB。对于l0阶范数参数,取β=10和κ=3×10-5。对于恒定步长算法,μ=0.01,变步长参数,γ=0.99,Q=4。对于AP类算法,ψ=0.01,投影阶数L=6。对于DCD算法,取H=2-10,Mb=12,Nu=10。采用学习曲线来描述算法的收敛性能和稳态归一化MSE(normalized MSE,NMSE)情况。最终的结果取1 000次统计平均。
稀疏突变信道条件下4种算法的性能如图 2所示。在信道的64根有效途径中,只有2根是非零值,并且随机分布。自适应滤波器的长度为64。在迭代2 500次后,2个非零值的幅度和位置发生了变化。这个实验的目的是为了测试算法在稀疏突变情况下的收敛性能和跟踪性能。从图 1中可以看出的看出l0-SH-WL-LMS算法和l0-SH-WL-AP算法能迅速的达到稳定状态并且他们的稳态误差比其他算法要小得多。在迭代的初始阶段,改进算法的NMSE下降的很快。在大约500次迭代后,LMS算法和AP算法达到稳定状态,稳态NMSE约为-15 dB,此时而l0-SH-WL-LMS算法和l0-SH-WL-AP算法的稳态误差远低于LMS算法和AP算法并且在持续下降。到大约800次迭代时,2种改进算法的稳态误差下降到约-30 dB以下,基本达到了稳定状态。当信道突然变化时,改进算法恢复到稳定状态用时更少,并且仍然达到最小的稳态误差。这表明相比于其他算法,改进算法在跟踪信道变化的方面更有优势。由于AP类算法能利用更多的信号信息,l0-SH-WL-AP算法比l0-SH-WL-LMS算法性能更好。对l0-SH-WL-AP算法进行降低计算复杂对处理并没有降低其性能。由于在仿真中精度取值较高,l0-SH-WL-DCD-AP算法的稳态误差反而更低。这说明,DCD是一种非常有效的方法,它可以在保持性能优势的同时降低算法计算复杂度。

|
Download:
|
| 图 2 改进算法的学习曲线 Fig. 2 Learning curves of different adaptive algorithms | |
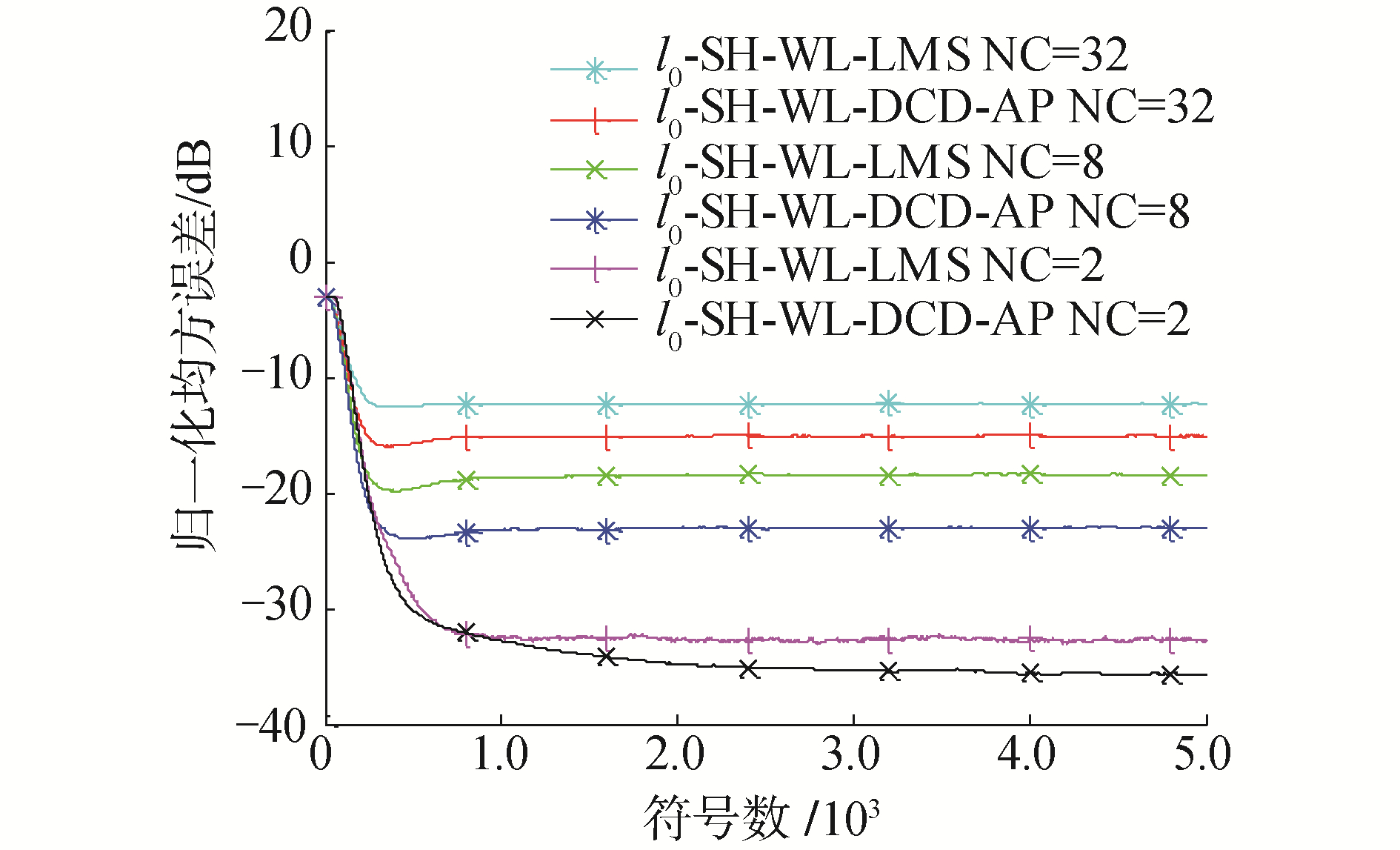
图 3比较了在不同稀疏度下l0-SH-WL-LMS算法和l0-SH-WL-DCD-AP算法的性能。此时,信道的长度为64不变,而非零值(non-zero coefficient, NC)的个数分别为2、8、32,位置仍然随机分布。传统算法由于没有考虑稀疏约束,在稀疏度变化时,算法的性能没有变化,因此图中未加入对比。从图中可以看出,改进算法对信道稀疏度变化敏感。随着信道稀疏度下降,算法收敛速度下降,稳态NMSE上升。这是由于当信道稀疏度下降时,l0范数约束逐渐失效,但是变化的步长还是会使改进算法的性能有所提高。
|
Download:
|
| 图 3 改进算法随稀疏度变化曲线 Fig. 3 Performance versus sparsity level | |
将改进的自适应算法应用到符号间隔的DFE中,验证改进接收机性能。信道仍为稀疏信道,长度为64,其中有2个随机分布的非零值。信号序列采用BPSK的调制方式,传输码元长度为2 000,训练序列长度为512,最终的误码率取1 000个数据包的结果做平均。噪声采用独立均匀分布的均值为零方差为1的高斯白噪声,信噪比SNR区间[0:10] dB。算法参数为β=10,κ=1×10-5,Q=2和L=2。LMS算法和AP算法的步长μ分别取0.01和0.1。仿真中采用非理想反馈的判决方式,将判决器硬判决得到的信号直接输入反馈滤波器[24]。仿真时所采用的前馈滤波器和反馈滤波器阶数分别为80和20。仿真结果如图 4所示。从图中可以看出,将改进算法应用到判决反馈均衡器中后,信道均衡的性能有了明显的提高。2种改进算法的误码率(bit error rate, BER)曲线相近,明显比LMS和AP算法低。随着信噪比的增大,改进算法误码率性能的提升逐渐明显,当信噪比达到10时,l0-SH-WL-LMS算法和l0-SH-WL-DCD-AP算法的误码率低至10-4以下。当信噪比继续增大时,2种改进算法的误码率均低至0,这充分说明改进的DFE接收机非常适合稀疏时变信道的均衡处理。

|
Download:
|
| 图 4 改进DFE接收机的BER性能 Fig. 4 BER performance of the improved DFE | |
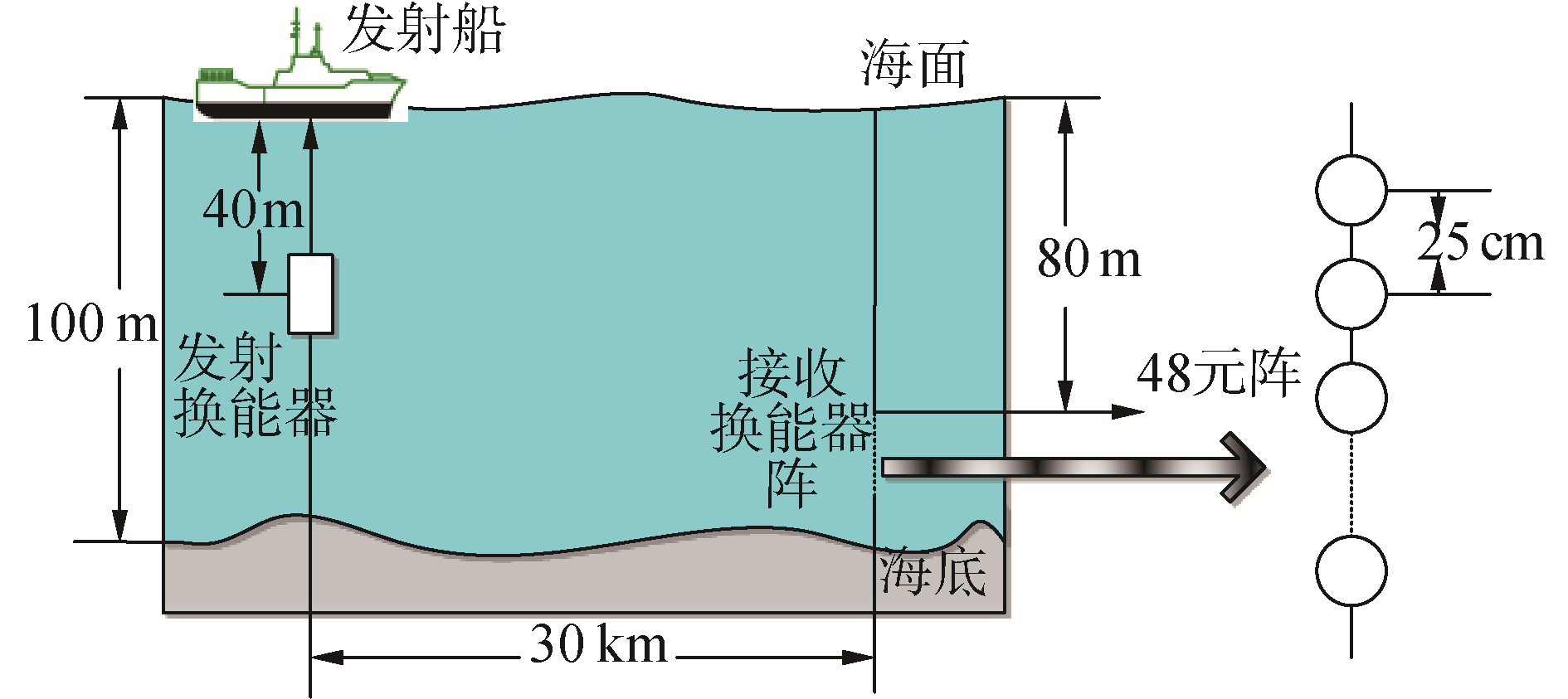
利用改进的DFE接收机处理2015-11在南海进行的单载波水声通信试验接收数据。信号调制方式为BPSK,符号率为250 symbols/s。每帧信号包含1 728个符号,其中前500个为训练序列。试验中设备布放距离和深度示意图如图 5所示。
|
Download:
|
| 图 5 试验装置布放示意 Fig. 5 Layout of experiment | |
由于传输距离较远,接收信号的信噪比较低(约为2 dB以下),直接均衡处理很难得到理想结果。利用48元阵进行空域滤波提高处理增益,滤波后信噪比约为18 dB。利用LMS-DFE, AP-DFE, l0-SH-WL-LMS-DFE和l0-SH-WL-DCD-AP-DFE接收机对上述接收信号进行均衡处理。LMS算法和AP算法的步长分别取μ=0.02和μ=0.3,其余参数分别取β=10,κ=5×10-4,Q=2。AP类算法的投影阶数L=3。为了提高处理效果,在均衡过程中加入了多普勒补偿技术。4种均衡器处理后的星座图如图 6所示。误码率和不同长度训练序列下的平均MSE如表 1所示。

|
Download:
|
| 图 6 判决反馈均衡后的星座图 Fig. 6 Constellation after different DFE | |
| 表 1 均衡后误码率和均方误差 Table 1 BER and average MSE after different DFE |
从图 6可以看出,改进的DFE接收机均衡后星座图的聚集度明显提高。改进算法由于利用了水声信道和通信信号特性,在进行多普勒补偿后,均衡结果明显好于基础算法。由于AP类算法对信号统计特性利用较多,AP-DFE和l0-SH-WL-DCD-AP-DFE分别好于LMS-DFE和l0-SH-WL-LMS-DFE。表2中结果表明采用改进算法的DFE得到的BER和稳态MSE性能明显提高。为了验证算法收敛速度对DFE性能的影响,缩短训练序列长度至100进行对比,结果表明基于改进算法的DFE可以在缩短训练序列长度的同时达到较好的均衡判决结果。数据处理结果证明了改进接收系统能有效的提高数据传输效率并提高接收信号可靠性。
3 结论1) 算法性能仿真结果表明改进算法具有更快的收敛速度和更低的稳态误差。在稀疏突变仿真条件下,改进算法的稳态误差比原算法低20 dB以上,采用改进算法的DFE均衡器的误码率在信噪比大于8 dB时,低于10-4。
2) 试验数据处理结果表明DFE接收机性能得到优化。
3) 相比于基础算法在训练序列较长时仍存在微小的误码,采用改进算法的DFE在利用较短的训练序列的同时可以到达到0误码。
| [1] |
STOJANOVIC M, CATIPOVIC J, PROAKIS J G. Adaptive multichannel combining and equalization for underwater acoustic communications[J]. The journal of the acoustical society of america, 1993, 94(3): 1621-1631. DOI:10.1121/1.408135 (  0) 0)
|
| [2] |
宁小玲, 刘忠, 罗亚松, 等. 水声信道快速收敛自适应均衡算法[J]. 系统工程与电子技术, 2010, 32(12): 2524-2527. NING Xiaoling, LIU Zhong, LUO Yasong, et al. Fast convergence adaptive equalization algorithm for underwater acoustic channels[J]. Systems engineering and electronics, 2010, 32(12): 2524-2527. DOI:10.3969/j.issn.1001-506X.2010.12.07 (  0) 0)
|
| [3] |
欧阳晓曦.自适应均衡技术在水声通信中的应用研究[D].西安: 西北工业大学, 2006. OUYANG Xiaoxi. Research on adaptive equalization in underwater acoustic communication system[D]. Xi'an: Northwestern Polytechnical University, 2006. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y930334 (  0) 0)
|
| [4] |
HAYKIN S.自适应滤波器原理[M].郑宝玉, 译. 4版.北京: 电子工业出版社, 2003. HAYKIN S. Adaptive filter theory[M]. ZHENG Baoyu, trans. 4th ed. Beijing: Publishing House of Electronics Industry, 2003. (  0) 0)
|
| [5] |
DUTTWEILER D L. Proportionate normalized least mean squares adaptation in echo cancelers[J]. IEEE transactions on speech and audio processing, 2000, 8(5): 508-518. DOI:10.1109/89.861368 (  0) 0)
|
| [6] |
BENESTY J, GAY S L. An improved PNLMS algorithm[C]//Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing. Orlando, FL, USA, 2002: Ⅱ-1881-Ⅱ-1884. https://www.researchgate.net/publication/238183235_An_improved_PNLMS_algorithm
(  0) 0)
|
| [7] |
DENG Hongyang, DOROSLOVACKI M. Proportionate adaptive algorithms for network echo cancellation[J]. IEEE transactions on signal processing, 2006, 54(5): 1794-1803. DOI:10.1109/TSP.2006.872533 (  0) 0)
|
| [8] |
DENG Hongyang, DYBA R A. Partial update PNLMS algorithm for network echo cancellation[C]//Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing. Taipei, Taiwan, 2009: 1329-1332. https://www.researchgate.net/publication/220733071_Partial_update_PNLMS_algorithm_for_network_echo_cancellation
(  0) 0)
|
| [9] |
SHI Yunmei, HUANG Lei, QIAN Cheng, et al. Shrinkage linear and widely linear complex-valued least mean squares algorithms for adaptive beamforming[J]. IEEE transactions on signal processing, 2015, 63(1): 119-131. (  0) 0)
|
| [10] |
CHEN Yilun, GU Yuantao, HERO A O. Sparse LMS for system identification[C]//Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing. Taipei, Taiwan, 2009: 3125-3128. https://www.researchgate.net/publication/220735276_Sparse_LMS_for_system_identification
(  0) 0)
|
| [11] |
TAHERI O, VOROBYOV S A. Sparse channel estimation with lp-norm and reweighted l1-norm penalized least mean squares[C]//Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing. Prague, Czech Republic, 2011: 2864-2867. https://www.researchgate.net/publication/220732564_Sparse_channel_estimation_with_Lp-norm_and_reweighted_L1-norm_penalized_least_mean_squares
(  0) 0)
|
| [12] |
CAND È S E J, WAKIN M B, BOYD S P. Enhancing sparsity by reweighted l1 minimization[J]. Journal of fourier analysis and applications, 2008, 14(5/6): 877-905. (  0) 0)
|
| [13] |
GU Yuantao, JIN Jian, MEI Shunliang. l0-norm constraint LMS algorithm for sparse system identification[J]. IEEE signal processing letters, 2009, 16(9): 774-777. DOI:10.1109/LSP.2009.2024736 (  0) 0)
|
| [14] |
刘立刚.稀疏冲激响应的自适应滤波算法及其应用研究[D].上海: 复旦大学, 2010. LIU Ligang. Research on adaptive filtering algorithms for sparse impulse response and their applications[D]. Shanghai: Fudan University, 2010. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2227165 (  0) 0)
|
| [15] |
ADALI T, SCHREIER P J, SCHARF L L. Complex-valued signal processing:The proper way to deal with impropriety[J]. IEEE transactions on signal processing, 2011, 59(11): 5101-5125. DOI:10.1109/TSP.2011.2162954 (  0) 0)
|
| [16] |
ZHANG Youwen, XIAO Shuang, HUANG Defeng, et al. l0-norm penalised shrinkage linear and widely linear LMS algorithms for sparse system identification[J]. IET signal processing, 2017, 11(1): 86-94. DOI:10.1049/iet-spr.2015.0218 (  0) 0)
|
| [17] |
SHI Yunmei, HUANG Lei, QIAN Cheng, SO H C. Shrinkage Linear and Widely Linear Complex Valued Least Mean Squares Algorithms for Adaptive Beamforming[J]. IEEE transactions on signal processing, 2015, 63(1): 119-131. (  0) 0)
|
| [18] |
PICINBONO B, CHEVALIER P. Widely linear estimation with complex data[J]. IEEE transactions on signal processing, 1995, 43(8): 2030-2033. DOI:10.1109/78.403373 (  0) 0)
|
| [19] |
QU Jinyou, ZHANG Jianyun, ZHANG Xinan. A widely-linear LMS algorithm for adaptive beamformer[C]//IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications. Hangzhou, China, 2007: 1060-1063. http://www.researchgate.net/publication/4296027_A_Widely-Linear_LMS_Algorithm_for_Adaptive_Beamformer
(  0) 0)
|
| [20] |
ZHANG Youwen, XIAO Shuang, SUN Dajun, et al. Low-complexity l0-norm penalized shrinkage linear and widely linear affine projection algorithms[J]. Circuits, systems, and signal processing, 2017, 36(8): 3385-3408. DOI:10.1007/s00034-016-0465-6 (  0) 0)
|
| [21] |
DAUBECHIES I, DEFRISE M, DEMOL C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on pure and applied mathematics, 2004, 57(11): 1413-1457. DOI:10.1002/(ISSN)1097-0312 (  0) 0)
|
| [22] |
ZIBULEVSKY M, ELAD M. l1-l2 optimization in signal and image processing[J]. IEEE transactions on signal processing magazine, 2010, 27(3): 76-88. DOI:10.1109/MSP.2010.936023 (  0) 0)
|
| [23] |
CHEN Teyan. Novel Adaptive Signal Processing Techniques for Underwater Acoustic Communications[D]. New York: University of York, 2011. https://ethos.bl.uk/OrderDetails.do?uin=uk.bl.ethos.550272
(  0) 0)
|
| [24] |
裴晓黎, 宁小玲, 刘忠, 等. 水声信道均衡算法比较研究[J]. 计算机工程与应用, 2014, 50(1): 111-115. PEI Xiaoli, NING Xiaoling, LIU Zhong, et al. Comparison of equalization algorithms for underwater acoustic channels[J]. Computer engineering and applications, 2014, 50(1): 111-115. DOI:10.3778/j.issn.1002-8331.1203-0149 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


