2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
收发合置声呐在浅水信道中对小目标的定位能力受到强混响制约。近年来,已开展了很多利用目标的前向散射进行目标探测和定位的研究,通常采用由垂直发射阵和垂直接收阵构成的声屏障系统[1]进行实验。目前用于声屏障系统的定位方法主要有时间反转法和扰动声线法。Prada[2]利用时间反转分解(decomposition of the time-reversal operator,DORT)方法第一次在实际浅海环境实现了目标定位。但是时反技术比一般的收发系统需要更复杂的硬件支持,为实现信号时反重发的功能,需要收发合置阵[1]或者进行远距离的数据传输[3]。罗方方[4]将虚拟时间反转镜与最小方差无失真响应(minimum variance distortionless response,MVDR)算法结合用于被动目标探测,充分利用了水声信道的多途信息,减小复杂的水声环境对高分辨率算法的影响,但该方法的被动探测方式对于小目标的探测能力有限。扰动声线法是一种利用因目标存在而受到扰动的声线所包含的位置信息实现定位的方法。不同学者利用扰动声线所包含的不同物理信息实现目标定位,Folegot[5]利用扰动声线的几何路径实现定位,而Marandet[6]利用扰动声线的声压敏感核来估计目标位置。敏感核是近年来从地球物理学引入到水声学的,用于描述声场观测量对声场扰动的敏感性和空间特性[7]。根据引起声场扰动的不同原因(局部声速的变化、局部密度的变化或水面的起伏等)分类,敏感核可用于实现声层析[8-11]、波导中目标定位[6, 12-13]和分析表面重力波[14-15]等。
本文将针对大目标定位的扰动声线声压敏感核方法应用于小目标的定位研究,分析了3种水底模型精度下的定位性能,并开展了沿深度非等声速分布环境下的湖上实验。
1 基于扰动声线声压敏感核的定位方法 1.1 目标引起声压相对变化的原理目标进入探测区域会对声场产生扰动,引起格林函数的变化,格林函数的变化量ΔG(ω; rr, r′, rs)与目标位置r′和目标的散射形态函数f∞(ω, φs+φr)有:
| $ \begin{array}{*{20}{c}} {\Delta G\left( {\omega ;{\mathit{\boldsymbol{r}}_{\rm{r}}}, {\mathit{\boldsymbol{r}}^\prime }, {\mathit{\boldsymbol{r}}_{\rm{s}}}} \right) = - 4\pi {f_\infty }\left( {\omega , {\varphi _{\rm{s}}} + {\varphi _{\rm{r}}}} \right) \cdot }\\ {G\left( {\omega ;{\mathit{\boldsymbol{r}}_{\rm{r}}}, {\mathit{\boldsymbol{r}}^\prime }} \right)G\left( {\omega ;{\mathit{\boldsymbol{r}}^\prime }, {\mathit{\boldsymbol{r}}_{\rm{s}}}} \right)} \end{array} $ | (1) |
式中:rs和rr分别表示发射点和接收点的位置;r′表示目标位置;G(ω; r′, rs)和G(ω; rr, r′)分别表示发射点到目标的格林函数和目标到接收点的格林函数;ω为角频率;f∞(ω, φs+φr)是目标的散射形态函数;φs是向量rr-rs和向量r′-rs之间的夹角;φr是向量rs-rr和向量r′-rr之间的夹角。而接收阵元的声压扰动量ΔP与格林函数的扰动量ΔG的关系为:
| $ \Delta P\left(t ; \boldsymbol{r}_{\mathrm{r}}, \boldsymbol{r}^{\prime}, \boldsymbol{r}_{\mathrm{s}}\right)=\frac{1}{2 \pi} \int \Delta G\left(\omega ; \boldsymbol{r}_{\mathrm{r}}, \boldsymbol{r}^{\prime}, \boldsymbol{r}_{\mathrm{s}}\right) P_{\mathrm{s}}(\boldsymbol{\omega}) \mathrm{e}^{\mathrm{i} \omega t} \mathrm{d} \omega $ | (2) |
式中:Ps(ω)是发射信号的频谱; ΔP是声压扰动的时域。声压P的时域表示为:
| $ P\left(t ; \boldsymbol{r}_{\mathrm{r}}, \boldsymbol{r}_{\mathrm{s}}\right)=\frac{1}{2 \pi} \int G\left(\boldsymbol{\omega} ; \boldsymbol{r}_{\mathrm{r}}, \boldsymbol{r}_{\mathrm{s}}\right) P_{\mathrm{s}}(\boldsymbol{\omega}) \mathrm{e}^{i \omega t} \mathrm{d} \omega $ | (3) |
根据式(1)~(3),可以得到目标引起接收声压的相对变化的表达式为:
| $ \begin{array}{c}{\Delta P\left(t ; \boldsymbol{r}_{\mathrm{r}}, \boldsymbol{r}^{\prime}, \boldsymbol{r}_{\mathrm{s}}\right) / P\left(t ; \boldsymbol{r}_{\mathrm{r}}, \boldsymbol{r}_{\mathrm{s}}\right)=-4 \pi \int f_{\infty}\left(\omega, \varphi_{\mathrm{s}}+\right.} \\ {\varphi_{\mathrm{r}} ) G\left(\omega ; \boldsymbol{r}_{\mathrm{r}}, \boldsymbol{r}^{\prime}\right) G\left(\omega ; \boldsymbol{r}^{\prime}, \boldsymbol{r}_{\mathrm{s}}\right) P_{\mathrm{s}}(\omega) \mathrm{e}^{\mathrm{i} \omega t} \mathrm{d} \omega /} \\ {\int G\left(\omega ; \boldsymbol{r}_{\mathrm{r}}, \boldsymbol{r}_{\mathrm{s}}\right) P_{\mathrm{s}}(\omega) \mathrm{e}^{\mathrm{i} \omega t} \mathrm{d} \omega}\end{array} $ | (4) |
当目标为半径为a的球体且满足一阶波恩近似条件(目标满足弱散射条件[16])时,散射形态函数可表示为:
| $ \begin{aligned} f_{\infty}\left(\omega, \varphi_{{\rm s}}+\varphi_{\mathrm{r}}\right)=& 2 / 3 k^{2} a^{3}\left[\Delta c\left(\boldsymbol{r}^{\prime}\right) / c\left(\boldsymbol{r}^{\prime}\right)+\right.\\ & \Delta \boldsymbol{\rho}\left(\boldsymbol{r}^{\prime}\right) / \boldsymbol{\rho}\left(\boldsymbol{r}^{\prime}\right)\left(1+\cos \left(\varphi_{\mathrm{s}}+\right.\right.\\ & \varphi_{\mathrm{r}} ) ) / 2 ] \end{aligned} $ | (5) |
式中k为波数,k=ω/c。将式(5)代入式(4),接收声压相对变化为:
| $ \begin{array}{c}{\Delta P\left(t ; \boldsymbol{r}_{\mathrm{r}}, \boldsymbol{r}^{\prime}, \boldsymbol{r}_{\mathrm{s}}\right) / P\left(t ; \boldsymbol{r}_{\mathrm{r}}, \boldsymbol{r}_{\mathrm{s}}\right)=\int\left[\Delta c\left(\boldsymbol{r}^{\prime}\right) / c\left(\boldsymbol{r}^{\prime}\right)+\right.} \\ {\Delta \boldsymbol{\rho}\left(\boldsymbol{r}^{\prime}\right) / \boldsymbol{\rho}\left(\boldsymbol{r}^{\prime}\right)\left(1+\cos \left(\varphi_{\mathrm{s}}+\varphi_{\mathrm{r}}\right)\right) / 2 ]}\cdot \\ {Q\left(\omega ; \boldsymbol{r}_{\mathrm{r}}, \boldsymbol{r}^{\prime}, \boldsymbol{r}_{\mathrm{s}}\right) V P_{\mathrm{s}}(\boldsymbol{\omega}) \mathrm{e}^{i \omega t} \mathrm{d} \omega}/ \\ {\int G\left(\omega ; \boldsymbol{r}_{\mathrm{r}}, \boldsymbol{r}_{\mathrm{s}}\right) P_{\mathrm{s}}(\omega) \mathrm{e}^{i \omega t} \mathrm{d} \omega}\end{array} $ | (6) |
式中:V为球体体积;Q(ω; rr, r′, rs)为文献[8]定义的声压敏感核,Q(ω; rr, r′, rs)=-2k2G(ω; rr, r′) ·G(ω; r′, rs),从式(6)中可发现声压敏感核反映的是声压场对r′处局部扰动(Δc和Δρ)的敏感性,与目标位置r′有关,所以可以利用声压敏感核的空间特性进行目标定位。
式(6)表示目标引起的声压相对变化ΔP/P与局部的声速相对变化Δc/c和密度相对变化Δρ/ρ成线性关系,但前提条件是目标满足弱散射条件。当目标为更一般的固体球时,应将式(5)表示为式(7)[17]计算散射形态函数f∞(ω, φs+φr),再代入式(4)求得声压相对变化:
| $ \begin{aligned} f_{\infty}\left(\omega, \varphi_{\mathrm{s}}+\varphi_{\mathrm{r}}\right)=& \frac{1}{k} \sum\limits_{n=0}^{\infty}(2 n+1) \sin \eta_{n} ·\\ & \exp \left(\mathrm{i} \eta_{n}\right) \mathrm{P}_{n}\left(\cos \left(\varphi_{\mathrm{s}}+\varphi_{\mathrm{r}}\right)\right) \end{aligned} $ | (7) |
式中ηn为中间变量,与目标密度、声速和半径等参数有关; Pn(·)为勒让德多项式。
1.2 基于声压敏感核的目标定位方法从声源出发经过一定的路径到达接收点的声线称为本征声线,本征声线是射线理论描述声场的关键。目标进入波导会对原有的部分本征声线产生扰动,引起接收信号幅度、相位等的变化,受目标扰动的本征声线称为扰动声线。
扰动声线声压相对变化的计算流程分为以下3步:1)根据实际声速梯度、布放位置和目标空间网格位置,利用Bellhop模型计算格林函数库G(ω; rr, rs)、G(ω; r′, rs)和G(ω; rr, r′),为之后的计算做数据准备;2)根据扰动声线的收发位置,利用式(4),计算目标处于不同网格位置时接收声压的相对变化;3)根据每一点的计算结果画出扰动声线的声压相对变化。图 1为根据上述流程计算得到的某条扰动声线的声压相对变化,从图中可以看出引起本征声线声压相对变化较大的区域主要集中在声线附近,且目标在不同位置所引起的变化正负交替出现。

|
Download:
|
| 图 1 某条扰动声线的声压相对变化 Fig. 1 Relative pressure changes of a perturbed eigenray | |
图 1体现了声压敏感核的空间特性,即目标处于不同位置所引起的声压相对变化不同。而扰动声线是因目标出现而影响到的本征声线,其声压相对变化包含了目标的位置信息。
Marandet[6]统计了一次实验室等比缩放实验中7 000条本征声线的声压相对变化,发现多数扰动声线的声压是减弱的。所以本文利用声压相对变化为负的扰动声线进行目标定位,该集合用M表示。目标处于不同位置所引起的声压相对变化ΔP/P有正有负,那么一条声压相对变化为负的扰动声线所提供的目标位置信息是目标应该在ΔP/P < 0的区域。因此只保留ΔP/P < 0的区域的计算结果,用Ψm(r′)表示,其中下角标表示第m条扰动声线的结果。将所有声压相对变化为负的扰动声线的计算结果相加,并求得绝对值最大的位置rt:
| $ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( {{\mathit{\boldsymbol{r}}^\prime }} \right) = \sum\limits_{m \in M} {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\rm{m}}}} \left( {{\mathit{\boldsymbol{r}}^\prime }} \right) $ | (8) |
| $ {\mathit{\boldsymbol{r}}_{\rm{t}}} = \max \left( {\left| {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( {{\mathit{\boldsymbol{r}}^\prime }} \right)} \right|} \right) $ | (9) |
式中rt为目标位置。
1.3 定位方法的信号处理流程利用扰动声线声压敏感核进行小目标定位的处理过程:1)对接收到的所有本征声线进行分离,筛选得到所有声压相对变化为负的扰动声线。由于波导边界的存在,接收换能器实际接收到的是发射信号经过信道扩展的多途信号。分离本征声线的目的是得到每条途径的接收信号,而不受其他途径干扰;2)计算每条分离的本征声线的声压相对变化,筛选出用于目标定位的所有声压相对变化为负的扰动声线;3)利用式(4)计算每条筛选出的扰动声线的声压相对变化。这些计算结果包含了目标的位置信息;4)根据式(8)和式(9),将所有筛选出的扰动声线的计算结果求和,确定目标位置。
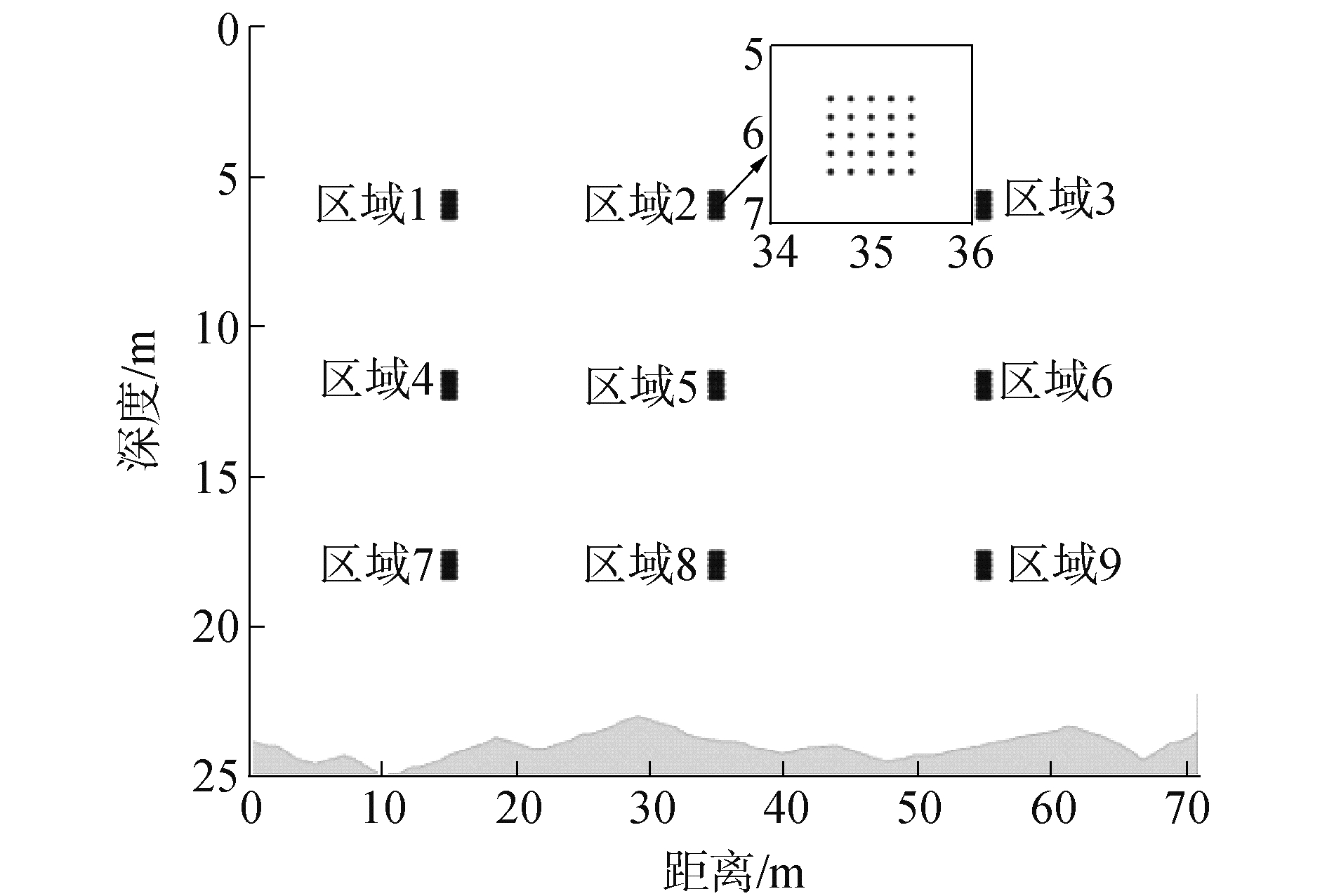
2 仿真实验及性能分析为分析前文介绍的定位方法的定位精度,本节进行了3种不同水底模型精度下的理论仿真。第1种是精确已知水底地形;第2种是测得的水底地形存在0.1%和0.3%的测量误差(国内商用测深仪的精度一般为水深的0.1%~0.3%);第3种是利用平底假设对起伏水底进行近似。定位区域及目标位置的示意如图 2所示,仿真参数如下:发射接收距离71 m,水深约24 m,水底在23~25 m起伏;16个发射阵元均匀分布在4~19 m,16个接收阵元均匀分布在4.2~19.2 m,发射信号为24 kHz单频脉冲,目标为半径0.2 m的铁球,位于如图 3所示的9个区域,每个区域内选择25个目标位置,间隔0.2 m,9个区域的中心分为3个深度(6、12和18 m)和3个距离(距发射15、35和55 m)。
|
Download:
|
| 图 2 定位区域及目标位置示意图 Fig. 2 Schematic diagram of location area and target locations | |

|
Download:
|
| 图 3 精确已知水底地形的定位结果 Fig. 3 Location results under accurate bottom model | |
图 3所示为精确已知水底地形情况下,目标位于9个区域中心位置的定位结果,可以发现不同扰动声线的声压敏感核在实际目标位置处能够很好的交汇,从而实现目标定位。图 3中的每幅图是不同扰动声线的声压相对变化求和后再归一化的结果。
统计9个区域中25个目标位置的平均定位精度,结果如表 1所示,可以发现因算法引起的误差很小,说明该算法是有效的。
| 表 1 精确已知水底地形时的平均定位误差 Table 1 Average location error under accurate bottom model |
利用测深仪对水底地形进行测量时,会存在测量误差,目前国内商用测深仪的测量精度为水深的0.1%~0.3%,所以分析当水底地形存在0.1%和0.3%测量误差时,本文所述基于扰动声线声压敏感核的定位方法的定位性能。
图 4为2种测量精度下测量值与实际深度的相对误差的仿真结果,其中所有测量点的相对误差服从正态分布,并且最大相对误差的绝对值分别约为0.1%和0.3%。根据图 4所示的2个水底地形的仿真结果,利用本文所述方法计算目标位于9个区域的平均定位结果,结果如图 5所示。观察图 5发现:1)本方法的深度定位精度高于距离定位精度,距离定位误差是主要误差。这是由于发射阵和接收阵均采用垂直阵的原因;2)水底测量误差越大,定位误差越大。水底的测量误差会影响跟水底有关的扰动声线的声压敏感核,造成交汇变差,进而引起定位误差;3)扰动声线中与水底有关的声线所占比例越高,定位结果越易受水底测量误差的影响。在仿真参数下,本文分析讨论的9个区域中,区域8、9、7、5的上述比例分别为85.1%、74.4%、72.9%和55.3%,其余区域均在35.2%以下。图 5显示接近水底的7、8、9三个区域定位误差最大,其次是区域5,最后是其他区域,规律与扰动声线中与水底有关的声线所占比例一致。

|
Download:
|
| 图 4 2种测量精度下的测量值与实际深度的相对误差的仿真结果 Fig. 4 Simulation results of depth relative error between true value and measurement value under two measurement precisions | |

|
Download:
|
| 图 5 存在地形测量误差时不同区域的平均定位误差 Fig. 5 Average location error of different areas under bottom models with measurement error | |
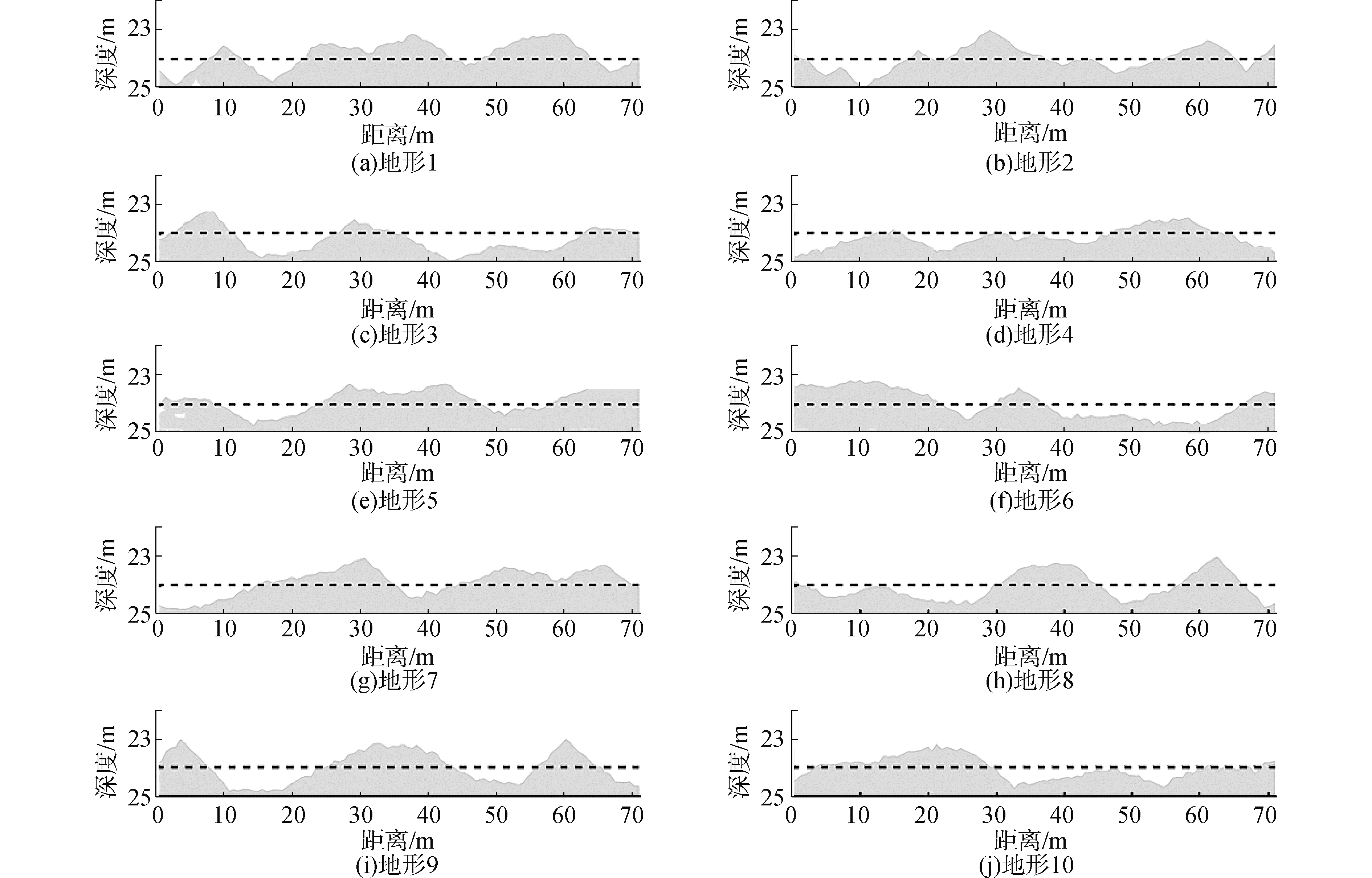
在实际应用中,并不总是具备测量水底地形的条件,这种情况下就需要将实际起伏水底近似为平底来定位目标。图 6为10种在23~25 m随机起伏的水底地形,定位过程中将水底近似为24 m的平底,图中用虚线表示。
|
Download:
|
| 图 6 10种随机起伏的水底地形 Fig. 6 10 different bottoms of random fluctuation | |
上文分析得出本方法的距离定位误差是主要误差,表 2给出了10种地形下利用本文所述方法计算目标位于9个区域的距离平均误差。观察表 2总结出以下4点结论:1)整体观察,仍然是接近水底的7、8、9三个区域定位误差最大,其次是区域5;2)与测量水底地形存在测量误差的定位结果相比,近似为平底的误差更大;3)由于地形的不同,同样是近似为平底,对同一个区域造成的影响也不同;4)虽然相比于其他情况近似为平底时误差较大,但当测量条件有限时该方法仍能确定目标的大致位置,其中对于水体中上部的目标定位效果更好。原因与存在测量误差时的分析类似,目标位于水体中上部,扰动声线中与水底有关的声线所占比例更少,定位结果受水底模型近似的影响更小,所以定位效果更好。
| 表 2 起伏水底近似为平底时不同区域的距离平均定位误差 Table 2 Average distance error of different areas under flat bottom approximation |
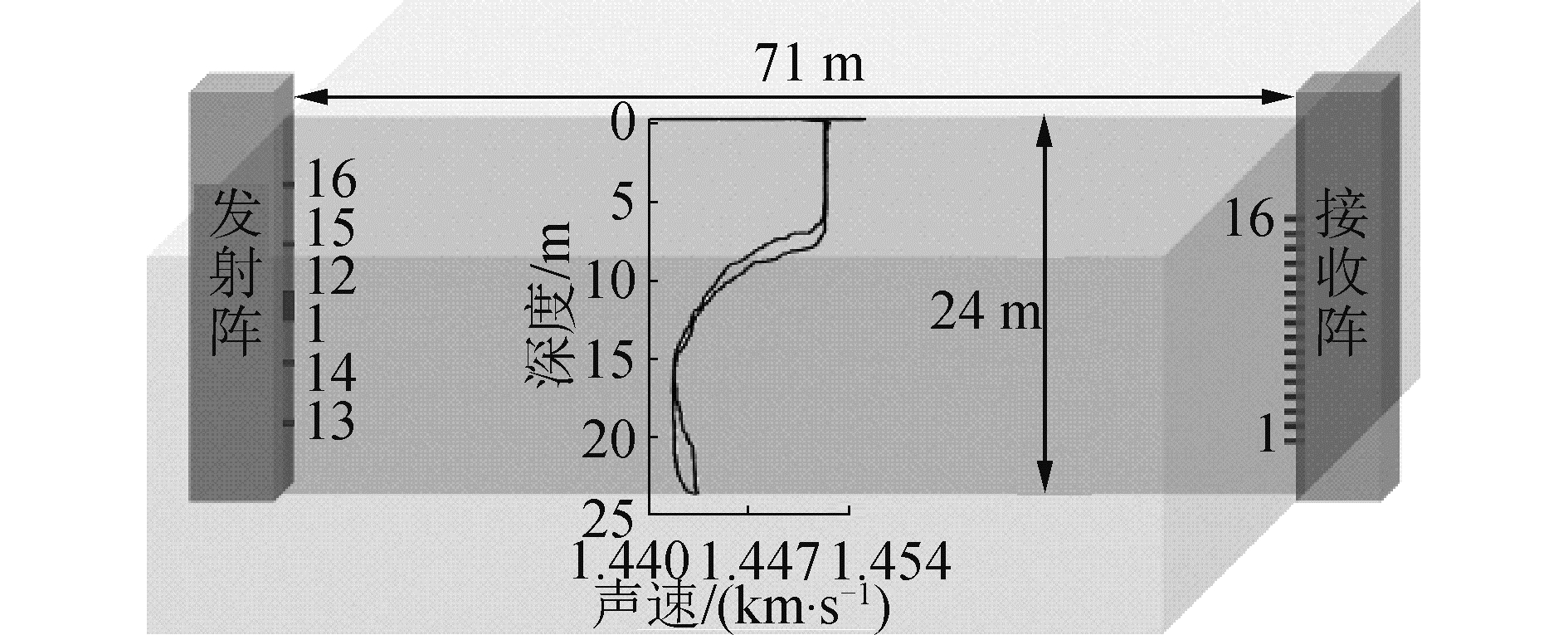
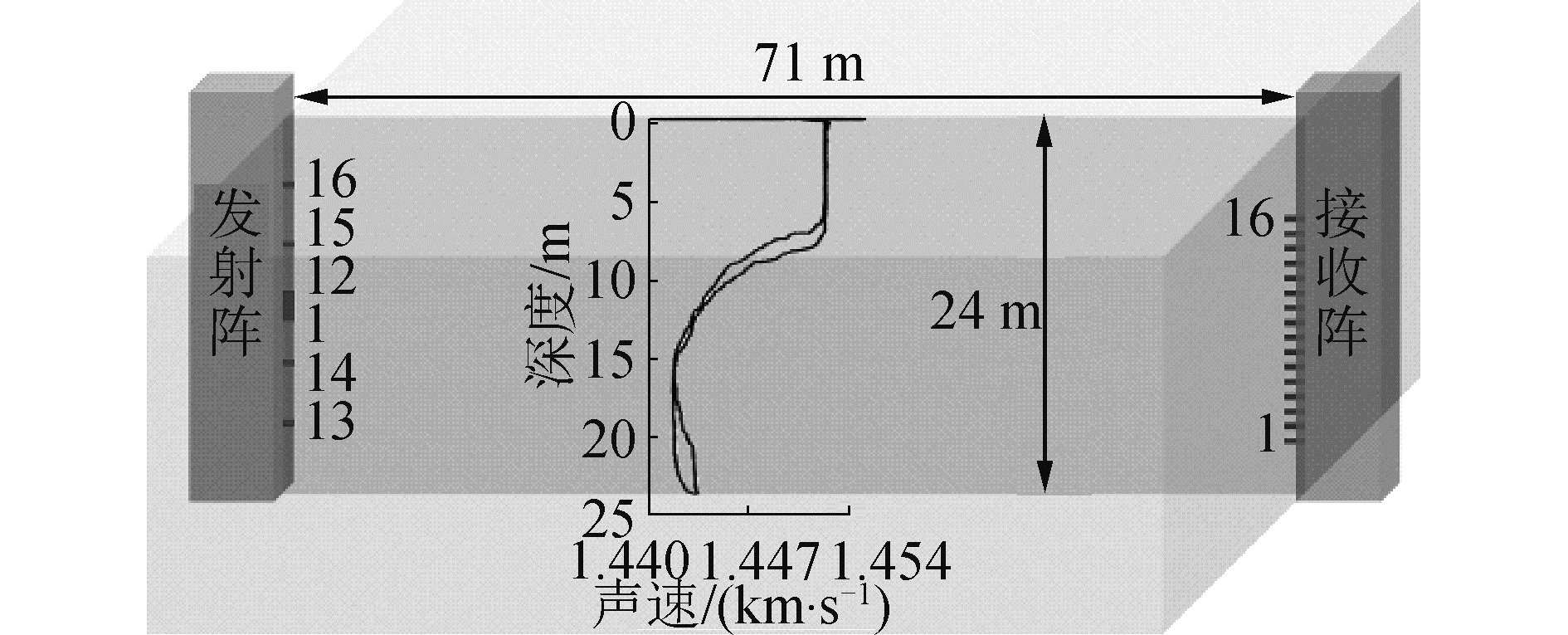
整个实验系统的水下部分由一条垂直发射阵和一条垂直接收阵组成,布放情况如图 7所示,水深约24 m,没有测量水底具体地形,发射阵和接收阵均为刚性连接,相距约71 m。发射阵由16个阵元组成,1~12号阵元均匀分布在9.8~10.8 m深度,13~16号阵元的深度分别为18.1、14.1、6.1和2.1 m。接收阵由16个子阵组成(每个子阵包含4个阵元),1~16号子阵均匀分布在4.2~16.2 m深度。图 7还给出了利用CTD测得的水中声速梯度。
|
Download:
|
| 图 7 实验布局示意 Fig. 7 Schematic diagram of experimental layout | |
实验过程中,目标为直径0.4 m的充水铁球壳,目标球通过绳子与水面浮子相连,利用GPS对浮子进行定位,进而间接确定目标球在水下的位置。目标静止于收发连线某点,GPS的定位结果显示目标与发射阵的直线距离为8.0 m(该值为利用GPS在一段时间内的平均值计算得到,该段时间GPS的定位结果与平均值的最大差值为1.9 cm),目标与浮子间绳子的长度约为14.1 m。综上,目标的坐标为(8.0 m, 14.1 m),其中坐标系以发射阵与水面的交点为坐标原点,发射阵与接收阵连线为横坐标,竖直方向为纵坐标,接收阵为横坐标正方向,竖直向下为纵坐标正方向。根据目标实际的位置和发射阵元的垂直开角,选择深度为9.9、10.3、10.7、14.1、18.1 m的阵元依次发射LFM信号(参数为:中心频率24 kHz,带宽8 kHz,脉宽10 ms),16个接收子阵同时采集信号并进行存储。
3.2 实验结果根据前文介绍的信号处理流程,首先,对接收信号进行脉冲压缩处理分离本征声线,结果如图 8所示,由于通道数较多,每隔4个通道画出1个通道的脉冲压缩信号,并对该结果进行归一化处理,从图 8中可以观察到明显的多途结构。根据分离的结果,计算每条本征声线的声压相对变化,筛选出实际声压相对变化超过设定阈值且为负的扰动声线,图 8中放大的第5通道的直达途径就是一条扰动声线,可以观察到当目标存在时,引起了该途径声压变小。其次,计算每条筛选出的扰动声线的声压相对变化。由于实验过程中没有对水底地形进行精确测量,只利用单波束测深仪确认水深在23~25 m起伏,平均深度约24 m,所以在计算过程中将水底近似为24 m深平底。最后,将所有筛选出的扰动声线的计算结果求和,并进行归一化,结果如图 9所示,定位结果为(7.2 m, 14.4 m)。
|
Download:
|
| 图 8 经过脉冲压缩后的本征声线 Fig. 8 Eigenrays after pulse compression | |

|
Download:
|
| 图 9 湖试定位结果 Fig. 9 Location result of lake trial | |
1) 本仿真分析方法自身的定位误差很小。测深精度优于测距精度,测距误差是主要误差。适用于存在水底测量误差的情况,而且当水底起伏不大时,直接将其近似为平底仍可确定目标的大致位置,其中对于水体中上部的目标定位效果更好。
2) 扰动声线中与水底有关的声线所占比例越高,定位结果越易受水底模型不精确的影响。
3) 基于扰动声线声压敏感核的定位方法在自然环境下仍然适用。将起伏水底近似为平底,目标位于水体的中部略偏下的位置,利用本文方法仍能较好对其定位,与仿真分析的性能一致。与之前文献中在实验室进行的等声速等比例缩放实验相比,更能说明该方法的实用性。
| [1] |
SONG H, KUPERMAN W A, HODGKISS W S, et al. Demonstration of a high-frequency acoustic barrier with a time-reversal mirror[J]. IEEE Journal of oceanic engineering, 2003, 28(2): 246-249. DOI:10.1109/JOE.2003.811900 (  0) 0)
|
| [2] |
PRADA C, DE ROSNY J, CLORENNEC D, et al. Experimental detection and focusing in shallow water by decomposition of the time reversal operator[J]. The journal of the acoustical society of America, 2007, 122(2): 761-768. DOI:10.1121/1.2749442 (  0) 0)
|
| [3] |
ROUX P, KUPERMAN W A, HODGKISS W S, et al. A nonreciprocal implementation of time reversal in the ocean[J]. The journal of the acoustical society of America, 2004, 116(2): 1009-1015. DOI:10.1121/1.1707089 (  0) 0)
|
| [4] |
罗方方, 生雪莉, 梅继丹, 等. 基于MVDR高分辨算法的时反定位技术研究[J]. 哈尔滨工程大学学报, 2010, 31(7): 945-950. LUO Fangfang, SHENG Xueli, MEI Jidan, et al. Time reversal mirror localization technology based on a high-resolution MVDR algorithm[J]. Journal of Harbin Engineering University, 2010, 31(7): 945-950. DOI:10.3969/j.issn.1006-7043.2010.07.021 (  0) 0)
|
| [5] |
FOLEGOT T, MARTINELLI G, GUERRINI P, et al. An active acoustic tripwire for simultaneous detection and localization of multiple underwater intruders[J]. The journal of the acoustical society of America, 2008, 124(5): 2852-2860. DOI:10.1121/1.2977675 (  0) 0)
|
| [6] |
MARANDET C, ROUX P, NICOLAS B, et al. Target detection and localization in shallow water:an experimental demonstration of the acoustic barrier problem at the laboratory scale[J]. The journal of the acoustical society of America, 2011, 129(1): 85-97. DOI:10.1121/1.3514503 (  0) 0)
|
| [7] |
温凤丹, 林巨. 浅海环境下的声学灵敏度核函数研究[J]. 南京大学学报(自然科学), 2017, 53(1): 135-143. WEN Fengdan, LIN Ju. The study of sensitivity kernels in shallow water environments[J]. Journal of Nanjing University (natural sciences), 2017, 53(1): 135-143. (  0) 0)
|
| [8] |
SKARSOULIS E K, CORNUELLE B D. Travel-time sensitivity kernels in ocean acoustic tomography[J]. The journal of the acoustical society of America, 2004, 116(1): 227-238. DOI:10.1121/1.1753292 (  0) 0)
|
| [9] |
ROUX P, ITURBE I, NICOLAS B, et al. Travel-time tomography in shallow water:Experimental demonstration at an ultrasonic scale[J]. The journal of the acoustical society of America, 2011, 130(3): 1232-1241. DOI:10.1121/1.3621271 (  0) 0)
|
| [10] |
AULANIER F, NICOLAS B, MARS J I, et al. Shallow-water acoustic tomography from angle measurements instead of travel-time measurements[J]. The journal of the acoustical society of America, 2013, 134(4): EL373-EL379. DOI:10.1121/1.4820468 (  0) 0)
|
| [11] |
HUANG Ying, ZHAO Hangfang, WANG Feiyi. Ocean acoustic tomography using travel-time sensitivity kernel[C]//Proceedings of OCEANS 2016. Shanghai, China, 2016: 1-7. https://ieeexplore.ieee.org/document/7485418/
(  0) 0)
|
| [12] |
ROUX P, MARANDET C, NICOLAS B, et al. Experimental measurement of the acoustic sensitivity kernel[J]. The journal of the acoustical society of America, 2013, 134(1): EL38-EL44. DOI:10.1121/1.4808111 (  0) 0)
|
| [13] |
YILDIZ S, ROUX P, RAKOTONARIVO S T, et al. Target localization through a data-based sensitivity kernel:A perturbation approach applied to a multistatic configuration[J]. The journal of the acoustical society of America, 2014, 135(4): 1800-1807. DOI:10.1121/1.4868362 (  0) 0)
|
| [14] |
SARKAR J, MARANDET C, ROUX P, et al. Sensitivity kernel for surface scattering in a waveguide[J]. The journal of the acoustical society of America, 2012, 131(1): 111-118. DOI:10.1121/1.3665999 (  0) 0)
|
| [15] |
ROUX P, NICOLAS B. Inverting for a deterministic surface gravity wave using the sensitivity-kernel approach[J]. The journal of the acoustical society of America, 2014, 135(4): 1789-1799. DOI:10.1121/1.4867374 (  0) 0)
|
| [16] |
张培珍, 王朔中, 王润田, 等. 修正一阶Born近似改进水中弱散射目标的散射声场预报[J]. 声学学报, 2014, 39(3): 331-338. ZHANG Peizhen, WANG Shuozhong, WANG Runtian, et al. Modification to first-order Born approximation for improved prediction of scattered sound from weakly scattering objects[J]. Acta acustica, 2014, 39(3): 331-338. (  0) 0)
|
| [17] |
FARAN J J JR. Sound scattering by solid cylinders and spheres[J]. The journal of the acoustical society of America, 1951, 23(4): 405-418. DOI:10.1121/1.1906780 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


