随着社会的发展,海洋资源与空间的开发和利用逐渐受到了人们的重视,海洋平台结构、浮式风机等海上结构物得到了广泛的应用[1-2]。定位系统对于海上建筑物的安全、稳定工作等方面都起到了至关重要的作用,解决系泊装置波漂移力过大等问题成为了学者研究的热点[3]。此前研究主要着眼于改变结构物的形状等方面,并没有考虑改善浮体所处的环境,从根本上降低浮体所受的波漂移力等载荷。何广华等[4]和Zhang等[5-6]研究表明:通过在浮体周围合理布置小型浮体群,利用浮体间的群遮效应,中心浮体所受到的波漂移力可得到显著降低,可从根本上达到保护浮体的目的。
“Cloaking”现象被应用在电磁波、声波和地震波等领域[7-9]。它指波运动中向外传播的散射波波幅的减小或完全消散[10]。根据动量守恒,波漂移力可以通过散射波幅来计算:即没有散射波存在时,平均漂移力数值减小至0;散射波幅减小时,漂移力也得到减小。对于水波领域,学者们对cloaking现象也开展了初步的研究:文献[11-13]通过使用一个优化的可变化深度的环形区域,实现了一个坐底圆柱的cloaking现象。然而,在深海远海情况中,改变海底地形很难适用于工程应用。受Farhat等[14]的启发,Newman[15]通过在单浮体周围环绕布置多个尺寸优化的外围浮体,实现了特定波数下截断圆柱的cloaking现象;Iida等[16]通过模型试验,验证了该尺寸优化的浮体阵列的群遮效应现象。何广华等[4]对Newman[15]的cloaking模型进一步展开了波漂移力方面的研究。
对于cloaking模型[4, 15-16],作用于浮体上的波漂移力的降低与浮体周围波面分布变化密切相关;对于结构周围波浪场的分布,目前还没有细致的研究。本文对无外围浮体(N=0)及外围浮体数为4时(N=4)中心浮体周围的波面分布进行了系统的研究。为了验证本数值模型的准确性,浮体参数与布置形式参考Newman[15]和何广华等[4]的设置。粘性对波浪传播、多浮体作用中波浪场的分布情况起到了不可忽略的影响[17-18],故本文考虑了粘性效应对数值结果的影响。通过对CFD软件FLUENT进行二次开发,建立了可以分析多浮体群遮效应的多相流数值水池,并进行了网格与时间步长的收敛性验证,保证了数值水池的精确性和稳定性;研究了不同波数的波浪作用下结构周围波浪场的分布情况,分析了多浮体的复杂相互干涉作用发生下中心浮体波漂移力的变化机理;并给出了中心浮体的一阶力与波面分布的对应关系。
1 数值水池的建立 1.1 控制方程控制方程采用粘性不可压缩流体的Navier-Stokes方程和连续性方程,方程以速度和压力为变量:
| $ \frac{\partial u_{i}}{\partial x_{i}}=0 $ | (1) |
| $ \rho \frac{\partial u_{i}}{\partial t}+\rho u_{j} \frac{\partial u_{i}}{\partial x_{j}}=\mu\left(\frac{\partial^{2} u_{i}}{\partial x_{j}^{2}}\right)-\frac{\partial p}{\partial x_{i}}+S_{i}+f_{i} $ | (2) |
式中:ρ为密度;ui代表x、y、z方向的速度分量;p代表压力;fi为质量力;μ表示动力粘度系数;Si表示x、y、z方向的附加动量源项。
采用流体体积函数方法捕捉自由液面的形状,流体体积分数函数满足方程:
| $ \frac{\partial \alpha_{q}}{\partial t}+u_{i} \frac{\partial \alpha_{q}}{\partial x_{i}}=0 $ | (3) |
式中:αq为流体的体积分数。通过将计算域划分为一定数目的控制单元,并在每个单元中引入体积分数,即:单元中第q相流体所占体积与单元总体积的比值;如αq=1表示单元内充满了第q相流体,αq=0表示单元内没有第q相流体,0 < αq < 1表示该单元处于交界面,为交接面单元。
对于本文所研究的水波问题,涉及气液两相,即q为1或2,αq满足方程:
| $ \sum\limits_{q=1}^{2} \alpha_{q}=1 $ | (4) |
此时,每个控制体中,式(1)、(2)中的ρ可表示为:
| $ \rho=\sum\limits_{q=1}^{2} \alpha_{q} \rho_{q} $ | (5) |
式中ρq为第q相流体的密度。
1.2 数值造波与消波本文通过对FLUENT二次开发,建立了可模拟弱非线性水波的造波水池。造波方法采用设置造波边界法:通过定义边界处的水面抬高和水质点速度,实现波浪的生成。为防止波浪在水槽末端产生反射进而影响计算结果,本文采用人工阻尼进行消波,通过在动量方程中添加附加源项的方法来消除流体的波动和能量。具体理论及实现方法可参考文献[19]。从后文波浪的模拟及收敛性验证中可验证所建水池造波及消波的精确性与有效性。
控制方程扩散项由中心差分格式离散,对流项离散方法如下:压力方程采用体积力加权计算离散格式,动量方程采用二阶迎风格式离散,压力速度耦合采用瞬态问题的PISO算法。
2 收敛性验证在研究群遮效应现象前,本文对建立的多相流粘性数值波浪水池分别进行了网格和时间步长的收敛性验证,以确保数值水池工作的准确性及高效性。另外,数值水池末端2L长度的消波区x向网格,采取节点分布逐渐稀疏的渐变方式,以减少计算时间并提供额外的数值耗散来进行波能的消耗。
2.1 网格收敛性验证以波数k=1.0,波高H=0.2 m的波浪为研究对象,对x方向和自由面附近y方向的最小网格尺寸δx、δy进行了系统的收敛性验证,δx及δy的具体值如表 1所示,表 1同时给出了各算例的代指名称。如名称4020表示x方向最小网格尺寸δx = L/40、y方向最小网格尺寸δy =H/20的算例。
| 表 1 网格收敛性验证的具体参数 Table 1 Specific parameters for mesh convergence verification |
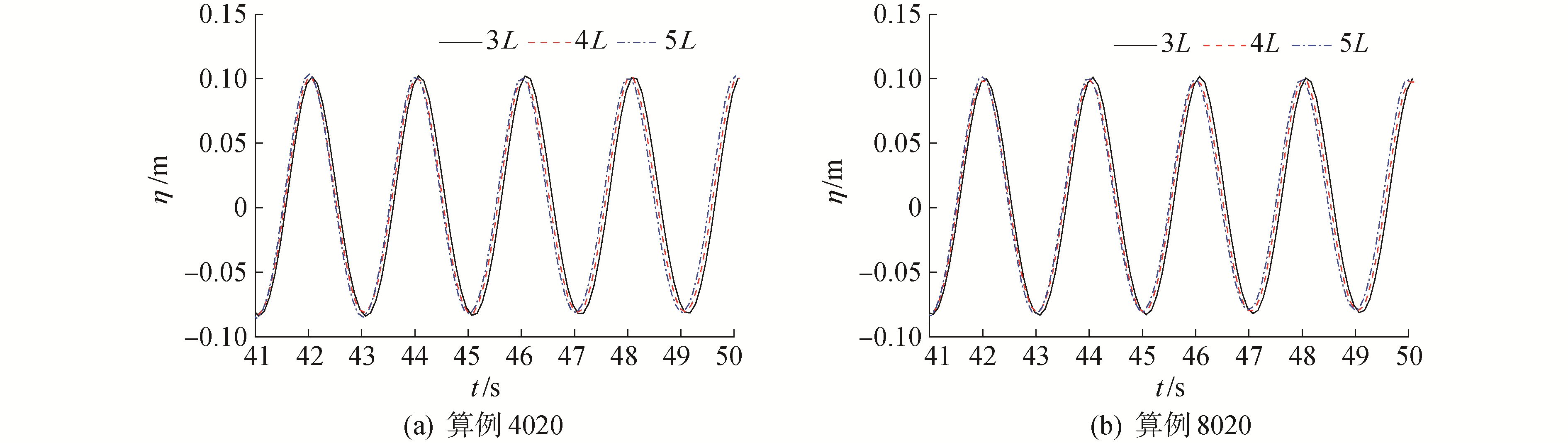
首先保持y方向网格尺寸确定,改变计算域x方向网格尺寸:从每波长均分40个网格逐渐增加到每波长剖分80个网格。图 1分别给出了名称为4020及8020的算例,距离造波边界分别为3L、4L及5L处波面抬高的时历曲线。由图 1可知,同一算例中,3L、4L及5L处的波面抬高时历曲线变化基本一致,所以在后文网格收敛性验证中,仅对比不同算例间距离造波边界3L处的波面抬高变化。
|
Download:
|
| 图 1 距离造波边界3L、4L及5L处的波面抬高时间历程 Fig. 1 Time histories of wave elevations at 3L, 4L and 5L from the wave generation boundary | |
图 2(a)为4020~8020的算例中距造波边界3L处的波面抬高序列对比,除4020的算例,其余算例的波面变化趋于一致,并与解析结果吻合较好。考虑到计算效率与精度的平衡,在后文的算例中,如无特别指明,x方向网格尺寸δx保持δx =L/50。然后保持x方向网格尺寸不变,改变计算域自由面附近y方向最小网格尺寸:从每波高均分10个网格逐渐增加到每波高剖分30个网格。

|
Download:
|
| 图 2 距离造波边界3L处的波面抬高时间历程 Fig. 2 Time histories of wave elevations at 3L from the wave generation boundary | |
同上,图 2(b)为5010~5030的算例中距造波边界3L处的波面抬高时间序列对比,可以看出:波面抬高变化随δy的减小,数值结果逐渐收敛于解析结果;且算例5020~5030的波面抬高变化曲线几乎一致。考虑到数值计算所要求的准确性及三维CFD模拟的耗时性,在后文的数值算例中,均采用算例5020对应的网格尺寸进行计算域的离散。
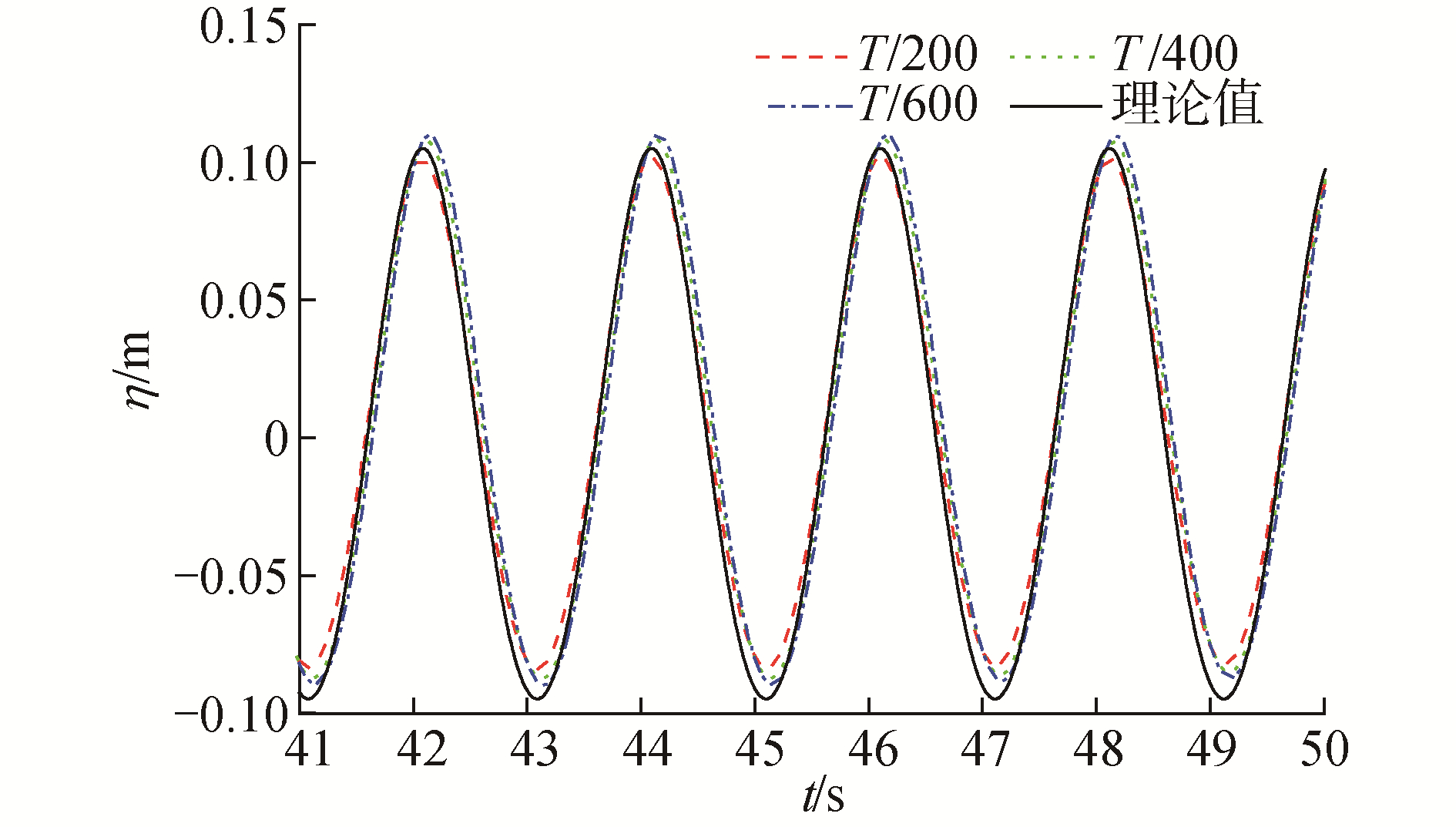
2.2 时间步长收敛性验证本节对数值波浪水池进行了时间步长收敛性的验证。同上,以波数k=1.0,波高H=0.2 m的波浪为研究对象,网格尺寸同算例5020,分别取时间步长δt为T/200、T/400及T/600。距造波边界3L处波面抬高的时间序列如图 3所示:随时间步长的减小,曲线趋于期望波解,且时间步长δt=T/400和δt=T/600的算例所模拟出的波浪基本一致,考虑到δt=T/400较δt=T/600的算例模拟所需时间显著减少,在此后的模拟中,时间步长均取δt=T/400。此外,基于本数值模型的波浪与多浮体相互作用的系统性验证研究可参考文献[19]。
|
Download:
|
| 图 3 不同时间步长的算例距离造波边界3L处的波面抬高时间历程 Fig. 3 Time histories of wave elevations at 3L from the wave generation boundary of cases with different time step | |
Newman[15]和何广华等[4]研究了K=1.0(K=kd0, d0为中心浮体吃水)的波浪作用下,多浮体结构发生群遮效应现象时的总散射波能量和波漂移力。本文基于上述建立的粘性数值波浪水池,对N=4的多浮体模型的群遮效应现象进行了系统的研究。研究了波数K为0.75、1.0、1.25、1.5的波浪作用时,N=0和N=4的浮体群周围波浪场的分布情况;分析了波浪载荷的低减机理,验证了群遮效应对中心浮体的保护作用,并与相关高阶边界元结果进行了对比,验证了本文结果的准确性。
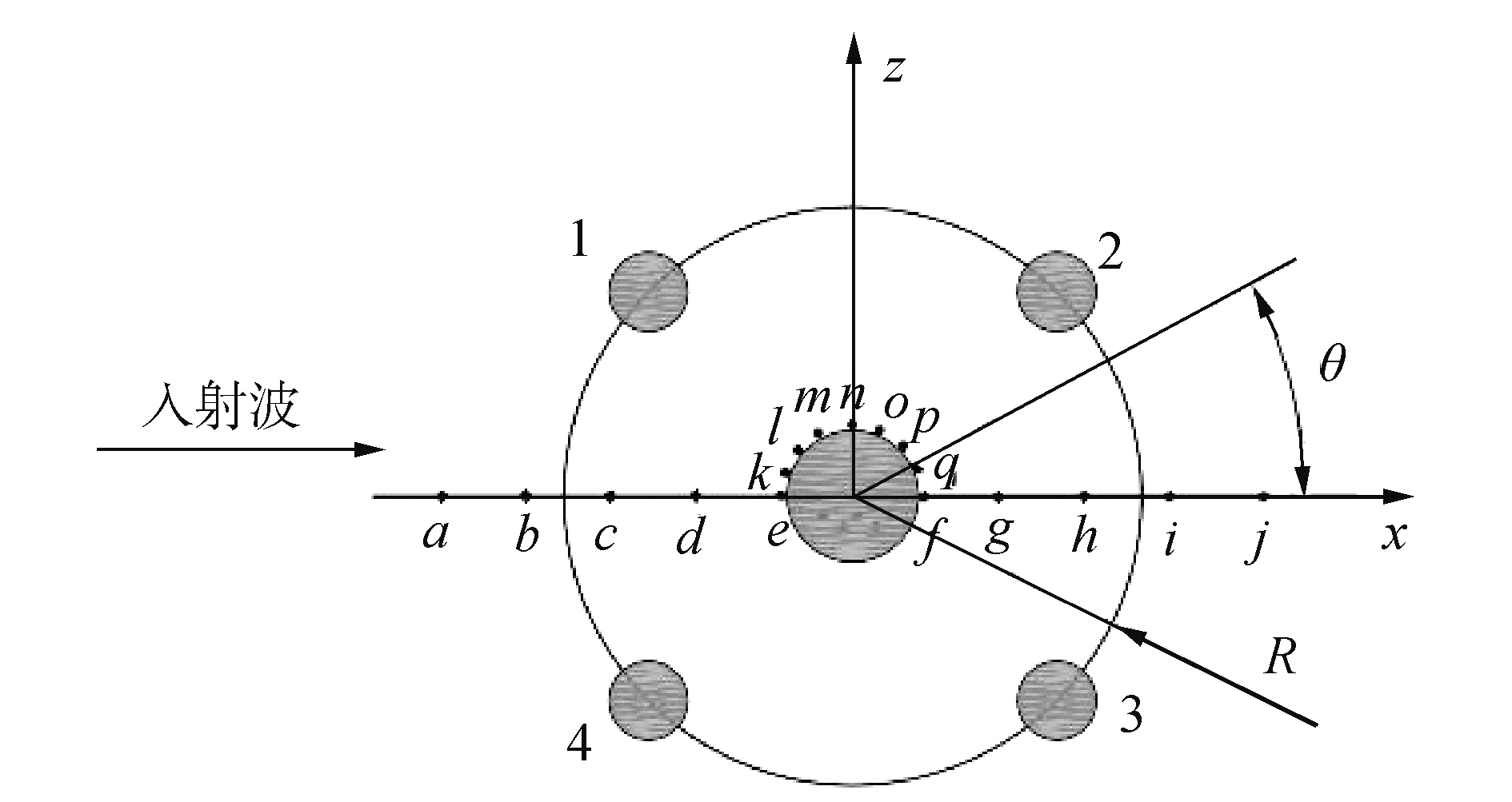
3.1 模型布置与网格剖分N=0和N=4时模型布置、优化的几何尺寸参数与Newman[15]中的相同。N=4时浮体布置如图 4所示:外围浮体编号1~4;a~q表示监测波浪场变化的浪高仪,其中圆柱环向的浪高仪(即e、f、k~q)距圆柱壁面0.02 m,圆柱迎浪及背浪侧的浪高仪(即a~e、f~j)间距为0.65 m;笛卡尔坐标系定义为:y坐标竖直向上,坐标原点处于静水面与受保护物体中心轴的交点;波浪从x轴负方向入射。浮体的几何尺寸见表 2。其中,中心浮体吃水为1 m,表中几何尺寸均以中心浮体吃水为无量纲因子进行无量纲化。
|
Download:
|
| 图 4 Cloaking模型布置(N=4, 俯视图) Fig. 4 Cloaking model layout (N=4, top view) | |
| 表 2 浮体几何尺寸参数 Table 2 Geometric parameters of floating bodies |
网格尺寸同第2.1节中算例5020对应的尺寸,为了保持计算精度并减少模拟时间;根据文献[19]的收敛性验证,本文圆柱环向单元剖分数目为88。N=4模型对应的计算域尺寸及网格划分如图 5所示。从图 5可以看出:三维数值水槽长度尺寸超过8L,其中中心浮体与造波边界的距离为5L,侧壁距临近浮体的宽度尺寸为1.2L,足够的间距减小了边壁效应对结果的影响。

|
Download:
|
| 图 5 N=4的模型布置 Fig. 5 Model layout of N=4 | |
在中心浮体周围环绕分布尺寸优化的浮体群,可以降低中心浮体上的波漂移力。本文对作用在浮体上总的波浪载荷的时历曲线进行快速傅里叶分析,得到了浮体上的一阶波浪力和波漂移力。
图 6给出了不同波数下,本文方法(CFD)与高阶边界元方法(higher-order boundary element method, HOBEM)[4]计算所得的x方向波漂移力;波漂移力Fx(2)无量纲形式同文献[4]。

|
Download:
|
| 图 6 中心浮体在波浪下的波漂移力 Fig. 6 Wave drift force of the central floating body | |
由图 6可知:1)在计算无外围浮体,即单柱情况(N=0)的波漂移力时,随着波数的增加,波长变短,结构物对波浪的阻碍作用逐渐明显,波漂移力呈单调递增的趋势。在长波作用下(K为0.75、1.0),本文方法与HOBEM计算的结果一致,但随着波长变短,波浪反射作用增强,CFD结果较HOBEM结果略有减小。总体来看,CFD方法与HOBEM方法计算结果基本趋于一致; 2)中心浮体在周围布设4个尺寸优化后的外围浮体后(N=4),其波漂移力数值与无外围浮体存在时(N=0)显著不同;且在优化波数K=1.0时,波漂移力较N=0的波漂移力明显减小,如图 6中箭头所示,验证了群遮效应可显著减小中心浮体的波漂移力。当0.75 < K < 1.5时,N=4的中心浮体波漂移力比N=0的波漂移力明显减小,当K>1.5时,减小作用已不明显,这表明:对于不同的入射波频率,需要分别优化外围浮体尺寸来减小中心浮体上的波漂移力。
多浮体模型发生群遮效应现象时,作用在中心浮体上的波漂移力较单柱情况得到了显著的降低,这是由于波浪在柱群之间产生了复杂的相互干涉作用,使得波漂移力的数值得到了低减。本节接着研究了在复杂波浪干涉下,作用在中心浮体上的一阶波浪力(N=4)较单柱(N=0)的变化情况。
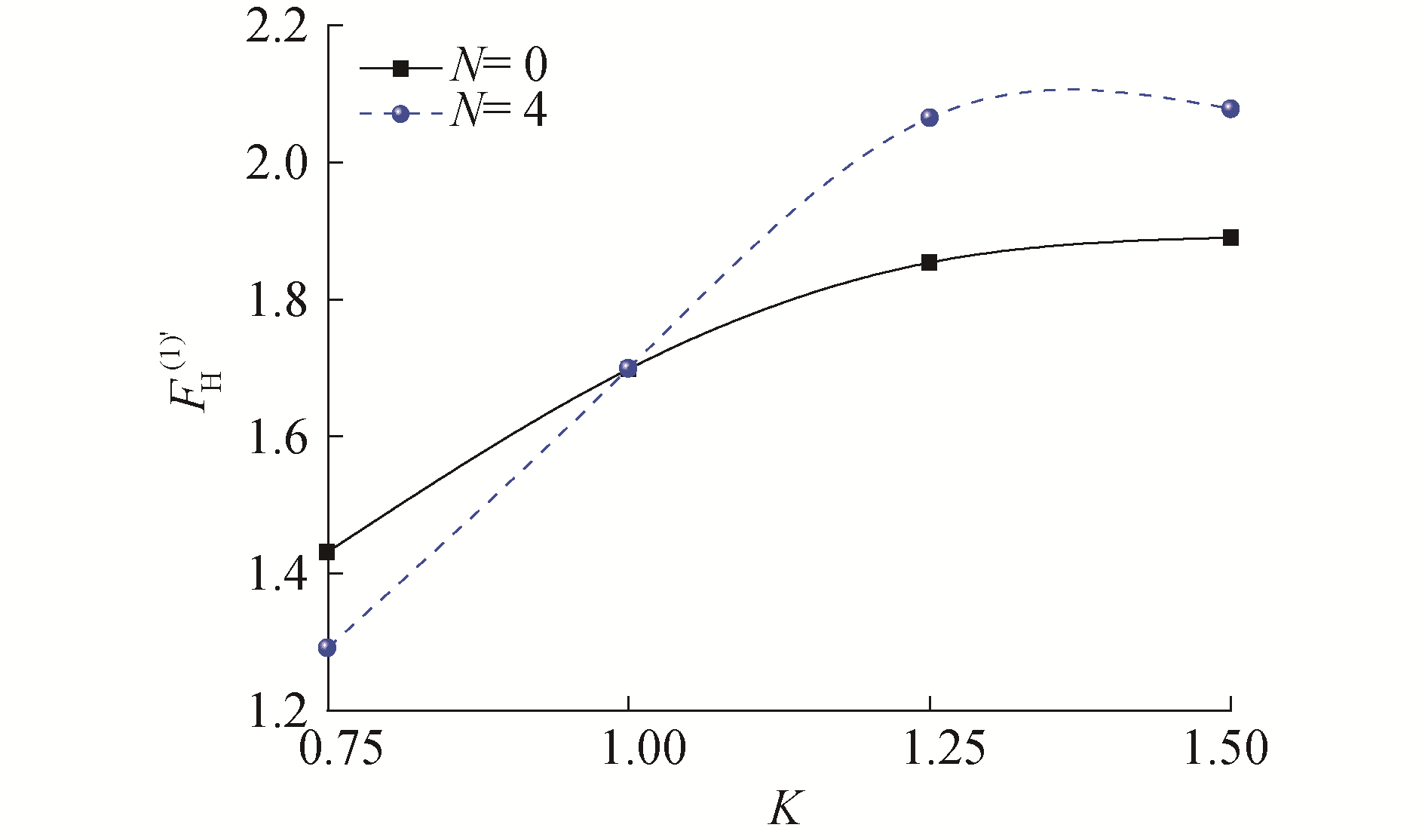
图 7给出了N=0和N=4时,作用在中心浮体上的一阶水平波浪力随波数的变化情况,波浪力的无量纲形式为:
|
Download:
|
| 图 7 中心浮体的水平波浪力 Fig. 7 Horizontal wave force of central floating body | |
| $ F{_{\rm{H}}^{{{(1)}^\prime }}} = \frac{{F{{_{\rm{H}}}^{(1)}}}}{{\rho g{\eta _{\rm{I}}}dr}} $ | (6) |
式中:g表示重力加速度,ηI表示入射波波面最大抬高,d表示浮体吃水,r表示浮体半径。
从图 7可以看出:N=0时,在0.75 < K < 1.5内,一阶水平波浪力随波数的增大而增大,N=4的波浪力变化趋势与之基本一致;当K < 1.0时,N=4的波浪力比单柱的要小,K>1.0时,N=4的波浪力相较单柱的有所增大,在群遮效应最显著的K=1.0时,N=0与N=4的水平波浪力数值基本没有变化,这表明群遮效应并没有对浮体的一阶力产生不利影响。
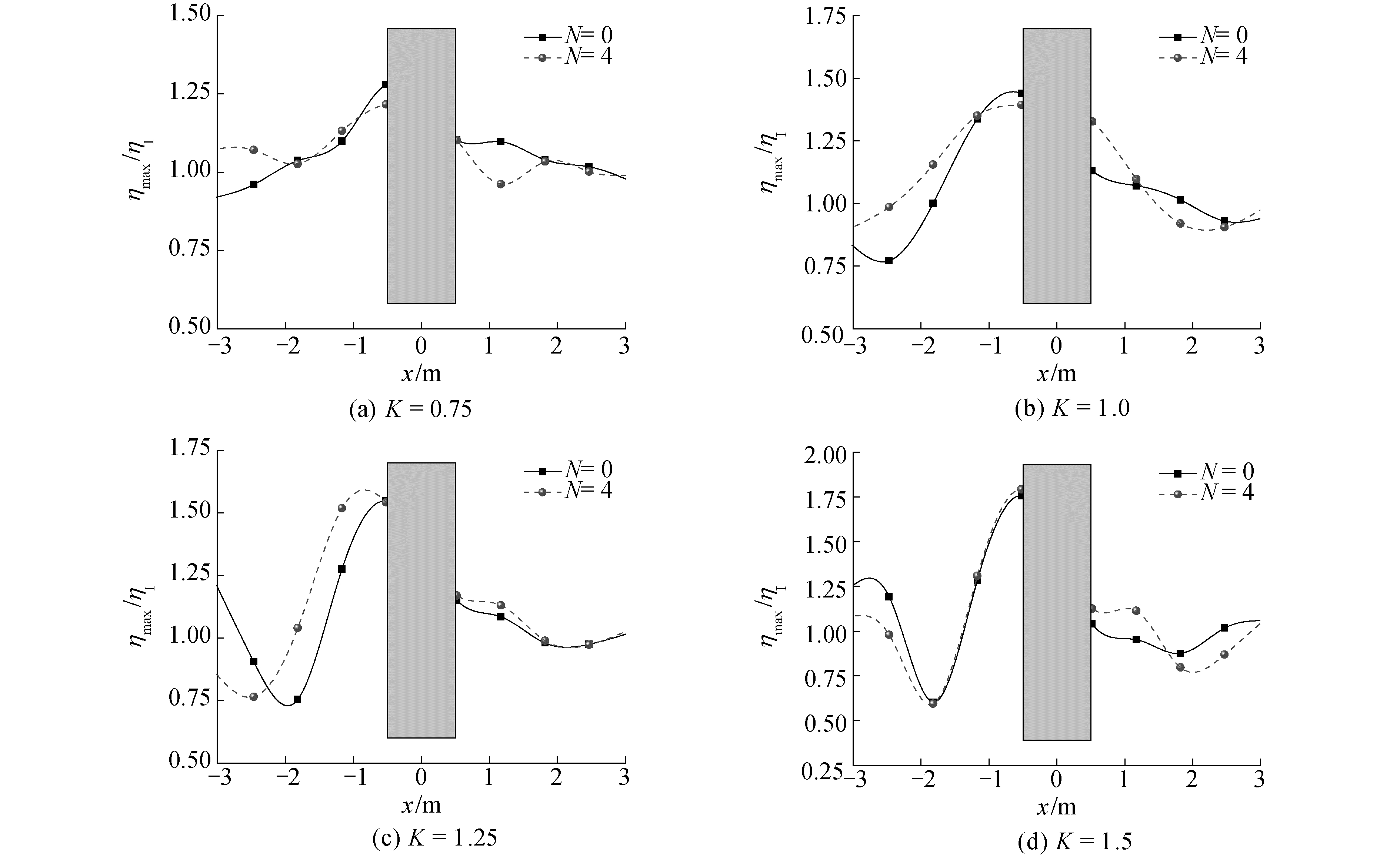
3.3 波浪场分布浮体的波浪载荷与其周围的波浪场分布密切相关,目前鲜有从波面角度分析群遮效应对波浪载荷影响机理的研究。本文通过在中心浮体周围布设浪高仪来记录波面的变化,浪高仪位置如图 4所示。图 8给出了不同波数下中心浮体迎浪、背浪侧波面最大抬高的分布情况。从图 8可以看出,N=0时,浮体迎浪侧波面最大抬高比背浪侧要大,且随着波数的增加,迎浪侧、背浪侧波面抬高的差值逐渐增加,这也导致了中心浮体波漂移力的加大(如图 6,N=0)。而对于N=4的算例,在K=0.75的波浪作用下,中心浮体两侧波面抬高的差值较N=0算例有所减小,这也解释了图 6中,N=4情况下中心浮体波漂移力(K=0.75)较N=0波漂移力(K=0.75)的减小;而在优化波数K=1.0时,N=4中心浮体两侧波面最大抬高几乎一致,此时结构内部发生复杂的波浪干涉叠加,作用在中心浮体上的波漂移力得到显著减小,如图 6中箭头所示;随着波数的增加(K=1.25, 1.5),波浪透射能力减弱,浮体迎浪侧波面抬高数值显著大于背浪侧,且N=0与N=4波面分布情况趋于一致,这同样与图 6中N=0与N=4情况浮体波漂移力数值逐渐接近的结论一致。
|
Download:
|
| 图 8 中心浮体迎浪、背浪侧最大波面抬高 Fig. 8 Maximum wave elevation of central floating body in weatherside and leeside | |
图 7中,在K=1.0时,N=0与N=4的中心浮体一阶水平波浪力数值近似。一阶力数值不仅与波面抬高的数值有关,还与相位变化有关。图 9给出了K=1.0时,中心浮体迎浪侧e点与背浪侧f点的波面抬高时历曲线。由图可知,虽然N=4时中心浮体迎浪、背浪侧波面最大抬高近似,但是相位差明显,使得一阶波浪力的数值与N=0时近似。

|
Download:
|
| 图 9 K=1.0时中心浮体迎浪侧(e点)、背浪侧(f点)波面抬高变化 Fig. 9 Time histories of wave elevation at weatherside (point e) and leeside (point f) of central floating body at K=1.0 | |
为了从波面角度更深入地了解群遮效应对中心浮体波漂移力低减的作用机理,图 10给出了K=1.0时中心浮体周围的波面最大抬高分布,即图 4中浪高仪e、f和k~q的波面数据。图 10中横坐标θ为迎浪侧位置,θ=180°;背浪侧位置,θ=0°。影响浮体x方向波漂移力数值的波面主要分布在45°>θ>0°和180°>θ>135°两个区域,如图 10中背浪侧主要贡献区和迎浪侧主要贡献区。N=4时,中心浮体迎浪侧主要贡献区波面抬高与背浪侧近似,且图中虚线关于θ=90°近似对称,这使得作用在中心浮体上的波漂移力得到显著减小。而实线(N=0)迎浪侧及背浪侧波面抬高差异明显,且最小波面抬高约为θ=45°,趋向于圆柱下游移动。

|
Download:
|
| 图 10 K=1.0时中心浮体周围最大波面抬高 Fig. 10 Maximum wave elevation around the central floating body at K=1.0 | |
1) 在中心浮体周围合理布设尺寸优化的浮体群,本文验证了群遮效应对中心浮体的保护作用。群遮效应发生时中心浮体波漂移力得到显著降低。
2) 对于不同的入射波浪频率,需要分别优化外围浮体的尺寸参数以实现群遮效应。
3) 波浪载荷与结构周围波面分布密切相关,通过系统研究中心浮体周围的波面分布情况,本文揭示了浮体波浪载荷的变化机理:浮体波漂移力的低减可归因于浮体迎浪侧与背浪侧间波面抬高差别的减小;一阶波浪力数值不仅与最大波面分布有关,还与波浪抬高的相位密切相关。
4) 考虑流体粘性的本文结果与实际情况更相符,对群遮效应的工程应用有实际指导意义。
| [1] |
郑崇伟. 21世纪海上丝绸之路:风能资源详查[J]. 哈尔滨工程大学学报, 2018, 39(1): 16-22. ZHENG Chongwei. Wind energy evaluation of the 21st Century Maritime Silk Road[J]. Journal of Harbin Engineering University, 2018, 39(1): 16-22. (  0) 0)
|
| [2] |
喻言, 欧进萍. 海洋平台结构振动监测的无线传感实验研究[J]. 哈尔滨工业大学学报, 2007, 39(2): 187-190. YU Yan, OU Jinping. Wireless sensing experiments for structural vibration monitoring of offshore platform[J]. Journal of Harbin Institute of Technology, 2007, 39(2): 187-190. DOI:10.3321/j.issn:0367-6234.2007.02.005 (  0) 0)
|
| [3] |
王科, 许旺. FPSO型采油平台波浪漂移力的分析研究[J]. 哈尔滨工程大学学报, 2008, 29(12): 1261-1265. WANG Ke, XU Wang. Study of wave drift forces affecting FPSO systems[J]. Journal of Harbin Engineering University, 2008, 29(12): 1261-1265. DOI:10.3969/j.issn.1006-7043.2008.12.002 (  0) 0)
|
| [4] |
何广华, 张志刚, 张子豪, 等. 群遮效应对海上结构物波漂移力的低减作用[J]. 哈尔滨工程大学学报, 2017, 38(11): 1676-1681. HE Guanghua, ZHANG Zhigang, ZHANG Zihao, et al. Reduction in wave drift force on marine structures by cloaking phenomenon[J]. Journal of Harbin Engineering University, 2017, 38(11): 1676-1681. (  0) 0)
|
| [5] |
ZHANG Zhigang, HE Guanghua, KASHIWAGI M, et al. A quasi-cloaking phenomenon to reduce the wave drift force on an array of adjacent floating bodies[J]. Applied ocean research, 2018, 71: 1-10. DOI:10.1016/j.apor.2017.11.011 (  0) 0)
|
| [6] |
ZHANG Zhigang, HE Guanghua, WANG Zhengke. Real-coded genetic algorithm optimization in reduction of wave drift forces on an array of truncated cylinders[J]. Journal of marine science and technology: (2018). https://doi.org/10.1007/s00773-018-0597-4.
(  0) 0)
|
| [7] |
PENDRY J B, SCHURIG D, SMITH D R. Controlling electromagnetic fields[J]. Science, 2006, 312(5781): 1780-1782. DOI:10.1126/science.1125907 (  0) 0)
|
| [8] |
ZIGONEANU L, POPA B I, CUMMER S A. Three-dimensional broadband omnidirectional acoustic ground cloak[J]. Nature materials, 2014, 13(4): 352-355. DOI:10.1038/nmat3901 (  0) 0)
|
| [9] |
BRÛLÉ S, JAVELAUD E H, ENOCH S, et al. Experiments on seismic metamaterials:molding surface waves[J]. Physical review letters, 2014, 112(13): 133901. DOI:10.1103/PhysRevLett.112.133901 (  0) 0)
|
| [10] |
NEWMAN J N. Cloaking a circular cylinder in water waves[J]. European journal of mechanics-B/fluids, 2014, 47: 145-150. DOI:10.1016/j.euromechflu.2013.11.005 (  0) 0)
|
| [11] |
PORTER R. Cloaking of a cylinder in waves[C]//Proceedings of the 26th International Workshop on Water Waves and Floating Bodies. Athens, Greece, 2011: 1-4.
(  0) 0)
|
| [12] |
NEWMAN J N. Scattering by a cylinder with variable bathymetry[C]//Proceedings of the 27th International Workshop on Water Waves and Floating Bodies. Copenhagen, Denmark, 2012: 129-132.
(  0) 0)
|
| [13] |
PORTER R, NEWMAN J N. Cloaking of a vertical cylinder in waves using variable bathymetry[J]. Journal of fluid mechanics, 2014, 750: 124-143. DOI:10.1017/jfm.2014.254 (  0) 0)
|
| [14] |
FARHAT M, ENOCH S, GUENNEAU S, et al. Broadband cylindrical acoustic cloak for linear surface waves in a fluid[J]. Physical review letters, 2008, 101(13): 134501. DOI:10.1103/PhysRevLett.101.134501 (  0) 0)
|
| [15] |
NEWMAN J N. Cloaking a circular cylinder in deep water[C]//Proceedings of the 28th International Workshop on Water Waves and Floating Bodies. L'isle surla Sorgue, France, 2013: 157-160.
(  0) 0)
|
| [16] |
IIDA T, KASHIWAGI M, MIKI M. Wave pattern in cloaking phenomenon around a body surrounded by multiple vertical circular cylinders[J]. International journal of offshore and polar engineering, 2016, 26(1): 13-19. (  0) 0)
|
| [17] |
ZHAN J M, DONG Z, JIANG W, et al. Numerical simulation of wave transformation and runup incorporating porous media wave absorber and turbulence models[J]. Ocean engineering, 2010, 37(14/15): 1261-1272. (  0) 0)
|
| [18] |
KAGEMOTO H, MURAI M, FUJII T. Second-order resonance among an array of two rows of vertical circular cylinders[J]. Applied ocean research, 2014, 47: 192-198. DOI:10.1016/j.apor.2014.05.002 (  0) 0)
|
| [19] |
WANG Zhengke, HE Guanghua, ZHANG Zhigang, et al. Viscous-flow-based analysis of wave near-trapped in a four-cylinder structure[J]. Journal of marine science and application, 2018, 17(3): 371-379. DOI:10.1007/s11804-018-0047-z (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


