2. 武汉理工大学 高性能船舶技术教育部重点实验室, 湖北 武汉 430063
2. Key Laboratory of High Performance Ship Technology(Wuhan University of Technology), Ministry of Education, Wuhan 430063, China
在极端恶劣海况以及碰撞、地震等突发事件中,船舶与海洋结构物所承受的环境载荷必须按动态载荷处理。当含裂纹结构受到动态载荷作用时,载荷的影响通过材料以应力波的形式传播到裂纹,在载荷与裂纹相互作用期间,裂纹面可能会产生闭合接触,在接触区会产生接触力。在动态断裂力学中,由于接触区域和非接触区域是随时间变化的,裂纹面接触作用将对断裂力学特性产生很大的影响。如果忽略裂纹面的接触作用,会得到负的Ⅰ型动态应力强度因子以及实际上不可能出现的裂纹面互相穿透或重叠现象。因此,在动态载荷作用下,更准确的裂纹分析应该考虑裂纹面的接触作用。
已有的动态裂纹研究中,最为经典的是Chen问题。Chen[1]首先采用拉格朗日有限差分法研究了阶跃载荷作用下中心裂纹板的动态应力强度因子,其后Lin等[2]采用相同的方法对Chen问题进行了复算。Song等[3]采用相互作用积分法;Saribay等[4]采用扩展有限单元法;Idesman等[5]采用波动问题中的数值技术计算了冲击载荷下的动态应力强度因子。在国内,解德等[6]采用虚拟裂纹闭合技术(VCCT)计算了一些经典的动态固定裂纹问题;姜伟[7]采用有限元软件ANSYS和相互作用积分法计算了平板穿透裂纹尖端的动态应力强度因子,但没有考虑裂纹面的接触作用;王立清[8-9]采用位移外插法计算了孔边斜裂纹、双-边裂纹板的动态应力强度因子,并考虑了裂纹面接触的影响。
本文不考虑裂纹扩展,在文献[7]的基础上,考虑了裂纹面的接触作用,采用有限元软件ANSYS研究了接触刚度、摩擦系数、冲击载荷形式和裂纹长度等裂纹参数对动态应力强度因子(DSIFs)的影响,并进一步阐述了裂纹面上的接触压力和摩擦力随时间的变化情况。
1 基本理论在复合型裂纹中采用相互作用积分法可以提取应力强度因子KⅠ和KⅡ,相互作用积分来源于J积分,是一个在包含裂纹尖端的回路Γ上的能量积分,如图 1所示,其定义式为[10]:
| $ I=\int_{\mathit{\Gamma}}\left[\boldsymbol{W}^{(1, 2)} \delta_{1 j}-\sigma_{i j}^{(1)} \frac{\partial\left(u_{i}^{(2)}\right)}{\partial x_{1}}-\sigma_{i j}^{(2)} \frac{\partial\left(u_{i}^{(1)}\right)}{\partial x_{1}}\right] n_{j} \mathrm{d} \mathit{\Gamma} $ | (1) |

|
Download:
|
| 图 1 相互作用积分示意 Fig. 1 The diagram of interaction integral | |
式中:
当回路Γ接近裂纹尖端时,相互作用积分与真实场和辅助场的应力强度因子之间的关系为[10]:
| $ I=\frac{2}{E^{*}}\left(K_{\mathrm{I}}^{(1)} K_{\mathrm{I}}^{(2)}+K_{\mathrm{II}}^{(1)} K_{\mathrm{II}}^{(2)}\right) $ | (2) |
式中E*为材料弹性模量E和泊松比v的组合项:
| $ {E^*} = \left\{ {\begin{array}{*{20}{c}} {E, ~~~~平面应力}\\ {\frac{E}{{1 - {v^2}}}, ~~~~平面应变} \end{array}} \right. $ | (3) |
将KⅠ(2)=1,KⅡ(2)=0和KⅠ(2)=0,KⅡ(2)=1分别代入式(2)中,可求得Ⅰ型和Ⅱ型应力强度因子:
| $ K_{\mathrm{I}}=\frac{E^{*}}{2} I^{(1)}, K_{\mathrm{II}}=\frac{E^{*}}{2} I^{(2)} $ | (4) |
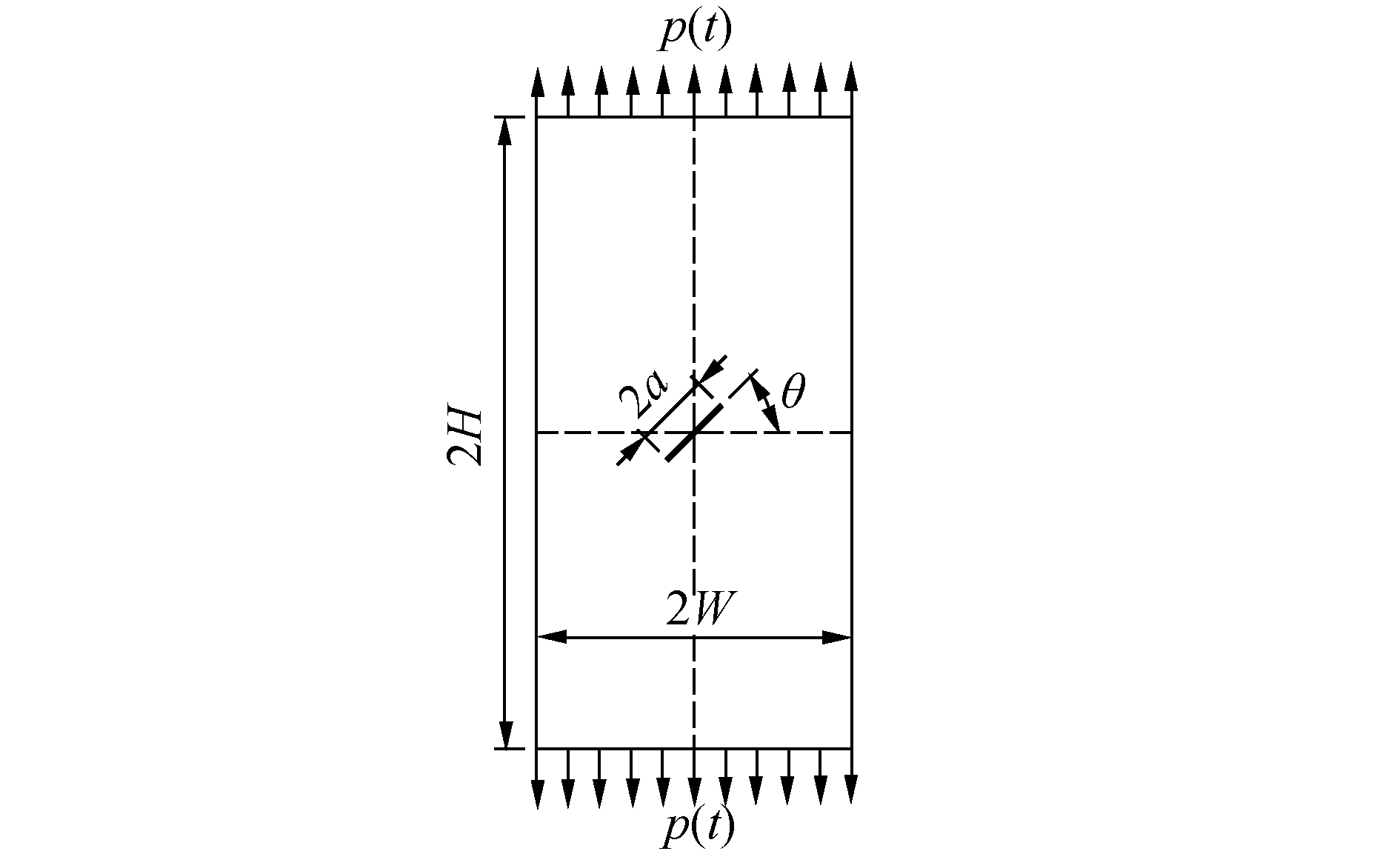
为了便于比较,采用文献[7]中的算例作为本文研究对象。具有中心穿透斜裂纹的有限平板两端受冲击拉伸载荷作用,矩形板宽度2W=20 mm、长度2H=40 mm,斜裂纹长度2a=4.8 mm,夹角为θ,如图 2所示。假设矩形板的材料均匀、各向同性、线弹性,其弹性模量E=199.992 GPa,泊松比ν=0.3,密度ρ=5 000 kg/m3。在矩形板的宽度边上作用阶跃载荷p(t),大小取p(0)=10 MPa,载荷作用时间t=14 μs。考虑到结构不对称,并且还要计算裂纹面的接触情况,建立平面应变状态下的整体有限元模型。矩形板选用PLANE183单元,裂纹尖端采用1/4节点奇异单元,接触设置在上下裂纹面处,通过目标单元TARGE169和接触单元CONTA172模拟裂纹的上下表面不能彼此穿透现象。当取θ=0°时,模型演变为Chen问题。文中对计算的随时间变化的动态应力强度因子进行无量纲化处理:
| $ K_{{\mathrm{I}d}}^{n}=K_{{\mathrm{I}d}}(t) / K_{{\mathrm{I}s}}, K_{{\mathrm{II}d}}^{n}=K_{{\mathrm{II}d}}(t) / K_{I s} $ | (5) |
|
Download:
|
| 图 2 中心穿透斜裂纹板几何模型 Fig. 2 Geometric model of finite plate with a central through inclined crack | |
式中:
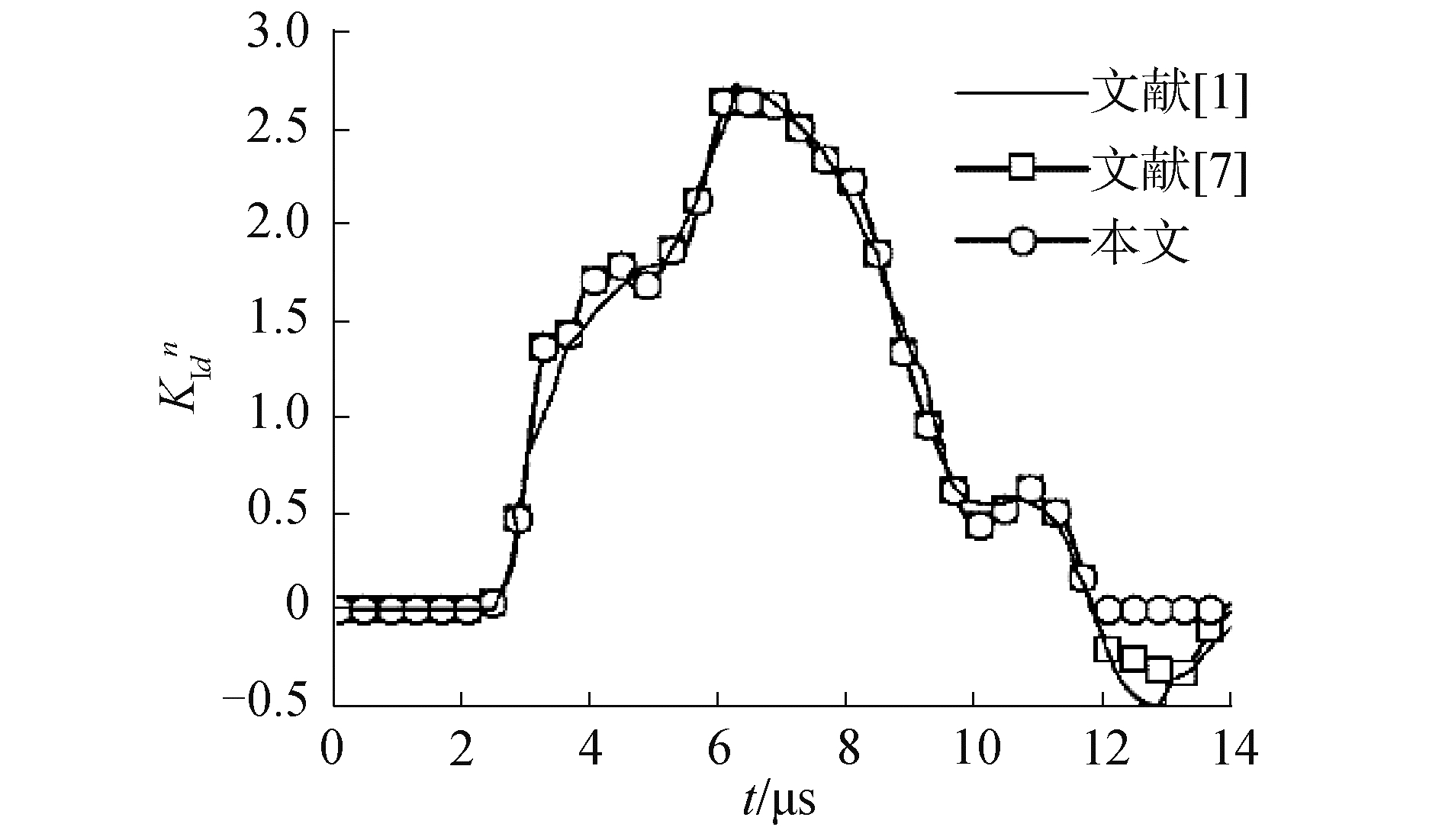
图 3给出了本文考虑裂纹面接触作用时的计算结果与Chen等结果的对比。从图中可见,在0~12 μs,裂纹面没有发生接触,本文的计算结果与Chen等结果比较吻合。在12~14 μs,由于Chen等没有考虑裂纹面的接触作用,出现了负的Ⅰ型DSIFs,而本文考虑裂纹面接触作用后,Ⅰ型DSIFs接近于0,这说明裂纹面接触作用避免了裂纹面发生相互穿透或重叠,是符合实际情况的。
|
Download:
|
| 图 3 本文计算结果与Chen等结果的对比 Fig. 3 Comparison between the present result and the reference solutions by Chen | |
如无特殊说明,以下仅对裂纹夹角θ=45°时的情况进行分析。接触刚度kn和摩擦系数μ分别取1.0和0.1,时间增量Δt取0.1 μs。
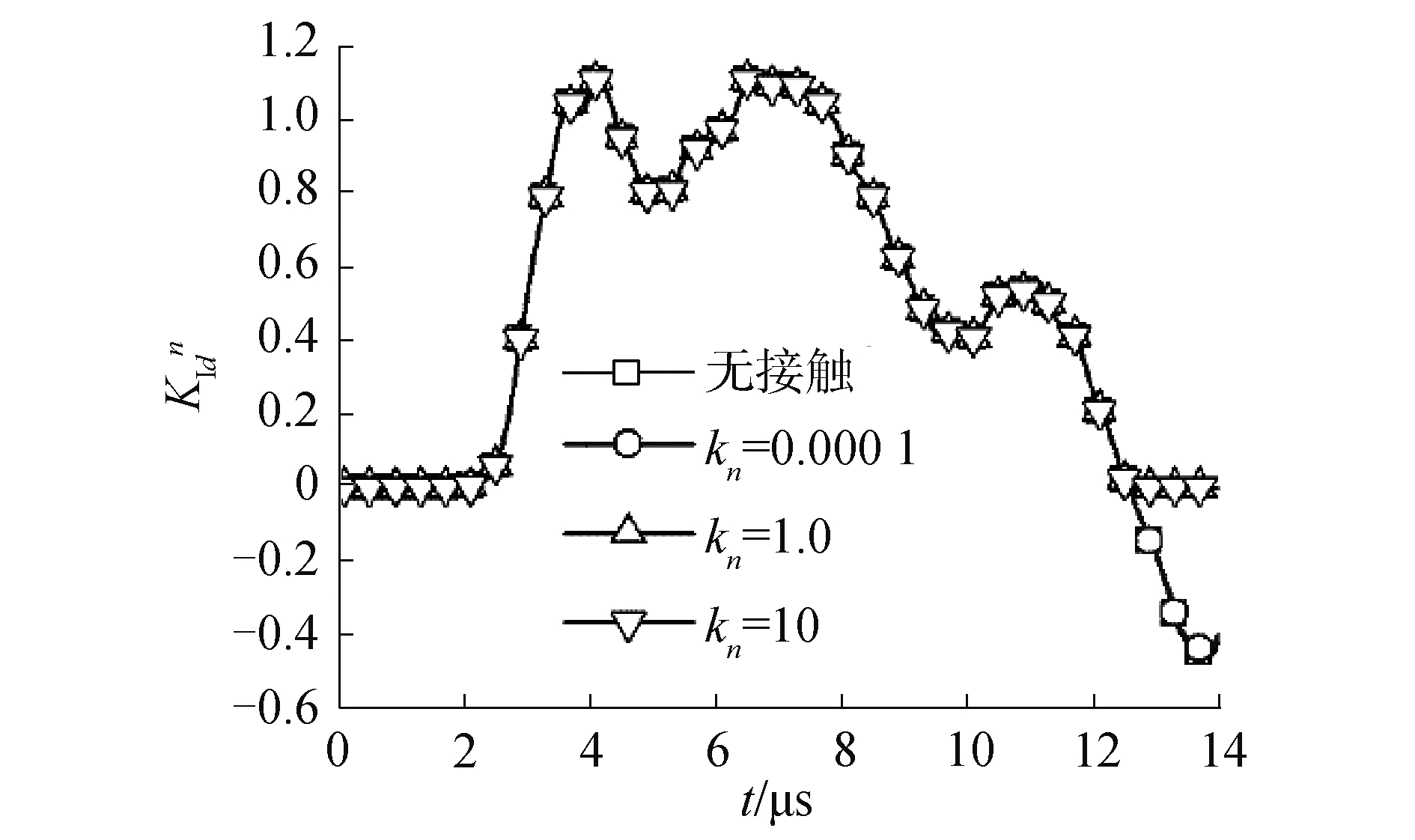
3.1 接触刚度kn对DSIFs的影响接触问题属于不定边界问题,即使是简单的弹性接触问题也具有非线性。过低的接触刚度将导致穿透问题,而过高的接触刚度又会导致收敛困难。因此选择合适的接触刚度对计算结果的稳定性非常重要。图 4给出了裂纹面没有接触单元,接触刚度系数分别取kn=0.000 1,1.0,10时裂尖的Ⅰ型DSIFs。从图中可以看出,当kn=0.000 1时,计算结果与无接触单元时的结果十分吻合,说明在接触刚度很小时,考虑裂纹面接触的情况退化为无接触状态。当kn=1.0时,负的Ⅰ型DSIFs接近于0,其余几乎不变,可见接触单元只有在裂纹面接触时起作用,在裂纹面张开时自然退化为无接触状态,而随着裂纹面接触刚度的增加,裂纹面相互穿透量逐渐减小直至消失。当kn=10时,计算结果与kn=1.0时基本重合,说明本模型选取kn=1.0已能满足计算要求。
|
Download:
|
| 图 4 不同接触刚度下的无量纲KⅠ(t)曲线 Fig. 4 Normalized KⅠ(t) for different contact stiffness | |
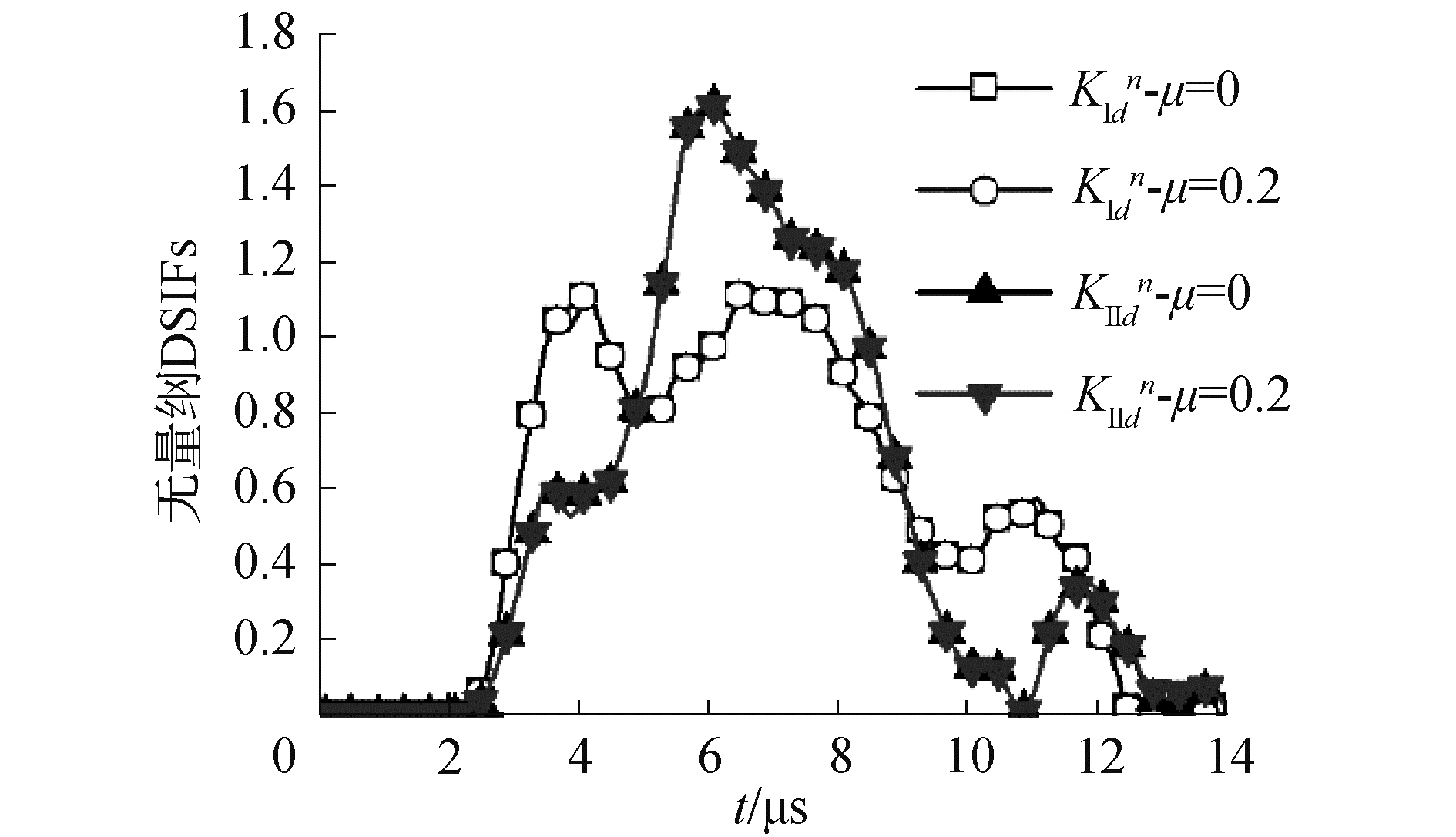
裂纹接触面的摩擦采用库仑摩擦模型,图 5给出了摩擦系数μ=0,0.2时裂尖的Ⅰ型、Ⅱ型DSIFs。从图 5可以看出,裂纹面摩擦系数对Ⅰ型DSIFs几乎没有影响;在0~12.5 μs,由于裂纹处于张开状态,所以裂纹面摩擦系数对Ⅱ型DSIFs也不产生影响。在12.5 μs之后,裂纹面发生闭合接触,裂纹面的接触作用避免了裂纹面发生相互穿透或重叠,消除了负Ⅰ型DSIFs,此时裂纹面的摩擦将对Ⅱ型DSIFs产生影响。
|
Download:
|
| 图 5 不同摩擦系数下的无量纲KⅠ(t)、KⅡ(t)曲线 Fig. 5 Normalized KⅠ(t) and KⅡ(t) for different friction coefficients | |
为了进一步研究裂纹体的动态特征,将载荷形式由阶跃载荷改为三角形载荷,但总冲量保持不变,如图 6所示。图 7给出了不同载荷形式下裂尖的Ⅰ型、Ⅱ型DSIFs,从图 7可以看出,即使载荷的总冲量保持不变,改变载荷形式仍会对DSIFs产生显著影响。三角形载荷下裂纹面发生闭合的时间比阶跃载荷早,当裂纹面发生闭合时,三角形载荷下Ⅱ型DSIFs峰值接近于裂纹闭合前的峰值,远远大于阶跃载荷下的Ⅱ型DSIFs。图 8为不同载荷形式下加载不同时刻矩形板的von-Mises应力云图,从图 8也可以看出,在裂纹闭合以前2种载荷形式下的应力分布十分接近,当t=10 μs时,三角形载荷下裂纹已经基本闭合,而阶跃载荷下裂纹仍然张开,这与DSIFs曲线反应的规律完全一致。

|
Download:
|
| 图 6 三角形冲击载荷 Fig. 6 Triangular impact loading | |

|
Download:
|
| 图 7 不同载荷形式下的无量纲DSIFs曲线 Fig. 7 Normalized KⅠ(t) and KⅡ(t) for different load styles | |

|
Download:
|
| 图 8 不同载荷形式下不同时刻板的von-Mises应力云图 Fig. 8 Von-Mises stress distributions at different times for different load styles | |
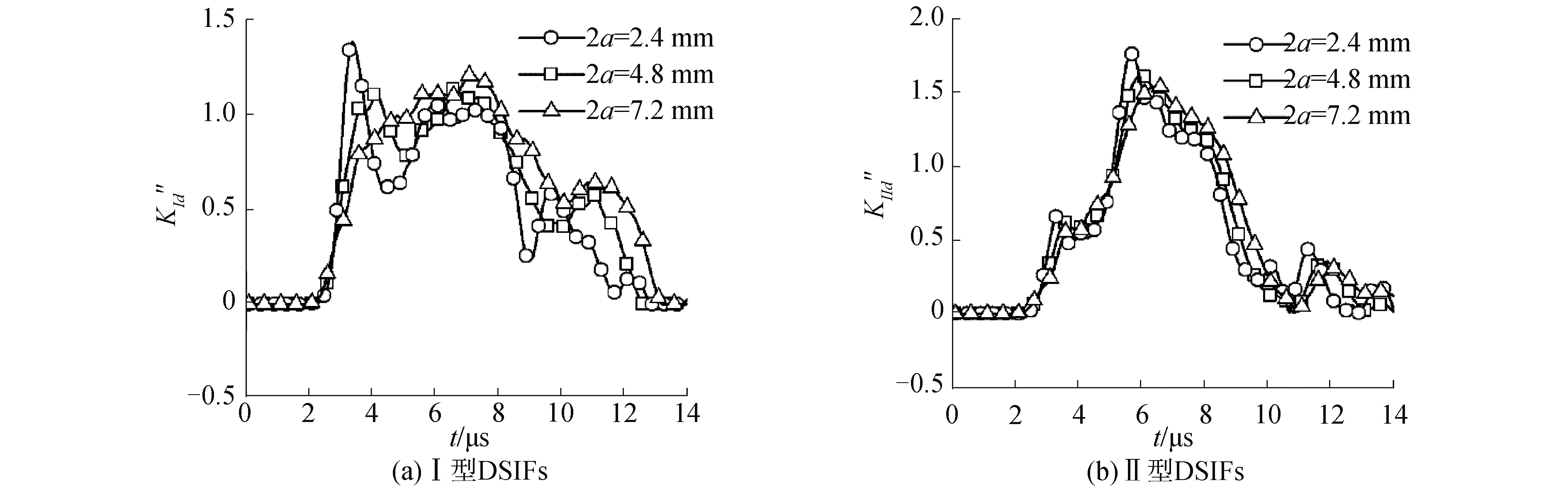
分别取裂纹长度2a为2.4,4.8,7.2 mm,计算在各裂纹长度下裂尖的Ⅰ型、Ⅱ型DSIFs,如图 9所示。图 9可以看出,裂纹长度的变化对Ⅰ型DSIFs的影响更为明显,裂纹越短,裂纹尖端动态响应越剧烈,裂纹面发生闭合接触的时间也有所不同。随着裂纹长度的增加,Ⅱ型DSIFs的峰值逐渐减小,并且峰值发生的时间逐渐延后,但是随时间变化的总趋势基本一致。图 10给出了不同裂纹长度下不同时刻矩形板的von-Mises应力云图,从图 10也可以看出,裂纹长度对板的应力分布影响十分明显。
|
Download:
|
| 图 9 不同裂纹长度下的无量纲DSIFs曲线 Fig. 9 Normalized DSIFs for different crack length | |

|
Download:
|
| 图 10 不同裂纹长度下不同时刻板的von-Mises应力云图 Fig. 10 Von-Mises stress distributions at different times for different crack length | |
实际工程结构中,裂纹绝大部分为复合型裂纹,研究裂纹角度对动态应力强度因子的影响尤为重要。分别取裂纹角度θ为30°,45°,60°,计算在各裂纹角度下裂尖的Ⅰ型、Ⅱ型DSIFs,如图 11所示。从图 11可以看出,随着裂纹角度的增加,Ⅰ型DSIFs逐渐减小,由于裂纹尖端距离载荷作用的距离减短,峰值发生的时间逐渐提前,裂纹面发生闭合接触的时间却逐渐延后。当θ=45°时,Ⅱ型DSIFs达到最大,θ=30°,60°的Ⅱ型DSIFs相差不大,并且Ⅱ型DSIFs峰值发生的时间基本不随角度改变。图 12给出了不同裂纹角度下不同时刻板的von-Mises应力云图,从图 12中也可以看出,裂纹角度对板的应力分布影响明显,在裂纹闭合以前,相同时刻下裂纹角度越大,裂纹张开得越小。

|
Download:
|
| 图 11 不同裂纹角度下的无量纲DSIFs曲线 Fig. 11 Normalized DSIFs for different crack angles | |

|
Download:
|
| 图 12 不同裂纹角度下不同时刻板的von-Mises应力云图 Fig. 12 Von-Mises stress distributions at different times for different crack angles | |
为了研究裂纹位置对动态应力强度因子的影响情况,裂纹中心距纵边的横向距离保持不变,沿着纵向移动,分别取裂纹中心距底端2H/3、H、4H/3,计算在各裂纹位置下裂尖的Ⅰ型、Ⅱ型DSIFs,如图 13(a)~(b)所示;裂纹中心纵向距离保持不变,沿着横向移动,裂纹中心距左端分别为2W/3、W、4W/3时裂尖的Ⅰ型、Ⅱ型DSIFs如图 13(c)~(d)所示。从图 13中可以看出,改变裂纹的纵向位置,由于裂纹尖端距离载荷作用的距离减短,动态应力强度因子的起始时间逐渐提前,Ⅰ型DSIFs的第1次峰值明显增加,第2次峰值变化不大;Ⅱ型DSIFs的峰值逐渐减小,并且峰值发生的时间逐渐延后。改变裂纹的横向位置,DSIFs曲线变化不大,这主要是因为改变裂纹的横向位置,虽然裂纹尖端距离纵向边界更近,但与载荷作用的距离并没有发生变化。由此可见,裂纹位置对DSIFs的影响主要是由于有限平板模型的边界效应,而其中裂纹尖端与载荷作用的距离的影响最大。限于篇幅,仅给出了裂纹纵向位置变化时不同时刻矩形板的von-Mises应力云图,如图 14所示。从图中也可以看出,裂纹纵向位置对板的应力分布影响明显,由于对称性,2H/3和4H/3处的应力云图关于板的横向中心对称。

|
Download:
|
| 图 13 不同裂纹位置下的无量纲DSIFs曲线 Fig. 13 Normalized DSIFs for different crack locations | |

|
Download:
|
| 图 14 纵向位置变化时不同时刻板的von-Mises应力云图 Fig. 14 Von-Mises stress distributions at different times for different crack longitudinal location | |
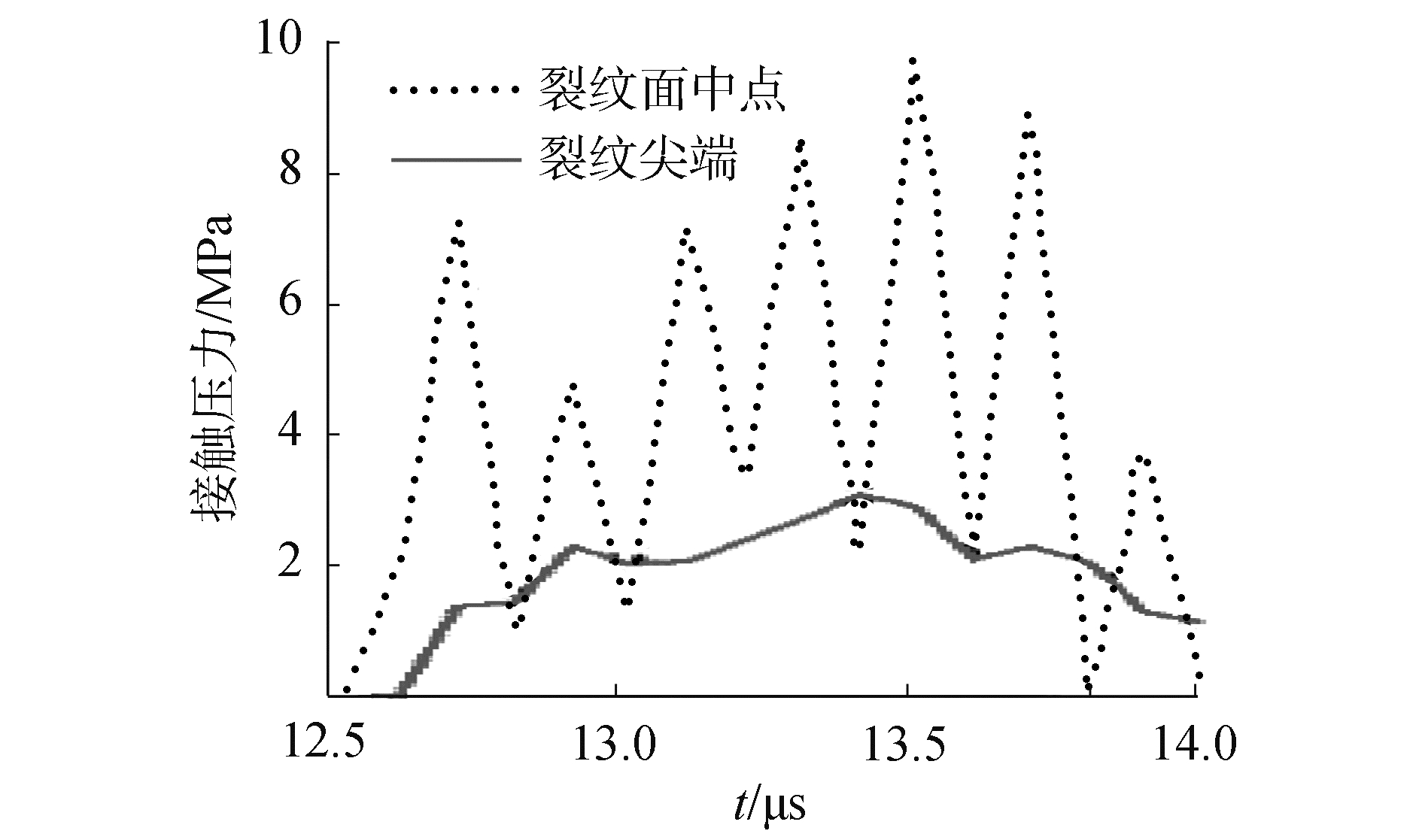
裂纹面中点和裂尖处的接触压力和接触摩擦力随时间的变化曲线如图 15、16所示。从图 15中可以看出,当本算例的裂纹面处于接触状态后,在所计算的时间内始终处于接触状态,而且裂纹面中点和裂尖处的接触压力随时间的变化规律相似,都是在接触后迅速达到最大值,但压力幅值和作用的起止时间有着明显的差异。
|
Download:
|
| 图 15 裂纹面上随时间变化的接触压力 Fig. 15 Dynamic response curves of contact pressure on the crack faces | |

|
Download:
|
| 图 16 裂纹面上随时间变化的接触摩擦力 Fig. 16 Dynamic response curves of contact friction stress on the crack faces | |
图 16给出了裂纹面中点和裂尖处的接触摩擦力随时间的变化曲线。从图 16中可以看出,当接触压力达到最大时,相应的接触摩擦力也达到最大,其中接触摩擦力方向的改变是由于裂纹面切向相对位移的方向发生了变化,这是符合实际情况的,进一步验证了本文考虑接触作用的正确性。
5 结论1) 考虑裂纹面的接触作用,可以避免裂纹面发生相互穿透或重叠,从而消除了负Ⅰ型动态应力强度因子。
2) 选择合适的接触刚度对计算的收敛性和准确性十分重要,而摩擦系数对动态应力强度因子的影响在本算例中并不十分明显。载荷形式在总冲量不变的情况下对动态应力强度因子的影响也非常大,而裂纹长度等裂纹参数对Ⅰ型动态应力强度因子的影响比Ⅱ型显著。
3) 当裂纹面发生闭合接触时,接触压力迅速达到最大,相应的接触摩擦力也达到最大,这是符合实际情况的。
| [1] |
CHEN Y M. Numerical computation of dynamic stress intensity factors by a Lagrangian finite-difference method (the HEMP code)[J]. Engineering fracture mechanics, 1975, 7(4): 653-660. DOI:10.1016/0013-7944(75)90021-1 (  0) 0)
|
| [2] |
LIN X, BALLMANN J. Re-consideration of Chen's problem by finite difference method[J]. Engineering fracture mechanics, 1993, 44(5): 735-739. DOI:10.1016/0013-7944(93)90202-4 (  0) 0)
|
| [3] |
SONG S H, PAULINO G H. Dynamic stress intensity factors for homogeneous and smoothly heterogeneous materials using the interaction integral method[J]. International journal of solids and structures, 2006, 43(16): 4830-4866. DOI:10.1016/j.ijsolstr.2005.06.102 (  0) 0)
|
| [4] |
SARIBAY M, NIED H F. Dynamic stress intensity factors for suddenly loaded structures using enriched finite element[J]. Theoretical and applied fracture mechanics, 2014, 70: 59-67. DOI:10.1016/j.tafmec.2014.02.003 (  0) 0)
|
| [5] |
IDESMAN A, BHUIYAN A, FOLEY J R. Accurate finite element simulation of stresses for stationary dynamic cracks under impact loading[J]. Finite elements in analysis and design, 2017, 126: 26-38. DOI:10.1016/j.finel.2016.12.004 (  0) 0)
|
| [6] |
解德, 钱勤, 李长安. 断裂力学中的数值计算方法及工程应用[M]. 北京: 科学出版社, 2009: 134-139.
(  0) 0)
|
| [7] |
姜伟, 杨平, 董琴. 平板穿透裂纹尖端动态应力强度因子研究[J]. 武汉理工大学学报(交通科学与工程版), 2016, 40(5): 820-825. JIANG Wei, YANG Ping, DONG Qin. Research on dynamic stress intensity factors for through-cracked plates[J]. Journal of Wuhan University of Technology (transportation science & engineering), 2016, 40(5): 820-825. DOI:10.3963/j.issn.2095-3844.2016.05.012 (  0) 0)
|
| [8] |
王立清, 盖秉政. 有限板中圆孔边单边斜裂纹动态应力强度因子的数值计算[J]. 工程力学, 2009, 26(3): 9-14. WANG Liqing, GAI Bingzheng. Numerical calculation of dynamic stress intensity factors for a single hole-edge slant crack in a finite plate[J]. Engineering mechanics, 2009, 26(3): 9-14. (  0) 0)
|
| [9] |
王立清, 盖秉政. 裂纹面接触摩擦对双-边裂纹板动态应力强度因子的影响[J]. 工程力学, 2009, 26(7): 7-11. WANG Liqing, GAI Bingzheng. Effect of crack face contact and friction on dynamic stress intensity factors for a double-edge cracked plate[J]. Engineering mechanics, 2009, 26(7): 7-11. (  0) 0)
|
| [10] |
MOËS N, DOLBOW J, BELYTSCHKO T. A finite element method for crack growth without remeshing[J]. International journal for numerical methods in engineering, 1999, 46(1): 131-150. DOI:10.1002/(ISSN)1097-0207 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


