由于从自然界中取用的工程材料以各种各样的形式存在,不可避免地存在各种复合缺陷。在动态荷载作用下,缺陷会对实际工程产生很大影响,因此,研究SH波的散射对隧道及地铁工程等具有重要的意义。Wong等[1]和Trifunac[2]运用Mathieu函数分别分析了半椭圆形峡谷对SH波散射问题。Eshelby[3]研究了椭球体中的夹杂在弹性场中的静力问题。汪越胜等[4]结合错位密度函数分析了衬砌与孔洞脱胶对SH波散射的解析解。刘殿魁等[5-6]将复变函数法结合多级坐标变换原理,求解了半空间中的孔洞以及夹杂对SH波散射动应力集中数值解。杨在林等[7-8]研究了椭圆夹杂及直线裂纹同时存在时,SH波散射产生的动应力集中系数、位移幅值等情况。齐辉等[9-10]研究了直角域中圆形夹杂、椭圆形夹杂等复合缺陷对SH波的散射问题。
关于SH波的散射问题已经积累了丰富的理论成果[11-15],但是含有部分脱胶的任意形状的弹性夹杂与另一弹性夹杂同时存在问题很少分析。本文采用复变函数的方法,结合保角映射的原理、Green函数法,研究了含有部分脱胶的椭圆夹杂与圆夹杂对SH波的散射问题,通过具体的数值计算,讨论了椭圆夹杂周围动应力集中系数的变化情况。
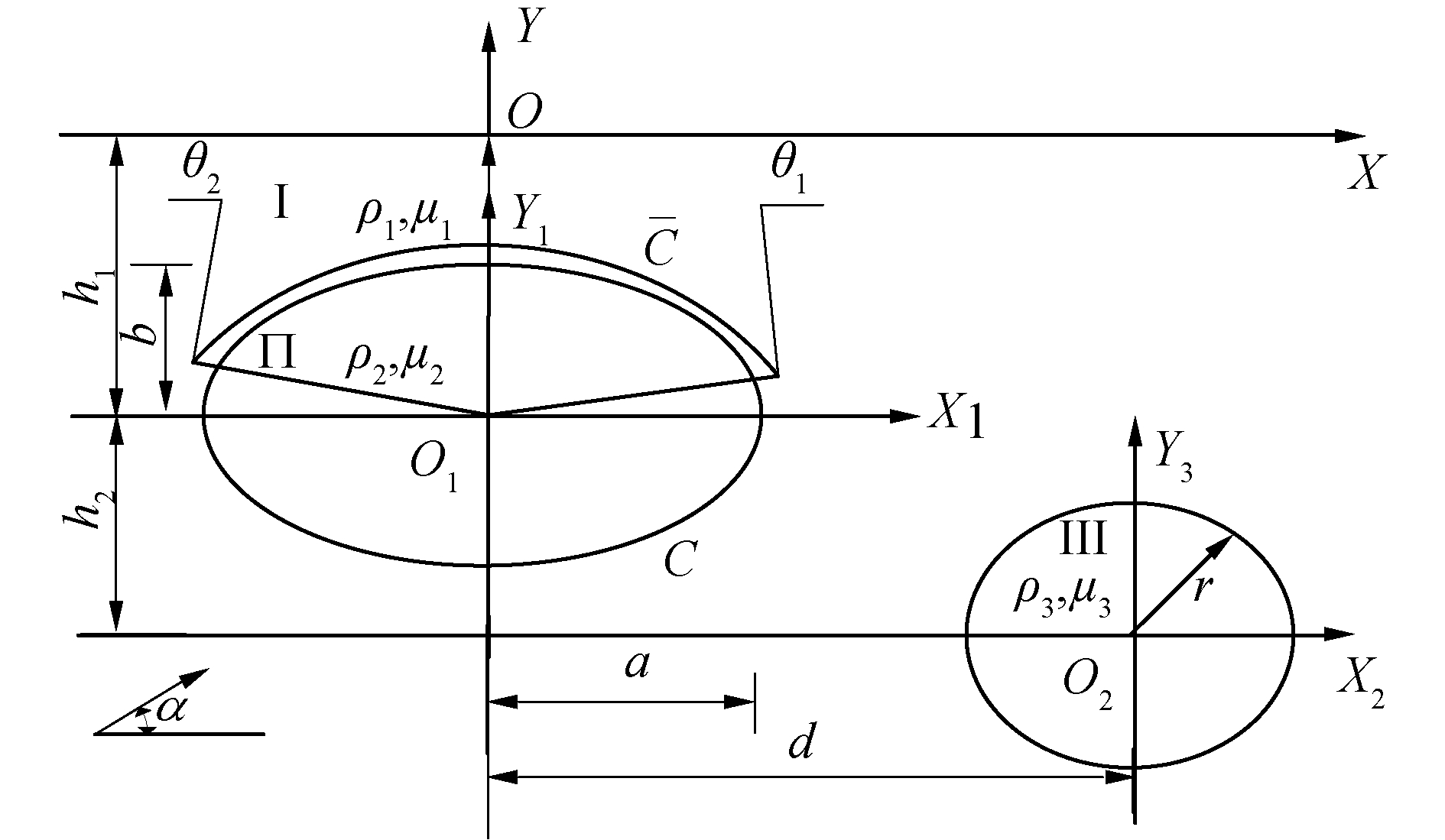
1 理论模型图 1为弹性含有部分脱胶的椭圆夹杂及圆形夹杂对SH波散射的理论模型,SH波的入射角度为α0,建立一个半空间整体坐标系XOY,在椭圆形、圆形弹性夹杂的中心分别建立局部坐标系X1O1Y1、X2O2Y2,区域Ⅰ、Ⅱ、Ⅲ介质密度和弹性模量分别为ρ1和μ1、ρ2和μ2、ρ3和μ3。脱胶部分起点、终点角度分别为θ1和θ2。图 1中坐标关系为:
|
Download:
|
| 图 1 半空间含有部分脱胶的椭圆夹杂及圆形夹杂的模型 Fig. 1 The model of elliptical inclusion with a partially debond curve and circular cavity in half space | |
| $ \left\{ \begin{array}{l} {x_1} = x,{y_1} = y + {h_1}\\ {x_2} = x - d,{y_2} = y + {h_1} + {h_2} \end{array} \right. $ | (1) |
位移函数G与时间因子的依赖关系为e-iwt,满足Helmholtz控制方程[11]:
| $ \frac{{{\partial ^2}G}}{{\partial {x^2}}} + \frac{{{\partial ^2}G}}{{\partial {y^2}}} + {k^2}G = 0 $ | (2) |
根据保角变换原理,应力表达式则可以表示为:
| $ {\tau _{rz}} = \frac{\mu }{{R\left| {\omega '\left( \eta \right)} \right|}}\left( {\eta \frac{{\partial G}}{{\partial \eta }} + \bar \eta \frac{{\partial G}}{{\partial \bar \eta }}} \right) $ | (3) |
| $ {\tau _{\theta z}} = \frac{{{\rm{i}}\mu }}{{R\left| {\omega '\left( \eta \right)} \right|}}\left( {\eta \frac{{\partial G}}{{\partial \eta }} - \bar \eta \frac{{\partial G}}{{\partial \bar \eta }}} \right) $ | (4) |
根据参考文献[11-12],通过SH波散射的对称特性以及“镜像法”,构造出散射波场。
在复平面(
| $ W_{\rm{I}}^{\left( s \right)}\left( {z,\bar z} \right) = W_{{\rm{I}}C}^{\left( s \right)} + W_{{\rm{I}}T}^{\left( s \right)} $ |
由椭圆夹杂产生的散射波WΙC(s):
| $ \begin{array}{*{20}{c}} {W_{{\rm{IC}}}^{(s)} = \sum\limits_{n = - \infty }^{ + \infty } {{A_n}} \left\{ {H_n^{(1)}\left[ {{k_1}\left| {{z_1}} \right|} \right]{{\left[ {\frac{{{z_1}}}{{\left| {{z_1}} \right|}}} \right]}^n} + } \right.}\\ {H_n^{(1)}\left[ {{k_1}\left| {{z_1} - 2i{h_1}} \right|} \right]{{\left[ {\frac{{{z_1} - 2i{h_1}}}{{\left| {{z_1} - 2i{h_1}} \right|}}} \right]}^{ - n}}\} } \end{array} $ | (5) |
由圆形夹杂所产生的散射波WΙT(s):
| $ W_{{\rm{I}}T}^{(s)} = \sum\limits_{n = - \infty }^{ + \infty } {{B_n}} \left\{ {{s_1} + {s_2}} \right\} $ | (6) |
式中:
| $ s_{2}=H_{n}^{(1)}\left[k_{1}\left|m_{1}-2 i h_{1}-i h_{2}\right|\right]\left[\frac{m_{1}-2 i h_{1}-i h_{2}}{\left|m_{1}-2 i h_{1}-i h_{2}\right|}\right]^{-n} $ |
An、Bn是待定系数,椭圆夹杂产生的散射波式(5)代入式(3)、(4)可得椭圆夹杂的应力表达式:
| $ \tau _{rz,{\rm{I}}C}^{\left( s \right)} = \frac{{{\mu _1}{k_1}}}{2}\sum\limits_{n = - \infty }^{ + \infty } {{A_n}\left[ {{\phi _1} - {\phi _2}} \right]} $ | (7) |
| $ \tau _{\theta z,{\rm{I}}C}^{\left( s \right)} = \frac{{i{\mu _1}{k_1}}}{2}\sum\limits_{n = - \infty }^{ + \infty } {{A_n}\left[ {{\phi _1} + {\phi _2}} \right]} $ | (8) |
| $ \begin{array}{*{20}{c}} {{\phi _1} = \left[ {H_{n - 1}^{\left( 1 \right)}\left[ {{k_1}\left| {{z_1}} \right|} \right]{{\left[ {\frac{{{z_1}}}{{\left| {{z_1}} \right|}}} \right]}^{n - 1}} - } \right.}\\ {\left. {H_{n + 1}^{\left( 1 \right)}\left[ {{k_1}\left| {{z_1} - 2i{h_1}} \right|} \right]{{\left[ {\frac{{{z_1} - 2i{h_1}}}{{\left| {{z_1}} \right| - 2i{h_1}}}} \right]}^{ - \left( {n + 1} \right)}}} \right]\frac{{\eta {{z_1}'}}}{{R\left| {{z_1}'} \right|}}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{\phi _2} = \left[ {H_{n + 1}^{\left( 1 \right)}\left[ {{k_1}\left| {{z_1}} \right|} \right]{{\left[ {\frac{{{z_1}}}{{\left| {{z_1}} \right|}}} \right]}^{n + 1}} - } \right.}\\ {\left. {H_{n - 1}^{\left( 1 \right)}\left[ {{k_1}\left| {{z_1} - 2i{h_1}} \right|} \right]{{\left[ {\frac{{{z_1} - 2i{h_1}}}{{\left| {{z_1}} \right| - 2i{h_1}}}} \right]}^{ - \left( {n - 1} \right)}}} \right]\frac{{\bar \eta \overline {{z_1}^\prime }}}{{R\left| {{z_1}'} \right|}}} \end{array} $ |
将式(6)代入式(3)、(4)得到圆夹杂的应力:
| $ \tau _{rz,{\rm{I}}T}^{\left( s \right)} = \frac{{{\mu _1}{k_1}}}{2}\sum\limits_{n = - \infty }^{ + \infty } {{B_n}\left[ {{\phi _3} - {\phi _4}} \right]\frac{{\eta {{z_1}'}}}{{R\left| {{z_1}'} \right|}}} $ | (9) |
| $ \tau _{\theta z,{\rm{I}}T}^{\left( s \right)} = \frac{{i{\mu _1}{k_1}}}{2}\sum\limits_{n = - \infty }^{ + \infty } {{B_n}\left[ {{\phi _3} + {\phi _4}} \right]\frac{{\bar \eta \overline {{z_1}^\prime }}}{{R\left| {{z_1}'} \right|}}} $ | (10) |
式中:
| $ \begin{array}{*{20}{c}} {{\phi _3} = \left[ {H_{n - 1}^{\left( 1 \right)}\left[ {{k_1}\left| {{m_1}} \right|} \right]{{\left[ {\frac{{{m_1} + i{h_2}}}{{\left| {{m_1} + i{h_2}} \right|}}} \right]}^{n - 1}} - } \right.}\\ {\left. {H_{n + 1}^{\left( 1 \right)}\left[ {{k_1}\left| {{m_1} - 2i{h_1} - i{h_2}} \right|} \right]{{\left[ {\frac{{{m_1} - 2i{h_1} - i{h_2}}}{{\left| {{m_1} - 2i{h_1} - i{h_2}} \right|}}} \right]}^{ - \left( {n + 1} \right)}}} \right]} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{\phi _4} = \left[ {H_{n + 1}^{\left( 1 \right)}\left[ {{k_1}\left| {{m_1}} \right|} \right]{{\left[ {\frac{{{m_1} - i{h_2}}}{{\left| {{m_1} - i{h_2}} \right|}}} \right]}^{n + 1}} - } \right.}\\ {\left. {H_{n - 1}^{\left( 1 \right)}\left[ {{k_1}\left| {{m_1} - 2i{h_1} - i{h_2}} \right|} \right]{{\left[ {\frac{{{m_1} - 2i{h_1} - i{h_2}}}{{\left| {{m_1} - 2i{h_1} - i{h_2}} \right|}}} \right]}^{ - \left( {n - 1} \right)}}} \right]} \end{array} $ |
式中m1=z1-d, z1=ω(η)。
在复平面(
| $ \begin{array}{*{20}{c}} {W_{\Pi C}^{\left( s \right)} = \sum\limits_{n = - \infty }^{ + \infty } {{A_n}\left\{ {H_n^{\left( 1 \right)}\left[ {{k_1}\left| {{m_2} - i{h_2}} \right|} \right]{{\left[ {\frac{{{m_2} - i{h_2}}}{{\left| {{m_2} - i{h_2}} \right|}}} \right]}^n} + } \right.} }\\ {\left. {H_n^{\left( 1 \right)}\left[ {{k_1}\left| {{m_2} - 2i{h_2} - i{h_2}} \right|} \right]{{\left[ {\frac{{{m_2} - 2i{h_1} - i{h_2}}}{{\left| {{m_2} - 2i{h_1} - i{h_2}} \right|}}} \right]}^{ - n}}} \right\}} \end{array} $ | (11) |
圆形夹杂产生的散射波可以表示为:
| $ \begin{array}{*{20}{c}} {W_{\Pi T}^{\left( s \right)} = \sum\limits_{n = - \infty }^{ + \infty } {{B_n}\left\{ {H_n^{\left( 1 \right)}\left[ {{k_1}\left| {{z_2}} \right|} \right]{{\left[ {\frac{{{z_2}}}{{\left| {{z_2}} \right|}}} \right]}^n} + } \right.} }\\ {\left. {H_n^{\left( 1 \right)}\left[ {{k_1}\left| {{z_2} - 2i\left( {{h_1} + {h_2}} \right)} \right|} \right]{{\left[ {\frac{{{z_2} - 2i\left( {{h_1} + {h_2}} \right)}}{{\left| {{z_2} - 2i\left( {{h_1} + {h_2}} \right)} \right|}}} \right]}^{ - n}}} \right\}} \end{array} $ | (12) |
将式(11)分别代入式(3)、(4),得到椭圆夹杂产生的散射波应力表示为:
| $ \tau _{rz,\prod C }^{\left( s \right)} = \frac{{{k_1}{\mu _1}}}{2}\sum\limits_{n = - \infty }^\infty {{A_n}\left[ {{\varphi _1}{{\rm{e}}^{{\rm{i}}{\theta _1}}} - {\varphi _2}{{\rm{e}}^{{\rm{i}}{\theta _1}}}} \right]} $ | (13) |
| $ \tau _{\theta z,\prod C }^{\left( s \right)} = \frac{{i{k_1}{\mu _1}}}{2}\sum\limits_{n = - \infty }^\infty {{A_n}\left[ {{\varphi _1}{{\rm{e}}^{{\rm{i}}{\theta _1}}} + {\varphi _2}{{\rm{e}}^{ - {\rm{i}}{\theta _1}}}} \right]} $ | (14) |
式中:
| $ \begin{array}{*{20}{c}} {{\varphi _1} = H_{n - 1}^{\left( 1 \right)}\left( {{k_1}\left| {{m_2} - i{h_2}} \right|} \right){{\left[ {\frac{{{m_2} - i{h_2}}}{{\left| {{m_2} - i{h_2}} \right|}}} \right]}^{n - 1}} - }\\ {H_{n + 1}^{\left( 1 \right)}\left( {{k_1}\left| {{m_2} - 2i{h_1} - i{h_2}} \right|} \right){{\left[ {\frac{{{m_2} - 2i{h_1} - i{h_2}}}{{\left| {{m_2} - 2i{h_1} - i{h_2}} \right|}}} \right]}^{ - \left( {n + 1} \right)}}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{\varphi _2} = H_{n + 1}^{\left( 1 \right)}\left( {{k_1}\left| {{m_2} - i{h_2}} \right|} \right){{\left[ {\frac{{{m_2} - i{h_2}}}{{\left| {{m_2} - i{h_2}} \right|}}} \right]}^{n + 1}} - }\\ {H_{n - 1}^{\left( 1 \right)}\left( {{k_1}\left| {{m_2} - 2i{h_1} - i{h_2}} \right|} \right){{\left[ {\frac{{{m_2} - 2i{h_1} - i{h_2}}}{{\left| {{m_2} - 2i{h_1} - i{h_2}} \right|}}} \right]}^{ - \left( {n - 1} \right)}}} \end{array} $ |
将圆形夹杂产生的散射波位移式(12)分别代入式(3)、(4),得到圆形夹杂产生的散射波应力表示:
| $ \tau _{rz,\prod T }^{(s)} = \frac{{{k_1}{\mu _1}}}{2}\sum\limits_{n = - \infty }^\infty {{B_n}} \left[ {{\varphi _3}{{\rm{e}}^{{\rm{i}}{\theta _1}}} - {\varphi _4}{{\rm{e}}^{ - {\rm{i}}{\theta _1}}}} \right] $ | (15) |
| $ \tau _{\theta z,\prod T }^{(s)} = \frac{{i{k_1}{\mu _1}}}{2}\sum\limits_{n = - \infty }^\infty {{B_n}} \left[ {{\varphi _3}{{\rm{e}}^{{\rm{i}}{\theta _1}}} + {\varphi _4}{{\rm{e}}^{ - {\rm{i}}{\theta _1}}}} \right] $ | (16) |
式中:
| $ \begin{array}{*{20}{c}} {{\varphi _3} = H_{n - 1}^{(1)}\left( {{k_1}\left| {{z_2}} \right|} \right){{\left[ {\frac{{{z_2}}}{{\left| {{z_2}} \right|}}} \right]}^{n - 1}} - }\\ {H_{n + 1}^{(1)}\left( {{k_1}\left| {{z_2} - 2i\left( {{h_1} + {h_2}} \right)} \right|} \right){{\left[ {\frac{{{z_2} - 2i\left( {{h_1} + {h_2}} \right)}}{{\left| {{z_2} - 2i\left( {{h_1} + {h_2}} \right)} \right|}}} \right]}^{ - (n + 1)}}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{\varphi _4} = H_{n + 1}^{(1)}\left( {{k_1}\left| {{z_2}} \right|} \right){{\left[ {\frac{{{z_2}}}{{\left| {{z_2}} \right|}}} \right]}^{n + 1}} - }\\ {H_{n - 1}^{(1)}\left( {{k_1}\left| {{z_2} - 2i\left( {{h_1} + {h_2}} \right)} \right|} \right){{\left[ {\frac{{{z_2} - 2i\left( {{h_1} + {h_2}} \right)}}{{\left| {{z_2} - 2i\left( {{h_1} + {h_2}} \right)} \right|}}} \right]}^{ - (n - 1)}}} \end{array} $ |
在椭圆形弹性夹杂内,构造一驻波WΠ(st),使其在没有发生脱胶时满足应力连续的边界条件,同时,对应的驻波表示为:
| $ W_\Pi ^{\left( {st} \right)} = \sum\limits_{n = - \infty }^{ + \infty } {{C_n}\left\{ {{J_n}\left( {{k_2}\left| {{z_1}} \right|} \right){{\left[ {\frac{{{z_1}}}{{\left| {{z_1}} \right|}}} \right]}^n}} \right\}} $ | (17) |
驻波的位移式(17)分别代入式(3)、(4),应力表示为:
| $ \tau_{r z}^{(s t)}=\frac{\mu_{2} k_{2}}{2} \sum\limits_{n=-\infty}^{+\infty} C_{n}\left(\psi_{1}-\psi_{2}\right) $ | (18) |
| $ \tau_{\theta z}^{(s t)}=\frac{i \mu_{2} k_{2}}{2} \sum\limits_{n=-\infty}^{+\infty} C_{n}\left(\psi_{1}+\psi_{2}\right) $ | (19) |
式中:
| $ \psi_{1}=J_{n-1}\left[k_{2}\left|z_{1}\right|\right]\left[\frac{z_{1}}{\left|z_{1}\right|}\right]^{n-1} \frac{\eta {z_1}^{\prime}}{R\left|{z_1}^{\prime}\right|} $ |
| $ \psi_{2}=J_{n+1}\left[k_{2}\left|z_{1}\right|\right]\left[\frac{z_{1}}{\left|z_{1}\right|}\right]^{n+1} \frac{\overline{\eta} \overline{{z_1}^{\prime}}}{R\left|{{z^\prime}_1}\right|} $ |
式中Cn为待求的未知系数。
在圆形夹杂内构造一驻波WΟ(sto),根据圆形夹杂周边位移连续、应力连续的边界条件,其位移表达式为:
| $ W_{\mathrm{O}}^{(\mathrm{sto})}=\sum\limits_{n=-\infty}^{+\infty} D_{n}\left\{J_{n}\left(k_{3}\left|z_{2}\right|\right)\left[\frac{z_{2}}{\left|z_{2}\right|}\right]^{n}\right\} $ | (20) |
将位移式(20)代入应力表达式(3)、(4),得应力式为:
| $ \tau_{r z}^{(\mathrm{sto})}=\frac{\mu_{3} k_{3}}{2} \sum\limits_{n=-\infty}^{+\infty} D_{n}\left[\psi_{1} \mathrm{e}^{i \theta}-\psi_{2} \mathrm{e}^{-i \theta}\right] $ | (21) |
| $ \tau_{\theta z}^{(\mathrm{sto})}=\frac{i \mu_{3} k_{3}}{2} \sum\limits_{n==-\infty}^{+\infty} D_{n}\left[\psi_{1} \mathrm{e}^{i \theta}+\psi_{2} \mathrm{e}^{-i \theta}\right] $ | (22) |
式中:
| $ \psi_{1}=J_{n-1}\left[k_{3}\left|z_{2}\right|\right]\left[\frac{z_{2}}{\left|z_{2}\right|}\right]^{n-1} $ |
| $ \psi_{2}=J_{n+1}\left[k_{3}\left|z_{2}\right|\right]\left[\frac{z_{2}}{\left|z_{2}\right|}\right]^{n+1} $ |
式中Dn为待求的未知系数。
4 Green函数的构造如图 2,出平面线源荷载作用在脱胶部分的任意一点,利用GΙ来表示在复平面(

|
Download:
|
| 图 2 SH波垂直入射时τθz*随着k1a的分布 Fig. 2 Distribution of τθz* with k1a by SH-wave vertically | |
| $ \left\{\begin{array}{ll}{G_{1}=G_{\Pi}^{\mathrm{st}},} & {\tau_{r z, \mathrm{I}}=\tau_{r z, \Pi}^{\mathrm{st}}} \\ {G_{\Pi}=G_{\Pi}^{\mathrm{sto}},} & {\tau_{r z, \Pi}=\tau_{r z, \Pi}^{\mathrm{sto}}}\end{array}\right. $ | (23) |
在一个完整的弹性全空间内,根据文献[7], 在出平面线源荷载δ(z-z0)扰动下,在复平面(
| $ G_{\mathrm{I}}^{(i)}=\frac{i}{4 \mu_{1}} H_{0}^{(1)}\left(k_{1}\left|z_{1}-z_{0}\right|\right) $ | (24) |
稳态的SH波GΙ(i)入射,从而在水平界面激发出反射波GΙ(r)表示为:
| $ G_{\mathrm{I}}^{(r)}=\frac{i}{4 \mu_{1}} H_{0}^{(1)}\left(k_{1}\left|z_{1}-\overline{z_{0}}-2 i h_{1}\right|\right) $ | (25) |
式(24)、(25)分别代入式(3)、(4)式得应力表达式:
| $ \tau_{r z, \mathrm{I}}^{(i)}=-\left(i k_{1} / 8\right)\left(s_{1}+s_{2}\right) $ | (26) |
| $ \tau_{\theta z, \mathrm{I}}^{(i)}=\left(k_{1} / 8\right)\left(s_{1}-s_{2}\right) $ | (27) |
| $ \tau_{r z, \mathrm{I}}^{(r)}=-\left(i k_{1} / 8\right)\left(s_{3}+s_{4}\right) $ | (28) |
| $ \tau_{\theta z, \mathrm{I}}^{(r)}=\left(k_{1} / 8\right)\left(s_{3}-s_{4}\right) $ | (29) |
式中:
| $ s_{1}=H_{1}^{(1)}\left(k_{1}\left|z_{1}-z_{0}\right|\right) \frac{\overline{z_{1}}-\overline{z_{0}}}{\left|z_{1}-z_{0}\right|} \frac{\eta z_{1}^{\prime}}{R\left|z_{1}^{\prime}\right|} $ |
| $ s_{2}=H_{1}^{(1)}\left(k_{1}\left|z_{1}-z_{0}\right|\right) \frac{z_{1}-z_{0}}{\left|z_{1}-z_{0}\right|} \frac{\overline{\eta} \overline{z_{1}^{\prime}}}{R\left|z_{1}^{\prime}\right|} $ |
| $ s_{3}=H_{1}^{(1)}\left(k_{1}\left|z_{1}-\overline{z_{0}}-2 i h_{1}\right|\right) \frac{\overline{z_{1}}-z_{0}+2 i h_{1}}{\left|z_{1}-\overline{z_{0}}-2 i h_{1}\right|} \frac{\eta z_{1}^{\prime}}{R\left|z_{1}^{\prime}\right|} $ |
| $ s_{4}=H_{1}^{(1)}\left(k_{1}\left|z_{1}-\overline{z_{0}}-2 i h_{1}\right|\right) \frac{z_{1}-\overline{z_{0}}-2 i h_{1}}{\left|z_{1}-\overline{z_{0}}-2 i h_{1}\right|} \frac{\overline{\eta} \overline{z_{1}^{\prime}}}{R\left|z_{1}^{\prime}\right|} $ |
要求得这4个未知系数An、Bn、Cn、Dn,建立线性代数方程组,本文根据椭圆夹杂周边的位移连续、径向应力连续,圆形夹杂周边的位移连续、径向应力连续的边界条件,得到问题解的积分方程组:
| $ \left\{ \begin{array}{l} G_{\rm{I}}^{(i)} + G_{\rm{I}}^{(r)} + G_{{\rm{I}}C}^{(s)} + G_{{\rm{I}}T}^{(s)} = W_\Pi ^{({\rm{st}})}\\ \tau _{rz,{\rm{I}}}^{(i)} + \tau _{rz,{\rm{I}}}^{(r)} + \tau _{rz,{\rm{I}}C}^{(s)} + \tau _{rz,{\rm{I}}T}^{(s)} = \tau _{rz,\Pi }^{({\rm{st}})}\\ {\bf{ \pmb{\mathsf{ τ}} }}_{rz,\Pi }^{(i)} + {\bf{ \pmb{\mathsf{ τ}} }}_{rz,\Pi }^{(r)} + {\bf{ \pmb{\mathsf{ τ}} }}_{rz,\Pi C}^{(s)} + {\bf{ \pmb{\mathsf{ τ}} }}_{rz,\Pi T}^{(s)} = {\bf{ \pmb{\mathsf{ τ}} }}_{rz,\Pi }^{({\rm{sto}})}\\ G_\Pi ^{(i)} + G_\Pi ^{(r)} + G_{\Pi C}^{(s)} + G_{\Pi T}^{(s)} = W_\Pi ^{({\rm{sto}})} \end{array} \right. $ | (30) |
将式(30)的位移和应力表达式分别代入得:
| $ \left\{ \begin{array}{l} \sum\limits_{n = - \infty }^\infty {{A_n}} \xi _n^{(11)} + {B_n}\xi _n^{(12)} + {C_n}\xi _n^{(13)} = {\xi ^{(1)}}\\ \sum\limits_{n = - \infty }^\infty {{A_n}} \xi _n^{(21)} + {B_n}\xi _n^{(22)} + {C_n}\xi _n^{(23)} = {\xi ^{(2)}}\\ \sum\limits_{n = - \infty }^\infty {{A_n}} \xi _n^{(31)} + {B_n}\xi _n^{(32)} + {D_n}\xi _n^{(34)} = {\xi ^{(3)}}\\ \sum\limits_{n = - \infty }^\infty {{A_n}} \xi _n^{(41)} + {B_n}\xi _n^{(42)} + {D_n}\xi _n^{(44)} = {\xi ^{(4)}} \end{array} \right. $ | (31) |
用exp(-imθ)同时乘以式(31)的等式两边,并在(-π, π)上对所求等式进行积分,即得待定系数An、Bn、Cn、Dn的线性代数方程组,通过控制精度截断有限项,求得未知待定系数,最终得到Green函数的解答。
在半空间内存在一稳态SH波入射WΙ(i),其入射夹角为α0,本文模型为半空间水平界面,在水平界面会产生反射波WΙ(r),其入射波、反射波为:
| $ \begin{array}{*{20}{c}} {W_{\rm{I}}^{(i)} = {W_0}\exp \left\{ {\left( {{\rm{i}}{k_1}/2} \right)\left[ {(z - {\rm{i}}h){{\rm{e}}^{ - {\rm{i}}{\alpha _0}}} + } \right.} \right.}\\ {(\bar z + {\rm{i}}h){{\rm{e}}^{{\rm{i}}{\alpha _0}}}]\} } \end{array} $ | (32) |
| $ \begin{array}{c}{W_{\mathrm{I}}^{(r)}=W_{0} \exp \left\{\left(\mathrm{i} k_{1} / 2\right)\left[(z-\mathrm{i} h) \mathrm{e}^{\mathrm{i} \alpha_{0}}+\right.\right.} \\ {(\overline{z}+\mathrm{i} h) \mathrm{e}^{-\mathrm{i} \alpha_{0}} ] \}}\end{array} $ | (33) |
本文通过设计“脱胶模型”,根据Green函数求出的应力,在脱胶部分施加大小相等,方向相反的应力,使其脱胶部分应力自由即为零。
首先,在SH波的作用下,没有发生脱胶时的总位移场可以表示为:
| $ {W_{\rm{I}}} = W_{\rm{I}}^{(i)} + W_{\rm{I}}^{(r)} + W_{{\rm{I}}C}^{(s)} + W_{{\rm{I}}T}^{(s)} $ | (34) |
其次,根据脱胶部分的应力是自由的,在发生脱胶的部分,施加大小相等、方向相反的应力,可以得到:
| $ \begin{array}{*{20}{c}} {W_{\rm{I}}^{(ct)} = W_{\rm{I}}^{(i)} + W_{\rm{I}}^{(r)} + W_{{\rm{I}}C}^{(s)} + W_{{\rm{I}}T}^{(s)} - }\\ {\int_{{\theta _1}}^{{\theta _2}} {{{\left. {{\tau _{\theta z,{\rm{I}}}}} \right|}_{\eta = {\eta _0}}}} {G_{\rm{I}}}\left( {\eta ,{\eta _0},\theta ,{\theta _0}} \right){\rm{d}}\theta } \end{array} $ | (35) |
由于在实际工程中,通常存在各种不同形式的复合缺陷或者不规则缺陷,而椭圆形且存在脱胶的缺陷更接近工程的实际情况,因此本文着重讨论椭圆夹杂周围动应力集中系数的变化情况,动应力集中系数可以被定义为:
| $ \tau _{\theta z}^* = \left| {\tau _{\theta z,{\rm{I}}}^{(ct)}/{\tau _0}} \right| $ | (36) |
式中:τθz*表示椭圆夹杂周边的动应力集中系数;τθz, Ι(ct)表示椭圆夹杂周边的应力;SH波入射产生的最大幅值为τ0,且τ0=W0μ1k1。
5 算例及分析本文讨论了半空间内含有部分脱胶的椭圆夹杂和圆形夹杂同时存在时对SH波的散射,通过对入射角度、入射波频率、介质参数、夹杂的埋深,分析了含有部分脱胶的椭圆夹杂周围动应力集中系数τθz*的分布情况。引入无量纲参数k1*=k2/k1,k2*=k3/k1,μ1*=μ2/μ1,μ2*=μ3/μ1,椭圆长、短轴之比a/b,椭圆埋深用h1/a表示,椭圆夹杂与圆形夹杂的位置用d/r、h2/r表示,脱胶角度为θ1*=θ2-θ1,SH波的入射角度表示为α0。
为了验证本文计算结果的准确性,将本文模型退化为和文献[5]相同的模型,即在半空间内含有一个圆形孔洞,取与文献[5]一致的参数,即k1*=1.0,a/b=1.0,μ1*=0,h1/a=12,在SH波以α0=90°垂直入射到半空间内含有一个圆形孔洞的模型内,本文图 2为模型退化为圆孔后周围动应力集中系数τθz*的分布情况,与文献[5]中的结果一致,因此,可以证明本文的研究方法是正确的。
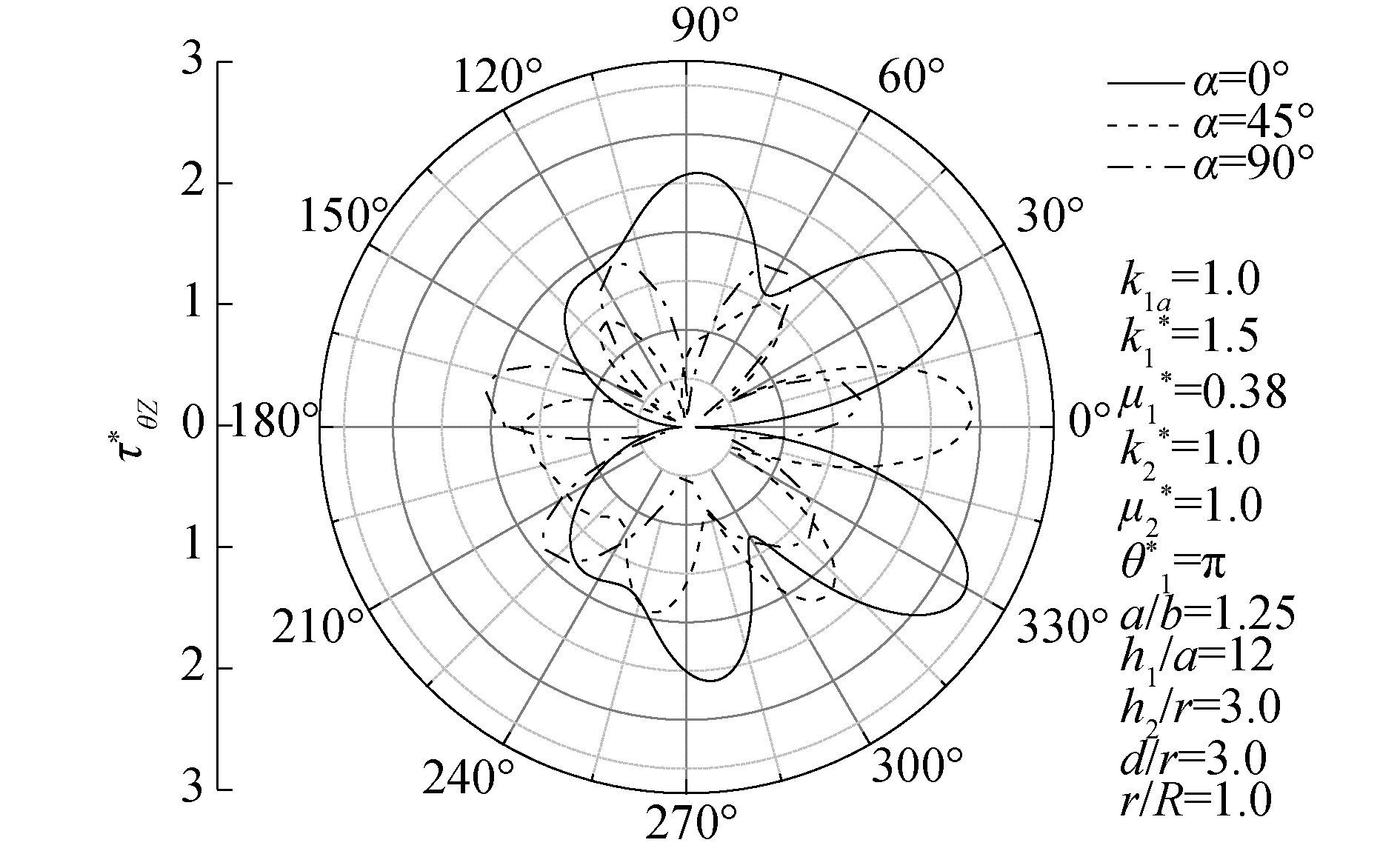
图 3给出了SH波以不同的角度入射到半空间内含有部分脱胶的椭圆夹杂以及圆形夹杂时,椭圆夹杂周围动应力集中系数τθz*的变化情况。当SH波入射频率为k1a=1.0时,SH波入射角度为α=0°时,动应力集中系数τθz*最大值在θ=328°为3.3,比α=45°动应力集中系数τθz*的最大值时大12%,比α=90°时动应力集中系数τθz*的最大值增加了42%,因此,在α=0°入射时,动应力集中系数τθz*的最大值比SH波以α=45°和α=90°入射时,动应力集中系数更大,所以本文中主要讨论SH波以α=0°水平入射时,动应力集中系数的分布情况。
|
Download:
|
| 图 3 SH波以不同的角度α入射时τθz*的分布 Fig. 3 Distribution of τθz* with different incident angles by SH-wave horizontally | |
图 4给出了SH波水平入射时,动应力集中系数τθz*随着波数比k1*变化的分布情况。当入射波频率在k1a=0.5时,由图 4(a)可以看出,k1*=0.5与k1*=1.0的图像接近重合,因此,在波数比k1*≤1.0时,动应力集中系数τθz*的变化不大。在入射波以k1a=0.5频率入射时,动应力集中系数τθz*在波数比为k1*=4.0时达到最大值3.5,比k1*=2.0的动应力集中系数τθz*的最大值增加了16%,波数比为k1*=4.0图像出现明显的震荡,因此,在波数比较小时,τθz*的变化非常小,而随着k1*的增大,动应力集中系数τθz*的变化非常大,产生明显的影响。

|
Download:
|
| 图 4 SH波水平入射随着k1*的变化τθz*的分布情况 Fig. 4 Distribution of τθz* with k1* by SH-wave horizontally | |
图 5给出了SH波水平入射时,随着夹杂介质参数k1*及μ1*的不同,含有部分脱胶的椭圆夹杂周围动应力集中系数τθz*的变化情况,其中,图 5(a)中k1*=1.5,μ1*=0.38表示花岗岩中含有混凝土夹杂,图 5(b)中k1*=0.7,μ1*=3.23表示混凝土中含有钢夹杂的情况。图 5(a)中,在入射波频率为k1a=0.5时,动应力集中系数τθz*的最大值在θ=281°达到最大值3.0,当入射波由软夹杂入射到硬夹杂时如图 5(b)所示,在同等入射频率k1a=0.5下,此时动应力集中系数的最大值为0.9,比图 5(a)中动应力集中系数τθz*的最大值降低了67%。在k1a=2.0时,图像出现明显的震动,动应力集中系数在θ=324°的最大值为2.9,比图(b)中k1a=2.0时动应力集中系数τθz*的最大值提高了62%。因此,当夹杂与基体比更软时,τθz*的变化较大,夹杂比基体较硬时,τθz*相对较小,所以,在实际工程中可以根据介质参数不同,选择合适的施工材料。

|
Download:
|
| 图 5 SH波水平入射时τθz*随着k1*及μ1*的分布情况 Fig. 5 Distribution of τθz* with k1*andμ1*by SH-wave horizontally | |
图 6(a)给出了当SH波水平入射时,在不同入射频率k1a下,椭圆夹杂周围动应力集中系数τθz*随着夹杂埋深h1/a的不同的分布情况。由图 6可以看出,h1/a=1.5时动应力集中系数在θ=90°时达到最大值4.5,此外,h1/a=5.0与h1/a=12.0的图像几乎重合,最大值在θ=90°为3.0,比h1/a=1.5时的最大值降低了33%,因此,当h1/a < 5.0,动应力集中系数τθz*随着夹杂的埋深越小,其动应力集中系数变化越大,而在h1/a≥5.0时,夹杂的埋深对于动应力集中系数的变化影响不大。

|
Download:
|
| 图 6 SH波水平入射时τθz*的分布 Fig. 6 Distribution of τθz* with h2/r by SH-wave horizontally | |
图 6(b)给出了SH波水平入射时,随着圆形夹杂与椭圆夹杂距离h2/r的不同,椭圆夹杂周围动应力集中系数τθz*的分布情况。当入射波频率为k1a=2.0,在h2/r=1.0时,动应力集中系数τθz*在θ=110°达到最大值3.76,比h2/r=3.0时的动应力集中系数最大值提高了13%,比h2/r=4.0时的动应力集中系数最大值提高了15%,因此,圆形夹杂距离椭圆夹杂越近,椭圆夹杂周围的动应力集中系数τθz*越大,应该重视缺陷之间的距离对动应力集中系数分布产生的影响。
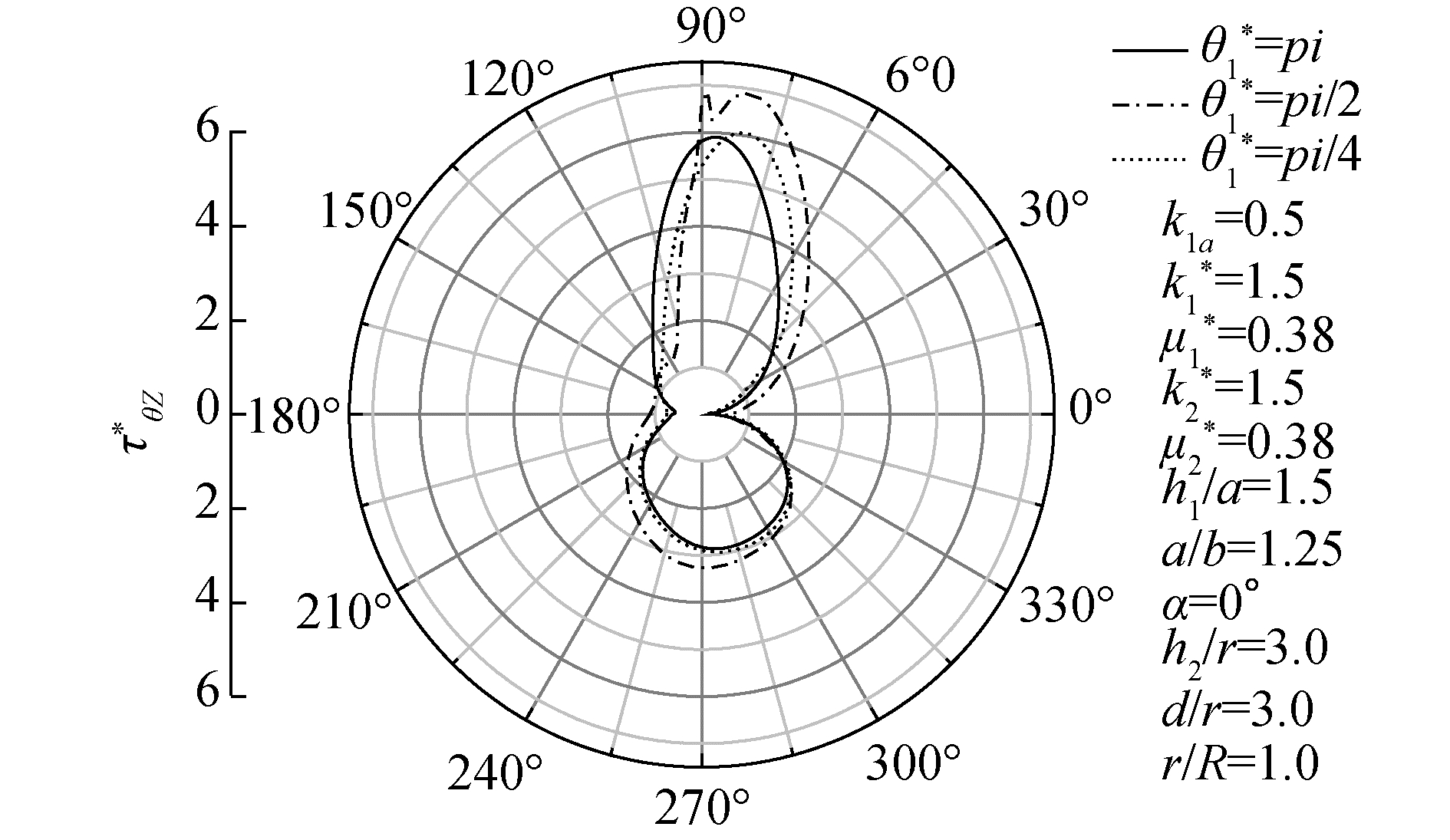
图 7给出了在SH波水平入射到半空间含有部分脱胶的椭圆夹杂以及圆形夹杂界面内时,随着脱胶角度θ1*的不同,椭圆夹杂周围动应力集中系数τθz*的变化情况。由图中可以看出,当脱胶角度为θ1*=π/2时,动应力集中系数τθz*在θ=82°达到最大值6.88,比脱胶角度为θ1*=π的最大值增加了17%,因此,脱胶角度的不同对椭圆夹杂周围动应力集中系数具有一定的影响。其次,在θ从180°~360°的椭圆夹杂未发生脱胶的下半部分,动应力集中系数τθz*的最大值在θ=270°为2.9,比发生脱胶部分的动应力集中系数的最大值降低了57%,因此,和未脱胶部分比,脱胶结构对动应力集中系数的变化产生较大的影响,在实际工程结构中,脱胶可能会导致结构发生直接破坏,因此,应该重视对于脱胶结构的处理。
|
Download:
|
| 图 7 SH波水平入射时随着θ1*的不同τθz*的分布情况 Fig. 7 Distribution of τθz* with θ1* by SH-wave horizontally | |
1) 入射频率、入射波数比越大,动应力集中系数越大,在达到一定数值后趋于稳定,但变化更加复杂,容易出现明显的震荡。
2) 缺陷埋深越小,2个缺陷之间的距离越近,对动应力集中系数的影响越大。
3) 脱胶角度对浅埋缺陷的动应力影响较大,脱胶部分比未脱胶部分的动应力集中更大,应该引起重视。
4) 根据介质参数的不同,对动应力集中系数产生的不同影响,可以在工程实际中选择合适的材料进行施工或者结构设计。
本文分析了半空间内含有部分脱胶的椭圆夹杂以及圆形夹杂对SH波的散射,可以再在圆夹杂周围加入衬砌,分析圆形夹杂周围动应力集中系数的变化情况。
| [1] |
WONG H L, TRIFUNAC M D. Scattering of plane SH waves by a semi-elliptical canyon[J]. Earthquake engineering & structural dynamics, 1974, 3(2): 157-169. (  0) 0)
|
| [2] |
TRIFUNAC M D. Scattering of plane SH waves by a semi-cylindrical canyon[J]. Earthquake engineering & structural dynamics, 1972, 1(3): 267-281. (  0) 0)
|
| [3] |
ESHELBY J D. The determination of the elastic field of an ellipsoidal inclusion, and related problems[J]. Proceedings of the Royal Society of London. Series A. Mathematical and physical sciences, 1957, 241(1226): 376-396. (  0) 0)
|
| [4] |
汪越胜, 王铎. SH波对有部分脱胶衬砌的圆形孔洞的散射[J]. 力学学报, 1994, 26(4): 462-469. WANG Yuesheng, WANG Duo. Diffraction of SH-waves by a circular cavity with a partially debonded liner[J]. Acta mechanica sinica, 1994, 26(4): 462-469. (  0) 0)
|
| [5] |
林宏, 刘殿魁. 半无限空间中圆形孔洞周围SH波的散射[J]. 地震工程与工程振动, 2002, 22(2): 9-16. LIN Hong, LIU Diankui. Scattering of SH-wave around a circular cavity in half space[J]. Earthquake engineering and engineering vibration, 2002, 22(2): 9-16. DOI:10.3969/j.issn.1000-1301.2002.02.002 (  0) 0)
|
| [6] |
李宏亮, 刘殿魁. SH波作用下圆形夹杂与裂纹的相互作用[J]. 哈尔滨工程大学学报, 2004, 25(5): 618-622. LI Hongliang, LIU Diankui. Interaction of SH-wave by cracks with a circular inclusion[J]. Journal of Harbin Engineering University, 2004, 25(5): 618-622. DOI:10.3969/j.issn.1006-7043.2004.05.016 (  0) 0)
|
| [7] |
杨在林, 许华南, 黑宝平. 半空间椭圆夹杂与裂纹对SH波的散射[J]. 振动与冲击, 2013, 32(11): 56-61, 79. YANG Zailin, XU Huanan, HEI Baoping. Interaction of elliptical inclusion and crack under incident SH-wave in a half-space[J]. Journal of vibration and shock, 2013, 32(7): 56-61, 79. (  0) 0)
|
| [8] |
XU Huanan, YANG Zailin, WANG Shasha. Dynamics response of complex defects near bimaterials interface by incident out-plane waves[J]. Acta mechanica, 2016, 227(5): 1251-1264. (  0) 0)
|
| [9] |
丁晓浩, 齐辉, 赵元博. 含有直线裂纹的直角域中椭圆形夹杂对SH波的散射[J]. 天津大学学报(自然科学与工程技术版), 2016, 49(4): 415-421. DING Xiaohao, QI Hui, ZHAO Yuanbo. Scattering of SH-wave by elliptic inclusion in right-angle plane with beeline crack[J]. Journal of Tianjin University (science and technology), 2016, 49(4): 415-421. (  0) 0)
|
| [10] |
QI Hui, YANG Jie. Dynamic analysis for circular inclusions of arbitrary positions near interfacial crack impacted by SH-wave in half-space[J]. European Journal of Mechanics-A/Solids, 2012, 36: 18-24. (  0) 0)
|
| [11] |
QI H, ZHANG X M, CHEN H Y, et al. Scattering of SH wave by a cylindrical inclusion and a semi-cylindrical hollow near vertical interface crack in the Bi-material half space[J]. Journal of mechanics, 2017, 33(5): 619-629. (  0) 0)
|
| [12] |
陈志刚, 杨在林, 刘殿魁. SH波在浅埋椭圆孔上的散射对地震动的影响[J]. 哈尔滨工程大学学报, 2006, 27(1): 5-9. CHEN Zhigang, YANG Zailin, LIU Diankui. Effect of scattering on the ground motion above a subsurface elliptic cavity by incident SH-waves[J]. Journal of Harbin Engineering University, 2006, 27(1): 5-9. DOI:10.3969/j.issn.1006-7043.2006.01.002 (  0) 0)
|
| [13] |
张希萌, 齐辉, 项梦. 半空间双相压电介质垂直边界附近圆孔对SH波的散射[J]. 爆炸与冲击, 2017, 37(4): 591-599. ZHANG Ximeng, QI Hui, XIANG Meng. Scattering of SH-wave by a circular cavity near the vertical boundary in the piezoelectric bi-material half-space[J]. Explosion and shock waves, 2017, 37(4): 591-599. (  0) 0)
|
| [14] |
QI Hui, ZHANG Ximeng. Scattering of SH wave by a semi-cylindrical salient near vertical interface in the bi-material half space[J]. Waves in random and complex media, 2017, 27(4): 751-767. (  0) 0)
|
| [15] |
ZHAO Chunxiang, QI Hui, NAN Jingfu. Scattering of SH-wave by an interface cylindrical elastic inclusion with a semicircular debonded above subsurface cavity[J]. Advanced materials research, 2013, 753-755: 1846-1850. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


