2. 哈尔滨工业大学 计算机科学与技术系, 黑龙江 哈尔滨 150001
2. Department of Computer Science and Technology, Harbin Institute of Technology, Harbin 150001, China
信息化时代下,数据已变成与资产同等重要的资源广泛应用于各领域中。大量的数据和多样的数据类型都有可能导致信息的重叠和冲突,即描述相同实体同一属性的值不同。因此如何在大数据的冲突信息中发现真实值变得十分重要[1],称之为大数据的真值发现。
目前,大数据真值发现面临一系列的技术挑战。首先数据的规模非常庞大,因此真值发现框架需要不断扩大规模,降低由于数据规模较大导致的处理时间大幅度延长效应,增加效率[2-4]。其次,数据的增长速度非常快,因此处理数据的真值发现框架需要较好适应增量式的输入,不间断快速检测冲突并解决冲突。
基于真值发现的重要性,研究人员提出了不同真值发现的方法[5]。Yin等[6]提出了真值发现的概念,并给出了一个解决方案TruthFinder,该方案通过迭代计算数据源的准确度和值的信心度来达到真值发现的目的。Dong等[7]考虑了数据源之间的依赖关系,通过给数据源增加评价维度,即依赖度,从而使独立的数据源在投票过程中具有更高的权重。这种方法大大提高了真值发现的准确度,但是仅适用于解决单值问题。Zhao等[8]给出一个基于贝叶斯推理模型的MAP算法,该方法对数据源不使用确定的评价维度且推理得到的真值须满足最大后验概率。但由于MAP算法的指数复杂度较高,难以实际应用。Pasternak等[9]将先验知识加入了真值发现的过程之中,通过线性规划进行调整。相关研究表明真值往往由可靠的数据源提供,并且真值的发现与数据源的可靠程度密切相关。而在最近的研究中,该原则被形式化建模成一个优化问题,其目标是最小化由多个数据源提供的观察值与真值的总距离[10]。文献提出了一个基于最小-最大熵的优化框架来进行真值发现的方法,该方法也是通过迭代更新真值和数据源可信度来进行优化[11]。另外,文献[12-16]利用概率方法来解决真值发现问题。其基本思路是研究多个数据源的数据混合分布,并将数据源的可信度作为随机变量加入概率模型来进行真值发现。这些方法均试图最大似然概率或后验分布,不断地迭代更新模型的参数和真值。
综上,当前已有处理真值发现的方法在特定的领域表现良好,但仍难以解决大数据中真值发现的问题[17]。一方面,当前的方法主要考虑在小型数据集上的执行效率,并未过多地考虑在大数据上的可扩展性问题。当数据量增大时,算法往往难以运行,且时间上的消耗的代价难以承担[18-19]。另一方面,当前方法主要在处理静态数据上具有很好的可靠性和准确度,但没有考虑数据随时间增长的动态变化的特点。而大数据变化速度快的特点要求算法可以快速判定更新数据的真值,当前的方法都没有考虑到这一点。
针对上述问题,本文将并行框架Map-Reduce应用于真值发现, 从而提出了一种基于Map-Reduce的增量真值发现算法。由于Map-Reduce框架可以将大规模数据拆分成数据块,每个数据块均可独立计算,因此可以并行快速处理大数据,提高了系统的性能和可扩展性。为了适应大数据更新速度快的特点,本文在MTPF算法的基础上,引入了将增量技术Incoop,并对于Map过程和Reduce进行了优化,从而提出了增量真值发现算法IncooMPTF,从而可以达到使数据的输入能够增量化的目的,有效对快速更新的数据进行真值发现。
本文面向大数据提出了Map-Reduce模型下的真值发现算法MPTF,该算法将传统的单机真值发现算法扩展到集群,对大数据进行并行处理,探索了基于Map-Reduce模型的真值发现方法。在MPTF的基础上提出增量真值发现算法IncooMPTF,该算法结合了Incoop增量框架和Map-Reduce计算模型的特点,有效解决了并行增量真值发现快速变化的问题。通过真实数据集上的扩展实验验证了本文提出的算法具有较高的效率和可扩展性。
1 基于Map-Reduce的真值发现算法 1.1 问题定义本文主要立足于解决多数据源中冲突数据的真值发现问题,因此输入由多个数据源。下面给出基于贝叶斯的串行真值发现算法的基本概念以及问题定义。
本文中使用的其他常见符号如表 1所示。
| 表 1 符号表 Table 1 Symbol table |
定义1 假设数据D = {source1, source2, …, sourcem}组成,其中每个数据源是一系列声明的集合sourcei = {claim1, claim2, …, claimn},每个声明均是一个包含数据源id, 属性id和属性值value的记录claimj = {source_id, object_id, value}。
定义2 假设真值标签t是布尔类型的随机变量,则t是否为真表示是否可以由贝叶斯模型计算。声明中已计算的标签o是布尔类型的随机变量,表示当真值确定并且t是其标签,某个claim为真的可能性。
定义3 通过比较o和t,定义如下4个属性:
True Positives (TPs),当o = true, t = true;
False Positives (FPs),当o = false, t = true;
False Negatives(FNs),当o = true, t = false;
True Negatives(TNs),当o = false, t = false;
定义3中定义的4个属性值表示了每个source的质量,因此,高质量的数据源中包含更多的基于TPs和TNs的真值声明。
为描述整个模型的方便,给出如下假设。
假设1 数据源中对象的质量都是已知的。即声明Claimi包含的object_id所表示的对象质量已知。
假设2 每一个数据源中只提供一个对象的声明,并且在真值发现以前,整个实体解析已经完成。
如果数据质量过差,无法得到高质量的结果。因此,获取的数据对于预测要足够可靠,从而可以保证从数据获取的知识可以用于后续的分析和计算。
1.2 贝叶斯模型在本文中,根据来源的质量,使用贝叶斯图模型推断给定值为真的可能性;同时,基于先验知识采用贝叶斯模型来更新数据源的质量。通过真值发现和数据源质量计算定义模型,然后给出数据源评价策略,然后基于通过迭代计算数据源的质量推断真值提出基于贝叶斯推理的真值发现算法。
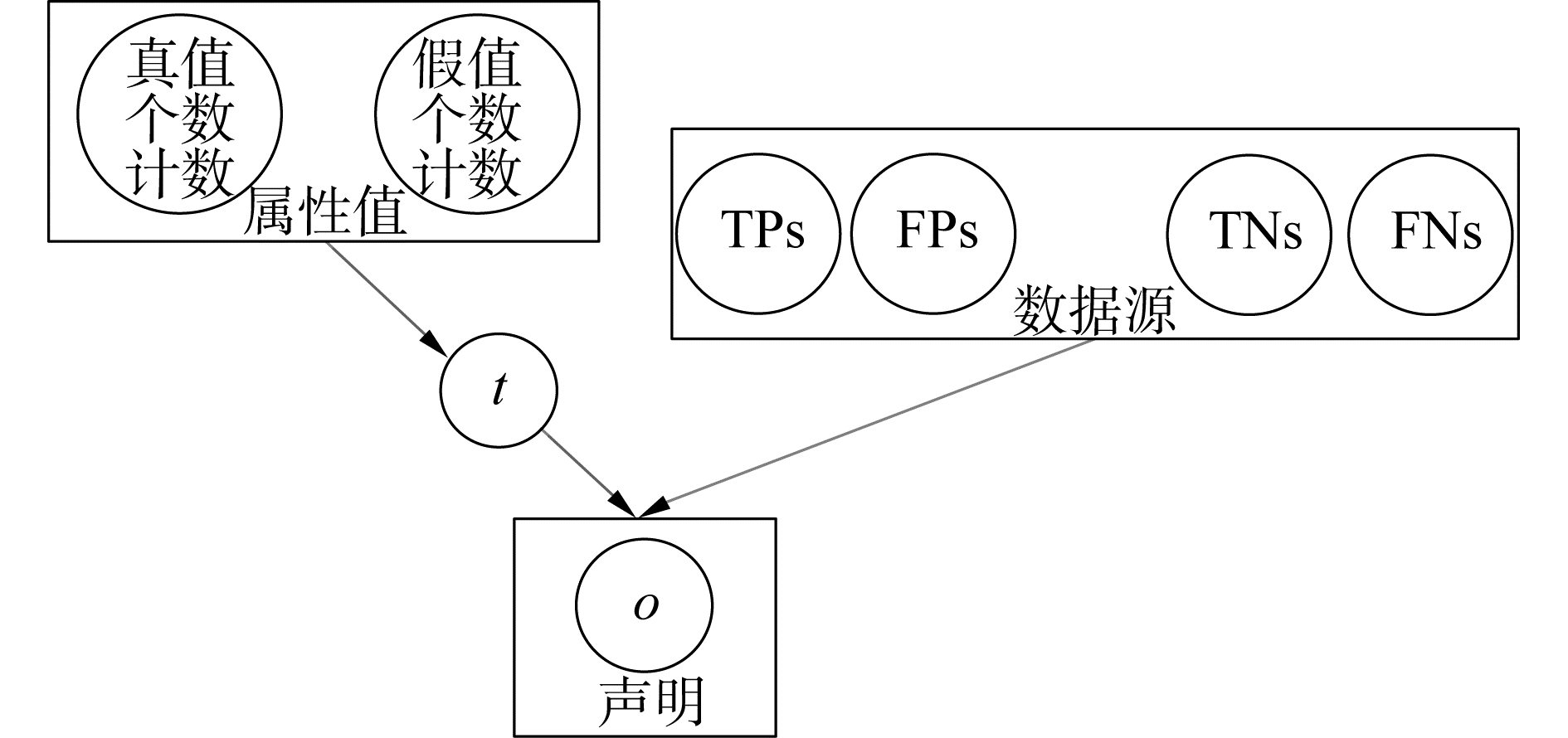
整个模型框架如图 1所示,基于贝叶斯推理的真值发现算法BaseTF(算法1)主要如下步骤:首先,计算每个数据的质量,并对真值数据进行选择和标记;其次,通过定义3中Positive-Negative 2个方面的计数来计算数据源的质量;再次,比较观测值和已有真值来更新数据和数据源的质量;最后,判断给定值的正确值。若大于阈值,则确定其为真值,并计算其概率。若小于阈值,则更新结果集Result Set,同时更新TPs、TNs、FPs、FNs。
|
Download:
|
| 图 1 贝叶斯概率图模型 Fig. 1 Bias probability diagram model | |
本算法中通过对比当前支持value为真的数据源个数pt与支持value为假的数据源个数pε,可以得到value为真的概率。对于当前pti和pεi可以通过之前的pti-1和pεi-1来计算:
| $ {p_t}^i = {\rm{ }}\frac{{{p_t}^{i-1} \times ({\rm{TP}}{{\rm{s}}_{\rm{c}}}{\rm{ + TPs}})}}{{{\rm{TP}}{{\rm{s}}_{\rm{c}}}{\rm{ + TN}}{{\rm{s}}_{\rm{c}}}{\rm{ + TPs + TNs}}}}{\rm{ifo}} = {\rm{true}} $ | (1) |
| $ {\rm{ }}{p_\varepsilon }^i = {\rm{ }}\frac{{{p_t}^{i-1} \times ({\rm{FP}}{{\rm{s}}_{\rm{c}}}{\rm{ + TPs}})}}{{{\rm{FP}}{{\rm{s}}_{\rm{c}}}{\rm{ + FN}}{{\rm{s}}_{\rm{c}}}{\rm{ + FPs + FNs}}}}{\rm{ifo}} = {\rm{false}} $ | (2) |
综述所述,本文提出基于贝叶斯推理的真值发现算法BaseTF的时间复杂度为O(m×n),其中m×n为所有数据源的声明数量,具体伪代码如下:
算法1 基于贝叶斯推理的真值发现算法BaseTF
输入:由多个数据源组成的数据记录D = {source1, source2, …, sourcem},准确度下限σ;
输出:结果集Result Set。
1) 用训练集执行贝叶斯算法
2) for each sourcei in D:
3) 初始化TPs、TNs、FPs、FNs、Result Set
4) for each value in each source:
5) 初始化先验真值个数pt
6) 初始化先验假值个数pt
7) while Result Set的准确率小于σ:
8) for each source:
9) for each value:
10) for each claim:
11) 计算当前pti和pεi
12) if pti+pεi≥0
13) t is true;
14) else t is false;
15) 更新TPs, TNs, FPs, FNs;
16) Add t to Result Set
17) for each value in each source:
18) if t is true : p(t = true) =
本节将Map-Reduce框架应用到贝叶斯真值发现算法BaseTF,从而提出基于Map-Reduce的真值发现算法MPTF。而由于算法中需要对每个记录进行扫描,确定冲突记录并计算真值概率,在计算概率的过程中,将相关计数全部放入内存供推理更新是不现实的。经过分析,将整个算法分为6个过程,即预处理、全局数据处理、分割过程、描述更新过程、值更新过程和结果集更新。在这6个过程中,每个Job的输入串行承接其他Job的输出,各模块内部的记录运算均是相对独立的,不需要其他模块参加,因此每个模块内部可以利用Map-Reduce框架进行并行运算。
MPTF算法中预处理模块用于数据格式的变换,同时将无须发现真值数据的记录剔除;全局数据处理模块负责提取全局数据,即先验质量,包括TPs、TNs、FPs、FNs,以及Result Set结果集;接下来将重点介绍如何将Map-Reduce框架应用于分割、描述更新和值更新过程。
1.3.1 分割过程该模块的任务是利用拆分算法将全局数据分拆为各个模块需要的数据,同时在分拆的过程中伴随着一些计算(如先验参数等)。
由于在Map-Reduce中不能像单机算法一样一次性获得数据源、值以及描述的相关信息,因此只能将它们按对(Pair)分开。其中,原始数据格式表示为:
〈key = LineNum, value = SourceID, ValueID, ClaimID, Tuple_content〉
其中,Tuple_content指元组内容,包括元组所有属性的值。为表述方便,本文中用SID表示SourceID; VID表示ValueID;CID表示ClaimID以及T表示Tuple_content。根据算法需求,在Map阶段将原始数据转化两两对应序对,即
| $ \begin{array}{*{20}{l}} {\left\langle {{\rm{key}} = {\rm{SID}}, {\rm{value}} = {\rm{VID}}} \right\rangle }\\ {\left\langle {{\rm{key}} = {\rm{VID}}, {\rm{value}} = {\rm{SID}}} \right\rangle }\\ {\left\langle {{\rm{key}} = {\rm{CID}}, {\rm{value}} = {\rm{SID}}} \right\rangle }\\ {\left\langle {{\rm{key}} = {\rm{VID}}, {\rm{value}} = {\rm{CID}}} \right\rangle }\\ {\left\langle {{\rm{key}} = {\rm{SID}}, {\rm{value}} = {\rm{CID}}} \right\rangle } \end{array} $ |
其中,应在Reduce阶段将序对聚集成需要的信息。
1.3.2 描述处理过程该模块的任务是计算, 当前支持value为真的数据源个数pt中的系数代表了数据源质量的描述。由式(1)可知,系数部分为:
| $ \frac{{{\rm{TP}}{{\rm{s}}_{\rm{c}}}{\rm{ + TPs}}}}{{{\rm{TP}}{{\rm{s}}_{\rm{c}}}{\rm{ + TN}}{{\rm{s}}_{\rm{c}}}{\rm{ + TPs + TNs}}}} $ |
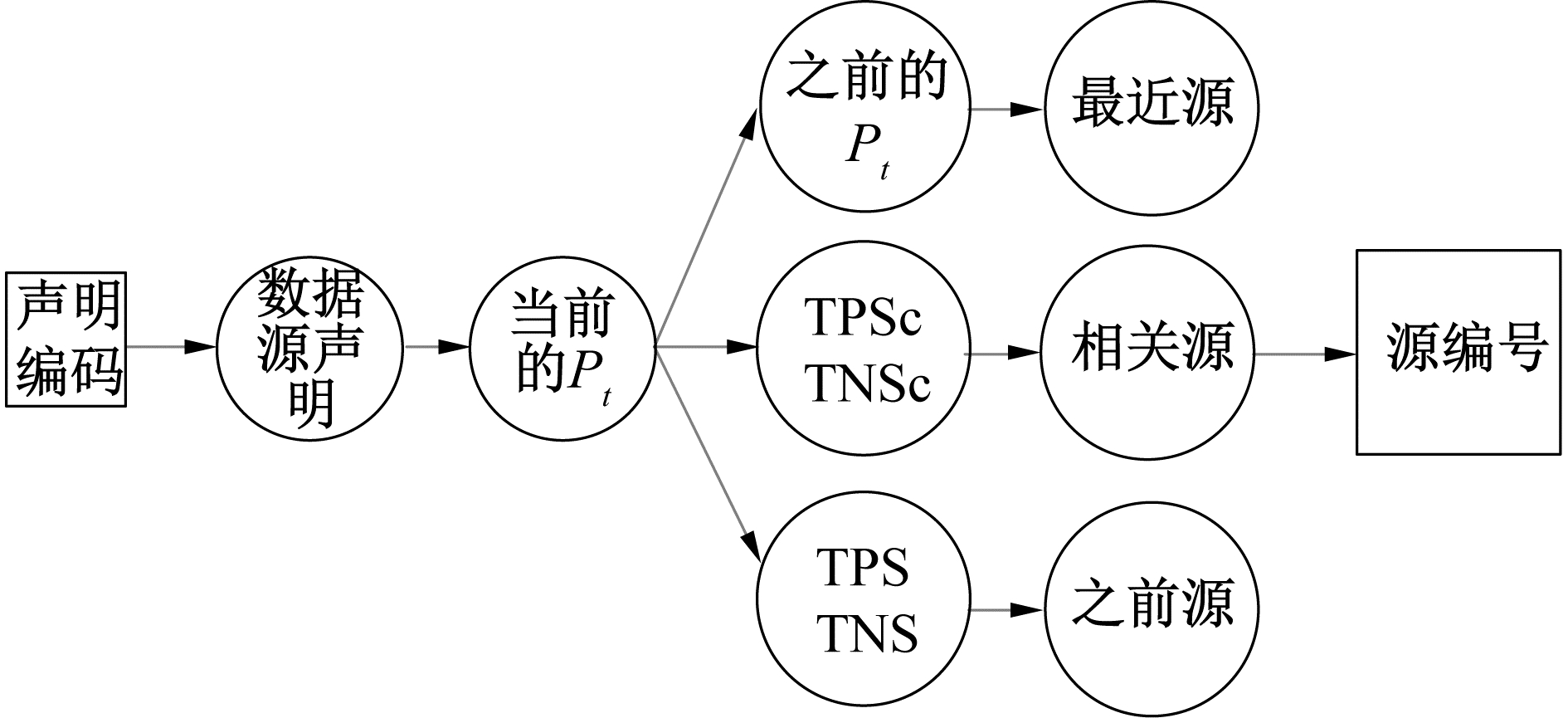
要想计算数据源质量pti,首先需要聚集Claim到Source的关系。由图 2中可知,在计算Claim的过程中,需要得到全局数据TPs、TNs、FPs、FNs,并且claim须知道与之相关的数据源SID的TPsc、TNsc、FPsc、FNsc。全局数据TPs、TNs、FPs、FNs在分拆的过程中存入的全局数据文档可以通过Map调用得到。数据源SID的TPsc、TNsc、FPsc、FNsc通过分拆模块中的当前参数获得。其中Claim的计算过程需要接受前面模块产生的2个不同的输入,由于在前面没有Claim到TP、TN、FP、FN直接对应的输出导致输入TP、TN、FP、FN无法直接获得。
|
Download:
|
| 图 2 各个变量之间的依赖关系 Fig. 2 Dependencies between variables | |
值处理过程关键要计算当前支持value为真的数据源个数pt,并将其作为数据源的质量和真值的质量互相给出评价用来迭代更新。值处理过程是整个Map-Reduce真值发现算法的核心步骤。该过程首先将VID->CID聚集claim来计算每个数据源质量当前pti,然后将VID->SID聚集数据源SID,并更新SID的TP、TN、FP、FN等信息。
2 基于Map-Reduce的增量真值发现算法 2.1 系统模型在MPTF算法的基础上,通过使用进行Incoop增量框架进行大数据增量真值发现,从而提出了基于Map-Reduce的增量真值发现算法——IncooMPTF,该算法模型主要考虑以下2点:
1) 新加入的数据应该尽量不要影响已有的计算结果和节点,这就要求IncooMPTF尽量在新加入的节点上给予计算。
2) 将新加入节点和已有节点的计算结果汇总得到最终的结果。
基于以上2点考虑,IncooMPTF算法的主要思想是基于投票的多分类器集成策略。把MPTF中Map-Reduce的真值发现策略作为基本训练分类器算法,用Map过程来训练每个子分类器,每个Reducer均可作为预测器并集成各个子分类器的结果。而在算法的实现过程中由于每个子分类器是由许多Map-Reduce过程构成的,这就会导致Map和Reduce过程需要嵌套调动,因此需要在Map-Reduce的节点上再次启动一个Map-Reduce任务,在节点间形成一个近似树状的层次结构,具体过程如图 3所示。

|
Download:
|
| 图 3 增量真值发现示意 Fig. 3 Schematic diagram of incremental truth value discovery | |
分类难度是指分类器分类实体的难度,对于每个分类器Mi,如果p(t = true)>τ,则将Mi视为在特定实体object上是有效的,反之,M不参与投票。类似的,如果p(t = true)>τ, 则将M视为具有高权重参与对该实体的投票。这样可以将输出分为3个部分(part A表示分类非常有把握的描述, part B表示能够分类的描述, part C表示不确定的描述),将由该分类器推断出的每个真值truth都打上A、B、C的标签。
假设Ws(o)为数据源在实体上投票的权重。如果在该实体上值投票的源平均真值概率高,则认为数据源在实体的票数也高。因此可以用Ws(o)相关值的平均真值概率来计算:
| $ {W_s}\left( o \right) ={\rm{lb}}\left| {{V_s}} \right| \frac{{{\sum _v}p({V_s}\left( o \right) = {\rm{true}})}}{{{V_s}}} $ | (3) |
同理,假设H(o)为一个实体在一个子模型上可以被推断概率的难度。一个分类器推断时越困难,在投票时权重也越小。在式(4)中,由于与当前实体相关的数据源的权重越高,实体被推断难度越大,因此一个实体被分辨的难度可以用式(3)中的Ws(o)进行计算,其中sup(v→0)指现有数据中实体和值的支持度,ρ是一个调节参数。
| $ H\left( o \right) = \rho \times {\rm{ }}\frac{{\left| {{W_s}} \right|}}{{{\rm{lbsup}}\left( {v \to o} \right){\sum _s}{W_s}\left( o \right)}} $ | (4) |
综上所述,IncooMPTF算法的伪代码如算法2所示。
算法2 基于Map-Reduce的增量真值发现算法IncooMPTF
1) 设置blocksize,假设数据分为N块。
2) Map过程:
输入:新加入的增量数据块ΔS (ti),将其映射到第Mi个分类器上。
输出:Mi (一个分类器), 计算其属性HMi(o)。
3) Reduce过程:
输入:ti时刻所有子分类器,所有的数据集S+ΔS(ti)+…+ΔS(tj)
Reduce()
{
① 聚集Map中在相同实体o上相关的分类器Mi
② 计算其分类难度和错误率
③ 对不同的值进行投票,计算其confidence,并判断值是否为真
}
输出:给出每个分类器的投票权重,给出最终分类结果,给出真值Truth
2.2 模型分析与优化本文提出的增量真值发现算法运行过程中,算法首先分析用于真值发现,假设最初有n个Map节点,m个Reduce节点用于处理离线的真值发现,而k个Map节点和l个Reduce节点用于处理增量数据。由于贝叶斯基础算法的复杂度函数为O(n),那么使用没有进行增量计算之前的Map和Reduce节点来训练这个分类器,则基于海量数据S的真值发现f(S)的代价也是线性的,即O(f(S)) = O(n)。
分析算法用于投票的Map和Reduce节点的代价。假设Map和Reduce节点的个数分别为n′和m′,那么在增量数据上进行基础计算的时间复杂度近似是,由此这些节点的复杂度O (Map)都是相似的,即每一个Map结点对应一个投票节点,那么Map过程和Reduce过程的时间复杂度如下:
| $ \begin{array}{l} O\left( {{\rm{Map}}} \right) = O\left( {\frac{{\Delta {S_i}}}{{S + {\sum _\Delta }{S_i}}}g\left( {\Delta {S_i}} \right)} \right)\\ O\left( {{\rm{Reduce}}} \right) = O\left( {\frac{1}{{m\prime }} \times n\prime \times h\left( {\Delta {S_i}} \right) + b} \right) \end{array} $ |
式中:g(ΔSi)和h(ΔSi)分别表示Map和Reduce阶段操作;b表示所有Reduce汇总的代价。故需要处理一个数据,增量算法总的时间为:
| $ \begin{array}{l} O\left( {{\rm{Map}}} \right) + O\left( {{\rm{Reduce}}} \right) = O\left( {\frac{{\Delta {S_i}}}{{S + {\sum _\Delta }{S_i}}}g\left( {\Delta {S_i}} \right)} \right) + \\ {\rm{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;O\left( {\frac{1}{{m\prime }} \times n\prime \times h\left( {\Delta {S_i}} \right) + b} \right) \ll \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;O\left( {n \times f\left( {\frac{{2S}}{n} + \Delta {S_i}} \right)} \right) = O\left( {{n^2}} \right) \end{array} $ |
综上所述,Map-Reduce算法时间复杂度高于线性,因此为提高算法效率,本模型分别从Map过程和Reduce过程进行优化。
2.2.1 Map过程的优化策略1) 调整缓冲值。Mapper在运行过程中会在内存中对应一个缓存,通过在缓存中排序来优化性能,其默认参数是100 Mb。当集群节点较少时,Mapper的缓存会相应的比较大,单个节点输出的数据比较多,从而影响磁盘读取的性能。因此设置一个较大的缓存来加快磁盘读取的速度。
2) 调整溢出值。每当缓存满的时候数据将会溢出,因此调整任务参数使其在缓存快满的时候就溢出,减少等待计算的时间。
3) 调整归并值。每当Mapper退出时会对已经产生的输出文件进行合并,因此通过增大每次可以合并的文件个数来降低合并的次数。
4) 调整组合器。Map和Reduce中间有一个用于合并mapper结果组合过程,该过程能减少传输带宽,因此通过调整参数对组合器运行进行加速。
2.2.2 Reduce过程的优化策略1) shuttle过程的优化。Reduce过程分成3个阶段,分别为shuttle->sort->reduce。本文算法包含多轮Map-Reduce过程。等待所有的Map执行完毕后再Reduce显然会浪费大量等待时间。因此通过调整每个reduce并行下载Map结果的最大线程数,使shuttle过程尽快完成。
2) 出错处理。当集群出现错误时Reduce会长时间等待,因此可以调整下载线程的最大等待时间来减少时间消耗。
3) 调整归并值。通过调整Reduce可以合并不同Map的最大个数来加快单次Reduce运行时间。
2.3 模型应用讨论在实际中,基于Map-Reduce的增量真值发现算法中的数据增量可能存在2种情况,第1种情况是数据源大量新增,从而增加了相应的claim,第2种情况是数据源数量基本稳定,但是数据源中增加很多的新的claim。
基于上述2种情况,采取本文方法均可有效实现增量数据真值的发现。针对第1种情况,本文提出的方法可以直接对新增数据源的数据实现真值发现,再采用投票机制保证结果的准确性;针对第2种情况,即使数据源的质量估计可能会由于增量数据发生变化,但由于本文提出的方法中采用式(4)重新估计了实体的数据源投票(算法2中Reduce函数),因此仍能够保证投票机制的有效性。
3 实验对比分析本文算法均基于Hadoop2.0平台用Java语言实现。本过程实验集群包含八台PC机,配置是:Intel(R) Core(TM) i5-2400的处理器,主频3.10 GHz,内存大小4 GB,操作系统Windows7,实验数据来自真实数据集DBLP,阈值的改变范围是0.5~1.0。通过设置不同的适用形式,本文提出的MPTF算法和IncooMPTF算法分别与BaseTF、INC-Drift1、INC-Drift2以及INC-Drift3进行了准确率的对比实验。此外,为证明本文提出算法的优势和有效性,分别从算法的加速比、数据更新类型以及可扩展性等方面进行的对比实验。实验过程中,从数据集中随机选取100个记录进行人工标记,将其作为真实结果,而将运行算法的结果与人工标记的真实结果相比来衡量算法的准确度。
3.1 准确率为了验证本文算法的优势,分别基于静态更新、Sources added one by one、Big task coming one by one和Data stream 4种使用情形下,进行了不同算法的准确度对比实验,实验结果如表 2所示。通过实验结果可以看到并行算法和非并行算法精确度上区别不大,但由于并行的增量策略为适应Hadoop有了细微调整,从而导致IncooMPTF和INC之间存在细微差别。此外,由于本文提出的算法结合了Incoop增量框架,从而可以通过检测数据变化来更新输出,因此整个过程是增量的,且该增量具有更新粒度较细、可拓展性与稳定性较好等特点,同时由于本文算法对更新数据的进行真值发现时,将更新的数据和系统中已经存在大数据进行先融合后再计算,因此可以保证本文提出的算法在真实数据集上表现出良好的准确性。从实验结果也可以看出,尽管充分考虑了可扩展性和快速的数据更新,本文提出的算法依然保证了最好的正确率。
| 表 2 不同的算法的准确率且阈值高于0.5 Table 2 Accuracy of different algorithm and the threshold is higher than 0.5 |
为验证本文中提出的算法在加速比方面的优势,本实验分别在数据量为10 MB、50 MB、100 MB和150 MB 4种情况下,比较了分别采用基于Map-Reduce的真值发现算法与其他非Map-Reduce算法进行真值发现的时间消耗,从而得到其加速比。
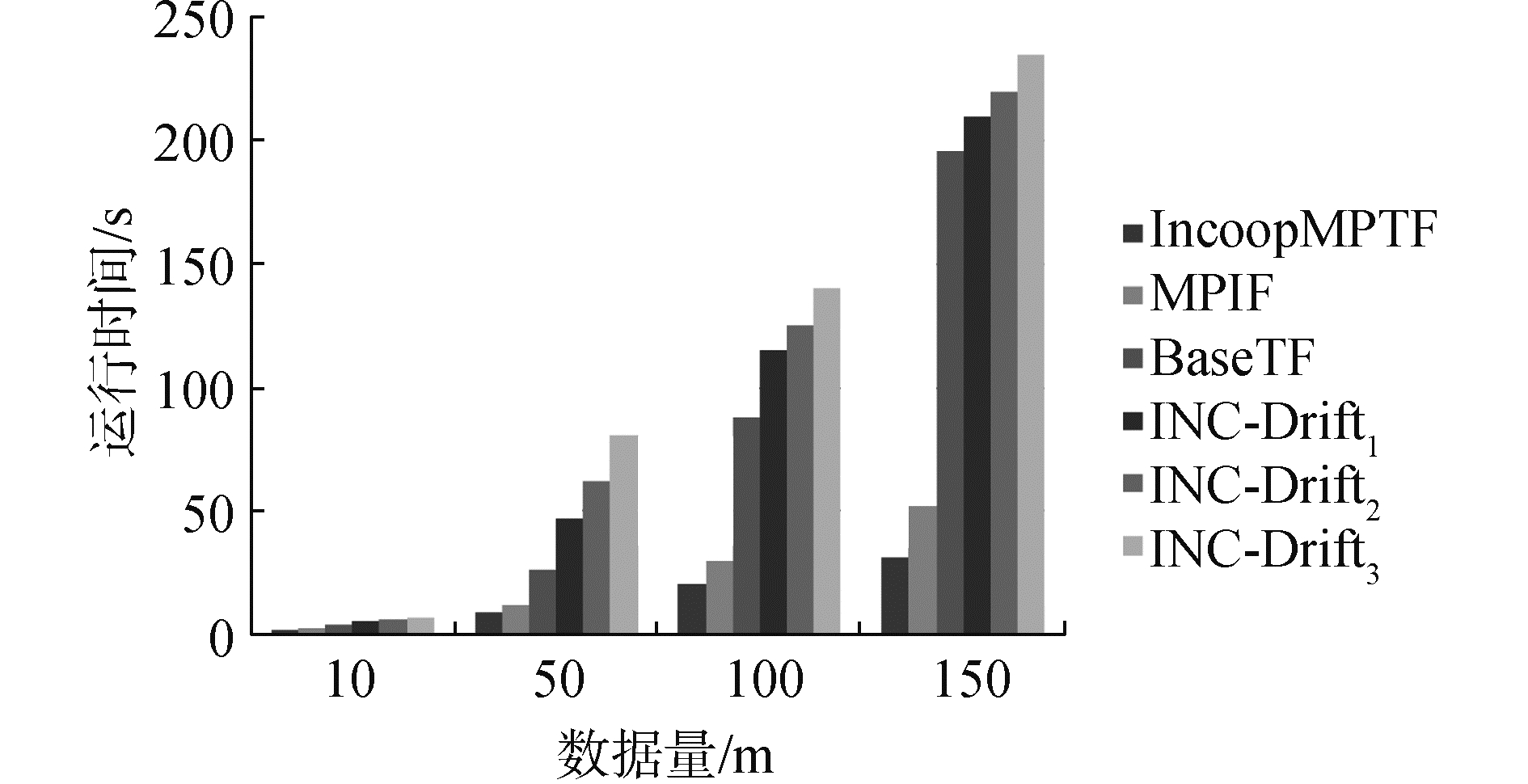
由于本文提出的算法中每个Job的输入都与其他Job的输出是串行承接的,同时各模块内部的运算均是相对独立的,不需要其他模块参加,因此每个模块内部可以利用Map-Reduce框架进行并行运算,这样就可以大大提高整个真值发现的效率,减少算法运行的时间代价。具体实验结果如图 4所示,随着数据量的不断增加,相比于其他非Map-Reduce算法,IncooMPTF算法和MPTF算法在加速比方面表现出更好的性能,具体的实验效果如图 4所示。
|
Download:
|
| 图 4 基于数据量变化的算法运行时间 Fig. 4 The running time of algorithms based on data volume changing | |
为了测试数据更新类型对算法效率的影响,本实验采用统一100 M的数据量,测试了基于4种更新类型(静态:S1;数据源逐个输入:S2;批量数据:S3;数据流:S4)的情况下,IncoopMPTF算法、MPTF算法、BaseTF算法、NC-Drift1算法、INC-Drift2算法以及INC-Drift3算法的时间效率。由于IncoopMPTF算法中的Incoop技术采用监测数据变化来更新数据的输出,同时整个增量更新过程数据更新粒度更细;此外,相比于其他算法,IncooMPTF在进行真值发现过程中,首先将更新的数据和系统中已经存在的大数据进行动态融合,然后再进行发现计算,因此IncooMPTF可以适用于快速更新的动态,特别适用于系统中已经存在大规模数据的情况下的真值发现。数据更新类型的实验结果如图 5所示。从图中可以看出,MPTF的耗费时间最多,IncooMPTF在批量数据和数据流情况下可以大幅提高增量时间。

|
Download:
|
| 图 5 基于不同数据更新类型的算法运行时间 Fig. 5 The running time of algorithms based on different data updating | |
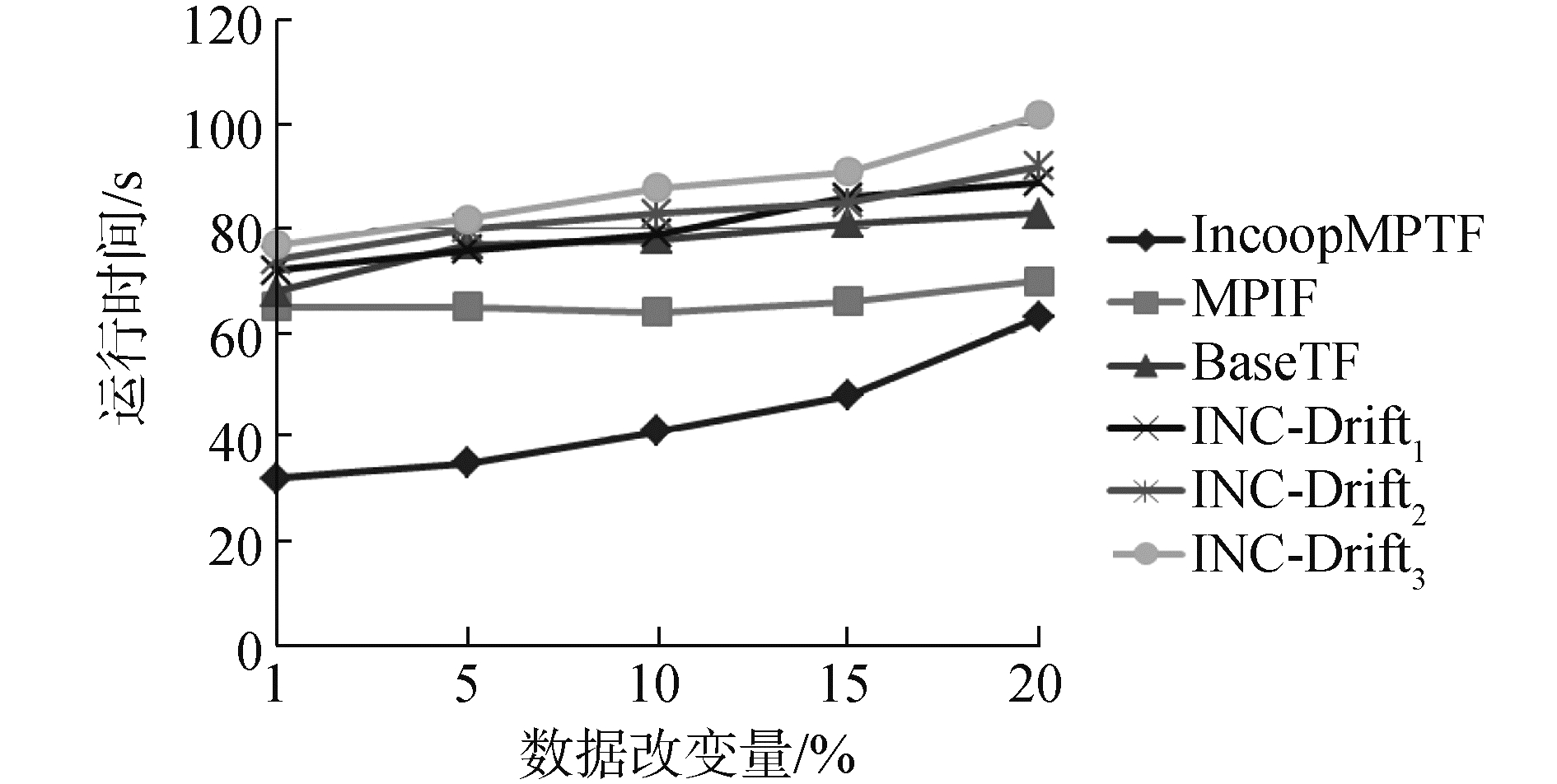
为验证数据输入改变程度的方面对并行算法的影响,本实验中,实验数据量统一采用100 M,增量过程仅执行一次,分别选择数据改变程度为1%、5%、10%、15%和20%,进行算法运行效率的比较。相比于其他算法,IncooMPTF算法运行过程中分别进行了Map过程的优化(调整缓冲值、调整溢出值、调整归并值以及调整组合器)和Reduce过程的优化(shuttle过程的优化、出错处理和调整归并值),特别是Reduce过程中的shuttle过程的优化,可以减少大量的等待时间,从而使得shuttle过程尽快完成。因此,通过上述优化过程可以大大提高整个算法真值的发现效率,从而可以使得IncooMPTF算法时间复杂度不高于线性。具体实验结果如图 6所示。当输入改变在20%以内时,IncooMPTF算法表现出很好性能。
|
Download:
|
| 图 6 基于不同的数据改变量算法的运行时间 Fig. 6 The running time of algorithms based on different data changing | |
为了有效测试系统的可扩展性,本实验通过拷贝DBLP数据集将数据扩大为5倍、10倍、15倍、20倍、25倍,分别测试了本文提出的基于Map-Reduce的真值发现算法(IncoopMPTF算法和MPTF算法)以及传统的非Map-Reduce的真值发现算法(BaseTF算法、NC-Drift1算法、INC-Drift2算法以及INC-Drift3算法)在进行发现真值的运行效率。由于本文中提出的基于Map-Reduce的真值发现算法在进行真值发现过程中,在不同的数据分组中进行相同操作,同时可以保证操作间相互独立;此外,利用Map-Reduce框架将真值发现的每个过程并行化,从而大大提高整个真值发现的可扩展性。此外,IncoopMPTF算法在进行真值发现过程中分别进行了Map过程的优化和Reduce优化,从而可以大大降低算法运行的时间代价,提高运行效率。从实验结果可以看出,本文提出算法的运行时间随数据量呈线性增长,系统在数据量增大时有较好的可扩展性。具体实验结果如图 7所示。

|
Download:
|
| 图 7 可扩展性实验 Fig. 7 Scalability experiment | |
1) 该算法将Incoop增量框架和并行框架Map-Reduce应用于真值发现,不仅可以实现大规模数据的并行真值发现,而且可以有效地对快速更新数据进行真值发现。
2) 通过引入基于投票机制的分类器集成策略,把Map-Reduce的真值发现策略作为基本分类器训练算法,不仅保证了分类的准确率,而且实现了对于增量真值的高效发现。
3) 在提高效率的同时,本文中优化了传统真值发现方法中的Map和Reduce过程,并考虑到一些较为复杂的状况,使真值发现模型更加稳定,适用范围更加广泛。
未来的工作主要是利用数据之外的知识对数据进行清洗处理,从而进一步研究基于上下文的背景的真值发现。
| [1] |
JIA Li, WANG Hongzhi, LI Jianzhong, et al. Incremental truth discovery for information from multiple data sources[M]//GAO Y. Web-Age Information Management. Berlin: Springer, 2013: 56-66.
(  0) 0)
|
| [2] |
HUANG Chao, WANG Dong, CHAWLA N. Scalable uncertainty-aware truth discovery in big data social sensing applications for cyber-physical systems[J/OL]. IEEE Transactions on Big Data: (2017-02-14). https://ieeexplore.ieee.org/document/7855694. DOI:10.1109/TBDATA.2017.2669308.
(  0) 0)
|
| [3] |
ZHANG D Y, WANG Dong, ZHANG Yang. Constraint-aware dynamic truth discovery in big data social media sensing[C]//2017 IEEE International Conference on Big Data (Big Data). Boston, MA, USA: IEEE, 2017: 57-66.
(  0) 0)
|
| [4] |
ZHANG D, WANG Dong, VANCE N, et al. On scalable and robust truth discovery in big data social media sensing applications[J/OL]. IEEE Transactions on Big Data: (2018-04-10). https://www.computer.org/csdl/trans/bd/preprint/08334619-abs.html. DOI:10.1109/TBDATA.2018.2824812.
(  0) 0)
|
| [5] |
LI Yaliang, GAO Jing, MENG Chuisi, et al. A survey on truth discovery[J]. ACM SIGKDD Explorations Newsletter, 2016, 17(2): 1-16. DOI:10.1145/2897350 (  0) 0)
|
| [6] |
YIN Xiaoxin, HAN Jiawei, YU P S. Truth discovery with multiple conflicting information providers on the web[J]. IEEE Transactions on Knowledge and Data Engineering, 2008, 20(6): 796-808. DOI:10.1109/TKDE.2007.190745 (  0) 0)
|
| [7] |
DONG X L, BERTI-EQUILLE L, SRIVASTAVA D. Truth discovery and copying detection in a dynamic world[J]. Proceedings of the VLDB Endowment, 2009, 2(1): 562-573. DOI:10.14778/1687627 (  0) 0)
|
| [8] |
ZHAO Bo, RUBINSTEIN B I P, GEMMELL J, et al. A Bayesian approach to discovering truth from conflicting sources for data integration[J]. Proceedings of the VLDB Endowment, 2012, 5(6): 550-561. DOI:10.14778/2168651 (  0) 0)
|
| [9] |
PASTERNACK J, ROTH D. Knowing what to believe (when you already know something)[C]//Proceedings of the 23rd International Conference on Computational Linguistics. Stroudsburg, PA: Association for Computational Linguistics, 2010: 877-885.
(  0) 0)
|
| [10] |
LI Qi, LI Yaliang, GAO Jing, et al. Resolving conflicts in heterogeneous data by truth discovery and source reliability estimation[C]//Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data. New York, NY, USA: ACM, 2014: 1187-1198.
(  0) 0)
|
| [11] |
ZHOU Dengyong, PLATT J C, BASU S, et al. Learning from the wisdom of crowds by minimax entropy[C]//Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe, Nevada: Curran Associates Inc., 2012: 2204-2212.
(  0) 0)
|
| [12] |
MARSHALL J, ARGUETA A, WANG Dong. A neural network approach for truth discovery in social sensing[C]//2017 IEEE 14th International Conference on Mobile Ad Hoc and Sensor Systems (MASS). Orlando, FL, USA: IEEE, 2017: 343-347.
(  0) 0)
|
| [13] |
ZHANG D Y, BADILLA J, ZHANG Yang, et al. Towards reliable missing truth discovery in online social media sensing applications[C]//2018 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM). Barcelona, Spain: IEEE, 2018: 143-150.
(  0) 0)
|
| [14] |
BAKHTIARI B, YAZDI H S. Bayesian filter based on the wisdom of crowds[J]. Neurocomputing, 2018, 283: 181-195. DOI:10.1016/j.neucom.2017.12.037 (  0) 0)
|
| [15] |
FANG X S, SHENG Q Z, WANG Xianzi, et al. SmartVote: a full-fledged graph-based model for multi-valued truth discovery[J]. World Wide Web: (2018-08-22). https://link.springer.com/article/10.1007%2Fs11280-018-0629-3. DOI:10.1007/s11280-018-0629-3.
(  0) 0)
|
| [16] |
ZHAO Bo, RUBINSTEIN B I P, GEMMELL J, et al. A Bayesian approach to discovering truth from conflicting sources for data integration[J]. Proceedings of the VLDB Endowment, 2012, 5(6): 550-561. DOI:10.14778/2168651 (  0) 0)
|
| [17] |
GARCIA-ULLOA D A, XIONG Li, SUNDERAM V. Truth discovery for spatio-temporal events from crowdsourced data[J]. Proceedings of the VLDB Endowment, 2017, 10(11): 1562-1573. DOI:10.14778/3137628 (  0) 0)
|
| [18] |
THIYAGARAJ M P B, ALOYSIUS A. A survey on truth discovery methods for big data[J]. International Journal of Computational Intelligence Research, 2017, 13(7): 1799-1810. (  0) 0)
|
| [19] |
XU Guowen, LI Hongwei, TAN Chen, et al. Achieving efficient and privacy-preserving truth discovery in crowd sensing systems[J]. Computers & Security, 2017, 69: 114-126. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


