2. 吉林大学 符号计算与知识工程教育部重点实验室, 吉林 长春 130012
2. Key Laboratory of Symbolic Computation and Knowledge Engineering(Jilin University), Ministry of Education, Changchun 130012, China
Davis和Putnam等提出DPLL算法是求解SAT问题的完备算法。先进的SAT求解器普遍基于回溯的DPLL算法,其中包含了子句学习(clause learning)等技术[1-3]。
在DPLL的改进过程中,子句学习发挥着重要的作用。将子句学习的概念引入到DPLL框架中,构成了冲突驱动的子句学习。随着子句学习技术的不断成熟,各种不同的学习机制也相继提出。利用子句学习技术的Chaff、Glucose、COMiniSat[4-5]等求解器能够解决包含百万个变元和子句的工业算例,这是其他推理算法无法做到的[6]。
P系统是一种细胞膜计算模型[7-8]。该模型相继出现了许多变型,其中多半表达能力都与图灵机等价。根据细胞新陈代谢的特点如:消融、分裂或创建等,可知膜系统的格局及它们之间转移的概念[9-10]。
细胞膜演算是基于细胞膜计算提出的形式化方法[11-12]。在膜计算的基础上,膜演算增加了移入、移出、传入和传出等细胞膜之间的反应规则。
本文利用细胞膜演算形式化描述带子句学习的DPLL算法的整个推理过程,分别给出了DPLL的一般过程和冲突分析过程的描述,为DPLL算法提供了一种新的形式化描述方法。
1 伴随子句学习的DPLL算法 1.1 DPLL过程与子句学习目前,先进的求解器皆基于DPLL算法。经典的DPLL算法过程如下:对于合取范式F和部分赋值α,若α满足F,则该合取范式判定为SAT;若α导致其中某个子句为空,则该合取范式判定为UNSAT。一个变元x通过启发式被α选中,α通过x: = 0或x: = 1,会递归调用该判定程序2次。若某一次递归调用判定为SAT,则该合取范式可满足;若两次递归调用都判定为UNSAT,则该合取范式不可满足。
若在单元传播过程中发生了一次冲突,且α的子集α′是导致这个冲突的赋值,则将其保存到一个新的子句C并将其添加到公式中,在之后的搜索中若再次出现部分赋值α′时,可以更早地回溯。
算法 DPLL with clause learning[13]
输入 CNF formula F
输出 A solution of F or UNSAT if F is not satisfiable
1) P←Unit propagate
2) If P assigns a value to every variable
3) return success
4) Else
5) P contains a conflict
6) choose a conflict graph G to find c under P and add it to F
7) rollback variable or back jump
上述算法为带子句学习的DPLL算法的一般过程。其中,第6行的子句学习过程即在真值赋值发生冲突时,分析冲突产生的原因,找到导致冲突的赋值序列并添加到子句集中,避免再次发生相同的冲突。
1.2 冲突分析在求解过程中,变元的赋值序列可以通过蕴含图表示。图中每个顶点代表一个文字,正文字代表变元被赋值为1,负文字代表变元被赋值为0;边表示导致一个变元被赋值的原因。每一个决策变元对应着一个决策层[14]。
原始的DPLL算法具备较简单的冲突分析机制:求解器为每个决策变元存储一个标记,用作记录变元赋值次数。当出现空子句后,算法会检测当前标记:若标记1次,则强制反转当前赋值;若标记2次,则回溯到上一层并强制反转赋值。
非时序性回溯是基于蕴含图的更先进的冲突分析机制。通过对冲突的分析,学习得到一些子句并将其添加到子句集中,这个过程称为冲突驱动子句学习,用于在将来搜索过程中避免相同的错误发生。若返回的最大层为0,意味着算法已经无法再回溯,即整个问题不可满足。
1.3 重启机制当求解器在搜索过程中发生了k(k>1)次冲突后,激活重启功能,求解器终止当前求解过程并返回到第0层,即重新求解该子句集。冲突上界由参数k来决定[15]。
2 细胞膜演算 2.1 基本概念细胞膜演算主要包括:膜结构、对象和反应规则。膜结构表达多个事务的嵌套关系,对象有不同类,对象之间可用反应规则来描述[7-10]。
细胞膜演算模型定义如下。
定义 细胞膜是一个元组MM = (Σ, μ, O1, …, Om, R1, …, Rm, C),其中:
1) Σ是一个有限非空的类型集合,包含所有出现对象的类型;
2) μ是一个细胞膜结构,包含m个细胞膜;
3) Oi(1≤i≤m)是第i个细胞膜的对象多集;
4) Ri(1≤i≤m)是第i个细胞膜的反应规则多集;
5) C是类型映射函数,定义为o∈Oi→Σ。该函数定义对象o的类型C(o)→Σ。直观上讲,所有对象都是类型化的。
2.2 语法定义类型集合为Σ,其元素为T,对象多集中的元素为a, b, c, …,反应规则为R,标识符为i, j, k, …。细胞膜演算定义如下:
| $ M,M':: = 0\left| {\left[ {{}_iO,R,M} \right]} \right|M,M' $ |
| $ O,O':: = 0\left| {a:T} \right|OO' $ |
| $ \begin{array}{l} R,R':: = 0\left| {O \to O'} \right|O \to {{O'}_{{\rm{out}}}}\left| {O \to {{O'}_{{\rm{in}}\left( f \right)}}} \right|\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;O \to \lambda \left| R \right|R' \end{array} $ |
| $ \lambda :: = \delta \left| {\delta k} \right|\eta k\left| M \right. $ |
在该语法表述中,首先定义了一系列的细胞膜M、M′等,然后定义细胞膜中的对象类O、O′和反应规则类R、R′。细胞膜用[0[1][2]…]的嵌套形式表达彼此间的关系[9]。
2.3 反应规则下面为反应规则的作用和效果的定义(O, O′, O″为对象多集,M、M′、M″、M"'为细胞膜多集,R、R′、R″为规则多集,i、j、k为标识符):
对象迁移规则:O→O′out。将对象O变为O′。
| $ \left[ {{}_iOO'',O \to O'\left| {R',M} \right.} \right] \to \left[ {{}_iO'O'',O \to O'\left| {R',M} \right.} \right] $ |
对象传出规则:O→O′out。将对象传送到其父细胞膜。
| $ \begin{array}{l} \left[ {{}_iO',R,\left[ {{}_jO'O'',O \to {{O''}_{{\rm{out}}}}\left| {R',M} \right.} \right]M} \right] \to \left[ {{}_iO'O''',} \right.\\ \left. {R,\left[ {{}_jO''O \to {{O''}_{{\rm{out}}}}\left| {R',M'} \right.} \right]M} \right] \end{array} $ |
对象传入规则:O→O′in(j)。将对象传送到其子细胞膜。
| $ \begin{array}{l} \left[ {{}_iOO',O \to {{O''}_{{\rm{in}}\left( j \right)}}\left| R \right.,\left[ {{}_jO''',R',M'} \right]M} \right] \to \left[ {{}_iO',} \right.\\ \left. {O \to {{O''}_{{\rm{in}}\left( j \right)}}\left| R \right.,\left[ {{}_jO''O''',R',M'} \right]M} \right] \end{array} $ |
对象溶解规则:O→δ。将该细胞膜溶解,将其对象保留于父细胞膜中。
| $ \left[ {{}_iO'',R,\left[ {{}_jOO',O \to \delta \left| {R',M'} \right.} \right]M} \right] \to \left[ {{}_iO'',O',R,M} \right] $ |
细胞膜移出规则:O→σi。将子细胞膜i从父细胞膜中移出,成为兄弟细胞膜。
| $ \begin{array}{l} \left[ {{}_iO'',R,\left[ {{}_jOO',O \to \sigma i\left| {R',M'} \right.} \right]M} \right] \to \left[ {{}_iO'',R,} \right.\\ \left. M \right]\left[ {{}_jOO',O \to \sigma i\left| {R',M'} \right.} \right] \end{array} $ |
细胞膜移入规则:O→ηi。将兄弟细胞膜i移入到其子细胞膜,成为子细胞膜。
| $ \begin{array}{l} \left[ {{}_iO'',R,M} \right]\left[ {{}_jOO',O \to \eta i\left| {R',M'} \right.} \right] \to \left[ {{}_iO'',R,} \right.\\ \left. {\left[ {{}_jOO',O \to \eta i\left| {R',M'} \right.} \right]M} \right] \end{array} $ |
细胞膜生成规则:O→M。将创建一个细胞膜M。
| $ \left[ {{}_iOO',O \to M\left| {R',M'} \right.} \right] \to \left[ {{}_iO',O \to M\left| {R,MM'} \right.} \right] $ |
反应规则是区别细胞膜演算和细胞膜计算的根本要素。只有定义对象的反应规则,才能真正实现形式化描述的过程。
3 细胞膜演算描述子句学习 3.1 细胞膜演算规则带有子句学习的DPLL算法包含部分赋值、变元反转、回溯、回跳等核心步骤。多个对象集合表示为l、li、
1) 部分赋值(细胞膜的产生)。
决策文字表示为li,变元集表示为L,子膜的反应规则表示为R′,父细胞膜表示为M,产生的新细胞膜表示为M′,是M的子膜。即:在决策变元被赋值后,对象li触发了反应规则,并产生了新的子细胞膜M′,其他不变。
| $ \left[ {{}_i{l_i}L,{l_i} \to M'\left| {R',M} \right.} \right] \to \left[ {_iL,{l_i} \to M'\left| {R',MM'} \right.} \right] $ |
2) 变元反转。
变元反转li后的值表示为
| $ \left[ {{}_i{l_i}L,{l_i} \to \neg {l_i}\left| {R,M} \right.} \right] \to \left[ {{}_i\neg {l_i}L,{l_i} \to \neg {l_i}\left| {R,M} \right.} \right] $ |
3) 回溯。
上一层的赋值被强制反转后表示为
| $ \left[ {{}_i{l_i}L,{l_i} \to \neg {l_{i - 1}}\left| {R,M} \right.} \right] \to \left[ {{}_i\neg {l_{t - 1}}L,{l_i} \to \neg {l_{i - 1}}\left| {R,M} \right.} \right] $ |
4) 回跳最大层。
回跳最大层的决策变元表示为lt,强制反转最大层变元表示为
| $ \left[ {{}_i{l_i}L,{l_i} \to \neg {l_t}\left| {R,M} \right.} \right] \to \left[ {{}_i\neg {l_t}L,{l_i} \to \neg {l_t}\left| {R,M} \right.} \right] $ |
5) 细胞膜溶解。
由部分赋值规则可知,决策变元赋值后会产生新的细胞膜。赋值反转后同样会产生新的细胞膜,而原有的细胞膜会被溶解。
| $ \left[ {_iL,R,\left[ {{}_jl,l \to \delta \left| {R',M'} \right.} \right]M} \right] \to \left[ {_iL,R,M} \right] $ |
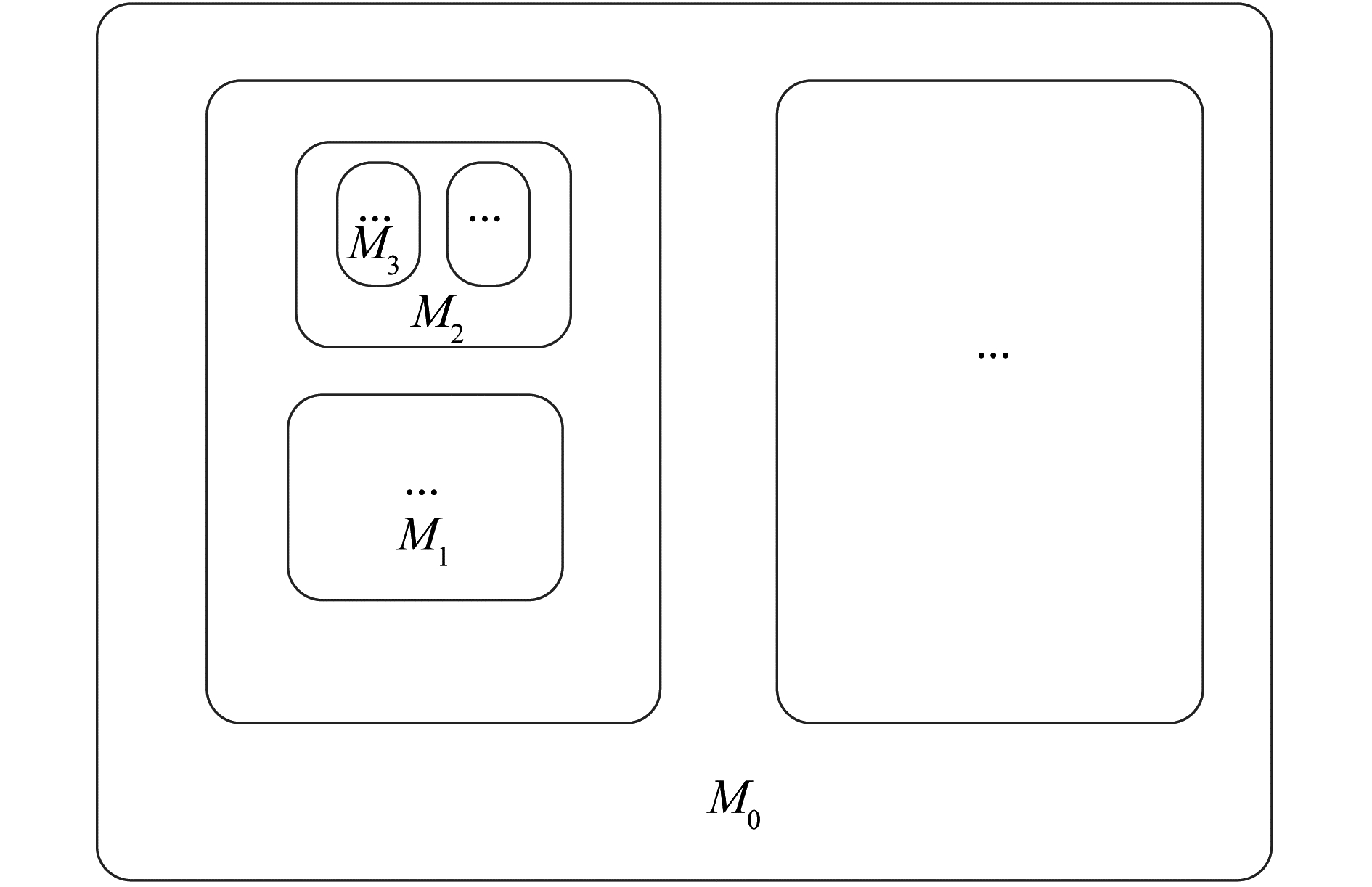
如图 1,首先定义对象集,决策类表示为p,单元传播类表示为q,反转类表示为r,冲突类表示为v,子句集表示为S。最外层的细胞膜表示为M0,主要用于判定该层的冲突次数。
| $ O = \left( {{p_i},\neg {q_i},\neg {q_{i - 1}},q,r,v,\neg v,\emptyset ,S,{T_p},{F_p},{T_q},{F_q},y} \right) $ |
| $ {M_0} = \left[ {S,{R_1},{M_j}} \right] $ |
| $ {R_0} = \left( {{r_{01}},{r_{02}},{r_{03}},{r_{04}},{r_{05}}} \right) $ |
| $ {r_{01}}:{p_i} \to {T_p}\left| {{F_p}} \right.;{T_p} \to {T_p}{M_{11}}\left| {{F_p} \to {F_p}{M_{10}}} \right. $ |
| $ {r_{02}}:q \to {T_q}\left| {{F_q}} \right. $ |
| $ {r_{03}}:{T_p} \to {T_{{\rm{pin}}M11}};{F_q} \to {F_{{\rm{pin}}M10}} $ |
| $ {r_{04}}:\left( {v,\neg v} \right) \to {\left( {v,\neg v} \right)_{{\rm{in}}\left( j \right)}},y \to \delta $ |
| $ {r_{05}}:S \to {\emptyset _{{\rm{out}}}} $ |
| $ {\rho _0} = \left\{ {{r_{04}} > {r_{02}} > {r_{01}} > {r_{03}} > {r_{05}}} \right\} $ |
| $ {R_j} = \left\{ {{r_{j1}},{r_{j2}}} \right\} $ |
| $ {r_{j1}}:{p_i} \to \neg {p_{{\rm{iout}}}} $ |
| $ {r_{j2}}:{p_i} \to \neg {p_{i - 1{\rm{out}}}} $ |
| $ {\rho _j} = {r_{j1}} > {r_{j2}} $ |
|
Download:
|
| 图 1 DPLL过程对应的细胞膜嵌套关系 Fig. 1 Nested relationship of membranes corresponding to DPLL process | |
DPLL求解首先对决策变元进行赋值。r01:pi→Tp|Fp; Tp→TpM11|Fp→FpM10对决策变元p进行赋值,若决策变元p赋值为T,则会产生新的子细胞膜M11。同理,若决策变元p赋值为F,会产生另一个新的子细胞膜M10。
决策变元赋值后子句集可能会产生部分单元子句,这时进行单元传播,即所有单文字都用q来代替。在r02:q→Tq|Fq中,q进行决策Tq或Fq。
规则r03:Tp→TpinM11; Fq→FpinM10将决策变元Tp传入新的子细胞膜M11中,并把决策变元Fp传入子细胞膜M10中。
在r04:(v,
最后一条r05:S→Øout表示子句集可满足。
规则的优先级顺序同样存在于父细胞膜M0中。其顺序用ρ0 = {r04>r02>r01>r03>r05}表示。反应规则必须按照优先级的排列顺序执行,当不符合当前规则的触发条件时,会跳转执行下一条规则的判定。
细胞膜Mj的判定仅有2条规则。该层的冲突次数在该层的子细胞膜中判定。在规则rj1:pi→
发生第2次冲突时触发规则rj2:
在有大量子句的子句集中,随着赋值变元增多,二叉树搜索也会相应变深。所以可以用Mij代替决策变元。
3.3 冲突分析冲突分析是找出引起冲突的变元并更改其赋值。回跳也被称为非时序性回溯,是基于冲突驱动子句学习所提出来的方法。经过分析后得知准确的回跳层数,并将学习到的子句添加到子句集中。
子句学习属于典型的长事务实例。这个过程中,当开始执行单元传播时,如果产出了空子句,即触发回跳规则,找出最大层并返回到相应层。根据细胞膜演算,得到相应的形式化描述。
| $ \begin{array}{*{20}{c}} {{M_C} = \left[ {{\rm{Begin}}:{\rm{State}},{R_1},{M_0},{M_L},{M_J}} \right]}\\ {{M_0} = \left[ {_00,{R_0},0} \right]}\\ {{M_L} = \left[ {_L0,{R_L},0} \right]}\\ {{M_F} = \left[ {_F0,{R_F},0} \right]}\\ {{M_J} = \left[ {_J0,{R_J},0} \right]} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{R_1} = }\\ {{\rm{Begin}}:{\rm{State}} \to {\rm{Begi}}{{\rm{n}}_0}:{\rm{State}}{_{\left( {{\rm{in}}\left( 0 \right)} \right.}}|}\\ {{\rm{Succes}}{{\rm{s}}_0}:{\rm{State}} \to {\rm{Begi}}{{\rm{n}}_1}:{\rm{State}}{_{{\rm{in}}\left( L \right)}}|}\\ {{\rm{Succes}}{{\rm{s}}_{\rm{L}}}:{\rm{State}} \to {\rm{Begi}}{{\rm{n}}_{\rm{F}}}:{\rm{State}}{_{{\rm{in}}\left( F \right)}}|}\\ {{\rm{Fai}}{{\rm{l}}_0}:{\rm{State}} \to {\rm{Learnin}}{{\rm{g}}_0}:{\rm{State}}{_{{\rm{in}}\left( L \right)}}}\\ {{\rm{Fai}}{{\rm{l}}_1}:{\rm{State}} \to {\rm{Judge}}:{\rm{State}}{_{\left( {{\rm{in}}} \right)J}}|}\\ {{\rm{Fai}}{{\rm{l}}_{0'}}:{\rm{State}} \to {\rm{Learnin}}{{\rm{g}}_{0'}}:{\rm{State}}{_{{\rm{in}}\left( F \right)}}|}\\ {{\rm{Fai}}{{\rm{l}}_{\rm{L}}}:{\rm{State}} \to {\rm{Learnin}}{{\rm{g}}_0}:{\rm{State}}{_{{\rm{in}}\left( F \right)}}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{R_0} = }\\ {{\rm{Begi}}{{\rm{n}}_0}:{\rm{State}} \to {{\rm{L}}_0}:{\rm{State}}|}\\ {{{\rm{L}}_0}:{\rm{State}} \to {\rm{Succes}}{{\rm{s}}_0}:{\rm{State}}{_{{\rm{out}}}}|}\\ {{{\rm{L}}_0}:{\rm{State}} \to {\rm{Fail:}}{\rm{State}}{_{{\rm{out}}}}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{R_L} = }\\ {{\rm{Begin}}{{\rm{L}}_1}:{\rm{State}} \to {{\rm{L}}_1}:{\rm{State}}|}\\ {{{\rm{L}}_1}:{\rm{State}} \to {\rm{SuccessL:}}{\rm{State}}{_{{\rm{out}}}}|}\\ {{{\rm{L}}_1}:{\rm{State}} \to {\rm{Fai}}{{\rm{l}}_0}{\rm{:}}{\rm{State}}{_{{\rm{out}}}}|}\\ {{\rm{Fai}}{{\rm{l}}_0}{\rm{:}}{\rm{State}} \to {\rm{Learnin}}{{\rm{g}}_0}:{\rm{State}}{_{{\rm{out}}}}|}\\ {{\rm{Learnin}}{{\rm{g}}_0}:{\rm{State}} \to {\rm{Fai}}{{\rm{l}}_0}{\rm{:}}{\rm{State}}{_{{\rm{out}}}}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{R_F} = }\\ {{\rm{Begin}}{{\rm{L}}_1}:{\rm{State}} \to {{\rm{L}}_F}:{\rm{State}}}\\ {{{\rm{L}}_F}:{\rm{State}} \to {\rm{Success:}}{\rm{State}}{_{{\rm{out}}}}}\\ {{{\rm{L}}_1}:{\rm{State}} \to {\rm{Fai}}{{\rm{l}}_1}{\rm{:}}{\rm{State}}{_{{\rm{out}}}}|}\\ {{\rm{Learnin}}{{\rm{g}}_{0'}}:{\rm{State}} \to {\rm{Fail:}}{\rm{State}}{_{{\rm{out}}}}|}\\ {{\rm{Learnin}}{{\rm{g}}_L}:{\rm{State}} \to {\rm{Fai}}{{\rm{l}}_{\rm{L}}}{\rm{:}}{\rm{State}}{_{{\rm{out}}}}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{R_J} = }\\ {{\rm{Begi}}{{\rm{n}}_J}:{\rm{State}} \to {\rm{Fai}}{{\rm{l}}_L}:{\rm{State|}}}\\ {{\rm{Fai}}{{\rm{l}}_{\rm{I}}}:{\rm{State}} \to {\rm{Fai}}{{\rm{l}}_{0'}}:{\rm{Stat}}{{\rm{e}}_{{\rm{out}}}}|}\\ {{\rm{Fai}}{{\rm{l}}_{\rm{I}}}:{\rm{State}} \to {\rm{Fai}}{{\rm{l}}_L}:{\rm{Stat}}{{\rm{e}}_{{\rm{out}}}}} \end{array} $ |
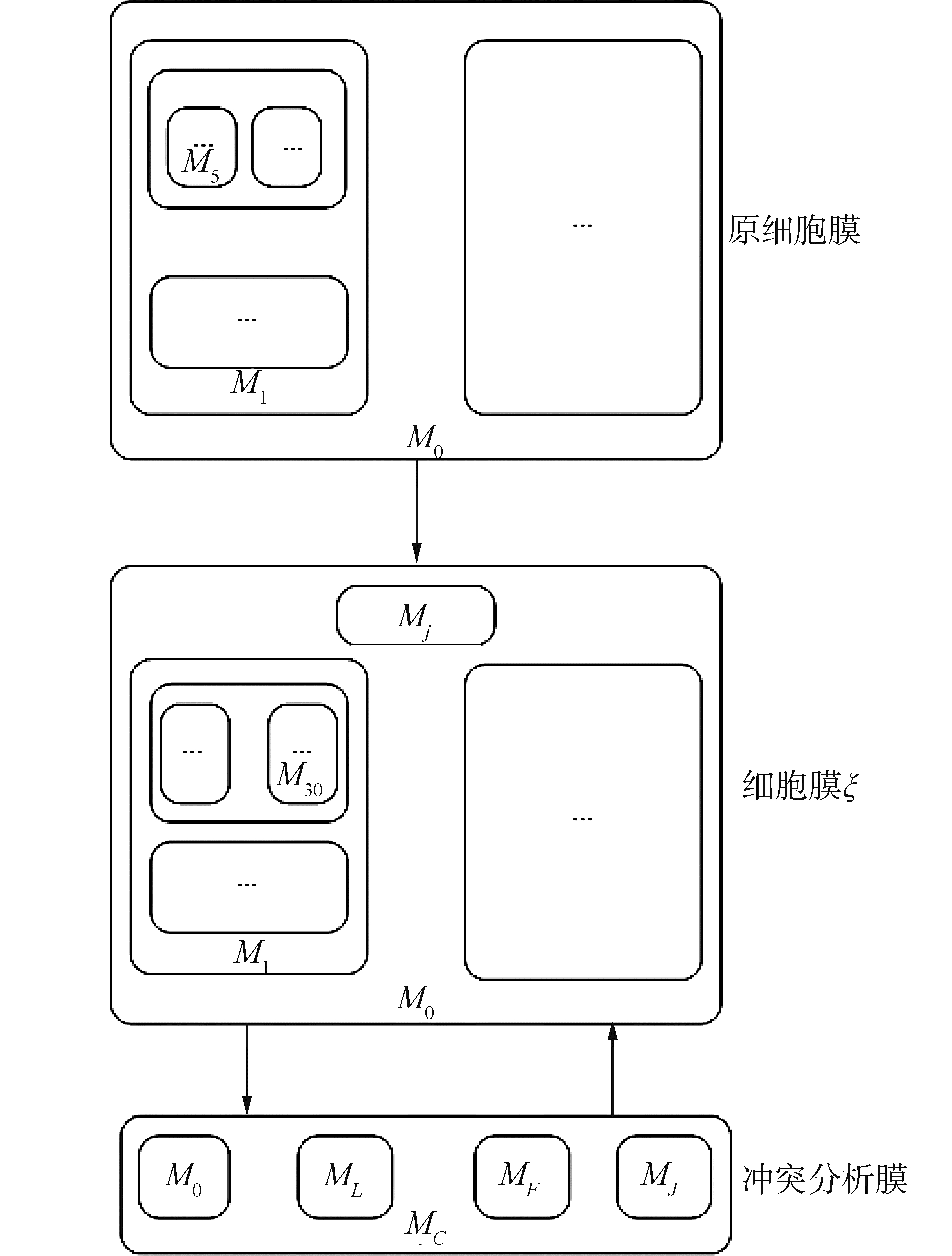
冲突分析的子事务表示为细胞膜MC,赋值第0层的子事务表示为细胞膜M0,决策层的子事务表示为细胞膜ML,冲突层的子事务表示为细胞膜MF,判定层的子事务表示为细胞膜MJ。在单元传播过程中,传播的成功和失败状态分别表示为Success、Fail,学习的子句表示为Learning,对冲突的判定表示为Judge。
开始时,细胞膜ζ从对象Judge开始,将子句集定义为重写规则Begin:State→Begin0:Statein(0),对象Begin被重写为Begin0并传入到子细胞膜M0中,即通过重写规则使子事务开始运行。若运行结果是成功的,则改写状态Success0并传入到子事务——细胞膜ML中;运行结果是失败的,则Fail并结束整个事务。若细胞膜ML成功,则传出到细胞膜MC。
同上,若细胞膜MC是成功的,那么子句集传出到细胞膜ζ判定整个事务成功。若冲突发生在子细胞膜ML中,则规则LI:State→Fail0:Stateout会将Fail0传出到规则,随后将再次传入细胞膜ML中,当规则Learning0返回到第0层而无法再次回溯时,返回到细胞膜ζ并结束整个过程。若细胞膜MC中发生冲突时,则冲突FailI会传入到另一个子细胞膜J中。这个冲突FailI为蕴含冲突,与Fail0冲突有着本质的不同:冲突FailI所包含的冲突,可能是决策层引起的冲突,亦可能是第0层引起的冲突。所以需要子细胞膜MJ对FailI进行判定。根据判定结果,若FailI是由某一决策层导致的,则将其状态判定为FailL,并根据回溯机制传出到细胞膜ML;若FailI是由第0层导致的,则根据回跳机制传出到细胞膜M0。
如图 2,假设冲突层是第5层,回跳层为第3层。带有子句学习的DPLL对决策变元赋值时,流程如下:当赋值存在于第0层时,当前层单元传播达到饱和状态后触发第0层产生第1层子细胞膜。当赋值到第0层时,以同样的顺序再传入第2层、第3层。当冲突出现在第5层时,冲突信息将由当前层反馈到上一层,随后强制反转当前层的决策赋值并再次进行单元传播。若第2次出现冲突,结束该膜的所有操作并传入冲突分析膜,进行冲突分析。
|
Download:
|
| 图 2 带子句学习的搜索过程 Fig. 2 Searching process with clause learning | |
本节对于例1所示的SAT算例展示经典的求解过程和细胞膜演算的形式化描述。
| $ 例\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {p \vee q \vee r}\\ {s \vee \neg r \vee p}\\ {\neg s \vee \neg t}\\ {u \vee \neg q}\\ t \end{array}} \right] $ |
该子句集包括6个变元、5条子句,经求解后存在若干个解。若变元u和p同时取F,便会导致一个冲突,从而使子句变得不可满足。
推理过程为:首先单元子句t = T,通过单元传播,使得s = F,进而子句集化简为:
随机选择变元u进行赋值u = F。通过单元传播使得q = F,进而子句集化简为:
若变元p赋值为p = F,通过单元传播使得r = T,所以
细胞膜描述过程为:
| $ \begin{array}{l} \left[ {{}_0t\left| {{S_0},t \to T,{S_0} \to {S_1},M} \right.} \right] \to \left[ {{}_1T\left| {{S_1},t \to T,} \right.} \right.\\ \left. {{S_0} \to {S_1},M} \right] \end{array} $ |
| $ \begin{array}{l} \left[ {{}_1s\left| {{S_1},s \to F,{S_0} \to {S_1},M} \right.} \right] \to \left[ {{}_1F\left| {{{S'}_1},S \to F,} \right.} \right.\\ \left. {{S_1} \to {{S'}_1},M} \right] \end{array} $ |
| $ \begin{array}{l} \left[ {{}_1u\left| {{{S'}_1},S \to F,{S_1} \to {{S'}_1},M} \right.} \right] \to \left[ {{}_2F\left| {{S_2},u \to F,} \right.} \right.\\ \left. {{{S'}_1} \to {S_2},M} \right] \end{array} $ |
| $ \begin{array}{l} \left[ {{}_2q\left| {{S_2},q \to F,{S_2} \to {{S'}_2},M} \right.} \right] \to \left[ {{}_2F\left| {{{S'}_2},q \to F,} \right.} \right.\\ \left. {{S_2} \to {{S'}_2},M} \right] \end{array} $ |
| $ \begin{array}{l} \left[ {{}_2p\left| {{{S'}_2},p \to F,{{S'}_2} \to {S_3},M} \right.} \right] \to \left[ {{}_3F\left| {{S_3},p \to F,} \right.} \right.\\ \left. {{{S'}_2} \to {S_3},M} \right] \end{array} $ |
| $ \begin{array}{l} \left[ {{}_3r\left| {{S_3},r \to T,{S_3} \to {{S'}_3},M} \right.} \right] \to \left[ {{}_3T\left| {{{S'}_3},r \to T,} \right.} \right.\\ \left. {{S_3} \to {{S'}_3},M} \right] \end{array} $ |
| $ \begin{array}{l} \left[ {{}_3\left( {r,\neg r} \right)\left| {{{S'}_3}} \right.,\left( {r,\neg r} \right) \to \emptyset ,{s_3} \to \emptyset ,M} \right] \to \\ \left[ {{}_3\emptyset \left| \emptyset \right.,{{S'}_3}\left( {r,\neg r} \right) \to \emptyset ,{S_3} \to \emptyset ,M} \right] \end{array} $ |
| $ \begin{array}{l} \left[ {{}_2p\left| {{{S'}_2},p \to T,{{S'}_2} \to {S_3},M} \right.} \right] \to \left[ {{}_2T\left| {{{S'}_3},p \to F,} \right.} \right.\\ \left. {{{S'}_2} \to {S_3},M} \right] \end{array} $ |
演化过程开始时,子句集产生于M0。当对象t赋值为真时,子细胞膜M1产生并与对象t建立了对应关系。由于s是单元传播决定的变元,所以s是同层变元,此时并不产生新的细胞膜,即仍然在细胞膜M1中。同上,当u赋值为假时,产生细胞膜M2。在DPLL过程中出现了互补文字对,即发生了冲突。该冲突导致当前层决策变元p取反,原变元所属的细胞膜溶解。此时,通过单元传播使子句集为空,子句集可满足。
5 结论1) 采用细胞膜演算的形式化方法描述带子句学习的DPLL算法,分别定义了部分赋值、变元反转、回溯、回跳最大层、细胞膜溶解等反应规则,给出了DPLL的一般过程和冲突分析过程的描述。最后通过一个算例来验证该形式化方法是可行的。
2) 选用计算机领域中最成功的SAT求解方法进行刻画,使得整个推理过程可以与细胞膜演算过程完全对应,展现了细胞膜演算的描述能力。
| [1] |
BEAME P, KAUTZ H, SABHARWAL A. Towards understanding and harnessing the potential of clause learning[J]. Journal of artificial intelligence research, 2004, 22: 319-351. DOI:10.1613/jair.1410 (  0) 0)
|
| [2] |
PIPATSRISAWAT K, DARWICHE A. On the power of clause-learning SAT solvers as resolution engines[J]. Artificial intelligence, 2011, 175(2): 512-525. DOI:10.1016/j.artint.2010.10.002 (  0) 0)
|
| [3] |
AUDEMARD G, LAGNIEZ J M, MAZURE B, et al. On freezing and reactivating learnt clauses[C]//Proceedings of the 14th International Conference on Theory and Applications of Satisfiability Testing. Ann Arbor, MI, USA: Springer, 2011: 188-200.
(  0) 0)
|
| [4] |
ATSERIAS A, FICHTE J K, THURLEY M. Clause-learning algorithms with many restarts and bounded-width resolution[J]. Journal of artificial intelligence research, 2011, 40: 353-373. DOI:10.1613/jair.3152 (  0) 0)
|
| [5] |
JABBOUR S, LONLAC J, SAIS L, et al. Revisiting the learned clauses database reduction strategies[J]. arXiv: 1402.1956, 2014.
(  0) 0)
|
| [6] |
HEULE M, JÄRVISALO M, LONSING F, et al. Clause elimination for SAT and QSAT[J]. Journal of artificial intelligence research, 2015, 53: 127-168. DOI:10.1613/jair.4694 (  0) 0)
|
| [7] |
戚正伟, 尤晋元. 基于细胞膜演算的Web服务事务处理形式化描述与验证[J]. 计算机学报, 2006, 29(7): 1137-1144. QI Zhengwei, YOU Jinyuan. The formal specification and verification of transaction processing in web services by membrane calculus[J]. Chinese journal of computers, 2006, 29(7): 1137-1144. DOI:10.3321/j.issn:0254-4164.2006.07.015 (  0) 0)
|
| [8] |
QI Zhengwei, LI Minglu, FU Cheng, et al. Membrane calculus:a formal method for Grid transactions:research articles[J]. Journal concurrency and computation:practice & experience, 2006, 18(14): 1799-1809. (  0) 0)
|
| [9] |
戚正伟, 尤晋元. 基于细胞膜演算的Web服务事务处理形式化描述与验证[J]. 计算机学报, 2006, 29(7): 1137-1144. QI Zhengwei, YOU Jinyuan. The formal specification and verification of transaction processing in web services by membrane calculus[J]. Chinese journal of computers, 2006, 29(7): 1137-1144. DOI:10.3321/j.issn:0254-4164.2006.07.015 (  0) 0)
|
| [10] |
戚正伟.细胞膜演算: 一种新的事务处理形式化方法研究[D].上海: 上海交通大学, 2005. QI Zhengwei. Membrane calculus: a new formal method for transaction processing[D]. Shanghai: Shanghai Jiao Tong University, 2005. (  0) 0)
|
| [11] |
任俊绮, 刘磊, 张鹏. 适用于演化过程建模的通信膜演算[J]. 哈尔滨工程大学学报, 2018, 39(4): 751-759. REN Junqi, LIU Lei, ZHANG Peng. Communication membrane calculus:a formal method for modeling the process of evolution[J]. Journal of Harbin Engineering University, 2018, 39(4): 751-759. (  0) 0)
|
| [12] |
刘磊, 刘丰, 任俊绮, 等. 基于细胞膜演算的Dryad形式化描述[J]. 哈尔滨工程大学学报, 2016, 37(11): 1539-1545. LIU Lei, LIU Feng, REN Junqi, et al. Formal description of Dryad based on membrane calculus[J]. Journal of Harbin Engineering University, 2016, 37(11): 1539-1545. (  0) 0)
|
| [13] |
LUO Mao, LI Chumin, XIAO Fan, et al. An effective learnt clause minimization approach for CDCL SAT solvers[C]//Proceedings of the 26th International Joint Conference on Artificial Intelligence. Melbourne, Australia: IJCAI, 2017: 703-711.
(  0) 0)
|
| [14] |
MOSKEWICZ M W, MADIGAN C F, ZHAO Ying, et al. Chaff: Engineering an efficient SAT solver[C]//Proceedings of the 38th Annual Design Automation Conference. Las Vegas, NV, USA: ACM, 2001: 530-535.
(  0) 0)
|
| [15] |
AUDEMARD G, SIMON L. Refining restarts strategies for SAT and UNSAT[C]//Proceedings of the 18th International Conference on Principles and Practice of Constraint Programming. Québec City, Canada: Springer, 2012: 118-126.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


