2. 哈尔滨工程大学, 海洋信息获取与安全工信部重点实验室, 黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001
2. Key Laboratory of Marine Information Acquisition and Security, Harbin Engineering University, Harbin 150001, China;
3. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
近年来随着现代水声信号处理技术和水声换能器技术的大幅度进步,水下目标精细探测和成像声呐技术已然成为了国内外研究的热点[1]。多波束测深声呐的接收换能器基阵通常具有几十至上百个基元,而基阵的指向性、目标方位波束响应等参数对多波束声呐的测量精度有很大影响,因此在进行系统调试前,应首先进行换能器基阵校准[2]。多波束测深声呐以及由其发展而来的多波束合成孔径声呐、多波束浅剖声呐等设备,通常需要按照预设波束角度成像,因此为了获得高质量的声呐图像必须得到准确的预设方位波束形成输出[3]。常用的海底地形检测方法(如时间加权平均算法)、基于相位差检测类的算法(如多子阵相位差检测算法)以及基于区间划分的多角度响应分类算法,同样依赖于精准的目标方位波束响应,因此对于声呐基阵系统参数的测量和校准是保证测量精度的前提条件[4]。常规的基阵指向性测量方法采用的是远场平面波模型,此方法的局限性在于平面波假设所需的远场测量距离很远,多阵元换能器基阵远场距离通常超过15 m,并且为避免池壁反射、混响等因素干扰,对测量水池的尺寸要求较为苛刻。当探测距离小于远场距离时,远场波束形成算法会引起目标方位模糊、图像散焦等问题[5]。常规方法中由于采用了自然累加的近似计算,忽略了阵元间距误差对波束形成算法产生的影响,此误差将导致回波到达方向(direction of arrival, DOA)估计的偏移。多阵元系统对接收信号存在阵增益效果,可以通过波束形成算法对信号进行相干叠加,提升声呐有效覆盖角度,因此基阵的波束指向性相比于自然指向性能够更准确地反映多波束测深系统的有效覆盖范围指标[6]。常规声呐校准方法一般仅单纯地进行换能器基阵校准,并没有综合考虑信号调理电路与基阵阵元耦合所导致的信号相位偏移,而这种相位偏移将引起信号处理算法中的相干累加相位误差,导致DOA估计出现偏差[7]。
针对以上问题,结合多波束测深系统实际工作需求,本文提出了一种多波束声呐基阵一体化自校准方法。在分析研究阵元间距误差对测深结果影响的基础上,通过聚焦波束形成技术在小尺寸水池条件下开展了实验研究,利用获得的目标方位波束角误差曲线对外场探测实验数据进行了归位补偿。该方法能够保障声呐的有效覆盖范围,具有较强的实用性和重要的工程应用价值与推广价值。
1 基础理论 1.1 换能器基阵信号模型在多波束测深系统中,一般采用一维均匀直线阵(ULA)作为信号接收基阵,其阵元间距设定为d = λ/2,其中λ为信号波长[8]。为了简化计算,接收信号形式一般近似于远场平面波假设,基阵由M阵元组成,当信号入射角为θ时,相邻两阵元之间的回波到达时延差为:
| $ {\tau _0} = \frac{d}{c}\sin \theta $ | (1) |
式中:d为阵元间距;c为当前时刻声速。为了在回波到达方向上形成一个主波束,需要对各阵元之间的时延差进行补偿,构造导向矢量为:
| $ \mathit{\boldsymbol{w}}\left( \theta \right) = {\left[ {\begin{array}{*{20}{c}} 1&{{{\rm{e}}^{ - {\rm{j}}\omega {\tau _0}}} \cdots {{\rm{e}}^{ - {\rm{j}}\omega \left( {M - 1} \right){\tau _0}}}} \end{array}} \right]^{\rm{T}}} $ | (2) |
通过基元接收到的信号构造协方差矩阵形如:
| $ \mathit{\boldsymbol{R}} = \frac{1}{N}\sum\limits_{t = 1}^N {\mathit{\boldsymbol{x}}\left( t \right){\mathit{\boldsymbol{x}}^{\rm{H}}}\left( t \right)} $ | (3) |
利用常规波束形成功率谱函数在观测区域内遍历各回波角度,得到常规波束形成输出:
| $ {P_{{\rm{CBF}}}}\left( \theta \right) = {\mathit{\boldsymbol{w}}^{\rm{H}}}\left( \theta \right)\mathit{\boldsymbol{Rw}}\left( \theta \right) $ | (4) |
为了实时向量化计算方便,PCBF(θ)可表示为:
| $ \begin{array}{*{20}{c}} {{P_{{\rm{CBF}}}}\left( \theta \right) = \frac{1}{N}\sum\limits_{t = 1}^N {{{\left| {y\left( {t,\theta } \right)} \right|}^2}} = }\\ {\frac{1}{N}\sum\limits_{t = 1}^N {{{\left| {\sum\limits_{i = 1}^M {{{\rm{e}}^{ - {\rm{j}}\left( {i - 1} \right)\omega {\tau _0}}}} } \right|}^2}} } \end{array} $ | (5) |
式中ω为信号在声速c条件下的角频率。
上述假设的有效范围是被测目标与基阵之间的距离rk

|
Download:
|
| 图 1 多波束基阵回波到达模型 Fig. 1 Echo model of the multibeam transducer array | |
此时需利用球面波扩展模型,计算目标到基阵的聚焦长度,采用Fresnel近似重新计算阵元间的时延差,修正导向矢量[10]。通过计算焦距得到扫描角度在θk时,第m号阵元与0阵元之间的相位差:
| $ {\varphi _{mk}} \approx - 2{\rm{ \mathsf{ π} }}\frac{{md}}{\lambda }\sin {\theta _k} + {m^2}{\rm{ \mathsf{ π} }}\frac{{{d^2}}}{{\lambda {r_k}}}{\cos ^2}{\theta _k} $ | (6) |
式中rk为扫描焦距,可以通过当前信号的采样序号n和系统采样频率fs计算得到。通过式(6)可以发现,远场平面波假设是近场球面波假设的一种近似情况,当焦距足够大的时候,式(6)中的第2项趋近于0,此时的相位差公式等价于远场条件,即在远场条件下直接应用近场聚焦波束形成算法其结果同样也是正确的。通过公式的对比,证明了在近场条件下的校准结果,是可以直接应用于目标处于远场的情况的。扫描角度θk方向上的波束形成输出结果可以表示为:
| $ V\left( {{\theta _k}} \right) = \sum\limits_{m = 0}^{M - 1} {{V_m}\left( {\cos {\varphi _{mk}} - {\rm{j}}\sin {\varphi _{mk}}} \right)} $ | (7) |
为了进一步验证近场聚焦波束形成对于近距离目标的成像效果,并评估该方法在小尺寸水池条件下对基阵进行校准的可行性,本文开展了目标回波模拟与成像算法仿真研究,仿真参数如表 1所示。
| 表 1 目标仿真参数 Table 1 Target simulation parameters |
通过图 2中的成像效果对比可以发现,当目标处于近场条件下时,回波按照球面波扩展,此时如仍然按照远场平面波假设进行波束形成会引起声呐图像散焦。靠近基阵一侧的目标无法分辨,分辨效果随目标距离的增加逐步好转。采用近场聚焦波束形成算法处理后的声呐图像较为清晰,在目标所处方位的回波能量集中,目标可以被分辨,因此该方法可以被应用于小尺寸水池环境下的基阵校准。

|
Download:
|
| 图 2 远场波束形成与近场聚焦波束形成输出对比 Fig. 2 Comparison of the far-field beamforming and the near-filed focused beamforming | |
对于声呐换能器的加工主要依赖于数控机床,其加工精度最高能达到0.01 mm(1丝),以中心频率为200 kHz的多波束声呐换能器基阵为例,其理论阵元间距d = λ/2 = 3.75 mm。由此可见,数控机床的加工误差已经能够影响到基阵的阵元间距精度,尤其是对于高频、多阵元系统,这种加工误差对声呐基阵的影响更为严重。伴随着上百阵元的切割进刀,此误差将会逐步累积,最终对阵元的平均间距产生较大影响[11-12]。由阵列信号处理理论可知,在基阵自然指向性函数中插入相移β可以得到所需扫描波束角方位θ的主极大输出,记为:
| $ \sin \theta = \frac{{\beta \lambda }}{{2{\rm{ \mathsf{ π} }}d}} $ | (8) |
当平均阵元间距存在误差Δd时,波束扫描角度发生偏移,记为:
| $ {\mathop{\rm si}\nolimits} n'\theta = \frac{{\beta \lambda }}{{2{\rm{ \mathsf{ π} }}\left( {d + \Delta d} \right)}} $ | (9) |
扫描得到的目标方位角误差Δθ = θ-θ′表示为:
| $ \Delta \theta = \arcsin \frac{{\beta \lambda }}{{2{\rm{ \mathsf{ π} }}d}} - \arcsin \frac{{\beta \lambda }}{{2{\rm{ \mathsf{ π} }}\left( {d + \Delta d} \right)}} $ | (10) |
在不同DOA情况下遍历平均阵元间距误差,得到目标方位波束角误差曲线如图 3所示。通过观察可以发现,DOA估计误差随着阵元间距误差的增大而增加,且呈不对称、非线性趋势。对于波达方向在θ = 70°的情况下,其DOA偏差将会超过1.2°,这将给近场聚焦波束形成计算和目标回波到达时间检测引入极大的误差。因此,为了保证多波束测深系统的测量精度,对基阵的平均阵元间距进行有效的估计与补偿是十分必要的。

|
Download:
|
| 图 3 波束到达方向误差曲线 Fig. 3 Error curves of the direction of arrival | |
多波束测深系统对于水底地形的检测首先需要利用预设波束角对波达时间进行空间归位,之后才能够获得测量目标的水深值及其水平坐标分布,因此如上文分析的DOA估计误差会对水底地形的检测与归位产生较大影响。给定目标所在真实深度H,当DOA估计存在偏差时,计算得到的深度值为:
| $ H' = \frac{H}{{\cos \theta }} \cdot \cos \left( {\theta + \Delta \theta } \right) $ | (11) |
测量值与真实值之间的误差ΔH = H-H′可表示为:
| $ \Delta H' = H\left( {1 - \frac{{\cos \left( {\theta + \Delta \theta } \right)}}{{\cos \theta }}} \right) $ | (12) |
选取波束到达角度在θ = 60°方位的不同深度值情况,在波束到达角度误差范围内遍历,得到深度值测量误差曲线如图 4(a)所示。通过观察可知,在波束到达角度相同的情况下,测量误差随着水深的增加而增大,逐渐超过IHO S-44标准所规定的误差范围[13-14]。选取深度值H = 20 m条件下的不同DOA方位情况,在波束到达角误差范围内遍历,得到深度值测量误差曲线如图 4(b)所示。通过观察可知,在深度值相同的情况下,测量误差随波束角的增加而增大,这将导致多波束测深系统外侧波束测量精度下降,声呐系统有效覆盖范围缩减。
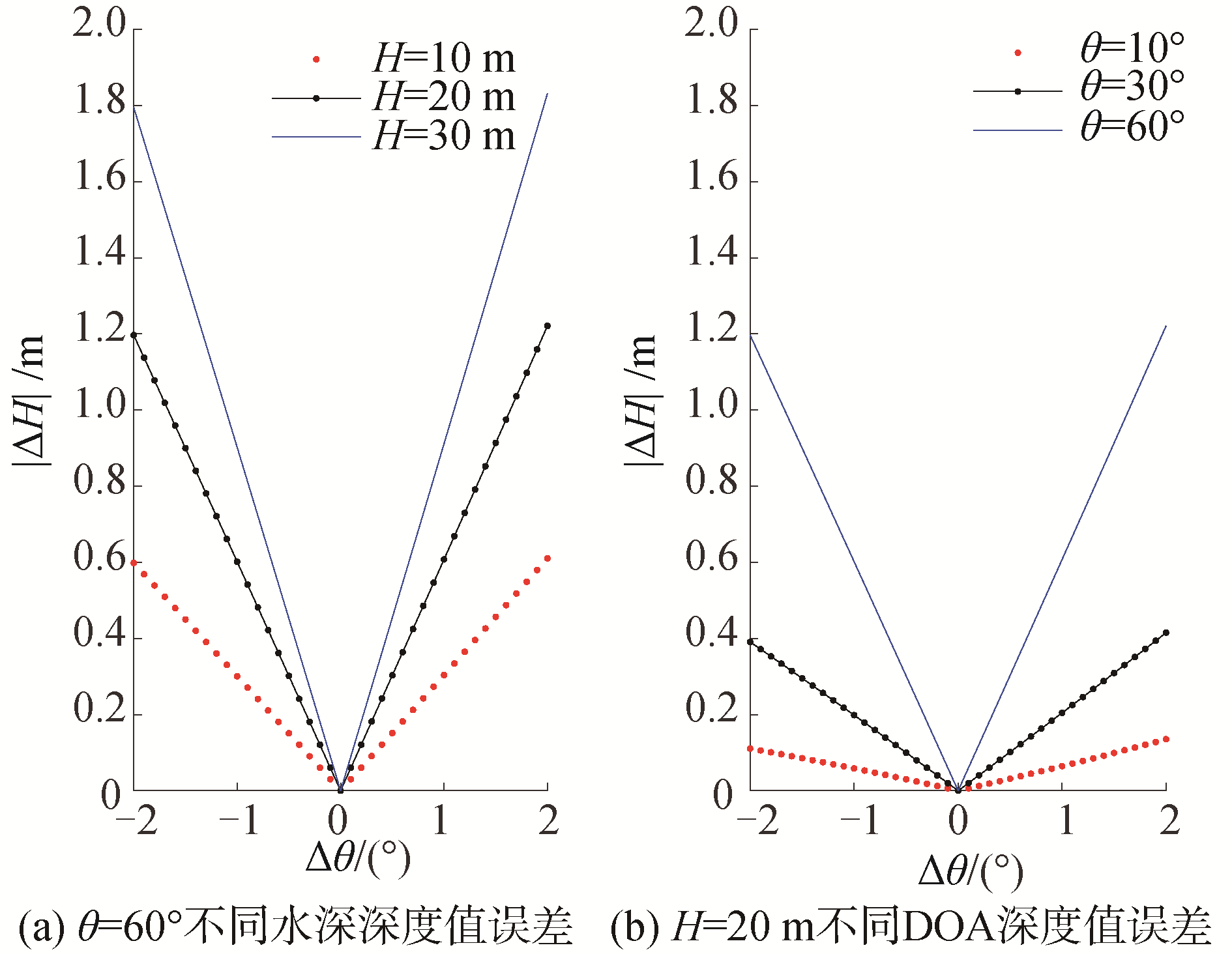
|
Download:
|
| 图 4 不同条件下深度测量误差曲线 Fig. 4 Depth error curve at different parameters | |
经过上述分析可知,当多波束声呐换能器基阵制造存在误差时,将会对系统的测量精度和有效覆盖范围产生较大的影响,并且由于换能器制造过程中的切割、硫化等工艺的特殊性及其产生误差的不均匀性、非对称性,无法直接利用机械原理测量误差[15-16]。因此,需要采取有效的测量方法对基阵误差进行测量,利用得到的波束到达方位误差曲线,对波束形成角度和深度值进行空间归位修正。
3 基阵一体化自校准方法研究 3.1 机械结构设定换能器测试水池需要使用高精度自动旋转定位装置,以固定角速度单向旋转基阵,避免频繁手动旋转引入空程误差。在待测换能器对向位置布放同频单基元发射换能器,布放深度正对待测换能器声中心,保持待测换能器水平放置。测量过程中,将发射换能器信号源与待测换能器电路同步信号相连,目标方位与采样时刻严格同步对应。利用声呐系统自有的信号调理电路、信号采集电路自动采集数据,数据文件按照采样时刻进行编号存储及索引,系统旋转机械结构如图 5所示,在每一个测量位置正对声源所在的方位角度都能够形成一个幅值最强的输出波束。

|
Download:
|
| 图 5 基阵旋转及波束指向性示意 Fig. 5 Rotating transducer array and the beam directivity | |
测量过程利用声呐基阵与电路系统的一体化测量,考虑电路系统与基阵耦合产生的信号相位偏移影响,评估待测声呐系统的目标方位波束响应特性。这种一体化测量方法,接近于声呐的实际工作条件,能够更加真实地反应换能器基阵的工作性能。本方法不需要直接测量阵元间距误差,而是通过测量在理论阵元间距参数下波束形成输出的DOA估计结果,得到目标方位波束角误差曲线,利用该曲线对系统预设波束角进行修正。
3.2 信号处理流程首先,根据待测换能器基阵与发射换能器的已知间距L计算指向波束角方向的回波到达斜距:
| $ {K_i} = L/\cos {\theta _i} $ | (13) |
实时采集当前测量水域声速c,将回波到达点数处于有效范围内的数据提取出来,压缩待测数据量,减少无效数据计算量,选取有效数据范围区间为:
| $ {N_i} \in \left[ {\left( {1 - \alpha } \right)\frac{{2{K_i}}}{{c{f_s}}},\left( {1 + \alpha } \right)\frac{{2{K_i}}}{{c{f_s}}}} \right] $ | (14) |
式中α为回波区间裕量。其次,按照式(6)、(7)对每Ping数据进行近场聚焦波束形成,其中波长λ和焦距等参数按照实时声速计算。对压缩后的数据输出选取波束包络极值并记录,在所有波束输出极值范围内遍历,寻找波束形成能量输出最大值位置D = argmax{D(n)}作为正对向发射换能器的中心波束。根据同相叠加原理,在待测换能器基阵正前方位置的波束同相叠加最充分,聚焦传输距离最近,波束形成输出最强,因此记录此位置文件号,作为中心波束位置。
再次,对中心波束位置所对应的数据文件再进行角度分辨率更高的近场聚焦波束形成,在角度轴上更细地划分出波束到达角刻度,找出波束输出极值位置对应的波束到达角度,观察其与0角度的偏差,修正各旋转位置对应的理论目标方位波束角。
最后,截取各波束文件输出最强波束所对应的回波角度,将其与理论目标方位波束角作差即可得到目标方位波束角误差曲线。记录各位置波束形成输出极值,经上述误差曲线修正后,选取回波极值-3 dB范围作为波束覆盖宽度,得到接收波束指向性图。对测量过程中双程往返测试数据求均值,用以降低测量误差。
4 实验验证 4.1 水池实验测量为了验证本文所提出方法的有效性,利用哈尔滨工程大学水声技术国家重点实验室消声水池对某国产多波束测深声呐系统接收换能器基阵进行校准。待测基阵中心频率200 kHz,阵元数目100,计算得到远场距离为18.75 m。本次实验为排除系统发射混响干扰和池壁反射回波影响,选择适当的测量间距8 m进行测试,水池结构示意图和待测换能器基阵布放相对位置如图 6所示。实验过程中只进行接收换能器的校准,因此需要将该多波束声呐的发射系统与声呐主机之间断开,不使用自身的发射换能器基阵,单独使用外置的单阵元发射换能器。
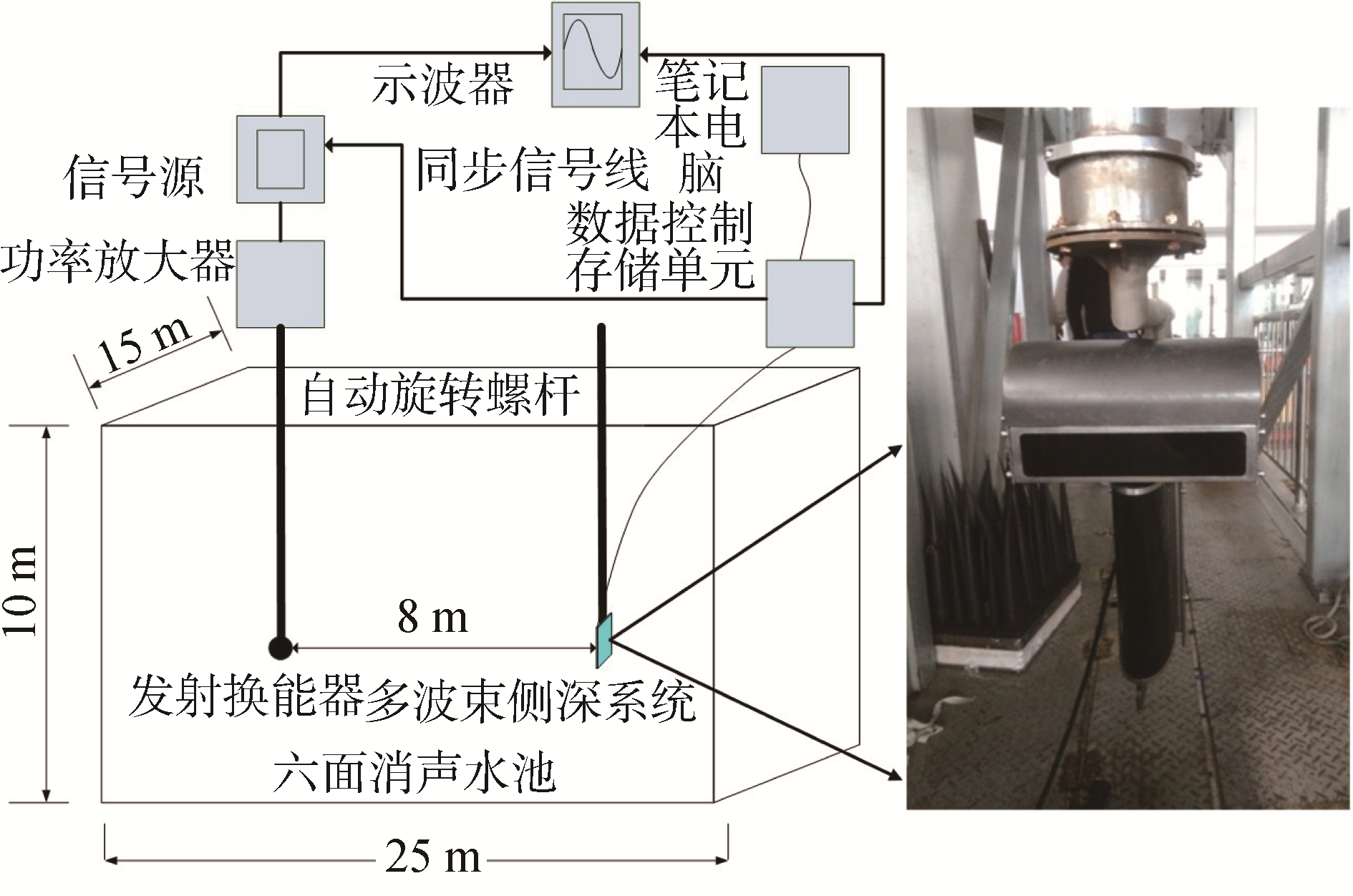
|
Download:
|
| 图 6 基阵布放位置示意 Fig. 6 Placement of the transducer array | |
实验现场使用到了高精度自动旋转装置单向定速旋转,自动采集回波数据。在发射换能器阵元和声呐主机之间建立同步信号,由声呐显控主机进行信号发射与采集的整体控制,确保信号发射与采集严格对时,保证声源所处方位与试验预设吻合。为了保证测量精度需使用较小的发射信号脉冲宽度,确保回波到达时刻估计准确,自动旋转机械与待测换能器工作参数如表 2所示。
| 表 2 实验现场工作参数 Table 2 Parameters of the field work |
经过数据压缩后的近场聚焦波束形成输出能量较为集中,对数据拼接后能够清晰地观察到波束到达方向曲线,如图 7所示。

|
Download:
|
| 图 7 波束到达方向输出 Fig. 7 Beamforming of the output of DOA | |
截取每Ping近场聚焦波束形成输出极值位置对应的波束到达角度方向,与理论波束角作差得到目标方位波束角误差曲线如图 8所示。通过观察可以发现,测量结果的最大波束角度误差达到0.6°,并且外侧波束误差较大,这将严重影响多波束测深系统的有效覆盖范围。利用该曲线进行多项式拟合,可以得到不同覆盖倍数工作参数下对应的所有预设波束角修正值,将经过修正后的波束角度作为多波束测深系统实时信号处理算法和图像后处理软件的预设波束角,就可以对声呐图像和水底检测结果进行空间归位修正。
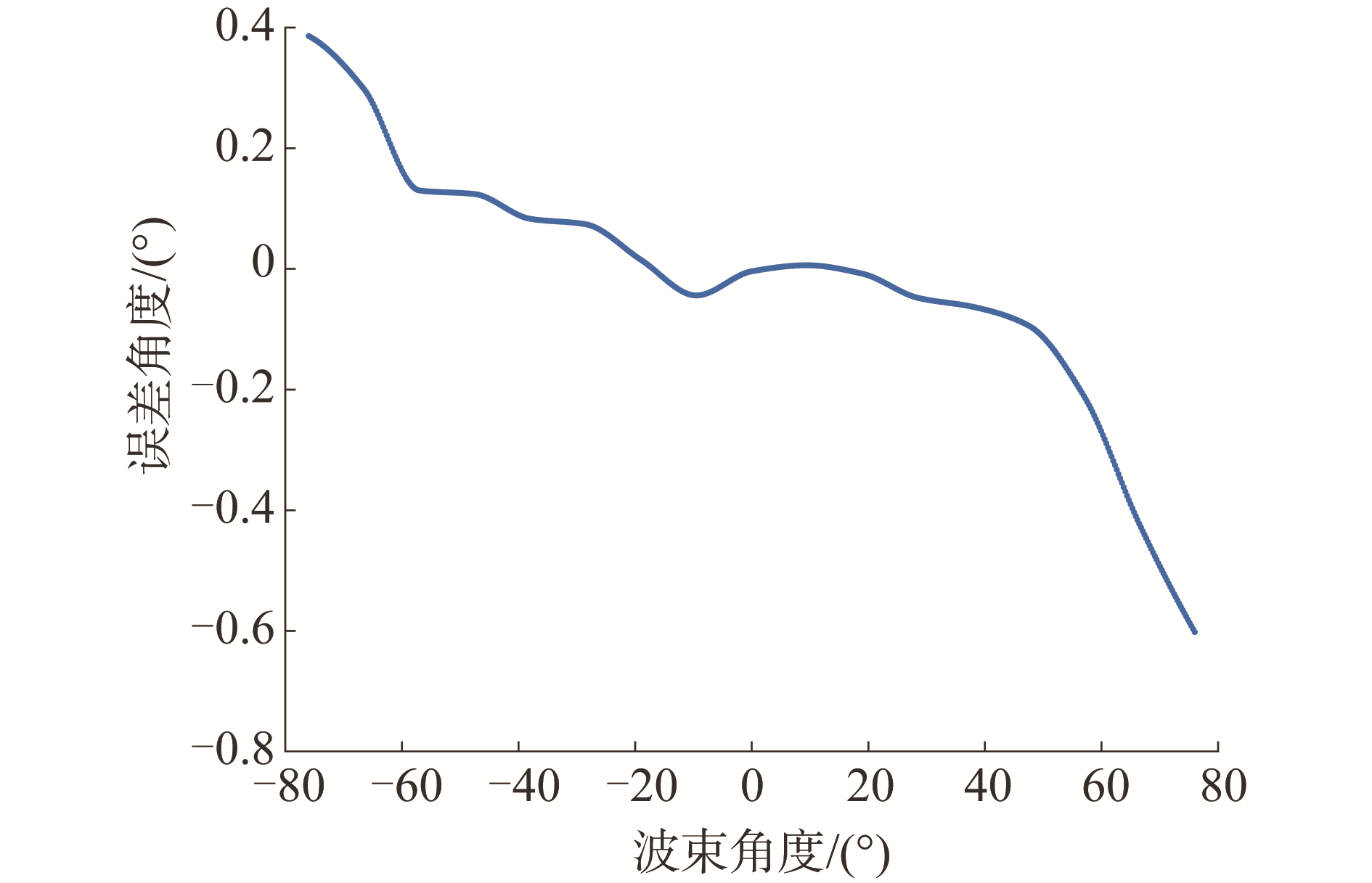
|
Download:
|
| 图 8 目标方位波束角误差曲线 Fig. 8 Error curve of the direction of arrival | |
遍历波束输出极值,选取回波极值-3 dB范围作为波束有效覆盖宽度,还得到接收波束指向性图如图 9所示。由该图可知,该基阵的-3 dB覆盖宽度超过130°,-6 dB覆盖宽度超过145°,能够满足该型号多波束测深系统的设计覆盖范围要求。
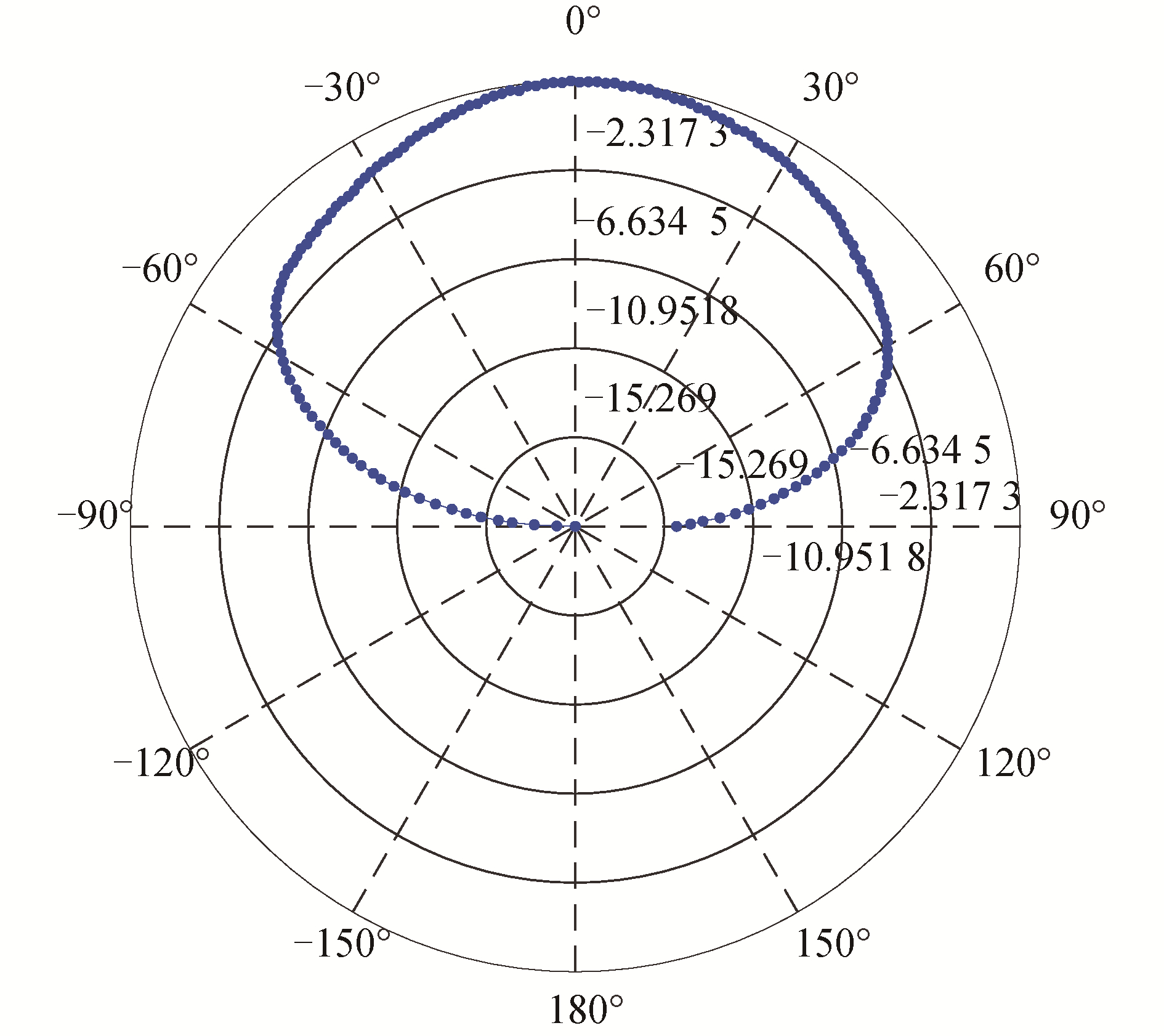
|
Download:
|
| 图 9 基阵波束指向性 Fig. 9 Beam directivity of the transducer array | |
为了进一步验证算法的有效性,本文针对被测多波束系统的某水域外场实验数据进行修正处理。其处理流程为:首先修正预设波束角度,其次进行波束形成算法处理,最后对检测到的回波斜距到达时间进行空间归位,修正前后测量结果对比如图 10所示。

|
Download:
|
| 图 10 波束角修正前后水底检测对比 Fig. 10 Comparison of the bottom detection results before and after the beam angle correction | |
图 10(a)为波束形成输出结果,表征了包含水体成像和水底探测结果的能量输出图像。通过观察可以得知,多波束测深声呐的水体成像能量输出较为散乱,并且外侧波束发生了展宽,不能够直接判定测量的水底深度值。此外,波束角修正前后的水体成像输出肉眼很难观测其差别,因此需要通过水底检测算法来详细对比修正前后的测量结果。通过图 10(b)的水底检测结果对比可以发现,未经过波束角修正的水底检测结果在外侧波束位置处测量值偏深,呈现弧形下垂虚假地形,测量可靠性较差,声呐的有效覆盖范围下降。经波束角修正后的水底地形检测结果处于正常区间内,地形未发生突变,声呐测量结果的可靠性和覆盖范围得到了有效的保证。修正前后的测量结果在中心波束位置吻合的较好,符合理论分析结果,这也验证了本文提出方法的有效性。
5 结论本文针对国产多波束测深系统的高精度探测需求,提出了一种多波束声呐基阵一体化自校准方法。分析了远场近似导致的目标方位探测误差,并推导了阵元间距误差对多波束测深系统测量结果产生的影响。通过换能器基阵和信号调理电路一体化自动测量的结构进行了换能器基阵自校准方法研究。在小尺寸水池条件下开展了实验,进行了换能器的指向性测量和目标方位波束响应校准,通过得到的目标方位波束角误差曲线对某声呐外场实验数据进行了归位补偿,其补偿结果显示,该方法能够保障声呐的有效覆盖范围。该方法具有较强的实用性和重要的工程应用性,具有可以在类似多阵元声呐系统校准中应用的推广价值。
| [1] |
周天, 欧阳永忠, 李海森. 浅水多波束测深声纳关键技术剖析[J]. 海洋测绘, 2016(03): 1-6. ZHOU Tian, OUYANG Yongzhong, LI Haisen. Key technologies of shallow water multibeam bathymetric sonar[J]. Hydro graphic surveying and charting, 2016(03): 1-6. DOI:10.3969/j.issn.1671-3044.2016.03.001 (  0) 0)
|
| [2] |
CHU D, BALDWIN K C, FOOTE K G, Y, et al. Multibeam sonar calibration: target localization in azimuth[C]//Oceans 2001. HI, USA, 2001: 2506-2510.
(  0) 0)
|
| [3] |
李海森, 魏波, 杜伟东. 多波束合成孔径声呐技术研究进展[J]. 测绘学报, 2017, 46(10): 1760-1769. LI Haisen, WEI Bo, DU Weidong. Technical progress in research of multibeam synthetic aperture sonar[J]. Cehui Xuebao/Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1760-1769. DOI:10.11947/j.AGCS.2017.20170410 (  0) 0)
|
| [4] |
XU C, LI H, CHEN B, et al. Angular response classification of multibeam sonar based on multi-angle interval division, Harbin, China, 2016[C]//Institute of Electrical and Electronics Engineers Inc., 2016: 1-4.
(  0) 0)
|
| [5] |
LI J, LIN Q, KANG C, et al. DOA estimation for underwater wideband weak targets based on coherent signal subspace and compressed sensing[J]. Sensors (Switzerland), 2018, 18(3): 1-19. (  0) 0)
|
| [6] |
TREES H L V. Detection, estimation, and modulation theory, Part Ⅳ, optimum array processing[J]. A papoulis probability random variables & stochastic processes, 2013, 8(10): 293-303. (  0) 0)
|
| [7] |
尹家亮.多波束测深声呐多通道接收机的设计与实现[D].哈尔滨: 哈尔滨工程大学, 2016. YIN Jialiang. Design and implementation of multi-channel receiver for multi-beam bathymetric sonar[D]. Harbin: Harbin Engineering University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10217-1017245294.htm (  0) 0)
|
| [8] |
吴自银. 高分辨率海底地形地貌:探测处理理论与技术[M]. 北京: 科学出版社, 2017: 78-80.
(  0) 0)
|
| [9] |
孙超. 水下多传感器阵列信号处理[M]. 西安: 西北工业大学出版社, 2007: 51-71.
(  0) 0)
|
| [10] |
李海森, 鲁东, 周天. 基于FPGA的多波束实时动态聚焦波束形成方法[J]. 振动与冲击, 2014(03): 83-88. LI Haisen, LU Dong, ZHOU Tian. Multi-beam real-time dynamic focused beam-forming method based on FPGA[J]. Journal of vibration and shock, 2014(03): 83-88. DOI:10.3969/j.issn.1000-3835.2014.03.017 (  0) 0)
|
| [11] |
刘瑞华.基于Sierpinski分形结构的小型宽带振动换能器的设计与制作[D].南京: 南京邮电大学, 2016. LIU Ruihua. Design and fabrication of a miniature broadband vibration transducer based on the sierpinski fractal structure[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10293-1016303288.htm (  0) 0)
|
| [12] |
孙继欣, 张宇, 朱永伟. 压电器件的精密超声复合电解加工技术[J]. 陕西师范大学学报(自然科学版), 2018(05): 32-38. SUN Ji-xin, ZHANG Yu, ZHU Yongwei. Design of precision ultrasonic compound electric maching for piezoelectric components[J]. Journal of Shaanxi Normal University(natural science edition), 2018(05): 32-38. (  0) 0)
|
| [13] |
董玉磊, 桑金. 海道测量规范与IHO标准的比较研究[J]. 海洋测绘, 2018(01): 59-62. DONG Yulei, SANG Jin. Comparative study on specifications for hydrographic survey and the IHO standard[J]. Hydro graphic surveying and charting, 2018(01): 59-62. DOI:10.3969/j.issn.1671-3044.2018.01.015 (  0) 0)
|
| [14] |
MALEIKA W, CZAPIEWSKI P. Visualisation of multibeam echosounder measurement data, Kolkata, India, 2013[C]//Springer Verlag, 2013: 373-380.
(  0) 0)
|
| [15] |
KUNTSAL E. A survey of transducer and sonar electroacoustic test and calibration facilities in the USA, 2010[C]//IEEE Computer Society, 2010: 1-6.
(  0) 0)
|
| [16] |
薛术.基于2-2型压电复合材料高频线阵换能器的仿真及工艺研究[D].西安: 西安电子科技大学, 2015. XUE Shu. Numerical simulation and process study of a high-frequency linear ultrasonic array based on 2-2 piezoelectric composite[D]. Xi'an: Xi'an Electronic and Science University, 2015. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D01068823 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


