2. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001
2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
水下人工目标在入射声波激励下产生的声散射成分的种类、数量及时序等参数与目标的尺度、形状、结构和材质等物理属性密切相关[1-2]。研究目标声散射成分的分离有助于分析和提取目标的声散射特征,对水下目标的探测和识别具有重要意义。但主动声呐工作系统受海底混响干扰,严重影响对目标的探测性能。盲源分离技术[3-4]是一种在缺少信源与信道先验知识的情况下,仅根据观测信号分离或恢复出目标信号的处理算法。其中,时频域盲分离算法[5-7]根据源信号在时频域的分布差异对源进行分离,其将混响等环境噪声干扰的能量散布在整个观测时频域中,提高了算法对背景干扰抑制的鲁棒性。该算法利用阵列接收数据构造观测信号的空间时频分布矩阵,需要选取目标回波的自项时频点,但实际测量环境存在混响及噪声等环境干扰,影响对自项时频点选取的准确性及分离性能。分数阶Fourier变换[8-10]从本质上来说可以看作是一种时频分析方法,它是将目标回波与混响时频面坐标轴在最佳角度下做逆时针旋转,并将信号的时频分布向旋转后的横坐标轴上做投影。由于目标回波具有较好的相位一致性,信号能量会聚集在一条脉冲上,表现为冲激形式。而混响是由大量散射信号叠加形成的,其声散射成分相位分布是随机的,不具有能量聚集性。因此,分数阶Fourier变换具有较好的抑制混响能力。分数阶Fourier变换适于处理具有线性调频性质的非平稳信号,具有与理想条件下匹配滤波相同的脉冲压缩性能,可以通过调整变换参数达到最佳匹配效果。文献[11]从理论上推导了目标几何声散射回波在分数阶Fourier变换域上的表达形式和特性,并分析了分数阶Fourier变换对多亮点分量的分辨能力。本文以此为基础,研究了目标声散射回波与混响在分数阶Fourier域的分离有效性。
1 主动声呐回波信号形成机理水下目标探测中,主动声呐接收的回波信号由目标回波、混响和环境噪声线性混合而成。对水下目标而言,严格的声散射理论会受到目标形状复杂,环境杂波干扰以及求解解析解难等条件的限制。而水下目标声散射回波的近似求解方法被广泛地应用于实际工程实践中。其中,亮点模型[12]可以较准确地描述水下简单目标的声散射传递函数。目标回波形成亮点是要满足一定条件:如目标为光滑凸面,kl>2π,k为波数,L为目标的尺度。
亮点模型将亮点回波的产生视为线性系统,利用包含幅度、相位、时延的传递函数进行描述。对于如图 1所示的半球头圆柱模型,仅考虑几何亮点,主要包括端面、圆柱侧面以及球头的镜反射和棱角1、2、3、4产生的棱角反射。用s(t)代表发射信号,目标回波信号可以视为若干个独立亮点信号的线性叠加,有:
| $ x\left( t \right) = \sum\limits_{i = 1}^I {{x_i}\left( t \right)} = \sum\limits_{i = 1}^I {{A_i}s\left( {t - {\tau _i}} \right){{\rm{e}}^{{\rm{j}}{\varphi _i}}}} $ | (1) |

|
Download:
|
| 图 1 目标模型结构 Fig. 1 The target model | |
式中:Ai、τi、φi分别是目标散射强度因子、时延因子与相位因子,与入射角度及具体亮点的类型有关;I是目标亮点数目。
混响是由小尺度、相互独立的随机散射体受激励产生的散射波线性叠加形成的。散射体在形状、尺度、密度上的不连续性,使得混响的时域波形表现出明显的随机性。假设海洋声场环境缓慢时变,且忽略散射过程的时变特性,用单元散射模型来描述混响的形成机理,混响本质上是水下众多散射体对入射声波散射的线性叠加[13-14]:
| $ R\left( t \right) = \sum\limits_{i = 1}^{N\left( t \right)} {K\left( t \right) \cdot s\left( {t - {\tau _i}} \right){{\rm{e}}^{{\rm{j}}{\varphi _i}}}} $ | (2) |
式中:K(t)代表信道传输损失、界面散射及收发设备指向性对混响幅度产生影响的因子,在目标时间尺度内,不会产生明显变化,近似是常数; N(t)是t时刻对混响有贡献的散射体数目;φi为随机相位,由信号的传输和散射过程决定。主动声呐接收回波用矩阵形式可以描述为:
| $ \mathit{\boldsymbol{x}}\left( t \right) = \mathit{\boldsymbol{As}}\left( t \right) + \mathit{\boldsymbol{n}}\left( t \right) = {\mathit{\boldsymbol{x}}_T}\left( t \right) + \mathit{\boldsymbol{r}}\left( t \right) + \mathit{\boldsymbol{n}}\left( t \right) $ | (3) |
式中:A代表从散射单元到接收系统的水下传输信道确定的混合矩阵。盲分离实质是以信号特性为基础建立一个以分离矩阵W为变元的目标函数J(W),并通过某种寻优算法使该对照函数达到极大(或极小)值时求解W,即为解混矩阵。
2 回波信号的分数阶Fourier域分布特性分数阶Fourier变换[15-16]将信号x(t)分解为u域上一组正交LFM基的线性组合,它既包含时(空)域信息,同时也包含频域信息。信号x(t)的分数阶Fourier变换定义为:
| $ {X_p}\left( u \right) = {F^p}\left[ {x\left( t \right)} \right] = \int_{ - \infty }^{ + \infty } {{K_p}\left( {t,u} \right)x\left( t \right){\rm{d}}t} $ | (4) |
式中:分数阶Fourier变换的阶数p可以取任意实数;Kp(t, u)为分数阶Fourier变换的变换核,有:
| $ {K_p}\left( {t,u} \right) = \left\{ \begin{array}{l} \left. {\sqrt {\left( {1 - {\rm{j}}\cot \alpha } \right)/2{\rm{ \mathsf{ π} }}} \cdot \exp \left( {{\rm{j}}\left( {{t^2} + {u^2}} \right)\cot \alpha - tu\csc \alpha } \right)/2} \right),\;\;\;\;\;\;\alpha \ne n{\rm{ \mathsf{ π} }}\\ \delta \left( {t - u} \right),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\alpha = 2n{\rm{ \mathsf{ π} }}\\ \delta \left( {t + u} \right),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\alpha = \left( {2n \pm 1} \right){\rm{ \mathsf{ π} }} \end{array} \right. $ | (5) |
式中:α(α = pπ/2)为旋转角度,若旋转α角度后信号的时频能量谱线垂直于横坐标轴,即信号能量聚集在一条脉冲上,此时的阶次p为最佳分数阶变换阶次。由分数阶Fourier变换的定义可以看出,分数阶Fourier变换是对信号x(t)的一维变换,不会产生交叉干扰项。分析其性质如下:
1) 线性叠加性质,即多个信号加权线性组合的分数阶傅里叶变换等效于对各信号作分数阶傅里叶变化后的加权线性组合,即:
| $ {\mathscr{F} ^p}\left[ {\sum\limits_n {{c_n}{x_n}\left( t \right)} } \right] = \sum\limits_n {c_n^p\left[ {{x_n}\left( t \right)} \right]} $ | (6) |
2) 阶次叠加性质,即:
| $ {\mathscr{F}^{{p_1}}}{\mathscr{F}^{{p_2}}} = {\mathscr{F}^{{p_1} + {p_2}}} $ | (7) |
由于0阶变换为信号本身,因此分数阶傅里叶变化存在着反变换形式。
3) 满足Parseval准则,即变换前后能量守恒:
| $ \int_{ - \infty }^{ + \infty } {{{\left| {x\left( t \right)} \right|}^2}{\rm{d}}t} = \int_{ - \infty }^{ + \infty } {{{\left| {{\mathscr{F}^p}\left[ {x\left( t \right)} \right]} \right|}^2}{\rm{d}}u} $ | (8) |
4) 时移性质,信号x(t)经时延τ形成的信号为x1(t) = x(t-τ),其分数阶傅里叶变换结果为:
| $ \begin{array}{*{20}{c}} {{X_{p1}}\left( u \right) = {}^p\left[ {{x_1}\left( t \right)} \right] = \exp \left( {{\rm{j \mathsf{ π} }}{\tau ^2}\sin \alpha \cos \alpha } \right) \cdot }\\ {\exp \left( { - {\rm{j}}2{\rm{ \mathsf{ π} }}u\tau \sin \alpha } \right){X_p}\left( {u - \tau \cos \alpha } \right)} \end{array} $ | (9) |
设目标回波的亮点模型如式(1),主动声呐发射LFM信号形式为:
| $ d\left( t \right) = \left\{ \begin{array}{l} {A_0}\exp \left( {{\rm{j}}2{\rm{ \mathsf{ π} }}{f_0}t + {\rm{j \mathsf{ π} }}u{t^2}} \right),\;\;\;\;t \in \left[ {0,T} \right]\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (10) |
时刻t亮点信号si(t) = Aid(t-τi)exp(jφi)的最佳分数阶Fourier变换为:
| $ {S_i}\left( \mu \right) = {A_{ip}}T\sin c\left[ {{\rm{ \mathsf{ π} }}T\left( {{f_0} - {u_i}{\tau _i} - \mu \csc {\alpha _i}} \right)} \right] $ | (11) |
式中:单亮点的最佳分数阶Fourier变换是与亮点信号斜率和时延有关的sinc函数。与目标单亮点信号比较,t时刻混响是大量具有不同幅度、时延及相位的散射回波叠加形成的信号,对其做p阶分数阶Fourier变换,根据性质4,由于大部分散射回波成分与目标亮点回波间存在时延差,因而不具有能量聚集性。
采用均匀线列阵接收回波信号,假设某一阵元接收信号为xi(t),其p阶分数阶Fourier变换为:
| $ \begin{array}{*{20}{c}} {x_{i1}^p\left( u \right) = \sqrt {\frac{{1 - {\rm{j}}\cot \alpha }}{{2{\rm{ \mathsf{ π} }}}}} \exp \left( {{\rm{j}}\frac{{{u^2}}}{2}\cot \alpha } \right) \cdot }\\ {\int_{ - T/2}^{T/2} {\exp \left[ {{\rm{j}}\frac{{{t^2}}}{2}\left( {\cot \alpha + {\mu _i}} \right) - {\rm{j}}t\left( {u\csc \alpha - {\omega _i}} \right)} \right]{\rm{d}}t} } \end{array} $ | (12) |
式中T为信号的观测时间。
搜索LFM信号在分数阶Fourier变换域的最优阶数,从而实现对信号参数的估计。即在分数阶Fourier域对xi1p(u)的能量值进行二维搜索,找出其峰值点对应的u1 m和αi,则信号的参数可由式(13)进行估计:
| $ {{\hat \mu }_i} = - \cot {\alpha _i},\;\;\;\;{{\hat \omega }_i} = {u_{1m}}\csc {\alpha _i} $ | (13) |
分数阶Fourier变换的旋转角αi = -arccotμi时,xi1p(u)有最好的能量聚集性。由式(11)可得第k个阵元上接收信号xi(t-τki)的分数阶Fourier变换也会出现最好的能量聚集,
| $ \begin{array}{*{20}{c}} {x_{ik}^p\left( {{u_{km}}} \right) = \exp \left[ { - {\rm{j \mathsf{ π} }}\left( {\tau _{ki}^2\sin {\alpha _i}\cos {\alpha _i} + } \right.} \right.}\\ {\left. {\left. {2{u_{km}}{\tau _{ki}}\sin {\alpha _i}} \right)} \right] \cdot x_{i1}^p\left( {{u_{1m}}} \right)} \end{array} $ | (14) |
其峰值对应变换域位置为:
| $ {u_{km}} = {u_{1m}} + {\tau _{ki}}\cos {\alpha _i} $ | (15) |
由于时延τki非常小,其平方项可以忽略不计,式(14)可以近似为:
| $ x_{ik}^p\left( {{u_{km}}} \right) = \exp \left( { - {\rm{j}}2{\rm{ \mathsf{ π} }}{u_{km}}{\tau _{ki}}\sin {\alpha _i}} \right) \cdot x_{k1}^p\left( {{u_{1m}}} \right) $ | (16) |
此时,LFM信号已经变成了分数阶Fourier域的单频平稳信号,得到分数阶Fourier域信号的混合向量矩阵为:
| $ {\mathit{\boldsymbol{A}}_p} = \left[ {\begin{array}{*{20}{c}} 1\\ {\exp \left( { - {\rm{j}}2{\rm{ \mathsf{ π} }}{u_{1m}}{\tau _{2i}}\sin {\alpha _i}} \right)}\\ \vdots \\ {\exp \left( { - {\rm{j}}2{\rm{ \mathsf{ π} }}{u_{1m}}{\tau _{Mi}}\sin {\alpha _i}} \right)} \end{array}} \right] $ | (17) |
在u1 m和αi已知的条件下,方向向量只与时延有关。根据分数阶Fourier变换性质1,取声呐接收阵列信号分数阶Fourier变换结果xp(uim)的自相关运算为:
| $ \begin{array}{*{20}{c}} {R_{xx}^p = {\rm{E}}\left[ {{x^p}{{\left( {{x^p}} \right)}^{\rm{H}}}} \right] = }\\ {{\mathit{\boldsymbol{A}}_p}{\rm{E}}\left[ {s_{i1}^p\left( {{u_{im}}} \right)s_{i1}^p{{\left( {{u_{im}}} \right)}^{\rm{H}}}} \right]A_p^{\rm{H}} + {\rm{E}}\left[ {{n^p}\left( t \right)\;\;{{\left( {{n^p}\left( t \right)} \right)}^{\rm{H}}}} \right]} \end{array} $ | (18) |
盲分离通常假设源信号间满足独立或者弱相关的特性,那么n个源信号si的自相关函数矩阵Rs = diag (rs1, rs2, …, rsn)是一个对角阵,但在实际应用中由于环境干扰的存在以及对非平稳数据截断带来的计算误差,信号的完全对角化是不能实现的,通常通过对自相关矩阵进行近似对角化处理求解解混矩阵,即使自相关矩阵的非对角线元素之和最小:
| $ C\left( W \right) = \sum\limits_{i = 1}^K {{\rm{off}}\left( {{W^H}R_{xx}^pW} \right)} $ | (19) |
实际处理的声呐回波信号均为数字信号,利用采样型算法对分数阶Fourier变换进行离散化处理。
3 目标声散射回波与混响在FRFT域的盲分离1) 对阵元接收信号进行平稳化处理,并计算声散射信号的理论分数阶幂p;
2) 确定声散射信号的最优变换阶数。在理论分数阶幂周围进行L次的分数阶Fourier变换,得到一系列声散射回波在变换域的能量分布,并对其进行谱峰搜索,找出谱峰能量最大值对应的um,认为是目标实际的峰值点位置;
3) 设计u域窄带滤波器Wp,在u域构造观测数据的广义协方差矩阵
4) 对滤波后的广义协方差矩阵
研究FRFTBSS算法的分离性能,对比分析FRFTBSS算法和经典时频域盲分离(TFBSS)算法在不同输入信混比条件下对目标声散射信号的分离能力,结果如图 2所示。

|
Download:
|
| 图 2 算法分离性能比较 Fig. 2 The performance comparison of the different algorithms | |
从图 2中可以看出,在整个输入信混比变化范围内(-15 dB,0 dB),FRFTBSS算法的输出信混比增益变化不大,算法均有效。相比于FRFTBSS算法,当输入信混比从-15~-10 dB变化时,TFBSS算法的输出增益接近于零,即无输出增益,算法失效。这是因为TFBSS算法通过设定阈值对空间时频分布矩阵的迹和特征值进行约束来选取自项信息,信源自项时频点选取的准确性与阈值大小有关,而阈值设置受背景干扰影响严重。FRFTBSS算法根据目标回波与混响的能量聚集性差异,提高了对混响的抑制能力,分离目标回波信号信混比高。
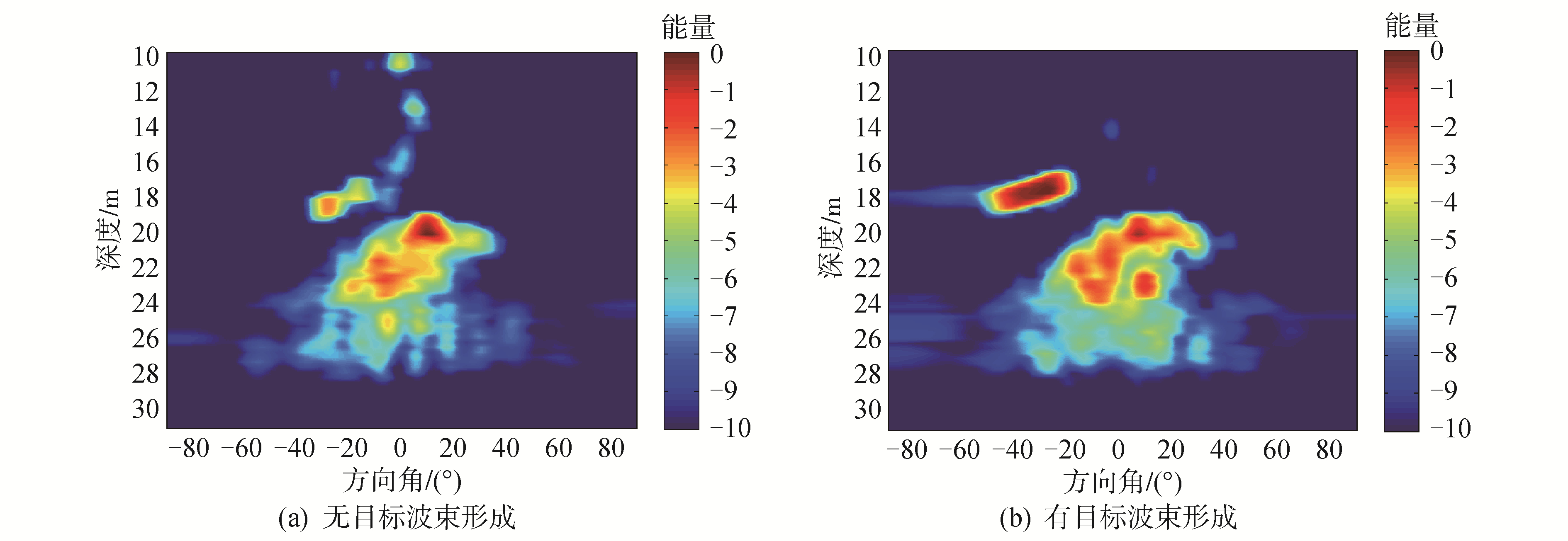
5 海试掩埋数据处理与分析为进一步验证本文方法在实际水下小目标探测中的应用效果,现对海上掩埋目标回波实验数据进行处理。实验采用收发合置声呐系统,发射宽带线性调频信号,归一化频率范围0.03~0.06,接收基阵为均匀线列阵。实验采用“走航梳理”的方式对回波信号进行采集,单航次数据中包含多个脉冲回波信号,为了将盲分离算法高效地应用于对目标声散射信号分离中,需要在每一航次的大量回波文件中预判包含掩埋目标的回波文件。实验以与掩埋目标相连的悬浮目标做参考,标示可能存在掩埋目标回波的文件号。根据水深、基阵下水位置、基阵掠射角、目标掩埋深度等参数,可以在回波时间波形上大概确定悬浮目标回波与掩埋目标回波的存在位置。利用FRFT域分离算法对存在掩埋目标回波的数据段进行处理,达到抑制混响,分离目标声散射回波的目的。选取悬浮目标所在脉冲,给出脉冲回波数据的方位-深度空间谱,进而判断掩埋目标存在与否。空间谱计算如下:对接收数据加窗处理,取与发射信号脉宽相同的窗函数长度,重叠步长取窗长的1/10,在窗长内取各个阵元信号的加权和作为窗内目标回波的能量,空间谱估计结果如图 3所示。
|
Download:
|
| 图 3 回波数据波束形成结果 Fig. 3 Beamform results of the sonar echoes | |
分别取无目标和有目标的回波文件处理得到的空间谱图。从图 3中可以看出,海底散射能量散布在一定方位角度范围内,其强度主要集中在水深20 m处,悬浮目标能量主要集中在水深约16 m处,目标方位-30°处。与图 3(a)无目标时的空间谱图对比,图 3(b)中在水深23 m处的信号能量可能是由掩埋目标产生的。
取存在掩埋目标回波的数据进行处理与分析,图 4(a)是取掩埋目标回波所在数据段的时频分布,观测信号在时频域的图像是随机的点或面状区域,信号能量随机散布在整个信号持续时间及频带内,不能判断是否存在掩埋目标回波。对数据进行时频盲分离处理,给出分离信号的时频结构分布,为了便于观察分析,对分离信号的时频结构进行时频滤波进一步抑制干扰,结果如图 4(b)所示,得到间断的线谱,并不能判断其是目标亮点的自项时频谱,TFBSS分离算法失效。采用FRFTBSS算法对数据进行处理,图 4(c)是信号FRFT谱在u域投影,根据信号FRFT谱信息进行分离处理,得到目标声散射信号的时频结构滤波结果,如图 4(d)所示。分离信号在时频面是一条连续的亮点谱线,由于所分析的数据是根据实验设计选择的掩埋目标所在位置,因而可以判断分离出的线谱为掩埋目标的几何散射回波,利用FRFTBSS算法实现了对掩埋目标声散射回波的分离,提高了信混比,验证了算法的分离有效性。

|
Download:
|
| 图 4 掠射角75°的掩埋目标分离 Fig. 4 Buried target separation at grazing angle 75° | |
1) 依据在分数阶Fourier域中海底混响和目标回波时频能量聚集特性的差异性,构建了最佳分数阶Fourier域广义相关矩阵构建目标函数。
2) 采用分数阶Fourier域构建的目标函数,实现了目标声散射回波与混响的分离。解决了时频域盲分离算法受混响干扰严重,不能准确地选取目标亮点的自项时频信息的局限性,
3) 仿真研究与海试掩埋数据处理结果表明,与时频域盲分离算法相比分数阶Fourier域盲分离算法在低信混比下分离目标回波信号是可行性和有效性。
研究的混响背景下的目标回波信号分离方法,也可用于水下沉船和考古等探测领域。
| [1] |
WATERMAN P C. New formulation of acoustic scattering[J]. The journal of the acoustical society of America, 1969, 45(6): 1417-1429. DOI:10.1121/1.1911619 (  0) 0)
|
| [2] |
DERBESSE L, PERNOD P, LATARD V, et al. Acoustic scattering from complex elastic shells:visualization of S0, A0 and A waves[J]. Ultrasonics, 2000, 38(1/2/3/4/5/6/7/8): 860-863. (  0) 0)
|
| [3] |
GINOLHAC G, JOURDAIN G. "Principal component inverse" algorithm for detection in the presence of reverberation[J]. IEEE journal of oceanic engineering, 2002, 27(2): 310-321. DOI:10.1109/JOE.2002.1002486 (  0) 0)
|
| [4] |
GINOLHAC G, JOURDAIN G. "Principal component inverse" algorithm for detection in the presence of reverberation[J]. IEEE journal of oceanic engineering, 2002, 27(2): 310-321. DOI:10.1109/JOE.2002.1002486 (  0) 0)
|
| [5] |
杨阳, 李秀坤. 水下目标声散射信号的时频域盲抽取[J]. 物理学报, 2016, 65(16): 164301. YANG Yang, LI Xiukun. Blind source extraction based on time-frequency characteristics for underwater object acoustic scattering[J]. Acta physica sinica, 2016, 65(16): 164301. DOI:10.7498/aps.65.164301 (  0) 0)
|
| [6] |
ANDERSON S D, SABRA S G, ZAKHARIA M E, et al. Time-frequency analysis of the bistatic acoustic scattering from a spherical elastic shell[J]. The journal of the acoustical society of America, 2012, 131(1): 164-173. DOI:10.1121/1.3669995 (  0) 0)
|
| [7] |
ANDERSON S D. Time-frequency methods for the analysis of multistaic acoustic scattering of elastic shells in shallow water[D]. Atlanta, USA: Georgia Institute of Technology, 2011: 1-20.
(  0) 0)
|
| [8] |
WANG Ruhang, HUANG Jianugo, ZHANG Yujie. An improved prewhitening method for LFM reverberation in shallow sea using frequency focusing transformation[C]//20102nd International Conference on Signal Processing Systems. Dalian, China, 2010.
(  0) 0)
|
| [9] |
JIA Hongjian, LI Xiukun, MENG Xiangxia. Rigid and elastic acoustic scattering signal separation for underwater target[J]. The journal of the acoustical society of America, 2017, 142(2): 653-665. DOI:10.1121/1.4996127 (  0) 0)
|
| [10] |
王强, 潘翔. 水下沉底小目标回波的短时FrFT滤波分析[J]. 浙江大学学报:工学版, 2008, 42(6): 918-922. WANG Qiang, PAN Xiang. Analysis of small underwater bottomed target echo time-frequency filter characteristics based on short-time FrFT[J]. Journal of Zhejiang university:engineering science, 2008, 42(6): 918-922. (  0) 0)
|
| [11] |
李秀坤, 孟祥夏, 夏峙. 水下目标几何声散射回波在分数阶傅里叶变换域中的特性[J]. 物理学报, 2015, 64(6): 064302. LI Xiukun, MENG Xiangxia, XIA Zhi. Characteristics of the geometrical scattering waves from underwater target in fractional Fourier transform domain[J]. Acta physica sinica, 2015, 64(6): 064302. (  0) 0)
|
| [12] |
汤渭霖. 声呐目标回波的亮点模型[J]. 声学学报, 1994, 19(2): 92-100. TANG Weilin. Highlight model of echoes from sonar targets[J]. Acta acustica, 1994, 19(2): 92-100. (  0) 0)
|
| [13] |
HARRISON C H. An approximate form of the Rayleigh reflection loss and its phase:application to reverberation calculation[J]. The journal of the acoustical society of America, 2010, 128(1): 50-57. DOI:10.1121/1.3372731 (  0) 0)
|
| [14] |
TANG Dajun, JACKSON D R. Application of small-roughness perturbation theory to reverberation in range-dependent waveguides[J]. The journal of the acoustical society of America, 2012, 131(6): 4428-4441. DOI:10.1121/1.4707437 (  0) 0)
|
| [15] |
QI Lin, TAO Ran, ZHOU Siyong, et al. Detection and parameter estimation of multicomponent LFM signal based on the fractional Fourier transform[J]. Science in China F:information sciences, 2004, 47(2): 184-198. DOI:10.1360/02yf0456 (  0) 0)
|
| [16] |
ZHAO Yanbo, YU Hua, WEI Gang, et al. Parameter estimation of wideband underwater acoustic multipath channels based on fractional fourier transform[J]. IEEE transactions on signal processing, 2016, 64(20): 5396-5408. DOI:10.1109/TSP.2016.2582466 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


