2. 中国科学院 水声环境特性重点实验室, 北京 100190
2. Key laboratory of underwater Acoustics Environment, Chinese Academy of Sciences, Beijing 100190, China
声传播问题一直是水声工作者们研究的热点和难点[1-6]。对于中远距离的声场预报,尤其对于浅海或者存在等温层表面声道的水声环境,粗糙海面对声传播的影响较为显著。Zhou等[7]指出海面作用在混响或者声传播模型中具有重要作用,即使单次碰撞的海面作用产生较小的影响,但在长距离的混响或传播中却具有累积效果,因此粗糙海面下的声传播模型的研究具有重要意义,关于粗糙海面对声传播影响的研究在早期就已经引起了学者们的广泛关注[8-12]。
Williams等[13]基于PM谱[14]研究了粗糙海面反射系数问题;Jones等[15-17]基于PM谱粗糙海面比较了KA(kirchhoff approximation,KA)散射方法和SSA(small slope approximation,SSA)散射方法计算的海面反射损失,并与海试数据做了比较,还利用Bellhop仿真计算了平滑海面、粗糙海面不考虑气泡影响和粗糙海面考虑气泡影响时的传播曲线。
学者们对粗糙海面反射系数和粗糙海面反射损失的研究最终是为了解决粗糙海面下的声传播问题,本文直接着眼于粗糙海面声传播计算方法,比较分析了几种典型的粗糙海面声传播计算方法:Krakenc-KA声传播模型、Krakenc-SSA声传播模型和Ramsurf声传播模型,为粗糙海面下的声传播研究提供模型基础。Krakenc粗糙海面声传播模型是通过TRC(top reflection coefficient)文件输入平均海面反射系数,平均海面反射系数可以根据不同的散射理论计算得到,例如常用的KA方法、适用性较广的SSA方法等。而Ramsurf粗糙海面声传播模型是基于monte-carlo方法产生一维粗糙海面,可根据海区的具体情况选取多种不同的风浪谱模型。Ramsurf计算海底地形变化条件下的粗糙海面下的声场更为方便。
Ramsurf、Krakenc是已有的粗糙海面传播模型,Krakenc-KA和Krakenc-SSA分别是作者基于KA散射理论和SSA散射理论提出的;本文通过仿真实验比较了几种典型的粗糙海面声传播计算方法,并通过海试数据分析了Ramsurf粗糙海面声传播计算方法的有效性。
1 粗糙海面下的声传播模型 1.1 单粗糙海面下的声传播模型:Krakenc-KA和Krakenc-SSA粗糙海面条件下可根据实际情况选择不同散射理论计算海面反射系数。例如较常用的KA方法、适用性较广的SSA方法等。据此,典型的粗糙海面声传播模型有Krakenc-KA模型和Krakenc-SSA模型, 下面将给出KA方法和SSA方法计算平均海面反射系数的公式。
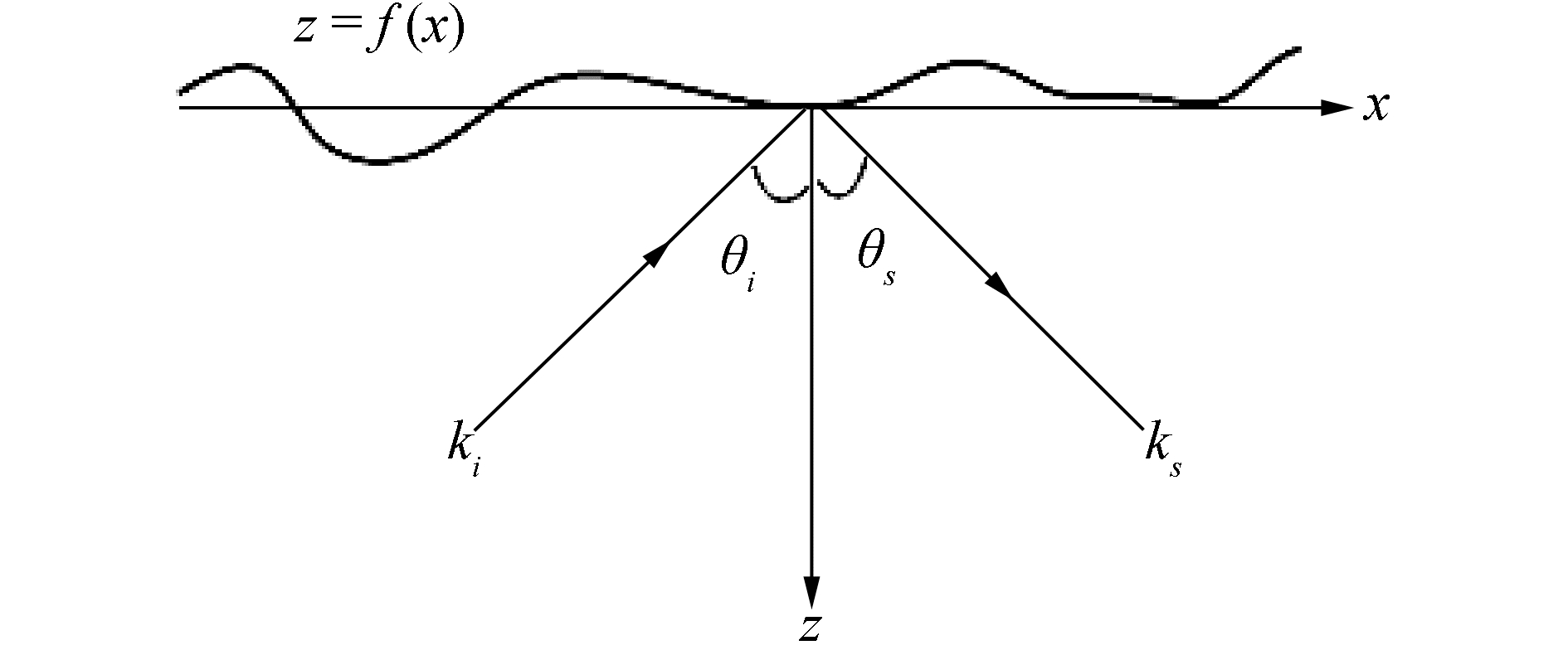
考虑入射到粗糙海面z = f(x)上的入射平面波为exp(iki · r),其中,
| $ \mathit{\boldsymbol{r}} = \left( {x, z} \right), {k_i} = ({k_{ix}}, {k_{iz}}) = ({k_{ix}}, -{\kappa _{iz}}) $ |
并且有:
| $ {\kappa _{iz}} = {[{k^2}-{k_{ix}}^2]^{1/2}} > 0 $ |
式中k = ω/c是辐射波数。
|
Download:
|
| 图 1 一维粗糙海面散射示意 Fig. 1 Scattering sketch map for one-dimensional rough sea surface | |
令
| $ \mathit{\boldsymbol{v}} = {\mathit{\boldsymbol{k}}_i}-{\mathit{\boldsymbol{k}}_s} = ({\mathit{\boldsymbol{v}}_x}, -{\mathit{\boldsymbol{v}}_z}), \;{\mathit{\boldsymbol{v}}_x} = {\mathit{\boldsymbol{k}}_{ix}}-{\mathit{\boldsymbol{k}}_{sx}} $ |
| $ {\mathit{\boldsymbol{v}}_z} = {\mathit{\boldsymbol{\kappa }}_{iz}} + {\mathit{\boldsymbol{k}}_{sz}}, {\rm{ }}k{\beta _{1 + i}} = {[{k^2}-{({K_1} + {k_{ix}})^2}]^{1/2}} $ |
并且有:
| $ {\rm{Im}}[{\beta _{1 + i}}] > 0, {\rm{ }}k{\beta _{s - 1}} = [{k^2}-{({k_{sx}}-{K_1})^2}] $ |
式中:
最终可以得到小斜率近似下的反射系数为:
| $ {R_A}({k_{ix}}) \approx {\rm{exp}}\left[{-\frac{{{v_z}^2{h^2}}}{2}} \right][-1 + {\kappa _{iz}}\int {{\rm{d}}{K_1}W({K_1})g({K_1})}] $ | (1) |
式中:等号右侧的第1项是KA模型的反射系数计算结果,注意到KA模型只需要用到粗糙海面的波高均方根h。
1.2 粗糙海面下的声传播模型:Ramsurf粗糙海面边界条件下的Ramsurf声传播模型是一种修正的PE算法声场模型,它可基于不同波浪谱的粗糙海面模型,利用Monte-Carlo方法生成一维粗糙海面,作为粗糙海面边界条件下的Ramsurf声场传播模型的海面边界条件输入,可计算粗糙海面条件下的声场。这种方法考虑了不同粗糙海表剖面斜率下的影区衍射效应和不同程度的透射效应,另外,Ramsurf模型只考虑了前向散射,不适用于强界面引起的后向散射问题。
下面介绍一维粗糙海面建模的Monte-Carlo方法。
粗糙表面被认为是由大量的谐波叠加而成,谐波的振幅是独立的高斯随机变量,其方差正比于特定波数的功率谱S(kj)。可以由下式生成长度为L的一维粗糙表面样本,即:
| $ f({x_n}) = \frac{1}{L}\sum\limits_{{\rm{ }}j = -N/2 + 1}^{N/2} {F({k_j}){{\rm{e}}^{{\rm{i}}{k_j}{x_n}}}} $ | (2) |
式中:xn = nΔx,(n = -N/2+1, …, N/2)表示粗糙表面上第n个采样点,F(kj)与f(xn)称为Fourier变换对,定义为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;F({k_j}) = \frac{{2{\rm{ \mathsf{ π} }}}}{{\sqrt {2\Delta k} }}\sqrt {S({k_j})} \cdot\\ \left\{ \begin{array}{l} [N\left( {0, 1} \right) + iN\left( {0, 1} \right)], {\rm{ }}\;\;\;\;\;\;j = -N/2 + 1, \ldots, -1\\ N\left( {0, 1} \right), {\rm{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;j = 0, N/2 \end{array} \right. \end{array} $ | (3) |
式中:定义离散波数kj的表达式为kj = 2πj/L;Δk为谱域相邻的谐波样本的空间波数差;S(kj)为粗糙海面的功率谱密度,代表海浪能量相对于空间波数的分布;N(0, 1)表示均值为0,方差为1的正态分布的随机数。当j>0时,F(kj)满足共轭对称关系F(kj) = F(k-j)*。
高斯分布随机粗糙面的功率谱密度为:
| $ S\left( k \right) = \frac{{{h^2}l}}{{2\sqrt {\rm{ \mathsf{ π} }} }}{\rm{exp}}\left( {\frac{{-{k^2}{l^2}}}{4}} \right) $ | (4) |
式中:h为高斯粗糙面的高度起伏均方根,它是反映粗糙面粗糙程度的一个基本量;l是表面相关长度,是描述随机粗糙面各统计量中的一个最基本量,它提供了估计表面上2点相互独立的一种基准,即如果表面上2点在水平距离上相隔距离大于l,那么该两点的高度值从统计意义上说是近似独立的。将式(4)代入式(3)中,再进行逆傅里叶变换,即可得到粗糙海表剖面f(x)。
在实际建模时,可根据已知的海况和有效波高[18],并进一步估算波高均方根,可作为monte-carlo方法的参数。一维粗糙海面建模的monte-carlo方法的物理意义是在一定的海面粗糙度下给出海面最可能存在的形态,因此,当进行基于粗糙海面建模的后续计算时,一般应采用多次平均的方法。
2 数值仿真 2.1 粗糙海面声传播模型:Krakenc-KA和Krakenc-SSA 2.1.1 Krakenc-KA粗糙海面声场模型Krakenc-KA声场模型有2种实现方法:1)直接设置ENV文件中的sigma参数(海面粗糙度参数);2)首先通过KA方法计算出平均海面反射系数,再通过TRC(top reflection coefficient)文件输入到Krakenc中。
在30 m深的水声环境中,声速剖面为1 500 m/s等声速剖面,频率为300 Hz,声源深度为7 m,接收深度为15 m。图中实线是平滑海面下的传播损失曲线,虚线是直接设置ENV文件中的sigma参数为0.5计算得到的传播损失曲线,点划线是通过TRC文件输入平均海面反射系数后计算得到的传播损失曲线,其中平均海面反射系数是在波高均方根为0.5的粗糙海面下由KA方法计算得到。
由图 2可见,虚线和点划线基本一致。Krakenc中在ENV文件中直接设置波高均方根sigma参数时,默认采用KA方法计算平均海面反射系数,因此,我们将在相同波高均方根条件下利用KA方法计算的平均海面反射系数通过TRC文件输入到Krakenc的声场计算结果与在ENV文件中直接设置sigma参数的声场计算结果基本一致。在ENV文件中直接设置波高均方根sigma参数较为简单直观,但是通过TRC文件将平均海面反射系数输入到Krakenc中除了选取KA方法来计算平均海面反射系数,还可以根据实际情况选择更为合适的散射方法,例如适用性较广的SSA方法,下面就对利用不同散射方法来计算平均海面反射系数后的声场计算结果进行比较。

|
Download:
|
| 图 2 Krakenc-KA粗糙海面声传播模型2种实现方法的比较 Fig. 2 Comparison of two realization methods for Krakenc-KA propagation model with rough sea surface | |
利用Krakenc-SSA粗糙海面声场的计算方法是首先通过SSA理论计算平均海面反射系数,再通过TRC文件输入平均海面反射系数,平均海面反射系数由SSA方法得到。
保持水声环境条件不变,图 3是考虑不同散射理论下的海面平均反射系数时传播损失曲线的比较,其中实线是平滑海面下的传播损失曲线,虚线是在波高均方根为0.5的高斯谱粗糙海面下基于KA方法计算平均海面反射系数时的传播损失曲线,点划线是在波高均方根为0.5的高斯谱粗糙海面下基于SSA方法计算平均海面反射系数时的传播损失曲线。

|
Download:
|
| 图 3 不同散射方法计算海面平均反射系数时所得传播损失曲线的比较 Fig. 3 Comparison of transmission loss curves by different scattering method to calculate mean reflection coefficient | |
由图 3可见,随着水平距离的增加,虚线和点划线的差别更加明显,这也是两者的差异在水平距离上的累积结果。另外,虚线与实线的干涉峰谷的水平位置一致,而点划线的干涉峰谷的水平位置相对于实线有明显的偏移。
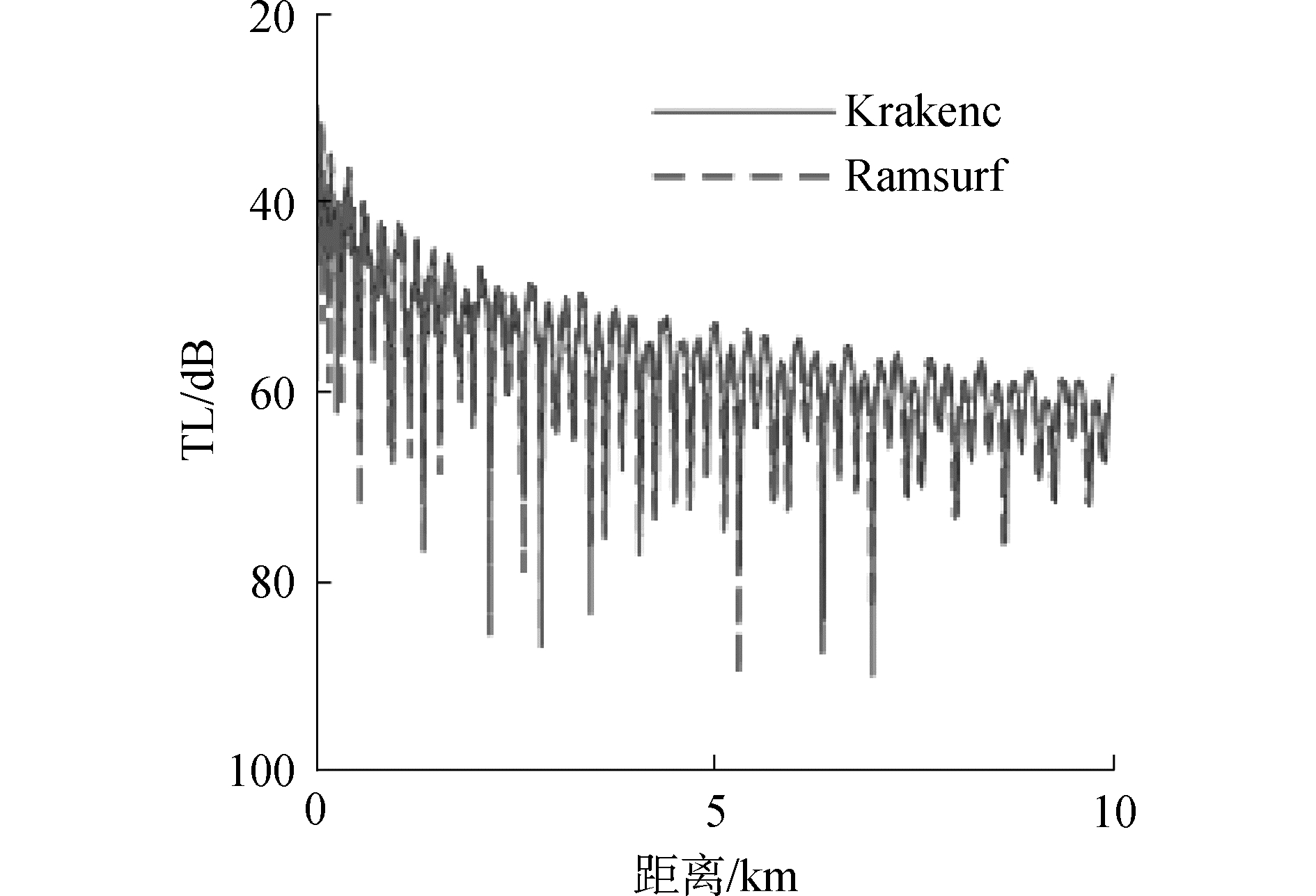
2.2 粗糙海面下的Krakenc模型与Ramsurf模型比较 2.2.1 平滑海面下保持水声环境不变,图 4中实线是平滑海面下Krakenc声传播模型的传播损失计算结果,虚线是平滑海面下Ramsurf声传播模型的传播损失计算结果,可见平滑海面下Krakenc声传播模型与Ramsurf声传播模型的计算结果基本一致。
|
Download:
|
| 图 4 平滑海面下Krakenc和Ramsurf的比较 Fig. 4 Comparison of transmission loss curves by Krakenc model and Ramsurf model with smooth sea surface | |
Krakenc粗糙海面声传播模型是基于海面反射系数计算模型来计算平均海面反射系数,可根据实际需要选取多种不同的海面反射系数计算模型;而Ramsurf粗糙海面声传播模型是基于monte-carlo方法产生一维粗糙海面,可根据海区的具体情况选取多种不同的风浪谱模型。另外,Ramsurf可计算海底地形变化条件下的粗糙海面下的声场。
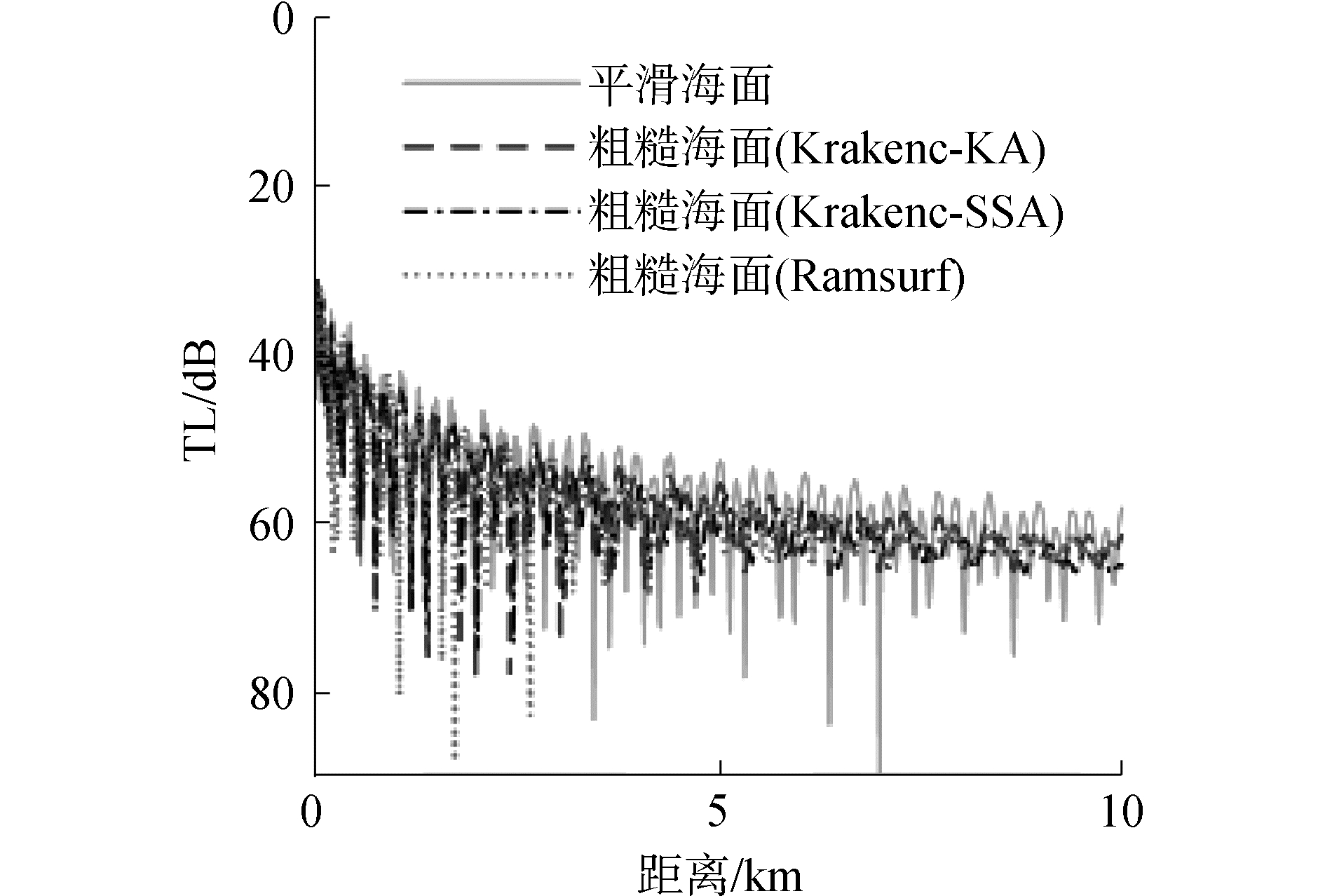
图 5是在高斯波浪谱下波高均方根值相同的基础上,对Krakenc粗糙海面声传播模型和Ramsurf粗糙海面声传播模型的比较。
|
Download:
|
| 图 5 粗糙海面下Krakenc-KA、Krakenc-SSA、和Ramsurf的比较 Fig. 5 Comparison of transmission loss curves by Krakenc-KA model, Krakenc-SSA model and Ramsurf model with rough sea surface | |
高斯谱粗糙海面的波高均方根为0.5,Ramsurf以monte-carlo方法(40次平均)产生高斯谱一维粗糙海面,声场计算结果为实线。
3 数据处理某次声传播试验过程中海面波浪有效波高为1.5 m左右,在接收阵处放置CTD进行声速剖面测量,试验船在走航测量过程中投掷200 m-1kg弹型的爆炸声源,由接收阵接收到的爆炸声源信号进行传播损失计算并与粗糙海面边界条件下的声传播模型Ramsurf仿真结果进行对比。试验海区海底地形与声速剖面如图所示,采样获得的海底参数如表 1所示。
| 表 1 试验海区海底参数 Table 1 Seabed parameters of the sea area |

|
Download:
|
| 图 6 试验地区声速剖面 Fig. 6 Sound speed profile of the sea area | |

|
Download:
|
| 图 7 试验地区海底地形 Fig. 7 Topography of the sea area | |
首先根据实验过程中观察到的有效波高值估算粗糙海面的波高均方根值[18],有效波高在1.5 m左右时,估算平均波高为1 m左右,估算高斯谱的波高均方根h取值为1.2。根据实验时的实际情况,相关长度l取值为1 m。波浪谱选取较为常用的高斯波浪谱,可根据Monte-Carlo方法生成一维高斯谱粗糙海面,作为Ramsurf模型的海面边界输入;声速剖面、海底地形和海底底质参数均参考海试中的实测数据,可仿真得到粗糙海面下的传播损失。保持其他条件不变,将海面设置为平滑海面,可仿真得到平滑海面下的传播损失。
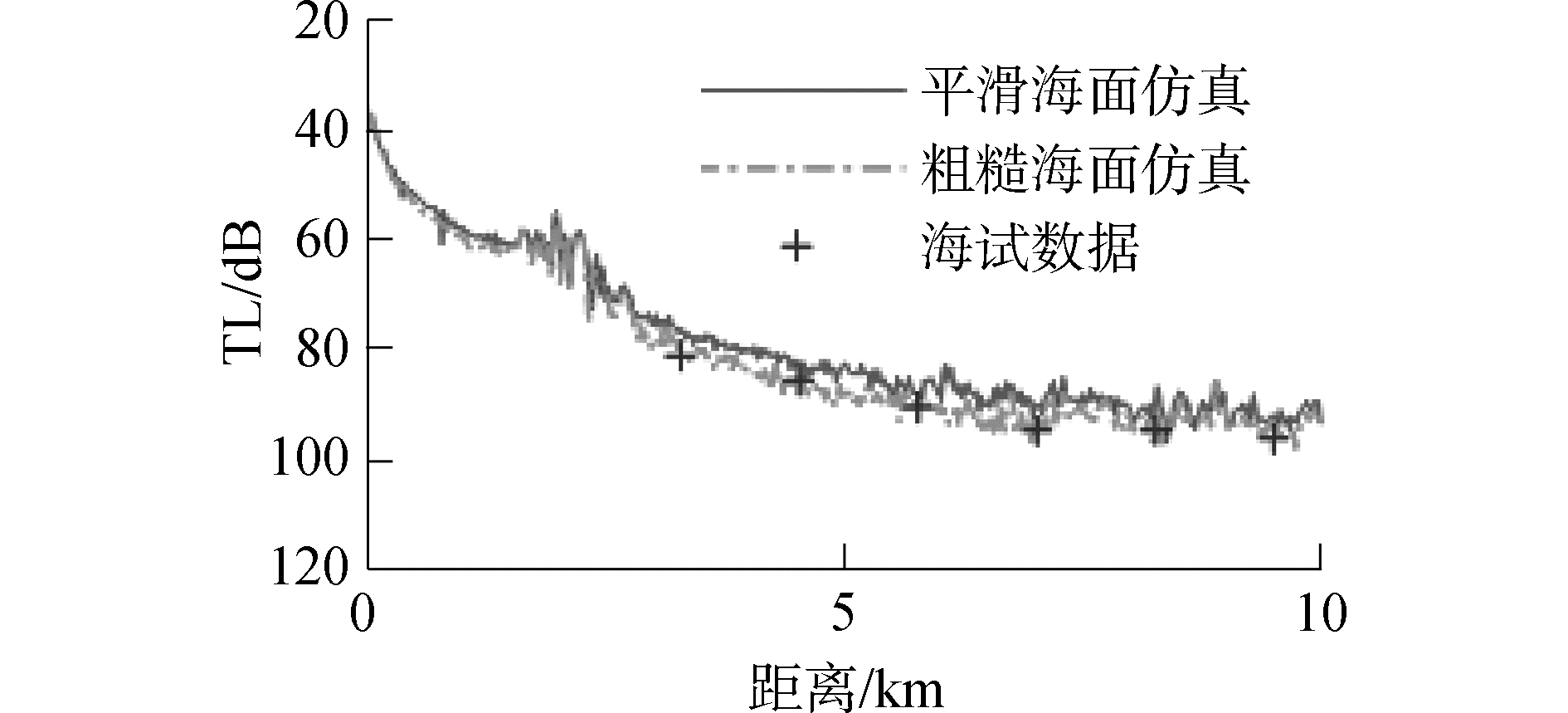
图 8是数据处理结果和仿真结果的对比:利用Ramsurf分别仿真平滑海面与粗糙海面下3 kHz声场的传播损失曲线,由宽带非相干方法计算,其中实线为平滑海面下的仿真结果,点划线为粗糙海面下的仿真结果;实验数据处理以1/3倍频程的带宽计算中心频率为3 kHz的传播损失曲线,以符号“+”标记。由图可见,在2.5~8.5 km范围内,在同一距离上,粗糙海面下的Ramsurf传播损失计算结果比平滑海面下的Ramsurf传播损失计算结果大4~6 dB,粗糙海面下的Ramsurf传播损失计算结果与实验数据得到的传播损失结果较为吻合,可见Ramsurf声传播模型较为有效。
|
Download:
|
| 图 8 Ramsurf传播损失仿真与海试处理结果比较(3 kHz) Fig. 8 Comparison of transmission loss curves by Ramsurf model and sea trial data with rough sea surface (3 kHz) | |
本文研究并比较了几种典型的粗糙海面下的声传播模型-Krakenc-KA粗糙海面声传播模型、Krakenc-SSA粗糙海面声传播模型和Ramsurf粗糙海面声传播模型,这对于粗糙海面下的声场预报和声呐性能预报具有重要意义。通过研究得出以下结论:
1) KA方法计算的平均海面反射系数不改变声场的相位,而SSA方法计算的平均海面反射系数改变了声场的相位。因此,利用Krakenc-KA方法计算平均海面反射系数后得到的声场干涉峰谷的水平位置没有改变,而利用Krakenc-SSA方法计算平均海面反射系数后得到的声场改变了声场干涉峰谷的水平位置。
2) krakenc粗糙海面声传播模型是基于海面反射系数计算模型来计算平均海面反射系数,可根据实际需要选取多种不同的散射方法来计算平均海面反射系数;而Ramsurf粗糙海面声传播模型是基于monte-carlo方法产生一维粗糙海面,一般要进行40次以上的蒙特卡罗计算最后求得平均值,因此krakenc计算效率更高。
3) 通过实验数据验证Ramsurf是较为有效的粗糙海面下的声传播模型,并且可以计算粗糙海面下水平非均匀条件下的声场。
4) Krakenc-KA模型和Krakenc-SSA模型适用于水平均匀条件,文中的实验数据是海底地形变化条件下的数据,因此没有对其他两种模型进行验证。下一步的工作方向是获取更多的实验数据以开展对水平均匀条件下的Krakenc-KA模型和Krakenc-SSA模型的验证以及进一步的模型间的对比分析工作。
| [1] |
QIN Jixing, LUO Wenyu, ZHANG Renhe, et al. Analysis and comparison between two coupled-mode methods for acoustic propagation in range-dependent waveguides[J]. Chinese journal of acoustics, 2014, 33(1): 1-20. (  0) 0)
|
| [2] |
LI Zhenglin, WANG Yaojun, MA Li, et al. Effects of sediment parameters on the low frequency acoustic wave propagation in shallow water[J]. Chinese journal of acoustics, 2000, 19(3): 221-229. (  0) 0)
|
| [3] |
MO Yaxiao, PIAO Shengchun, ZHANG Haigang, et al. An energy-conserving two-way coupled mode model for underwater acoustic propagation[J]. Chinese journal of acoustics, 2016, 35(2): 97-110. (  0) 0)
|
| [4] |
ZHANG Lingshan, PENG Zhaohui, WANG Guangxu, et al. Experimental analysis on air-to-water sound transmission loss in shallow water[J]. Chinese journal of acoustics, 2017, 36(2): 217-230. (  0) 0)
|
| [5] |
KIM I C, SUH K D. Effect of sea level rise and offshore wave height change on nearshore waves and coastal structures[J]. Journal of marine science and application, 2018(2): 192-207. (  0) 0)
|
| [6] |
BADIEV M, WAN L, LUO J. Shallow water modal evolution due to nonlinear internal waves[J]. Journal of marine science and application, 2017(3): 362-369. (  0) 0)
|
| [7] |
ZHOU Jixun, ZHANG Xuezhen, PENG Zhaohui, et al. Sea surface effect on shallow-water reverberation[J]. The journal of the acoustical society of America, 2007, 121(1): 98-107. DOI:10.1121/1.2400623 (  0) 0)
|
| [8] |
THORSOS E I. The validity of the Kirchhoff approximation for rough surface scattering using a Gaussian roughness spectrum[J]. The journal of the acoustical society of America, 1988, 83(1): 78-92. DOI:10.1121/1.396188 (  0) 0)
|
| [9] |
CHAPMAN D M F. An improved Kirchhoff formula for reflection loss at a rough ocean surface at low grazing angles[J]. The journal of the acoustical society of America, 1983, 73(2): 520-527. DOI:10.1121/1.388997 (  0) 0)
|
| [10] |
THORSOS E I. The validity of the Perturbation approximation for rough surface scattering using a Gaussian roughness spectrum[J]. J.Acoust.Soc.Am., 1989, 86(1): 261-277. DOI:10.1121/1.398342 (  0) 0)
|
| [11] |
SCHNEIDER H G. Surface loss, scattering, and reverberation with the split-step parabolic wave equation model[J]. The journal of the acoustical society of America, 1993, 93(2): 770-781. DOI:10.1121/1.405439 (  0) 0)
|
| [12] |
LEISHMAN T W, TICHY J. On the significance of reflection coefficients produced by active surfaces bounding one-dimensional sound fields[J]. The journal of the acoustical society of America, 2003, 113(3): 1475-1482. DOI:10.1121/1.1550924 (  0) 0)
|
| [13] |
WILLIAMS K L, THORSOS E I, ELAM W T. Examination of coherent surface reflection coefficient (CSRC) approximations in shallow water propagation[J]. The journal of the acoustical society of America, 2004, 116(4): 1975-1984. DOI:10.1121/1.1785617 (  0) 0)
|
| [14] |
THORSOS E I. Acoustic scattering from a "Pierson-Moskowitz" sea surface[J]. The journal of the acoustical society of America, 1990, 88(1): 335-349. DOI:10.1121/1.399909 (  0) 0)
|
| [15] |
JONES A D, MAGGI A L, CLARKE P A, et al. Analysis and simulation of an extended data set of waveforms received from small explosions in shallow oceans[C]//Proceedings of ACOUSTICS 2006. Christchurch, New Zealand, 2006.
(  0) 0)
|
| [16] |
JONES A D, SENDT J, DUNCAN A J, et al. Modelling the acoustic reflection loss at the rough ocean surface[C]//Proceedings of ACOUSTICS 2009. Adelaide, Australia, 2009: 1-8.
(  0) 0)
|
| [17] |
JONES A D, DUNCAN A J, MAGGI A L, et al. A detailed comparison between a small-slope model of acoustical scattering from a rough sea surface and stochastic modeling of the coherent surface loss[J]. IEEE journal of oceanic engineering, 2016, 41(3): 689-708. DOI:10.1109/JOE.2015.2464551 (  0) 0)
|
| [18] |
汪德昭, 尚尔昌.水声学[M].科学出版社, 2013
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


