混响是主动声呐检测水下目标的主要背景干扰。动目标的检测可利用目标回波与混响在多普勒速度上的差异^[1]。当混响较强且目标运动较慢时，常规波束形成(beamforming, BF)加频率搜索的匹配滤波(matched filtering, MF)方法(BF & MF)得到的单ping输出仍难以改善检测效果。港口蛙人警戒场景中，发射信号、基阵、探测空间中的环境在一定时间和空间内是缓变的，因此多ping接收信号所蕴含的信息有极大利用价值。

根据多ping之间混响的一致性，将混响视为包含慢变成分(主要来自海底)和快变成分的量，通过多ping递归平均来估计并抑制慢变成分可以提高检测增益^[2]，但当目标强度与混响快变部分的强度相当时该方法失效。蛙人声呐处理中常用帧差法序列图像来检测目标，该方法虽计算简单却极易出现“空洞”和“双影”现象^[3]。视频信号处理可以利用多帧图像中同一像素点之间的统计差异来检测跟踪运动目标^[4]，常用非参数估计来刻画某一像素点的概率密度函数在每帧图像中的变化^[5]。在对核密度估计(kernel density estimation, KDE)算法改进的基础上，用于自适应背景更新的基于像素时间信息窗的核密度估计方法提高了检测性能^[6]。然而这些目前只用于视频目标检测的方法，因其帧率高、分辨力高而未能被直接引入主动声呐探测应用。基于混响与目标的统计特征存在差异的事实^[7-9]，虽然因环境中各分辨元的散射时空起伏有所差异，在某个分辨元内，没有目标侵入时应是弱散射贡献。一旦目标侵入，原则上是强反射(相对弱散射)。使用核函数方法估计此时的概率密度，就可利用目标和混响概率密度函数的差异实现自动检测。非参量核密度函数估计可以利用多ping数据获得统计样本。

本文首先研究了混响和目标回波输出包络的统计模型及它们之间的统计特性差异，在此基础上利用核函数方法估计多ping的BF & MF输出的概率密度函数，提出动目标检测的新方法。对新方法在不同信混比下的ROC曲线进行理论分析。通过仿真数据和海上实验数据验证该方法相较于普通单ping检测的性能改进。

1 BF & MF输出包络的分布

海洋混响可以视为由一些随机固定于平整海底上的以及一些随机浮动在海面和水体中的散射体引起。设发射脉冲s(t)的复包络为|s(t)|e^jψ(t)。接收信号经过波束形成后可表示为：

$ {X_\theta }\left( t \right) = {A_0}s\left( {t - {\tau _0}} \right) + \sum\limits_{i = 1}^{n\left( t \right)} {{A_i}s\left( {t - {\tau _i}} \right)} + {V_\theta }\left( t \right) $

式中：下标θ表示第θ个波束；n(t)是对特定波束θ在t时刻接收到混响有贡献的散射体数；τ_i为接收脉冲相对t时刻的时延；V_θ(t)为随机噪声，接收脉冲幅度A_i=b(r_i)|α_i|e^jφ_i，b(r_i)表示双程传播损失；r_i、α_i、φ_i为第i个散射元的位置，散射系数和相移；α_i、φ_i为随机变量，可认为具有均匀性和遍历性^[10]。

将匹配滤波后得到的X(t)移到基带并低通滤波可输出复包络：

$ \begin{array}{*{20}{c}} {\tilde X\left( t \right) = {A_0}{{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}{f_c}{\tau _i}}}{{\tilde R}_{ss}}\left( {t - {\tau _0}} \right) + }\\ {\sum\limits_{i = 1}^m {{A_i}{{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}{f_c}{\tau _i}}}{{\tilde R}_{ss}}\left( {t - {\tau _i}} \right)} + \tilde V\left( t \right)} \end{array} $

式中：${{\tilde R}_{ss}}\left( t \right)$是发射波形的基带互相关函数；$\tilde V\left( t \right)$是随机噪声经过匹配滤波的复包络；f_c为中心频率。匹配滤波能很大程度上提高目标回波和混响相对噪声的功率之比，因此在一定信噪比下，混响背景下混响级远大于噪声级的情况下分析时只考虑混响对目标回波的影响。通过假设互相关函数是二值的(即只要散射体处于分辨元内则${{\tilde R}_{ss}}$(t-τ_i)=1)可得：

$ \tilde X\left( t \right) \approx {A_0}{{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}{f_c}{\tau _0}}} + \sum\limits_{i = 1}^{n\left( t \right)} {{A_i}{{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}{f_c}{\tau _i}}}} $

(1)

1.1 混响输出包络概率分布

目标不存在时式(1)可以简化为：

$ \tilde X\left( t \right) \approx \sum\limits_{i = 1}^m {{A_i}{{\rm{e}}^{ - j 2{\rm{ \mathsf{ π} }}{f_c}{\tau _i}}}{{\tilde R}_{ss}}\left( {t - {\tau _i}} \right)} \approx \sum\limits_{i = 1}^{n\left( t \right)} {{A_i}{{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}{f_c}{\tau _i}}}} $

对各次发射的同一方位距离单元观察，衰减因子f(r_i)可视为常量。设单元内包含的散射元数n(t)服从同一分布，而随机变量α_i、φ_i具有均匀性和遍历性，因此多次发射所得方位距离图的同一单元输出包络服从同一分布。

1.2 目标回波输出包络概率分布

输出目标回波的统计模型分为2类^[11]，非起伏信号和起伏信号。非起伏目标模型是将目标看作一个点散射元，此时输出是幅度非随机、相位随机的复随机变量。起伏目标模型是将目标看作由多个散射体组成，复包络的幅值和相位均随机。

当目标和混响同时存在于某一分辨单元，输出包络的概率密度函数可以用联合特征函数的方法计算。特别地，当n(t)固定且趋于无穷，信号为非起伏时，只含混响的单元的输出包络服从瑞利分布，目标出现后该单元输出包络服从莱斯分布^[12]。由以上分析可知，当方位距离单元内含目标回波时的输出包络概率分布与仅有混响背景时概率分布不同。

2 基于核密度估计的动目标检测 2.1 利用核密度函数构造检验统计量

考虑双择假设，即：

$ {H_0}:x = r + n $

$ {H_1}:x = s + r + n $

式中s、r、n分别表示目标回波、混响和噪声。

每ping的BF & MF处理结果在每一方位距离单元的输出被视为一个随机过程。由于混响的复杂性，实际中难以用一种模型准确描述，其概率分布也就无法提前假设。因此，采用由多ping输出数据估计其概率密度的非参量KDE这种完全基于测量数据的方法。

输出方位距离图包含若干方位距离单元，以第i个方位距离单元为研究对象。KDE方法需要选取样本。由2.1节知，一段时间内每ping中各个方位距离单元混响的输出包络应服从相同的概率密度分布，因此取该单元连续输出的Nping混响包络数据为一组，把这组数据作为样本集{x_{i, 1}, x_{i, 2}, …, x_{i, N}}。当被观测ping输出包络x_i后，用KDE方法估计概率密度$\hat f\left( {{x_i}} \right)$为：

$ \hat f\left( {{x_i}} \right) = \frac{1}{N}\sum\limits_{j = 1}^N {K\left( {{x_i} - {x_{i,j}}} \right)} $

(2)

式中：x_i表示第i个单元被观测ping的输出包络；x_{i, j}表示第i个单元输出包络的第j个样本；N₀表示样本个数；K为核估计子，选择常用的高斯核函数$K\left( u \right) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} }}{{\rm{e}}^{ - \frac{{{u^2}}}{2}}}$，带入式(2)可得：

$ \hat f\left( x \right) = \frac{1}{N}\sum\limits_{i = 1}^N {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} h}}{{\rm{e}}^{ - \frac{{{{\left( {x - {x_i}} \right)}^2}}}{{2{h^2}}}}}} $

(3)

若被观测ping输出包络无目标，那么其概率密度分布应与作为样本的N ping基本保持一致，得到的$\hat f\left( {{x_i}} \right)$应该较大；反之，若被观测ping出现目标，那么其输出包络概率密度分布应与前面样本输出包络出现差异，得到的$\hat f\left( {{x_i}} \right)$应该较小。找到方位距离图中与混响背景的概率密度明显不同的单元即可检测出目标。最大似然比准则是常用的判决准则。本文研究的检测方法不事先假设目标回波的统计模型，是只利用背景信息的方法，因此直接用log似然函数作为检验统计量进行判决：

$ \mathit{\Lambda }\left( x \right) = - \lg \left[ {{f_{X\left| {{H_0}} \right.}}\left( x \right)} \right]\begin{array}{*{20}{c}} {{H_1}}\\ > \\ < \\ {{H_0}} \end{array}{t_h} $

式中：t_h是合适的的检测门限，将在2.3节中讨论。f_X|H0(x)的取值可以趋于0，取对数可以将数量级的差异更清晰地显示在输出检验统计量中，负号是为了使输出检验统计量为正数，且目标单元输出值较大，混响单元输出值较小，使最终检测结果的显示更直观。

2.2 核宽选择

式(3)中h为核宽，决定了每个样本对概率密度估计值所做贡献的影响范围。理论上，当样本的数量趋于无穷时，核宽的选择对估计值的影响并不明显，估计值总能趋于真实值^[13]。但实际中样本数量有限且需要实时计算，核宽的选择就显得十分重要。核宽影响KDE的平滑度，核宽选择过小会使概率密度估计曲线参差不齐，核宽选择过大又容易导致概率密度曲线过于平滑^[14]。常用的核宽选择方法是基于样本值的固定核宽核密度估计(fixed kernel density estimation, FKDE)。对固定核宽进行优化，常用的方法是通过最小化积分均方误差(mean integrated error, MISE)的方法，KDE值的M_MISE为：

$ \begin{array}{*{20}{c}} {{M_{{\rm{MISE}}}} = \left[ {\hat f\left( x \right)} \right] = {\rm{E}}\int {{{\left[ {\hat f\left( x \right) - f\left( x \right)} \right]}^2}{\rm{d}}x} = }\\ {\int {{{\left[ {{\rm{E}}\hat f\left( x \right) - f\left( x \right)} \right]}^2}{\rm{d}}x} + \int {{\mathop{\rm var}} \hat f\left( x \right){\rm{d}}x} } \end{array} $

上式的前一项是估计值的期望与真实概率密度的差值平方的积分，后一项是概率密度估计值的方差的积分，由泰勒公式可得：

$ \begin{array}{*{20}{c}} {{M_{{\rm{MISE}}}}\left[ {\hat f\left( x \right)} \right] = \frac{1}{4}{h^4}\int {{u^2}K\left( u \right){\rm{d}}u} \int {\left[ {f''{{\left( x \right)}^2}} \right]{\rm{d}}x} + }\\ {\frac{1}{{nh}}\int {{{\left[ {K\left( u \right)} \right]}^2}{\rm{d}}u} + o\left( {{h^4} + \frac{1}{{nh}}} \right)} \end{array} $

(4)

对式(4)求导得M_MISE取极小值时对应的核宽为：

$ h = {\left( {\frac{{\int {{K^2}\left( u \right){\rm{d}}u} }}{{\int {\left[ {f''{{\left( x \right)}^2}} \right]{\rm{d}}x} {{\left[ {\int {{u^2}K\left( u \right){\rm{d}}u} } \right]}^2}}}} \right)^{\frac{1}{5}}}{N^{ - \frac{1}{5}}} $

(5)

式(5)的优化核宽与概率密度真实值有关，这是无法获得的，常用方法是先假设服从正态分布，带入式(5)，可以获得优化固定核宽：

$ h = 1.059\sigma {N^{ - 1/5}} $

FKDE方法虽计算简单，但实际上核宽不仅与样本有关，也与被估计点有关。本文采用改进的基于被估计点的核宽，可以弥补固定核宽只考虑样本值的不足。对每个被估计点都计算最小均方误差：

$ \begin{array}{*{20}{c}} {{M_{{\rm{MISE}}}}\left[ {\hat f\left( x \right)} \right] = {\rm{E}}\left\{ {{{\left[ {\hat f\left( x \right) - f\left( x \right)} \right]}^2}} \right\} = }\\ {{{\left( {{\rm{E}}\left[ {\hat f\left( x \right)} \right] - f\left( x \right)} \right)}^2} + {V_{{\rm{var}}}}\left[ {\hat f\left( x \right)} \right]} \end{array} $

式中：

$ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;{\rm{E}}\left[ {\hat f\left( x \right)} \right] = \int {K\left( u \right)f\left( {x + hu} \right){\rm{d}}u} \\ {V_{{\rm{ar}}}}\left[ {\hat f\left( x \right)} \right] = \frac{1}{N}\left[ {\frac{1}{h}\int {{K^2}\left( u \right)f\left( {x + hu} \right){\rm{d}}u} - {E^2}\left[ {\hat f\left( x \right)} \right.} \right] \end{array} $

令均方误差最小，$h = {\rm{arg }}\mathop {{\rm{min}}}\limits_h \left\{ {{M_{{\rm{MSE}}}}\left[{\hat f\left( {{x}} \right)} \right]} \right\}$

$ h = {\left( {\frac{{f\left( x \right)\int {{K^2}\left( u \right){\rm{d}}u} }}{{{{\left[ {f''\left( x \right)\int {{u^2}K\left( u \right){\rm{d}}u} } \right]}^2}}}} \right)^{\frac{1}{5}}}{N^{ - \frac{1}{5}}} $

(6)

式(6)中未知的真实概率密度不直接由正态分布假设代替，选择用优化固定核宽通过核密度估计得到的概率密度估计式(3)计算，这样做比直接使用正态分布假设更接近真实的概率密度函数。

2.3 门限选择

2.1节中提到的检测判决方法为：

$ \Lambda \left( x \right) = - \lg \left[ {{f_{X\left| {{H_0}} \right.}}\left( x \right)} \right]\begin{array}{*{20}{c}} {{H_1}}\\ > \\ < \\ {{H_0}} \end{array}{t_h} $

KDE是基于数据统计的估计方法，因此根据统计的方法确定t_h。为了避免固定门限无法反映环境变化的不足，使用自适应门限t_h，根据被观测ping统计量的分布更新门限。

显然混响单元的统计量Λ(x)较大且在方位距离图中所占方位距离单元数目较多，而目标的出现相对于混响的存在是小概率事件，对于尺寸较小的目标所占方位距离单元数目较少。因此可以通过统计被观测ping所有方位单元的Λ(x)的概率分布直方图H_Λ来确定检测门限t_h。

被观测ping的方位距离图包含若干个方位距离单元，遍历所有单元的统计量Λ(x)，可得Λ(x)的概率分布直方图H_Λ，将Λ(x)的取值范围分为j个区间[u_j, w_j]：

$ {H_\mathit{\Lambda }}\left( j \right) = \left\{ \begin{array}{l} {H_\mathit{\Lambda }}\left( j \right) + 1,\;\;\;\;\;{u_j} \le \mathit{\Lambda }\left( x \right) < {w_j}\\ {H_\mathit{\Lambda }}\left( j \right),\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $

(7)

根据式(7)统计出的Λ(x)概率分布直方图如图 1(a)所示。可将图 1(a)中落于Λ(x)>b内的单元判断为背景单元(对应图 1(a)的0部分)。为更好地观察细节，将直方图H_Λ中的Λ(x) < b部分提取出来进行细化统计，统计满足 < Λ(x) < b的f(x)的概率分布直方图H_p(j)。为减小极端值对门限选取的影响，对概率分布直方图H_p(j)用三次样条插值处理，结果记为H_ps(j)，如图 1(b)。H_ps(j)可分成A、B两段。区间A内单元数目相对区间B较多且迅速减少，这个区间内可认为有目标存在。区间B内单元数目少且随概率密度估计值大小的变化不明显，可以认为这个区间是目标和混响背景之间的过渡区域，区域A、B之间的分界点可以作为目标和混响的区分标准，记分界点的值为a。定义差分函数：

$ {H_d}\left( j \right) = \left| {{H_{ps}}\left( j \right) - {H_{ps}}\left( {j + 1} \right)} \right| $

寻找H_d(j)的第1个零点即可得到a。从而可以确定检测门限：

$ {t_h} = - \lg a $

至此，检测算法流程为：

1) 选取一个方位距离单元，按照式(6)计算核宽；

2) 用该单元的混响输出包络样本按照式(3)计算当前ping的KDE值，并计算检验统计量；

3) 根据2.3节选择门限，并将检验统计量与门限比较，若大于门限，判断该单元存在目标，否则该单元判定为无目标；

4) 待遍历所有方位距离单元后，输出该ping检测结果。

3 检测性能分析

为从理论上分析新方法对检测性能的提高，推导新方法检测器的ROC曲线。选取一个方位距离单元，概率密度估计值式(3)可以改写为：

$ z = \sum\limits_{j = 1}^N {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} h}}{{\rm{e}}^{ - \frac{{{{\left( {x - {x_j}} \right)}^2}}}{{2{h^2}}}}}} = \sum\limits_{i = 1}^N {{m_j}} $

记y_j=x-x_j，${m_j} = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} h}}{{\rm{e}}^{ - \frac{{y_j^2}}{{2{h^2}}}}}$，x_j、y_j、m_j、z_j为随机变量X_j、Y_j、M_j、Z_j的一个取值。

在目标未出现在该单元之前，设第j个输出包络样本X_j(t)的概率密度函数为f_Xj(x_j)，待检测ping的输出包络X(t)的概率密度函数为f_X(x)。Y_j=X-X_j的分布函数可由f_X(x)、f_Xj(x_j)求得：

$ \begin{array}{*{20}{c}} {{F_{{Y_j}}}\left( {{y_j}} \right) = \int\limits_{ - \infty }^\infty {\int\limits_{x - {x_j} \le {y_j}} {{f_{X{X_j}}}\left( {x,{x_j}} \right){\rm{d}}x{\rm{d}}{x_j}} } = }\\ {\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^{{y_j}} {{f_{X{X_j}}}\left( {{x_j} + u,{x_j}} \right){\rm{d}}u{\rm{d}}{x_j}} } } \end{array} $

可以认为随机变量是相互独立的，对分布函数求导可得概率密度函数：

$ {f_{{Y_j}}}\left( {{y_j}} \right) = \frac{{{\rm{d}}{F_{{Y_J}}}\left( {{y_j}} \right)}}{{{\rm{d}}{y_i}}} = \int\limits_{ - \infty }^\infty {{f_X}\left( {{y_j} + {x_j}} \right){f_{{X_j}}}\left( {{x_j}} \right){\rm{d}}{x_j}} $

(8)

从而可以得到随机变量M_j的概率密度为：

$ {f_{{M_j}}}\left( {{m_j}} \right) = {f_{{Y_j}}}\left( {{y_j}} \right)\frac{{{\rm{d}}{y_j}}}{{{\rm{d}}{m_j}}} $

(9)

由此可得M_j的特征函数为：

$ {\mathit{\Phi }_{{M_j}}}\left( \omega \right) = \int\limits_{ - \infty }^\infty {{f_{{M_j}}}\left( {{m_j}} \right){{\rm{e}}^{{\rm{j}}\omega {m_j}}}{\rm{d}}{m_j}} $

(10)

由于m₁, m₂, …, m_N为独立同分布的随机变量，根据特征函数的性质可得随机变量Z的特征函数

$ {\mathit{\Phi }_Z}\left( \omega \right) = \prod\limits_{j = 1}^{{N_0}} {{\mathit{\Phi }_{{M_j}}}\left( \omega \right)} $

(11)

做逆变换可得KDE值的概率密度函数

$ {f_Z}\left( z \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int\limits_{ - \infty }^\infty {{\Phi _Z}\left( \omega \right){{\rm{e}}^{ - {\rm{j}}\omega z}}{\rm{d}}\omega } $

(12)

真实的f_X(x)、f_Xj(x_j)是未知的，因此下面以特定分布的混响输出包络为例，计算并比较该方法和传统方法检测的ROC曲线，如图 2。设混响输出包络样本服从瑞利分布：${X_j} \sim {f_{{X_j}}}({x_j}) = \frac{{2{x_j}}}{{{{\rm{ \mathsf{ λ} }}_0}}}{{\rm{e}}^{ - \frac{{{x_j}^2}}{{{\lambda _0}}}}},{{\rm{ \mathsf{ λ} }}_0}$表示混响的输出功率。当单元内无目标时，输出包络分布与混响样本一致，代入式(8)~(12)可得无目标情况的估计值的概率密度，记为f_Z(z)；当输出含目标时，包络服从$X\left( t \right) \sim {g_X}\left( x \right) = \frac{x}{{{\rm{ \mathsf{ π} }}{{\rm{ \mathsf{ λ} }}_0}}}{{\rm{e}}^{ - \frac{{{x^2} + {b_0}^2}}{{{{\rm{ \mathsf{ λ} }}_0}}}}}\int_0^{2{\rm{ \mathsf{ π} }}} {{{\rm{e}}^{2x{b_0}{\rm{cos}}\psi /{{\rm{ \mathsf{ λ} }}_0}}}} {\rm{d}}\psi $，b₀表示目标信号的输出功率的平方根^[15]，同样代入式(8)~(12)可求出包含目标情况下估计值的概率密度，记为g_Z(z)。由f_Z(z)、g_Z(z)可以计算检测器的虚警概率和检测概率:

$ {P_{fa}} = P\left\{ { - \lg z \ge {\rm{th}}\left| {{H_0}} \right.} \right\} = \int_{ - \infty }^{{{10}^{ - t}}h} {{f_Z}\left( z \right){\rm{d}}z} $

(13)

$ {P_d} = P\left\{ { - \lg z \ge {\rm{th}}\left| {{H_1}} \right.} \right\} = \int_{ - \infty }^{{{10}^{ - t}}h} {{g_Z}\left( z \right){\rm{d}}z} $

(14)

定义经过BF & MF后的输出信混比为b₀²/λ₀。根据式(13)、(14)可以绘制不同信混比条件下目标检测和虚警概率对应的ROC曲线，如图 3。

比较图 3、4可知，在相同的低信混比条件下，新方法检测器的检测性能要明显高于普通检测器。在保证虚警概率不高于0.01，检测概率不低于0.5的条件下，本文方法可以将检测到目标所需的最低信混比由普通检测器的9 dB降到3 dB。随着信混比的提高，低虚警概率条件下，新方法检测器的检测概率迅速上升，而普通检测器的检测概率上升速度较缓。

4 试验验证 4.1 仿真试验

通过蛙人声呐的仿真数据检验本文方法的有效性。仿真试验的参数如下:输入信混比和信噪比均为-28 dB；发射信号中心频率10 kHz、带宽2 kHz、脉宽50 ms；每次发射间隔1 s；接收水听器阵为16元等间距线阵，阵元间隔为0.2倍波长。目标初始位于60°方位角，370 m；目标运动径向速度为1 m/s。为便于比较，竖坐标均进行了归一化处理。

由图 5可以看出，单ping输出结果中弱目标完全被强混响掩盖。首先选择20ping作为初始样本，归一化检验统计量的输出如图 5(a)所示，此时运动目标所处单元的检验统计量明显大于混响背景单元的检验统计量，表明目标所在单元的概率密度估计值明显较小。再经过门限判决即可得到检测结果，如图 5(b)。图 6、图 7分别为选择50ping、100ping作为初始样本得到的输出结果，其中图 6(a)、图 7(a)为输出归一化检验统计量的结果，图 6(b)、图 7(b)是通过门限后的结果。比较图 6~8可明显看出，随着样本数的增加，新方法对混响背景抑制效果明显增加。这是由于增加样本数量减少了混响背景极端值对概率密度估计的影响，增加了估计精度。

4.2 海上试验

为进一步验证本文方法对检测真实动目标的有效性，选取海试数据进行处理。数据源于中国东海海域试验，在同一时段有20次发射并记录接收数据。所用阵列为固定32元阵，阵元间隔1.5 m；发射LFM信号，中心频率420 Hz，带宽80 Hz，脉宽2 s；接收信号的采样率为10 kHz。发射多ping信号的ping间隔为10 s。目标运动的径向速度为1 m/s。目标所在的初始位置为4 500 m，深度约为20 m。

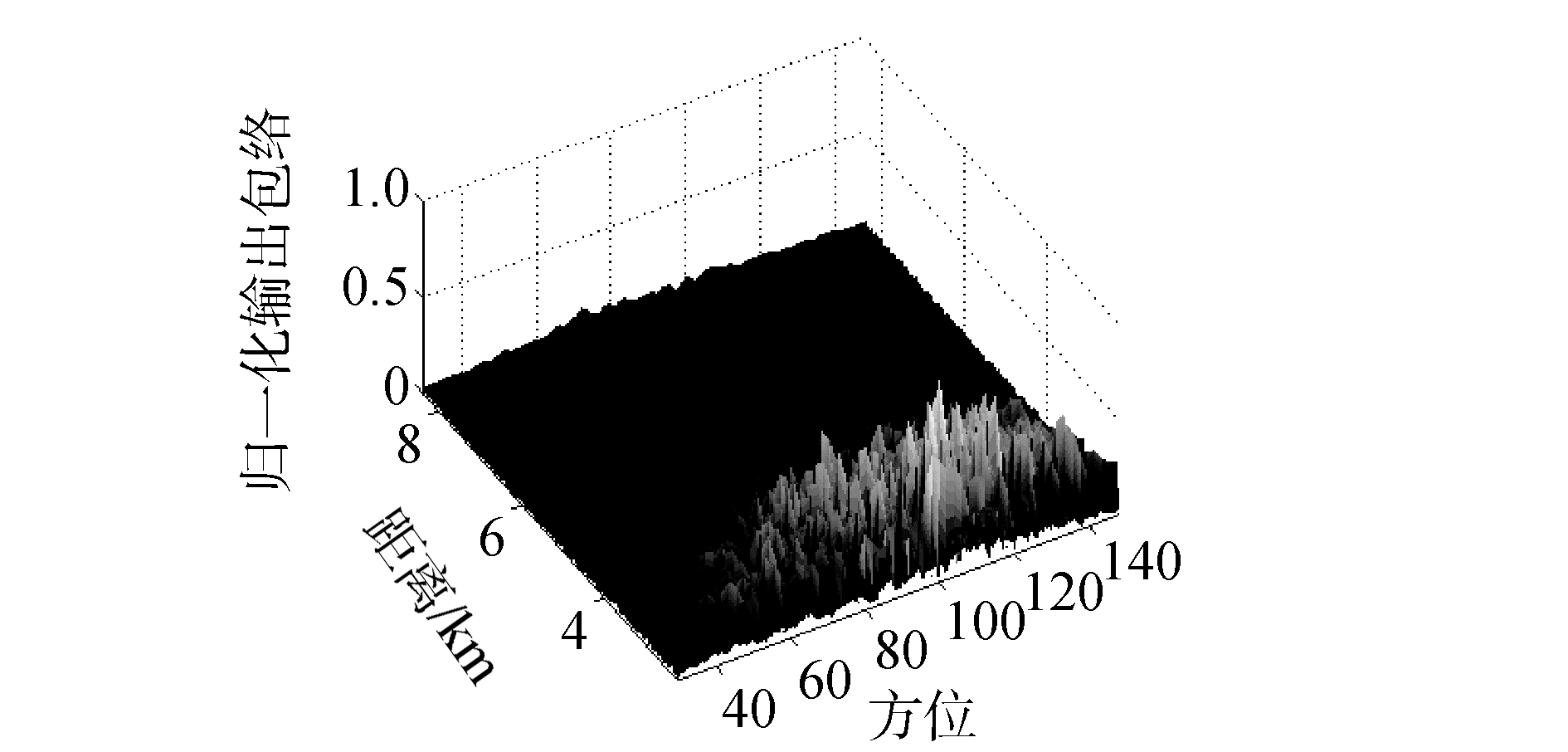
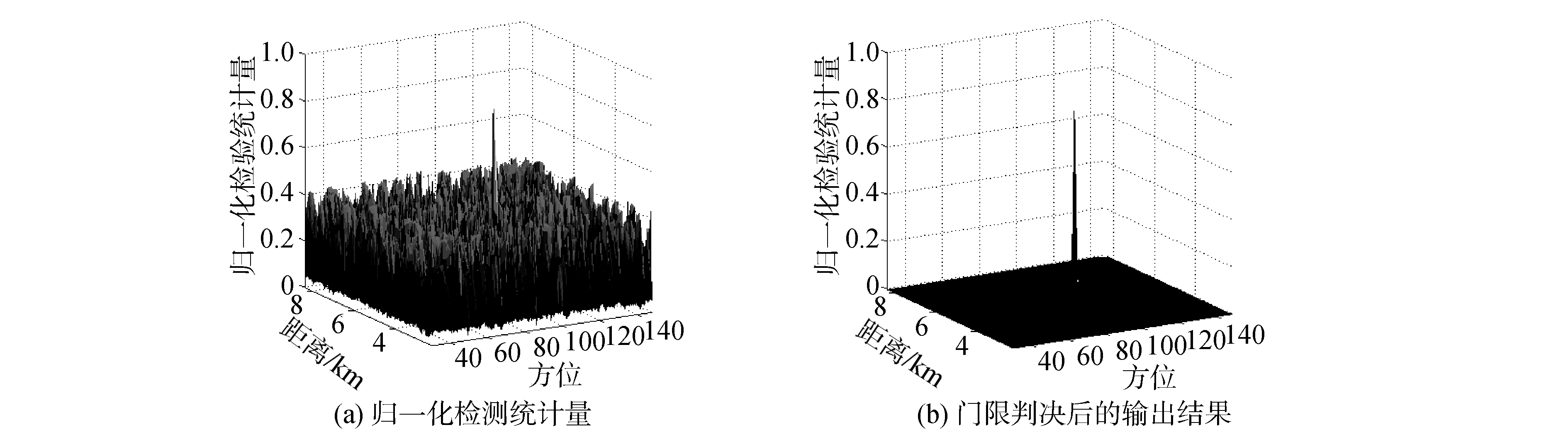
选择海试中20次发射接收数据的MF & BF输出包络作为样本(即N=20)。在混响较强的情况下本文方法仍能清晰地突出目标(图 8(a))，而普通单ping方法目标完全被强混响掩盖(如图 9)。由于海试试验发射次数有限，用于背景学习的样本量偏少，处理结果仍有背景干扰的残留，但已被抑制到了较均匀的水平，并可以通过门限将目标检测出来(如图 8(b))。

5 结论

1) 采用非参量核密度估计可以充分利用多ping数据，不需要假设目标和混响的概率的先验知识，可以避免概率模型失配对检测的影响。针对主动声呐的特点，改进了核密度估计算法中核宽和门限选择方法，仿真和海试数据处理均证实新方法的检测性能优于传统上广泛使用的BF & MF检测方法。而且，随着样本数的增加，检测性能可进一步提高。

2) 新检测方法理论分析与数值计算结果表明，低信混比下的检测性能要明显高于普通检测器，相比较而言，在保证虚警概率小于0.01，检测概率大于0.5的条件下，相同检测水平所需最小可检测信混比将降低6 dB。

3) 目前并未考虑混响背景在检测过程中有较大变化的情况，这涉及到背景样本集的自动更新问题，有待于进一步研究。