2. 海洋石油工程股份有限公司, 天津 300384
2. Offshore Oil Engineering Co. Ltd., Tianjin 300384, China
导管桨是在工程类船舶采用较多的一种特种推进方式,导管在保护螺旋桨的同时还能产生推力,提高推进系统效率,改善螺旋桨空化、噪声性能,尤其是在重载状态下性能更优。研究表明,导管推力的产生与导管的剖面形状及导管内表面附着涡相关,为进一步了解导管回收尾涡能量的作用机理,深入对导管桨内流场的流动特性(特别是涡结构特性)分析十分有必要[1]。
现阶段导管桨内流场特性主要采用数值计算方法,早期开展的研究大多基于势流理论进行数值计算[2-3],苏玉民等[4]、解学参等[5]基于面元法对导管桨的水动力性能和内流场进行了计算,势流方法计算效率高但很难准确模拟复杂流动;随着计算机性能的不断发展,基于粘流的多种数值计算方法被应用到导管桨不同方向的数值模拟中[6-9],胡健等[10]、时立攀等[11]基于雷诺平均方法(Reynolds-averaged navier-stokes, RANS)对导管桨的周围流场及尾涡特性进行了预报,孙瑜等[12]对导管结构改进前后的导管桨水动力性能进行了数值模拟;Bhattacharyya等[13-15]基于RANS方法对导管桨的尺度效应问题进行了研究,并探讨了不同导管类型对导管桨水动力性能的影响;Gaggero等[16]对导管桨的空化梢涡进行了数值预报,其网格划分及加密拓扑对拟捕捉流动细节的数值模拟研究方向具有较高参考价值。
本文基于分离涡模拟(detached eddy simulation, DES)方法进行导管桨敞水试验数值模拟,通过与模型试验结果相比验证数值计算精度与可信度,叙述数值模型的网格类型、湍流模型选择及计算方法等,重点分析导管桨内流场典型物理量分布特征,研究导管桨内流场涡系组成,分析导管内壁面附着涡具体形态与分布特性。
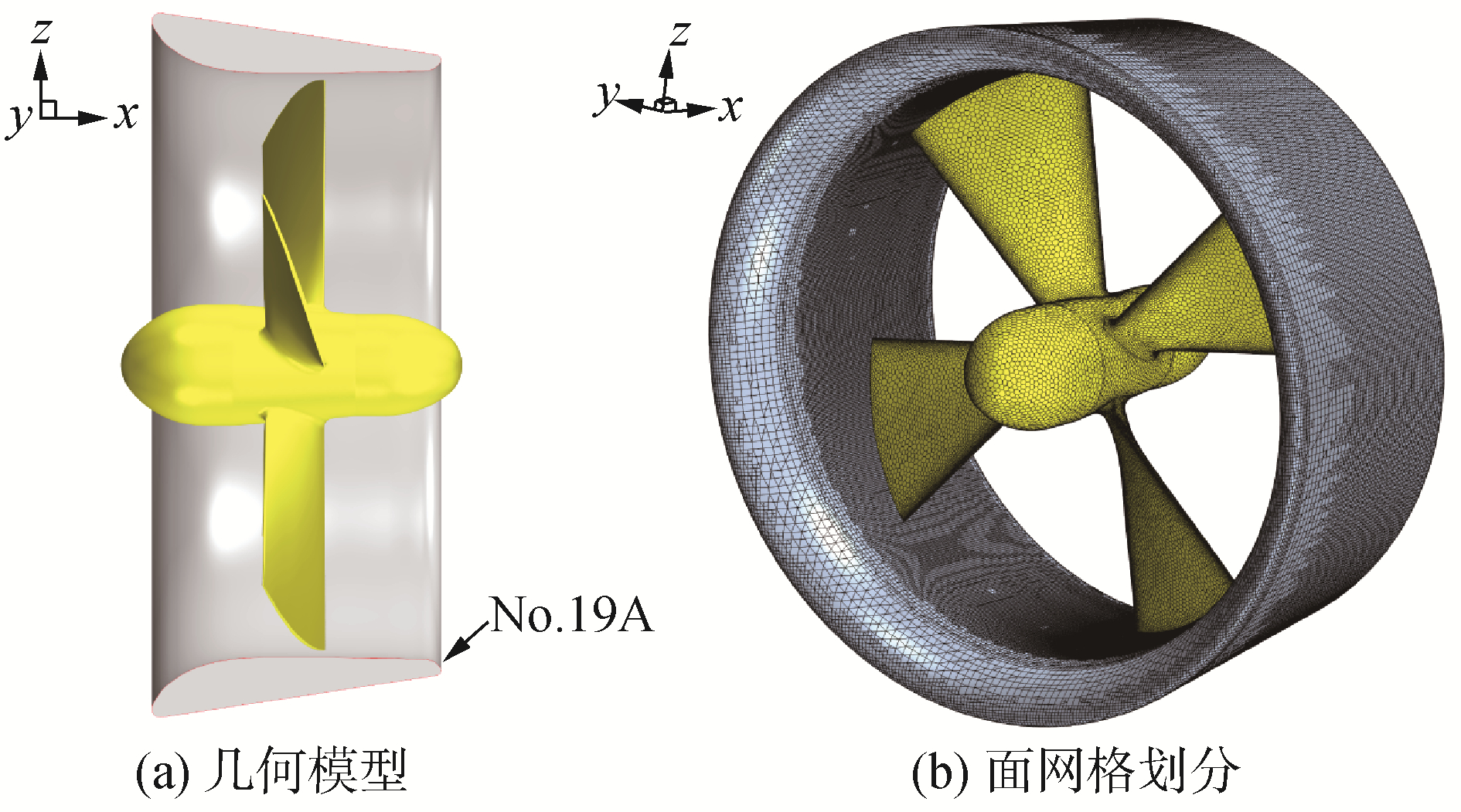
1 几何模型与计算区域数值计算几何模型为某动力定位系统导管桨模型,螺旋桨为定螺距4叶桨,桨模直径D=0.240 m(半径R=0.120 m),毂径比为0.190,盘面比为0.417,导管剖面为荷兰MARIN设计的No.19A导管(图 1(a)),叶梢间隙为2 mm。参考坐标系为笛卡尔坐标系O-xyz,坐标系O原点位于螺旋桨的几何中心,顺流方向为x轴正向,y轴、z轴正向按右手定则确立。
|
Download:
|
| 图 1 导管桨几何模型与网格划分 Fig. 1 Geometry model and mesh generation of ducted propeller | |
数值计算域为圆柱形,圆柱直径为6D,数值计算域向上游延伸2D,向下游延伸8D距离以避免产生限制效应。螺旋桨的旋转运动通过滑移网格技术实现,计算域被分为静态域和旋转域2个子域。计算域边界条件设定如下:进口及圆柱形外边界为速度入口,出口为压力出口,螺旋桨及导管模型表面为非滑移壁面,静态域和旋转域的交界面设定为interface以实现2个子域内数据交换和迭代。
2 数值模型建立 2.1 湍流模型与离散方法数值模拟为三维黏性、不可压缩、常密度的非稳态数值计算,应用滑移网格技术实现导管桨的敞水性能试验数值模拟。分离涡模型(DES)是一种混合模型[17],其应用RANS方法处理近壁区湍流,应用大涡模拟方法(large eddy simulation, LES)求解距离壁面较远的大涡结构,因此DES方法能用相对较少的计算资源提高对小尺度涡结构的计模拟精度。所有的DES模拟中均应用Spalart & Allmaras一方程湍流模型用于流场中湍流结构求解。
基于Spalart & Allmaras一方程模型的DES方法简要介绍如下,湍流粘性系数通过设置辅助变量求解,代数方程为:
| $ \nu_{t}=\tilde{\nu} f_{\nu 1} $ | (1) |
| $ f_{\nu 1}=\chi^{3} /\left(\chi^{3}+C_{\nu 1}^{3}\right) $ | (2) |
| $ \chi=\tilde{\nu} / \nu $ | (3) |
式中Cν13为常数。辅助变量根据涡粘性输运方程求解:
| $ \begin{array}{c}{\frac{\partial \tilde{\nu}}{\partial t}+u_{j} \frac{\partial \tilde{\nu}}{\partial x_{j}}=\frac{1}{\sigma}\{\nabla \cdot[(\nu+\tilde{\nu}) \nabla \tilde{\nu}]+} \\ {C_{b 2}\left|\nabla_{\nu}\right|^{2} \}+C_{b 1}\left[1-f_{t 2}\right] \tilde{S} \tilde{\nu}-} \\ {\left[C_{w 1} f_{w}-\frac{C_{b 1}}{\kappa^{2}} f_{l 2}\right]\left(\frac{\tilde{\nu}}{d}\right)^{2}+f_{t 1} \Delta U^{2}}\end{array} $ | (4) |
式中:等号右侧波形括号内第1项为扩散项,第2项诱导层流区内诱导湍流向前传播,第3项和第4项代表湍流的生成项和耗散项,最后一项用于在特定位置触发湍流。诸多C项和σ项均为常数,冯卡曼常数κ=0.41,f是壁面距离d的函数,
定义一个新的壁面距离
| $\tilde{d}=\min \left(d, C_{\mathrm{DES}} \mathit{\Delta}\right) $ | (5) |
式中:CDES是常数;Δ=max(Δx, Δy, Δz)。
DES模拟采用SIMPLE算法完成压力-速度耦合方程的求解。其中,对流项通过二阶迎风格式进行离散,扩散项通过中心差分格式进行离散,时间项二阶隐式格式离散,均采用Spalart-Allmaras湍流模型封闭N-S方程组。
2.2 网格划分计算域网格类型为混合网格,其中静态域为切割体网格,旋转域为多面体网格。数值计算域整体网格尺寸需逐渐过渡以避免发生较大的数值耗散[19]叶梢和导管之间的计算属于近壁面相对运动问题,因此需要进行更为精细的离散处理以提升网格质量。叶梢区域内设定包含叶梢的环状圆柱进行区域体加密处理,同时,叶梢与导管间隙区域设定间隙加密区域;叶片表面通过设定导边和随边特征线加密以控制体网格生成;螺旋桨和导管物面设置8层棱柱层网格完成边界层模拟,为满足DES算法要求,壁面y+值控制在(-∞,1)[20]。最终确认计算域网格总数约为951万(其中静态域736万,旋转域215万), 导管桨部件面网格划分结果见图 1(b)。
3 计算结果与讨论 3.1 敞水性能计算结果验证导管桨的水动力系数定义如下:
| $ \left\{\begin{array}{l}{J=V_{x} / n D} \\ {K_{t p}=T_{p} / \rho n^{2} D^{4}} \\ {K_{t d}=T_{d} / \rho n^{2} D^{4}} \\ {K_{q}=Q_{0} / \rho n^{2} D^{5}} \\ {\eta_{0}=\frac{J}{2 \pi} \frac{K_{t p}+K_{t d}}{K_{q}}}\end{array}\right. $ | (6) |
式中:J为进速系数;Vx为进流速度;n为转速;D为螺旋桨直径;Tp为螺旋桨推力;Td为导管推力;Q0为螺旋桨扭矩;ρ为水密度;Ktp、Ktd为螺旋桨、导管的推力系数;Kq为导管桨扭矩系数;η0为导管桨效率。
数值计算工况选定J为0.3, 0.4, 0.5这3个进速系数,转速设定为n=11 r/s,相应的雷诺数范围为3.5×105~3.6×105,时间步长设定为1°。
导管桨模型前期已经基于船模拖曳水池进行过敞水试验,数值计算结果与敞水试验结果对比如表 1所示。从对比结果来看,导管推力系数Ktd的最大相对偏差达到4.42%,螺旋桨周期性旋转导致导管推力产生明显脉动;螺旋桨的推力系数、扭矩系数和试验结果吻合良好,偏差均在3%以内。上述结果说明数值计算模型的数值计算精度较高,后续关于内流场特性及涡特性的分析具备一定的可信度。
| 表 1 导管桨数值计算与模型试验结果对比 Table 1 Comparison of numerical calculation and model test results of ducted propeller |
选取计算域内典型的剖面进行内流场特性分析,其中,横剖面(y-z平面)分别选定桨前盘面(x=-0.5R)和桨后盘面(x=0.3R),剖面坐标系均基于螺旋桨半径进行无因次化。后文详细地对上述盘面内瞬态的轴向速度场分布、涡量分布、压力分布等进行分析,选定分析工况为进速系数J=0.5。
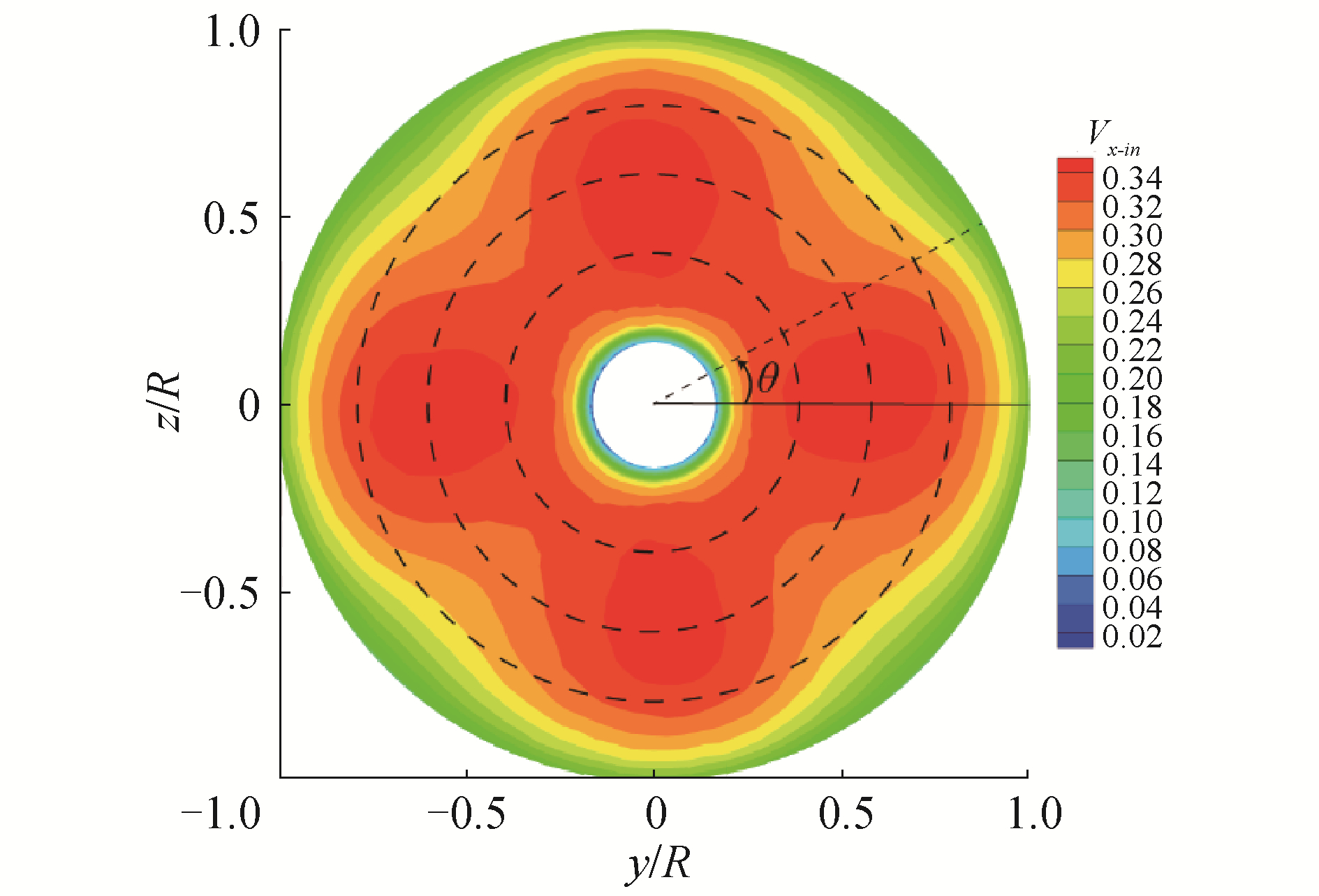
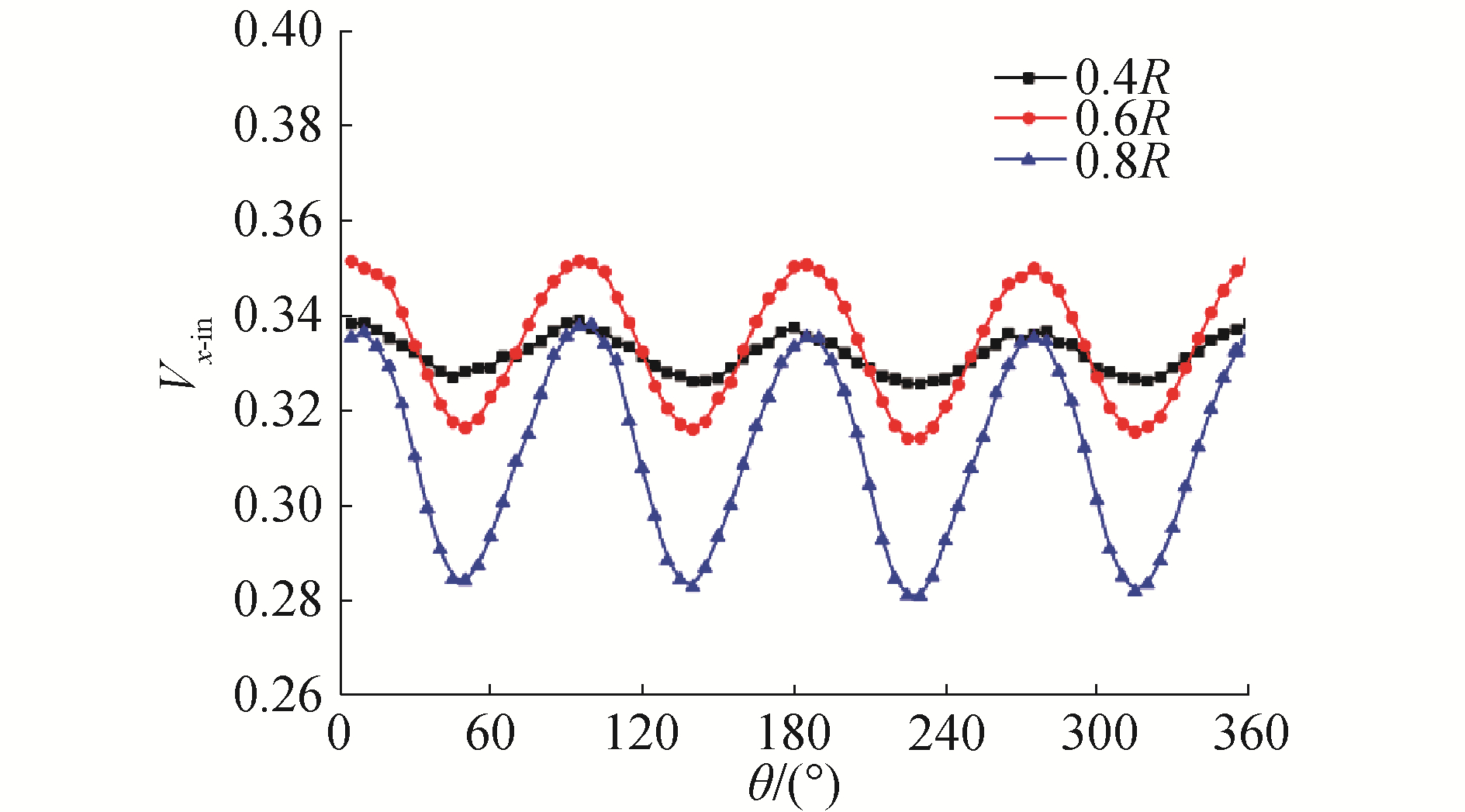
导管的存在增强了螺旋桨对桨前区域的诱导作用,桨前盘面内水流的速度场明显发生改变。从径向变化规律来看,导管桨桨前盘面(x=-0.5R)的轴向诱导速度(Vx-in=(Vx-V0)/V0)沿径向呈现先增加再减小的趋势(图 2),这与导管壁面和桨毂对水流流动存在阻滞作用有关。一周范围内盘面不同半径处(0.4R, 0.6R, 0.8R)轴向诱导速度分布如图 3所示,从周向变化规律来看,Vx-in沿周向呈现出明显的周期性,轴向诱导速度峰、谷值数与桨叶数一致,图 3中可见,0.8R位置轴向诱导作用波动最为强烈,整体来看,越靠近盘面外侧轴向诱导速度沿周向的波动幅度越大。
|
Download:
|
| 图 2 桨前盘面(x=-0.5R)轴向诱导速度分布 Fig. 2 Axial induced velocity profiles of the front disk (x=-0.5R) | |
|
Download:
|
| 图 3 不同半径处一周内轴向诱导速度分布 Fig. 3 Axial induced velocity profiles at different radii within one circle | |
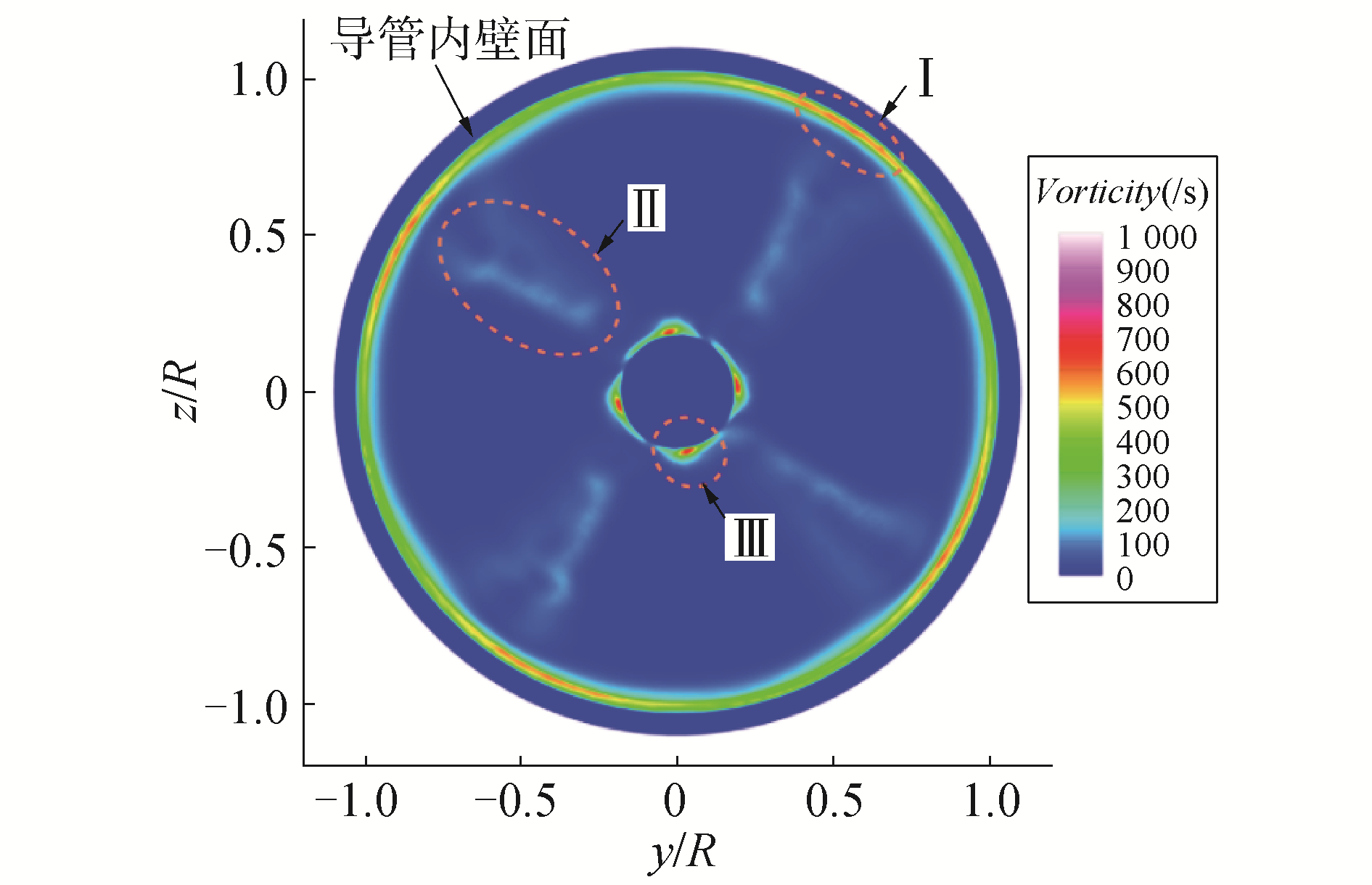
桨前水流经由桨叶加速后,导管桨内流场产生剧烈变化且涡特征明显。从桨后盘面(x=0.3R)的瞬态轴向速度分布(图 4(a))来看,桨叶对尾流的加速作用集中体现在0.5~0.8R,无因次轴向速度Vx/V0分布在1.4~1.8,由于粘性作用,导管壁面和桨毂附近区域流体以一定的速度梯度流动。桨后盘面内涡量分布(图 4(b))能体现出导管内流场涡系的组成成分:导管内壁面的剪切层流产生剪切层涡,剪切层涡在横剖面内体现为贴近导管内壁面的圆环形状,螺旋桨产生的涡系由外到内依次为叶梢梢涡(图 4(b)(Ⅰ))、叶片脱落涡(图 4(b)(Ⅱ))及叶根涡(图 4(b)(Ⅲ)),漩涡涡核分布于涡强最大值附近;湍流粘度反映涡扩散运动,从分析结果来看湍流粘度值在梢涡分布区、叶梢及叶根区较大,湍流粘度分布特性与涡分布特性保持一致。

|
Download:
|
| 图 4 x=0.3R盘面速度分布 Fig. 4 Velocity of the back disk x=0.3R | |
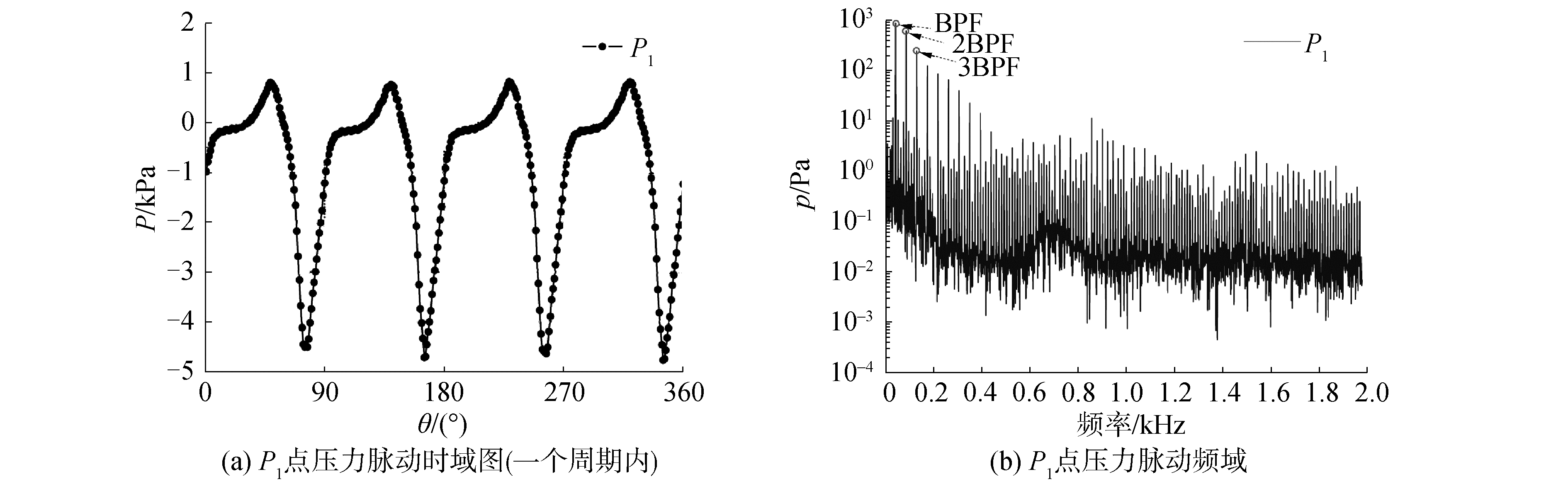
导管表面的瞬态压力分布如图 5所示,导管内表面叶梢前后附近存在压力峰值与谷值点。在导管内壁面x=0截面处设定探点P1(图 5),监测在导管桨正常工作过程中P1处压力脉动变化。从时域范围内分析结果来看(图 6(a)),螺旋桨旋转一周的过程中,探点P1处经历4个压力峰值与谷值,导管内表面压力脉动幅度大,流场变化剧烈,探点处的压力值与桨叶的位置直接相关;从频域来看(图 6(b)),压力脉动在叶频(BPF)处峰值最高,整个频域范围内多倍叶频处连续出现峰值,说明导管内壁面压力脉动特征与叶频相关。
|
Download:
|
| 图 5 导管表面瞬态压力分布 Fig. 5 Transient pressure profile of the duct surface | |

|
Download:
|
| 图 6 P1点压力脉动时域图(一个周期内) Fig. 6 Pressure fluctuation in the time domain of probe P1 within one period | |
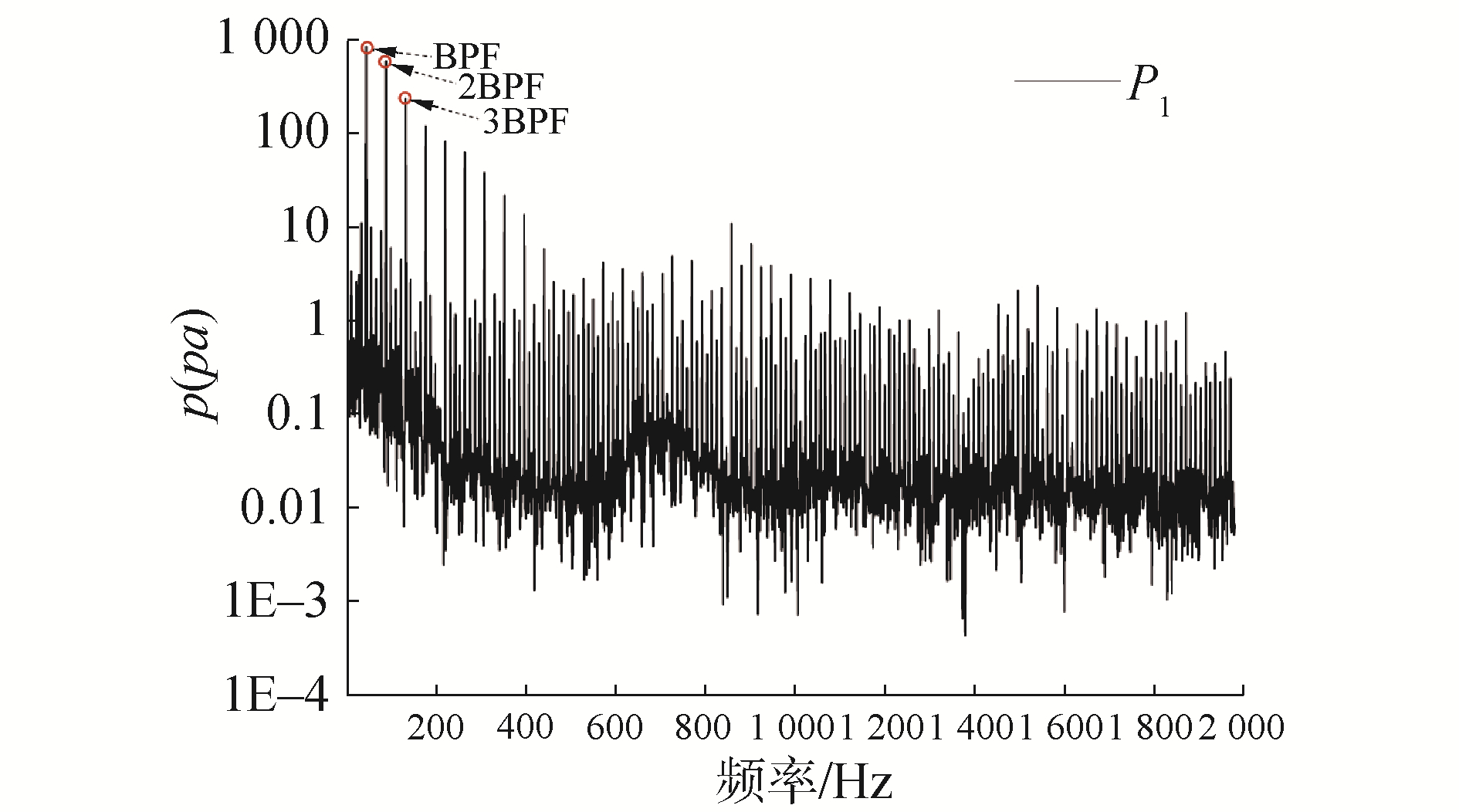
导管桨内流场涡特性及其分布规律直接影响导管桨的水动力性能,选定水平剖面(z=0)分析内流场涡量沿流向的分布规律。如图 7所示,导管与螺旋桨之间的强相互作用导致叶梢间隙附近及导管内壁面区域(Ⅰ框内)分布大量泄出涡,螺旋桨叶根涡(Ⅱ框内)和毂涡(Ⅲ框内)的分布相对清晰,导管剪切层涡与内流场泄出涡在导管尾缘产生相互复杂干扰,尾涡能量相互传递并向下游传输,导管桨近尾流场中涡量出现连续椭圆形分布(Ⅳ框内)。
|
Download:
|
| 图 7 水平剖面(z=0)内瞬态涡量分布 Fig. 7 Instantaneous vorticity distribution of the horizontal section (z=0) | |
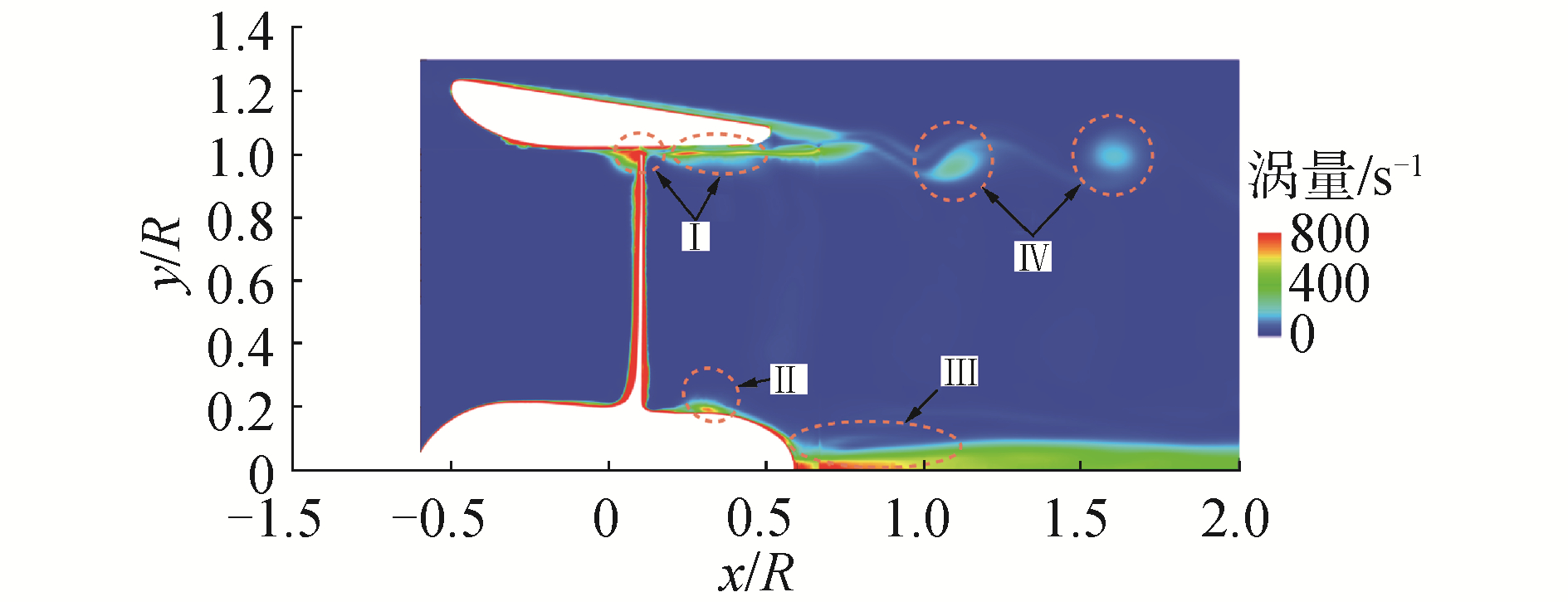
通过体渲染方式对导管桨内流场三维空间涡量分布进行分析,图 8中可以清晰分辨出螺旋桨叶片随边处产生的片状脱落涡,脱落涡连接叶梢涡与叶根涡,涡量大小随着向尾流中扩散迅速降低,不同桨叶叶根涡呈螺旋状发展并逐步汇集于桨毂处;叶梢涡分布于导管内壁面区域,梢涡的形态明显产生变形,而且还与导管内壁面剪切层涡发生融合与干扰,因此梢涡涡能的分布发生明显变化,涡量更大面积地分布于导管内壁面,引起导管表面产生更强的环流进而产生导管推力。
|
Download:
|
| 图 8 导管桨内流场三维空间涡量分布结果 Fig. 8 Three-dimensional vorticity distribution in internal flow field of ducted propeller | |
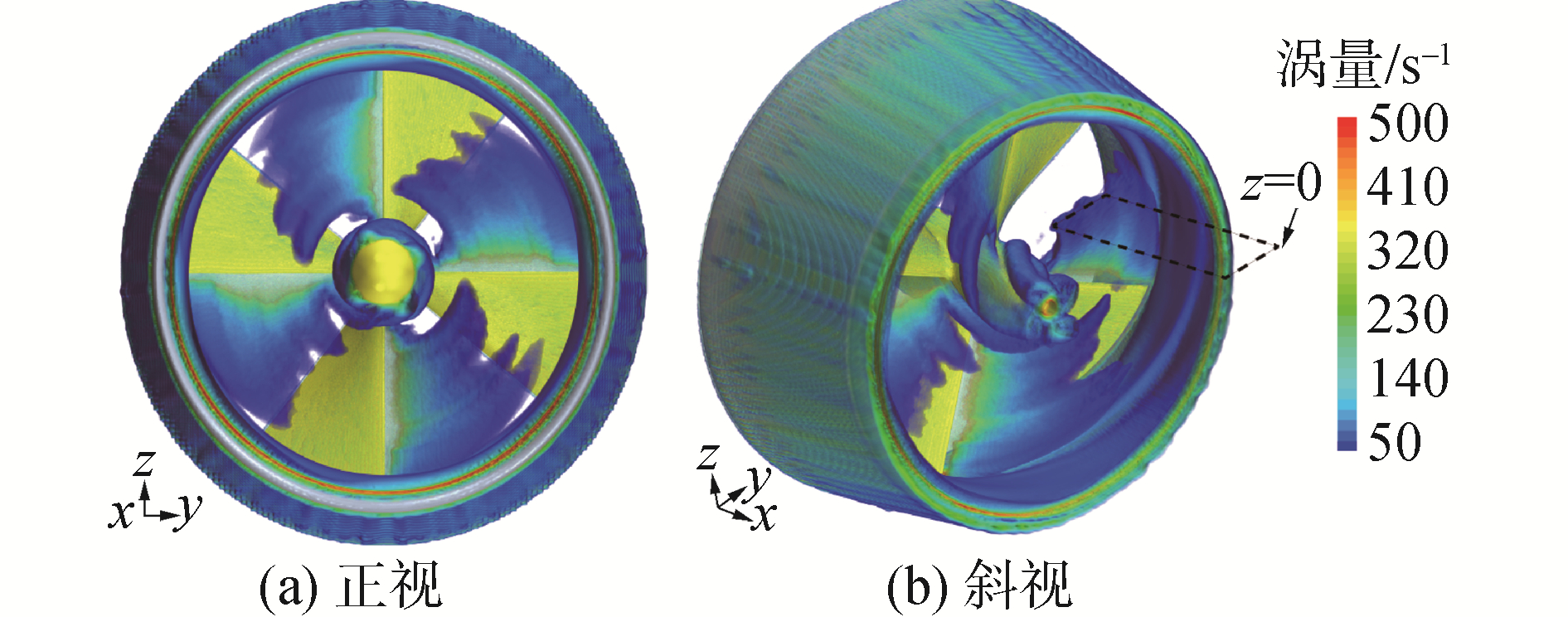
通过局部流动特性分析可以对变形梢涡结构内部特征进行深入辨析,图 9是z=0平面内梢涡截面内流线结果。黑色虚线为涡量/s-1=100 s-1等值线,其外部轮廓与图 8中一致,在投影视角上呈现“W”形,流线分布可以看到梢涡管内部诱导速度存在2个漩涡中心,这与独立螺旋桨梢涡涡量的分布特征存在明显差异。进一步读取y/R=1位置处涡管范围(0.2 < x/R < 0.5)内的涡量大小(图 10),发现2个漩涡中心涡量沿顺流方向逐渐下降。
|
Download:
|
| 图 9 梢涡结构形态及内部流线结果 Fig. 9 The morphology of the vorticity contour and the internal streamlines | |
|
Download:
|
| 图 10 y/R=1位置处涡量分布 Fig. 10 Vorticity distribution diagram at y/R=1 | |
1) 导管内壁区域流动复杂,导管内壁面压力脉动特性与螺旋桨叶频相关;
2) 导管桨尾涡系包含导管剪切层涡、叶梢涡、叶片脱落涡、叶根涡和毂涡,叶片脱落涡向下游传输过程中能量迅速扩散;
3) 导管的存在直接影响螺旋桨梢涡的分布,梢涡形态发生变化,涡量更大面积的分布于导管内壁面,导管有助于螺旋桨尾流的涡能回收从而提高系统推进效率。
| [1] |
盛振邦, 刘应中. 船舶原理[M]. 上海: 上海交通大学出版社, 2004: 177-188.
(  0) 0)
|
| [2] |
王国强, 刘小龙. 用基于速度势的面元法预估导管桨的非定常性能[J]. 船舶力学, 2006, 10(1): 36-42. WANG Guoqiang, LIU Xiaolong. Prediction of unsteady performance of ducted propellers by potential based panel method[J]. Journal of ship mechanics, 2006, 10(1): 36-42. DOI:10.3969/j.issn.1007-7294.2006.01.006 (  0) 0)
|
| [3] |
胡健, 黄胜, 马骋, 等. 影响导管桨内部流场的几个因素[J]. 天津大学学报, 2009, 42(4): 340-344. HU Jian, HUANG Sheng, MA Cheng, et al. Several influence factors for the inner flow field of ducted propeller[J]. Journal of Tianjin University, 2009, 42(4): 340-344. DOI:10.3969/j.issn.0493-2137.2009.04.011 (  0) 0)
|
| [4] |
苏玉民, 刘业宝, 沈海龙, 等. 基于面元法预报导管桨性能的数值计算方法[J]. 华中科技大学学报(自然科学版), 2012, 40(8): 57-61. SU Yumin, LIU Yebao, SHEN Hailong, et al. Surface panel method-based numerical calculation for predicting ducted propeller performances[J]. Journal of Huazhong University of Science and Technology (natural science edition), 2012, 40(8): 57-61. (  0) 0)
|
| [5] |
解学参, 黄胜, 胡健, 等. 导管桨内部流场的数值计算[J]. 哈尔滨工程大学学报, 2009, 30(1): 7-12, 45. XIE Xueshen, HUANG Sheng, HU Jian, et al. Inner flow field calculations for ducted propellers[J]. Journal of Harbin Engineering University, 2009, 30(1): 7-12, 45. DOI:10.3969/j.issn.1006-7043.2009.01.002 (  0) 0)
|
| [6] |
龚杰, 郭春雨, 吴铁成, 等. 基于分离涡模拟方法的导管桨近尾流场及尾涡特性分析[J]. 上海交通大学学报, 2018, 52(6): 674-680. GONG Jie, GUO Chunyu, WU Tiecheng, et al. Detached eddy simulation of near wake field and vortex characteristics for a ducted propeller[J]. Journal of Shanghai Jiao Tong University, 2018, 52(6): 674-680. (  0) 0)
|
| [7] |
刘业宝, 苏玉民, 赵金鑫, 等. 环流理论与泵理论相结合的导管桨设计优化[J]. 哈尔滨工程大学学报, 2014, 35(11): 1307-1313. LIU Yebao, SU Yumin, ZHAO Jinxin, et al. Optimal design of a ducted propeller based on the circulation theory and pump theory[J]. Journal of Harbin Engineering University, 2014, 35(11): 1307-1313. (  0) 0)
|
| [8] |
GONG Jie, GUO Chunyu, ZHAO Dagang, et al. A comparative DES study of wake vortex evolution for ducted and non-ducted propellers[J]. Ocean Engineering, 2018, 160: 78-93. DOI:10.1016/j.oceaneng.2018.04.054 (  0) 0)
|
| [9] |
胡健, 王楠, 胡洋. 加速导管和减速导管的性能比较[J]. 北京航空航天大学学报, 2017, 43(2): 240-252. HU Jian, WANG Nan, HU Yang. Performance comparison of accelerating duct and decelerating duct[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(2): 240-252. (  0) 0)
|
| [10] |
胡健, 王楠, 胡洋. 导管桨水动力特性的数值研究[J]. 哈尔滨工程大学学报, 2017, 38(6): 815-821. HU Jian, WANG Nan, HU Yang. Numerical study on the hydrodynamic performance of ducted propellers[J]. Journal of Harbin Engineering University, 2017, 38(6): 815-821. (  0) 0)
|
| [11] |
时立攀, 熊鹰, 杨勇, 等. 导管桨周围流场的数值模拟[J]. 哈尔滨工程大学学报, 2016, 37(3): 344-348. SHI Lipan, XIONG Ying, YANG Yong, et al. Numerical simulation of the flow around a ducted propeller using Reynolds-averaged Navier-Stokes equations[J]. Journal of Harbin Engineering University, 2016, 37(3): 344-348. (  0) 0)
|
| [12] |
孙瑜, 苏玉民, 刘伟. 导管结构改进后导管桨的水动力性能研究[J]. 华中科技大学学报(自然科学版), 2016, 44(6): 68-71. SUN Yu, SU Yumin, LIU Wei. Research on hydrodynamic performance of ducted propeller after structure improvement of duct[J]. Journal of Huazhong University of Science and Technology (natural science edition), 2016, 44(6): 68-71. (  0) 0)
|
| [13] |
BHATTACHARYYA A, KRASILNIKOV V, STEEN S. A CFD-based scaling approach for ducted propellers[J]. Ocean engineering, 2016, 123: 116-130. DOI:10.1016/j.oceaneng.2016.06.011 (  0) 0)
|
| [14] |
BHATTACHARYYA A, KRASILNIKOV V, STEEN S. Scale effects on a 4-bladed propeller operating in ducts of different design in open water[C]//Fourth International Symposium on Marine Propulsors smp'15, USA, 2015.
(  0) 0)
|
| [15] |
BHATTACHARYYA A, KRASILNIKOV V, STEEN S. Scale effects on open water characteristics of a controllable pitch propeller working within different duct designs[J]. Ocean engineering, 2016, 112: 226-242. DOI:10.1016/j.oceaneng.2015.12.024 (  0) 0)
|
| [16] |
GAGGERO S, TANI G, VIVIANI M, et al. A study on the numerical prediction of propellers cavitating tip vortex[J]. Ocean engineering, 2014, 92: 137-161. DOI:10.1016/j.oceaneng.2014.09.042 (  0) 0)
|
| [17] |
SHUR M L, SPALART P R, STRELETS M K, et al. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities[J]. International journal of heat and fluid flow, 2008, 29(6): 1638-1649. DOI:10.1016/j.ijheatfluidflow.2008.07.001 (  0) 0)
|
| [18] |
龚杰, 郭春雨, 张海鹏. 喷水推进船模旋转叶轮流场的数值分析[J]. 上海交通大学学报, 2017, 51(3): 326-331. GONG Jie, GUO Chunyu, ZHANG Haipeng. Numerical analysis of impeller flow field of waterjet self-propelled ship model[J]. Journal of Shanghai Jiao Tong University, 2017, 51(3): 326-331. (  0) 0)
|
| [19] |
SPALART P R. Detached-eddy simulation[J]. Annual review of fluid mechanics, 2009, 41: 181-202. DOI:10.1146/annurev.fluid.010908.165130 (  0) 0)
|
| [20] |
DI MASCIO A, MUSCARI R, DUBBIOSO G. On the wake dynamics of a propeller operating in drift[J]. Journal of fluid mechanics, 2014, 754: 263-307. DOI:10.1017/jfm.2014.390 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


