高光谱图像的解混问题是近年来遥感技术的一个重点研究内容。由于传感器空间分辨率不足，在获取像元对应的地面单元时可能包含不同的地物，形成混合像元^[1]，这会影响高光谱图像的分类精度和目标探测的效果。因此，高光谱图像的解混问题越来越受到学者们的广泛关注。

现有的高光谱图像的解混模型可分为线性光谱解混模型^[2]和非线性光谱解混模型^[3]。由于非线性光谱解混模型结构复杂，难以实现，目前国内外研究大多采用模型简单且物理意义明确的线性光谱解混模型。在线性光谱解混模型中，随着压缩感知和稀疏表示理论蓬勃发展，基于稀疏性的解混思想已经成为解混技术的热点。Bioucas-Dias等^[4]2010年提出了利用可变分和增广拉格朗日的稀疏解混算法(sparse unmixing via variable splitting and augmented Lagrangian，SUnSAL)，它将有约束问题转换为无约束问题，取得了很好的解混效果，目前大多数的稀疏解混算法都是在此基础上改进实现的。但是该模型仍存在一些问题，首先，上述稀疏解混方法将非凸的l₀范数替换为l₁范数，只能得到近似解，这将导致解混精度的降低。其次，上述稀疏解混方法用正则化的权重参数将2个或多个目标函数整合为一个目标函数进行优化，这些参数的设置直接影响解混精度，使解混结果具有不确定性。为了解决上述2个问题，Gong等^[5]将多目标优化思想引入到高光谱稀疏解混模型中，取得了很好的效果。该方法直接对l₀范数进行优化，也无需正则化参数，但是由于该算法采用的随机分组策略不能考虑3个以上决策变量间的相关性，且拐点选解策略具有单一性，使得高光谱数据解混精度仍有提升空间。

为此，本文提出一种基于大规格多目标优化(large-scale many-objective evolutionary optimization, LMEA)^[6]的高光谱稀疏解混算法，采用具有决策变量聚类和相关性分组策略的多目标优化算法，并提出有约束拐点区域选择策略来提高稀疏解混的精度。在模拟和真实的高光谱数据对比实验中，本文算法均获得了更优的解混结果。

1 理论基础知识 1.1 高光谱图像的稀疏解混模型

高光谱图像的线性光谱解混模型如下：

$ {y_i} = \sum\limits_{j = 1}^q {{m_{ij}}} {\alpha _j} + {n_i} $

(1)

式中：y_i表示在第i个光谱频带处像元的反射率；q表示端元个数；端元代表混合像元中的多种地物；每个端元只包含一种地物信息；m_ij表示第j个端元在第i个光谱频带上的反射率；α_j表示第j个端元的丰度系数；n_i表示第i个光谱频带上的误差项。如果将高光谱数据用矩阵形式表示，则式(1)可以重新写成：

$ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{M\alpha }} + \mathit{\boldsymbol{n}} $

(2)

式中：M∈R^L×q表示端元集合；L表示光谱频带数；y∈R^L×1表示高光谱数据中某一像元在第L个光谱频带上的观测值；α∈R^q×1表示每个端元对应的丰度系数；n表示误差项。一般来说，丰度系数α还应该满足和为一约束(abundance sum-to-one constraint, ASC)和非负性约束(abundance non-negativity constraint, ANC)：

$ \left\{ {\begin{array}{*{20}{l}} {{\rm{ASC}}:\sum\limits_{j = 1}^q {{\alpha _j}} = 1}\\ {{\rm{ANC}}:{\alpha _j} \ge 0} \end{array}} \right.j = 1, 2, \cdots , q $

(3)

稀疏解混模型就是采用已知的光谱库A来替代端元集合M，进一步求解出高光谱数据解混的丰度图，因此式(2)也可以写成：

$ \mathit{\boldsymbol{y}}{\rm{ = }}\mathit{\boldsymbol{A x}}{\rm{ + }}\mathit{\boldsymbol{n}} $

(4)

式中：A∈R^L×m表示已知的光谱库，m为光谱库A中包含的端元数量；x∈R^m×1表示丰度系数向量。

由于在光谱库A中仅有几个端元是对混合像元y有贡献，因此丰度向量x是稀疏的，那么式(4)也可以转换为^[7]：

$ \left\{ {\begin{array}{*{20}{l}} {\mathop {\min }\limits_\mathit{x} {{\left\| \mathit{\boldsymbol{x}} \right\|}_0}}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}{{\left\| {\mathit{\boldsymbol{y - Ax}}} \right\|}_2} \le \delta , \mathit{\boldsymbol{x}} \ge 0, {\bf{1}}_{m \times 1}^{\rm{T}}\mathit{\boldsymbol{x}} = 1} \end{array}} \right. $

(5)

式中：${{{\left\| \mathit{\boldsymbol{x}} \right\|}_0}}$表示丰度向量x中非零元素的个数，它代表稀疏项；${{{\left\| {\mathit{\boldsymbol{y - Ax}}} \right\|}_2}}$代表的是重建误差项，δ≥0是由于噪声和建模等原因导致的误差。

式(5)是一个NP-hard问题，不能直接进行求解。Candes等^[8]已经证明，只有当噪声项n为稀疏项的时候，才能将l₀范数替换为l₁范数。那么式(5)可以替换成：

$ \left\{ {\begin{array}{*{20}{l}} {\mathop {\min }\limits_x {{\left\| \mathit{\boldsymbol{x}} \right\|}_1}}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}{{\left\| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{Ax}}} \right\|}_2} \le \delta , \mathit{\boldsymbol{x}} \ge 0, {\bf{1}}_{m \times 1}^{\rm{T}}\mathit{\boldsymbol{x}} = 1} \end{array}} \right. $

(6)

式中：${{{\left\| \mathit{\boldsymbol{x}} \right\|}_1}}$表示丰度向量x的l₁范数。SUnSAL^[5]将2个约束条件加入式(6)中，将式(6)由有约束问题转换为无约束问题：

$ \mathop {\min }\limits_x \frac{1}{2}\left\| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{Ax}}} \right\|_2^2 + \lambda {\left\| \mathit{\boldsymbol{x}} \right\|_1} + {\mathit{\boldsymbol{\iota }}_{\{ 1\} }}\left( {{\bf{1}}_{m \times 1}^{\rm{T}}\mathit{\boldsymbol{x}}} \right) + {\mathit{\boldsymbol{\iota }}_{R_ + ^m}}(\mathit{\boldsymbol{x}}) $

(7)

式中：λ≥0是控制解稀疏度的权重系数；${\mathit{\boldsymbol{\iota }}_{\{ 1\} }}\left( {{\bf{1}}_{m \times 1}^{\rm{T}}\mathit{\boldsymbol{x}}} \right)$和${\mathit{\boldsymbol{\iota }}_{R_ + ^m}}(\mathit{\boldsymbol{x}})$分别是ASC和ANC 2种约束。

1.2 多目标优化算法

多目标优化算法^[9]能同时优化多个目标函数。其表达式如下：

$ \left\{ {\begin{array}{*{20}{l}} {\min F(\mathit{\boldsymbol{x}}) = {{\left( {{f_1}(\mathit{\boldsymbol{x}}), {f_2}(\mathit{\boldsymbol{x}}), \cdots , {f_m}(\mathit{\boldsymbol{x}})} \right)}^{\rm{T}}}}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}\mathit{\boldsymbol{x}} \in \mathit{\Omega }} \end{array}} \right. $

(8)

式中：x=(x₁, x₂, …, x_n)是一个n维的决策变量；Ω是n维的可行决策空间；F(x)是一个包含了m个目标函数的向量。当且仅当∀i=1, 2, …, m，f_i(x_u)≤f_i(x_v)，$\wedge \;\;\exists j = 1, 2, \cdots, m, {f_i}\left( {{\mathit{\boldsymbol{x}}_u}} \right) < {f_i}\left( {{\mathit{\boldsymbol{x}}_v}} \right)$时，称决策变量x_u支配决策变量x_v(表示为${\mathit{\boldsymbol{x}}_u} \succ {\mathit{\boldsymbol{x}}_v}$)。

对于一个解x^*，如果不存在另一解x∈Ω使得$\mathit{\boldsymbol{x}} \succ {\mathit{\boldsymbol{x}}^*}$，那么x^*为Pareto最优解。Pareto最优解集为所有的Pareto最优解的集合，其定义为：

$ {P^*} = \left\{ {{\mathit{\boldsymbol{x}}^*} \in \mathit{\Omega }|\neg \;\exists \mathit{\boldsymbol{x}} \in \mathit{\Omega }, \mathit{\boldsymbol{x}} \succ {\mathit{\boldsymbol{x}}^*}} \right\} $

(9)

Pareto最优解集在目标函数空间上对应的图像称为Pareto最优前沿面(pareto front, PF)，其数学表达式为：

$ \begin{array}{l} {\rm{P}}{{\rm{F}}^*} \buildrel \Delta \over = \left\{ {F\left( {{x^*}} \right) = \left( {{f_1}\left( {{x^*}} \right), {f_2}\left( {{x^*}} \right), \cdots } \right.} \right., \\ {f_m}\left( {{x^*}} \right))|{x^*} \in {P^*}\} \end{array} $

(10)

2 基于LMEA多目标优化稀疏解混算法 2.1 多目标稀疏解混框架

基于式(5)的高光谱稀疏解混模型对应了2个目标函数，其中$\left\| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{Ax}}} \right\|_2^2$表示重建误差项RSE，${\left\| \mathit{\boldsymbol{x}} \right\|_0}$表示稀疏项SPA。标准光谱库A∈R^L×m通常包含成百上千个端元光谱样本，这意味着在进行多目标优化时，丰度向量x的维度会很大，因此高光谱稀疏解混问题是一个大规模多优化问题。普通的多目标优化算法在解决大规模优化问题时，随着空间搜索维度的增加，性能会恶化，因此只能选择适合解决大规模优化问题的多目标优化算法才能得到良好的解混结果。

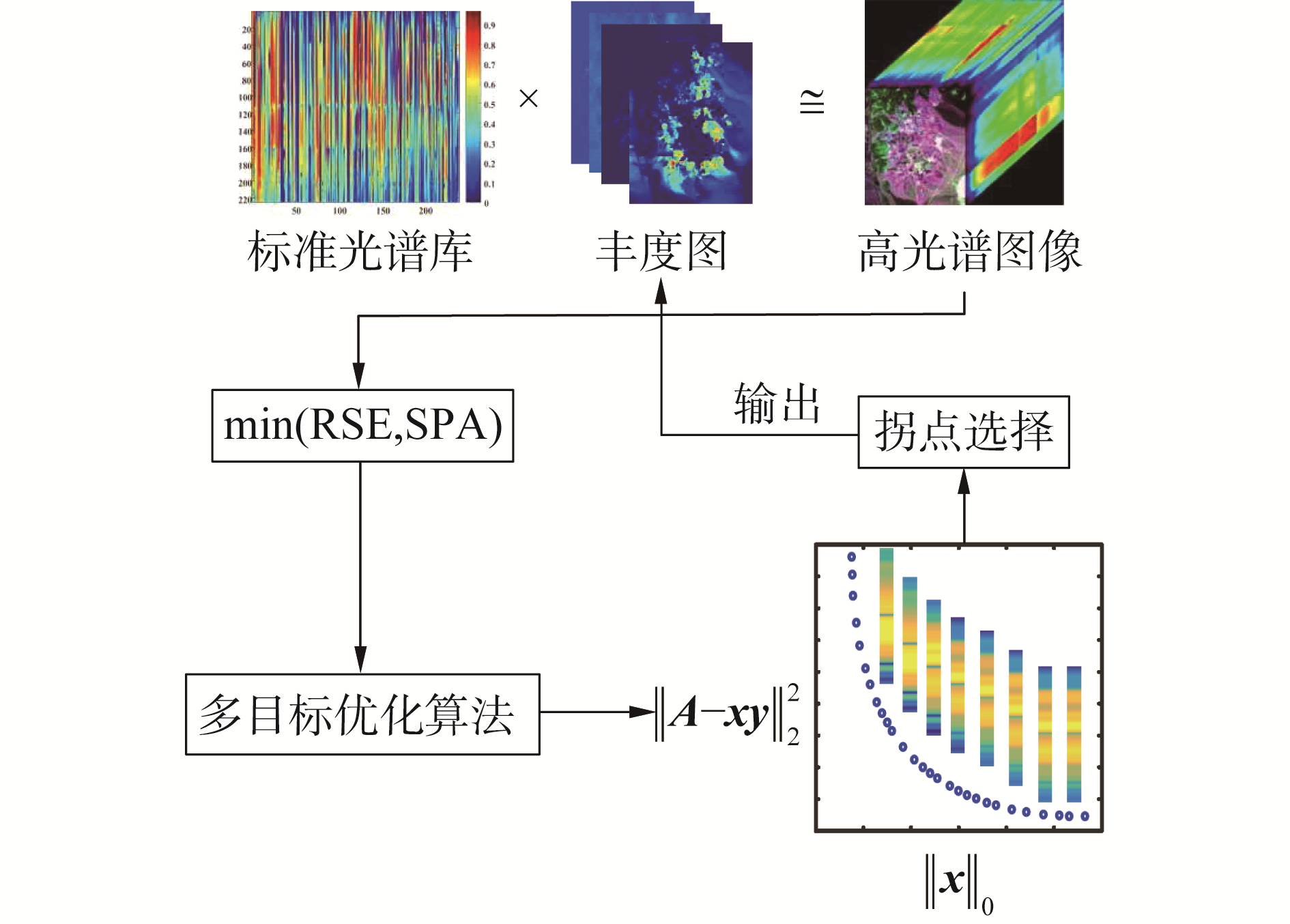
多目标稀疏解混算法的具体操作如图 1所示，首先输入标准光谱库和高光谱图像，选择RSE和SPA作为待优化的2个目标函数；然后采用多目标优化算法对其进行优化，满足终止条件后，从得到的PF中采用拐点选择策略选择最佳丰度向量；最后将每一个像元得到的丰度向量进行组合即为所求的丰度图。

2.2 基于LMEA多目标优化的稀疏解混算法

本文采用Zhang等^[6]提出的LMEA多目标优化算法，该算法采用了一种决策变量聚类分组的方法，将决策变量分为收敛性相关变量和多样性相关变量，再依据相关性分析将收敛性相关变量分成几个子组，最后将多样性相关变量和收敛性相关变量子组分别进行优化，这样的分组策略可以改善文献[5]中随机分组策略的缺陷。文献[5]将协同进化策略结合到多目标优化算法中，用以解决多目标稀疏解混框架中出现的大规模优化问题，选用随机分组策略来解决决策变量非独立不可分优化问题，通过随机分组可以有效地提高相互作用的2个决策变量分到同一组的概率。但是随机分组策略有一个缺陷，当存在多于3个彼此相关的决策变量时，将他们同时放到一个分组里进行优化的可能性几乎为零，不能充分考虑决策变量之间的相关性。而使用上述提及的LMEA多目标优化中的分组策略，即使多个决策变量彼此相关，也能分到同一组进一步的优化。

本文还提出一种有约束拐点区域选择策略。选择一个拐点区域，并以拐点区域重建误差最小的个体作为最佳丰度向量，避免了文献[5]在拐点选解时，只选择了单一的拐点解作为最终丰度估计向量，从而进一步提高解混精度。本文基于上述思想，提出一种基于LMEA多目标优化的高光谱稀疏解混算法。

2.2.1 决策变量的分组策略

将采用LMEA多目标优化算法中的决策变量聚类方法和相关性分析方法来对决策变量进行分组，该分组策略充分考虑了多个决策变量之间相关性，有效改进了随机分组中的不足。

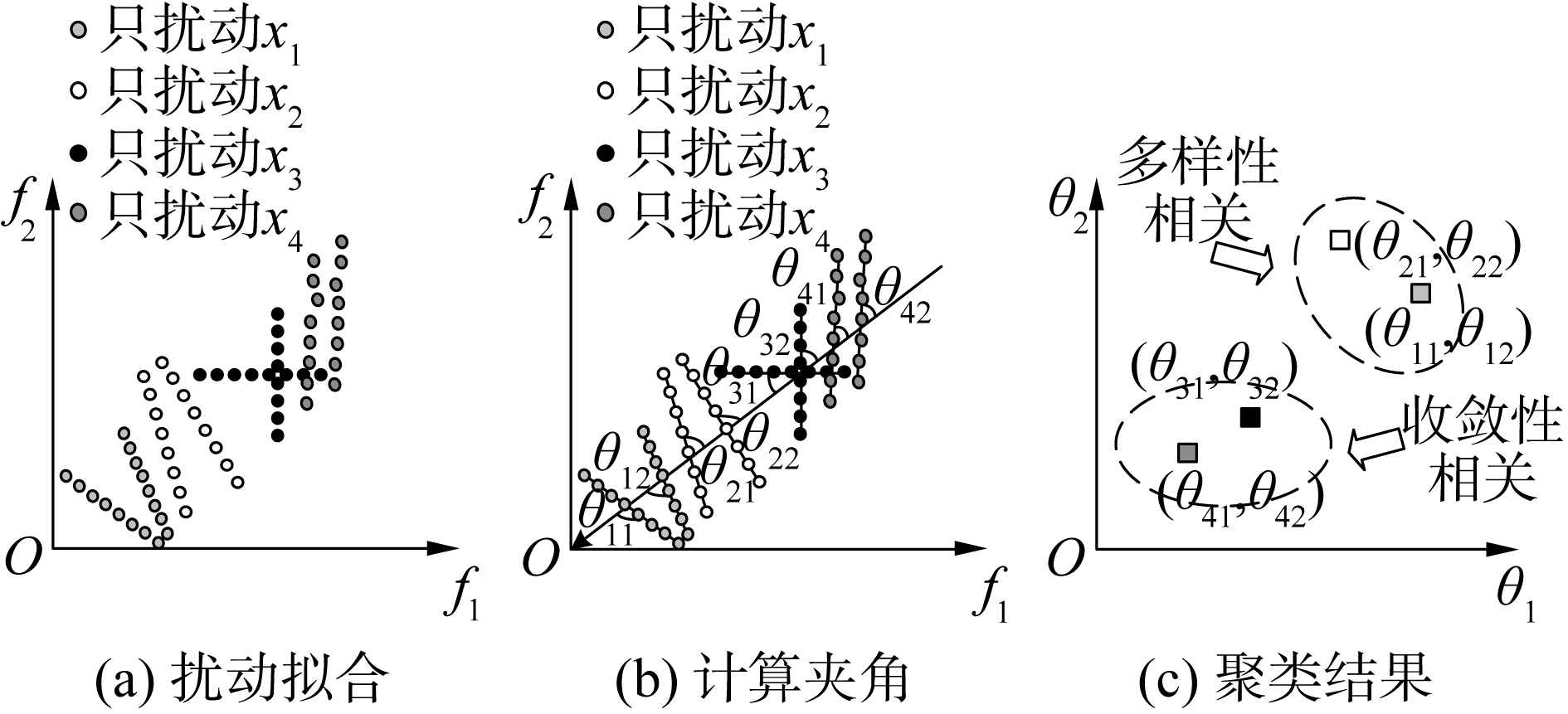
本文举例来说明决策变量聚类方法的主要思想，如图 2所示。

图 2中包含了4个决策变量，为了确定这4个决策变量是收敛性相关变量还是多样性相关变量，如图 2(a)所示，对每一个决策变量都执行8个扰动，将扰动后的采样解进行归一化，生成直线L以拟合每个归一化的采样解，并计算收敛方向与每个拟合线之间的夹角，如图 2(b)所示。其中夹角较大的意味着决策变量的收敛性更强，夹角较小的意味着决策变量的多样性更强。之后利用k均值聚类方法，根据每个变量的角度特征将决策变量分为2类，角度较大的变量划分为收敛性相关变量，角度较小的变量划分为多样性相关变量。那么按照这种方法，图 2(c)中的x₁和x₂被识别为多样性相关变量，而x₃和x₄被识别为收敛性相关变量。

在根据图 2所示的决策变量分析方法将所有的决策变量分成收敛性相关变量和多样性相关变量后，接下来，对收敛性相关变量进行了进一步的分组。首先，将收敛性相关变量的子组subCV初始化为空集，然后基于它们之间的相关性将CV中的收敛性相关变量分配给不同的subCV。其中相关性定义为：给定一个多目标优化问题$\min f = \min \left( {{f_1}} \right., {f_2}, \cdots, {f_m})$，如果存在x、a₁、a₂、b₁、b₂和至少一个f_k，1≤k≤m，满足：

$ \left\{ {\begin{array}{*{20}{l}} {{f_k}{{\left. {(\mathit{\boldsymbol{x}})} \right|}_{{\mathit{\boldsymbol{x}}_i} = {\mathit{\boldsymbol{a}}_2}, {\mathit{\boldsymbol{x}}_j} = {\mathit{\boldsymbol{b}}_1}}} < {f_k}{{\left. {(\mathit{\boldsymbol{x}})} \right|}_{{\mathit{\boldsymbol{x}}_i} = {\mathit{\boldsymbol{a}}_1}, {\mathit{\boldsymbol{x}}_j} = {\mathit{\boldsymbol{b}}_1}}}}\\ {{f_k}{{\left. {(\mathit{\boldsymbol{x}})} \right|}_{{\mathit{\boldsymbol{x}}_i} = {\mathit{\boldsymbol{a}}_2}, {\mathit{\boldsymbol{x}}_j} = {\mathit{\boldsymbol{b}}_2}}} > {f_k}{{\left. {(\mathit{\boldsymbol{x}})} \right|}_{{\mathit{\boldsymbol{x}}_i} = {\mathit{\boldsymbol{a}}_1}{\rm{, }}{\mathit{\boldsymbol{x}}_j} = {\mathit{\boldsymbol{b}}_2}}}} \end{array}} \right. $

(11)

则2个决策变量x_i和x_j被认为具有相关性。具体来说，如果变量与subCV中的至少1个变量是相关的，则将2个变量分配到同1个子组中，否则将它分配到1个新的子组中。因此，在十分极端的情况下，最多会有|CV|个子组，每个子组只包含1个决策变量。若决策变量是完全不可分的，则只有1个子组。

2.2.2 收敛性优化策略和多样性优化策略

本文使用决策变量聚类方法将多目标稀疏解混算法中的全部决策变量分为收敛性相关变量和多样性相关变量，再将收敛性相关变量依照相关性分析分为几个子组后，采用文献[6]中2种不同的优化策略分别优化收敛性相关变量子组和多样性相关变量。

在收敛性优化策略中，LMEA多目标优化算法提出T-ENS对父代种群进行非支配排序，并计算每个解到理想点之间的欧几里德距离，通过独立优化每个子组内的收敛性相关变量来生成子代解。在多样性优化策略中，首先通过使用模拟二进制交叉算子优化所有多样性相关变量，从种群P^t中生成的NP个子代解；然后将子代解和父代解组合，并对组合后的解进行环境选择。

通过上面2种优化策略，对于每一个新生成的解x, x中的每一个元素x_i(i=1, 2, …, n)做如下调整：

$ \left\{ {\begin{array}{*{20}{c}} {{\rm{ANC}}:{x_i} = \left\{ {\begin{array}{*{20}{l}} {0\;\;\;\;{\mathit{x}_\mathit{i}}{\rm{ < 0}}}\\ {{x_i}\;\;\;其他} \end{array}} \right.}\\ {{\rm{ASC}}:{x_i} = \frac{{{x_i}}}{{\sum\limits_{i = 1}^n {{x_i}} }}\;\;\;\;\;\;\;\;\;} \end{array}} \right. $

(12)

以保证其满足ANC和ASC这2个约束条件。然后根据得到的解更新种群P^t，计算种群P^t的目标函数值，进行非支配排序，更新PF，重复循环2种优化策略，直到满足终止条件。

2.2.3 有约束拐点区域选择策略

在多目标稀疏解混模型中，拐点是PF上最有价值的点，如图 3(a)中的大圆圈所示。在拐点之前，RSE随着SPA的增加急剧减小，在拐点之后，随着SPA的增加，RSE只能少量的减少。为了平衡这2个相互冲突的目标函数，选择PF上的拐点作为最佳丰度向量是很合理的。拐点选择的好坏直接影响稀疏解混的最终结果，本文提出了一种有约束拐点区域选择策略去选择最佳丰度向量。

在实际的选解中，由于多目标优化算法的特性，每一次得到的PF前沿面不同，只选择单一的拐点解直接作为最终的丰度向量有很大的随机性，因此，本文将选解的过程进行改进。首先如图 3(b)所示，在PF上找到RSE的最大极端解和SPA的最大极端解，并根据2个极端解做一条超线。PF上的解与超线的欧几里德距离越大，这个解就越有可能被看作拐点。之后，求PF上的解与超线之间的欧几里德距离，将每个解按照欧几里德距离由大到小进行排序，如图 3(c)所示，选择距离相对较大的几个解作为拐点区域，然后，选择重建误差值作为一个约束条件，对区域中的每个解计算重建误差值，选择重建误差最小的解作为最佳丰度向量，以保证其解混结果更接近真实丰度向量。计算的重建误差值如下：

$ {\rm{Error}} = \left\| {\mathit{\boldsymbol{A\tilde x}} - \mathit{\boldsymbol{y}}} \right\|_2^2 $

(13)

式中：${\mathit{\boldsymbol{\tilde x}}}$为拐点区域中的某个解对应的丰度向量。

最后，将每一个混合像元对应的最佳丰度向量进行组合，得到的丰度估计图就是最终稀疏解混的输出结果。

3 实验仿真与分析

本文采用常用的一组模拟数据集和一组真实高光谱数据集进行实验仿真。对比算法选取Bi-MOSU多目标稀疏解混算法^[5]和比较有代表性的NCLS算法^[4]与SUnSAL算法^[4]。为了公平对比，本文算法初始种群和迭代次数的设置与Bi-MOSU算法相同，种群规模设置为100，种群最大迭代次数为200，在进化收敛性相关变量和多样性相关变量时，最大迭代次数为10。其他对比算法中的参数设置都参见文献中给出的参数进行实验。所有算法均独立运行20次，最终结果是20次实验结果的平均值。

本文算法采用的精度评价指标是与大多数文献相同的信号与重构误差之比(signal to reconstruction error, SRE^[10])和均方根误差(root mean square error, RMSE^[11])。SRE和RMSE的定义如下：

$ {\rm{SRE}} = 10\lg \left( {\frac{{{\rm{E}}\left[ {\left\| \mathit{\boldsymbol{x}} \right\|_2^2} \right]}}{{{\rm{E}}\left[ {\left\| {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{\widehat x}}} \right\|_2^2} \right.}}} \right) $

(14)

$ {\mathop{\rm RMSE}\nolimits} = \frac{1}{q}\sum\limits_{i = 1}^q {\sqrt {\frac{1}{L}\sum\limits_{j = 1}^L {\left( {{\mathit{\boldsymbol{x}}_{ij}} - {{\mathit{\boldsymbol{\widehat x}}}_{ij}}} \right)} } } $

(15)

式中：${\mathit{\boldsymbol{\tilde x}}}$表示估计的丰度向量，x_ij表示第j个像元的第i个端元的丰度真实值，${{{\mathit{\boldsymbol{\widehat x}}}_{ij}}}$表示第j个像元的第i个端元的丰度估计值。由式(14)、(15)可知，SRE的值越大或者RMSE的值越好，说明解混的结果越好。

本文所有实验的硬件平台采用Inter(R)Core(TM)i5-5250U CPU, 1.60 GHz，内存4 GB，软件平台采用MATLAB R2017a。

3.1 模拟数据仿真实验

本文使用的模拟数据集^[12]是一个包含了224个波段，大小为75×75的模拟图像，该数据集是在考虑了ASC和ANC的约束条件下，从光谱库A₁中随机抽取5个端元线性组合而成的。在模拟数据集中，混合像元区域和纯净像元区域分布在不同的正方形块中，混合像元区域包含了2~5种不等的纯净像元。背景像元是由这5个端元线性混合而成，相应的丰度值分别为0.114 9、0.074 1、0.200 3、0.205 5、0.405 1。该模拟数据集使用的光谱库A是从美国地质调查局(united states geologic, USGS)光谱库splib06中随机选取的240个光谱信号。为了验证本文算法对噪声的鲁棒性，在该数据集上增加了不同信噪比(signal to noise ratio, SNR)的高斯白噪声，SNR的值分别是20、30、40 dB。

表 1给出NCLS、SUnSAL、Bi-MOSU和本文算法在模拟数据集1上的解混精度SRE和RMSE的值。从表 1的数据可以定量分析，在对模拟数据集增加了不同信噪比的高斯白噪声后，所有算法的解混精度SRE都随着信噪比的增加而提高，其中本文算法的解混精度SRE随着信噪比的增加，提升的幅度最大。在信噪比相同的情况下，将本文算法的SRE值与3种对比算法的SRE值进行比较，本文算法得到的结果都是最高的。随着信噪比水平的升高，所有算法的RMSE都逐渐变小，而本文方法在不同信噪比条件下均获得了最小的RMSE值，说明本文算法具有最好的解混精度。

图 4给出模拟数据集中端元1、端元2和端元5的原始丰度图像及4种算法在受到信噪比为30 dB高斯白噪声污染下的模拟数据集上随机选取的端元1、端元2和端元5的丰度估计结果图。从图 4中可以定性看出，虽然这4种算法的稀疏解混结果都包含了很多的噪声点，但本文算法的噪声点要少于其他3种算法，且在背景颜色上更接近于真实丰度图像，效果更佳。

3.2 真实数据仿真实验

本文真实数据实验采用的数据集为著名的AVIRIS Cuprite高光谱数据集。该数据集目前已被广泛应用于混合像元分解、端元提取等应用算法中。图 5为软件Tricorder3.3对USGS光谱库进行分析得到的不同矿物分布的丰度图像。

本文采用与文献[5]相同的AVIRIS Cuprite数据集的子集进行实验，该子集大小为250×191，其中每个像元由188个波段组成(去掉了低信噪比和高水汽吸收的波段)。光谱库仍选取USGS光谱库用于实验。图 6给出了4种算法在AVIRIS Cuprite数据集中，明矾石和水铵长石这2种矿物质估计的丰度图。

从图 6中观察可知，这4种算法得到的明矾石估计结果很相似，但仔细观察存在细微的差别。在明矾石图像中，本文算法估计出的结果，丰度值较大的区域与SUnSAL算法和NCLS算法的颜色相近，但是都亮于Bi-MOSU算法的结果。丰度值较小的背景区域，本文算法和Bi-MOSU算法得到的图像明显要比其他2幅图像干净，并且本文算法得到的图像轮廓更为清晰。在水铵长石图像中，本文算法的背景要比其他3种对比算法更干净，解混出的地物更明显。总体来说，本文算法在真实数据集中边缘细节的处理更好一些，抗噪性能更强一些。

4 结论

1) 本文提出将LMEA算法引入高光谱稀疏解混模型，将决策变量分为收敛性相关变量和多样性相关变量，并分别进行优化，充分考虑了决策变量之间的相关性。

2) 本文提出有约束拐点区域选择策略在得到的PF上进行选解，提升了算法的解混精度。

3) 本文通过模拟和真实的高光谱数据集进行实验，本文算法和其他3种对比算法相比，得到了最优的高光谱数据解混精度，并且随着信噪比的增加，本文算法的解混精度得到了明显的提升，这对解决实际复杂的高光谱图像的解混问题具有重要的意义。

今后的工作将考虑引入空间相关性以充分利用空间信息，以期进一步提升高光谱稀疏解混的效果和精度。