现代通信技术的迅猛发展,特别是无线通信迅猛发展对数据传输速率,传输效率和频带利用率提出了更高要求,选择高效可行的调制解调手段,对提高信号的有效性和可靠性起着至关重要的作用。正交调制将数据分为两路,分别进行载波调制,两路载波相互正交,提高了频谱利用率。同时,在现代战争中,战斗机的飞行速度越来越快,在飞行速度达到几马赫的高动态场景下,多普勒频移(Doppler frequency shift, DFS)会造成大大降低了通信系统的可靠性。因此,定量的分析正交调制的抗DFS能力显得非常有意义。文献[1-3]研究了相位噪声对正交相移键QPSK信号的影响,并且给出了数学模型,但是忽略了信道中的高斯白噪声;文献[4]从多载波的角度分析了频偏对通信系统性能的影响,推导出了系统误码率随归一化频偏的近似公式;文献[5-6]研究了正交调制在衰落信道下的性能;文献[7]分析了定时偏差和载波恢复相差对误符号率的影响;文[8-10]从抗干扰的角度定量的推出了QAM信号的误符号率公式。本文以在L频段下,带宽在100 MHz左右,运行速度为1 Ma以上的高动态场景下研究正交调制系统对DFS的响应机理为目标,建立了正交调制信号在DFS下的一般性数学模型,得出了一般性的结论,并以MPSK和MQAM信号为例推导出了存在DFS和高斯白噪声时的误符号率公式,并用仿真验证推导公式的正确性。
1 正交调制的DFS响应模型正交调制的调制的原理图如图 1所示,输入的二进制流经过串并转换再经过2路正交载波调制后。(以下将2路信号分别称为I路和Q路)得到最终的信号为:

|
Download:
|
| 图 1 正交调制星座图 Fig. 1 Constellation of orthogonal modulation | |
| $ x(t) = a_{\mathrm{I}}\cos (2{\rm{ \mathsf{ π} }}ft) + {a_\rm{Q}}\sin (2{\rm{ \mathsf{ π} }}ft) $ |
在信道中由于受到DFS以及高斯白噪声的影响,在接收端收到的信号为:
| $ \begin{array}{l} y(t) = {a_{\rm{I}}}\cos (2{\rm{ \mathsf{ π} }}(f + \Delta f))t + {a_\rm{Q}}\sin (2{\rm{ \mathsf{ π} }}(f + \Delta f))t + \\ {n_c}\cos (2{\rm{ \mathsf{ π} }}ft) + {n_s}\sin (2{\rm{ \mathsf{ π} }}ft) \end{array} $ |
式中:Δf为接收端相对于发射载波的频偏,假设发送信号为短帧,则将Δf近似看做是恒定不变的,信道中的噪声可以看作是窄带高斯过程[11]。为了单独分析DFS对解调性能的影响,暂时将加性的高斯白噪声忽略掉。收端框图如图 2所示。

|
Download:
|
| 图 2 正交解调框图 Fig. 2 Block diagram of orthogonal demodulation | |
对于I路,y(t)与I路的本地载波相乘后为:
| $ \begin{aligned} y_{\mathrm{I}}(t)=&\left[a_{\mathrm{I}} \cos (2 {\rm{ \mathsf{ π} }}(f+\Delta f) t)+a_{Q} \sin (2 {\rm{ \mathsf{ π} }}(f+\Delta f) t)\right] \times \\ & \cos (2 {\rm{ \mathsf{ π} }} f t) \end{aligned} $ |
该信号经过低通滤波器滤除高频项,则:
| $ {y_{\rm{I}}}(t) = {a_{\rm{I}}}\cos (2{\rm{ \mathsf{ π} }}\Delta ft) + {a_{\rm{Q}}}\sin (2{\rm{ \mathsf{ π} }}\Delta ft) $ |
同理,Q路信号与本地载波相乘并经过低通滤波器滤除高频项后可写为:
| $ {y_{\rm{Q}}}(t) = {a_{\rm{Q}}}\cos (2{\rm{ \mathsf{ π} }}\Delta ft) - a_{\mathrm{I}}\sin (2{\rm{ \mathsf{ π} }}\Delta ft) $ |
引入归一化频偏ε,定义为频偏与带宽的比值,即
| $ \left\{ {\begin{array}{*{20}{l}} {{y_{\rm{I}}} = {a_{\rm{I}}}\cos ({\rm{ \mathsf{ π} }}\varepsilon ) + {a_{\rm{Q}}}\sin ({\rm{ \mathsf{ π} }}\varepsilon )}\\ {{y_{\rm{Q}}} = {a_{\rm{Q}}}\cos ({\rm{ \mathsf{ π} }}\varepsilon ) - {a_{\rm{I}}}\sin ({\rm{ \mathsf{ π} }}\varepsilon )} \end{array}} \right. $ | (1) |
式中yI、yQ分别对应接收信号的实部和虚部,也是对应接受信号星座点的横坐标和纵坐标。可见相对于发送信号的实部和虚部,接收信号的实部和虚部都有了改变。
接收信号的模值平方和相位分别为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\rho ^2} = y_{\mathrm{I}}^2 + y_{\rm{Q}}^2 = a_{\mathrm{I}}^2 + a_{\rm{Q}}^2}\\ {\varphi = \arctan \left( {\frac{{{y_{\rm{Q}}}}}{{{y_{\mathrm{I}}}}}} \right) = \arctan \left( {\frac{{{a_{\rm{Q}}}}}{{a_{\mathrm{I}}}}} \right) - {\rm{ \mathsf{ π} }} \varepsilon } \end{array}} \right. $ | (2) |
假设接收端相对于发送端的运动速度为v,则:
| $ \varepsilon = 2{T_s}\Delta f = 2\Delta f/{R_s} = 2{\rm{ \mathsf{ π} }}vf/c{R_s} $ | (3) |
式中:c为光速;Rs为符号速率;f为载波频率。由式(2)、(3)可见,DFS使得正交调制信号的相位减少了
从星座图的角度而言,DFS对正交信号的影响是星座点的旋转。而MPSK信号和MQAM信号由于其星座图和判决区域不同导致其误符号率的计算方式不同。
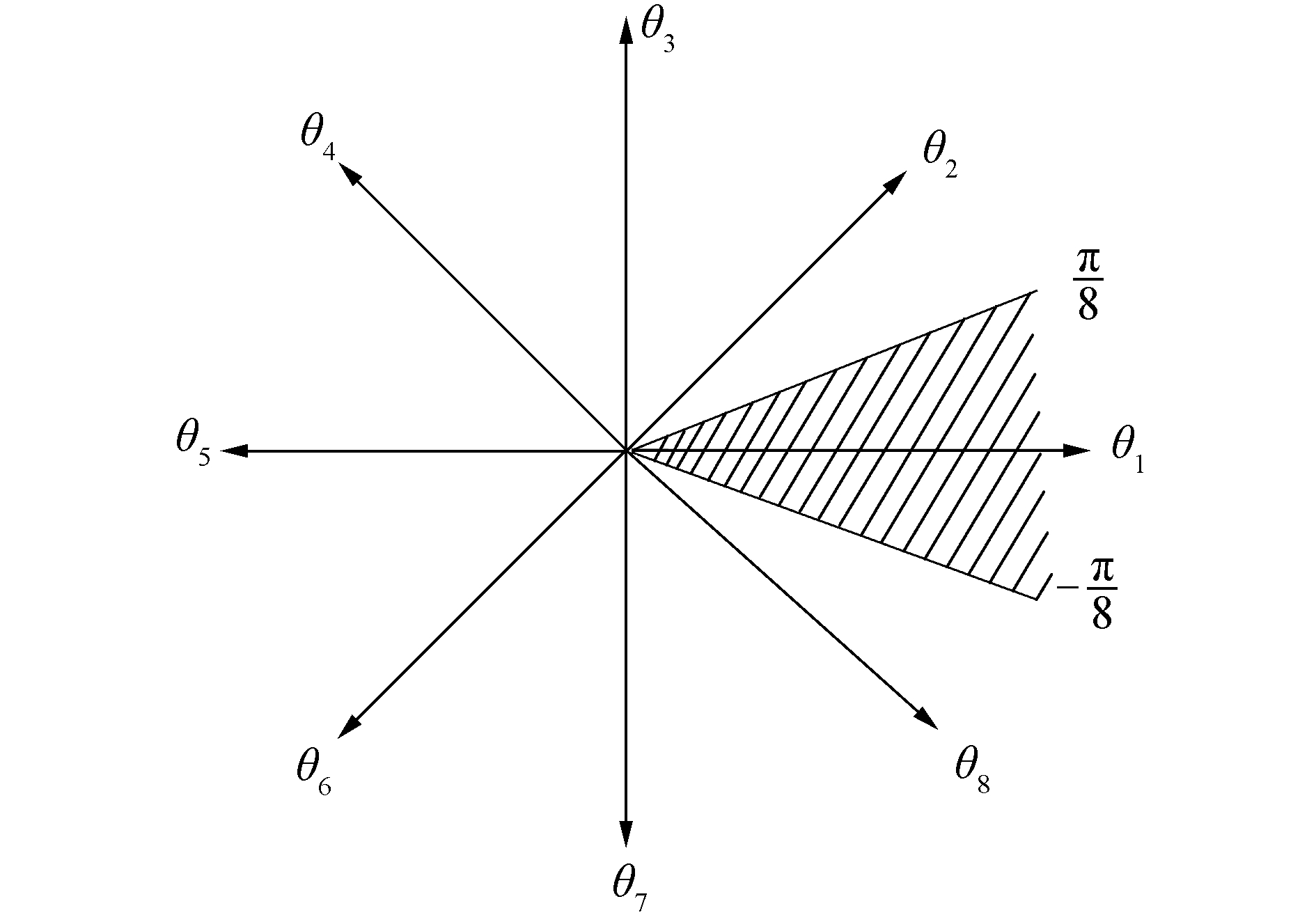
2 MPSK信号的DFS响应建模MPSK信号星座点和和判决区域如图 3(以8PSK为例)所示,8个信号矢量把相位平面分为8等份,若发送信号为零相位,接收信号的相位在-π/8 < θ < π/8时不会产生误判由于星座图的对称性,发送端对应星座图上任何一个点,在接收端的误符号率是相同的,为简便,以在零相位的点分析。考虑噪声的影响,则接收信号经过载波相干以及低通滤波器后并在Ts进行判决前的I路和Q路信号分别为:
|
Download:
|
| 图 3 8PSK星座图及判决区域 Fig. 3 Constellation of 8PSK and its verdict area | |
| $ \left\{ {\begin{array}{*{20}{l}} {{y_{\rm{I}}} = {a_{\rm{I}}} + {n_c}}\\ {{y_{\rm{Q}}} = {n_s}} \end{array}} \right. $ |
式中:yI、yQ相互独立;nc、ns则分别是I路和Q路的窄带高斯白噪声,服从均值为0,方差为σ2的高斯分布,yI、yQ的联合概率密度函数为:
| $ \begin{array}{l} f\left( {{y_{\rm{I}}}, {y_{\rm{Q}}}} \right) = f\left( {{y_{\rm{I}}}} \right)f\left( {{y_{\rm{Q}}}} \right) = \\ \frac{1}{{2{\rm{ \mathsf{ π} }}{\sigma ^2}}}\exp \left( {\frac{{ - {{\left( {{y_{\rm{I}}} - {a_{\rm{I}}}} \right)}^2} + y_{\rm{Q}}^2}}{{2{\sigma ^2}}}} \right) \end{array} $ |
其中:
| $ \begin{array}{l} f(\rho , \varphi ) = \left| {\begin{array}{*{20}{c}} {\cos \varphi }&{\sin \varphi }\\ { - \rho \sin \varphi }&{\rho \cos \varphi } \end{array}} \right|f\left( {{y_{\rm{I}}}, {y_{\rm{Q}}}} \right) = \rho f\left( {{y_{\rm{I}}}, {y_{\rm{Q}}}} \right) = \\ \frac{\rho }{{2{\rm{ \mathsf{ π} }}{\sigma ^2}}}\exp \left( { - \frac{{{\rho ^2} + a_{\rm{I}}^2 - 2{a_{\rm{I}}}\rho \cos \varphi }}{{2{\sigma ^2}}}} \right) \end{array} $ |
则相位密度可以化简为:
| $ \begin{array}{l} f(\varphi ) = \int_{ - \infty }^{ + \infty } f (\rho , \varphi ){\rm{d}}\varphi = \\ \frac{{{{\rm{e}}^{ - r}}}}{{2{\rm{ \mathsf{ π} }}}} + \frac{{{{\rm{e}}^{ - \mathit{r}{\rm{si}}{{\rm{n}}^2}\varphi }}}}{{2\sqrt {\rm{ \mathsf{ π} }} }} \times \sqrt r \cos \varphi \times (1 + {\mathop{\rm erf}\nolimits} (\sqrt r \cos \varphi )) \end{array} $ |
式中r为信噪比。当相位满足-π/M < φ < π/M时就不会产生误判。则MPSK信号在无DFS情况下的误符号率为:
| $ {P_e} = 1 - \int_{ - \frac{{\rm{ \mathsf{ π} }}}{M}}^{\frac{{\rm{ \mathsf{ π} }}}{M}} f (\varphi ){\rm{d}}\varphi $ |
从上节可知,DFS对MPSK影响只是相位顺时针旋转了
| $ \begin{array}{l} {P_e} = 1 - \int_{ - \frac{{\rm{ \mathsf{ π} }}}{M} + {\rm{ \mathsf{ π} }}\varepsilon }^{\frac{{\rm{ \mathsf{ π} }}}{M} + {\rm{ \mathsf{ π} }}\varepsilon } f (\varphi ){\rm{d}}\varphi = \\ \begin{array}{*{20}{l}} {1 - \frac{{{{\rm{e}}^r}}}{M} - \frac{1}{4}{\mathop{\rm erfc}\nolimits} \left( {\sqrt r \sin \left( {\frac{\pi }{M} + {\rm{ \mathsf{ π} }}\varepsilon } \right)} \right) + }\\ {\frac{1}{4}{\mathop{\rm erfc}\nolimits} \left( {\sqrt r \sin \left( { - \frac{\pi }{M} + {\rm{ \mathsf{ π} }}\varepsilon } \right)} \right) - }\\ {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} }}\int_{\sqrt r \sin \left( { - \frac{\pi }{M} + {\rm{ \mathsf{ π} }}\varepsilon } \right)}^{\sqrt r \sin \left( {\frac{\pi }{M} + {\rm{ \mathsf{ π} }}\varepsilon } \right)} {\exp } \left( { - {x^2}} \right){\mathop{\rm erf}\nolimits} (x){\rm{d}}x} \end{array} \end{array} $ | (4) |
其中:
MQAM信号的星座点及判决区域如图 4所示,(仅以最常用的正方形星座图为例)。星座点的横、纵坐标的表达式如下:

|
Download:
|
| 图 4 QAM星座图及判决区域 Fig. 4 Constellation of QAM and its verdict area | |
| $ \left\{ {\begin{array}{*{20}{l}} {{X_i} = id + \frac{d}{2}, }&{i = 0, 1, 2, \cdots , \frac{{\sqrt M }}{2} - 1}\\ {{X_j} = jd + \frac{d}{2}, }&{j = 0, 1, 2, \cdots , \frac{{\sqrt M }}{2} - 1} \end{array}} \right. $ | (5) |
式中:M为调制指数;d为任意2个星座点之间的距离。由于信道中的噪声和DFS影响导致接收信号的实部和虚部发生了变化,当接收信号的点变化到所属虚线区域以外时则判决错误。由于其星座图的对称性,仅以第一象限的点为例,可见QAM信星座图由4种不同的判决区域的点构成,如图 4所示将星座图上的点分为4类点。下面将对4类点进行分析。
3.1 第1类点的误符号率分析第1类点如图 4所示,设
| $ {P_{1x}} = P\left( {\left| {{y_i} - {x_i} + {n_c}} \right| \le \frac{d}{2}} \right) $ | (6) |
式中:nc是I路的噪声,服从均值为0,方差为σ2的高斯分布;yi为接收信号的实部;xi为发送信号的实部;yi为接收信号的虚部;xj为发送信号的虚部。由式(1)得:
| $ \left\{ {\begin{array}{*{20}{l}} {{y_i} = {x_i}\cos ({\rm{ \mathsf{ π} }}\varepsilon ) + {x_j}\sin ({\rm{ \mathsf{ π} }}\varepsilon )}\\ {{y_j} = {x_j}\cos ({\rm{ \mathsf{ π} }}\varepsilon ) - {x_i}\sin ({\rm{ \mathsf{ π} }}\varepsilon )} \end{array}} \right. $ | (7) |
式中:
| $ \begin{array}{l} {P_{1x}} = P\left( {|\left( {i + \frac{1}{2}} \right)d(\cos ({\rm{ \mathsf{ π} }}\varepsilon ) - 1) + } \right.\\ \left( {j + \frac{1}{2}} \right)d\sin ({\rm{ \mathsf{ π} }}\varepsilon ) + {n_c}| \le \frac{d}{2}) \end{array} $ | (8) |
令:
| $ {I_{ij}} = \left( {i + \frac{1}{2}} \right)(\cos ({\rm{ \mathsf{ π} }}\varepsilon ) - 1) + \left( {j + \frac{1}{2}} \right)\sin ({\rm{ \mathsf{ π} }}\varepsilon ) $ | (9) |
令
| $ {P_{1x}} = \frac{1}{2}\left( {{\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( { - \frac{1}{2} - {I_{i, j}}} \right)} \right) - {\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( {\frac{1}{2} - {I_{i, j}}} \right)} \right)} \right) $ |
同理,
ns是Q路的噪声,服从均值为0,方差为σ2的高斯分布。则:
| $ \begin{array}{l} {P_{1y}} = P\left( {|\left( {j + \frac{1}{2}} \right)d(\cos ({\rm{ \mathsf{ π} }}\varepsilon ) - 1) - } \right.\\ \left( {i + \frac{1}{2}} \right)d\sin ({\rm{ \mathsf{ π} }}\varepsilon ) + {n_s}| \le \frac{d}{2}) \end{array} $ | (10) |
令:
| $ {Q_{ij}} = \left( {j + \frac{1}{2}} \right)(\cos ({\rm{ \mathsf{ π} }}\varepsilon ) - 1) - \left( {i + \frac{1}{2}} \right)\sin ({\rm{ \mathsf{ π} }}\varepsilon ) $ | (11) |
将式(7)、(11)代入式(10)可得:
| $ {P_{1y}} = \frac{1}{2}{\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( { - \frac{1}{2} - {Q_{ij}}} \right)} \right) - \frac{1}{2}{\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( {\frac{1}{2} - {Q_{ij}}} \right)} \right) $ | (12) |
对于接收端来说,I路和Q路的判决是相互独立的,则:
| $ \begin{array}{l} {{\rm{P}}_{{\rm{1}}\mathit{ij}}}{\rm{ = }}{{\rm{P}}_{{\rm{1}}\mathit{x}}}{{\rm{P}}_{{\rm{1}}\mathit{y}}}{\rm{ = }}\\ \frac{1}{4}\left( {{\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( { - \frac{1}{2} - {I_{i, j}}} \right)} \right) - {\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( {\frac{1}{2} - {I_{i, j}}} \right)} \right)} \right)\\ \left( {{\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( { - \frac{1}{2} - {Q_{i, j}}} \right)} \right) - {\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( {\frac{1}{2} - {Q_{i, j}}} \right)} \right)} \right) \end{array} $ |
第2类点如图 4所示,设
| $ \begin{array}{l} {P_{2x}} = {P_{1x}}|\left( {j = \frac{{\sqrt M }}{2} - 1} \right) = \\ \frac{1}{2}{\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( { - \frac{1}{2} - {I_{i, \frac{\pi }{2} - 1}}} \right)} \right) - \\ \frac{1}{2}{\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( {\frac{1}{2} - {I_{i, \frac{{\sqrt M }}{2} - 1}}} \right)} \right)\\ {P_{2y}} = P\left( {{y_j} + {n_s} \ge \left( {\frac{{\sqrt M }}{2} - 1} \right)d} \right) = \\ \frac{1}{2}{\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( {\frac{{\sqrt M - 1}}{2} - {Q_{i, \frac{{\sqrt M - 1}}{2}}} + i} \right)} \right)\\ {{\rm{P}}_{{\rm{2}}\mathit{i}}}{\rm{ = }}{{\rm{P}}_{{\rm{2}}\mathit{x}}}{{\rm{P}}_{{\rm{2}}\mathit{y}}}{\rm{ = }}\\ \frac{1}{4}\left( {{\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( { - \frac{1}{2} - {I_{i, \frac{{\sqrt M }}{2} - 1}}} \right)} \right) - } \right.\\ {\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( {\frac{1}{2} - {I_{i, \frac{{\sqrt M }}{2} - 1}}} \right)} \right)\\ {\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( {\frac{{\sqrt M - 1}}{2} - {Q_{i, \frac{{\sqrt {M - 1} }}{2}}} + i} \right)} \right) \end{array} $ |
第3类点如图 4所示,设P3j为第3类点判决正确的概率,同理可得:
| $ \begin{array}{l} {P_{3j}} = \frac{1}{4}\left( {{\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( { - \frac{1}{2} - {Q_{\frac{\pi }{2} - 1, j}}} \right)} \right) - } \right.\\ {\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( {\frac{1}{2} - Q\frac{{\sqrt M }}{2} - 1, j} \right)} \right)) \cdot \\ {\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( {\frac{{\sqrt M - 1}}{2} - {I_{i, \frac{{\sqrt M - 1}}{2}}} + j} \right)} \right) \end{array} $ |
第4类点如图 5所示。设P4、P4x、P4y分别为本类点判决正确的概率,本类点实部判决正确的概率,本类点虚部判决正确的概率。则:
| $ \begin{array}{l} {P_{4x}} = {P_{3x}}|\left( {j = \frac{{\sqrt M }}{2} - 1} \right) = \\ \frac{1}{2}{\mathop{\rm erfc}\nolimits} (\sqrt {{r_1}} (\sqrt M - 1 - ({\mathit{I}_{\frac{{\sqrt M - 1}}{2}, \frac{{\sqrt M - 1}}{2}}}))\\ {P_{4y}} = {P_{2y}}|\left( {i = \frac{{\sqrt M }}{2} - 1} \right) = \\ \frac{1}{2}{\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( {\sqrt M - 1 - {Q_{\frac{{\sqrt M - 1}}{2}, \frac{{\sqrt M - 1}}{2}}}} \right)} \right)\\ {{\rm{P}}_{\rm{4}}}{\rm{ = }}{{\rm{P}}_{{\rm{4}}\mathit{x}}}{{\rm{P}}_{{\rm{4}}\mathit{y}}}{\rm{ = }}\\ \frac{1}{4}{\mathop{\rm erfc}\nolimits} (\sqrt {{r_1}} (\sqrt M - 1 - ({\mathit{I}_{\frac{{\sqrt M - 1}}{2}, \frac{{\sqrt M - 1}}{2}}})) \cdot \\ {\mathop{\rm erfc}\nolimits} \left( {\sqrt {{r_1}} \left( {\sqrt M - 1 - {Q_{\frac{{\sqrt M - 1}}{2}, \frac{{\sqrt M - 1}}{2}}}} \right)} \right) \end{array} $ |
对于发送端来说,发送上述4类点是随机的并且服从均匀分布,则在存在DFS和高斯白噪声的信道下MQAM信号的误符号率的表达式为:
| $ P = 1 - \frac{4}{M}\left( {\sum\limits_{i = 0}^{\frac{{\sqrt M }}{2} - 2} {\sum\limits_{j = 0}^{\frac{{\sqrt M }}{2} - 2} {{P_{1ij}}} } + \sum\limits_{i = 0}^{\frac{{\sqrt M }}{2} - 2} {{P_{2i}}} + \sum\limits_{j = 0}^{\frac{{\sqrt M }}{2} - 2} {{P_{3j}}} + {P_4}} \right) $ | (13) |
仿真1:接收端不同的运动速度对MPSK调制信号性能的影响。
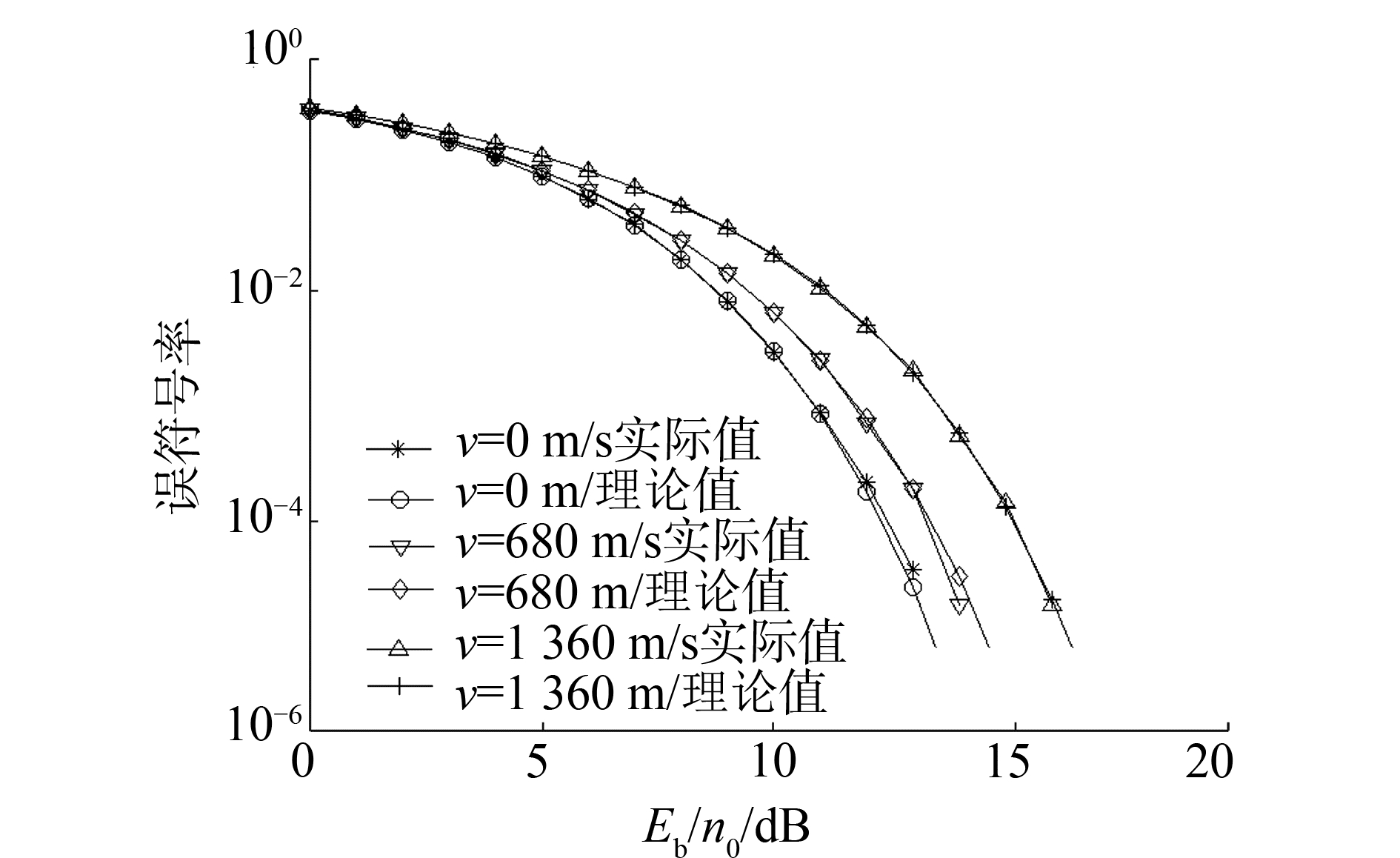
仿真参数:模仿在L频段的高动态场景下,其中载波频率f=2 GHz,符号速率Rs=50 Mbit/s, 信道为高斯白噪声信道,调制方式为8PSK调制。图 5给出了8PSK调制信号在接收机运动速度分别为0、680、1 360 m/s的误符号率随着信噪比在上述条件下的曲线,可见实际曲线和理论曲线基本重合,验证了推导的正确性,当飞行速度增加时,系统的性能显著下降。
|
Download:
|
| 图 5 8PSK信号在不同运动速度下性能曲线 Fig. 5 Performance curves of 8PSK signals under different speeds | |
仿真2:调制指数对MPSK调制信号性能的影响。
仿真参数:载波频率f=2 GHz,符号速率Rs=50 Mbit/s,信道为高斯白噪声信道,信噪比Eb/n0=20 dB。图 6给出了8PSK、16PSK、32PSK信号的误符号率随着运动速度的理论和实际曲线,可见实际误符号率和理论误符号率基本重合,验证了推导的正确性。在仿真中设置的信噪比很大,设为20 dB,是为了减小噪声对信号的影响。由图可知:随着调制指数增大,系统性能下降,误符号率上升速率也越快。由此可得出结论:随着调制指数增大,系统抗DFS能力越弱。

|
Download:
|
| 图 6 MPSK信号误符号率随运动速度变化曲线 Fig. 6 Curves of error symbol rate of MPSK signal with speeds | |
仿真3:接收端不同的运动速度对MQAM调制信号性能的影响。
仿真参数:载波频率f=2 GHz,符号速率Rs=50 Mbit/s,信道为高斯白噪声信道,调制方式为16QAM调制。图 7给出了16QAM调制信号在接收端运动速度分别为0、680、1 360 m/s的误符号率随着信噪比在上述条件下的曲线,可见实际曲线和理论曲线基本重合,验证了推导的正确性,当运动速度增加时,系统的性能显著下降。

|
Download:
|
| 图 7 16QAM信号在不同运动速度下性能曲线 Fig. 7 Performance curve of 16QAM signal under different speeds | |
仿真4:调制指数对MQAM调制信号性能的影响。
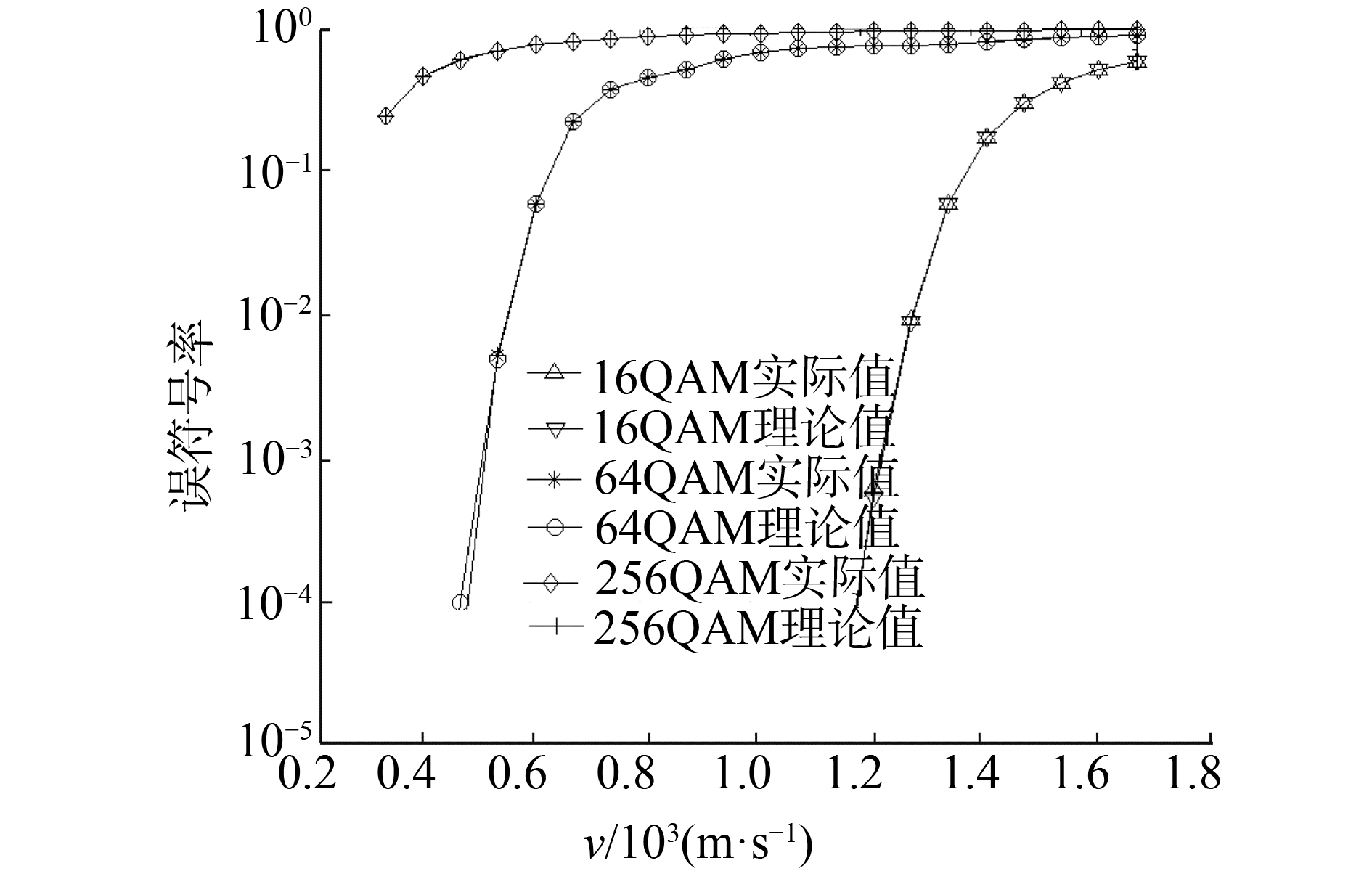
仿真参数:载波频率f=2 GHz,符号速率Rs=50 Mbit/s, 信道为高斯白噪声信道,信噪比Eb/n0=20 dB。图 8给出了16QAM,64QAM,256QAM信号的误符号率随着飞行速度的理论和实际曲线图,可见实际误符号率和理论误符号率基本重合,验证了推导的正确性。在仿真中设置的信噪比很大,设为20 dB,是为了减小噪声对信号的影响。由图可知:随着调制指数增大,系统性能下降, 误符号率上升速率也越快。由此可得出结论:随着调制指数增大,系统抗DFS能力越弱。
|
Download:
|
| 图 8 MQAM信号误符号率随运动速度变化曲线 Fig. 8 Curves of error symbol rate of MQAM signal with speeds | |
且随着运动速度的增加,MQAM信号的误符号率比MPSK信号上升更快,可见MQAM的抗DFS能力弱于MPSK信号。
5 结论1) DFS破坏了正交调制信号的两路载波的正交性,总体来说是信号相位的旋转,幅度并未改变。
2) 随着运动速度的增加,正交调制的性能会严重下降。
3) 系统对DFS的敏感性随调制指数的增加而增大。
4) 在相同信噪比且信噪比较大情况下,MPSK相比MQAM调制具有更好的抗DFS特性。这些结论对于在高动态场景下设计正交调制系统提供了理论基础。
| [1] |
TAGGART D, KUMAR R. Impact of phase noise on the performance of the QPSK modulated signal[C]//Proceedings of 2011 IEEE Aerospace Conference. Big Sky, MT, USA, 2011: 1-10.
(  0) 0)
|
| [2] |
BIALER O, RAPHAELI D. Analysis of optimum detector of trellis coded MPSK in phase noise channels[J]. IEEE transactions on communications, 2011, 59(1): 130-140. DOI:10.1109/TCOMM.2011.120710.090467 (  0) 0)
|
| [3] |
SLIMANE E B, JARBOUI S, BOUALLEGUE A. Blind phase estimation algorithm for trellis coded modulation over both AWGN and Rayleigh flat fading channels[C]//Proceedings of the 9th International Wireless Communications and Mobile Computing Conference. Sardinia, Italy, 2013.
(  0) 0)
|
| [4] |
POLLET T, VAN BLADEL M, MOENECLAEY M. BER sensitivity of OFDM systems to carrier frequency offset and wiener phase noise[J]. IEEE transactions on communications, 1995, 43. (  0) 0)
|
| [5] |
HOU Weikun, CHAMPAGNE B. Semiblind channel estimation for OFDM/OQAM systems[J]. IEEE signal processing letters, 2015, 22(4): 400-403. DOI:10.1109/LSP.2014.2361663 (  0) 0)
|
| [6] |
LIU Kaiming, RUAN Chunqing, LIU Yuanan, et al. An efficient joint subcarrier pairing and resource allocation for multi-relay OFDM systems[J]. Applied mechanics and materials, 2014, 696: 207-214. DOI:10.4028/www.scientific.net/AMM.696 (  0) 0)
|
| [7] |
MEHTA R, LOBIYAL D K. Energy optimization in ad-hoc networks with MQAM, MFSK, MPSK and MPAM modulations[C]//Proceedings of the 8th International Conference on Computing, Communication and Networking Technologies. Delhi, India, 2017.
(  0) 0)
|
| [8] |
孙志国, 徐天宇, 邓昌青, 等. 16-QAM信号的最佳干扰分析[J]. 哈尔滨工程大学学报, 2018, 39(7): 1245-1250. SUN Zhiguo, XU Tianyu, DENG Changqing, et al. Analysis on optimal jamming against 16-QAM signal[J]. Journal of Harbin Engineering University, 2018, 39(7): 1245-1250. (  0) 0)
|
| [9] |
DA ROS F, GAJDA A, LIEBIG E, et al. Dual-polarization wavelength conversion of 16-QAM signals in a single silicon waveguide with a lateral p-i-n diode[Invited][J]. Photonics research, 2018, 6(5): B23-B29. DOI:10.1364/PRJ.6.000B23 (  0) 0)
|
| [10] |
LI Chao, GUI Chengcheng, XIAO Xi, et al. On-chip all-optical wavelength conversion of multicarrier, multilevel modulation (OFDM m-QAM) signals using a silicon waveguide[J]. Optics letters, 2014, 39(15): 4583-4586. DOI:10.1364/OL.39.004583 (  0) 0)
|
| [11] |
郭黎利, 李清伟, 戴佳, 等. 频谱重叠因子对数字调制系统的性能影响分析[J]. 哈尔滨工程大学学报, 2016, 37(4): 619-624. GUO Lili, LI Qingwei, DAI Jia, et al. Effect of the spectrum overlap factor on digital modulation systems[J]. Journal of Harbin Engineering University, 2016, 37(4): 619-624. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


