2. 西安邮电大学 通信与信息工程学院, 陕西 西安 710121
2. School of Telecommunication and Information Engineering, Xi'an University of Post & Telecommunications, Xi'an 710121, China
在电磁环境日益复杂的现代战场中,电子攻击、反辐射导弹及日益成熟的低截获技术严重地威胁着雷达的生存空间。为了获得生存,雷达必须通过缩减自身射频信号的特征来降低无源探测系统的截获概率,从而提升雷达的抗侦察、抗干扰能力,该技术被称为射频隐身技术[1]。射频隐身技术的研究在各国军事技术中的地位愈来愈重要,隐身使得敌方处于不断的猜测和分析中,使得我方优先获取有利的战机。近年来,具备射频隐身特性的波形设计已经成为各国学者的研究热点之一[2]。
最初, 射频隐身波形的研究对象均为单一调制类型的信号,主要有调频类和调相类[2]。由于单一调制信号的时频等特征非常明显,敌方容易从较高的旁瓣信号中截获有用信息。其中,在满足各频率正交的情况下,Costas频率编码信号[3]不仅时宽带宽积大,而且距离速度分辨性能较高。然而Costas信号每个子脉内的频率总是恒定,易被敌方从多个脉冲串中积累得到该信号的频率捷变特征,且Costas信号的自相关旁瓣较高,辐射能量较强,也容易被截获。非线性调频(nonlinear frequency modulation,NLFM)信号[4-5]具有良好的非周期自相关特性,主要体现在峰值旁瓣电平(peak sidelobe level,PSL)、积分旁瓣电平(integral sidelobe level,ISL)和-3 dB主瓣宽度等3个方面,且具有反S型非线性时频特性。
近年来,国内外学者逐渐将射频隐身波形的研究重心转向组合调制方式,以得到复杂度更高的信号,通常采用调频与调相的复合调制方式[6-12]。FSK/PSK雷达信号[6]实现了脉间频率编码与脉内巴克码的复合,截获因子得到一定改善,而巴克码长度有限,影响信号的距离分辨率,因此频率编码信号与多相码的复合逐渐成为后续的研究趋势[7-10]。该类复合信号在跳频编码信号的每个子脉冲持续时间内增加原信号的相位复杂度和随机性,从而有效地降低信号的功率谱及自相关旁瓣电平,具有较低的截获概率。LFM-Costas信号[11]采用脉间跳频脉内线性调频的复合调制方式,修正了Costas信号的脉内恒定频率特征,获得了大的信号带宽、低的截获因子和低的功率谱峰值。然而,LFM-Costas信号存在较高的自相关旁瓣,存在被敌方截获的风险[12]。总体来看,采用脉间Costas跳频、脉内调相或调频的组合所得的复杂调制信号具备较强的抗截获性和抗干扰能力。
为了获得射频隐身性能更好的雷达信号,可以通过增加信号子脉间及子脉内各主要特征的复杂性和随机性来实现。本文通过以下2步设计复杂调制信号:1)利用NLFM信号的非线性时频特性调制Costas信号的脉内恒定频率,使得脉间频率呈现非线性的跳频特征,得到脉内复合调频的NLFM-Costas信号;2)在NLFM-Costas信号每个子脉内利用多相码序列进行相位调制,增加相位的多样性和随机性,得到脉间复合调频脉内相位编码(interpulse NLFM and Costas hybrid frequency modulation and intrapulse polyphase coded,IPNC-PC)雷达信号。
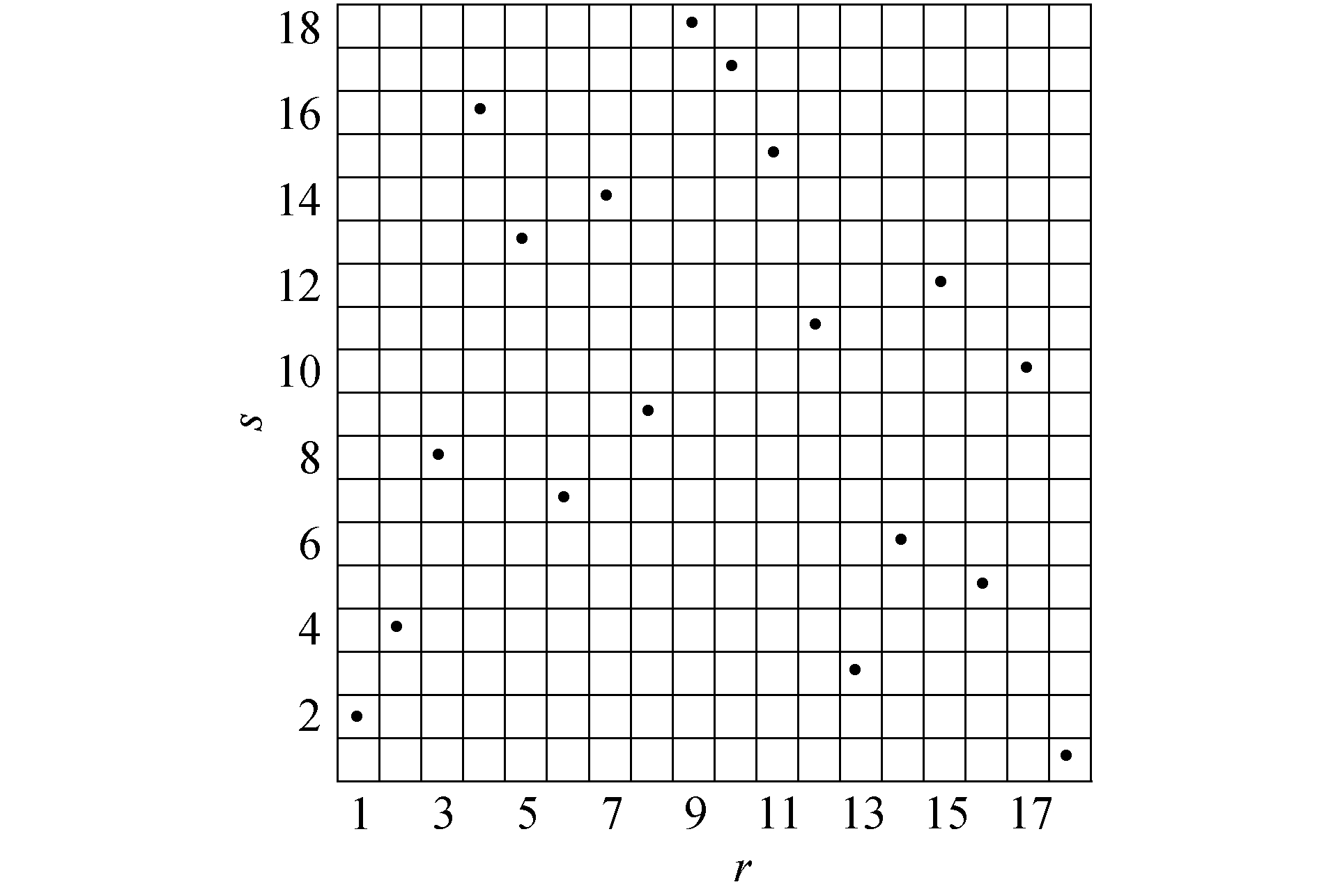
1 单一调制信号 1.1 Costas阵列Costas信号各脉间频率随机出现,且仅出现1次,下面以生成18位(N=18)Costas阵列为例。首先,选择合适的素数g,一般将g选为不小于N的最小奇素数,取g=19。其次,计算有限域GF(p)的本原元素b,其中b=2为本原元素之一。最后,根据Costas阵列Welch构造法[13]产生18位Costas序列{2, 4, 8, 16, 13, 7, 14, 9, 18, 17, 15, 11, 3, 6, 12, 5, 10, 1},其时频分布如图 1所示,时间和频率之间的对应关系可以用置换矩阵A={aij}N×N来表示,且aij=0或1。由矩阵A得到的Costas阵列的非周期自相关函数[14]为:
|
Download:
|
| 图 1 Costas信号的时频分布 Fig. 1 Time-frequency curve of Costas signal | |
| $ C(r, s)=\sum\limits_{i=1}^{N} \sum\limits_{j=1}^{N} a_{i j} a_{(i+r)(j+s)} $ | (1) |
当i+r或j+s不属于[1, N]时,取a(i+r)(j+s)为0。C(r, s)满足如下特征:
| $ \left\{\begin{array}{ll}{C(r, s)=n, } & {(r, s)=(0, 0)} \\ {0 \leqslant C(r, s)<n, } & {(r, s) \neq(0, 0)}\end{array}\right. $ | (2) |
在给定矩阵A中的任意2个位置后,可以找到某个延迟A*使得A*与A在指定的位置处重合,则有
| $ \mathop {\max }\limits_{(r,s) \ne (0,0)} C(r,s) = 1 $ | (3) |
的阵列就是模糊函数旁瓣最小的Costas信号,它可以准确地确定目标的距离和速度特征。
|
Download:
|
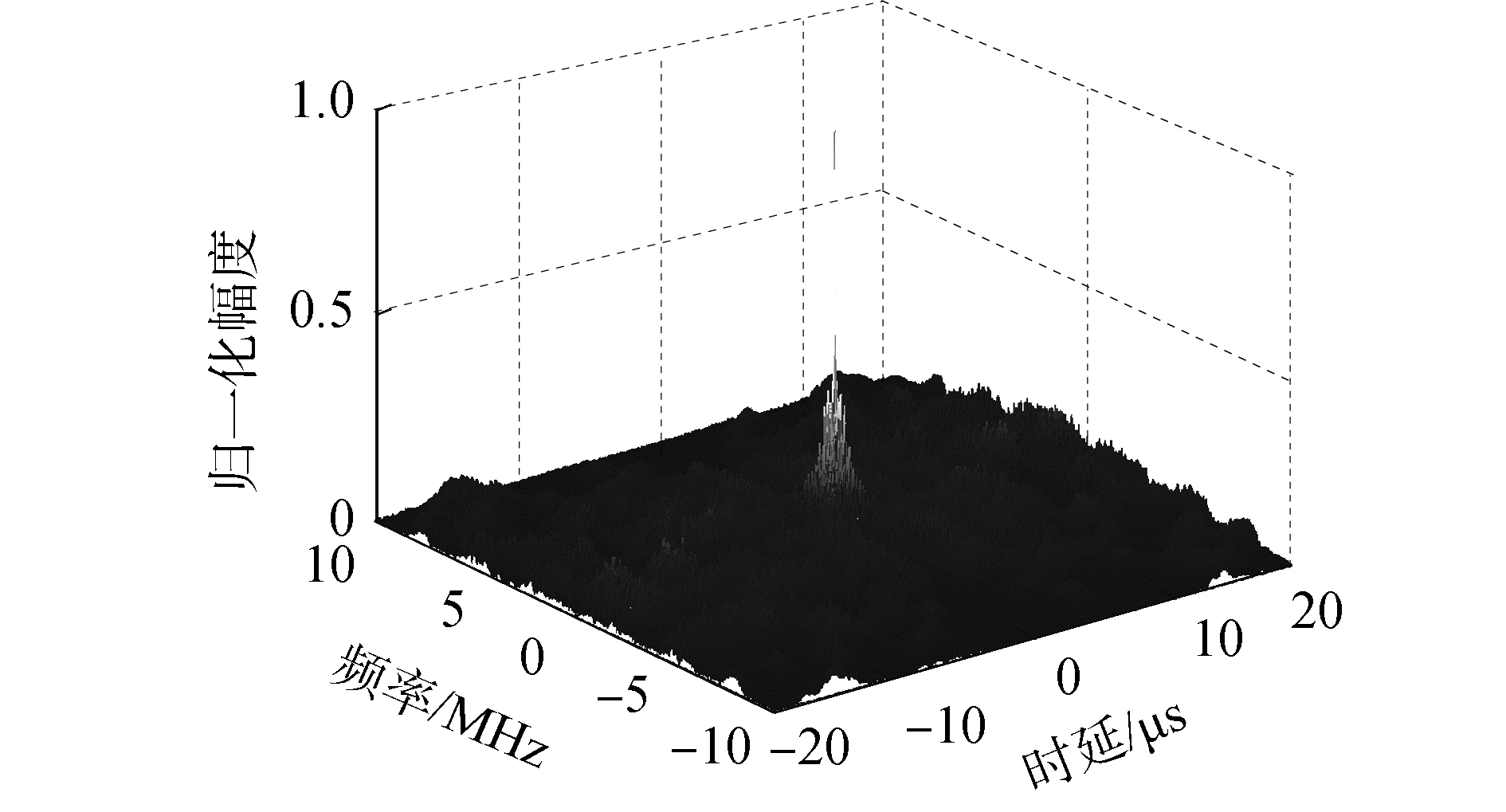
| 图 2 Costas信号的模糊图 Fig. 2 Ambiguity graph of Costas signal | |
基于Costas序列产生的Costas信号具有频率捷变性,是一种大时宽带宽积信号。该信号的主瓣能量集中在原点位置处,模糊图呈理想“图钉型”,旁瓣平坦,具有较高的距离速度分辨性能。
1.2 NLFM信号设NLFM信号为s(t),傅里叶变换为S(f),则模糊函数[15]为:
| $ \begin{array}{l} \chi (\tau ,\xi ) = \int_{ - \infty }^{ + \infty } s (t){s^*}(t + \tau )\exp ({\rm{j}}2{\rm{\mathsf{ π}}}\xi t){\rm{d}}t{\rm{ = }}\\ \int_{ - \infty }^{ + \infty } S (f - \xi ){S^*}(f)\exp ({\rm{j}}2{\rm{\mathsf{ π}}}f\tau ){\rm{d}}f \end{array} $ | (4) |
令ξ=0,则信号的距离模糊函数:
| $ \chi(\tau, 0)=\int_{-\infty}^{+\infty}|S(f)|^{2} \exp ({\rm{j}} 2 {\rm{\mathsf{ π}}} f \tau) \mathrm{d} f $ | (5) |
窗函数W(f)的能量主要集中在主瓣上,旁瓣较低,故可以假定信号的幅度谱|S(f)|与窗函数的谱分布特征一致:
| $ |S(f)|^{2}=W(f) $ | (6) |
根据给定功率谱,利用驻留相位原理计算群时延函数和时频函数,并积分得到相位函数,从而产生NLFM波形[16]。常用的窗函数有Hamming窗、Blackman窗、Hanning窗和Taylor窗等。本文采用性能较好的Hamming窗,仿真参数设置如下:NLFM信号的时宽Tb=1 μs,带宽BNLFM=20 MHz,采样频率fs=320 MHz。
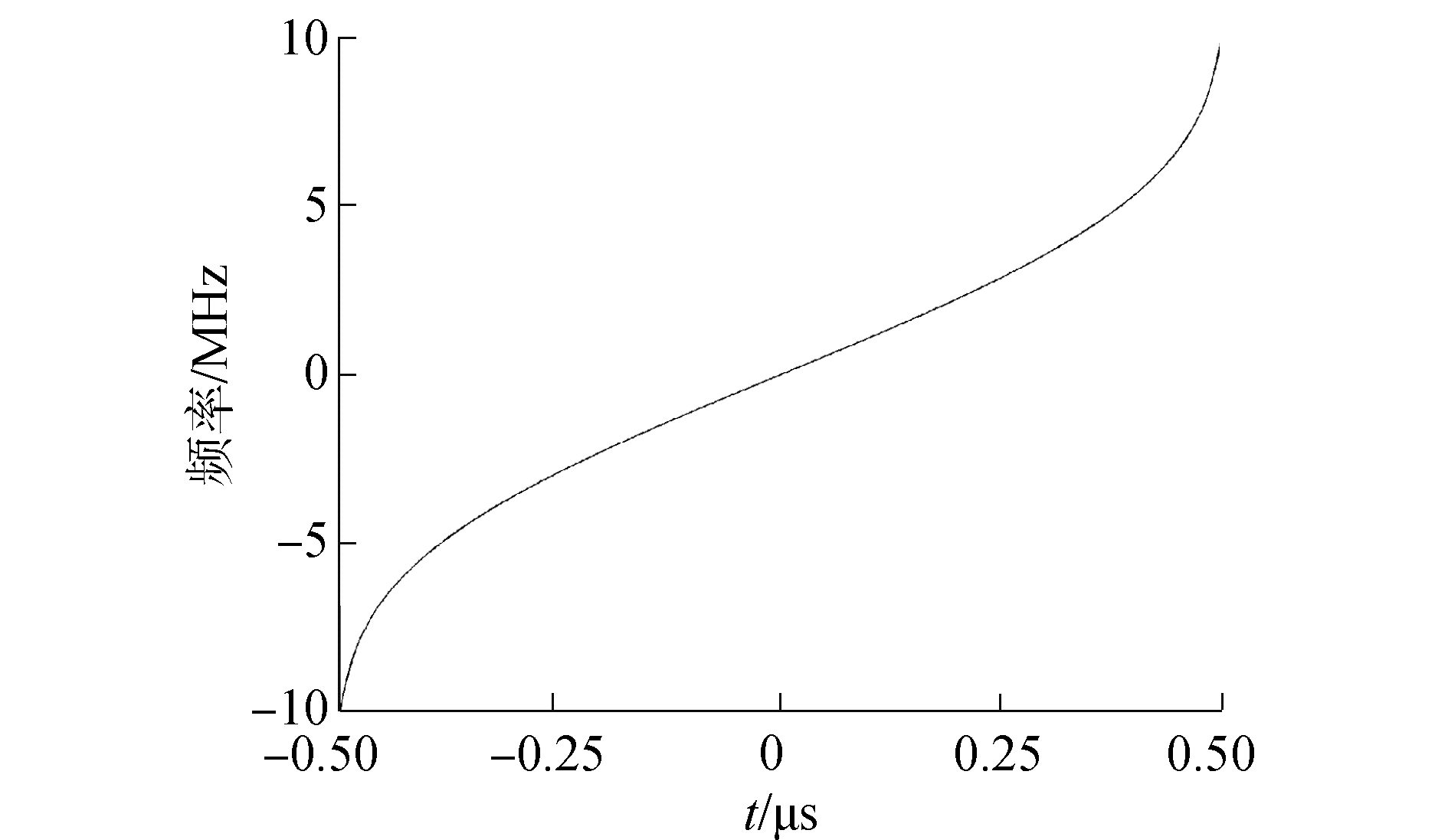
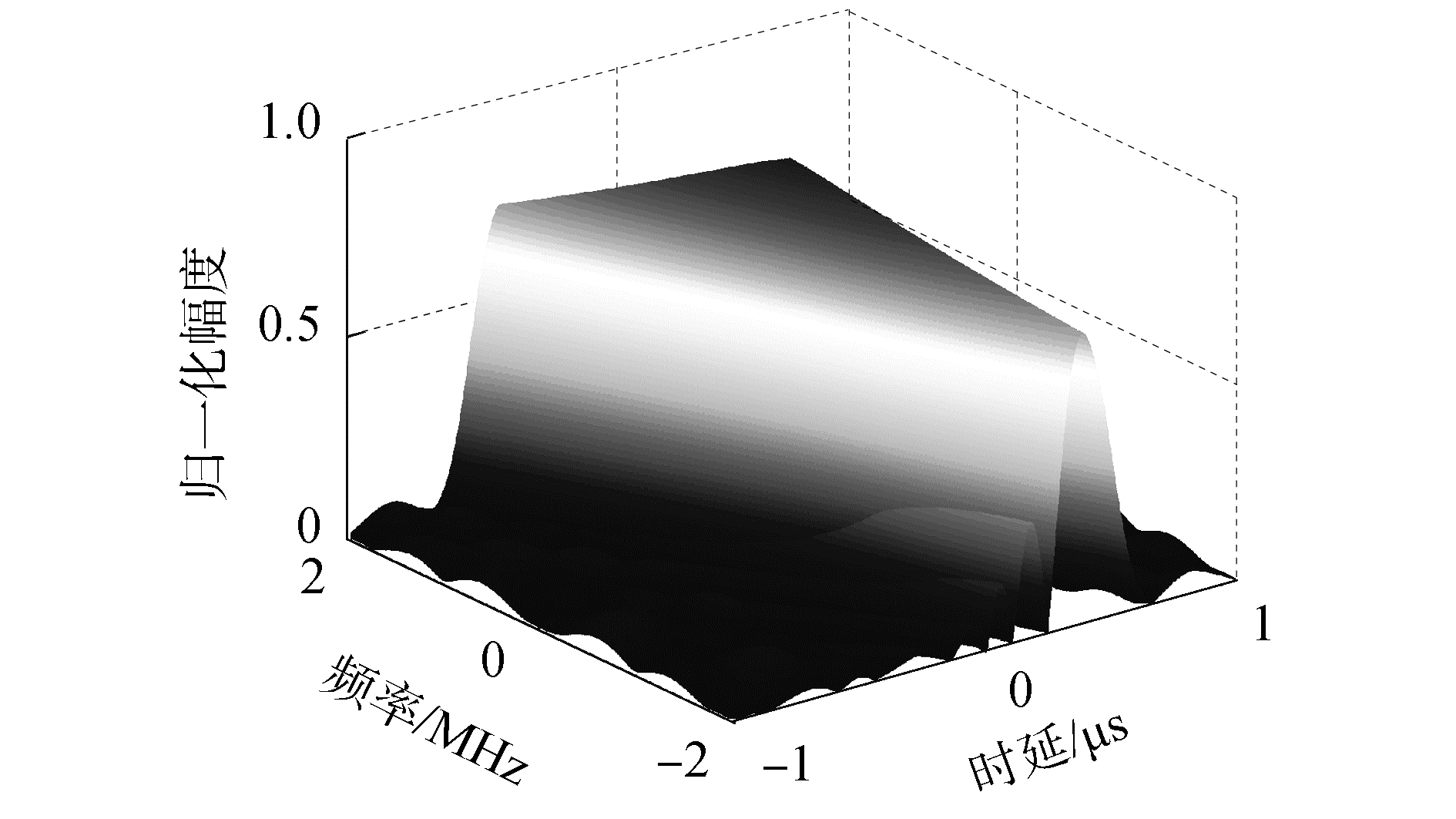
图 3~5分别为NLFM信号的时频分布、自相关函数及模糊图。由图 3、图 4可知,NLFM信号具有非线性时频特性,具有较低的PSL和ISL,分别为-22.50、-18.22 dB。由图 5可知,“斜刀刃型”模糊函数的能量主要集中在原点附近,较窄的主瓣宽度可以提高信号的距离分辨性能,较低的旁瓣电平可以增强信号的抗截获性能。
|
Download:
|
| 图 3 NLFM信号的时频分布 Fig. 3 Time-frequency curve of NLFM signal | |

|
Download:
|
| 图 4 NLFM信号的自相关函数 Fig. 4 Autocorrelation function of NLFM signal | |
|
Download:
|
| 图 5 NLFM信号的模糊图 Fig. 5 Ambiguity graph of NLFM signal | |
Costas各子脉冲载波频率为恒定值,使其分别与具备反S型调频特性的NLFM信号进行复合,信号的表达式为:
| $ s(t)=\sum\limits_{n=1}^{N} \omega_{n} u_{c}\left[t-(n-1) T_{b}\right] \exp \left\{{\rm{j}}\left[2 {\rm{\mathsf{ π}}} f_{n} t+\varphi(t)\right]\right\} $ | (7) |
式中:N为Costas频率编码序列长度;ωn为第n个载波上的归一化频率复加权因子,满足
在Costas信号各子脉间采用非线性调频与Costas跳频的复合调频方式后,在各子脉内采用相位编码方式,最终得到脉间复合调频脉内相位编码的IPNC-PC信号。其中,相位编码序列的二相码有巴克码、M序列等,多相码有Frank码、P1~P4码及Zadoff-Chu码等。IPNC-PC信号的表达式为:
| $ \begin{array}{l} s(t) = &&\sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {{\omega _n}} } {a_{n, m}}u\left[ {t - (n - 1){T_{\rm{b}}} - (m - 1){t_{\rm{b}}}} \right] \cdot \\ &&\exp \left\{ {{\rm{j}}\left[ {2{\rm{\mathsf{ π}}} {f_n}t + \varphi (t)} \right]} \right\} \end{array} $ | (8) |
式中:
由步进线性调频或线性调频信号导出的多相编码序列具有近似“图钉型”模糊函数,有利于获得良好的距离速度分辨率;大的时宽带宽积和低的峰值发射功率具备一定的低截获性及抗干扰性。设脉内相位编码采用P4码,其相位表达式为:
| $ \begin{aligned} \varphi_{n, m} &=\frac{{\rm{\mathsf{ π}}}(m-1)^{2}}{M}-{\rm{\mathsf{ π}}}(m-1) \\ m &=1, 2, \cdots, M ; n=1, 2, \cdots, N \end{aligned} $ | (9) |
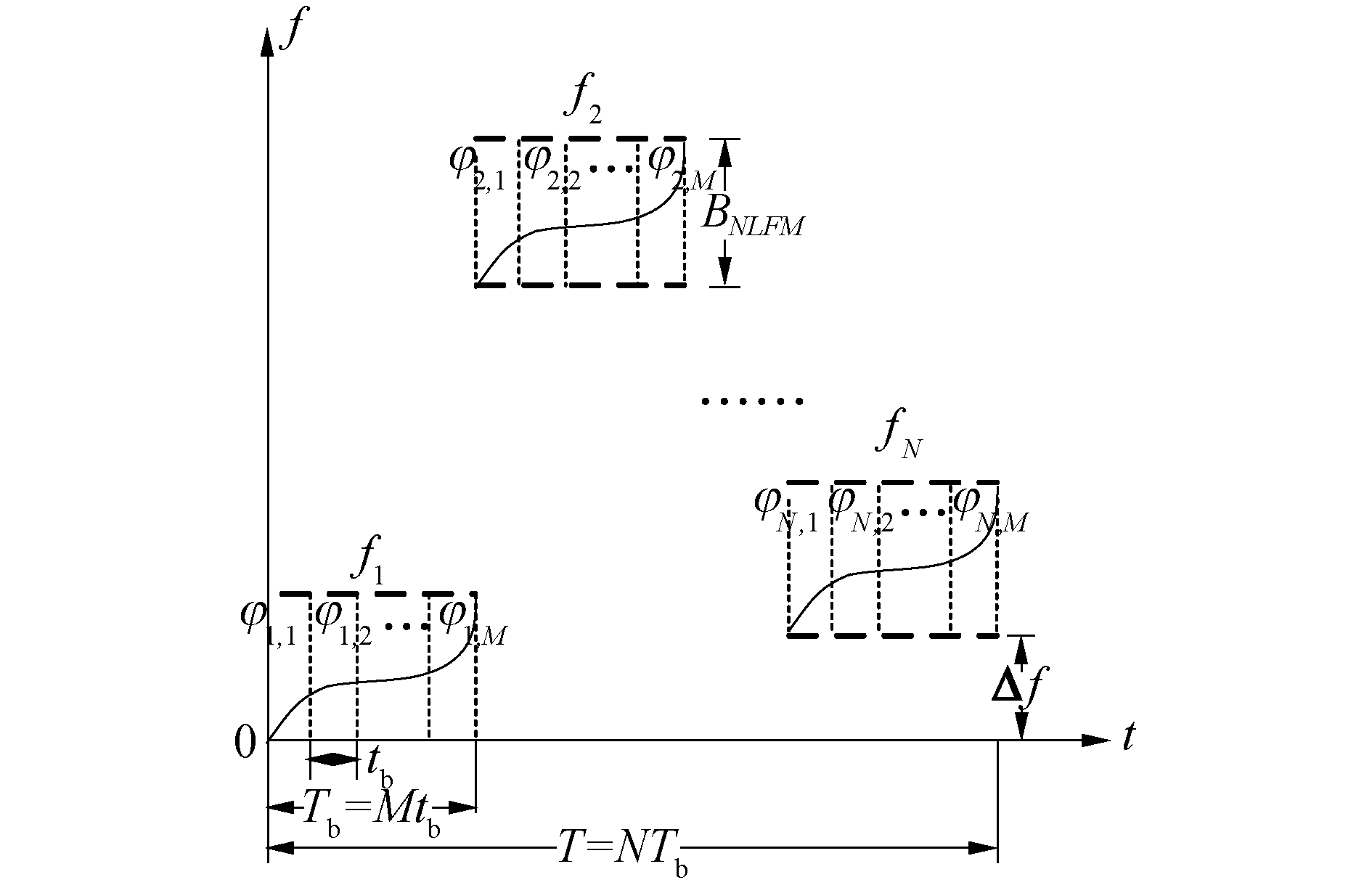
式中:φn, m表示第n个子载波基于多相码产生的第m个相位,则an, m=ejφn, m表示第n个子载波基于多相码产生的第m个相位编码,且|an, m|=1。利用多相编码实现复合调频子脉冲的M个相位调制,其结构如图 6所示。
|
Download:
|
| 图 6 IPNC-PC信号结构图 Fig. 6 Structure chart of IPNC-PC signal | |
IPNC-PC信号的带宽为B=(N-1)Δf+BNLFM,其中BNLFM为NLFM信号的带宽。IPNC-PC信号采用脉内与脉间共同调制的方式,脉间复合调频增加了信号的时频复杂度,脉内相位调制的多样性和随机性增加了信号的相位复杂度,对于想要获取我方雷达信号重要特征的无源探测系统而言是困难重重,故IPNC-PC信号具有较强的射频隐身性能。
3 模糊函数分析模糊函数可以用来衡量雷达信号对具有不同距离和不同速度的目标的辨识能力,反映出不同信号的性能优劣。模糊函数是雷达发射波形复包络的时间-频率的复合自相关函数,信号s(t)的模糊函数χ(τ, ξ)定义[15]为:
| $ \chi(\tau, \xi)=\int_{-\infty}^{+\infty} s(t) s^{*}(t+\tau) \exp (\mathrm{j} 2 {\rm{\mathsf{ π}}} \xi t) \mathrm{d} t $ | (10) |
结合式(8)和式(10),推导IPNC-PC信号的模糊函数:
| $ \begin{array}{l} \chi (\tau , \xi ) = \int_{ - \infty }^{ + \infty } s (t){s^*}(t + \tau )\exp ({\rm{j}}2{\rm{\mathsf{ π}}} \xi t){\rm{d}}t = \\ \sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {\sum\limits_{{n_1} = 1}^N {\sum\limits_{{m_1} = 1}^M {{\omega _n}} } } } \omega _{{n_1}}^*{a_{n, m}}a_{{n_1}, {m_1}}^*\exp \left( { - {\rm{j}}2{\rm{\mathsf{ π}}} {f_{{n_1}}}\tau } \right) \cdot \\ \int_{ - \infty }^{ + \infty } {\exp } \left[ {{\rm{j}}2{\rm{\mathsf{ π}}} \left( {{f_n} - {f_{{n_1}}} + \xi } \right)t} \right]\exp [{\rm{j}}\varphi (t) - \\ {\rm{j}}\varphi (t + \tau )] \cdot u\left[ {t - (n - 1){T_b} - (m - 1){t_b}} \right] \cdot \\ {u^*}\left[ {t + \tau - \left( {{n_1} - 1} \right){T_b} - \left( {{m_1} - 1} \right){t_b}} \right]{\rm{d}}t \end{array} $ | (11) |
设fn=f0+(Cn-1)B,fn1=f0+(Cn1-1)B,故式(11)简化为:
| $ \begin{array}{l} \chi (\tau , \xi ) = \sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {\sum\limits_{{n_1} = 1}^N {\sum\limits_{{m_1} = 1}^M {{\omega _n}} } } } \omega _{{n_1}}^*{a_{n, m}}a_{{n_1}, {m_1}}^*\exp \left( { - {\rm{j}}2{\rm{\mathsf{ π}}} {f_{{n_1}}}\tau } \right) \cdot \\ \int_{ - \infty }^{ + \infty } {\exp } \left[ {{\rm{j}}2{\rm{\mathsf{ π}}} \left( {({C_n} - {C_{{n_1}}})B + \xi } \right)t} \right]\exp [{\rm{j}}\varphi (t) - \\ {\rm{j}}\varphi (t + \tau )] \cdot u\left[ {t - (n - 1){T_b} - (m - 1){t_b}} \right] \cdot \\ {u^*}\left[ {t + \tau - \left( {{n_1} - 1} \right){T_b} - \left( {{m_1} - 1} \right){t_b}} \right]{\rm{d}}t \end{array} $ | (12) |
令(Cn-Cn1)B+ξ=Fd,t-(n-1)Tb-(m-1)tb=t′,式(12)中的积分化简为:
| $ \begin{array}{l} \int_{ - \infty }^{ + \infty } {\exp } \left\{ {{\rm{j}}2{\rm{\mathsf{ π}}} {F_d}\left[ {{t^\prime } + (n - 1){T_b} + (m - 1){t_b}} \right]} \right\} \cdot \\ \exp \left\{ {{\rm{j}}\varphi \left[ {{t^\prime } + (n - 1){T_b} + (m - 1){t_b}} \right] - } \right.\\ {\rm{j}}\varphi \left[ {{t^\prime } + \tau + (n - 1){T_b} + (m - 1){t_b}} \right]\} \cdot u\left( {{t^\prime }} \right)\\ \begin{array}{*{20}{l}} {{u^*}\left[ {{t^\prime } + \tau + \left( {n - {n_1}} \right){T_b} + \left( {m - {m_1}} \right){t_b}} \right]{\rm{d}}{t^\prime } = }\\ {\exp \left\{ {{\rm{j}}2{\rm{\mathsf{ π}}} {F_d}\left[ {(n - 1){T_b} + (m - 1){t_b}} \right] \cdot } \right.}\\ {\int_{ - \infty }^{ + \infty } u (t) \cdot {u^*}\left[ {t + \tau + \left( {n - {n_1}} \right){T_b} + \left( {m - {m_1}} \right){t_b}} \right] \cdot } \end{array}\\ \begin{array}{*{20}{l}} {\exp \left( {{\rm{j}}2{\rm{\mathsf{ π}}} {F_d}t} \right) \cdot \exp \left\{ {{\rm{j}}\varphi \left[ {t + (n - 1){T_b} + (m - 1){t_b}} \right] - } \right.}\\ {{\rm{j}}\varphi \left[ {t + \tau + (n - 1){T_b} + (m - 1){t_b}} \right]\} {\rm{d}}t} \end{array} \end{array} $ | (13) |
该积分仅在
| $ \begin{array}{l}{\exp \left\{\mathrm{j} 2 {\rm{\mathsf{ π}}} F_{d}\left[(n-1) T_{b}+(m-1) t_{b}\right]\right\}} \\ {\quad \int_{-\infty}^{+\infty} u(t) \cdot u^{*}\left(t+t_{s}\right) \exp \left(\mathrm{j} 2 {\rm{\mathsf{ π}}} F_{d} t\right)} \\ {\quad \exp \left\{{\rm{j}} \varphi\left[t+(n-1) T_{b}+(m-1) t_{b}\right]-\right.} \\ {\quad \mathrm{j} \varphi\left[t+t_{s}+\left(n_{1}-1\right) T_{b}+\left(m_{1}-1\right) t_{b}\right] \} \mathrm{d} t}\end{array} $ | (14) |
此时,式(12)化简为:
| $ \begin{aligned} \chi(\tau, \xi)=& \sum\limits_{n=1}^{N} \sum\limits_{m=1}^{M} \sum\limits_{n=1}^{N} \sum\limits_{m_{1}=1}^{M} \omega_{n} \omega_{n_{1}}^{*} a_{n, m} a_{n_{1}, m_{1}}^{*} \exp \left(-{\rm{j}} 2 {\rm{\mathsf{ π}}} f_{n_{1}} \tau\right) \\ & \exp \left\{{\rm{j}} 2 {\rm{\mathsf{ π}}} F_{d}\left[(n-1) T_{b}+(m-1) t_{b}\right]\right\} \\ & \int_{-\infty}^{+\infty} u(t) \cdot u^{*}\left(t+t_{s}\right) \exp \left({\rm{j}} 2 {\rm{\mathsf{ π}}} F_{d} t\right) \\ & \exp \left\{{\rm{j}} \varphi\left[t+(n-1) T_{b}+(m-1) t_{b}\right]-\right.\\ & {\rm{j}} \varphi\left[t+t_{s}+\left(n_{1}-1\right) T_{b}+\left(m_{1}-1\right) t_{b}\right] \} \mathrm{d} t \end{aligned} $ | (15) |
式(15)为IPNC-PC信号的模糊函数表达式。
4 IPNC-PC信号特性分析首先,将NLFM-Costas复合信号与NLFM信号和Costas信号的自相关旁瓣电平和-3 dB主瓣宽度等主要指标进行比较。其次,将INPC-PC复合信号与LFM-Costas复合信号[12]、NLFM-Costas复合信号的自相关指标、模糊函数及功率谱等进行对比。文中的仿真参数设为:Costas编码序列长度N=18,多相码序列长度M=16,子脉冲时宽Tb=10-6 s,各子脉内相位时宽tb=Tb/M,总时宽T=NTb,带宽BNLFM=20 MHz,采样频率fs=320 MHz,|ωn|=1。
4.1 自相关性能分析将NLFM-Costas信号与单一调制的NLFM信号和Costas信号的自相关性能做以对比(如表 1)。由表 1可得,NLFM-Costas信号的PSL不仅优于Costas信号,更优于NLFM信号,至少降低5.61 dB;由于Costas信号每个子脉内的频率受非线性调频调制,故NLFM-Costas信号的PSL、ISL和主瓣宽度均优于Costas信号对应的参数。
| 表 1 NLFM-Costas与单一调制信号比较 Table 1 Comparisons of NLFM-Costas and single modulated signals |
当脉内分别采用16位P4码、Frank码和Zadoff-Chu码调制时,得到3种形式的IPNC-PC信号,将其自相关性能与NLFM-Costas信号进行比较(如表 2)。从表 2可见,各IPNC-PC信号的自相关性能均有明显改善:PSL最多降低12.83 dB,ISL最多降低4.33 dB,主瓣宽度变窄率最高达到39%。
| 表 2 脉间复合调频与非线性调频信号比较 Table 2 Comparisons of signals with interpulse hybrid and nonlinear frequency modulation |
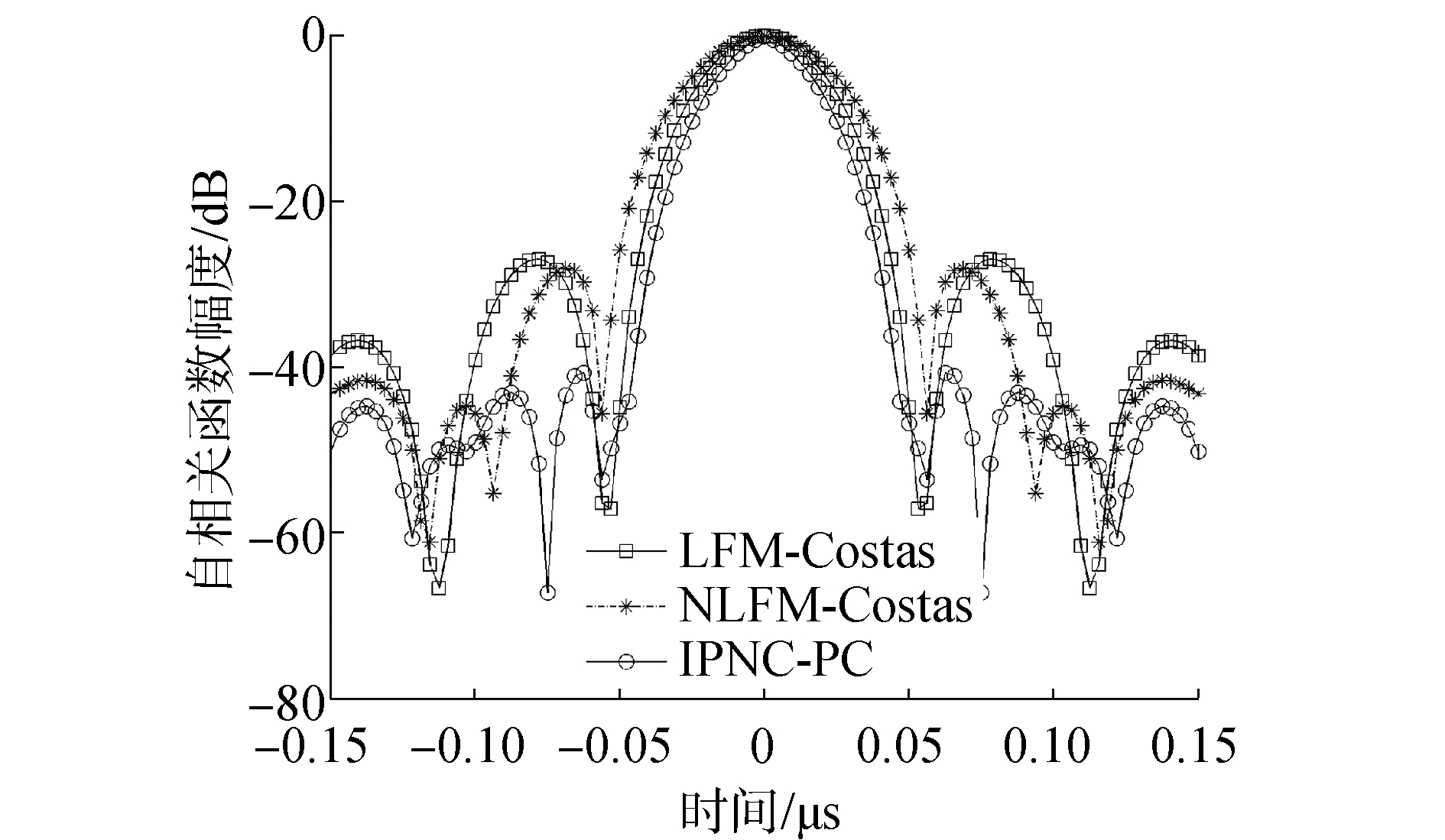
文献[12]对Costas信号子脉内的频率做线性调频调制而得到LFM-Costas信号,此时的信号频率特性变得比较复杂。在相同的仿真条件下,取BLFM=BNLFM=20 MHz,则LFM-Costas信号的带宽和IPNC-PC信号的带宽相同。表 3中比较了LFM-Costas信号、NLFM-Costas信号和IPNC-PC信号的自相关指标,并将其局部特征体现在图 7中。可以得出,IPNC-PC信号的PSL最低,相对LFM-Costas信号和NLFM-Costas信号分别降低了13.73 dB和12.58dB。IPNC-PC信号的主瓣宽度最窄,相对LFM-Costas信号和NLFM-Costas信号分别变窄了27%和39%。
| 表 3 脉间复合调频与单一调频信号比较 Table 3 Comparisons of signals with interpulse hybrid and single frequency mudulation |
|
Download:
|
| 图 7 自相关性能比较 Fig. 7 Comparison of autocorrelation properties | |
在雷达对抗中,发射信号若具备较窄的自相关主瓣,则可以提高系统的距离分辨率;若具备较低的自相关旁瓣,则信号旁瓣携带较少能量,即使敌方侦察机截获该信号,也很难从旁瓣中分选和识别有用信息,从而增强了我方雷达的射频隐身能力。
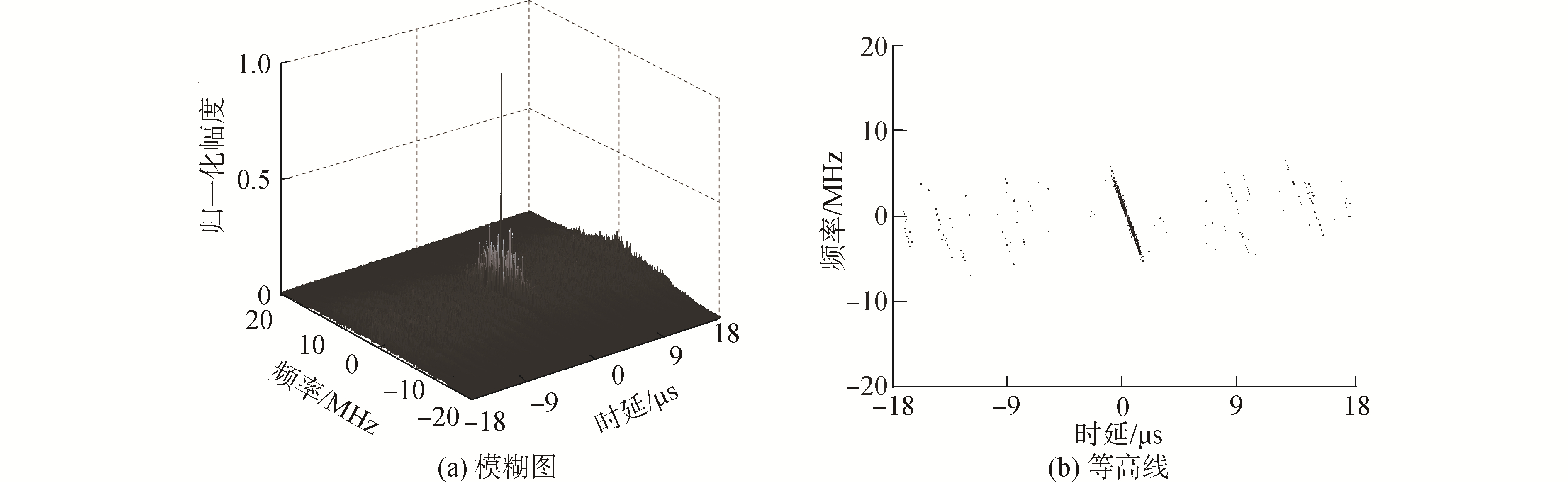
4.2 模糊函数分析由图 8(a)、图 9(a)和图 10(a)知,LFM-Costas信号、NLFM-Costas信号和IPNC-PC信号的模糊图均近似“图钉型”,信号能量集中在主峰附近,主峰尖而高,具有较高的距离速度分辨性能;旁瓣较低、较平坦,能量分布较少。对比图 8(b)、图 9(b)和图 10(b)的各等高线,相比LFM-Costas信号和NLFM-Costas信号,IPNC-PC信号主瓣集中的能量最多、旁瓣分散的能量最少,当敌方无源探测系统截获到该信号的旁瓣特征时最难以获取有用信息,故IPNC-PC信号具有最强的射频隐身能力。

|
Download:
|
| 图 8 LFM-Costas信号 Fig. 8 LFM-Costas signal | |
|
Download:
|
| 图 9 NLFM-Costas信号 Fig. 9 NLFM-Costas signal | |

|
Download:
|
| 图 10 IPNC-PC信号 Fig. 10 IPNC-PC signal | |
图 11给出了相同仿真条件下3种信号的功率谱特征,由图 11可见,当Costas信号的脉内进行线性、非线性及复合调频后,不仅获得较大的带宽和较低的截获因子,而且复合信号的频谱特征越来越复杂。脉内多相位调制的随机性和多样性不仅使IPNC-PC信号功率谱的起始和截止频率的边界不够清晰,而且带内频谱也随机化。另外,LFM-Costas信号和NLFM-Costas信号的功率谱均高于-10 dB,而IPNC-PC信号的功率谱整体都低于-10 dB。IPNC-PC信号较低的功率谱峰值和随机性的谱分布给敌方的截获工作带来一定困难,故该信号具备较强的射频隐身能力。

|
Download:
|
| 图 11 功率谱比较 Fig. 11 Comparision of PSD | |
1) 相对单一调制信号,NLFM-Costas信号的射频隐身指标具有一定的优势。该信号可获得大时宽带宽积和低截获因子,自相关旁瓣电平和-3 dB主瓣宽度均得到一定程度的改善。
2) 与LFM-Costas信号、NLFM-Costas信号相比,IPNC-PC信号增加了相位的随机性和多样性,具备更强的保密性;IPNC-PC信号具有更优良的自相关性能,PSL、ISL及主瓣宽度均获得了较大改善,增加了侦察接收机的截获难度,是一种性能良好的射频隐身波形,在雷达战场上具有广泛的应用前景。
后续可以通过调整各单一调制信号的主要参数或信号脉内与脉间、调频与调相的复合方式,设计出众多类型的复杂调制信号,并分析参数或复合方式对射频隐身性能的影响。
| [1] |
LYNCH JR D. Introduction to RF stealth[M]. Raleigh: SciTech Publishing Inc. Press, 2004: 23-25.
(  0) 0)
|
| [2] |
汪飞, 李海林, 夏伟杰, 等. 低截获概率机载雷达信号处理技术[M]. 北京: 科学出版社, 2017: 233-241.
(  0) 0)
|
| [3] |
COSTAS J P. A study of a class of detection waveforms having nearly ideal range-Doppler ambiguity properties[J]. Proceedings of the IEEE, 1984, 72(8): 996-1009. DOI:10.1109/PROC.1984.12967 (  0) 0)
|
| [4] |
PAN Yichun, PENG Shirui, YANG Kefeng, et al. Optimization design of NLFM signal and its pulse compression simulation[C]//IEEE International Radar Conference. Arlington, VA: IEEE, 2005: 383-386.
(  0) 0)
|
| [5] |
GAO Caicai, THE K C, LIU Aifei. Frequency diversity waveform with NLFM signals[C]//201510th International Conference on Information, Communications and Signal Processing. Singapore: IEEE, 2015: 1-4.
(  0) 0)
|
| [6] |
李英祥, 周先敏. 一种具有LPI特性的雷达信号-新的FSK/PSK信号[J]. 信号处理, 2002, 18(2): 177-179. LI Yingxiang, ZHOU Xianmin. A new FSK/PSK radar signal characterized with LPI[J]. Signal processing, 2002, 18(2): 177-179. DOI:10.3969/j.issn.1003-0530.2002.02.021 (  0) 0)
|
| [7] |
TOUATI N, TATKEU C, CHONAVEL T, et al. Design and performances evaluation of new Costas-based radar waveforms with pulse coding diversity[J]. IET radar, sonar & navigation, 2016, 10(5): 877-891. (  0) 0)
|
| [8] |
TOUATI N, TATKEU C, CHONAVEL T, et al. Phase coded Costas signals for ambiguity function improvement and grating lobes suppression[C]//Proceedings of the 78th Vehicular Technology Conference. Las Vegas, NV: IEEE, 2013: 1-5.
(  0) 0)
|
| [9] |
TOUATI N, TATKEU C, RIVENQ A, et al. Multiuser phase coded Costas signals with improved cross-correlation and partial cross-ambiguity properties[C]//Proceedings of 2014 IEEE International Radar Conference. Lille, France: IEEE, 2014: 1-6.
(  0) 0)
|
| [10] |
彭智慧, 林明. 一种新型组合低截获雷达波形研究[J]. 计算机仿真, 2014, 31(3): 46-50. PENG Zhihui, LIN Ming. Analysis of hybrid radar waveform with LPI[J]. Computer simulation, 2014, 31(3): 46-50. DOI:10.3969/j.issn.1006-9348.2014.03.011 (  0) 0)
|
| [11] |
LIU Feng, MU Shanxiang, LYU Wanghan, et al. MIMO SAR waveform separation based on Costas-LFM signal and co-arrays for maritime surveillance[J]. Chinese journal of electronics, 2017, 26(1): 211-217. DOI:10.1049/cje.2016.11.015 (  0) 0)
|
| [12] |
罗美方, 郝志梅, 王强. LFM-频率编码复合低截获波形信号处理方法[J]. 电子科技大学学报, 2017, 46(2): 335-339. LUO Meifang, HAO Zhimei, WANG Qiang. Signal processing technique for LFM/FSK hybrid LPI waveform[J]. Journal of University of Electronic Science and Technology of China, 2017, 46(2): 335-339. DOI:10.3969/j.issn.1001-0548.2017.02.003 (  0) 0)
|
| [13] |
黄琼丹, 李勇, 卢光跃. 脉间Costas跳频脉内多载波混沌相位编码雷达信号设计与分析[J]. 电子与信息学报, 2015, 37(6): 1483-1489. HUANG Qiongdan, LI Yong, LU Guangyue. Design and analysis of inter-pulse Costas frequency hopping and intra-pulse multi-carrier chaotic phase coded radar signal[J]. Journal of electronics & information technology, 2015, 37(6): 1483-1489. (  0) 0)
|
| [14] |
何元.编码复合调制信号分析与处理技术研究[D].长沙: 国防科学技术大学, 2009: 15-22. HE Yuan. Study on the coded multi-modulation signal analysis and processing[D]. Changsha: National University of Defense Technology, 2009: 15-22. http://cdmd.cnki.com.cn/Article/CDMD-90002-2010165067.htm (  0) 0)
|
| [15] |
LEVANON N, MOZESON E. Radar signals[M]. New York: John Wiley & Sons, 2004: 74-95.
(  0) 0)
|
| [16] |
何学辉, 陶海红, 吴兆平, 等. 一种改进的非线性调频信号设计[J]. 电子学报, 2009, 37(8): 1784-1788. HE Xuehui, TAO Haihong, WU Zhaoping, et al. An improved design for non-linear frequency modulation signal[J]. Acta electronica sinica, 2009, 37(8): 1784-1788. DOI:10.3321/j.issn:0372-2112.2009.08.028 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


