2. 哈尔滨工程大学 自动化学院, 黑龙江 哈尔滨 150000;
3. 哈尔滨工业大学 自动化学院, 黑龙江 哈尔滨 150001
2. College of Automation, Harbin Engineering University, Harbin 150001, China;
3. College of Automation, Harbin Engineering University, Harbin 150080, China
波达方向估计是阵列信号处理的一个重要问题,在雷达、声呐、通讯和地震信号处理具有广泛的应用前景[1-2]。许多高分辨率算法都是基于空间白噪声模型的情形下展开的,其中包括熟知的MUSIC算法[3-4]、ESPRIT算法[5]、最大似然估计算法[6-7]。在实际情况中,噪声和信号的信息往往是未知的,当入射信号相干时,MUSIC算法和ESPRIT算法性能严重衰减或者它们可能无法检测到所有的信号源,为了解决相干源的定位问题,Johnson等[8]提出了空间平滑技术方案,Shan等[9]也做出了一些相关研究,此类方法是把均匀线性阵列分割成更小的子阵,将这些子阵的数据平均,即可得到相干源的统计数据。在Johnson提出方案的基础上,一些处理相干源的算法不断地被提出,改进MUSIC算法[10-11]、改进MMUSIC算法[12]、前向平滑技术[13]、双向平滑技术[14]。这些算法的共同缺陷是需要对接收信号的协方差进行特征值分解才能得到信号的波达方向,这将使算法的计算复杂度比较高,在阵元数目较大的情况下尤其突出。为了解决这个问题,Macros等[15-16]提出了只需要使用线性运算的传播因子算法,但是传播因子算法不能完全消除未知噪声的影响。而由前后向平滑技术改进的广义差分GCD算法[17]可以完全消除空间非均匀噪声,也可以适用于一般的噪声场和低信噪比环境,本文通过对传播因子算法和空间平滑技术的结合,在保持空间平滑技术良好性能的基础上,进一步降低计算复杂度。
1 波达方向估计模型空间谱估计测向采用多元天线阵,是利用信号来波在各天线阵元上感应产生的电压幅度和相位与来波方向有关这一特性来实现对空间多个信号同时测向的,多元天线阵主要用于接收目标空间的无线电信号,并将电磁波信号转化为电信号,再将其送给接收机多元天线阵有线阵排列、圆阵排列及面阵排列等形式。线阵排列是天线单元在一条直线上均匀分布,因为其数学关系比较简单,所以我们多以此为例来介绍空间谱估计测向原理。天线间距与电磁波波长之比(d/λ)不能大于0.5,否则会出现相位模糊。此要求在高频段将导致天线间严重互耦,影响测向系统的精度。
假设N个远场的窄带信号Sn(t)(n=1, 2, …, N)入射到阵元间距为d的等距直线阵列,其中阵列天线由M个阵元组成,设阵元间距d为信号波长的一半,假设信号是不完全相关的,使用检测方法正确获N个信号源[18, 21],则阵元输出矢量可以写成:
| $ \mathit{\boldsymbol{X}}\left( t \right) = \sum\limits_{n = 1}^N {\mathit{\boldsymbol{a}}\left( {{\theta _i}} \right){\mathit{\boldsymbol{s}}_n}\left( t \right)} + \mathit{\boldsymbol{N}}\left( t \right) = \mathit{\boldsymbol{A}}\left( \theta \right)\mathit{\boldsymbol{S}}\left( t \right) + \mathit{\boldsymbol{N}}\left( t \right) $ | (1) |
对阵列输出做相关处理,得到其协方差矩阵:
| $ \mathit{\boldsymbol{R}} = {\rm{E}}\left\{ {\mathit{\boldsymbol{X}}\left( t \right){\mathit{\boldsymbol{X}}^{\rm{H}}}\left( t \right)} \right\} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{R}}_S}\mathit{\boldsymbol{A + }}{\mathit{\boldsymbol{R}}_N} $ | (2) |
式中:(·)H为埃尔米特矩阵,RS=E{ S(t) SH(t)}∈ CN×N代表信号协方差矩阵;RN=E{N(t) N H(t)}∈ CM×M代表噪声协方差矩阵。
若信号是相关的,si(t)=αs0(t)则相关信号源模型为:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}}\left( t \right) = \sum\limits_{n = 1}^N {\mathit{\boldsymbol{a}}\left( {{\theta _i}} \right){\mathit{\boldsymbol{s}}_n}\left( t \right)} + \mathit{\boldsymbol{N}}\left( t \right) = }\\ {\mathit{\boldsymbol{A}}\left( \theta \right)\left[ {\begin{array}{*{20}{c}} {{s_1}\left( t \right)}\\ {{s_2}\left( t \right)}\\ \vdots \\ {{s_N}\left( t \right)} \end{array}} \right] + \mathit{\boldsymbol{N}}\left( t \right) - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{s}}_0}\left( t \right) + \mathit{\boldsymbol{N}}\left( t \right)} \end{array} $ | (3) |
此时的协方差矩阵:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{R}} = {\rm{E}}\left\{ {\mathit{\boldsymbol{X}}\left( t \right){\mathit{\boldsymbol{X}}^{\rm{H}}}\left( t \right)} \right\} = \mathit{\boldsymbol{G}} \cdot \mathit{\boldsymbol{E}}\left\{ {{\mathit{\boldsymbol{s}}_0}\left( t \right){\mathit{\boldsymbol{s}}_0}^{\rm{H}}\left( t \right)} \right\} \cdot }\\ {{\mathit{\boldsymbol{G}}^{\rm{H}}} + {\mathit{\boldsymbol{R}}_N} = \mathit{\boldsymbol{G\rho }}{\mathit{\boldsymbol{G}}^{\rm{H}}} + {\mathit{\boldsymbol{R}}_N}} \end{array} $ | (4) |
式中ρ =E{ s0(t)s0H(t)}。
从式(4)可知,对于相关信号源,阵列流行矩阵G ∈ CN×1,对协方差矩阵进行特征分解,可以发现信号子空间降为1维,而噪声子空间扩展到N-1维。方向矢量不再反应信号源的真实方向,这种情况下,特征值分解的DOA估计方法不能准确地估计波达方向。
2 空间平滑技术波达方向估计算法 2.1 空间平滑算法MUSIC算法在理想状态下具有良好的性能,但在信号源相关时,算法的性能变得很坏; 在相干信号源的情况下,正确估计信号方向的核心问题是,如何通过一系列处理或变换使得信号协方差矩阵得到有效恢复,从而正确估计信号源的方向。空间平滑MUSIC[15-16]可以利用子阵平滑恢复数据协方差矩阵,再处理相干信号源时,有良好的性能。将系统模型里M个阵元的均匀线阵分成相互交错的p个子阵,每个子阵的阵元数为m, 即有M=p+m-1。前向平滑技术方法,一般取第1个子阵为参考矩阵,则对于第k个子阵数据模型满足:
| $ \mathit{\boldsymbol{x}}_k^t = {\mathit{\boldsymbol{Z}}_k}\mathit{\boldsymbol{X}}\left( t \right) $ | (5) |
前向平滑技术的协方差矩阵:
| $ {\mathit{\boldsymbol{R}}_f} = \frac{1}{p}\sum\limits_{k = 1}^p {{\mathit{\boldsymbol{Z}}_k}\mathit{\boldsymbol{RZ}}_k^{\rm{H}}} $ | (6) |
式中Zk=[0m×(k-1)| Im×m| 0 m×(p-k)]。
对比前向平滑技术,后向平滑技术的协方差矩阵:
| $ {\mathit{\boldsymbol{R}}_b} = \frac{1}{p}\sum\limits_{k = 1}^p {{\mathit{\boldsymbol{Q}}_k}{\mathit{\boldsymbol{R}}^ * }\mathit{\boldsymbol{Q}}_k^H} $ | (7) |
式中:Qk=[0m×(k-1)|Jm×m|0m×(p-k)];{ ·}*代表共轭矩阵,可以看出前向平滑与后向平滑满足:
| $ {\mathit{\boldsymbol{R}}_b} = \mathit{\boldsymbol{JR}}_f^ * \mathit{\boldsymbol{J}} $ | (8) |
Jm×m是反对角线为1的置换矩阵,即:
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} 0& \cdots &1\\ \vdots &{}& \vdots \\ 1& \cdots &0 \end{array}} \right] $ | (9) |
由式(5)和式(6)可推导前后向平滑的协方差矩阵为:
| $ {\mathit{\boldsymbol{R}}_{fb}} = \frac{1}{{2p}}\sum\limits_{k = 1}^p {{\mathit{\boldsymbol{Z}}_k}\left( {\mathit{\boldsymbol{R}} + \mathit{\boldsymbol{J}}{\mathit{\boldsymbol{R}}^ * }\mathit{\boldsymbol{J}}} \right)\mathit{\boldsymbol{Z}}_k^{\rm{H}}} $ | (10) |
为解决M个相关信号源,前向平滑技术和后向平滑技术最小需要为2M和3M/2个传感器[15]。空间平滑技术,又由于分割成相互交错的子矩阵,增加了计算复杂度,所以需要利用改进算法提升运算的速度。
2.2 传播因子类快速算法传播因子类快速算法(PM)通过对接收数据或者协方差矩阵进行简单的线性运算以快速估计出噪声子空间。这类算法运算量小,角分辨率高。
假设N个信号入射于M个阵元线性矩阵上,对阵列流型矩阵做如下处理:
| $ \mathit{\boldsymbol{A}}\left( \theta \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_1}\left( \theta \right)}\\ {{\mathit{\boldsymbol{A}}_2}\left( \theta \right)} \end{array}} \right] $ | (11) |
式中A1(θ)和A2(θ)分别由A(θ)的前N和M-N行构成,假设A1(θ)为非奇异矩阵,则存在唯一的传播算子P使得A2(θ)= PH A1(θ)成立,按照式(11)的分割方法对接收信号矩阵进行分割:
| $ \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_1}}\\ {{\mathit{\boldsymbol{X}}_2}} \end{array}} \right] $ | (12) |
则在无噪声的情况下有X2= PHX1,当存在噪声时,可利用最小二乘法可得到P:
| $ \mathit{\boldsymbol{P}} = {\left( {{\mathit{\boldsymbol{X}}_1}\mathit{\boldsymbol{X}}_1^{\rm{H}}} \right)^{ - 1}}{\mathit{\boldsymbol{X}}_1}\mathit{\boldsymbol{X}}_2^{\rm{H}} $ | (13) |
利用求得的P构造Q =[PT-IM-N]T使得QH A (θ)=0, 即可找到与方向向量正交的向量空间Q,这就是PM算法估计出的噪声子空间。结合MUSIC算法即可估算出信号的方向角,即搜索下式的最小值:
| $ {\mathit{\boldsymbol{F}}_{PM}}\left( \theta \right) = {\mathit{\boldsymbol{a}}^{\rm{H}}}\left( \theta \right)\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{Q}}^{\rm{H}}}\mathit{\boldsymbol{a}}\left( \theta \right) $ | (14) |
由于式中的噪声子空间Q的列向量之间不是相互正交的,为进一步提高角度的估计精度,对Q进行正交变换Q0= Q (QHQ)-1/2,然后将Q0代入式中进行角度估计,即:
| $ {\mathit{\boldsymbol{F}}_{{\rm{OPM}}}}\left( \theta \right) = {\mathit{\boldsymbol{a}}^{\rm{H}}}\left( \theta \right){\mathit{\boldsymbol{Q}}_0}\mathit{\boldsymbol{Q}}_0^{\rm{H}}\mathit{\boldsymbol{a}}\left( \theta \right) $ | (15) |
简单的和常识性的运算公式和推导过程不要列写。
2.3 空间平滑算法的改进1) 利用OPM算法进行空间平滑技术分解,从而得到波达方向估计,由式(10)可知前后向平滑技术协方差矩阵为:
| $ {\mathit{\boldsymbol{R}}_{fb}} = \frac{1}{{2p}}\sum\limits_{k = 1}^p {{\mathit{\boldsymbol{Z}}_k}\left( {\mathit{\boldsymbol{R}} + \mathit{\boldsymbol{J}}{\mathit{\boldsymbol{R}}^ * }\mathit{\boldsymbol{J}}} \right)\mathit{\boldsymbol{Z}}_k^{\rm{H}}} $ | (16) |
利用协方差矩阵来估计传播算子P,首先对Rfb进行如下分割:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{fb}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_1}}\\ {{\mathit{\boldsymbol{A}}_2}} \end{array}} \right]{\mathit{\boldsymbol{R}}_S}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_1}}&{{\mathit{\boldsymbol{A}}_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{R}}_S}\mathit{\boldsymbol{A}}_1^{\rm{H}}}&{{\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{R}}_S}\mathit{\boldsymbol{A}}_2^{\rm{H}}}\\ {{\mathit{\boldsymbol{A}}_2}{\mathit{\boldsymbol{R}}_S}\mathit{\boldsymbol{A}}_1^{\rm{H}}}&{{\mathit{\boldsymbol{A}}_2}{\mathit{\boldsymbol{R}}_S}\mathit{\boldsymbol{A}}_2^{\rm{H}}} \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{R}}_S}\mathit{\boldsymbol{A}}_1^{\rm{H}}}&{{\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{R}}_S}\mathit{\boldsymbol{A}}_1^{\rm{H}}\mathit{\boldsymbol{P}}}\\ {{\mathit{\boldsymbol{A}}_2}{\mathit{\boldsymbol{R}}_S}\mathit{\boldsymbol{A}}_1^{\rm{H}}}&{{\mathit{\boldsymbol{A}}_\mathit{\boldsymbol{R}}}_S\mathit{\boldsymbol{A}}_1^{\rm{H}}\mathit{\boldsymbol{P}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{G}}&\mathit{\boldsymbol{H}} \end{array}} \right]} \end{array} $ | (17) |
式中:G和H分别是由Rfb的前N列和后M-N列构成的矩阵,在无噪声的情况下有H = GP,当存在噪声时,利用最小二乘‖ H - GP ‖F2可得到P的估值为:
| $ \mathit{\boldsymbol{P}} = {\left( {{\mathit{\boldsymbol{G}}^{\rm{H}}}\mathit{\boldsymbol{G}}} \right)^{ - 1}}{\mathit{\boldsymbol{G}}^{\rm{H}}}\mathit{\boldsymbol{H}} $ | (18) |
| $ \mathit{\boldsymbol{Q}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}^{\rm{T}}}}&{ - {\mathit{\boldsymbol{I}}_{M - N}}} \end{array}} \right]^{\rm{T}}} $ | (19) |
对Q进行正交变换Q0= Q(Q H Q)-1/2可以得到前后向平滑技术OPM空间谱:
| $ {F_{{\rm{fb - OPM}}}}\left( \theta \right) = \frac{1}{{{{\left\| {{\mathit{\boldsymbol{Q}}_0}\mathit{\boldsymbol{a}}\left( \theta \right)} \right\|}^2}}} $ | (20) |
2) 对前后向平滑协方差Rfb取共轭矩阵:
| $ \mathit{\boldsymbol{R}}_{fb}^ * = \frac{1}{{2p}}\sum\limits_{k = 1}^p {{\mathit{\boldsymbol{Z}}_k}\left( {{\mathit{\boldsymbol{R}}^ * } + \mathit{\boldsymbol{JRJ}}} \right)\mathit{\boldsymbol{Z}}_k^{\rm{H}}} $ | (21) |
广义差分协方差GCD可以表示为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{{\rm{GCD}}}} = {\mathit{\boldsymbol{R}}_{fb}} - \mathit{\boldsymbol{R}}_{fb}^ * = \frac{1}{{2p}}\sum\limits_{k = 1}^p {{\mathit{\boldsymbol{Z}}_k}\left( {\mathit{\boldsymbol{R}} + \mathit{\boldsymbol{J}}{\mathit{\boldsymbol{R}}^ * }\mathit{\boldsymbol{J}} - } \right.} }\\ {\left. {{\mathit{\boldsymbol{R}}^ * } - \mathit{\boldsymbol{JRJ}}} \right)\mathit{\boldsymbol{Z}}_k^{\rm{T}}} \end{array} $ | (22) |
令ΔR = R + JR * J - R *- JRJ,可知Δ R是纯虚矩阵[19],对比式(16), 对RGCD进行OPM分解估计,即RGCD技术OPM空间谱:
| $ {F_{{\rm{GCD - OPM}}}}\left( \theta \right) = \frac{1}{{{{\left\| {{\mathit{\boldsymbol{Q}}_0}\mathit{\boldsymbol{a}}\left( \theta \right)} \right\|}^2}}} $ | (23) |
对所提出的方法进行仿真检验,仿真在阵元间距为信号波长一半的均匀线阵下进行。假设快拍数为1 024,阵元数为8,阵元间距d=λ/2,2个信号源分别从10°和30°方向入射到ULA上,信噪比为10。
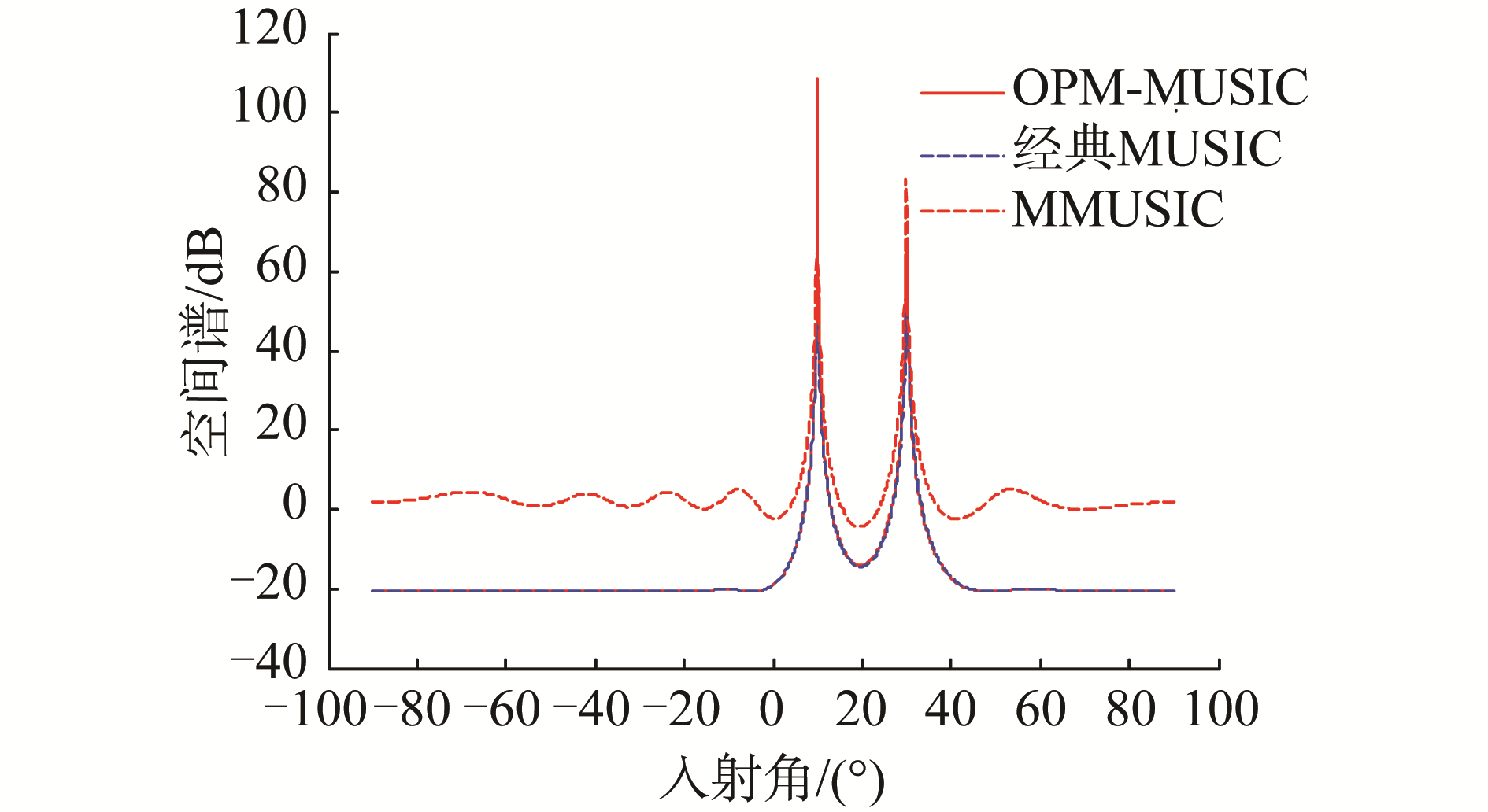
从图 1看出,经典MUSIC、MMUSIC、OPM-MUSIC空间谱波形,都具有良好的性能,性能差别不大。从图 4可以看出传播因子双向平滑相对于双向平滑波形收敛稍快,谱峰尖锐程度较弱些,总体性能差别不大。
|
Download:
|
| 图 1 3种MUSIC算法对比曲线 Fig. 1 Comparison curves of three MUSIC algorithms | |
假设快拍数为1 024,阵元数为8,阵元间距设置为d=λ/2,一个信号源从15°方向入射到ULA上,信噪比为10,从图 3可以看出OPM-GCD平滑相对于GCD平滑波形收敛稍快,两者的谱峰尖锐程度相差无几。另外也可以看出GCD平滑技术有一个-15°方向的峰值。因为GCD平滑技术有关于原点对称分布的特征值。

|
Download:
|
| 图 2 2种双向平滑算法对比曲线 Fig. 2 Comparison curves of two kinds of spatial smoothing techniques | |

|
Download:
|
| 图 3 2种GCD平滑算法对比曲线 Fig. 3 Comparison curves of two kinds of GCD-spatial smoothing techniques | |
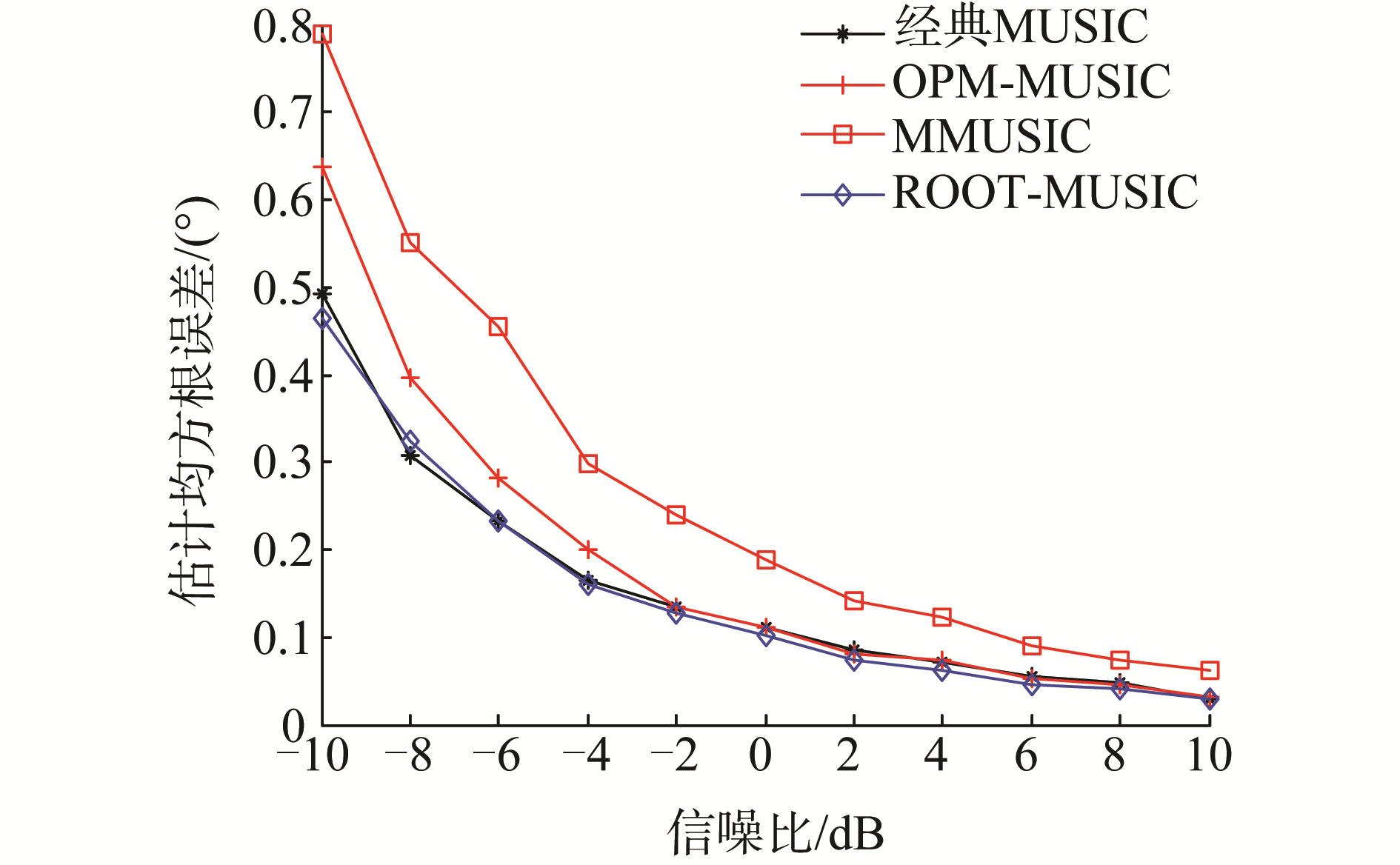
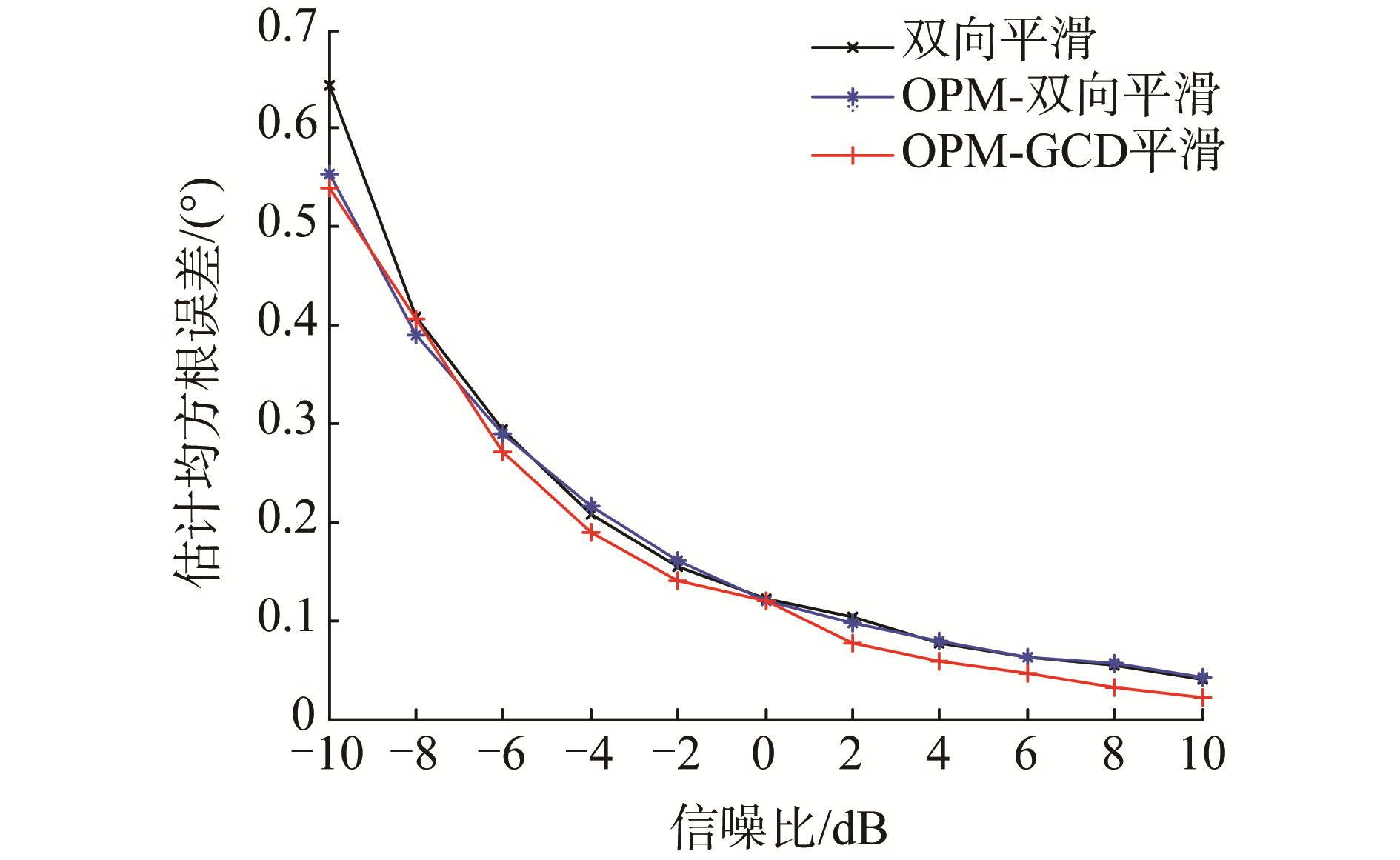
综合图 4、图 5可以看出结合传播因子类方法的双向平滑技术仍可以保持其原有的性能,但传播因子类算法也可以应用到空间平滑技术中,通过简单的线性分割变换来快速估计噪声子空间,避免了传统子空间算法中运算量极大的特征分解,从而降低了计算量。
|
Download:
|
| 图 4 4种MUSIC算法的RMSE随SNR变化曲线 Fig. 4 RMSE curves of four kinds of MUSIC algorithms with SNR | |
|
Download:
|
| 图 5 3种平滑算法的RMSE随SNR变化曲线 Fig. 5 RMSE curves of three kinds of smoothing algorithms with SNR | |
1) 结合传播因子类方法的双向平滑技术、GCD平滑技术,在不影响良好的精确度的情况下,进一步降低了运算复杂度。
2) 算法存在不足之处,如其他环境因素的限制,精度方面没有太大提高,因此还需要在这些方面加以改进。
| [1] |
王永良. 空间谱估计理论与算法[M]. 北京: 清华大学社, 2004.
(  0) 0)
|
| [2] |
张贤达, 保铮. 通信信号处理[M]. 北京: 国防工业出版社, 2000.
(  0) 0)
|
| [3] |
SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE transactions on antennas and propagation, 1986, 34(3): 276-280. DOI:10.1109/TAP.1986.1143830 (  0) 0)
|
| [4] |
宋虎, 蒋迺倜, 刘溶, 等. 基于稀疏采样阵列优化的APG-MUSIC算法[J]. 电子与信息学报, 2018, 40(6): 1390-1396. SONG Hu, JIANG Naiti, LIU Rong, et al. APG-MUSIC algorithm based on sparse sampling array optimization[J]. Journal of electronics & information technology, 2018, 40(6): 1390-1396. (  0) 0)
|
| [5] |
ROY R, KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE transactions on acoustics, speech, and signal processing, 1989, 37(7): 984-995. DOI:10.1109/29.32276 (  0) 0)
|
| [6] |
STOICA P, NEHORAI A. MUSIC, maximum likelihood, and Cramer-Rao bound:further results and comparisons[J]. IEEE transactions on acoustics, speech, and signal processing, 1990, 38(12): 2140-2150. DOI:10.1109/29.61541 (  0) 0)
|
| [7] |
STOICA P, NEHORAI A. Performance study of conditional and unconditional direction-of-arrival estimation[J]. IEEE transactions on acoustics, speech, and signal processing, 1990, 38(10): 1783-1795. DOI:10.1109/29.60109 (  0) 0)
|
| [8] |
EVANS J E, JOHNSON J R, SUN D F.High resolution angular spectrum estimation techniques for terrain scattering analysis and angle of arrival estimation[C]//Proceedings of the 1st ASSP Workshop Spectral Estimation.Hamilton, Ontario, Canada, 1981.
(  0) 0)
|
| [9] |
SHAN Tiejun, WAX M, KAILATH T. On spatial smoothing for direction-of-arrival estimation of coherent signals[J]. IEEE transactions on acoustics, speech, and signal processing, 1985, 33(4): 806-811. DOI:10.1109/TASSP.1985.1164649 (  0) 0)
|
| [10] |
KUNDU D. Modified MUSIC algorithm for estimating DOA of signals[J]. Signal processing, 1996, 48(1): 85-90. DOI:10.1016/0165-1684(95)00126-3 (  0) 0)
|
| [11] |
ZHAO Yongbo, ZHANG Shouhong.A fast algorithm for DOA estimation in unknown correlated noise[C]//Proceedings of the IEEE 6th Circuits and Systems Symposium on Emerging Technologies: Frontiers of Mobile and Wireless Communication.Shanghai, China, 2004, 2: 757-759. https://www.researchgate.net/publication/4086273_A_fast_algorithm_for_DOA_estimation_in_unknown_correlated_noise
(  0) 0)
|
| [12] |
张聪, 胡谋法, 卢焕章. 基于虚拟阵列空间平滑的相干信号DOA估计[J]. 电子学报, 2010, 38(4): 929-933. ZHANG Cong, HU Moufa, LU Huanzhang. Virtual array-based spatial smoothing method for direction finding of coherent signals[J]. Acta electronica sinica, 2010, 38(4): 929-933. (  0) 0)
|
| [13] |
PILLAI S U, KWON B H. Forward/backward spatial smoothing techniques for coherent signal identification[J]. IEEE transactions on acoustics, speech, and signal processing, 1989, 37(1): 8-15. DOI:10.1109/29.17496 (  0) 0)
|
| [14] |
MARCOS S, MARSAL A, BENIDIR M. The propagator method for source bearing estimation[J]. Signal processing, 1995, 42(2): 121-138. DOI:10.1016/0165-1684(94)00122-G (  0) 0)
|
| [15] |
MARCOS S, MARSAL A, BENIDIR M.Performances analysis of the propagator method for source bearing estimation[C]//Proceedings of ICASSP'94.IEEE International Conference on Acoustics, Speech and Signal Processing.Adelaide, SA, Australia, 1994: IV/237-IV/240. https://www.researchgate.net/publication/232629004_Performances_analysis_of_the_propagator_method_for_source_bearing_estimation
(  0) 0)
|
| [16] |
QI Chongying, CHEN Zhijie, WANG Yongliang, et al. DOA estimation for coherent sources in unknown nonuniform noise fields[J]. IEEE transactions on aerospace and electronic systems, 2007, 43(3): 1195-1204. DOI:10.1109/TAES.2007.4383611 (  0) 0)
|
| [17] |
AOUADA S, ZOUBIR A M, SEE C M S.Source detection in the presence of nonuniform noise[C]//Proceedings of 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing.Montreal, Que., Canada, 2004, 2: 165-168. https://www.researchgate.net/publication/4087619_Source_detection_in_the_presence_of_nonuniform_noise
(  0) 0)
|
| [18] |
AOUADA S, TRASKOV D, D'HEUREUSE N, et al.Application of the bootstrap to source detection in nonuniform noise[C]//Proceedings.(ICASSP'05).IEEE International Conference on Acoustics, Speech, and Signal Processing.Philadelphia, PA, USA, 2005, 4: iv/997-iv1000. https://www.researchgate.net/publication/224612704_Application_of_the_bootstrap_to_source_detection_in_nonuniform_noise
(  0) 0)
|
| [19] |
黄家才, 石要武, 陶建武. 多径循环平稳信号二维波达方向估计--极化域平滑法[J]. 电子与信息学报, 2007, 29(5): 1110-1114. HUANG Jiacai, SHI Yaowu, TAO Jianwu. 2-D direction finding of cyclostationary signals with Polarization smoothing algorithm in multipath environment[J]. Journal of electronics & information technology, 2007, 29(5): 1110-1114. (  0) 0)
|
| [20] |
DIVERSI R, GUIDORZI R, SOVERINI U.Estimating the number of signals in the presence of nonuniform noise[C]//Proceedings of 2014 IEEE International Conference on Acoustics, Speech and Signal Processing.Florence, Italy, 2014: 2967-2971. https://www.researchgate.net/publication/269295503_Estimating_the_number_of_signals_in_the_presence_of_nonuniform_noise
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


