2. 江苏大学 电气信息工程学院, 江苏 镇江 212013
2. Electrical and Information Engineering College, Jiangsu University, Zhenjiang 212013, China
目前,海上航行的大多数船舶依靠螺旋桨主推进器和舵装置控制船舶水平面位置和艏摇角3个自由度的运动,这属于典型的欠驱动系统。欠驱动船舶在海洋中的航线通常由一系列转向点构成,转向点间为可近似为直线的恒向线,并且以定常或者近乎定常的速度进行长距离的直线航迹航行的情况最为常见[1-2]。欠驱动船舶在航行过程中受到强烈的风、浪、流时变干扰作用,不仅产生较大的航迹跟踪误差,并且会出现剧烈的横摇运动,危害航行安全。
舵不仅能够产生艏摇力矩,还能够产生横摇力矩,利用舵产生的横摇力矩可以在控制航向的同时,还能够达到减摇的效果。与其他减摇设备相比,舵减摇具有投资少,占用空间小,减摇效果好等特点。目前国内外的研究分别从欠驱动船舶航迹跟踪的鲁棒性和舵减摇效果两方面单独设计,其中控制器设计方法有模糊控制和神经网络等[3-4]。但是,上述文献都较少考虑航迹跟踪和减摇耦合协调问题,即实现如何在保证减摇效果的同时,尽可能地降低对航向控制的影响,在航迹跟踪控制性能和横摇角约束之间进行有效折衷。
模型预测控制可以事先将输出约束和输入约束考虑到控制器设计中,是目前解决系统约束的有效方法之一,并且在很多方面得以研究和利用[5-7]。文献[8]利用了预测控制的在线约束优化特点,保证了横摇角在安全范围内,但却没有考虑控制系统的鲁棒性。文献[9]利用复合的预测控制器和干扰观测器,解决了约束和时变干扰问题,保证了系统的稳定性和鲁棒性,但每个控制周期需要两次在线优化分别求解控制量和前馈补偿量,计算量大。但是,上述应用研究仍然存在局限性,假设了船舶的全运动状态可以精确获得,实际上船舶只有部分状态可测,并且观测量里夹杂随机噪声。同时,基于名义系统的预测控制不能有效抑制时变风浪流干扰,会造成闭环控制系能恶化。为解决这些问题,本文提出一种考虑横摇角约束的自适应卡尔曼状态估计和鲁棒预测控制器的综合设计方法。
1 欠驱动船舶航迹跟踪模型建立对于船舶的航迹跟踪问题,引入Serret-Frenet坐标系一定程度上简化了控制器的设计。其中图 1表示采用Serret-Frenet坐标系下研究航迹跟踪问题,{SF}的原点位于船舶重心在Ω上的正交投影,Ω为设定的目标航迹,e为{B}的原点与{SF}的原点之间的距离,ψSF为目标航向,ψ为船舶的航向角。

|
Download:
|
| 图 1 Serret-Frenet坐标系 Fig. 1 Serret-Frenet coordinates | |
在Serret-Frenet坐标系下的航迹跟踪的误差动态方程为[13]:
| $ \left\{ \begin{array}{l} \dot e = u\sin \bar \psi + v\cos \bar \psi \\ \dot {\bar \psi} = \dot \psi - {{\dot \psi }_{{\rm{SF}}}} = \frac{\kappa }{{1 - e\kappa }}\left( {u\sin \bar \psi - v\cos \bar \psi } \right) + r \end{array} \right. $ | (1) |
式中:ψ =ψ-ψSF为航向角偏差;κ为目标航迹的曲率。对于大多数欠驱动船舶航迹跟踪问题,航迹是由一个直线或分段连续的直线,即κ=0组成,并且在航行中横荡速度很小,这里假设v=0,因此误差动态方程(1)可以简化为:
| $ \left\{ \begin{array}{l} \dot e \approx u\sin \bar \psi \\ \dot {\bar \psi} = r \end{array} \right. $ | (2) |
为了实现期望航迹的跟踪,可以通过控制航向角误差ψ收敛到零使航迹误差e也收敛到0,从而达到跟踪轨迹的效果。为了控制欠驱动船舶的横摇角度在安全范围内,必须建立横摇动力学,而耦合的纵荡速度u、横荡速度v、横摇角速度p和艏摇角速度r 4个自由度上的非线性模型为[13]:
| $ \left\{ \begin{array}{l} m\left( {\dot u - vr - {X_G}{r^2} + {Z_G}pr} \right) = X\\ m\left( {\dot v + ur + {X_G}\dot r - {Z_G}\dot p} \right) = Y\\ {I_{XX}}\dot p - {I_{XZ}}\dot r - m{Z_G}\left( {\dot v + ur} \right) = K - mgG{M_T}\phi \\ {I_{ZZ}}\dot r - {I_{XZ}}\dot p + m{Z_G}\left( {\dot v + ur} \right) = N \end{array} \right. $ | (3) |
式中:m表示船的质量;Ixx和Ixz分别表示x轴与x、z轴耦合的力矩惯量;u和v分别表示船舶纵荡和横荡速度;r为艏摇角速度;ψ为航向角;p为横摇角速度;ϕ为横摇角;xG是x轴重心的位置;zG是z轴重心的位置;水动力X和Y,力矩K、N通常为非线性水动力常数的三阶泰勒级数多项式,参见文献[11]。
由于船舶的舵角工作范围有限,即|δ|≤35°,为了便于控制器的设计,将船舶运动模型分解为下面3个工作区域,在不同区域进行线性化处理,并通过切换模型描述非线性模型。3个工作区域为:
| $ \left\{ \begin{array}{l} {\mathit{\Omega }_1} = \left\{ {\delta \left| {, - {{10}^ \circ } \le \delta \le {{10}^ \circ }} \right.} \right\}\\ {\mathit{\Omega }_2} = \left\{ {\delta \left| {,{{10}^ \circ } \le \delta \le {{35}^ \circ }} \right.} \right\}\\ {\mathit{\Omega }_3} = \left\{ {\delta \left| {, - {{35}^ \circ } \le \delta \le - {{10}^ \circ }} \right.} \right\} \end{array} \right. $ | (4) |
而简化的切换模型具有下面的形式:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\hat x}} = {\mathit{\boldsymbol{A}}_i}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{B}}_i}\delta + {\mathit{\boldsymbol{B}}_d}\mathit{\boldsymbol{d}},\\ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Hx}} + \mathit{\boldsymbol{v}} \end{array} \right. $ | (5) |
式中:i=1, 2, 3;x ∈ X, δ∈U。
如果δ∈Ωi,则系统状态切换进入i模型,并且
| $ {\mathit{\boldsymbol{A}}_i} = \left[ {\begin{array}{*{20}{c}} 0&0&1&0&0\\ 0&{{a_{i11}}}&{{a_{i12}}}&{{a_{i13}}}&{{a_{i14}}}\\ 0&{{a_{i21}}}&{{a_{i22}}}&{{a_{i23}}}&{{a_{i24}}}\\ 0&{{a_{i31}}}&{{a_{i32}}}&{{a_{i33}}}&{{a_{i34}}}\\ 0&0&0&1&0 \end{array}} \right]\;\;\;\;{\mathit{\boldsymbol{B}}_i} = \left[ \begin{array}{l} 0\\ {b_{i1}}\\ {b_{i2}}\\ {b_{i3}}\\ 0 \end{array} \right] $ | (6) |
| $ \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0 \end{array}} \right] $ | (7) |
式中:[A1, B1]是模型(3)在平衡点δ=0的线性化模型,表示船舶在航向保持状态;[A2, B2]和[A3, B3]分别是模型(3)在平衡点δ=15和δ=-15的线性化模型。x =[ψ v r p ϕ]T表示系统的状态,系数aijm(i=1, 2, 3, j=1, 2, 3, m=1, 2, 3, 4)和bij(i=1, 2, 3, j=1, 2, 3)是常数,通过试验以及CFD软件获得[15]。d表示集总干扰,包含模型不确定性和外界干扰,并且假设其满足d(t) ≤dmax,
因此,在欠驱动切换模型(5)的基础上,需要设计自适应卡尔曼滤波消除量测噪声,估计出运动全状态和干扰,并进行干扰补偿。在满足输入约束的情况下,设计鲁棒预测控制,并求得复合控制器u(k)= umpc(k)+ ud(k),从而实现对期望航向角的跟踪、抑制随机干扰,并保证横摇角在安全的约束范围内。
2 基于扩展状态的自适应卡尔曼滤波欠驱动船舶在复杂海况航行中容易受到外界扰动和量测噪声的影响,系统状态难以准确获得,影响航迹跟踪效果。文献[12]将随机扰动作为白噪声进行卡尔曼估计有一定的近似误差,文献[13]通过成形滤波器将有色干扰白化进行干扰估计,计算比较复杂。这里采用卡尔曼滤波,并将集总干扰d作为系统的增广状态,对系统状态和干扰同时进行最优估计,从而减小随机干扰和量测噪声对系统的影响,并对估计的集总干扰
由于船舶具有低频运动特性,在状态估计周期内可以近似认为
| $ \begin{array}{l} \mathit{\boldsymbol{\bar x}}\left( {k + 1} \right) = {{\mathit{\boldsymbol{\bar A}}}_i}\mathit{\boldsymbol{\bar x}}\left( k \right) + {{\mathit{\boldsymbol{\bar B}}}_i}\delta \left( k \right)\\ \mathit{\boldsymbol{\bar y}}\left( k \right) = \mathit{\boldsymbol{\bar H\bar x}}\left( k \right) + \mathit{\boldsymbol{v}}\left( k \right) \end{array} $ | (8) |
式中:
滤波及估算状态、干扰的具体步骤为:
| $ \mathit{\boldsymbol{\bar x}}\left( {k\left| {k - 1} \right.} \right) = \mathit{\boldsymbol{\bar A\bar x}}\left( {k - 1} \right) + \mathit{\boldsymbol{\bar B}}u\left( k \right) $ | (9) |
| $ \mathit{\boldsymbol{\bar P}}\left( {k\left| {k - 1} \right.} \right) = \overline {\mathit{\boldsymbol{AP}}} \left( {k - 1\left| {k - 1} \right.} \right){{\mathit{\boldsymbol{\bar A}}}^{\rm{T}}} + \mathit{\boldsymbol{\bar Q}}\left( k \right) $ | (10) |
| $ \mathit{\boldsymbol{\bar K}}\left( k \right) = \frac{{\mathit{\boldsymbol{\bar P}}\left( {k\left| {k - 1} \right.} \right){{\mathit{\boldsymbol{\bar H}}}^{\rm{T}}}}}{{\overline {\mathit{\boldsymbol{HP}}} \left( {k\left| {k - 1} \right.} \right){{\mathit{\boldsymbol{\bar H}}}^{\rm{T}}} + \mathit{\boldsymbol{R}}\left( k \right)}} $ | (11) |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\bar x}}\left( {k\left| k \right.} \right) = \mathit{\boldsymbol{\bar x}}\left( {k\left| {k - 1} \right.} \right) + }\\ {\mathit{\boldsymbol{\bar K}}\left( k \right)\left( {\mathit{\boldsymbol{\bar y}}\left( k \right) - \mathit{\boldsymbol{\bar H\bar x}}\left( {k\left| {k - 1} \right.} \right)} \right)} \end{array} $ | (12) |
| $ \mathit{\boldsymbol{\hat d}}\left( k \right) = \mathit{\boldsymbol{\bar C\bar x}}\left( {k\left| k \right.} \right) $ | (13) |
| $ \mathit{\boldsymbol{\bar P}}\left( {k\left| k \right.} \right) = \left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{\bar K}}\left( k \right)\mathit{\boldsymbol{\bar H}}} \right)\mathit{\boldsymbol{\bar P}}\left( {k\left| {k - 1} \right.} \right) $ | (14) |
式中:C=[0 0 0 0 0 1]。由于模型(5)为欠驱动系统,并且d主要作用在艏摇的动力学中,干扰前馈补偿控制为:
| $ {\mathit{\boldsymbol{u}}_d}\left( k \right) = - \frac{{\mathit{\boldsymbol{\hat d}}\left( k \right)}}{{{b_{i2}}}} $ | (15) |
由于海面环境的复杂性导致了系统噪声及量测噪声统计特性难以事先确定,需要采用时变噪声统计的自适应Sage-Husa卡尔曼滤波算法对船舶进行估计状态,由滤波本身不断估计和修正系统噪声方差阵和量测噪声方差阵,防止所设计滤波器因状态估计较大的误差而造成滤波发散,具体公式可参考文献[15]。
3 舵减摇航迹跟踪鲁棒预测控制采用自适应卡尔曼的状态估计和干扰补偿后,船舶系统的真实运动状态与观测状态之间仍然会存在观测误差,并且干扰补偿过程中也存在估计误差。因此,在预测控制中处理状态和输入约束时需要不能忽略卡尔曼滤波器的影响,需要将控制器与滤波器综合一体化考虑,并提出基于状态估计和H2/H∞混合指标的直接约束鲁棒预测控制方法。在预测控制的性能指标与控制器设计中直接利用估计状态,保证了在满足横摇角的前提下,具有良好的航迹跟踪效果,并能够抑制估计误差和集总干扰。
经过前馈补偿后的模型可改写为含扰动的离散预测模型一般表达式[16-17]:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\hat x}}\left( {k + 1} \right) = {\mathit{\boldsymbol{A}}_i}\mathit{\boldsymbol{\hat x}}\left( k \right) + {\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{u}}_{{\rm{mpc}}}}\left( k \right) + {\mathit{\boldsymbol{B}}_d}{\mathit{\boldsymbol{d}}_1}\left( k \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{K}}\left( k \right)\left( {{\mathit{\boldsymbol{y}}_1}\left( k \right) - \mathit{\boldsymbol{H\hat x}}\left( k \right)} \right)\\ \mathit{\boldsymbol{y}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{Hx}}\left( k \right)}\\ {\mathit{\boldsymbol{R}}{u_{{\rm{mpc}}}}\left( k \right)} \end{array}} \right] \end{array} \right. $ | (16) |
式中:d1(k)= d (k)-
采用反馈控制律umpc(k)= Fx (k),设ϕ (k)= A i(k)+ Bi(k)F,那么式(16)可转化为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\hat x}}\left( {k + 1} \right) = \mathit{\boldsymbol{\varphi \hat x}}\left( k \right) + {\mathit{\boldsymbol{B}}_d}{\mathit{\boldsymbol{d}}_1}\left( k \right) + \mathit{\boldsymbol{K}}\left( k \right)\mathit{\boldsymbol{He}}\left( k \right)\\ \mathit{\boldsymbol{y}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{Hx}}\left( k \right)}\\ {\mathit{\boldsymbol{R}}{u_{{\rm{mpc}}}}\left( k \right)} \end{array}} \right] \end{array} \right. $ | (17) |
基于航迹跟踪最优目标和鲁棒稳定要求,提出下面H2/H∞指标。
1) H2性能指标:系统输出y(k)满足:
| $ \left\| \mathit{\boldsymbol{y}} \right\|_2^2 = \sum\limits_{k = 0}^\infty {{\mathit{\boldsymbol{y}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{y}}\left( k \right)} \le {\alpha ^2} $ | (18) |
2) H∞性能指标:扰动补偿估计误差d1(k)到输出y (k)的传递函数G满足:
| $ {\left\| {{\mathit{\boldsymbol{G}}_{y{\mathit{\boldsymbol{d}}_1}}}} \right\|_\infty } \le \gamma $ | (19) |
选取Lyapunov函数取为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{V}}\left( {\mathit{\boldsymbol{\hat x}}\left( {k + 1} \right)} \right) - \mathit{\boldsymbol{V}}\left( {\mathit{\boldsymbol{\hat x}}\left( k \right)} \right) = }\\ {\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat x}}}^{\rm{T}}}\left( k \right)}&{\mathit{\boldsymbol{d}}_1^{\rm{T}}\left( k \right)}&{{\mathit{\boldsymbol{e}}^{\rm{T}}}\left( k \right)} \end{array}} \right]}\\ {\mathit{\boldsymbol{N}}\left( k \right){{\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat x}}}^{\rm{T}}}\left( k \right)}&{{\mathit{\boldsymbol{d}}_1}\left( k \right)}&{{\mathit{\boldsymbol{e}}^{\rm{T}}}\left( k \right)} \end{array}} \right]}^{\rm{T}}} + }\\ {{\gamma ^2}\mathit{\boldsymbol{d}}_1^{\rm{T}}\left( k \right)\mathit{\boldsymbol{d}}_1^{\rm{T}}\left( k \right) - {\mathit{\boldsymbol{y}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{y}}\left( k \right)} \end{array} $ | (20) |
式中:χ = ϕ T(k) Pϕ (k)- P + H T H + F T R T RF,
| $ \mathit{\boldsymbol{N}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\chi }}&{{\mathit{\boldsymbol{\varphi }}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{B}}_d}}&{{\mathit{\boldsymbol{\varphi }}^{\rm{T}}}\mathit{\boldsymbol{PKH}}}\\ {\mathit{\boldsymbol{B}}_d^{\rm{T}}\mathit{\boldsymbol{P\varphi }}}&{\mathit{\boldsymbol{B}}_d^{\rm{T}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{B}}_d} - {\gamma ^2}\mathit{\boldsymbol{I}}}&{\mathit{\boldsymbol{B}}_d^{\rm{T}}\mathit{\boldsymbol{PKH}}}\\ {{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{P\varphi }}}&{{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{B}}_d}}&{{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{PKH}}} \end{array}} \right]。$ |
对于一个稳定的系统来说,有
| $ \sum\limits_{k = 0}^\infty {\left[ {\mathit{\boldsymbol{V}}\left( {\mathit{\boldsymbol{\hat x}}\left( {k + 1} \right)} \right) - \mathit{\boldsymbol{V}}\left( {\mathit{\boldsymbol{\hat x}}\left( k \right)} \right)} \right]} = - {{\mathit{\boldsymbol{\hat x}}}^{\rm{T}}}\left( 0 \right)\mathit{\boldsymbol{P\hat x}}\left( 0 \right) $ | (21) |
将H2性能指标改写,并与上式相加,可得:
| $ \begin{array}{*{20}{c}} {\sum\limits_{k = 0}^\infty {\left[ {{\mathit{\boldsymbol{y}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{y}}\left( k \right)} \right]} = \sum\limits_{k = 0}^\infty {{\gamma ^2}\mathit{\boldsymbol{d}}_1^{\rm{T}}\left( k \right){\mathit{\boldsymbol{d}}_1}\left( k \right)} + }\\ {{{\mathit{\boldsymbol{\hat x}}}^{\rm{T}}}\left( 0 \right)\mathit{\boldsymbol{P\hat x}}\left( 0 \right) + \sum\limits_{k = 0}^\infty {\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat x}}}^{\rm{T}}}\left( k \right)}&{\mathit{\boldsymbol{d}}_1^{\rm{T}}\left( k \right)}&{{\mathit{\boldsymbol{e}}^{\rm{T}}}\left( k \right)} \end{array}} \right]} \cdot }\\ {\mathit{\boldsymbol{N}}\left( k \right){{\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat x}}}^{\rm{T}}}\left( k \right)}&{\mathit{\boldsymbol{d}}_1^{\rm{T}}\left( k \right)}&{{\mathit{\boldsymbol{e}}^{\rm{T}}}\left( k \right)} \end{array}} \right]}^{\rm{T}}}} \end{array} $ | (22) |
由于H∞性能指标是扰动补偿估计误差d1(k)到输出y (k)的传递函数,可设当
| $ \sum\limits_{k = 0}^\infty {\left( {{\mathit{\boldsymbol{y}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{y}}\left( k \right) - {\gamma ^2}\mathit{\boldsymbol{d}}_1^{\rm{T}}\left( k \right){d_1}\left( k \right)} \right)} \le 0 $ | (23) |
即若要式(23)满足,由式(22)可知,则需N(k)≤0成立。换言之,若该条件满足,则式(23)成立,那么式(19)可满足。
由于N(k)≤0,基于Schur补理论,可得:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_1}}&{\mathit{\boldsymbol{M}}_2^{\rm{T}}}\\ {{\mathit{\boldsymbol{M}}_2}}&{{\mathit{\boldsymbol{M}}_3}} \end{array}} \right] \ge 0 $ | (24) |
式中:
| $ \begin{array}{l} {\mathit{\boldsymbol{M}}_1} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{Q}}&0&0&{\mathit{\boldsymbol{QA}}_i^{\rm{T}} + {\mathit{\boldsymbol{Y}}^{\rm{T}}}\mathit{\boldsymbol{B}}_i^{\rm{T}}}\\ 0&{{\gamma ^2}{\alpha ^2}\mathit{\boldsymbol{I}}}&0&{{\alpha ^2}\mathit{\boldsymbol{B}}_d^{\rm{T}}}\\ 0&0&0&{{\alpha ^2}{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{A}}_i}\mathit{\boldsymbol{Q}} + {\mathit{\boldsymbol{B}}_i}\mathit{\boldsymbol{Y}}}&{{\alpha ^2}{\mathit{\boldsymbol{B}}_d}}&{{\alpha ^2}\mathit{\boldsymbol{KH}}}&\mathit{\boldsymbol{Q}} \end{array}} \right],\\ \mathit{\boldsymbol{Q}} = {\alpha ^2}{\mathit{\boldsymbol{P}}^{ - 1}},\mathit{\boldsymbol{F}} = \mathit{\boldsymbol{Y}}{\mathit{\boldsymbol{Q}}^{ - 1}},i = 1,2,3。\end{array} $ |
在满足式(24)的情况下,由等式(22)可知:
| $ \sum\limits_{k = 0}^\infty {\left[ {{\mathit{\boldsymbol{y}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{y}}\left( k \right)} \right]} \le {{\mathit{\boldsymbol{\hat x}}}^{\rm{T}}}\left( 0 \right)\mathit{\boldsymbol{P\hat x}}\left( 0 \right) + {\mathit{\boldsymbol{\gamma }}^2}{{\mathit{\boldsymbol{\bar \omega }}}^2} $ |
如果H2性能指标满足,则有:
| $ \sum\limits_{k = 0}^\infty {\left[ {{\mathit{\boldsymbol{y}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{y}}\left( k \right)} \right]} \le {{\mathit{\boldsymbol{\hat x}}}^{\rm{T}}}\left( 0 \right)\mathit{\boldsymbol{P\hat x}}\left( 0 \right) + {\mathit{\boldsymbol{\gamma }}^2}{{\mathit{\boldsymbol{\bar \omega }}}^2} \le {\alpha ^2} $ | (25) |
根据Schur补理论,式(25)可转化为:
| $ \left[ {\begin{array}{*{20}{c}} 1&{{{\mathit{\boldsymbol{\hat x}}}^{\rm{T}}}\left( 0 \right)}&{{{\left( {{\gamma ^2}{{\mathit{\boldsymbol{\bar \omega }}}^2}} \right)}^{\rm{T}}}}\\ {\mathit{\boldsymbol{\hat x}}\left( 0 \right)}&\mathit{\boldsymbol{Q}}&0\\ {{\gamma ^2}{{\mathit{\boldsymbol{\bar \omega }}}^2}}&0&{{\gamma ^2}{\alpha ^2}{{\mathit{\boldsymbol{\bar \omega }}}^2}} \end{array}} \right] \ge 0 $ | (26) |
压缩不变集约束:从(20)可看出,只满足式(24),并不能保证系统的Lyapunov函数单调下降。因此,提出压缩约束不变集约束,保证
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat x}}{{\left( {k + 1} \right)}^{\rm{T}}}{\mathit{\boldsymbol{Q}}^{ - 1}}\left( {k + 1} \right)\mathit{\boldsymbol{\hat x}}\left( {k + 1} \right) \le }\\ {\mathit{\boldsymbol{\hat x}}{{\left( k \right)}^{\rm{T}}}{\mathit{\boldsymbol{Q}}^{ - 1}}\left( k \right)\mathit{\boldsymbol{\hat x}}\left( k \right) \le 1} \end{array} $ |
因此,不变集约束为:
| $ \mathit{\boldsymbol{Q}}\left( {k + 1} \right) \le \mathit{\boldsymbol{Q}}\left( k \right) $ | (27) |
输入约束:舵角作为控制输入是有幅值约束的,考虑前一节设计的前馈干扰补偿ud,新的预测控制输入约束为:
| $ \left\{ \begin{array}{l} {u_{n\max }} = {u_{\max }} - \left| {{u_d}} \right|\\ \left\| {{\mathit{\boldsymbol{u}}_{{\rm{mpc}}}}\left( {k + i} \right)} \right\|_2^2 \le u_{n\max }^2,i \ge 0 \end{array} \right. $ | (28) |
选取反馈控制律umpc= Fx = YQ -1 x,并采用Schur补理论,可得:
| $ \left[ {\begin{array}{*{20}{c}} {u_{n\max }^2}&\mathit{\boldsymbol{Y}}\\ {{\mathit{\boldsymbol{Y}}^T}}&\mathit{\boldsymbol{Q}} \end{array}} \right] \ge 0 $ | (29) |
横摇角约束:欠驱动船舶在受到强烈的外界干扰的情况下可能会出现大幅度的摇荡运动,而过大的横摇角会影响系统的性能和稳定性,因此需要考虑横摇角约束,即:
| $ \left\| {\phi \left( {k + i} \right)} \right\|_2^2 \le \phi _{\max }^2,i \ge 1 $ | (30) |
式中:ϕ(k+i)= H1 x (k+i);H1=[0 0 0 0 1]。经过计算并根据Schur补理论,上式可改写为:
| $ \left[ {\begin{array}{*{20}{c}} {\frac{\mathit{\boldsymbol{Q}}}{{\left( {1 + {{\mathit{\boldsymbol{\bar \omega }}}^2} + {\xi ^2}} \right)}}}&{\mathit{\boldsymbol{QA}}_i^{\rm{T}}\mathit{\boldsymbol{H}}_1^{\rm{T}} + {\mathit{\boldsymbol{Y}}^{\rm{T}}}\mathit{\boldsymbol{B}}_i^{\rm{T}}\mathit{\boldsymbol{H}}_1^{\rm{T}}}\\ {{\mathit{\boldsymbol{H}}_1}{\mathit{\boldsymbol{A}}_i}\mathit{\boldsymbol{Q}} + {\mathit{\boldsymbol{H}}_1}{\mathit{\boldsymbol{B}}_i}\mathit{\boldsymbol{Y}}}&\begin{array}{l} \left( {\mathit{\boldsymbol{x}}_5^2\mathit{\boldsymbol{I}} - \left( {1 + {{\mathit{\boldsymbol{\bar \omega }}}^2} + {\xi ^2}} \right)} \right.\\ {\mathit{\boldsymbol{H}}_1}{\mathit{\boldsymbol{B}}_d}\mathit{\boldsymbol{B}}_d^{\rm{T}}\mathit{\boldsymbol{H}}_1^{\rm{T}} + \\ \left. {{\mathit{\boldsymbol{H}}_1}\mathit{\boldsymbol{KHQ}}{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{H}}_1^{\rm{T}}} \right) \end{array} \end{array}} \right] \ge 0 $ | (31) |
式中:Q=α2P-1;F = YQ-1;i=1, 2, 3。注释:如果Bd= K =0,即不考虑系统扰动、状态估测误差,则式(31)可转化为文献[13]中无干扰时的结论。
定理1:基于LMI(15)、(24)、(26)、(27)、(29)、(31)约束的控制律u = umpc+ ud保证了闭环系统(16)鲁棒渐近稳定。
证明:LMI(15)是干扰补偿控制,LMI(24)、(27)约束保证了V(x (k))的单调递减性,LMI(26)是性能指标约束,LMI(29)保证了满足输入约束,LMI(31)是横摇角约束。假设该定理在k时刻可行,设最优解为{ Q0, …, QN-1, Y0, …, F0, …, FN-1, α*(k)}。由LMI(24)、(27)可知,在k+1时刻则存在可行解:{ Q1, …, QN-1, QN-1, Y1, …, YN-1, YN-1, F1, …, FN-1, FN-1, α*(k)},且存在α*(k)=α(k+1)。由优化原理可知,α*(k)≥α(k+1)≥α*(k+1)。
另外,由式(20)、(24)可知,当系统无扰动时,没有压缩不变集约束(27)也可保证系统Lyapunov函数的单调下降。因此,闭环系统(16)是鲁棒渐近稳定的。
4 仿真实验为验证算法有效性,对一船模进行仿真实验。欠驱动水面船舶模型具体参数A1、B1,A2、B2和A3、B3详见文献[8]。速度u=7 m/s。控制周期t=0.5 s。控制器参数Bd=0.02[0 0 1 0 0]T,C = I5×5,R=0.02,γ=2。船舶的初值状态为(ψ, v, r, p, ϕ)=(-20, 0, 0, 0, 0),横摇角要求小于5°,控制舵角
| $ S\left( \omega \right) = \frac{{172.75H_{1/3}^2}}{{{T^4}{\omega ^5}}}\exp \left( { - \frac{{691}}{{{T^4}{\omega ^4}}}} \right) $ |
式中:Η1/3为有义波高;T和ω分别为波浪平均周期和角速度;S表示能量密度。
1) 加入无量纲干扰
|
Download:
|
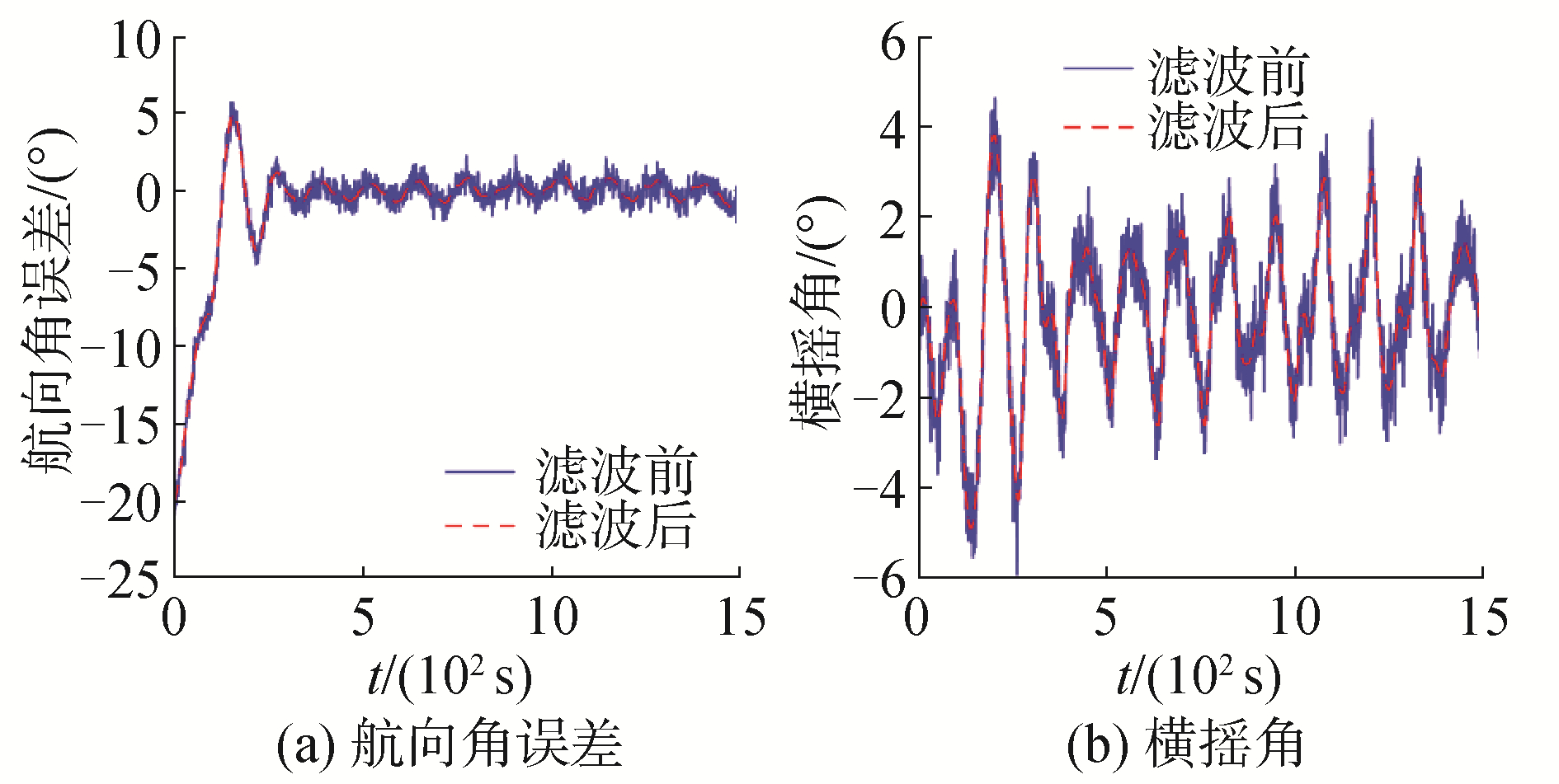
| 图 2 滤波前后的航向角偏差和横摇角 Fig. 2 Heading angle and roll angle with/without filtering | |

|
Download:
|
| 图 3 预测控制与干扰补偿鲁棒预测控制对比 Fig. 3 Comparisons of normal predictive control and robust predictive control with disturbance compensation | |
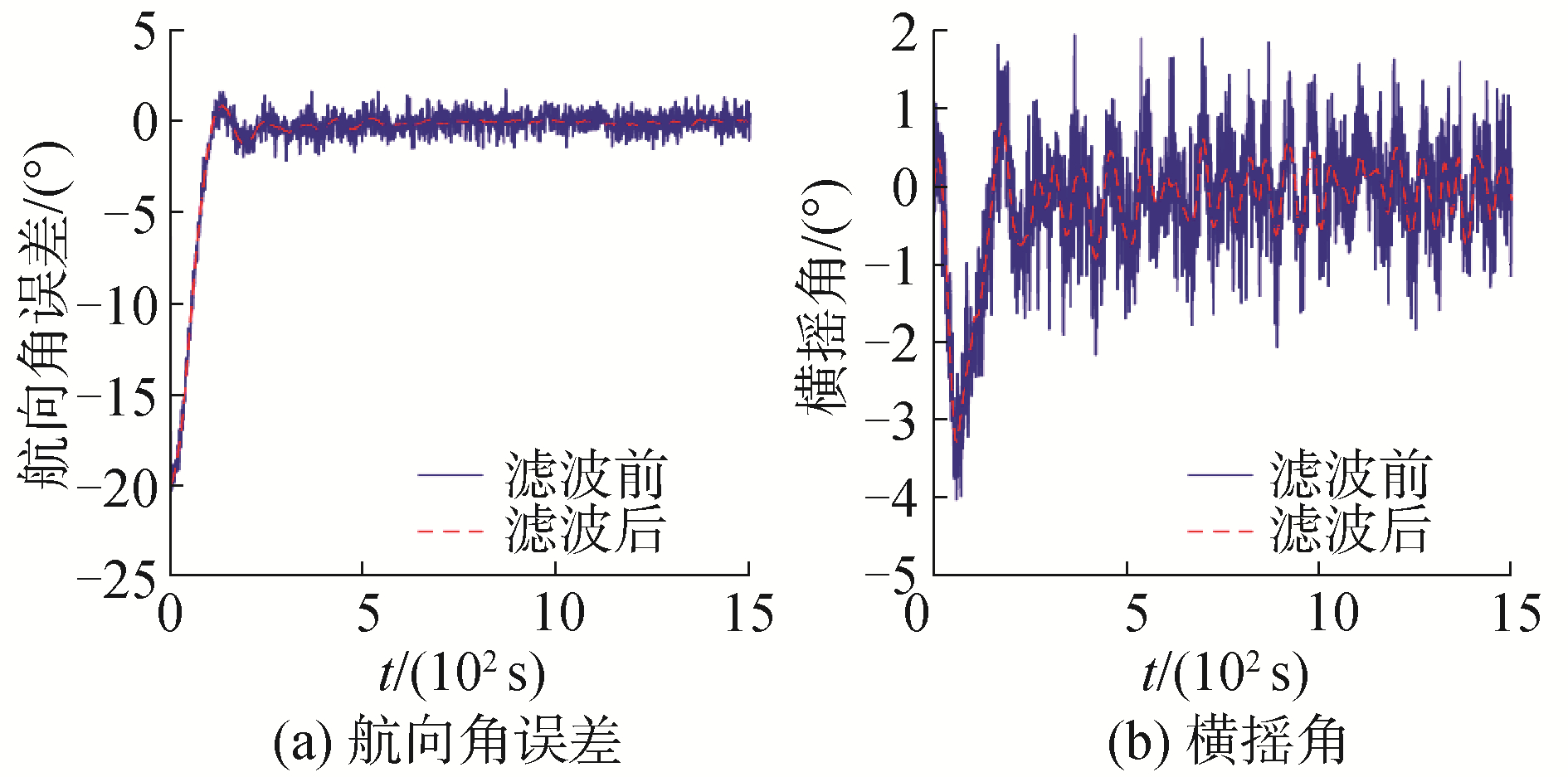
图 2、图 4是有无自适应卡尔曼滤波的航向角偏差及横摇角曲线,表明在不同干扰情况下,自适应卡尔曼滤波都能较好地滤除量测噪声。
|
Download:
|
| 图 4 滤波前后的航向角偏差和横摇角 Fig. 4 Heading angle and roll angle with/without filtering | |
图 3、图 5则是在不同干扰存在的条件下,比较了采用预测控制和采用干扰补偿的鲁棒预测控制这两种方法后的系统状态值。图 3、图 5(a)为航向角偏差对比曲线,可看出采用干扰补偿后的鲁棒预测控制收敛速度较快,偏差收敛范围较小。图 3、图 5(b)为横摇角对比曲线,从中可看出,采用干扰补偿后得出的横摇角收敛范围明显较小,并且满足状态约束;未采用干扰补偿的横摇角虽然也能收敛,但范围较大,收敛较慢。图 3、图 5(c)为控制舵角的对比曲线,可看出采用干扰补偿后舵角曲线较为光滑,波动范围也较小,并且满足输入约束;未采用干扰补偿的舵角值虽然也能够满足输入约束的要求,但是收敛较慢,变化波动较为剧烈,曲线不光滑,影响舵的使用寿命。图 3、图 5(d)为干扰估计值与实际值的对比曲线,从中可看出估计值在实际值处小范围波动,能够较好地估计出实际值。

|
Download:
|
| 图 5 预测控制与干扰补偿鲁棒预测控制对比 Fig. 5 Comparisons of normal predictive control and robust predictive control with disturbance compensation | |
通过仿真研究,表明基于扩展状态的自适应卡尔曼滤波和鲁棒预测控制的控制算法能较好地估计出系统的干扰值,干扰补偿后的控制系统能更快地实现收敛,使得横摇角、舵角振幅变小,满足输入约束,并且保证横摇角在更安全的约束范围内,从而对扰动有着更好的抑制作用。
5 结论1) 采用扩展状态的卡尔曼滤波和鲁棒预测控制所设计的控制方案通过仿真展现出较好的性能,表明其能够较好地完成具有横摇角约束的直线航迹跟踪任务;
2) 针对欠驱动水面船舶存在时变干扰、量测噪声以及部分运动状态可测的问题,采用扩展状态的卡尔曼滤波同时估计出系统状态和干扰,并对输入进行干扰补偿;在性能指标和控制器设计中使用观测状态,并结合鲁棒预测控制设计方法来有效抑制集总干扰。
所设计控制方法由于LMI计算量大等问题仍局限于仿真,下一步的工作主要集中如何将其运用于实际船模试验中,并将该方案与曲线航迹跟踪控制相结合。
| [1] |
LEFEBER E, PETTERSEN K Y, NIJMEIJER H. Tracking control of an underactuated ship[J]. IEEE transactions on control systems technology, 2003, 11(1): 52-61. DOI:10.1109/TCST.2002.806465 (  0) 0)
|
| [2] |
郭晨, 汪洋, 孙富春, 等. 欠驱动水面船舶运动控制研究综述[J]. 控制与决策, 2009, 24(3): 321-329. GUO Chen, WANG Yang, SUN Fuchun, et al. Survey for motion control of underactuated surface vessels[J]. Control and decision, 2009, 24(3): 321-329. DOI:10.3321/j.issn:1001-0920.2009.03.001 (  0) 0)
|
| [3] |
张文颖, 彭秀艳. 基于T-S模糊模型的船舶舵减横摇H∞状态反馈控制[J]. 船舶工程, 2013, 35(5): 51-54. ZHANG Wenying, PENG Xiuyan. H∞ state-feedback control for ship rudder roll damping system based on T-S fuzzy model[J]. Ship engineering, 2013, 35(5): 51-54. (  0) 0)
|
| [4] |
ALARÇÏN F. Internal model control using neural network for ship roll stabilization[J]. Journal of marine science and technology, 2007, 15(2): 141-147. (  0) 0)
|
| [5] |
ZHANG Jun, SUN Tairen, LIU Zhilin. Robust model predictive control for path-following of underactuated surface vessels with roll constraints[J]. Ocean engineering, 2017, 143: 125-132. DOI:10.1016/j.oceaneng.2017.07.057 (  0) 0)
|
| [6] |
ZHANG Jun, SUN Tairen, ZHAO Dean, et al. Robust model predictive control of the automatic operation boats for aquaculture[J]. Computers and electronics in agriculture, 2017, 142: 118-125. DOI:10.1016/j.compag.2017.08.016 (  0) 0)
|
| [7] |
MAYNE D Q, RAWLINGS J B, RAO C V, et al. Constrained model predictive control:stability and optimality[J]. Automatica, 2000, 36(6): 789-814. DOI:10.1016/S0005-1098(99)00214-9 (  0) 0)
|
| [8] |
LI Zhen, SUN Jing, OH S.Path following for marine surface vessels with rudder and roll constraints: An MPC approach[C]//Proceedings of 2009 American Control Conference.St.Louis, MO, USA, 2009: 3611-3616. https://www.researchgate.net/publication/224561016_Path_Following_for_Marine_Surface_Vessels_with_Rudder_and_Roll_Constraints_an_MPC_Approach
(  0) 0)
|
| [9] |
LI Zhen, SUN Jing. Disturbance compensating model predictive control with application to ship heading control[J]. IEEE transactions on control systems technology, 2012, 20(1): 257-265. (  0) 0)
|
| [10] |
LI Zhen.Path following with roll constraints for marine surface vessels in wave fields[D].Michigan: University of Michigan, 2009. https://www.researchgate.net/publication/30864428_Path_Following_with_Roll_Constraints_for_Marine_Surface_Vessels_in_Wave_Fields
(  0) 0)
|
| [11] |
于洋. 卡尔曼滤波器在船舶航迹跟踪中的应用[J]. 江苏船舶, 2005, 22(2): 31-33, 39. YU Yang. The application of Calman's wave filter in the shipping flight tracker[J]. Jiangsu ship, 2005, 22(2): 31-33, 39. DOI:10.3969/j.issn.1001-5388.2005.02.011 (  0) 0)
|
| [12] |
FOSSEN T I. Marine control systems[M]. Trondheim, Norway: Marine Cybernetics, 2002.
(  0) 0)
|
| [13] |
FOSSEN T I. Guidance and control of ocean vehicles[M]. New York: John Wiley & Sons, 1994.
(  0) 0)
|
| [14] |
OLALLA C, LEYVA R, EL AROUDI A, et al. Robust LQR control for PWM converters:an LMI approach[J]. IEEE transactions on industrial electronics, 2009, 56(7): 2548-2558. DOI:10.1109/TIE.2009.2017556 (  0) 0)
|
| [15] |
宋文尧, 张牙. 卡尔曼滤波[M]. 北京: 科学出版社, 1988.
(  0) 0)
|
| [16] |
黄鹤, 李德伟, 席裕庚. 基于多步控制策略的混合H2/H∞鲁棒预测控制器设计[J]. 自动化学报, 2012, 38(6): 944-950. HUANG He, LI Dewei, XI Yugeng. On design of mixed H2/H∞ RMPC based on multi-step control strategy[J]. Acta automatica sinica, 2012, 38(6): 944-950. (  0) 0)
|
| [17] |
ORUKPE P E, JAIMOUKHA I M, EL-ZOBAIDI H M H.Model predictive control based on mixed H2/H∞ control approach[C]//Proceedings of 2007 American Control Conference.New York, USA, 2007: 6417-6150. https://www.researchgate.net/publication/224718402_Model_Predictive_Control_based_on_Mixed_H2H_Control_Approach
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


