2. 中国工程物理研究院 化工材料研究所, 四川 绵阳 621000
2. Institute of Chemical Materials, China Academy of Engineering Physics, Mianyang 621000, China
随着机器人越来越多地应用于非结构环境下的接触操作任务,如柔顺装配、人机交互等,由于任务复杂,接触环境多变且不可预测,如何让机器人安全高效快速地执行新任务,精确地控制不同环境下的接触力,是机器人面临的新挑战。力控制特性决定于机器人的惯性、刚度和阻尼参数,为了得到良好的控制性能,需要对控制器设计及其参数有深入的认识,并需要根据任务特性手动调整控制参数[1]。特别是对于复杂任务,由于环境条件通常包含一些非线性和时变的因素,固定参数的阻抗控制方法很难实现目标任务。若阻抗控制参数能根据任务和环境的变化进行动态规划调整,则控制性能明显好于阻抗控制参数固定的情况[2]。Jesse等[3]研究了类人两足行走中的阻抗变化规律,发现变阻抗控制可以提升步态质量并能减少能量损失。基于任务改变系统阻抗特性的能力是生物力学系统具有鲁棒性和敏捷性等良好性能的关键因素之一[4-5]。所以,变阻抗控制已经成为现代机器人交互操作的一种基本能力,是安全完成复杂操作任务的关键。
强化学习算法只需要一个回报函数,即可通过试错找到高回报的策略,而不需要被控系统的模型或环境的先验知识,为机器人实现复杂的自主柔顺控制提供了新的途经。最近,很多学者研究了使用强化学习算法学习参数调整策略,动态地调整机器人的阻抗特性[6-8]。Du等[9]提出一种基于模糊强化学习的变导纳控制方法,通过动态调整导纳控制器中的变虚拟阻尼项,增强了机器人位置控制精度并降低了所需的能量。Izawa等[10]提出一种无模型的变阻抗控制算法,使用前向神经网络作为评价器,使机器人具备了类人的变阻抗控制能力。Mitrovic等[11]提出一种用于拮抗系统的变阻抗控制结构,使用监督学习算法学习系统的动力学与随机特性,扩展了随机最优控制理论,实现了系统精度、能耗和阻抗的权衡。Buchli等[4, 6, 12]提出的一种无模型的强化学习方法——PI2,通过路径积分同时调整参考轨迹和阻抗参数进行变阻抗控制,已经成功用于多种高维控制应用,需要1 000多次交互才能得到理想的控制策略。Florian等[13]提出一种C-PI2算法,考虑了多自由度的协同效应,与之前的学习变阻抗控制算法相比,学习速度提高了很多,仅需120次迭代过程即可得到稳定的控制策略。
虽然目前的学习变阻抗控制方法能很好地完成任务,但是,仍需要成百上千次的学习迭代才能得到满意的控制策略,这对于力敏感型控制任务而言是不切实际的。因为大量的物理交互尝试可能会对机器人或工件造成损坏,而且大量的采样数据费时且昂贵。为了提高学习变阻抗控制方法的学习效率,使机器人能在非结构环境中快速地自主学习完成力控制任务,本文提出一种高效的学习变阻抗控制方法。该方法使用高斯过程模型作为系统的变换动力学模型,以贝叶斯的方式概率化地推理预测并传递状态的不确定性,然后使用基于模型的强化学习算法搜索最优控制策略。为了使阻抗调整策略具有类似人的仿生特性,在成本函数中加入了能量损失项,实现能量和误差的权衡。
1 变阻抗控制人类经过多年的经验学习,具备了完善的变阻抗调节能力,能够通过动态地调整自身的骨骼肌肉系统调节阻抗特性控制接触力,可在各种环境下灵活地完成多种接触操作任务。人类针对特定任务,通过调节阻抗特性很好地整合了高刚性与柔顺性的优点,学习特定的控制策略:在需要精确跟踪或抑制未知扰动时,通过收缩肌肉群增大手臂的刚性;在需要安全地进行接触交互时,通过放松肌肉群使手臂具有柔顺性。如果把人类的这种阻抗调节策略应用到机器人中,则机器人可以像人类一样完成多种接触操作任务。
在机器人中,为获得较好的位置跟踪能力,通常使用高增益控制算法使机器人具有高刚性,但这并不适合需要力控制的交互任务。阻抗控制[14]为约束运动和非约束运动提供了一种统一的控制架构,已广泛应用于机器人的交互控制中。通过建立末端执行器或关节的虚拟质量-弹簧-阻尼模型,动态调整末端的期望轨迹,间接地控制接触力。由于阻抗控制参数的选择高度依赖任务,对于环境特性已知的结构化环境中的任务,可以指定合适的固定的阻抗参数,但是在非结构化环境中很难以固定的阻抗参数完成复杂的操作任务,若机器人能在任务中动态地调整阻抗参数,则可以得到更好的控制性能。而且,变阻抗控制的另一个优点是,通过主动控制阻抗参数,机器人可以很好地保证安全性。
机器人阻抗控制的理想模型为二阶阻抗模型:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{F}} - {\mathit{\boldsymbol{F}}_d} = {\mathit{\boldsymbol{M}}_d}\left( t \right)\left( {\mathit{\boldsymbol{\ddot X}} - {{\mathit{\boldsymbol{\ddot X}}}_d}} \right) + {\mathit{\boldsymbol{B}}_d}\left( t \right)\left( {\mathit{\boldsymbol{\dot X}} - {{\mathit{\boldsymbol{\dot X}}}_d}} \right) + }\\ {{\mathit{\boldsymbol{K}}_d}\left( t \right)\left( {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}_d}} \right)} \end{array} $ | (1) |
式中:Md(t)、Bd(t)、Kd(t)分别为阻抗模型中时变的目标惯性矩阵、目标阻尼矩阵与目标刚度矩阵;
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\ddot X}}}_d} = \mathit{\boldsymbol{\ddot X}} + \mathit{\boldsymbol{M}}_d^{ - 1}\left[ {{\mathit{\boldsymbol{B}}_d}\left( {\mathit{\boldsymbol{\dot X}} - {{\mathit{\boldsymbol{\dot X}}}_d}} \right) + {\mathit{\boldsymbol{K}}_d}\left( {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}_d}} \right) - } \right.}\\ {\left. {\left( {\mathit{\boldsymbol{F}} - {\mathit{\boldsymbol{F}}_d}} \right)} \right]} \end{array} $ | (2) |
由雅克比矩阵定义知:
| $ {{\mathit{\boldsymbol{\dot X}}}_d} = \mathit{\boldsymbol{J}} \cdot {{\mathit{\boldsymbol{\dot q}}}_d} $ | (3) |
| $ {{\mathit{\boldsymbol{\ddot X}}}_d} = \mathit{\boldsymbol{\dot J}} \cdot {{\mathit{\boldsymbol{\dot q}}}_d} + \mathit{\boldsymbol{J}} \cdot {{\mathit{\boldsymbol{\ddot q}}}_d} $ | (4) |
式中:J为雅克比矩阵;
| $ {{\mathit{\boldsymbol{\ddot q}}}_d} = {\mathit{\boldsymbol{J}}^{ - 1}}\left( {{{\mathit{\boldsymbol{\ddot X}}}_d} - \mathit{\boldsymbol{\dot J}} \cdot {{\mathit{\boldsymbol{\dot q}}}_d}} \right) $ | (5) |
然后,使用机器人的逆动力学控制即可计算期望关节力矩,在此不再赘述。
变阻抗控制就是通过在线不断调整阻抗参数Md(t)、Bd(t)、Kd(t),实现接触力的最优控制。为了简化计算,取目标惯性矩阵为常量Md(t)= I,所以在本文中执行力控制任务时,变阻抗控制器需要调节的参数有目标刚度Kd(t)与阻尼参数Bd(t)。
2 基于强化学习的学习变阻抗控制强化学习可以建模为有限范围的马尔可夫决策过程,只需给定一个回报函数,即可通过试错找到高回报的策略,而不需要被控系统和环境的模型或先验知识。强化学习算法大体上可分为基于模型的和无模型的两种类型,其中无模型算法不需要建立变换动力学模型,直接搜索最优策略参数,但是对于每个采样轨迹都需要与机器人实际交互,这非常耗时;基于模型的算法会明确地建立系统的变换动力学模型,然后用此模型进行内部仿真和预测系统的行为,最后通过评估与改进得到最优策略。基于模型的算法采样较少但是计算量比较密集,比无模型的方法效率更高[15]。
学习变阻抗控制不需要物理环境阻抗参数的具体值,使用强化学习算法学习得到基于任务的最优阻抗控制策略,根据状态自动调整阻抗参数,实现力跟踪控制,是一种理想的柔顺控制方式。本文为了提高学习效率,减少学习交互次数,使用基于模型的强化学习算法——概率推理学习控制算法(PILCO)学习变阻抗控制策略。PILCO[16]是由Deisenroth提出的一种基于模型的策略搜索强化学习算法,其特点是通过明确考虑动态模型中的不确定性,减少了模型偏差带来的负面影响,可以准确的预测策略的性能。这种算法可以从数据中提取更多有效的信息,能明显加速学习过程,减少交互时间,在连续的状态——动作空间具有目前最好的学习效率。目前,这种算法已经成功应用于倒立摆[16]、独轮车[17]等多种复杂的机器人系统中。
如图 1所示为基于强化学习的学习变阻抗控制方法结构图,根据采样数据建立系统的GP模型,然后根据此模型使用学习算法学习阻抗控制策略π。阻抗控制策略根据当前状态——末端接触力与末端位置——调整阻抗控制参数u=[Kd(t) Bd(t)],然后传递给变阻抗控制器,用于力控制。变阻抗控制器根据轨迹误差Xe和力跟踪误差Fe计算期望的末端加速度

|
Download:
|
| 图 1 基于强化学习的学习变阻抗控制方法结构图 Fig. 1 Scheme of the learning variable impedance control based on reinforcement learning algorithm | |
定义变阻抗控制策略为π: x | → u =π(x, θ),其中x =[X F]∈ R D为机械臂的可观测状态,策略输出u =[Kd(t) Bd(t)]∈ RF为阻抗控制器的目标刚度Kd(t)与阻尼系数Bd(t),θ为需要学习的控制策略参数。这里,选用GP控制器作为控制策略π:
| $ {\pi _t} = \pi \left( {{\mathit{\boldsymbol{x}}_t},\mathit{\boldsymbol{\theta }}} \right) = \sum\limits_{i = 1}^n {{\beta _{\pi ,i}}k\left( {{\mathit{\boldsymbol{x}}_\pi },{\mathit{\boldsymbol{x}}_t}} \right)} = \beta _\pi ^{\rm{T}}\mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{X}}_\pi },{\mathit{\boldsymbol{x}}_t}} \right) $ | (6) |
| $ {\mathit{\boldsymbol{\beta }}_\pi } = {\left( {\mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{X}}_\pi },{\mathit{\boldsymbol{X}}_\pi }} \right) + \sigma _{\varepsilon ,\pi }^2\mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{y}}_\pi } $ | (7) |
| $ k\left( {{\mathit{\boldsymbol{x}}_\pi },{\mathit{\boldsymbol{x}}_t}} \right) = \sigma _{f,\pi }^2\exp \left( { - \frac{1}{2}{{\left( {{\mathit{\boldsymbol{x}}_{\pi ,i}} - {\mathit{\boldsymbol{x}}_t}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{ - 1}}\left( {{\mathit{\boldsymbol{x}}_{\pi ,i}} - {\mathit{\boldsymbol{x}}_t}} \right)} \right) $ | (8) |
式中:n为GP控制器的个数; Xπ为训练输入; yπ为训练目标,初始化为接近零的随机值; Λ =diag(l12, l22, …, lD2)为每个状态的特征长度; σf, π2为信号方差,此处σf, π2=1,这样在功能上与RBF网络类似[16]; σε, π2为测量噪声方差。所以,GP控制策略π的超参数为θ={ Xπ, yπ, l1, l2, …, lD, σf, π2, σε, π2}。
在实际控制系统中,必须考虑控制参数u的物理边界,本文选用有界可微的梯形饱和函数,把控制变量u限制在区间[umin, umin+umax]内:
| $ S\left( {{\pi _t}} \right) = {u_{\min }} + {u_{\max }} + {u_{\max }}\frac{{9\sin {\pi _t} + \sin \left( {3{\pi _t}} \right)}}{8} $ | (9) |
阻抗控制策略的学习过程主要包括5个步骤:
1) 根据实际采样数据,建立系统的概率化GP动态模型,作为系统的变换动力学模型;
2) 使用学习得到的GP动态模型对状态进行长期推理预测p(x1|π), …, p(xT|π),并评估时间T内的期望总成本Jπ(θ);
3) 计算成本相对于策略参数的梯度信息dJπ(θ)/dθ,使用基于梯度的策略搜索算法寻找最优策略π*←π(θ);
4) 计算变阻抗控制器的阻抗控制参数,然后应用于系统进行力跟踪控制,并采集新的数据;
5) 重复步骤1)~4)直到得到满意的力跟踪效果,得到满意的控制策略。
2.2 高斯过程模型高斯过程是一种有效的回归方法[18],GP模型是一种非参数化的概率模型,用均值函数m(·)与半正定的协方差函数k(·, ·)表示。设描述系统的动力学方程为:
| $ {\mathit{\boldsymbol{x}}_t} = f\left( {{\mathit{\boldsymbol{x}}_{t - 1}},{\mathit{\boldsymbol{u}}_{t - 1}}} \right) $ | (10) |
| $ {\mathit{\boldsymbol{y}}_t} = {\mathit{\boldsymbol{x}}_t} + {\mathit{\boldsymbol{\varepsilon }}_t} $ | (11) |
式中:x ∈ RD为可观测状态; u ∈ RF为控制输入; y ∈ RE为训练目标; f为未知的变换函数; ε ~(0, σε2)为独立同分布的系统噪声。为了在预测及规划中考虑模型的不确定性,避免学习模型的确定性等价假设,根据获得的采样数据,使用高斯过程推测潜在函数f的后验分布,描述所有可能的动态模型。本文为了计算简便,选取先验均值为m≡0,并选取平方指数核函数:
| $ f\left( \mathit{\boldsymbol{x}} \right) \sim {\rm{GP}}\left( {m\left( \mathit{\boldsymbol{x}} \right),k\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{x'}}} \right)} \right) $ | (12) |
| $ k\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{x'}}} \right) = {\alpha ^2}\exp \left( { - \frac{1}{2}{{\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{x'}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{ - 1}}\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{x'}}} \right)} \right) + \sigma _\varepsilon ^2\mathit{\boldsymbol{I}} $ | (13) |
式中,α2为潜在函数f的信号方差;Λ =diag([l12, l22, …, lD2]);li是每个输入维度的特征长度。给定N组训练输入X =[x1 x2 … xn]及相应的训练目标y =[y1 y2 … yn]T,使用证据最大化算法即可学习到GP的超参数[Λ α2 σε2]。
给定确定性的测试输入x*,函数值f*=f(x*)的后验预测分布p(f*| x*)服从高斯分布:
| $ p\left( {{\mathit{\boldsymbol{f}}_ * }\left| {{\mathit{\boldsymbol{x}}_ * }} \right.} \right) \sim \left( {{\mathit{\boldsymbol{\mu }}_ * },{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_ * }} \right) $ | (14) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\mu }}_ * } = m\left( {{\mathit{\boldsymbol{x}}_ * }} \right) + k\left( {{\mathit{\boldsymbol{x}}_ * },\mathit{\boldsymbol{X}}} \right){{\left( {\mathit{\boldsymbol{K}} + \sigma _\varepsilon ^2\mathit{\boldsymbol{I}}} \right)}^{ - 1}} \cdot }\\ {\left( {\mathit{\boldsymbol{y}} - m\left( \mathit{\boldsymbol{X}} \right)} \right) = m\left( {{\mathit{\boldsymbol{x}}_ * }} \right) + k\left( {{\mathit{\boldsymbol{x}}_ * },\mathit{\boldsymbol{X}}} \right)\beta } \end{array} $ | (15) |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_ * } = k\left( {{\mathit{\boldsymbol{x}}_ * },{\mathit{\boldsymbol{x}}_ * }} \right) - k\left( {{\mathit{\boldsymbol{x}}_ * },\mathit{\boldsymbol{X}}} \right){\left( {\mathit{\boldsymbol{K}} + \sigma _\varepsilon ^2\mathit{\boldsymbol{I}}} \right)^{ - 1}}k\left( {\mathit{\boldsymbol{X}},{\mathit{\boldsymbol{x}}_ * }} \right) $ | (16) |
式中β=(K +σε2 I)-1(y -m(X)),K =k(X, X)为核函数矩阵。
使用的GP模型函数为f: RD+F→ RE,(xt-1, ut-1)| →Δt= xt- xt-1+ δt,其中
为得到最优的控制策略π: x | → u =π(x, θ),需要根据状态的长期预测演化,找到使成本Jπ(θ)最小化的策略参数θ *。使用GP模型表示实际系统的变换动力学模型,用于预测状态的长期分布p(x1), p(x2), …, p(xT)。由于GP模型可以传递输入的不确定性,把高斯分布的状态空间映射到目标空间,所以在长期规划中包含了模型的不确定性,减少了模型偏差带来的负面影响。状态预测的过程可简化为:
| $ p\left( {{\mathit{\boldsymbol{x}}_{t - 1}}} \right) \to p\left( {{\mathit{\boldsymbol{u}}_{t - 1}}} \right) \to p\left( {{\mathit{\boldsymbol{x}}_{t - 1}},{\mathit{\boldsymbol{u}}_{t - 1}}} \right) \to p\left( {{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_t}} \right) \to p\left( {{\mathit{\boldsymbol{x}}_t}} \right) $ | (17) |
若p(xt-1)已知,为了从p(xt-1)预测p(xt),需要根据控制变量ut-1=π(xt-1)的分布计算联合分布p(xt-1, ut-1)=p(
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{p}}\left( {{{\mathit{\boldsymbol{\hat x}}}_{t - 1}}} \right) = p\left( {{\mathit{\boldsymbol{x}}_{t - 1}},{\mathit{\boldsymbol{u}}_{t - 1}}} \right) = \left( {{{\mathit{\boldsymbol{\hat \mu }}}_{t - 1}},{{\mathit{\boldsymbol{ \boldsymbol{\hat \varSigma} }}}_{t - 1}}} \right) = }\\ {\left[ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\mu }}_{{x_{t - 1}}}}}\\ {{\mathit{\boldsymbol{\mu }}_{{u_{t - 1}}}}} \end{array}} \right]}&{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{{\rm{x}}_{{\rm{t}} - 1}}}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{{\rm{x}}_{{\rm{t}} - 1}},{{\rm{u}}_{{\rm{t}} - 1}}}}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{{\rm{x}}_{{\rm{t}} - 1}},{{\rm{u}}_{{\rm{t}} - 1}}}^T}&{{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{{\rm{u}}_{{\rm{t}} - 1}}}}} \end{array}} \right]} \end{array}} \right]} \end{array} $ | (18) |
训练目标Δt的预测分布为:
| $ p\left( {{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_t}} \right) = \int {p\left( {f\left( {{{\mathit{\boldsymbol{\hat x}}}_{t - 1}}} \right)\left| {{{\mathit{\boldsymbol{\hat x}}}_{t - 1}}} \right.} \right)p\left( {{{\mathit{\boldsymbol{\hat x}}}_{t - 1}}} \right){\rm{d}}{{\mathit{\boldsymbol{\hat x}}}_{t - 1}}} $ | (19) |
其中变换函数的后验预测分布
| $ p\left( {{\mathit{\boldsymbol{x}}_t}\left| {{{\mathit{\boldsymbol{\hat \mu }}}_{t - 1}},{{\mathit{\boldsymbol{ \boldsymbol{\hat \varSigma} }}}_{t - 1}}} \right.} \right) \sim \left( {{\mathit{\boldsymbol{\mu }}_t},{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_t}} \right) $ | (20) |
| $ {\mathit{\boldsymbol{\mu }}_t} = {\mathit{\boldsymbol{\mu }}_{t - 1}} + {\mathit{\boldsymbol{\mu }}_\Delta } $ | (21) |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_t} = {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{t - 1}}\mathit{\boldsymbol{ + }}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_\Delta } + {\mathop{\rm cov}} \left[ {{\mathit{\boldsymbol{x}}_{t - 1}},{\Delta _t}} \right] + {\mathop{\rm cov}} \left[ {{\Delta _t},{\mathit{\boldsymbol{x}}_{t - 1}}} \right] $ | (22) |
| $ {\mathop{\rm cov}} \left[ {{\mathit{\boldsymbol{x}}_{t - 1}},{\Delta _t}} \right] = {\mathop{\rm cov}} \left[ {{\mathit{\boldsymbol{x}}_{t - 1}},{\mathit{\boldsymbol{u}}_{t - 1}}} \right]\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_u^{ - 1}{\mathop{\rm cov}} \left[ {{\mathit{\boldsymbol{u}}_{t - 1}},{\Delta _t}} \right] $ | (23) |
由于ut-1=π(xt-1)是状态xt-1的函数,而p(xt-1)已知,显然,p(xt)的计算依赖策略π的参数θ。
2.4 成本函数为了使机器人在进行交互操作时,具备对环境的顺从能力,约束接触力以保证安全,控制增益不宜过高。小控制增益可以让系统具有多种期望特性,如鲁棒性与减少磨损等,而且通常控制增益越大,能量损耗也就越大。这也符合与人的变阻抗调节法则:尽可能的柔顺,只在任务需要的时候增大刚性,即在需要保证跟踪精度的时候增大阻抗,在需要保证安全时减小阻抗,并尽可能地减少能量损耗。这样,可以实现误差和能量最小化之间的权衡。为使机器人具备这种变阻抗特性,在成本函数中加入能量损耗项,通过惩罚控制动作降低完成任务所需的阻抗增益。定义瞬时成本函数为:
| $ {c_t} = {c_b}\left( {{\mathit{\boldsymbol{x}}_t}} \right) + {c_e}\left( {{\mathit{\boldsymbol{u}}_t}} \right) $ | (24) |
| $ {c_b}\left( {{\mathit{\boldsymbol{x}}_t}} \right) = 1 - \exp \left( { - \frac{1}{{2\sigma _c^2}}d{{\left( {{\mathit{\boldsymbol{x}}_t},{\mathit{\boldsymbol{x}}_{{\rm{target}}}}} \right)}^2}} \right) \in \left[ {0,1} \right] $ | (25) |
| $ {c_e}\left( {{\mathit{\boldsymbol{u}}_t}} \right) = {c_e}\left( {{\rm{ \mathsf{ π} }}\left( {{\mathit{\boldsymbol{x}}_t}} \right)} \right) = \zeta \cdot {\left( {{\mathit{\boldsymbol{u}}_t}/{\mathit{\boldsymbol{u}}_{\max }}} \right)^2} $ | (26) |
瞬时成本函数ct主要包括两项,cb(xt)为状态误差成本,是二次饱和成本函数,当距目标状态的偏差较大时饱和为1,d(·)为欧氏距离,σc是成本函数的宽度;ce(ut)为能量损耗项,即阻抗增益的均方能量损失函数,ζ为能量损失系数, ut为当前的控制量,umax为控制量的最大限幅。
为了评估控制策略π的性能,使用时间T内的总期望成本Jπ(θ)作为评价标准,总期望成本为:
| $ {J^{\rm{ \mathsf{ π} }}}\left( \theta \right) = \sum\limits_{t = 0}^T {{{\rm{E}}_{{x_t}}}\left[ {c\left( {{\mathit{\boldsymbol{x}}_t}} \right)} \right]} ,{\mathit{\boldsymbol{x}}_0} \sim \left( {{\mathit{\boldsymbol{\mu }}_0},{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_0}} \right) $ | (27) |
式中:c(xt)为t时刻的瞬时成本;Ext[c(xt)]为瞬时成本相对于预测状态分布的期望值:
| $ {{\rm{E}}_{{x_t}}}\left( {{c_t}} \right) = \int {{c_t}\left( {{\mathit{\boldsymbol{x}}_t}\left| {{\mathit{\boldsymbol{\mu }}_t},{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_t}} \right.} \right)d{\mathit{\boldsymbol{x}}_t}} $ | (28) |
然后,根据链式法则,计算期望成本相对于控制器参数θ的梯度,使用基于梯度的策略搜索方法,如L-BFGS算法,得到使得Jπ(θ)最小化的控制器参数θ *。
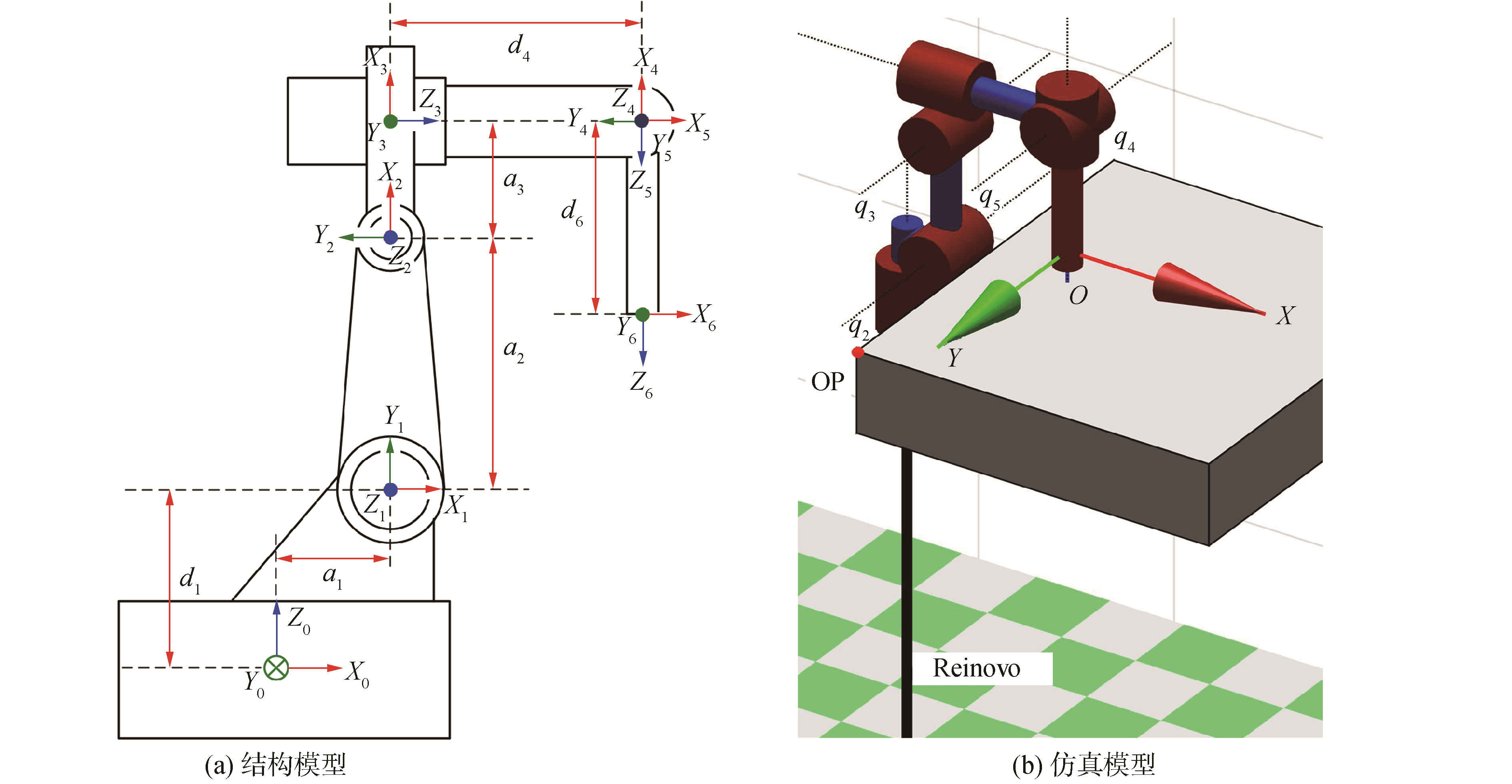
3 仿真实验与结果分析本文使用Matlab通过Reinovo六自由度工业机械臂的力控制仿真验证了本文方法的有效性与高效性。机械臂通过末端腕部的六维力/力矩传感器感知接触力,如图 2所示为机械臂的数学模型与仿真模型,相关的D-H参数如表 1所示。
|
Download:
|
| 图 2 机械臂的结构模型与仿真模型 Fig. 2 Mathematical model and simulated model of the robot | |
| 表 1 机械臂的D-H参数 Table 1 The D-H kinematic parameters of the robot |
在机械臂末端下方放置一个X-Y刚性接触面(图 2(b)),桌面的原点OP位于[0.2-0.5 0.15] m,设置接触桌面的阻尼与刚度分别为BE= [1 1 1] Ns ·m-1,KE=[5 000 5 000 5 000] N ·m-1,控制任务为机械臂自动的学习控制末端接触力达到期望值。选取机械臂的末端位置与接触力作为观测状态x=[X Y Z Fx Fy Fz]∈ R6,要学习的控制量为阻抗控制参数u =[Kdx Kdy Kdz Bdx Bdy Bdz]∈ R6,训练目标为机械臂的末端期望位置与接触力y = [Xd Yd Zd Fxd Fyd Fzd]=[0.41 0 0.226 5 0 0 15]∈ R6。机械臂末端垂直于X-Y刚性接触面,所以,在末端接触平面时,只在z轴方向产生接触力,而在x、y轴2个方向的接触力为0。z轴方向的期望接触力为15 N,若稳态力误差|Fz-Fzd|≤1 N,并且超调小于3 N,则认为任务成功,否则失败。关节位置、速度与接触力的测量噪声都设置为δ~(0, 0.012)。阻抗控制器的参数范围为Kd ∈ [0.1 25],Bd∈[50 1 000]。GP控制器的数量选取n=10,成本函数的能量损失系数ζ=0.03。
阻抗控制器的控制周期为0.01 s,学习算法的计算周期为0.01 s,不包括随机初始化在内,总学习迭代次数为N=20。初次试验时,阻抗控制参数u初始化为服从高斯分布(u0|0.25 umax, 0.1 umax)的随机变量,根据首次试验得到的数据,更新GP模型。然后根据GP模型对系统状态进行长期预测,搜索控制策略,计算阻抗控制参数并应用于系统,得到状态的实际轨迹。
3.2 仿真结果在仿真中,每次实验的持续时间T=1 s,学习变阻抗控制的仿真实验结果如图 3和图 4所示,图 3为学习过程的成本曲线,横坐标为学习次数,纵坐标为累积成本,点划线为策略搜索过程的预测累积成本,虚线为根据控制策略预测的成本均值,阴影为预测成本的95%置信区间,块状标志为实际试验的累积成本值,并表示任务成功与否,实线为实际成本曲线。每次学习迭代后,用新学习的阻抗控制策略进行力控制,图 4为力控制的学习过程。

|
Download:
|
| 图 3 学习过程的成本曲线 Fig. 3 The cost curve of learning process | |

|
Download:
|
| 图 4 力控制的学习过程 Fig. 4 Learning process of force control | |
由仿真实验结果可知,在初始化实验中(图 4中N=0),机械臂末端缓慢地向下移动搜索接触面,寻找环境面的时间较长,在T=0.7 s时才与环境面接触。为了降低累积成本,更快地接触环境面,学习算法不断地优化控制策略。但是由于超调过大,直到第5次学习才能成功完成力控制任务。经过第5次的学习(图 4中N=5),与初次实验相比,机械臂末端可以更快地在T=0.34 s时接触环境面。虽有小幅超调,但能快速地稳定到期望力。根据历史数据,学习算法不断优化调整阻抗参数,在尽快接触环境与抑制超调之间权衡,得到最优的控制策略。第7次学习后,力控制性能趋于稳定,接触力能很快地稳定到期望值并且无超调。经过20次的迭代学习,得到最优控制策略(图 4中N=20),累积成本最小,机械臂能在T=0.3 s时快速地接触环境面。
这一系列的学习训练调整过程都是在没有先验知识的情况下,通过学习调整自动实现的。由结果可知,需要5次交互过程就能得到较优的控制策略,成功学习完成任务,总的交互时间只有5 s,说明本文的算法具有数据高效性。
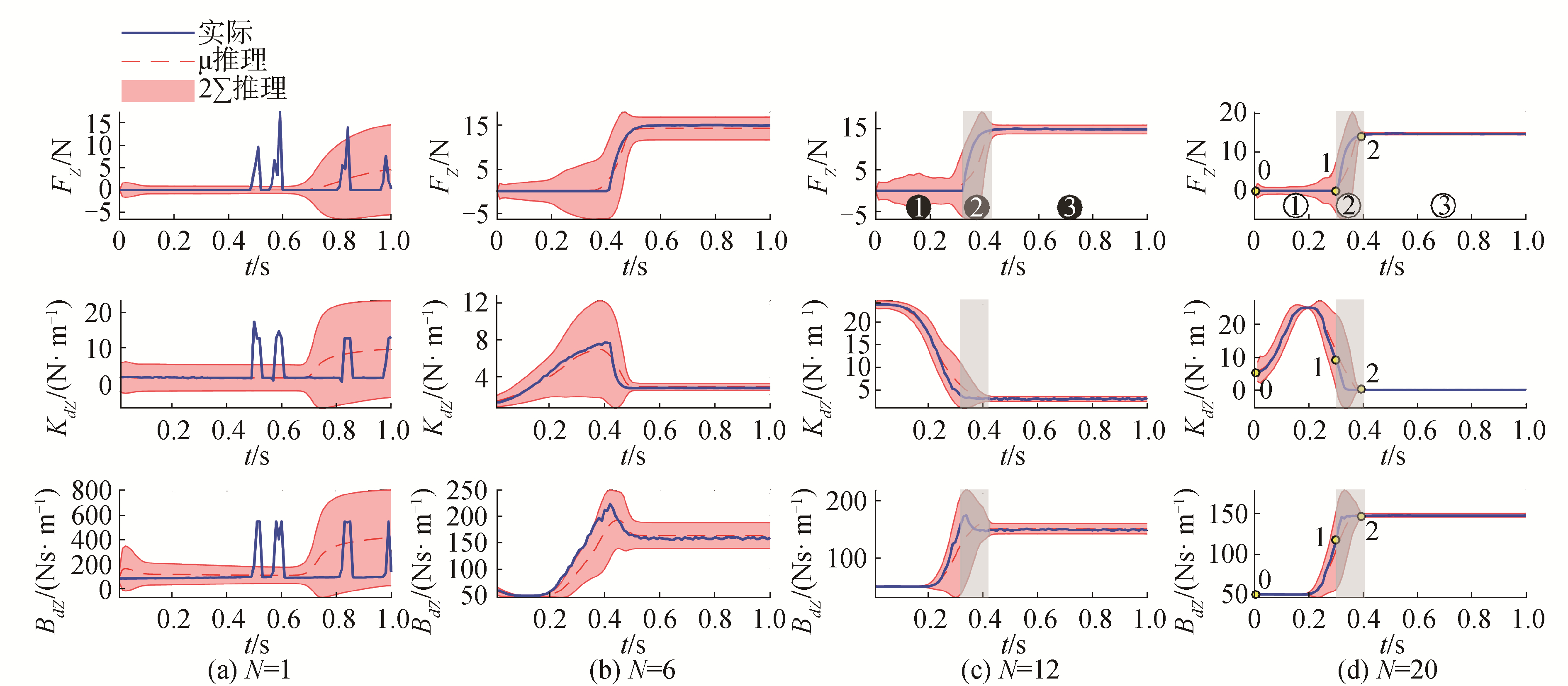
3.3 阻抗参数的调整过程如图 5所示为变阻抗控制中的预测状态与实际状态曲线,实线为实际状态轨迹,虚线与阴影分别为GP模型预测的状态均值与95%的置信区间。如图 6所示为第20次实验的关节空间轨迹与笛卡尔空间轨迹,图 6(a)为第20次实验的关节位置轨迹,图 6(b)为机械臂末端在笛卡尔空间的位置与速度轨迹。阴影部分把实验过程分为3个阶段,与图 5(d)相对应。第20次实验中各阶段的关键状态如表 2所示。
|
Download:
|
| 图 5 状态演变与阻抗调整过程 Fig. 5 States evolution and impedance regulation progress | |

|
Download:
|
| 图 6 关节空间轨迹与笛卡尔空间轨迹 Fig. 6 Joint space trajectories and Cartesian space trajectories | |
| 表 2 第20次实验的关键状态 Table 2 Key states of the 20th iteration |
如图 5的(c)、(d)列所示,阻抗参数的变化可以分为3个阶段:
1) T0~T1:接触环境面之前。机械臂在自由空间自由运动,为了尽快地接触平面,机械臂末端随着阻抗参数的增大,运动增量逐渐增大,在此阶段接触力为零。
2) T1~T2:与环境面接触阶段。当机械臂末端接触环境时,机械臂突然由自由空间运动变为约束空间运动,环境的刚度突然增大。控制器的刚度逐渐减小使系统变“软”以保证安全。同时,阻尼持续增大以使系统更“硬”,抑制环境扰动,系统通过权衡“软”和“硬”,得到合适的控制策略。在此阶段,接触力持续增大。
3) T2~T3:稳定接触环境面阶段。机械臂持续的接触环境,接触力稳定在期望值,在此阶段,控制器的刚度与阻尼保持在较小值,以使系统保持柔顺能力,并减小能量损耗。
在学习初期,由于历史数据不够丰富,GP模型预测的不确定性较大,但随着交互时间的增加,历史采样数据不断丰富,GP模型不断优化并趋于稳定,可以准确地预测状态的变化。为了减少总的累积成本,达到更好的控制效果,学习算法不断地探索改进控制策略,调整阻抗控制参数,在尽快接触环境与抑制超调之间权衡。得到的最优控制策略不仅使机械臂越来越快地接触环境,并能有效抑制超调。在自由空间时,通过高刚度低阻尼,使得末端可以快速地接触接触面;在接触环境后,通过低刚度高阻尼,使得末端具有柔顺性,可安全地稳定到期望接触力。
以上这些控制特性,与人的力跟踪控制策略类似:接触环境突变时,通过协同放松肌肉,增大手臂的柔性,保证安全性,或协同收缩肌肉,增大手臂刚性,抑制扰动;当稳定接触环境后,通过协同放松肌肉群,使手臂处于柔顺状态,实现接触力的稳定控制并能减少能量损耗。在需要保证安全时,减小阻抗,使机器人变“软”;在需要快速跟踪控制的时候,增大阻抗,使机器人变“硬”。
3.4 学习效率在整个实验过程中,总共有20次学习过程,在第5次学习之后,即只需5 s的交互时间即可学到成功完成力控制任务的控制策略,得到的稳定的变阻抗控制策略具有类似人的仿生功能,快速稳定地实现接触力控制,明显减少了学习完成力控制任务所需的交互时间。而其他学习变阻抗控制方法一般都需要成百上千次的迭代,很难达到这种速度。
这主要得益于该方法会明确地建立系统的变换动力学模型,然后用此模型在内部进行仿真并预测系统的变化,最后通过评估得到最优策略。这样能够在有限的观测数据中提取更多的有用信息,减少交互次数,效率更高。本文提出的基于强化学习的学习变阻抗控制方法在学习速度方面比其他学习变阻抗控制方法至少提高了一个数量级,具有明显的数据高效性。
4 结论1) 提出的基于强化学习的学习变阻抗控制方法具有明显的数据高效性,仅需数次交互即可自主学习得到用于力控制的稳定的阻抗控制策略,为非结构化环境中机器人自动学习完成力控制任务提供了一种高效的途经。
2) 根据交互数据构建系统的高斯过程模型,以贝叶斯的方式对系统进行长期推理与规划,并进行内部仿真,可以提高数据的利用效率。
3) 在成本函数中加入能量损耗项,通过惩罚控制动作降低完成任务所需的阻抗增益,学习得到的阻抗控制策略具有类人的仿生阻抗特性,而不需要环境的先验知识。
| [1] |
TSUJI T, TANAKA Y. On-line learning of robot arm impedance using neural networks[J]. Robotics and autonomous systems, 2005, 52(4): 257-271. DOI:10.1016/j.robot.2005.06.005 (  0) 0)
|
| [2] |
ARIMOTO S, HAN H Y, CHEAH C C, et al. Extension of impedance matching to nonlinear dynamics of robotic tasks[J]. Systems & control letters, 1999, 36(2): 109-119. (  0) 0)
|
| [3] |
VAN DEN KIEBOOM J, IJSPEERT A J.Exploiting natural dynamics in biped locomotion using variable impedance control[C]//Proceedings of the 2013 13th IEEE-RAS International Conference on Humanoid Robots.Atlanta, GA, USA, 2013: 348-353. https://www.researchgate.net/publication/282791880_Exploiting_natural_dynamics_in_biped_locomotion_using_variable_impedance_control
(  0) 0)
|
| [4] |
BUCHLI J, THEODOROU E, STULP F, et al.Variable impedance control: a reinforcement learning approach[C]//Proceedings of Robotics: Science and Systems.Zaragoza, Spain, 2010: 153. https://www.researchgate.net/publication/220122116_Learning_variable_impedance_control
(  0) 0)
|
| [5] |
付春江, 王如彬. 人体手臂阻抗控制研究[J]. 力学季刊, 2010, 31(1): 37-45. FU Chunjiang, WANG Rubin. On the human arm impedance control[J]. Chinese quarterly of mechanics, 2010, 31(1): 37-45. (  0) 0)
|
| [6] |
STULP F, BUCHLI J, ELLMER A, et al. Model-free reinforcement learning of impedance control in stochastic environments[J]. IEEE transactions on autonomous mental development, 2012, 4(4): 330-341. DOI:10.1109/TAMD.2012.2205924 (  0) 0)
|
| [7] |
黄瑞, 程洪, 郭宏亮. 基于增强学习的下肢助力外骨骼虚阻抗控制(英文)[J]. 电子科技大学学报, 2018, 47(3): 321-329. HUANG Rui, CHENG Hong, GUO Hongliang. Learning virtual impedance for control of a human-coupled lower exoskeleton[J]. Journal of University of Electronic Science and Technology of China, 2018, 47(3): 321-329. DOI:10.3969/j.issn.1001-0548.2018.03.001 (  0) 0)
|
| [8] |
邱静, 陈启明, 卢军, 等. 下肢助力外骨骼机器人自适应阻抗控制研究[J]. 电子科技大学学报, 2016, 45(4): 689-695. QIU Jing, CHEN Qiming, LU Jun, et al. Learning-based adaptive impedance control for a human-powered augmentation lower exoskeleton[J]. Journal of University of Electronic Science and Technology of China, 2016, 45(4): 689-695. DOI:10.3969/j.issn.1001-0548.2016.04.022 (  0) 0)
|
| [9] |
DU Zhijiang, WANG Wei, YAN Zhiyuan, et al. Variable admittance control based on fuzzy reinforcement learning for minimally invasive surgery manipulator[J]. Sensors, 2017, 17(4): 844. DOI:10.3390/s17040844 (  0) 0)
|
| [10] |
IZAWA J, KONDO T, ITO K. Biological arm motion through reinforcement learning[J]. Biological cybernetics, 2004, 91(1): 10-22. (  0) 0)
|
| [11] |
MITROVIC D, KLANKE S, HOWARD M, et al.Exploiting sensorimotor stochasticity for learning control of variable impedance actuators[C]//Proceedings of the 2010 10th IEEE-RAS International Conference on Humanoid Robots.Nashville, TN, USA, 2010: 536-541. https://www.researchgate.net/publication/224211500_Exploiting_Sensorimotor_Stochasticity_for_Learning_Control_of_Variable_Impedance_Actuators
(  0) 0)
|
| [12] |
BUCHLI J, STULP F, THEODOROU E, et al. Learning variable impedance control[J]. International journal of robotics research, 2011, 30(7): 820-833. DOI:10.1177/0278364911402527 (  0) 0)
|
| [13] |
WINTER F, SAVERIANO M, LEE D.The role of coupling terms in variable impedance policies learning[C]//Proceedings of International Workshop on Human-Friendly Robotics.2016.
(  0) 0)
|
| [14] |
HOGAN N. Impedance control:an approach to manipulation.Part I-Theory.Part Ⅱ-Implementation.Part Ⅲ-Applications[J]. Journal of dynamic systems, measurement, and control, 1985, 107(1): 1-24. DOI:10.1115/1.3140702 (  0) 0)
|
| [15] |
DEISENROTH M P, NEUMANN G, PETERS J. A survey on policy search for robotics[J]. Foundations and trends in robotics, 2013, 2(1-2): 1-142. (  0) 0)
|
| [16] |
DEISENROTH M P, RASMUSSEN C E.PILCO: a model-based and data-efficient approach to policy search[C]//Proceedings of the 28th International Conference on International Conference on Machine Learning.Bellevue, WA, USA, 2011: 465-472. https://www.researchgate.net/publication/221345233_PILCO_A_Model-Based_and_Data-Efficient_Approach_to_Policy_Search
(  0) 0)
|
| [17] |
DEISENROTH M P, FOX D, RASMUSSEN C E. Gaussian processes for data-efficient learning in robotics and control[J]. IEEE transactions on pattern analysis and machine intelligence, 2015, 37(2): 408-423. DOI:10.1109/TPAMI.2013.218 (  0) 0)
|
| [18] |
RASMUSSEN C E, WILLIAMS C K I. Gaussian processes for machine learning (adaptive computation and machine learning)[M]. Cambridge: MIT Press, 2006: 69-106.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


