离心泵以其流量范围大、运行稳定、结构简单和易于操作维护等优点,广泛应用于船舶、动力、能源和农业等诸多领域[1]。构建精确的离心泵数学模型对离心泵的理论分析[2-3]、性能预测[4]和设计优化[5-6]都具有重要的意义。
国内外学者针对离心泵的数学建模研究主要可以分为两大类:
1) 采用计算流体力学(CFD)的白箱建模方法,即在已知离心泵叶轮和流道等内部参数的基础上,构建离心泵流体三维模型,绘制网格后利用专业的CFD软件进行仿真,得到精确的泵内部流场和参数分布信息。这种方法建模工作量大,要实现实时仿真需要足够的硬件支撑,且对建模者的专业知识要求较高。任芸等[7]提出了一种考虑叶轮旋转和叶片曲率影响的离心泵分离流模型,通过仿真和实验对比发现,改进模型的扬程预测精确度比原始模型高出1%~7%。张帆等[8]对某型核电机组给水泵的第一级叶轮及蜗壳流道进行了建模,通过数值计算和实验对比分析了该型离心泵在汽蚀状态下的非稳态流动特性。Chalghoum等[9]对离心泵叶轮区域和蜗壳区域进行了建模,分别应用k-ω、SS和SST-CC湍流模型进行数值计算,结合实验数据分析了叶轮与蜗壳相互作用对离心泵内部运动参数的影响。王川等[10]等基于能量损失模型和计算流体力学方法提出了一种多级离心泵优化设计方法,揭示了圆盘摩擦损失与级间泄漏损失正相关、与容积泄漏损失的反相关关系,并通过实验验证了新方法能够有效优化泵效率。张玉良等[11]基于叶轮机械广义欧拉方程式对一台低转速比离心泵进行了外特性预测,并对其内流场进行了数值仿真,确定了离心泵流量突减时的瞬态过程特征。郭晓梅等[12]以一台带分离叶片诱导轮的高速离心泵为对象构建数值仿真模型,并在此基础上研究了汽蚀状态下泵的内部运动参数特性。
2) 利用实验数据拟合的黑箱建模方法,这种方法通常采用插值法或离心泵相似理论来解决不同转速条件下的函数拼接问题,得到的模型精度和适用条件较为有限。尹雅芹等[13]利用实验数据,基于最小二乘法对拟合出离心泵性能曲线函数,得到误差较小的拟合模型。李良等[14]在确定汽轮给水泵系统各部件机理模型的基础上,将非线性的模型线性化,再采用最小二乘法辨识模型未知参数得到系统模型。吴小平等[15]利用Matlab对离心泵实验数据进行拟合,得到精确度较高的N-Q、H-Q和ŋ-Q特性曲线。
本文以某型船用凝水泵为研究对象,基于差异演化(differential evolution,DE)算法[16]对该凝水泵模型结构和参数进行辨识;为提升模型精度,本文采用原始数据与所得模型的残差作为建模数据,并利用DE算法构建对象的残差模型,最终模型为原始模型和残差模型之和,以此实现对原始模型的修正。
1 离心泵机理模型离心泵叶轮内流体沿叶片型线的流动如图 1所示。假设离心泵叶轮以角速度ω逆时针旋转,单位时间内流过叶轮的液体流量为Qt,流体无黏性且不可压缩,离心泵的扭矩计算公式表示为:
| $ {{M}_{t}}=\rho {{Q}_{t}}\left( {{c}_{2}}{{r}_{2}}\cos {{\alpha }_{2}}-{{c}_{1}}{{r}_{1}}\cos {{\alpha }_{1}} \right) $ | (1) |

|
Download:
|
| 图 1 叶轮叶片进出口速度三角形 Fig. 1 Velocity triangle of impeller blade inlet and outlet | |
式中:Mt为作用在泵轴上的扭矩;ρ为液体密度;c为流体的绝对速度(脚标“2”代表叶轮出口处,“1”代表叶轮入口处,后同);r为叶轮半径;α为圆周速度与流体绝对速度的矢量夹角。
若角速度ω保持不变,则通过叶轮传递给流体的功率Pt:
| $ {{P}_{\text{t}}}={{M}_{\text{t}}}\omega =\rho {{Q}_{\text{t}}}\omega \left( {{c}_{2}}{{r}_{2}}\cos {{\alpha }_{2}}-{{c}_{1}}{{r}_{1}}\cos {{\alpha }_{1}} \right) $ | (2) |
若不考虑泵内各种损失,液体从叶轮获得的功率即为Pt,且满足:
| $ {{P}_{\text{t}}}=\rho g{{H}_{\text{t}}}{{Q}_{\text{t}}} $ | (3) |
联立式(1)~(3)可得离心泵的理论扬程Ht:
| $ {{H}_{\text{t}}}=\left( {{u}_{2}}{{c}_{2u}}-{{u}_{1}}{{c}_{1u}} \right)/g $ | (4) |
式中:u=0.104 72nr, 为叶轮半径r处的圆周速度;cu为液体绝对速度在叶轮旋转方向上的分量。
流体在叶轮内的圆周分速度cu和径向分速度cr可表示为:
| $ \left\{ \begin{align} & {{c}_{u}}=u-{{c}_{r}}/\tan \beta \\ & {{c}_{r}}=0.1592{{Q}_{t}}/\left( rb\psi \right) \\ \end{align} \right. $ | (5) |
式中:β为流体相对速度w与圆周速度的反向夹角;b、r和ψ为流体所在位置的叶轮高度、叶轮半径和叶片排挤系数。
在考虑流体黏性和泵过流部分形状及表面粗糙度的影响后,离心泵的实际扬程H:
| $ H={{H}_{t}}-{{k}_{1}}{{Q}^{2}}-{{k}_{2}}\left( {{Q}^{2}}-Q_{d}^{2} \right) $ | (6) |
式中:k1为流体流动的沿程阻力系数;k2为冲击阻力系数;Q为液体流量;Qd为离心泵设计流量。
联立式(4)~(6)可得离心泵实际扬程H与转速n和流量Q的关系为:
| $ \begin{align} & H=0.11{{n}^{2}}\left( r_{2}^{2}-r_{1}^{2} \right)-{{k}_{1}}{{Q}^{2}}-{{k}_{2}}\left( {{Q}^{2}}-Q_{d}^{2} \right)- \\ & \ \ \ \ \ \ nQ\left[ {{\left( {{b}_{2}}{{\psi }_{2}}\tan {{\beta }_{2}} \right)}^{-1}}-{{\left( {{b}_{1}}{{\psi }_{1}}\tan {{\beta }_{1}} \right)}^{-1}} \right]/60 \\ \end{align} $ | (7) |
由式(7)可见,计算离心泵扬程必须要知道叶轮的设计参数、流体的沿程阻力系数k1和冲击阻力系数k2。这些参数和系数通常通过实验数据拟合或设计工况反推得到,存在一定误差。
2 基于残差修正的差异演化建模差异演化算法的主要思路为:从目标种群中随机筛选2个个体向量并求差,将所得差向量作为变异个体生成的变异源,然后变异个体与原个体进行交叉操作并生成新个体。如果原个体的适应度劣于新个体,在下一代种群中其将被新个体取代,反之其将继续保留至下一代[17-18]。
2.1 算法过程本文利用基于残差修正的差异演化算法建立离心泵的扬程-转速-流量模型,流程如图 2所示。

|
Download:
|
| 图 2 基于残差修正的差异演化流程 Fig. 2 Flow chart of differential evolution based on residual correction | |
具体的操作步骤如下:
1) 算法初始化。根据模型需求设置算法的中止符集与函数集,设定常参数的取值范围;
2) 种群初始化。随机产生初代种群,种群个体数为n,令演化代数g=0;
3) 适应度计算。确定种群P(g)中所有个体的适应度,若满足算法结束条件,则输出演化结果并终止算法,反之进行下一步;
4) 差异演化。
① 种群P(g)中的个体ui发生变异,得到变异个体fi,具体过程:
| $ {{f}_{i}}={{u}_{i}}+F\left[ \left( {{u}_{\text{best}}}-{{u}_{i}} \right)+\left( {{u}_{r1}}-{{u}_{r2}} \right) \right] $ | (8) |
式中:F为变异因数,其决定了算法的收敛速度和新种群的多样性,常规取值在0.4~1;ubest为P(g)中的最优个体;ur1和ur2为P(g)中随机抽取的2个不同个体。
② 变异个体fi与原个体ui进行交叉,得到新个体ui,具体过程:
| $ u_{i}^{\mathit{'}}=\left\{ \begin{align} & {{f}_{i}}\ \ \ \ \text{rand}\left( 0, 1 \right)\le {{P}_{c}} \\ & {{u}_{i}}\ \ \ \ \text{rand}\left( 0, 1 \right)>{{P}_{c}} \\ \end{align} \right. $ | (9) |
式中:rand(0, 1)为随机数,取值在0~1;Pc为种群交概率。
③ 若新个体ui的适应度优于原始个体ui,则用ui替代ui,否则保留ui,最后产生新种群P(g+1),并通过适用度计算得到该种群中的最优个体ubest。
5) 残差修正,若4)执行完毕后仍不具备结束算法的条件,则需要进行残差修正。
① 计算原始实验数据与本次辨识结果的残差,得到残差样本。
② 采用差异演化算法对残差样本进行辨识,通过适应度计算获得残差种群最优个体rbest。
③ 将与求和合成新个体,并将该个体插入到下一代种群。
可见,差异演化算法基于种群个体间的差向量实现变异操作,其变异活跃度成正比于样本间的差异程度,使得算法在计算初期由于样本差异较大而具备充分的全局搜寻能力,而在计算末期,因为个体间差异不断减小而具备充分的局部搜寻能力,可以有效改善常规演化算法局部搜索能力较弱的缺陷[19]。
在此基础上,本文利用原始实验数据与所得模型的残差作为辨识对象,基于差异演化算法构建其模型,用所得残差模型对实验数据模型进行修正,可以有效提升最终模型的精确度。
2.2 参数设置将{+,-,×,/,sin,ln,^}设定为演化算法的函数集,相关参数中止符集:
| $ T\left( H \right)=\left\{ n, \mathit{Q}, \mathit{C} \right\} $ | (10) |
式中:C表示常数,其取值范围为[2.5, 5]。
差异演化和残差修正均采用子树交叉及轮盘赌选择。差异演化部分设置演化代数为1 500代,算法树最大深度为7,种群大小为95,交叉概率设为0.76,变异因数为0.8;残差修正部分设置演化代数为1 000代,算法树最大深度为7,种群大小为75,交叉概率为0.72,变异因数为0.75。
2.3 演化结果分析以凝水泵的原始实验数据为建模输入,经演化迭代计算,可以自动判定并得到一组高适应度的个体,从中选择最优个体,经编码还原[20],得到凝水泵的扬程-转速-流量模型:
| $ \begin{align} & H=0.1915+0.114\sin \left\{ \sin \left( \frac{5.5Q}{1000}+1.853 \right)+ \right. \\ & \left[ \left( -1.028 \right)2-\frac{n}{3600}+\frac{5.5Q}{1000}+0.723 \right]\times \\ & \left[ \frac{n}{1800}-\frac{5.5Q}{1000}-1.7505-\sin \left( \frac{n}{3600}- \right. \right. \\ & \left. \left. \left. \frac{5.5Q}{1000}-1.333 \right) \right] \right\}+0.8854\sin \left[ \left( \frac{0.18n}{1000}- \right. \right. \\ & \left. \left. \frac{2.4Q}{1000}+0.089 \right)\left( \frac{n}{3600}-1.028 \right) \right] \\ \end{align} $ | (11) |
式中:H为凝水泵压力扬程,MPa;n为汽轮凝水泵转速,r/min;Q为凝水泵的体积流量,m3/h。
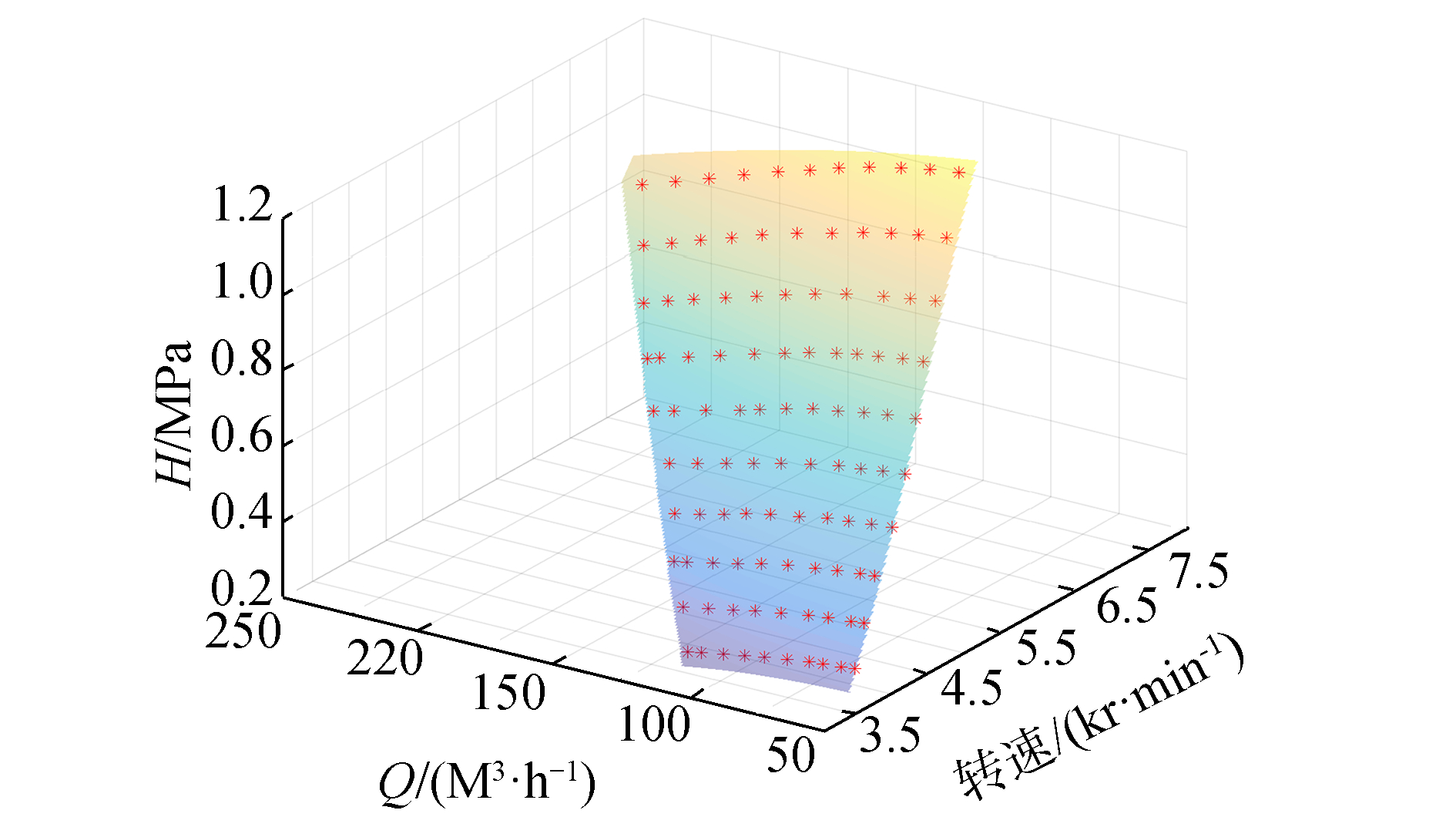
当温度为20 ℃、大气压力为0.101 3 MPa时,实验数据与演化模型计算结果的对比如图 3所示。图 3中,曲面为模型计算结果,标记点为实测值。
|
Download:
|
| 图 3 凝水泵模型计算结果与实验数据对比 Fig. 3 Comparison of calculation results of the condensate water pump model with experimental data | |
由图 3可见,模型计算结果与实验数据吻合得较好。为了定量评估模型的计算精度,对一次演化后的误差情况及残差修正后的误差情况进行了统计,结果如表 1所示。
| 表 1 模型误差统计结果 Table 1 Statistics of model errors |
由表 1可以发现,利用残差修正的方法可以进一步提升传统演化算法的建模精确度,在计算的最终结果中,最大相对误差小于1.4%,平均相对误差小于0.8%,说明本建模方法具有较高的精度。
3 凝水泵汽蚀特性分析 3.1 仿真对象某型船用凝水系统由冷凝器、凝水泵、除氧器、管路系统和其他辅助设备构成,2台凝水泵互为备用,其简化结构如图 4所示。

|
Download:
|
| 图 4 某型船用凝水系统结构 Fig. 4 Structure diagram of a marine condensate system | |
在额定条件下,冷凝器压力PC为0.01 MPa,冷凝器水位LC为500 mm,除氧器压力Pd为0.125 MPa。凝水泵额定转速为6 500 r/min,此时其流量和扬程分别为210 m3/h和0.75 MPa。以凝水泵入口所在平面为基准平面,冷凝器出水口高度HC为0.77 m,除氧器进水口高度Hd为9.3 m。
凝水泵入口压力Pr的计算公式为:
| $ {{P}_{r}}={{P}_{C}}+\rho g\left( {{H}_{C}}+{{L}_{C}} \right)-{{Q}_{m}}^{2}/{{R}^{2}} $ | (12) |
式中:PC为冷凝器压力,MPa;HC为冷凝器出水口高度;LC为冷凝器水位,mm;Qm为凝水泵质量流量,kg/s;R为凝水泵入口闸阀导纳系数[21]。
凝水由泵入口到达叶轮前缘的过程中压力将进一步下降,由于缺少凝水泵的几何参数和实验数据,无法求得叶轮前缘处压力。现假设Pr对应的饱和温度即为泵发生汽蚀的临界温度,当凝水泵入口水温高于该临界温度时,凝水泵发生汽蚀。
将之前得到的凝水泵扬程-转速-流量模型作为部件模型与已有的设备模型搭接,主要参数的连接关系如图 5所示。利用所得船用凝水系统的总体模型进行仿真实验,得到凝水泵转速、冷凝器压力和冷凝器水位变化会对凝水泵汽蚀特性的影响。

|
Download:
|
| 图 5 船用凝水系统各单元之间的参数连接关系 Fig. 5 Parameter connection diagram of each module for marine condensate system | |
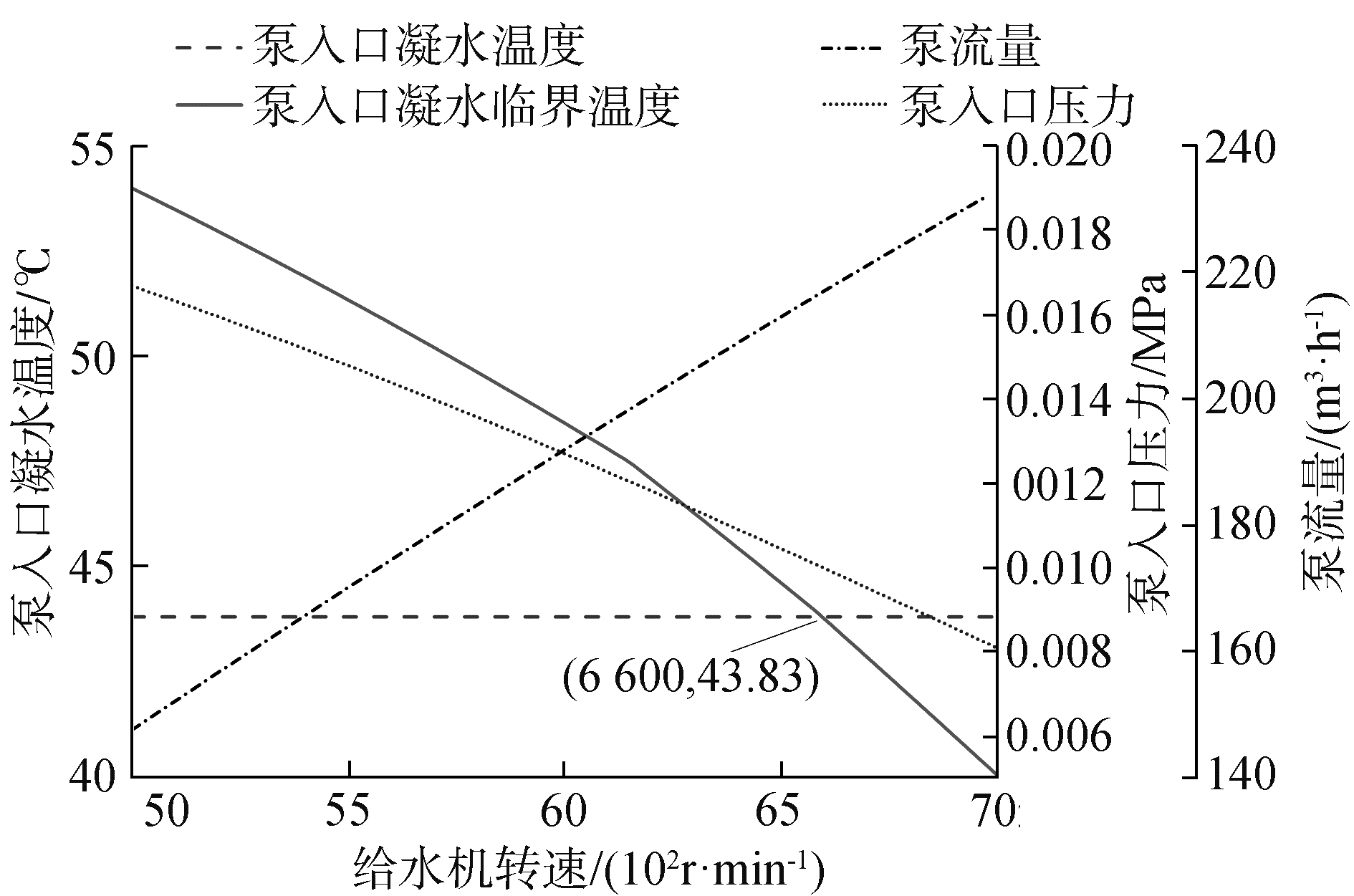
在额定条件下,将凝水泵转速由5 000 r/min增大至7 000 r/min,得凝水泵入口压力、凝水泵入口温度及凝水泵入口汽蚀临界温度的变化趋势如图 6所示。
|
Download:
|
| 图 6 凝水泵转速变化时凝水泵主要参数变化趋势 Fig. 6 Variation tendency of the main parameters of condensate pump when its rotate speed changes | |
由图 6可见,在凝水泵转速增大的过程中,凝水泵流量增大,凝水流经凝水泵入口管段时压力损失增大,导致凝水泵入口压力不断减小,进而导致泵入口凝水发生汽蚀的临界温度不断降低,由于冷凝器压力保持不变,在忽略泵入口凝水温度变化的条件下,当转速达到6 600 r/min时,凝水泵入口凝水发生汽蚀的临界温度降至泵入口凝水温度(43.83 ℃),凝水泵发生汽蚀。因此,在保留一定裕度的情况下,可将6 500 r/min设定为该工况下给水机组的高预警转速。
3.3 冷凝器压力对凝水泵汽蚀特性的影响调整仿真实验条件,将凝水泵转速设定为6 600 r/min,其余条件保持不变,在冷凝器压力由0.005 MPa上升至0.025 MPa的过程中,凝水泵入口凝水压力、凝水泵流量、泵入口凝水温度与凝水汽蚀临界温度差值的变化趋势如图 7所示。

|
Download:
|
| 图 7 冷凝器变化时凝水泵主要参数变化趋势 Fig. 7 Variation tendency of the main parameters of condensate pump when condenser pressure changes | |
由图 7可见,随着冷凝器压力的上升,凝水泵流量处于缓慢增大状态,凝水在流经泵入口管段时的压力损失增大幅度较小,因此凝水泵入口压力不断增大,且泵入口凝水发生汽蚀的临界温度随之上升;但是,随着冷凝器压力的上升,冷凝器内部凝水温度也会上升,到达凝水泵入口的凝水温度随之上升,泵是否发生汽蚀取决于两者的上升幅度。由泵入口凝水温度与该处凝水发生汽蚀的临界温度差值曲线可以看出,冷凝器压力为0.009 MPa时,温度差值为负值(-0.003 48 ℃),此时泵未发生汽蚀;冷凝器压力为0.009 5 MPa时,温度差值为正值(0.011 48 ℃),此时泵已发生汽蚀。因此,在保留一定裕度的情况下,可将0.008 5 MPa设定为该工况下冷凝器的高预警压力。
3.4 冷凝器水位对凝水泵汽蚀特性的影响调整仿真实验条件,将凝水泵转速设定为6 300 r/min,冷凝器压力设定为0.01 MPa,其余条件保持不变,在冷凝器水位由300 mm上升至500 mm的过程中,凝水泵入口凝水压力、凝水泵流量、凝水泵入口凝水温度及泵入口凝水汽蚀临界温度的变化趋势如图 8所示。

|
Download:
|
| 图 8 冷凝器水位变化时凝水泵主要参数变化趋势 Fig. 8 Variation tendency of the main parameters of condensate pump when condenser water level changes | |
由图 8可见,在给水机组转速保持在6 300 r/min的条件下,随着冷凝器水位的上升,冷凝器出水口压力增大,凝水泵流量处于微增趋势,凝水流过泵入口管段压力损失的增大幅度较小可忽略,因此凝水泵入口压力不断增大,导致凝水泵入口凝水汽蚀临界温度不断增大;由于冷凝器水位上升对冷凝器内部凝水温度的影响较小可忽略,因此凝水泵入口凝水温度可认为保持不变,在冷凝器水位小于等于360 mm时,凝水泵处于汽蚀状态。因此,在保留一定裕度的条件下,可将380 mm设为冷凝器在该运行工况下的低预警水位。
4 结论1) 利用基于残差修正的改进差异演化算法对某型船用凝水泵进行自动辨识建模,有效改善了利用理想状态下的实验数据作为建模参数所造成的误差,所得结果具有更高的精确度;
2) 对该型船用凝水系统凝水泵汽蚀特性进行仿真分析,结果表明,在特定运行条件下,过高的凝水泵转速、过高的冷凝器压力和过低的冷凝器水位,均会导致凝水泵发生汽蚀;
确定不同工况下相关参数预警值的方法,可为凝水系统监控系统设计和系统特性分析提供参考。
| [1] |
牟介刚, 李必祥. 离心泵设计实用技术[M]. 北京: 机械工业出版社, 2015. MOU Jiegang, LI Bixiang. Centrifugal pump design handbook[M]. Beijing: China Machine Press, 2015. (  0) 0)
|
| [2] |
率志君, 张权, 陈春来, 等. 多级离心泵整机流场三维非稳态湍流压力脉动特性分析[J]. 哈尔滨工程大学学报, 2013, 34(3): 306-311. SHUAI Zhijun, ZHANG Quan, CHEN Chunlai, et al. Characteristic analysis of three-dimensional unsteady turbulent pressure fluctuation in whole flow field of multi-stage centrifugal pump[J]. Journal of Harbin Engineering University, 2013, 34(3): 306-311. (  0) 0)
|
| [3] |
江伟, 李国君, 张新盛. 基于叶片载荷分布的离心泵叶轮水力性能优化[J]. 哈尔滨工程大学学报, 2015, 36(4): 505-510. JIANG Wei, LI Guojun, ZHANG Xinsheng. Optimization of the hydraulic performance of a centrifugal pump impeller based on the blade load distribution[J]. Journal of Harbin Engineering University, 2015, 36(4): 505-510. (  0) 0)
|
| [4] |
OMAR A K, KHALDI A, LADOUANI A. Prediction of centrifugal pump performance using energy loss analysis[J]. Australian journal of mechanical engineering, 2017, 15(3): 210-221. DOI:10.1080/14484846.2016.1252567 (  0) 0)
|
| [5] |
SAFIKHANI H, KHALKHALI A, FARAJPOOR M. Pareto based multi-objective optimization of centrifugal pumps using CFD, neural networks and genetic algorithms[J]. Engineering applications of computational fluid mechanics, 2011, 5(1): 37-48. DOI:10.1080/19942060.2011.11015351 (  0) 0)
|
| [6] |
ZHOU Ling, SHI Weidong, WU Suqing. Performance optimization in a centrifugal pump impeller by orthogonal experiment and numerical simulation[J]. Advances in mechanical engineering, 2013: 385809. (  0) 0)
|
| [7] |
REN Yun, ZHU Zuchao, WU Denghao, et al. An improved turbulence model for separation flow in a centrifugal pump[J]. Advances in mechanical engineering, 2016, 8(6): 1-10. (  0) 0)
|
| [8] |
ZHANG Fan, YUAN Shouqi, FU Qiang, et al. Cavitation-induced unsteady flow characteristics in the first stage of a centrifugal charging pump[J]. Journal of fluids engineering, 2017, 139(1): 011303. (  0) 0)
|
| [9] |
CHALGHOUM I, KANFOUDI H, ELAOUD S, et al. Numerical modeling of the flow inside a centrifugal pump:influence of impeller-volute interaction on velocity and pressure fields[J]. Arabian journal for science and engineering, 2016, 41(11): 4463-4476. DOI:10.1007/s13369-016-2157-8 (  0) 0)
|
| [10] |
WANG Chuan, SHI Weidong, WANG Xikun, et al. Optimal design of multistage centrifugal pump based on the combined energy loss model and computational fluid dynamics[J]. Applied energy, 2017, 187: 10-26. DOI:10.1016/j.apenergy.2016.11.046 (  0) 0)
|
| [11] |
张玉良, 肖俊建, 崔宝玲, 等. 离心泵快速变工况瞬态过程特性模拟[J]. 农业工程学报, 2014, 30(11): 68-75. ZHANG Yuliang, XIAO Junjian, CUI Baoling, et al. Simulation of transient behavior in prototype centrifugal pump during rapid regulating flow rate[J]. Transactions of the Chinese society of agricultural engineering, 2014, 30(11): 68-75. DOI:10.3969/j.issn.1002-6819.2014.11.009 (  0) 0)
|
| [12] |
GUO Xiaomei, ZHU Linhang, ZHU Zuchao, et al. Numerical and experimental investigations on the cavitation characteristics of a high-speed centrifugal pump with a splitter-blade inducer[J]. Journal of mechanical science and technology, 2015, 29(1): 259-267. DOI:10.1007/s12206-014-1232-x (  0) 0)
|
| [13] |
尹雅芹.基于MATLAB的多级离心泵性能预测建模的研究[D].合肥: 安徽大学, 2015. YIN Yaqin.Research on performance prediction model for multistage centrifugal pump based on MATLAB[D].Hefei: Anhui University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10357-1015376601.htm (  0) 0)
|
| [14] |
李良, 陈五星, 邹海.汽轮给水泵系统数学模型辨识[C]//第35届中国控制会议论文集(B).成都, 2016: 2182-2187. LI Liang, CHEN Wuxing, ZOU Hai.Identification of mathematical model for the steam turbine pump system[C]//Proceedings of the 35th Chinese Control Conference.Chengdu, 2016: 2182-2187. (  0) 0)
|
| [15] |
吴小平, 把多铎, 胡沙沙, 等. 基于MATLAB离心泵特性曲线的拟合与绘制[J]. 中国农村水利水电, 2010(11): 144-146. WU Xiaoping, BA Duoduo, HU Shasha, et al. Fitting and drawing of characteristic curve of centrifugal pump based on Matlab[J]. China rural water and hydropower, 2010(11): 144-146. (  0) 0)
|
| [16] |
STORN R, PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of global optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 (  0) 0)
|
| [17] |
武志峰.差异演化算法及其应用研究[D].北京: 北京交通大学, 2009. WU Zhifeng.Research on differential evolution algorithm and its application[D].Beijing: Beijing Jiaotong University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10004-2009205148.htm (  0) 0)
|
| [18] |
DAS S, MULLICK S S, SUGANTHAN P N. Recent advances in differential evolution:an updated survey[J]. Swarm and evolutionary computation, 2016, 27: 1-30. DOI:10.1016/j.swevo.2016.01.004 (  0) 0)
|
| [19] |
倪何, 肖航, 曾凡明, 等. 基于残差修正的涡轮增压机组差异演化建模与降负荷特性分析[J]. 上海交通大学学报, 2015, 49(5): 620-625, 632. NI He, XIAO Hang, ZENG Fanming, et al. Differential evolutionary modeling with residual correction and down-load characteristic analysis for marine turbocharged unit[J]. Journal of Shanghai Jiao Tong University, 2015, 49(5): 620-625, 632. (  0) 0)
|
| [20] |
倪何, 程刚, 孙丰瑞. 基于混合演化的自适应建模及其应用[J]. 浙江大学学报(工学版), 2010, 44(8): 1490-1495. NI He, CHENG Gang, SUN Fengrui. Adaptive hybrid evolutionary modeling method and its application[J]. Journal of Zhejiang University (engineering science), 2010, 44(8): 1490-1495. DOI:10.3785/j.issn.1008-973X.2010.08.010 (  0) 0)
|
| [21] |
倪何, 程刚, 孙丰瑞. 热工流体网络简易模块化建模方法[J]. 系统仿真学报, 2009, 21(12): 3536-3541. NI He, CHENG Gang, SUN Fengrui. Simple modular modeling method of thermo-fluid network[J]. Journal of system simulation, 2009, 21(12): 3536-3541. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


