2. 西安建筑科技大学 土木工程学院, 陕西 西安 710055;
3. 长安大学 建筑学院, 陕西 西安 710061
2. School of Civil Engineering, Xi'an University of Architecture and Technology, Xi'an 710055, China;
3. School of Architecture, Chang'an University, Xi'an 710061, China
既有钢结构梁柱连接形式多为刚接,梁柱连接处在往复位移作用下易发生脆性断裂[1-4],我国规范虽给出改进梁柱连接处的构造形式[5],但未作强制要求,加之老规范对节点区未作处理要求,在结构遭遇地震作用时,梁柱连接处始终为结构破坏的薄弱环节。在钢框架抗倒塌分析中,为保证结构稳定性,美国规范给出结构楼层位移角最大值限值为1/20[6]。依据强柱弱梁的设计理念,框架梁的刚度小于框架柱,结构临近倒塌破坏时,框架梁的变形应大于框架柱,而已有钢框架节点的抗震试验研究多集中于框架梁端在小位移循环加载下的疲劳破坏,很少研究大位移往复加载下钢框架节点的响应[7-8]。为合理评价钢结构梁柱节点在地震作用下响应,应研究节点在大位移往复加载下的力学特性。
本文设计了3种不同的大位移加载方式,钢框架节点试件进行低周反复加载试验,研究其在不同大位移加载下的破坏演化过程。
1 试验研究 1.1 试验概况考虑到已建成的钢框架结构多采用梁柱刚接形式,基于试验室设备加载能力,本文设计钢框架梁柱翼缘与腹板全焊接连接的边节点,制作比例尺取1 :2,试件梁柱均采用热轧H型钢,钢材型号均为Q235B,梁柱刚度比、板件宽厚比均满足《钢结构设计规范》(GB 50017-2003)[9]要求,节点试件截面尺寸与连接方法如图 1所示。

|
Download:
|
| 图 1 试件相关尺寸 Fig. 1 specimen size | |
已有研究钢框架节点抗震性能研究多集中于小位移往复加载下的疲劳破坏,不能反映结构结构临近倒塌状态时构件的大位移加载情形。结构弹塑性分析时所采用的构件本构关系通常基于变幅加载下构件损伤演化,因此,本次试验在变幅加载之外,设计3种大位移加载制度,等幅60 mm加载与等幅90 mm加载,相当于最大转角为0.04与0.06,3种大位移加载制度示意图如图 2所示。结合试验室加载能力,本试验采用悬臂梁式拟静力加载方法,采用30 t的电液伺服作动器来施加水平位移,并为了保证加载端侧向稳定,布置侧向支撑装置。试件编号及其具体信息如表 1所示。试件加载简图与装置见图 3和图 4。

|
Download:
|
| 图 2 试验加载制度 Fig. 2 Loading procedures of tests | |

|
Download:
|
| 图 3 钢框架节点加载装置 Fig. 3 Loading device and loading diagram of steel frame joint | |

|
Download:
|
| 图 4 加载装置 Fig. 4 Loading device photo | |
| 表 2 试件基本参数 Table 2 Design parameters of specimens |
本次试验,为研究不同大位移加载制度下试件的力学性能响应,以试件无法继续承担水平力为试验终点,试件破坏模态如图 5所示。

|
Download:
|
| 图 5 试件破坏形态 Fig. 5 Failure patterns of specimens | |
试验结果表明:
1) 试件在不同加载制度的大位移往复加载下,翼缘先于腹板产生塑性变形,屈曲变形不断累积,试件屈曲位置均发生在梁根部距离梁柱焊接处5~ 15 cm范围内。梁柱连接处为保证焊接质量,需对连接处的腹板局部开洞处理,此处截面抵抗力最低而弯矩与剪力值最大,但在距焊缝5 cm范围内无屈曲变形,表明端部刚性连接对距离焊缝5 cm范围内梁端有较强的约束作用;
2) 3个不同加载制度下试件破坏形态均表现为翼缘在焊缝通过孔位置处先出现裂纹,并随着位移加载不断发展,最终贯通翼缘,并撕裂腹板。分析其原因,翼缘与腹板出现裂缝的位置均为试件应力集中最明显的位置,易发生断裂。同时,当一侧翼缘裂缝明显发展时,另一侧将不再出现裂缝或已有裂缝不再发展;
3) 变幅加载与等幅60 mm循环加载下,试件破坏之前翼缘与腹板屈曲变形发展不充分,翼缘裂缝出现后发展迅速,很快贯穿,试件承载力降低突然,试件属脆性破坏。等幅90 mm循环加载下,试件屈曲变形发展较充分,承载力随着位移加载不断退化,板材裂缝除出现在应力集中区,即焊缝通过孔位置外,亦在翼缘屈曲变形曲率最大处出现裂纹,试件在裂缝贯通之前承载力已明显降低,试件属延性破坏。此外,焊接孔处的裂缝发生在应力集中最大的位置,出现较突然,发展迅速,而曲率最大处的裂缝发展缓慢,是由于试件屈曲变形过大且拉压循环引起的,等幅90 mm循环加载下的试件出现裂纹试件晚于变幅加载与等幅60 mm循环加载,可见翼缘屈曲变形减缓了焊接孔处的应力集中效应,即塑性变形区削弱大位移加载对梁柱焊接处的破坏作用。
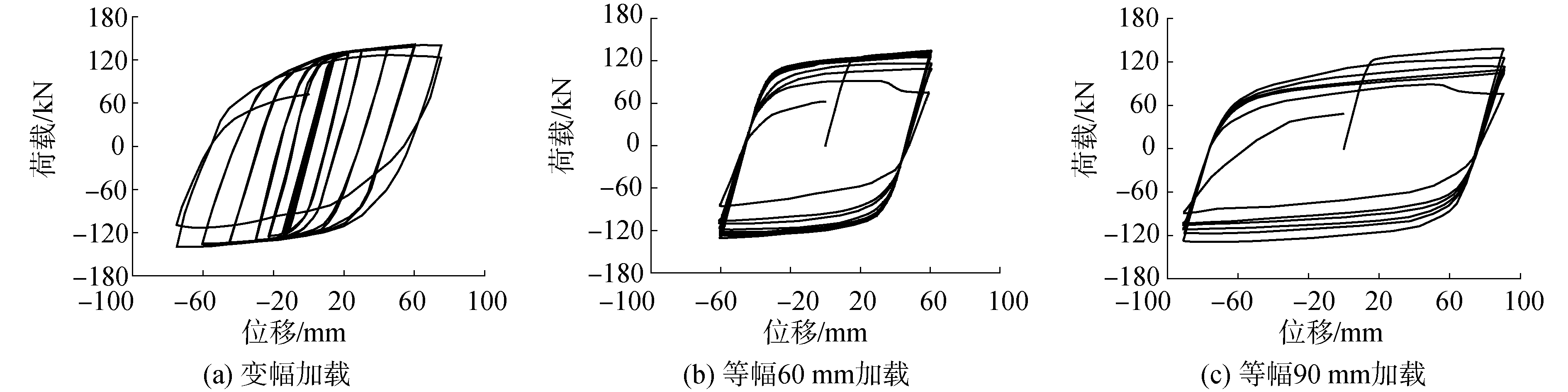
2.2 滞回性能3种大位移往复加载下3个试件的荷载-位移曲线如图 6所示,钢框架节点具有较高的承载力与较好的累积变形能力,滞回曲线均呈饱满,并无捏拢。变幅加载与等幅60 mm循环加载下滞回曲线在试件破坏之前无明显退化,而等幅90 mm循环加载下滞回曲线在试件破坏之前已有较大幅度的退化。
|
Download:
|
| 图 6 梁端荷载-位移滞回曲线 Fig. 6 Hysteresis curve of load-displacement | |
结构遭遇强烈地震作用时需依靠构件的塑性变形耗散地震能量,而结构的设计理念需保证构件破坏滞后于结构破坏,这对构件的耗能能力提出了较高的要求,钢框架梁通过梁端的塑性变形耗散地震能量,需研究其耗能能力。试件承载力降低15%之后,构件丧失承载能力,对比构件完全破坏与承载力降低15%两种状态下构件的变形能力与耗能能力,其中“有效”对应构件承载力降低15%状态,如表 3所示。
| 表 3 试件耗能能力 Table 3 Specimen energy dissipation |
对比各试件的在大位移往复加载下耗能响应,可作如下结论:
1) 对于本文设计的3种大位移加载制度,试件在完全破坏之前的累积耗能能力在等幅90 mm往复加载下最优,等幅60 mm往复加载下次之,变幅加载下最弱;
2) 若以试件承载力降低15%作为试件破坏临界点,试件耗能能力等幅60 mm往复加载下最优,等幅90 mm加载下次之,等幅90 mm往复加载下最弱,此时不同加载制度下试件耗能能力相近,差别较小;
3) 等幅90 mm往复加载下,试件耗能能力衰退是由于翼缘屈曲不断发展所导致的,而等幅60 mm往复加载与变幅加载下试件耗能能力衰退是由于翼缘裂缝发展所导致的。
2.4 损伤分析对于本次试验,考虑钢构件变形能力较好,并未获得其单调加载下的峰值承载力与变形极限,若将本在试验等幅90 mm往复加载中第一次正向加载到90 mm作为试件的单调加载,其对应的梁端截面转角位0.06,大于工程通常要求的截面转角0.05,此时试件并未表现出承载力下降趋势。因此,在试件的损伤分析中不应过度考虑试件的最大变形对其损伤的影响。
钢框架节点在往复加载下易发生脆性破坏,因此,应着重研究其在往复加载下的累积破坏。本次试验试件在变幅加载下的骨架曲线如图 7所示。可见试件在变幅加载下直至试件破坏亦未出现承载力降低趋势。因此在结构弹塑性分析时可采用不退化的滞回模型。

|
Download:
|
| 图 7 节点滞回骨架曲线 Fig. 7 Skeleton curves of the joint | |
对于钢构件,由于其较好的变形能力,结构失稳前,不可能达到其变形极限,因此在构件损伤分析时,无需考虑变形项。同时,已有损伤模型对于累积耗能项的分母,采用单调加载破坏之前的耗能值,并采用幂指数形式,通过试验获取指数,计算过于复杂,通用性较差,且结构中构件较多,并不适用于快速评价结构在地震作用下的损伤程度。本文中以试件承载力降低15%作为试件破坏临界点,则不同大位移往复加载下试件累积耗能能力相近,可作为试件累积破坏的极限耗能。熊俊等人采用等幅小位移循环往复加载研究梁柱焊接的钢框架节点的耗能能力,也得出试件属于脆性破坏,且不同位移幅值循环加载下试件耗能能力相近。Akbas等[10]统计了59个梁柱刚接的钢框架节点梁端在循环往复加载下的累积变形能力;Bojórquez[11]等对Akbas的统计结果进一步分析,指出梁端累积塑性转角服从对数正态分布,其平均值为0.23。此结论与本次试验差异较大,分析其原因:首先,本次试验破坏位置均为焊缝通过孔处翼缘断裂,并未出现焊缝断裂情形;其次,本次试验梁的截面高度较小,试件破坏对位移的敏感度较小。
综上所述,钢框架节点作为钢框架结构在遭遇地震作用的主要耗能构件,可建立钢框架节点构件适用于评价其在地震作用下破坏程度的损伤模型:
| $ D=\frac{\int _{0}^{t}M\left( t \right)\text{d}\theta }{{{W}_{E}}} $ | (1) |
式中:D为钢框架节点构件的损伤指数;M为t时刻构件的截面最大弯矩;
若采用不退化的滞回模型,则可假定构件屈服弯矩为常数,则式(1)可简化为:
| $ D=\frac{{{M}_{Y}}\int _{0}^{t}\text{d}\theta }{{{M}_{Y}}{{\theta }_{a}}}=\frac{\int _{0}^{t}\text{d}\theta }{{{\theta }_{a}}} $ | (2) |
式中:
对比不同损伤模型对评价构件损伤程度的影响,本文选取3个损伤模型:承载力损伤模型、双参数损伤模型与本文建立模型。3个损伤模型中,均选取承载力降低15%构件破坏。
承载力损伤模型可定义为:
| $ D=\frac{{{M}_{U}}-{{M}_{D}}\left( t \right)}{0.15{{M}_{U}}} $ | (3) |
由式(3)计算构件损伤程度时,构件达到承载力极限值之前,认为构件损伤程度为0。
双参数损伤模型选徐强等[12]针对钢构件提出的损伤模型:
| $ D=\alpha \frac{\theta \left( t \right)}{{{\theta }_{u}}}+\beta \frac{\int _{0}^{t}\text{d}\theta }{{{\theta }_{a}}} $ | (4) |
式中:θ(t)为构件在t时刻之前所经历的最大转角;θu为构件极限转角,取工程通常要求的截面转角能力0.05;α和β为权重组合系数,且α+β=1。考虑到节点区梁端以耗能为主,本文取α=0.3、β=0.7。
损伤模型的损伤曲线对比如图 8所示。

|
Download:
|
| 图 8 构件损伤演化曲线对比 Fig. 8 Comparison of damage evolution curves | |
由图 8可见,承载力损伤模型在构件达到承载力极限之前损伤值为0,而在构件达到承载力极限值之后损伤指标增长过快,不能表达构件在达到峰值承载力之前的塑性变形及累计损伤。双参数损伤模型中构件单调加载极限难以确定,且组合系数选取的主观性较大,同时,双参数模型中,耗能项采用Eu为试件单调加载的极限耗能,其适用于单调加载,而对于循环加载,由Eu作为构件耗能能力缺乏理论基础,且试验常数c对不同构件、不同加载制度取值均不同,不具有普遍适用性。本文提出的损伤模型构造简单,易于计算,能够表达节点区梁端的累积塑性变形下的损伤演化。由于损伤模型中构件累积塑性变形与损伤值呈线性关系,损伤曲线为直线,试验结果显示,构件在不同加载制度下,其有效累积耗能能力接近,因此对本次试验,本文提出的损伤模型已有计算且具有普遍适用性。
3 结论1) 设计了3个不同的大位移加载制度,对钢框架节点构件进行低周往复加载试验,3个试件的破坏位置均为焊缝通过孔处翼缘断裂,其中,变幅加载与等幅60 mm循环加载下试件为脆性破坏,等幅90 mm循环加载下试件为延性破坏。
2) 承载力降低15%时,构件翼缘开裂或发展较显著屈曲,其后试件承载力降低速度加快;不同大位移往复加载下构件的累积耗能能力差异较大,但试件承载力降低15%时所对应的累积耗能相近,可将承载力降低15%作为试件破坏的临界点。
3) 试验室很难直接获得构件的变形能力极限,且构件变形在地震作用下不可能达到其极限变形,针对钢框架节点,提出简单通用的累积破坏损伤模型。
| [1] |
CASTIGLIONI C A, PUCINOTTI R. Failure criteria and cumulative damage models for steel components under cyclic loading[J]. Journal of constructional steel research, 2009, 65(4): 751-765. DOI:10.1016/j.jcsr.2008.12.007 (  0) 0)
|
| [2] |
KRAWINKLER H, ZOHREI M. Cumulative damage in steel structures subjected to earthquake ground motions[J]. Computers & structures, 1983, 16(1/2/3/4): 531-541. (  0) 0)
|
| [3] |
郑山锁, 王晓飞, 孙龙飞, 等. 酸性大气环境下多龄期钢框架节点抗震性能试验研究[J]. 建筑结构学报, 2015, 36(10): 20-28. ZHENG Shansuo, WANG Xiaofei, SUN Longfei, et al. Experimental research on seismic behavior of multi-aged steel frame joint under acidic atmospheric environment[J]. Journal of building structures, 2015, 36(10): 20-28. (  0) 0)
|
| [4] |
国家自然科学基金委员会.学科发展战略研究报告一建筑、环境与土木工程Ⅱ[R].北京: 科学出版社, 2006. National Natural Science Foundation Committee.Subject development strategy research report-Construction, environment and civil engineering Ⅱ[R].Beijing: Science Press, 2006. (  0) 0)
|
| [5] |
中国建筑标准设计研究院.01SG519, 多、高层民用建筑钢结构节点构造详图[S].北京: 中国建筑标准设计研究院, 2004. China Institute of Building Stondard Design and Research.01SG519, Multistoriey and high-rise steel structune connection drawings[S].Beijing: China Institute of Building Standard Design and Research, 2004. (  0) 0)
|
| [6] |
Federal Emergency Management Agency (FEMA).FEMA 356 Commentary on the guidelines for the seismic rehabilitation of buildings[S].Washington, DC: Prepared by American Society of Civil Engineers, 2000.
(  0) 0)
|
| [7] |
熊俊.强震作用下钢框架焊接节点损伤性能和计算模型研究[D].北京: 清华大学, 2011. XIONG Jun.Research on the damage behavior and calculation model of welded connections in steel frames under earthquakes[D].Beijing: Tsinghua University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10003-1012035897.htm (  0) 0)
|
| [8] |
王萌, 石永久, 施刚, 等. 高层钢框架构件与节点滞回模型及损伤退化分析[J]. 工业建筑, 2009(S1): 973-981. WANG Meng, SHI Yongjiu, SHI Gang, et al. Analysis on degraded and damage hysteretic model of high-rise steel frame structures and connections[J]. Industrial construction, 2009(S1): 973-981. (  0) 0)
|
| [9] |
北京钢铁设计研究总院, 重庆大学, 西安建筑科技大学, 等.GB 50017-2003, 钢结构设计规范[S].北京: 中国计划出版社, 2003. Beijing Iron and Steel Design and Research Institute, Chongqing University, Xi'an University of Architecture and Technology.GB 50017-2003, Code for design of steel structures[S].Beijing: China Planning Press, 2003. (  0) 0)
|
| [10] |
AKBAS B.Energy-based earthquake resistant design of steel moment resisting frames[D].Chicago, USA: Illinois Institute of Technology, 1997.
(  0) 0)
|
| [11] |
BOJÓRQUEZ E, REYES-SALAZAR A, TERÁN-GILMORE A, et al. Energy-based damage index for steel structures[J]. Steel and composite structures, 2010, 10(4): 343-360. (  0) 0)
|
| [12] |
徐强, 郑山锁, 程洋, 等. 基于结构损伤的在役钢框架地震易损性研究[J]. 振动与冲击, 2015, 34(6): 162-167. XU Qiang, ZHENG Shansuo, CHENG Yang, et al. Based on the structural damage in service of steel framework seismic vulnerability research[J]. Journal of vibration and shock, 2015, 34(6): 162-167. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


