2. 悉尼科技大学 大数据中心, 新南威尔士 悉尼 2007
2. School of Electrical and Data Engineering Sydney University of Technology, Sydney 2007, Australia
近年来,地面自主车辆(unmanned ground vehicle,UGV)已成为人工智能领域里相当热门的一项研究课题。UGV系统通常由感知模块、融合模块、规划模块以及控制模块组成。其中路径规划模块需确保在有限计算资源内,依据环境、任务以及UGV自身状态进行规划,生成安全、有效的可执行路径。在能够有效检测出道路的情况下,规划模块就可以沿着道路方向生成引导UGV安全行驶的轨迹,并且可以根据道路弯曲程度提前进行方向以及速度的控制,确保UGV能够安全顺利地过弯。目前大部分道路检测方法都是基于视觉的方法,这些方法在结构化道路以及半结构化道路都有比较好的效果。而在结构化程度较低[1]的非结构化道路下,由于这类道路没有车道线、道路边界模糊、地表介质不均匀等问题,基于视觉的方法有时不能稳定地工作。而且视觉方法还容易受到恶劣光照(例如强光照、强阴影)和天气的影响,无法稳定地利用摄像机获得的图像进行道路检测。
激光雷达作为一种主动传感器,能够不受光照影响,全天时运作[2]。同时,非结构化道路两侧通常存在高于路面的植被、土堆和沙石,或者是低于路面的沟道。多线激光雷达可以检测到这些正、负障碍物,并提取出道路边界,以此作为在基于视觉的道路检测算法不能完全稳定工作时的一种补充手段。本文主要工作围绕如何从多线激光雷达生成的局部栅格地图中有效地提取道路或道路边界并进行路径规划而展开。
目前有许多经典的方法(如Voronoi图[3-4]和人工势场法[5])可以运用在激光雷达建立的栅格地图上来生成代价地图,而这代价地图则隐含了道路的信息,再利用搜索算法从代价地图中提取出道路。文献[6]提取了栅格地图的Voronoi图作为道路骨架,在此基础上使用快速行进法(fast marching method, FMM)进行路径搜索,但是得到的路径既不安全也不平滑。文献[7]提出的FM2算法则先对栅格地图使用FMM建立了一张传播速度地图,然后结合车辆运动学模型对传播速度地图再使用FMM生成了相对平滑且安全的路径,但是需要消耗相当多的计算资源。文献[8]提出了一种基于圆的空间探索算法,并使用启发式搜索生成一条远离障碍的路径。文献[9]利用线性鉴别分析(linear discriminant analysis, LDA)的分类思想对道路两侧障碍物进行划分并拟合得到道路的边界信息,该方法具有较好的实时性。文献[10]中将车辆行驶通道两侧的激光雷达点云数据进行聚类,得到两类数据,并使用线性支持向量机(support vector machine, SVM)对两类数据处理得到行驶通道的边界。然而,这些基于线性分类的边界检测方法无法运用于曲率较大的道路。因此,本文提出一种基于非线性支持向量机的局部路径规划算法,利用局部栅格地图来实时生成安全、平滑的UGV可执行路径,并在自主研发的UGV平台上验证了算法的有效性和正确性。
1 基于SVM的路径提取当视觉受到光照或天气影响,所获得的图像中道路边界模糊,如图 1所示。

|
Download:
|
| 图 1 受干扰的非结构化道路场景以及对应栅格地图 Fig. 1 Jamming scenes and corresponding grid maps in unstructured road | |
在这种情况下多线激光雷达仍然能够有效检测道路两侧障碍物,其中处于道路边界的障碍物包含了道路的边界信息,如何通过这些障碍物提取出道路,并用合适的模型来表示道路是本文的工作之一。
SVM[11]是一种二类分类模型,其最优分类超平面能够使得类间隔最大化。如图 1中的栅格地图所示,道路两侧的障碍物可以视作两类目标,以此作为训练样本进行训练得到的SVM分类超平面可以使得两侧障碍物具有最大间隔。分类超平面在二维栅格地图上的投影轨迹不仅平滑而且能够确保远离障碍物,因此可以作为UGV的可行驶路径。
首先定义(pi, γi)作为SVM的训练样本,其中pi=(xi, yi)表示在车体坐标系下第i个障碍物的坐标,γi∈{-1, +1}为类别标签。鉴于文献[10]中线性分类器不能处理弯道的问题,本文将使用径向基函数(radial basis function,RBF)作为核函数建立非线性SVM分类器,其定义为:
| $ K({{\mathit{\boldsymbol{p}}}_{i}}, {{\mathit{\boldsymbol{p}}}_{j}})=\text{exp}(-{{\left\| \text{ }{{\mathit{\boldsymbol{p}}}_{i}}-{{\mathit{\boldsymbol{p}}}_{j}} \right\|}^{2}}/{{\delta }^{2}}) $ | (1) |
非线性SVM超平面方程为:
| $ f\left( {{\mathit{\boldsymbol{p}}}_{j}} \right)=\sum\limits_{i=1}^{n}{{{\alpha }_{i}}{{\gamma }_{i}}K({{\mathit{\boldsymbol{p}}}_{i}}, {{\mathit{\boldsymbol{p}}}_{j}})+b=0~} $ | (2) |
式中:n为支持向量个数;αi为拉格朗日乘子。
在局部栅格地图中,满足式(2)的点构成的轨迹的一部分可作为行驶路径。如图 2所示,SVM超平面轨迹能够有效地将两侧障碍物分开,其中支持向量是离轨迹最近的点,因此都分布在路径上最狭窄的地方。

|
Download:
|
| 图 2 SVM超平面示意图 Fig. 2 SVM hyperplane schematic diagram | |
由于这个性质,支持向量所对应的障碍物可以用来判断路径的可通过性。
| $ D({{\mathit{\boldsymbol{p}}}_{i}})=\left| \mathit{\boldsymbol{w}}\cdot {{\mathit{\boldsymbol{p}}}_{i}}+b \right|/\left\| \mathit{\boldsymbol{w}} \right\| $ | (3) |
| $ D({\mathit{\boldsymbol{p}}_i}) < {\mathit{w}_{{\rm{car}}}}/2 + {d_{{\rm{safe}}}} $ | (4) |
式(3)可以计算得到支持向量到超平面的距离,式中w和b是在样本进行训练之后得到。若当存在支持向量pi满足式(4)时,说明路径并不安全。wcar是车宽,dsafe是一个安全参数,其值根据实验确定。
2 路径规划算法 2.1 栅格地图预处理与分类在UGV行驶过程中,局部地图会以固定周期进行更新。每次更新都会得到新的SVM超平面轨迹,由于存在环境感知的不确定性因素(如出现新的障碍物,车辆颠簸引起的测量误差等),所求得的超平面轨迹并不是完全一致的。
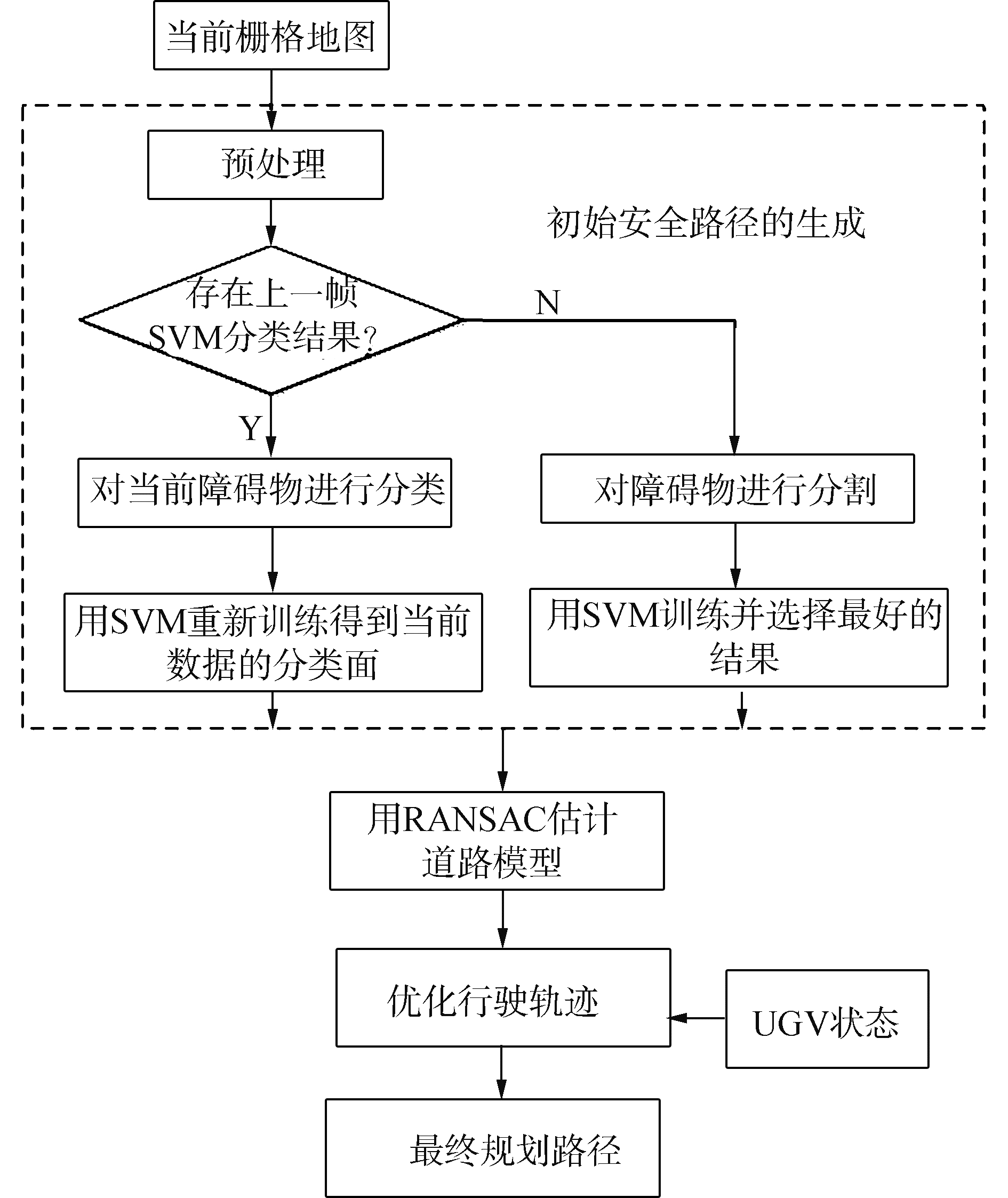
图 3是将多帧局部栅格地图以及SVM超平面轨迹投影到同一坐标系下的情形。可以看到SVM超平面轨迹线并不重合,这是由于UGV前进中感知到的环境不断变化所致。针对这一问题进行改进,利用随机采样一致性[12-14](random sample consensus, RANSAC)从多帧投影数据中估计道路模型。整个算法流程如图 4所示,主要有3个步骤:1)初始安全路径的生成;2)RANSAC估计道路模型;3)生成最终路径。

|
Download:
|
| 图 3 多帧数据示意 Fig. 3 Multi-frame data schematic diagram | |
|
Download:
|
| 图 4 路径规划算法流程 Fig. 4 Flow diagram of the path planning algorithm | |
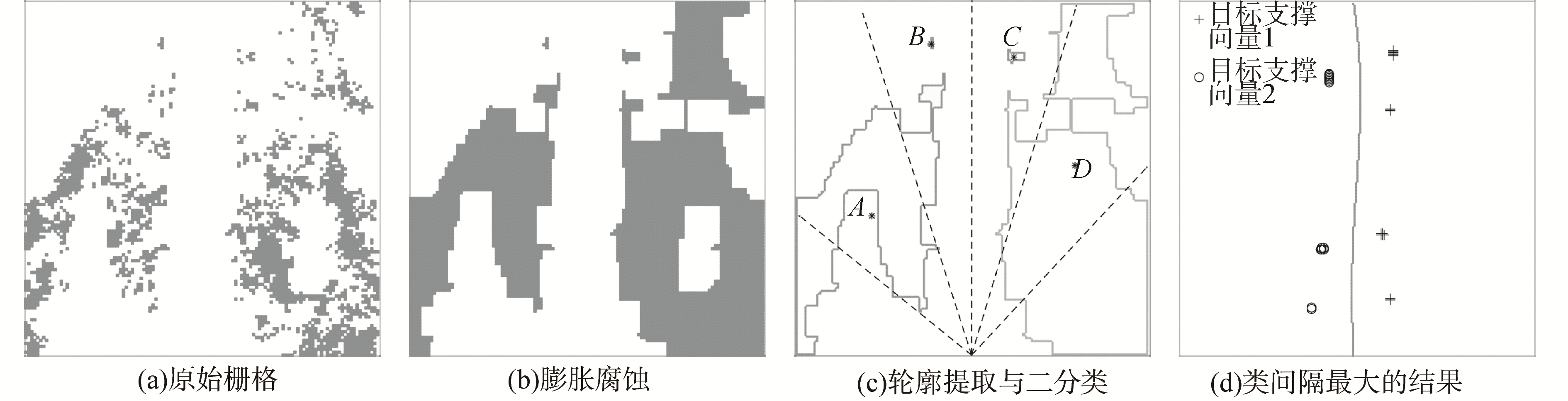
本文所使用的栅格地图大小为30 m×30 m,栅格分辨率为12.5 cm×12.5 cm,原始栅格数据如图 5(a)所示。原始栅格数据并不适合作为SVM训练样本,需要进行预处理与分类,具体步骤如下:
|
Download:
|
| 图 5 数据处理与分类 Fig. 5 Data processing and classification | |
1) 对原始栅格使用大小为一个车宽的窗口进行膨胀、腐蚀处理(见图 5(b))。将栅格数据作为二值图像,利用链码跟踪[15]算法提取障碍物的轮廓,每一个闭合轮廓被标记为一个障碍物目标(见图 5(c))。定义pij=(xij, yij)为第i个障碍物的第j个轮廓点坐标,pci=(xci, yci)为第i个障碍物的质心坐标,(pij, γi)为本文所使用的训练样本;
2) 将Nobs个障碍物转换到极坐标系下进行分割,将所有的障碍物分成两类,记分割线左侧的障碍物类别标签记为γi=-1,右侧为γi=+1。接着将所有的训练样本进行训练得到一组w和b。如图 5(c)中有4个障碍物,每次分割成两组,因此有5种分割方式。对Nobs+1种分割依次训练之后得到Nobs+1组w和b以及对应的超平面。最后,保留其中类间隔最大的一组w和b,其所构成的超平面Hmax则为当前所求的安全路径(见图 5(d))。
在UGV行驶过程中,道路衍生的趋势可以认为是在缓慢变化的,因此在新的一帧栅格数据到来时,可以直接使用上一帧的SVM训练结果H′对当前一帧的障碍物目标进行分类。接着对分类结果再次进行训练可以得到当前栅格数据的超平面H。具体过程如下:
将当前帧的Nobs个障碍物轮廓点坐标pij=(xij, yij)转换到上一帧的车体坐标系下,得到p′ij=(x′ij, y′ij),然后利用上一帧的H′对这些轮廓点p′ij进行分类,得到每个障碍物的类别标签γi。由前面假设道路衍生趋势变化缓慢可以得知相邻两帧之间同一个障碍物目标的类别标签γi不应该发生变化,因此可得到当前帧的训练样本(pij, γi),再次训练后得到当前帧的H。
2.2 基于RANSAC的路径提取由于多帧投影SVM超平面轨迹存在不一致的问题,本文提出在多帧轨迹的点集上使用RANSAC算法进行路径提取,而RANSAC算法使用的道路估计模型如下:
| $ f\left( y \right) = a + by + c{y^2} + d{y^3} $ | (5) |
使用RANSAC算法从散乱的多帧SVM超平面轨迹数据中提取出路径可以减少环境的不确定性所带来的干扰。同时相对SVM超平面方程,形式简单的三次多项式更易于求取轨迹的曲率。道路模型对应的曲率公式可表示为:
| $ k = \left| {f{{\left( y \right)}^{\prime \prime }}} \right|/{\left( {1 + f{{\left( y \right)}^\prime }^2} \right)^{3/2}} $ | (6) |
| $ \rho = {k^{ - 1}} $ | (7) |
根据曲率公式(6),可以评估路径的弯曲程度,为UGV速度控制提供依据。式(7)是相对应的道路半径。
用RANSAC算法估计道路模型,需要的参数如下:local_points为局部地图中的所有样本点;p为得到不含离群点子集的概率;s为估计模型M所需的最小样本数;τ为样本点被认为符合模型M时可容忍的误差;N为最大试验次数。RANSAC算法首先从总体样本中随机采样s个样本点,估计出模型M,然后用剩余的样本点对模型M的一致性评估并打分,重复这一过程得到一个评分最大的模型M。
本文在使用RANSAC算法进行模型估计前先要对使用的数据进行预处理,具体如下:
1) 在t时刻,首先将全局坐标系下的多帧SVM超平面轨迹点转换到局部车体坐标系下,然后合并t时刻求得的SVM超平面轨迹Ht,得到局部坐标系下的点集local_points。接着将local_points中位于车体前方的点qi转换到全局坐标系下,并保存在点集global_points中为下一帧处理做准备。
2) 根据式(5)可知,本文使用RANSAC算法需要在轨迹点集中随机采样4个点来估计道路模型M。而在UGV正常行驶过程中,道路可以认为是在车体坐标系下沿着y轴方向单调递增的,因此将投影点集沿着y轴方向分成4段,对每一段内的点集随机采样一个点。通过对点集进行分段归类,这样使得随机采样点有效分布在整个轨迹线上以提高RANSAC收敛速度。
图 6是2个场景下的RANSAC结果示意图。其中浅色的是多帧SVM超平面轨迹投影到t时刻车体坐标系下的结果,深色的轨迹是RANSAC的结果。RANSAC轨迹由大量的SVM轨迹点估计得到,不仅远离障碍物,并且将复杂的超平面方程转换到简单的3次多项式以便后续处理。

|
Download:
|
| 图 6 RANSAC结果示意 Fig. 6 Results of RANSAC schematic diagram | |
1) 更新策略
规划模块在每一个执行周期都会生成一条RANSAC路径,但是并不是每次都采用新的RANSAC路径,而是当满足一定条件时才进行更新,更新条件如下:
① t时刻,Ruse∩{1-Cfree}≠∅则进行更新。Ruse表示当前使用中的RANSAC轨迹,Cfree表示UGV的自由空间。在UGV行驶过程中,局部地图中出现了新的障碍物,导致沿着Ruse行驶将有碰撞的危险时,先去除local_points中有碰撞的点,然后重新生成t时刻的无碰撞RANSAC轨迹Rt,并更新Ruse=Rt和global_points。
② t时刻,Ruse剩下的可行驶长度drest满足drest < de,则重新生成t时刻的无碰撞RANSAC轨迹Rt并更新Ruse=Rt。其中de=v2/(2·amax),v为当前UGV速度,amax为UGV的最大制动加速度。
2) 最终路径生成
最终的路径通过结合UGV当前自身的状态以及剩余可行驶路径来选择控制点,最后用贝塞尔曲线拟合得到。具体步骤如下:
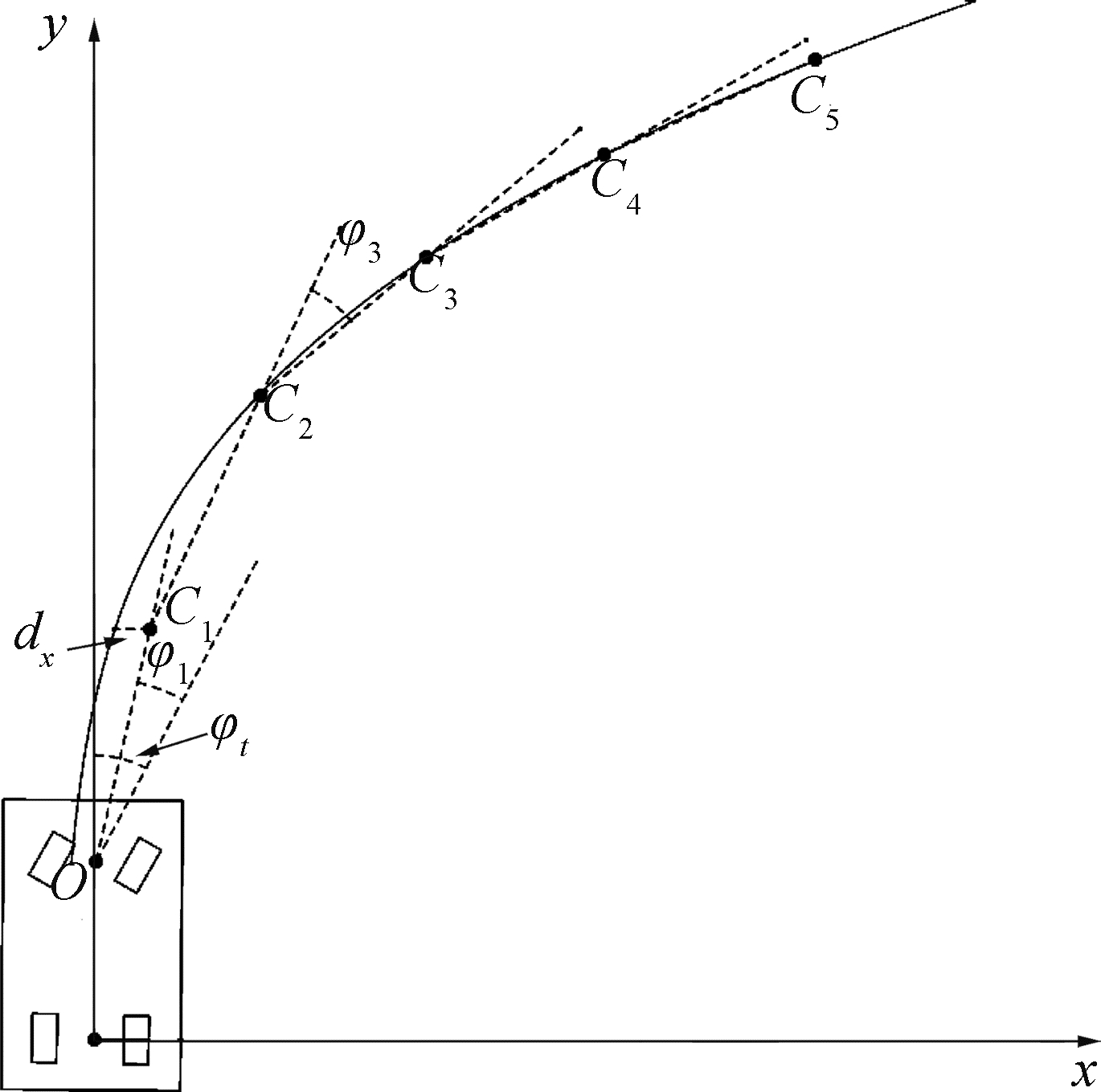
① 将剩余可行驶长度drest进行5等分得到每段长度dseg,接下来需要先确定控制点O1。见图 7,设
| $ \left\{ \begin{array}{l} {x_{{O_1}}} = {d_{{\rm{seg}}}} \cdot {\rm{sin}}\left( {{\varphi _1} + {\varphi _t}} \right)\\ {y_{{O_1}}} = {d_{{\rm{seg}}}} \cdot {\rm{cos}}\left( {{\varphi _1} + {\varphi _t}} \right) \end{array} \right. $ | (8) |
| $ {\varphi _i} = \mathop {{\rm{argmin}}}\limits_{\varphi \in \left[{-\Delta \varphi, \Delta \varphi } \right]} \left( {{c_1}\cdot\frac{{\left| \varphi \right|}}{{\Delta \varphi }} + {c_2} \cdot \frac{{{\rm{d}}\mathit{x}}}{{{\mathit{d}_{{\rm{max}}}}}}} \right) $ | (9) |
|
Download:
|
| 图 7 控制点选取 Fig. 7 The selection of control points | |
O1坐标可由式(8)计算得到,其中φ1取值应使得式(9)取到最小值。其中,式(9)前半部分用于控制曲线的曲率,后半部分用于控制曲线尽量靠近安全的区域。其中dx表示控制点Oi到Ruse的水平距离,
② 根据式(9)来确定后续控制点。确定第i个控制点Oi时,向量
| $ B\left( t \right) = \sum\limits_{i = 0}^5 {\frac{{5!}}{{i!\left( {5 - i} \right)!}}{{\left( {1 - t} \right)}^{5 - i}}{t^i}{O_i}, t \in \left[{0, 1} \right]} $ | (10) |
为了验证提出算法的有效性与正确性,利用实验平台“行健号”(见图 8)在非结构化道路上进行了大量测试。

|
Download:
|
| 图 8 实验平台 Fig. 8 Experiment platform | |
本节将本文提出的算法与文献[7-8]以及文献[10]的算法进行了对比。由于FM2算法和Circle-based算法需要起点和终点,因此将本文算法得到路径的两端作为FM2算法和Circle-based算法所需的起点和终点。
图 9(a)分别为强光、阴暗、雨天、植被覆盖以及岔道几个不同场景的视觉图像。其中部分场景下,图像受到光照、天气以及道路环境干扰,基于视觉的道路检测算法不能稳定工作。图 9(b)是本文算法的道路提取结果,图 9(c)是采用FM2算法得到的路径,图 9(d)是采用Circle-based算法得到的路径,图 9(e)是使用Linear SVM得到的检测结果。从图中可以看到本文算法、FM2算法和Circle-based算法各场景下都能生成有效路径,而Linear SVM无法处理道路曲率较大的情况。因此,在场景一的相关对比实验中没有Linear SVM的结果。

|
Download:
|
| 图 9 不同场景的提取路径对比 Fig. 9 The comparison of the path extracted in different scenes | |
图 10中的箱形图显示了各个场景下、不同算法生成的轨迹距离栅格地图中障碍物的最大值、平均值以及最小值。从图中可以看到,在安全性方面,本文算法结果整体优于Linear SVM的结果;在第1个和第3个场景下,本文算法是最优的;在第2个场景下,本文算法与最优的FM2算法较为接近,且优于Circle-based算法;在第4个场景下,由于栅格地图较为狭长,各个算法生成的轨迹较为接近,所以各算法结果都比较接近;在场景五中,FM2算法生成的路径会趋向更为安全的区域,而Circle-based算法在扩展过程中,后继圆的圆心是随机采样的,其中半径较大的圆会被优先扩展以保证路径的安全性,因此这2种算法在存在岔道的场景下生成的路径具有较高的安全性,但是路径长度并不是最优的。

|
Download:
|
| 图 10 离开障碍物距离的对比 Fig. 10 The comparison of the distance away from obstacles | |
图 11是各个场景下、不同算法生成轨迹的变化程度的对比。由于Linear SVM的线性特性生成的轨迹是直线,因此并没有将其加入对比。轨迹变化程度的定义如下:设qi-1、qi和qi+1是轨迹上的连续采样点。

|
Download:
|
| 图 11 曲线变化对比 Fig. 11 The comparison of the change of the curve | |
从图 11可以看到,本文算法生成的轨迹是变化程度是最小的,FM2算法和Circle-based算法虽然都结合了车辆运动学模型进行了优化,但是FM2生成轨迹趋向于远离障碍物区域,易受到障碍物分布的影响,而Circle-based则以类似快速扩展随机树(rapidly-exploring random tree, RRT)的方式进行空间搜索,同时扩展半径较大的圆以确保路径的安全,其结果具有一定的随机性。本文算法无论是初步生成的SVM轨迹,还是RANSAC估计出的道路轨迹都具有较好的安全性,而且变化程度较小,易作为UGV的可跟踪路径。
图 12的箱形图显示了各个场景下、不同算法生成轨迹所需的计算耗时的最大值、平均值以及最小值。相对较为耗时的FM2算法和Circle-based算法,本文算法和Linear SVM算法单位执行时间都基本在50 ms以内。相比Linear SVM算法,本文算需要利用RANSAC算法从多帧投影点中来估计最终的道路模型,因此本文算法相对Linear SVM算法要多出一部分开销。在使用RANSAC算法时,本文通过以下策略来减少时间开销:1)用上一帧的道路模型参数作为当前估计道路模型参数的初始值;2)SVM超平面轨迹进行投影时,增加采样点的步长;3)维护一个基于时间权值的SVM轨迹队列,新的SVM轨迹会被分配一个较高的时间权值,随着时间流逝该权值会逐渐减少,而当权值小于设定阈值时,该SVM轨迹会被移出队列。

|
Download:
|
| 图 12 运行时间对比 Fig. 12 The comparison of runtime | |
图 13分别为3个场景下的本文算法得到的最终路径。生成的路径对于底层控制来说是平滑且易于跟踪,对车辆来说也是远离两侧障碍物,能够保证车辆的安全。

|
Download:
|
| 图 13 本文算法生成的最终路径 Fig. 13 The final paths generated by proposed method | |
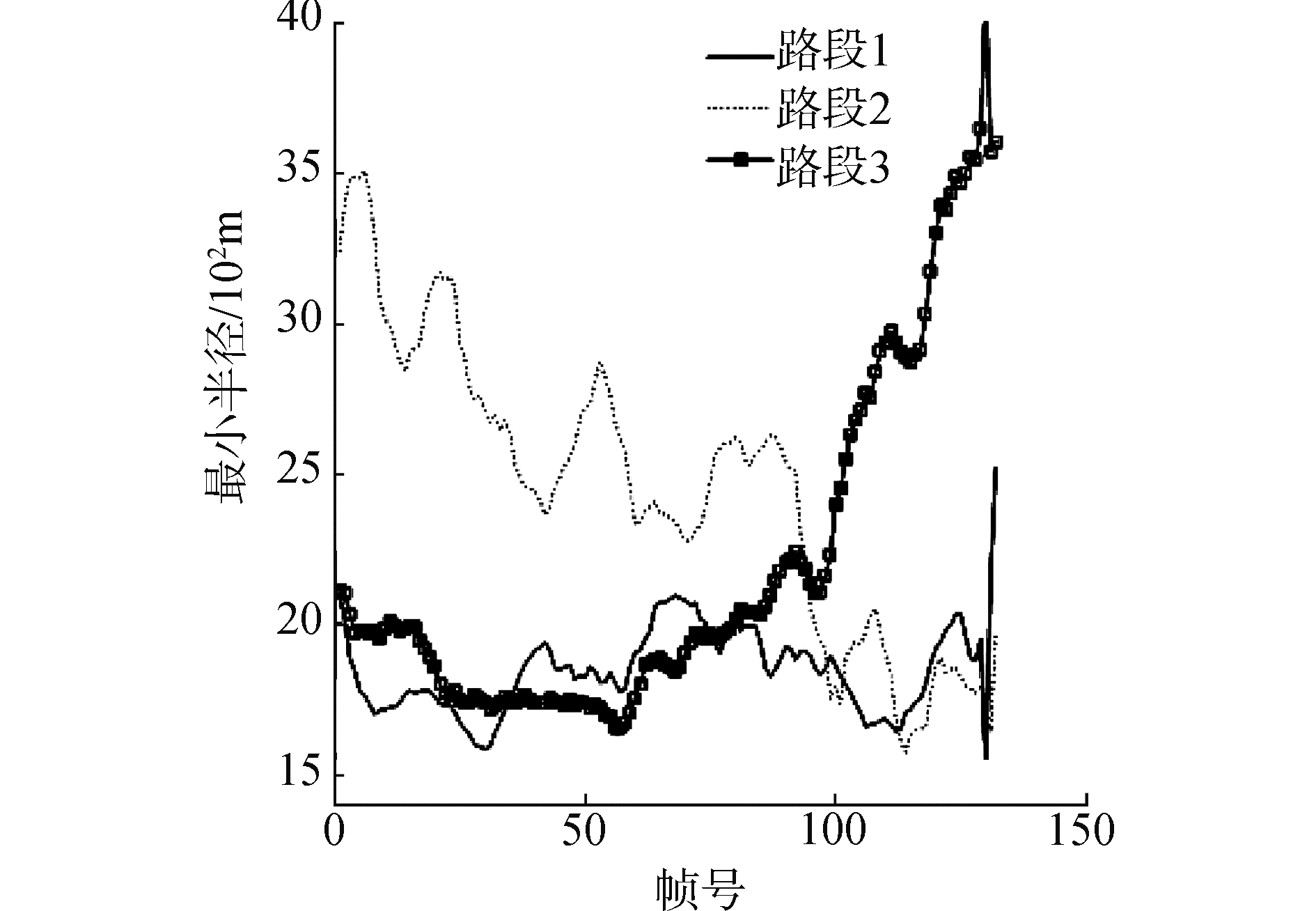
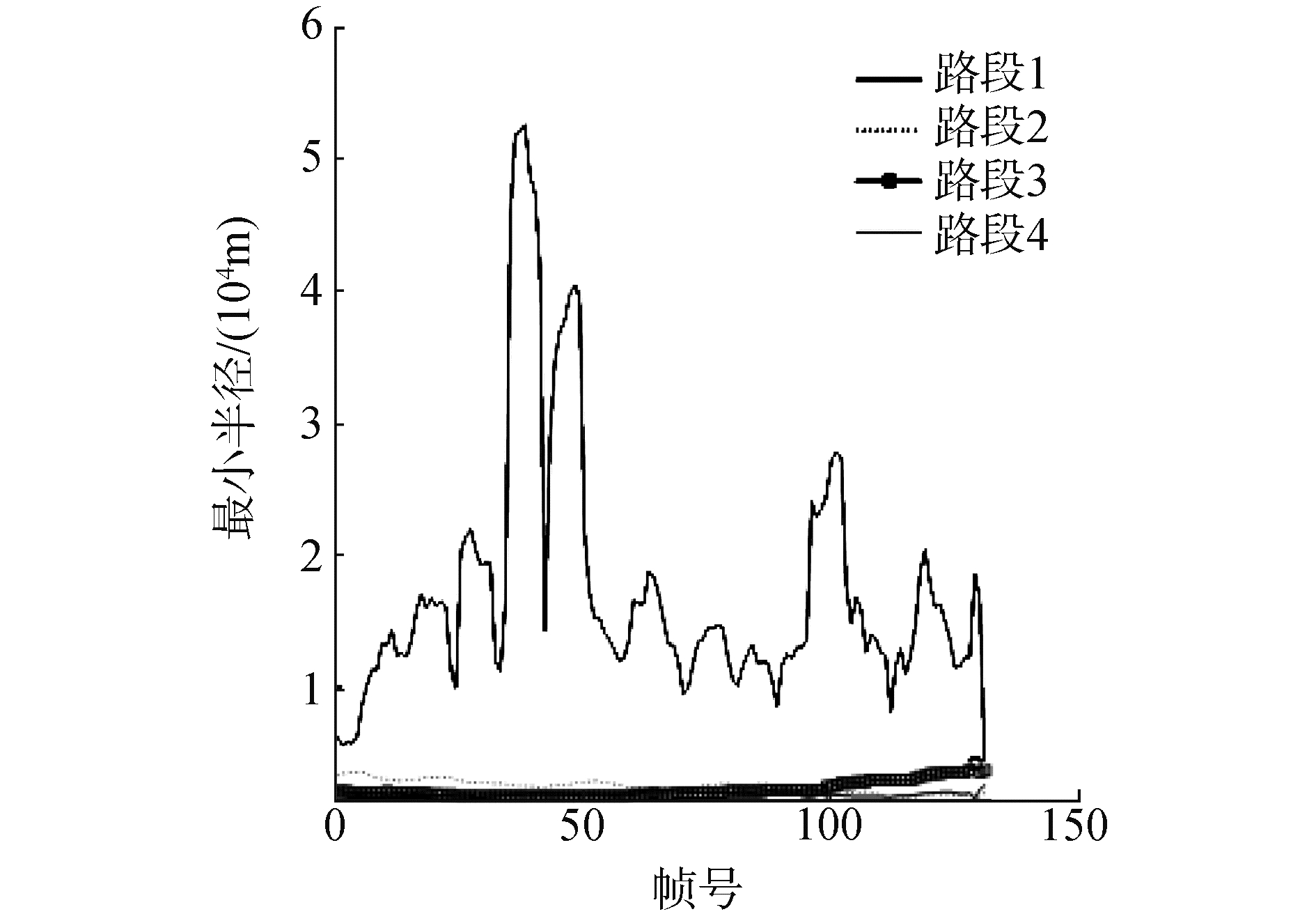
对于行驶路径曲率的分析能够有助于地面无人车辆对速度进行有效地控制,从而提高地面无人车辆自主行驶的安全性与舒适性。因此,本文在上述算法提取的三次多项式模型的基础上,对4种不同路段数据进行了对比分析。路段1是急弯的情况,路段2是由缓弯渐变为急弯的情况,路段3是出急弯的情况,路段4是直道的情况。根据式(7)、(8)可以得到每一帧RANSAC路径上的最小半径值。
图 14是3个弯道路段的对比。从图中可以看出曲线的变化是符合道路的变化情况的,路段1的最小半径值始终比较低,符合处于急弯的情况;路段2的数值则是逐渐变小,符合从缓弯进入急弯的情况;路段3的数值则是逐渐变大,符合从急弯驶出的情况。需要注意的是所求得的最小半径值并不是道路真正的半径。
|
Download:
|
| 图 14 不同弯道路段的最小半径对比 Fig. 14 The comparison of the minimal radius of different curves | |
从图 15可以看出,直线路段4的最小半径值明显大于其他3个弯道路段的数值,虽然路段4的最小半径值也有一定程度的波动,但其数值本身很高,从宏观上来说对应的RANSAC路径并不会发生剧烈变化,并不会影响将路段4判断为直道这一结果。
|
Download:
|
| 图 15 直道与弯道路段的最小半径对比 Fig. 15 The comparison of the minimal radius of straight and curves | |
1) 本文算法利用非线性SVM从栅格地图中有效地提取出安全的路径,在多帧SVM投影轨迹点集上使用RANSAC来估计道路模型,并得到RANSAC路径。在不同场景下,与文献[7-8]和文献[10]进行了对比实验,结果表明生成的RANSAC路径具有较好的安全性,而且平滑易于车辆进行跟踪。算法具有较好的实时性,能够满足UGV路径规划的实际需求。
2) 本文算法依据三次多项式建立道路模型,对道路的弯曲程度进行了初步的鉴别分析,实验数据分析得到结果与实际场景较为吻合。
对于道路曲率数据的进一步处理以及如何有效地结合地面无人车辆行驶速度控制将是今后开展的工作之一。
| [1] |
李青, 郑南宁, 马琳, 等. 基于主元神经网络的非结构化道路跟踪[J]. 机器人, 2005, 27(3): 247-251. LI Qing, ZHENG Nanning, MA Lin, et al. Tracking of unstructured road based on principal component analysis neural networks[J]. Robot, 2005, 27(3): 247-251. DOI:10.3321/j.issn:1002-0446.2005.03.011 (  0) 0)
|
| [2] |
朱株.基于三维数据面向无人车导航的非结构化场景理解[D].杭州: 浙江大学, 2014. ZHU Zhu. 3D data based understanding of unstructured scenes for vehicle navigation[D]. Hangzhou: Zhejiang University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10335-1015558799.htm (  0) 0)
|
| [3] |
GERAERTS R. Planning short paths with clearance using explicit corridors[C]//Proceedings of 2010 IEEE International Conference on Robotics and Automation. Anchorage, USA, 2010: 1997-2004. https://ieeexplore.ieee.org/document/5509263/
(  0) 0)
|
| [4] |
BHATTACHARYA P, GAVRILOVA M L. Roadmap-based path planning-using the voronoi diagram for a clearance-based shortest path[J]. IEEE robotics & automation magazine, 2008, 15(2): 58-66. (  0) 0)
|
| [5] |
RICHTER C, WARE J, ROY N. High-speed autonomous navigation of unknown environments using learned probabil-ities of collision[C]//Proceedings of 2014 IEEE International Conference on Robotics and Automation. Hong Kong, China, 2014: 6114-6121. http://www.mendeley.com/catalog/highspeed-autonomous-navigation-unknown-environments-using-learned-probabilities-collision/
(  0) 0)
|
| [6] |
YU Chong, QIU Qiwen, CHEN Xiong. A hybrid two-dimensional path planning model based on frothing construction algorithm and local fast marching method[J]. Computers & electrical engineering, 2013, 39(2): 475-487. (  0) 0)
|
| [7] |
GARRIDO S, MORENO L, GÓMEZ J V. Motion planning using fast marching squared method[M]//CARBONE G, GOMEZ-BRAVO F. Motion and Operation Planning of Robotic Systems: Background and Practical Approaches. Cham: Springer, 2015: 223-248.
(  0) 0)
|
| [8] |
CHEN Chao, RICKERT M, KNOLL A. Kinodynamic motion planning with space-time exploration guided heuristic search for car-like robots in dynamic environments[C]//Proceedings of 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems. Hamburg, Germany, 2015: 2666-2671. Kinodynamic motion planning with space-time exploration guided heuristic search for car-like robots in dynamic environment
(  0) 0)
|
| [9] |
刘梓, 唐振民, 任明武. 基于3D激光雷达的实时道路边界检测算法[J]. 华中科技大学学报(自然科学版), 2011, 39(S2): 351-354. LIU Zi, TANG Zhenmin, REN Mingwu. Algorithm of real-time road boundary detection based on 3D lidar[J]. Journal of Huazhong University of Science & Technology (natural science edition), 2011, 39(S2): 351-354. (  0) 0)
|
| [10] |
BAGCHI S. Rapid close surrounding evaluation for autonomous commercial vehicles[D]. Göteborg: Chalmers University of Technology, 2016. Rapid close surrounding evaluation for autonomous commercial vehicle
(  0) 0)
|
| [11] |
MARATHE A S, VYAS V, CHAVHAN M. Petrographic image classification using optimized radial basis function support vector machine & validation of its asymptotic behavior[C]//Proceedings of 2016 IEEE International Conference on Signal Processing, Communications and Computing. Hong Kong, China, 2016: 1-6. https://ieeexplore.ieee.org/document/7753703
(  0) 0)
|
| [12] |
FONTANELLI D, CAPPELLETTI M, MACⅡ D. A RANSAC-based fast road line detection algorithm for high-speed wheeled vehicles[C]//Proceedings of 2011 IEEE International Instrumentation and Measurement Technology Conference. Binjiang, China, 2011: 1-6. https://www.mendeley.com/catalogue/ransacbased-fast-road-line-detection-algorithm-highspeed-wheeled-vehicles/
(  0) 0)
|
| [13] |
SMADJA L, NINOT J, GAVRILOVIE T. Road extraction and environment interpretation from LiDAR sensors[J]. International archives of photogrammetry and remote sensing, 2010, 38: 281-286. (  0) 0)
|
| [14] |
LI Yingmao, GANS N R. Predictive-RANSAC: an effective data fitting and tracking method with application in curve tracking in video[C]//Proceedings of 2016 American Control Conference. Boston, USA, 2016: 3620-3625. https://ieeexplore.ieee.org/document/7525475
(  0) 0)
|
| [15] |
LI Wen, LI Yan, MA Yide. An efficient contour tracking and coding algorithm based on vertex chain code[C]//Proceedings of the 2012 8th International Conference on Intelligent Information Hiding and Multimedia Signal Processing. Piraeus, Greece, 2012: 514-517. https://ieeexplore.ieee.org/document/6274294
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


