2. 西安理工大学 高等技术学院, 陕西 西安 710048
2. Faculty of Higher Vacational and Technical Education, Xi'an University of Technology, Xi'an 710048, China
近年来,NAND闪存由于其高速、低能耗、抗震动和良好性能等优点已成为现代数据存储系统的存储介质[1-3]。MLC型NAND闪存通过一个单元存储4种不同电位表示2 bit数据来提高NAND闪存的数据存储密度。然而,目前NAND闪存芯片制作工艺已达到20 nm级别,MLC闪存相邻单元间的寄生耦合电容效应变强而导致的单元间干扰(cell-to-cell interference,CCI)成为影响闪存系统可靠性的主要原因[4-5]。
目前,提高MLC闪存存储系统可靠性的主要方法有2种,第1种是通过闪存存储信道检测技术来减弱CCI影响,进而可准确的读取MLC阈值电压,有效降低原始误比特率(raw bit error rate,RBER)[6-7]。第2种是通过纠错编码技术来提高闪存系统的可靠性。然而,随着半导体集成度的提高,传统的BCH纠错码已经不能满足MLC闪存系统数据存储可靠性要求。逼近容量限的低密度校验码(low-density parity-check codes,LDPC)由于其更强纠错能力而可用来提高闪存系统的可靠性[8-11]。
利用MLC闪存数据特征,Zhao等[9]借助LDPC码的最小和译码算法(min-sum,MS)来提高MLC型NAND闪存存储数据的可靠性。Dong等[10]给出了闪存信道LDPC码的对数似然比(log-likelihood ratio, LLR)的计算方法。然而,LDPC码的MS译码算法等软判决译码方法需要实数运算而增加了译码的复杂性。尽管比特翻转(bit-flipping,BF)译码算法的性能不如MS译码算法,但是BF译码算法具有计算过程简单和硬件实现复杂度低等特点,易于在闪存系统中实现。利用相同方差的4个AWGN信道来刻画MLC闪存信道模型,Hu等[11]提出基于比特翻转算法的SSD系统,但是这种刻画MLC闪存的信道模型不能准确描述MLC闪存阈值电压分布。
本文分析了CCI噪声影响下MLC阈值电压分布的准确数学统计模型[10]、MLC闪存数据存储信道错误规律。在CCI噪声原理的基础上,给出了利用蒙特卡罗仿真计算相邻阈值电压分布重叠区域的方法进而确定MLC阈值电压对应存储比特的可靠性,并将此可靠性引入到变量节点的翻转判定规则中,设计了MLC闪存的比特翻转规则,提出了一种适用于MLC闪存系统的BF译码算法,该算法具有良好的译码性能和更快的收敛速度,可以达到译码性能与译码复杂性之间更好折衷。
1 MLC型NAND闪存及其信道模型 1.1 MLC阈值电压模型建立MLC单元是MLC型NAND闪存的基本存储单元,可存储2 bit数据,其中左侧的比特称为最高有效位(most significant bit,MSB),右侧的比特称为最低有效位(least significant bit,LSB)。MLC闪存中四种不同的电位利用格雷码映射成不同的逻辑值(s0=00, s1=01, s2=11, s3=10),相邻状态的逻辑值仅有一比特发生变化,其中s0=00表示擦除状态阈值电压映射的逻辑值,s1=01, s2=11, s3=10分别表示三个不同编程状态阈值电压映射的逻辑值[12]。
1) 擦除状态(s0=00)的概率模型。MLC闪存执行块擦除之后每个MLC闪存单元阈值电压处于擦除状态,擦除状态的初始阈值电压分布可使用高斯分布近似表示[13-14]:
| $ {p_{{s_0}}}\left( x \right) = \frac{1}{{{\sigma _e}\sqrt {2{\rm{ \mathsf{ π} }}} }}{{\rm{e}}^{ - \frac{{{{\left( {x - {\mu _e}} \right)}^2}}}{{2\sigma _e^2}}}} $ | (1) |
式中:μe和σe分别表示擦除状态阈值电压分布的期望和标准差。
2) 编程状态(s1=01, s2=11和s3=10)的概率模型。MLC闪存单元编程操作是通过向浮栅中注入电荷改变其阈值电压进而实现不同逻辑值(s1=01, s2=11和s3=10)的写入[15]。每次迭代编程操作浮栅的阈值电压增量为ΔVpp,直到电压值达到目标校验电压Vp之后便停止注入电荷,MLC编程状态阈值电压的数学模型可近似表示为[Vp, Vp+ΔVpp]的均匀分布[13-14]。
| $ {p_{{s_1}\left| {{s_2}} \right.\left| {{s_3}} \right.}}\left( x \right) = \left\{ \begin{array}{l} \frac{1}{{\Delta {V_{pp}}}},\;\;\;\;{V_p} \le x \le {V_p} + \Delta {V_{pp}}\\ 0,\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (2) |
3) 读操作。MLC闪存单元存储信息的读操作分两步:
① 对MLC闪存单元阈值电压的感知。设2p(p≥2的整数)表示MLC闪存单元整个阈值电压区间划分的子区间个数(称p为MLC闪存单元阈值电压的感知精度)[10],2p个子区间需要2p-1个参考电压将MLC阈值电压区间进行划分。感知的方法是MLC闪存单元的控制门栅从小至大逐一加载参考电压,测试浮栅是否可以被导通。如果MLC闪存单元的浮栅可以导通,那么MLC闪存单元阈值电压处于该参考电压的子区间[Rl, Rr)内,其中Rl和Rr表示阈值电压区间的参考电压;
② 将感知的MLC阈值电压映射成相应的比特值。本文采用软判决感知读取MLC闪存单元中存储的比特值:针对第一步感知得到的MLC阈值电压区间[Rl, Rr),借助下式可计算出MLC闪存单元存储比特的LLR值[10]:
| $ \left\{ \begin{array}{l} {\rm{LL}}{{\rm{R}}_{{\rm{MSB}}}} = \log \frac{{\int_{{R_l}}^{{R_r}} {\left\{ {{p_{{s_2}}}\left( x \right) + {p_{{s_3}}}\left( x \right)} \right\}{\rm{d}}x} }}{{\int_{{R_l}}^{{R_r}} {\left\{ {{p_{{s_0}}}\left( x \right) + {p_{{s_1}}}\left( x \right)} \right\}{\rm{d}}x} }}\\ {\rm{LL}}{{\rm{R}}_{{\rm{LSB}}}} = \log \frac{{\int_{{R_l}}^{{R_r}} {\left\{ {{p_{{s_1}}}\left( x \right) + {p_{{s_2}}}\left( x \right)} \right\}{\rm{d}}x} }}{{\int_{{R_l}}^{{R_r}} {\left\{ {{p_{{s_0}}}\left( x \right) + {p_{{s_3}}}\left( x \right)} \right\}{\rm{d}}x} }} \end{array} \right. $ | (3) |
然后,通过比特信息的硬判决公式可得到MLC闪存单元中存储的比特值:
| $ {b_{{\rm{MSB}}\left| {{\rm{LSB}}} \right.}} = \left\{ \begin{array}{l} 1,\;\;\;\;{\rm{LL}}{{\rm{R}}_{{\rm{MSB}}\left| {{\rm{LSB}}} \right.}} > 0\\ 0,\;\;\;\;其他 \end{array} \right. $ | (4) |
由于相邻MLC闪存单元之间存在寄生耦合电容效应,MLC闪存单元的编程操作会对其相邻单元的阈值电压产生影响[16]。NAND闪存常用CCI干扰较小的全位线结构,该结构同一字线上的所有闪存单元同时进行编程操作,因此每个单元最多只受相邻字线上3个闪存单元的编程影响(如图 1所示)。

|
Download:
|
| 图 1 NAND闪存的阵列结构 Fig. 1 NAND flash memory array structure | |
设(i, j)表示第i个字线(word line,WL)和第j个位线(bit line,BL)上的MLC闪存单元,位于(i, j)的MLC单元阈值电压受到下一相邻字线(WL=i+1)CCI影响强度F可计算:
| $ \begin{array}{*{20}{c}} {{F_{\left( {i,j} \right)}} = \sum\limits_{k \in \left\{ {j - 1,j,j + 1} \right\}} {\left( {\Delta {V_{\left( {i + 1,k} \right)}} \cdot {\gamma _k}} \right)} = }\\ {{\gamma _{xy}} \cdot \Delta {V_{\left( {i + 1,j - 1} \right)}} + {\gamma _y} \cdot \Delta {V_{\left( {i + 1,j} \right)}} + {\gamma _{xy}} \cdot \Delta {V_{\left( {i + 1,j + 1} \right)}}} \end{array} $ | (5) |
式中:ΔV(i+1, k)表示相邻字线的MLC闪存单元编程操作前后阈值电压的增量,γy和γxy分别表示垂直耦合系数和对角线耦合系数。由于生产MLC闪存时工艺本身的振动问题,耦合系数系数γy和γxy服从有界高斯分布[6-14]:
| $ {p_\gamma }\left( x \right) = \left\{ \begin{array}{l} \frac{{{c_\gamma }}}{{{\sigma _\gamma }\sqrt {2{\rm{ \mathsf{ π} }}} }}{{\rm{e}}^{ - \frac{{{{\left( {x - {\mu _\gamma }} \right)}^2}}}{{2\sigma _\gamma ^2}}}},\;\;\;\;\left| {x - {\mu _\gamma }} \right| \le {w_\gamma },\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (6) |
式中:cγ用来确保有界高斯分布的积分值为1;σγ=0.3μγ;wγ=0.2μγ。
由于闪存不同字线之间干扰的程度不同,耦合系数γy和γxy的数学期望μγ服从有界高斯分布公式[6-14]:
| $ {p_{{\mu _\gamma }}}\left( t \right) = \left\{ \begin{array}{l} \frac{{{c_t}}}{{{\sigma _t}\sqrt {2{\rm{ \mathsf{ π} }}} }}{{\rm{e}}^{ - \frac{{{{\left( {t - {\mu _t}} \right)}^2}}}{{2\sigma _t^2}}}},\;\;\;\;\left| {t - {\mu _t}} \right| \le {w_t},\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (7) |
式中:ct确保有界高斯分布的积分值为1;σt=0.2μt和wt=0.2μt。设γy的期望μt为0.08s,γxy的期望μt为0.006s,参数s表示CCI噪声耦合强度系数,通过调节耦合强度系数s来改变CCI噪声的干扰强度[6]。
1.3 减弱CCI噪声的影响电路级噪声CCI造成MLC闪存单元的阈值电压与初始编程电压不同而导致MLC闪存存储数据错误。为了减弱CCI噪声对MLC闪存单元阈值电压的影响,可对感知后的MLC阈值电压进行修正。修正的思路是在感知后的MLC阈值电压基础上减去CCI噪声影响的估计值,从而得到的MLC阈值电压值更加准确。设位于(i, j)MLC闪存单元感知的阈值电压和修正后的阈值电压分别为V(i, j)和V′(i, j),其中V(i, j)=(Rl+Rr)/2,Rl和Rr表示MLC阈值电压感知过程中浮栅导通时的参考电压。CCI噪声影响强度的估计值为F′(i, j),擦除状态阈值电压分布的期望为μe[10]。因此,下一相邻字线的MLC闪存单元编程前后阈值电压的增量估计值为(V(i+1, k)-μe),可使用下式来估计CCI噪声大小F′(i, j):
| $ {{F'}_{\left( {i,j} \right)}} = \sum\limits_{k \in \left\{ {j - 1,j,j + 1} \right\}} {\left( {\left( {{V_{\left( {i + 1,k} \right)}} - {\mu _e}} \right) \cdot {\gamma _k}} \right)} $ | (8) |
并且计算修正后的MLC阈值电压公式为:
| $ \begin{array}{*{20}{c}} {{{V'}_{\left( {i,j} \right)}} = {V_{\left( {i,j} \right)}} - {{F'}_{\left( {i,j} \right)}} = }\\ {{V_{\left( {i,j} \right)}} - \sum\limits_{k \in \left\{ {j - 1,j,j + 1} \right\}} {\left( {\left( {{V_{\left( {i + 1,k} \right)}} - {\mu _e}} \right) \cdot {\gamma _k}} \right)} = }\\ {{V_{\left( {i,j} \right)}} - {\gamma _{xy}} \cdot \left( {{V_{\left( {i + 1,j - 1} \right)}} - {\mu _e}} \right) - }\\ {{\gamma _y} \cdot \left( {{V_{\left( {i + 1,j} \right)}} - {\mu _e}} \right) - {\gamma _{xy}} \cdot \left( {{V_{\left( {i + 1,j + 1} \right)}} - {\mu _e}} \right)} \end{array} $ | (9) |
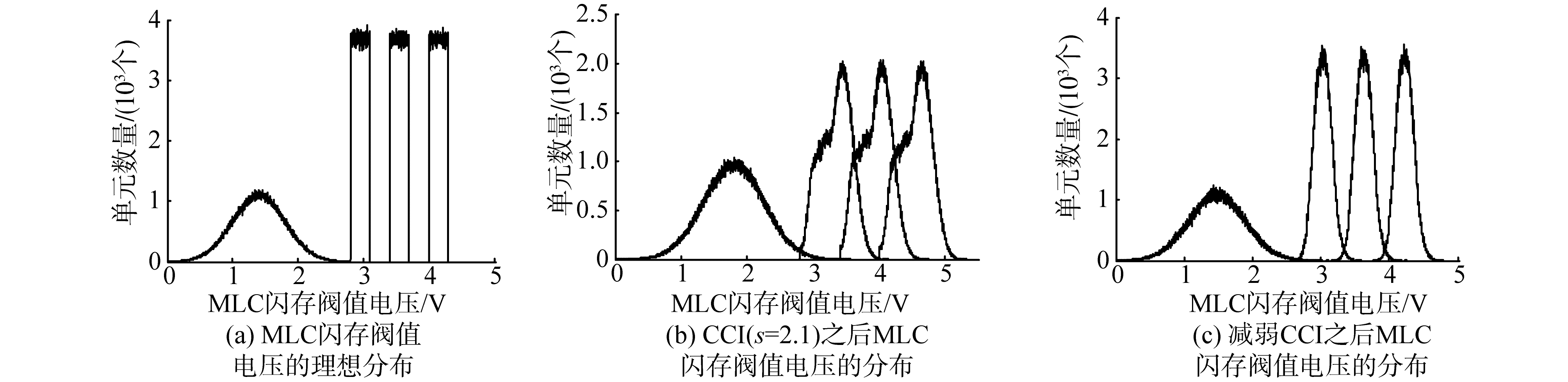
针对MLC闪存信道模型,利用计算机仿真验证上述减弱CCI影响方法的有效性。该模型中相关参数设置为[10]:擦除状态阈值电压分布的期望μe和标准差σe分别为1.2和0.35,ΔVpp等于0.3 V,校验电压Vp分别为2.80 V(s1=01),3.40 V(s2=11),4.00 V(s3=10),单元间耦合系数为s=2.1,仿真模拟100个闪存块,每个闪存块由32个闪存页组成,闪存页的长度为4 KB。通过蒙特卡罗仿真方法统计MLC闪存受CCI噪声前后的阈值电压分布直方图(如图 2所示)。与CCI干扰强度s=2.1的阈值电压分布图 2(b)相比,减弱CCI影响之后阈值电压分布图 2(c)更加符合图 2(a)的分布,有效减小了重叠区域面积,进而降低了原始误比特率。
|
Download:
|
| 图 2 减弱CCI影响前后MLC闪存单元的阈值电压分布 Fig. 2 Threshold voltage distribution for MLC flash memory before and after CCI cancellation | |
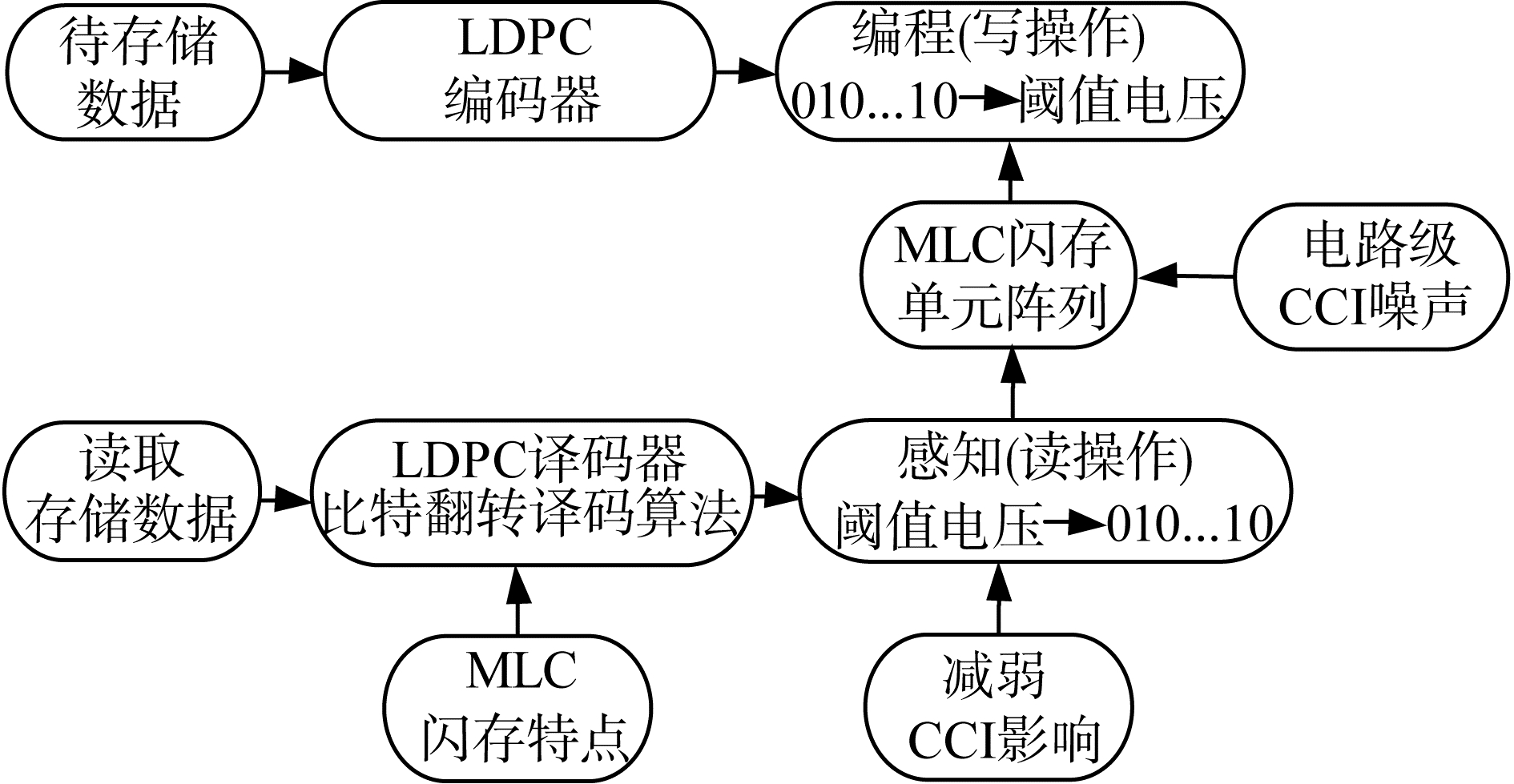
随着MLC单元比特存储密度的增加和半导体集成度的提高,CCI成为影响MLC闪存系统可靠性的主要存储信道噪声。本文的基本思想首先通过信号处理技术减弱CCI对MLC单元阈值电压的影响程度,有效减少相邻分布阈值电压的重叠区域面积,降低原始比特错误率;然后,利用蒙特卡罗仿真方法计算MLC闪存阈值电压分布的重叠区域,该区域是MLC闪存存储信息发生错误的主要区域。最后,借助主要错误区域的信息和MLC闪存存储信道错误的规律来确定MLC闪存页中存储比特的可靠性,从而提出了一种适用于MLC闪存系统的改进比特翻转译码算法(如图 3所示)。
|
Download:
|
| 图 3 MLC闪存系统的减弱CCI和LDPC译码器模块图 Fig. 3 Block diagram of CCI cancellation and LDPC decoder for MLC flash memory | |
MLC闪存的4个相互独立阈值电压分布经过不同CCI噪声之后相邻状态分布出现不同大小重叠区域,位于此重叠区域的MLC单元在比特判决时出错概率较高,因此该区域是MLC闪存存储信息发生错误的主要区域。
图 4为MLC闪存内部数据相关性分析示意图,分析可知当MLC闪存单元阈值电压位于阈值电压重叠区域A((q1, q2))和重叠区域C((q5, q6)),LSB位可能发生错误(矩形框表示),但MSB位不会发生错误;位于阈值电压重叠区域B((q3, q4)),MSB位可能发生错误(矩形框表示),但LSB位不会发生错误;其他区域不存在重叠,LSB位和MSB位均可正确读取。从图 4可知LSB位有两处跳变区域(s0=00

|
Download:
|
| 图 4 MLC闪存内部数据相关性分析示意图 Fig. 4 Schematic diagram of Intracell data dependence for MLC flash memory | |
利用MLC闪存存储信道错误的特点和主要错误区域边界的信息来确定MLC闪存页中存储比特的可靠性,并将该可靠性作为MLC闪存BF译码器比特翻转的重要判定条件来提高错误比特被正确翻转的准确度,因此,计算MLC相邻阈值电压分布的重叠区域边界至关重要。本文算法1借助蒙特卡罗仿真方法得到MLC闪存样本的阈值电压分布信息,通过对该信息进行统计可得不同CCI噪声下重叠区域的边界值,该方法适应于MLC闪存信道各种噪声影响下的阈值电压分布重叠区域计算,并且计算过程中对信道模型和重叠区域形状等条件不做限制。
算法1:计算相邻阈值电压分布重叠区域的边界值。
参数说明:
1) step_dist:MLC阈值电压的统计精度,初始化为1 000;
2) q[6]:存储3个重叠区域的边界值;
3) j:每个闪存块中字线的个数(初始化为32);
4) i:每个闪存页中MLC的个数(初始化为17 260);
5) max_step:最大阈值电压的统计范围(初始化为max_step=5.5 V×step_dist=5 500);
6) state_dist[4][max_step]:统计不同状态(s0=00, s1=01, s2=11和s3=10)下相同电压的单元个数;
7) cell_state[j][i]:位于(j, i)MLC单元所对应的电位(0表示s0,1表示s1,2表示s2和3表示s3);
8) cell_vth_output[j][i]:位于(j, i)MLC单元经过减弱CCI噪声影响之后的阈值电压;
//蒙特卡罗仿真100个闪存块样本的阈值电压分布
for j=(1, …, 32) do
for i=(1, …, 1726 0) do
//得到每个MLC闪存单元的阈值电压
temp=cell_vth_output[j][i]×step_dist
//统计得到闪存样本的阈值电压分布模型
state_dist[cell_state[j][i]][temp]++
end for
end for
for j=(2, 3, 4) do
//得到重叠区域左边界的值q1、q3和q5
for i=(0, …, max_step) do
if state_dist[j][i] > 0 then
q[2×(j-1)-1]=i/step_dist
break
end if
end for
end for
for j=(1, 2, 3) do
//得到重叠区域左边界的值q2、q4和q6
for i=(max_step, …, 0) do
if state_dist[j][i] > 0 then
q[2×j]=i/step_dist
break
end if
end for
end for
2.2 MLC闪存的比特翻转硬判决译码算法设计适用于MLC闪存系统的比特翻转译码算法动机是利用上述特点确定闪存页中存储比特的可靠性Ki(i∈[0, N-1]),并将此可靠性引入到变量节点的更新规则中,借助可靠性Ki(i∈[0, N-1])和“不满足校验方程的个数”作为硬判决序列中的比特是否进行翻转的判定条件(算法2)。假定MLC单元中存储的MSB位和LSB位这2个比特索引分别记为e(i mod 2=0)和o(si mod 2=1),那么MSB位和LSB位对应的可靠性参数Ke和Ko可表示为:
| $ {K_e} = \left\{ \begin{array}{l} 0,\;\;\left( {{V_{th}} > = {q_3}} \right)\& \& \left( {{V_{th}} < = {q_4}} \right),\\ 1,\;\;\;其他 \end{array} \right. $ | (10) |
| $ {K_o} = \left\{ \begin{array}{l} 0,\;\;\;\;\left( {\left( {{V_{th}} > = {q_1}} \right)\& \& \left( {{V_{th}} < = {q_2}} \right)} \right)\parallel \\ \;\;\;\;\;\;\left( {\left( {{V_{th}} > = {q_5}} \right)\& \& \left( {{V_{th}} < = {q_6}} \right)} \right),\\ 1,\;\;\;\;\;其他 \end{array} \right. $ | (11) |
式中:Ki=1表明第i个比特可靠而不需要翻转,而Ki=0表明第i个比特不可靠,满足翻转条件应被翻转。每次迭代过程中翻转“不满足校验方程个数最多”的不可靠比特,因此搜索需要翻转比特的范围要比BF译码算法小,同时避免了由于错误翻转正确比特而导致的链式效应。
算法2:适用于MLC闪存的改进比特翻转译码算法
参数说明:
1) 校验矩阵H=[hmn]为M×N的稀疏矩阵,码长为N,校验方程个数为M;
2) s=[s0, s1, …, sM-1]表示校验和;zi(i∈[0, N-1])存储硬判决的结果;
3) Ki(i∈[0, N-1])存储第i个比特对应的可靠性(0表示不可靠,1表示可靠);
① 对MLC闪存单元阈值电压进行感知和减弱CCI之后,得到MLC阈值电压区间[Rl, Rr);
② 利用式(3)计算MLC阈值电压所对应MSB和LSB的LLR值,通过式(4)得到存储的比特值;
③ 通过式(10)和(11)确定闪存页中每个MLC闪存单元MSB和LSB比特的可靠性K;
④ 计算校验和s=[s0, s1, …, sM-1], sm=
⑤ 统计码字中每一比特对应“不满足的校验方程的个数”,记作fn,n∈[0, N-1]:
| $ {f_n} = \sum\limits_{m \in M\left( n \right)} {{s_m},M\left( n \right)} = \left\{ {m:{{h}_{mn}} = 1} \right\},n \in \left[ {0,N - 1} \right]; $ |
⑥ 搜索Kn=0并且fn值最大的比特,若存在满足条件的比特,那么对满足条件的所有比特进行翻转;否则,搜索fn值最大的比特进行翻转;
⑦ 直到所有校验方程都满足(译码成功)或达到迭代次数设定的上限(译码失败)。
3 仿真实验及分析为了验证文中方法的有效性,对所提出算法的性能进行计算机仿真。MLC闪存信道模型的擦除状态阈值电压分布数学期望μe,标准差σe,阈值电压编程增量ΔVpp,校验电压Vp和MLC耦合强度系数s等参数与1.3节仿真程序参数相同[10]。BF译码算法[17-18]和改进的BF译码算法(算法2)采用码率为0.95,列重为4,行重为80的(34 520, 32 794)QC-LDPC码,最大迭代次数设为20。
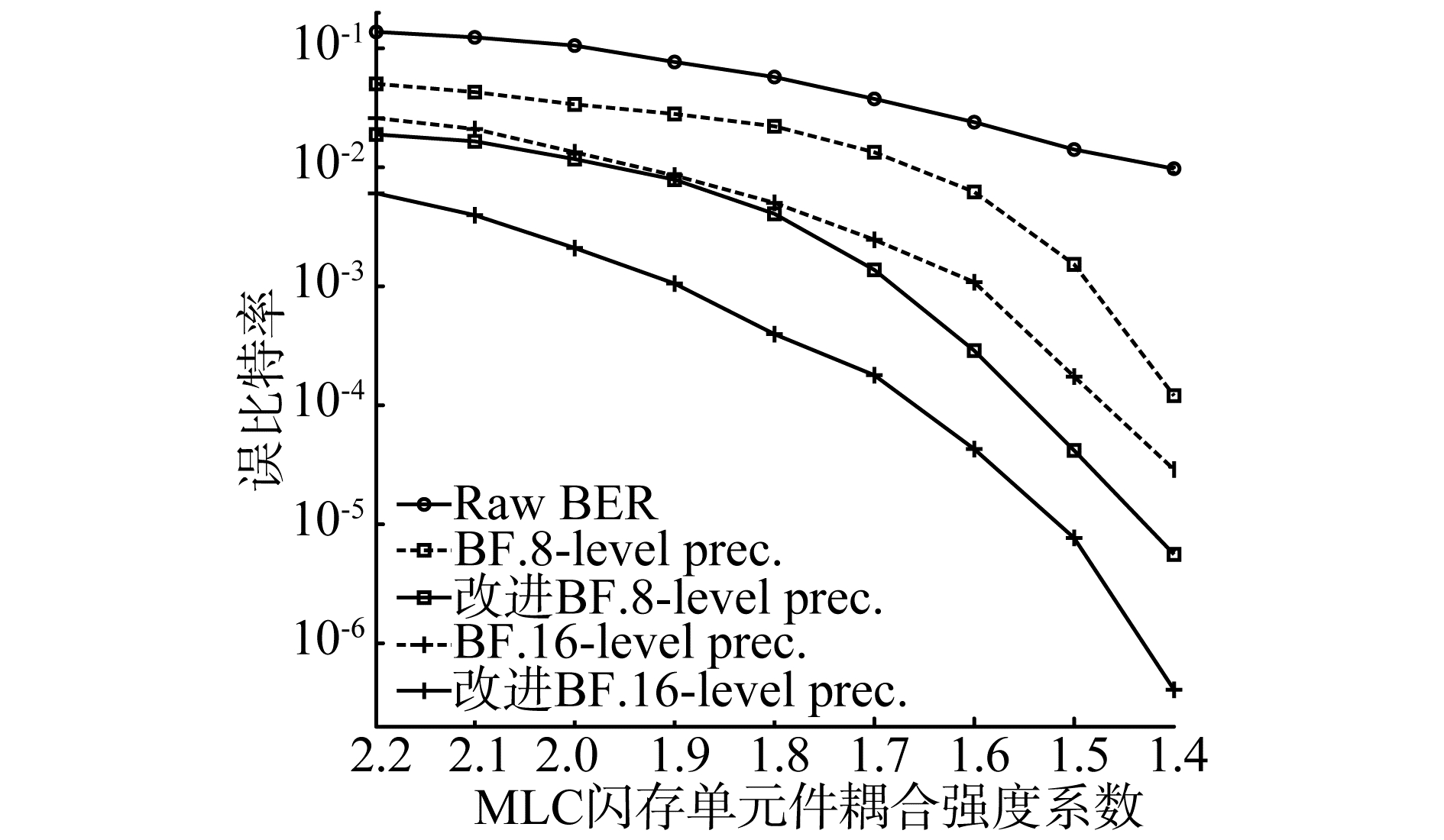
针对p=3(8-level prec.)和p=4(16-level prec.)2种感知精度,图 5给出了改进的BF译码算法与BF译码算法在不同耦合强度系数s下(34 520, 32 794) QC-LDPC码误比特率(bit error rate, BER)的比较。从图 5可知相同感知精度时改进的BF译码算法的译码性能明显优于BF译码算法的译码性能。当耦合强度系数s=1.8和感知精度为p=3时,原有MLC闪存BF译码算法的BER为2.19×10-2,改进的MLC闪存BF译码算法的BER为4.01×10-3,译码性能提升了81%;当感知精度增加到p=4时,原有MLC闪存BF译码算法的BER为5.02×10-3,改进的MLC闪存BF译码算法的BER为3.90×10-4,译码性能提升了91%。这是因为文中MLC闪存阈值电压分布主要错误区域的计算方法可以提高闪存页中翻转比特的可靠性和准确度,从而改进BF译码算法中错误比特被正确翻转的概率变大。同时,由于MLC闪存阈值电压感知精度越高,阈值电压感知子区间就变得越窄,这时感知得到的MLC闪存阈值电压和计算得到的LLR值就越准确,因此,对于相同译码算法下的LDPC码,感知精度p=4的BER译码性能优于感知精度p=3。但是,高感知精度会增加感知时间,影响闪存的读取速度。
|
Download:
|
| 图 5 感知精度p=3和p=4下MLC闪存两种比特翻转译码算法的(34 520, 32 794)QC-LDPC码性能比较 Fig. 5 The performances comparison of two bit-flipping decoding algorithms for (34 520, 32 794) QC-LDPC code with sensing precision p=3 and p=4 | |
图 6给出了改进的BF译码算法与BF译码算法在不同耦合强度系数s下的平均迭代次数比较。

|
Download:
|
| 图 6 感知精度p=3和p=4下MLC闪存两种比特翻转译算法的(34 520, 32 794)QC-LDPC码平均迭代次数比较 Fig. 6 The average number of iterations comparison of two bit-flipping decoding algorithms for (34 520, 32 794) QC-LDPC code with sensing precision p=3 and p=4 | |
由图 5、图 6可以看出,与BF译码算法相比较,改进的BF译码算法下LDPC码的BER译码性能明显改善,同时不增加译码的平均迭代次数。特别地,耦合强度系数s∈[1.8, 2.1] (16-level prec.)和s∈ [1.5, 1.8] (8-level prec.)时改进的BF译码算法的平均迭代次数有一些减少。例如,当耦合强度系数s=1.8和感知精度为p=3时,原有MLC闪存BF译码算法的平均迭代次数为19.98次,改进的MLC闪存BF译码算法的平均迭代次数为18.02次,平均迭代次数减少了9.8%左右;当感知精度增加到p=4时,原有MLC闪存BF译码算法的平均迭代次数为8.97次,改进的MLC闪存BF译码算法的平均迭代次数为7.07次,平均迭代次数减少了21%左右。
4 结论1) 文中通过信号处理技术减弱CCI噪声对MLC单元阈值电压的影响程度,有效减少相邻分布阈值电压的重叠区域面积,进而降低RBER。
2) 所提出MLC闪存BF算法的译码性能明显优于原有MLC闪存BF译码算法的性能。当耦合强度系数s=1.8与感知精度分别为p=3和p=4时,相比于原有MLC闪存BF译码算法,所提出MLC闪存BF译码算法的译码性能分别提升了81%和91%,并且译码的平均迭代次数减少了9.8%和21%。
3) 本文所提出的针对MLC闪存BF译码算法能够提高闪存页中翻转比特的可靠性和准确度,且其译码复杂度与BF译码算法相当,实现了译码性能和译码复杂性之间更好的折衷,适用于实时性要求较高的MLC闪存系统。
| [1] |
TAKEUCHI K. NAND flash application and solution[J]. IEEE solid-state circuits magazine, 2013, 5(4): 34-40. DOI:10.1109/MSSC.2013.2278087 (  0) 0)
|
| [2] |
DEAN K. The history of semiconductor memory:from magnetic tape to NAND flash memory[J]. IEEE solid-state circuits magazine, 2016, 8(2): 16-22. DOI:10.1109/MSSC.2016.2548422 (  0) 0)
|
| [3] |
LIU R, CHUANG M, YANG C, et al. Improving read performance of NAND flash SSDs by exploiting error locality[J]. IEEE transactions on computers, 2016, 64(4): 1090-1102. DOI:10.1109/TC.2014.2345387 (  0) 0)
|
| [4] |
CAI Y, Haratsch E, MUTLU O, et al. Threshold voltage distribution in MLC flash memory: characterization, analysis, and modeling[C]//Proceedings of the Conference on Design, Automation and Test in Europe, Grenoble, France, 2013: 1285-1290. DOI: 10.7873/DATE.2013.266. https://ieeexplore.ieee.org/document/6513712
(  0) 0)
|
| [5] |
SALA F, IMMINK K, DOLECEK L. Error control schemes for modern flash memories solutions for flash deficiencies[J]. IEEE consumer electronics magazine, 2015, 4(1): 66-73. DOI:10.1109/MCE.2014.2360965 (  0) 0)
|
| [6] |
DONG G, LI S, ZHANG T. Using data postcompensation and predistortion to tolerate cell-to-cell interference in MLC NAND flash memory[J]. IEEE transactions on circuits and systems Ⅰ:regular papers, 2010, 57(10): 2718-2728. DOI:10.1109/TCSI.2010.2046966 (  0) 0)
|
| [7] |
CHAUDHRY A, GUAN Y, CAI K. Detector for MLC NAND flash memory using neighbor-a-priori information[J]. IEEE transactions on very large scale integration (VLSI) systems, 2016, 24(9): 2827-2836. DOI:10.1109/TVLSI.2016.2523759 (  0) 0)
|
| [8] |
MICHELONI R, MARELLI A, RAVASIO R. Error correction codes for non-volatile memories[M]. Germany: springer, 2008: 85-101.
(  0) 0)
|
| [9] |
SUN H, ZHAO W, LV M, et al. Exploiting intracell bit-error characteristics to improve min-sum LDPC decoding for MLC NAND flash-based storage in mobile device[J]. IEEE transactions on very large scale integration (VLSI) sys-tems, 2016, 24(8): 2654-2664. DOI:10.1109/TVLSI.2016.2535224 (  0) 0)
|
| [10] |
DONG G, XIE N, ZHANG T. On the use of soft-decision error-correction codes in NAND flash memories[J]. IEEE transactions on circuits and systems Ⅰ:regular papers, 2011, 58(2): 429-439. DOI:10.1109/TCSI.2013.2244361 (  0) 0)
|
| [11] |
HU Y, SONG S, XIAO S, et al. A dominating error region strategy for improving the bit-flipping LDPC decoder of SSDs[J]. IEEE transactions on circuits and systems Ⅱ:express briefs, 2015, 62(6): 578-582. DOI:10.1109/TCSⅡ.2015.2407732 (  0) 0)
|
| [12] |
PARNELL T, DVNNER C, MITTELHOLZER T, et al. Capacity of the MLC NAND flash channel[J]. IEEE journal on selected areas in communications, 2016, 34(9): 2354-2365. DOI:10.1109/JSAC.2016.2603722 (  0) 0)
|
| [13] |
XU Q, GONG P, CHEN T, et al. Modelling and characterization of NAND flash memory channels[J]. Measurement, 2015, 70: 225-231. DOI:10.1016/j.measurement.2015.04.003 (  0) 0)
|
| [14] |
CHAUDHRY A, GUAN Y, CAI K. Read and write voltage signal optimization for multi-level-cell (MLC) NAND flash memory[J]. IEEE transactions on communications, 2016, 64(4): 1613-1623. DOI:10.1109/TCOMM.2016.2533498 (  0) 0)
|
| [15] |
SUH K, SUH B, LIM Y, et al. A 3.3V 32Mb NAND flash memory with incremental step pulse programming scheme[J]. IEEE journal of solid-state circuits, 1995, 30(11): 1149-1156. DOI:10.1109/ISSCC.1995.535460 (  0) 0)
|
| [16] |
PARK K, KANG M, KIM D, et al. A zeroing cell-to-cell interference page architecture with temporary LSB storing and parallel MSB program scheme for MLC NAND flash memories[J]. IEEE journal of solid-state circuits, 2008, 43(4): 919-928. DOI:10.1109/JSSC.2008.917558 (  0) 0)
|
| [17] |
张高远, 周亮, 文红. LDPC码加权比特翻转译码算法研究[J]. 电子与信息学报, 2014, 36(9): 2093-2097. ZHANG Gaoyuan, ZHOU Liang, WEN Hong. Research on weighted bit-flipping decoding algorithm for LDPC codes[J]. Journal of electronics & information technology, 2014, 36(9): 2093-2097. DOI:10.3724/SP.J.1146.2013.01622 (  0) 0)
|
| [18] |
TOFAR C, YU T. Dynamic weighted bit-flipping decoding algorithms for LDPC codes[J]. IEEE transactions on communications, 2015, 63(11): 3950-3963. DOI:10.1109/TCOMM.2015.2469780 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


