2. 济南大学 信息科学与工程学院, 山东 济南 250022
2. College of Information Sience and Engineering, University of Ji'nan, Ji'nan 250022, China
物体表面的结构特征可以通过纹理表现出来,纹理是图像的一个重要的属性,广泛应用于图像分割中,尤其在医学图像处理中应用更多。纹理图像分割中主要的3个步骤是:纹理特征的计算、相似区域的判断和分割轮廓线的光滑处理[1]。纹理图像分割的精度,在一定程度上由纹理特征向量的选取和计算,相似区域的合并以及分割轮廓线的光滑方法来决定的[2]。每个纹理特征对图像的代表性以及他们之间的相关度都有很大差异。不同的特征分别表示纹理的不同侧面和特点,所表示图像纹理的内容也有所不同,是不能完全相互替代的[3]。由于难以确定各特征的影响权重和计算效率等原因,目前比较典型的处理方法是选取几个主要的纹理特征进行计算。张翔等[4]为了寻找起决定因素作用的互补的主要特征提出一种极大熵加权方法,对分割结果有利的特征,则赋予较大的权重;反之,则赋予此特征较小的权重;但是,哪个是决定因素,权值达到什么程度,都由操作者自己判断,这里存在不确定性因素和人为因素影响分割结果准确率的问题。Zhang等[5]则根据每个纹理数据集的内在结构特征自动选择外部用户定义的抑制参数,使得所提出的方法对输入纹理数据集和初始条件的波动变得鲁棒。全卫澎等[6]提出一种依据纹理宏、微特性加权的新的特征融合的方法;赵泉华等[7]提出依据像素灰度的空间相关性选取纹理特征。这两种方法给纹理特征的权值选取提供了一定的依据,但是只是一定程度上减少了特征权重带来的不确定性,仅适合部分图像的特征权重的选取,普遍性上待研究。此外,一些研究人员为了尽可能多地选用纹理特征,采用通过编码转换的方式计算全部14种纹理特征,袁宝峰等[8]对局部二进制(LBP)纹理模型和灰度特征进行编码,将纹理特征进行转换;黄宁宁等[9]提出了基于灰度共生矩阵(GLCM)的特征转换方法。Singh等[10]提出了一种基于纹理特征的肝脏超声图像分割方法。该方法针对7个纹理特征,使用空间灰度级共生矩阵进行转换,用灰度级差异等纹理模型进行特征提取。然后使用线性分类器融合这些特征。该方法的优点是结合了不同纹理特征及其相应的加权分数权重作为计算肝脏分类的判别指数。这些转换方法虽然能够计算全部14种纹理特征,但是转换计算的方式也存在计算不准确的问题。这就需要探讨能否有更直接的不用转换就能计算全部纹理特征,而且不用人为的设置特征权重的计算方法,这是本文要研究和解决的第一个问题。在纹理特征的计算之后,图像分割中接下来的步骤就是相似区域的判断与分割轮廓线光滑问题。在这两个步骤的处理中都涉及到一个阈值设定的问题,即,区域相似程度超过多大的阈值能断定是相似,光滑轮廓线时,分段函数多小可以认定足够小进而可以进行光滑处理?针对此问题,王亭等[11]提出基于纹理测度与自适应模糊阈值的划分方法;张佳明等[12]将图像纹理信息加入到主动轮廓的能量函数中,提出通过实验分段确定阈值的主动轮廓模型的方法。这种设定阈值的方法有一定的人为因素和实验带来的不确定性进而导致分割不准确的问题[13]。这就需要探讨引入新的纹理特征计算方法避免阈值设定带来图像分割不准确的问题,这也是本文要研究的第二个问题。
针对纹理特征权重设置不准确或者不互补但重要的特征被忽略的问题,提出一种不用设置特征权重并且不用特征转换计算就计算全部特征的方法——基于纳什均衡理论的多纹理特征计算方法;并且在该方法的基础上提出基于纳什均衡理论的纹理相似区域判断的方法。针对分段阈值设定问题,本文提出不用设定阈值的改进的多纹理特征C-V模型。通过脑瘤图像分割对比实验,对本文提出方法的效果进行验证。
1 基于纳什均衡理论的纹理特征计算方法针对全面、有效计算纹理特征值问题,本文提出不用设置纹理特征权重,而是基于纳什均衡理论的多纹理特征计算公式;并且根据公式计算的结果,判断、合并相似区域,达到图像分割的目的。
1.1 基于纳什均衡理论的纹理特征计算公式纳什均衡解决的是一种非合作博弈的问题,以约翰·纳什命名。它以每一个个体的最大化收益作为判断平衡标准的策略,即同一时间内每一个个体的策略是对其他个体策略的相对最优反应。当每一个个体的收益都达到自己的最大值,纳什均衡就出现了。当其中任何一个个体策略要进行改变时,不仅要判断其自身的收益是否是最大值,还要判断其他个体是否时也是各自收益的最大值;只有所有个体都达到各自的相对最大值时,纳什均衡出现了,即:每次改变始终处于一个保持各方利益最大化的均衡状态[14]。
纳什均衡的非合作博弈的前提[14]:决策的个体是独立的,不合作的,不横向沟通的,每个个体的变化,要满足下面的两个条件:
1) 个体不变化是因为在新状态下没有更好的收益;
2) 个体改变是因为在新状态下收益没有变得更糟。
把纳什均衡理论引入到纹理特征计算中,用来判断2个区域是否是相似区域。本文分析认为,满足纳什均衡状态的前提条件是:收益变好,状态改变为一个新的均衡状态,收益没有变好,状态不改变,因为改变会导致失去均衡状态。那么在基于纹理特征的相似区域判断上,正好追求的是加入一个区域,使得原来区域的特征值没有变坏,甚至能够变好。这说明加入的区域和原来的区域在纹理特征上是相似的,所以两个区域是相似区域。
本文将纳什均衡理论引入到纹理特征计算和相似区域判断中。如果一个区域加入到另一个区域中,区域中的多种纹理特征值收益始终处于最大值。那么说明,区域在合并前后,区域中的纹理一直是保持均匀和相似的状态,进而,可以判断2个区域是相似区域。
本文提出纹理特征的纳什均衡计算公式,包括:个体、个体的收益和个体的策略。该计算公式具体定义如下。
当前状态中每个个体p的收益ωp*都大于或等于之前状态的个体的收益ωp,则达到一个新的纳什均衡状态,P为个体集合。即:
| $ \omega _p^ * \ge {\omega _p};p \in P $ | (1) |
| $ \omega _p^ * = \max \left( {\sum\limits_{p \in P} {{\omega _p}} } \right) $ | (2) |
每个个体p的策略σp定义为:
| $ {\sigma ^p} = \left\{ {s_p^1,s_p^2, \cdots ,s_p^i, \cdots ,s_p^M} \right\} $ | (3) |
式中:M是个体p的策略个数;spi是p的某个策略。
在本文的纹理图像中,个体p是图像中一个区域,区域p中有14个策略,即:区域p中的14个纹理特征值,策略的个数M=14。策略sp1表示的是角二阶矩(ASM)、sp2是对比度(CON)、sp3为相关度(COR)、sp4均值和(AV)、sp5是2个相关信息测量指标(IMC1)中的第一个、sp6是2个相关信息测量指标(IMC2)中的第二个、sp7是最大相关系数(MCC)、sp8是方差(VAR)、sp9是方差和(SOV)、sp10是熵(ENT)、sp11是和熵(SOE)、sp12是差熵(DOE),sp13是差的方差(DV), sp14是逆差矩(IDM)。
| $ \begin{array}{*{20}{c}} {{\sigma ^p} = \left\{ {s_p^1,s_p^2,s_p^3,s_p^4,s_p^5,} \right.}\\ {s_p^6,s_p^7, - s_p^8, - s_p^9, - s_p^{10},}\\ {\left. { - s_p^{11}, - s_p^{12}, - s_p^{13} - s_p^{14}} \right\}} \end{array} $ | (4) |
式中:负号是本文为了归一化特征值,将不同性质的特征值取反,使得每项特征值都是值越大,表示区域越均匀和相似。
为了计算区域纳什均衡收益,根据纳什均衡的理论原理,结合多纹理特征的特点,本文提出定义区域收益的纳什均衡的公式如下。
定义1 区域收益:
定义2 纳什均衡就是不断的求取14个纹理特征值是否保持各自收益最大值的过程,区域收益保持最大值:
针对现有的图像分割中相似区域的判断都是基于一个或者几个纹理特征值进行判断的局限性问题。本文提出一种基于纳什均衡理论的纹理相似区域判断方法,其出发点是基于纳什均衡理论,对全部14种纹理特征的区域收益值进行相似区域判断。
在加入新区域时,区域全部14种纹理特征的值要保持纳什均衡状态。保持了区域的纳什均衡状态,就说明新区域和原来的区域,在14种纹理特征的收益值保持最大,进而判断区域是均匀的、相似的。因此,基于纳什均衡的相似区域判断的过程是:随着区域的增加,要不断地判断区域14个特征值是否保持其自身的最大值,如果是,说明了保持纳什均衡状态,新加入的区域是相似区域;否则,纳什均衡状态被打破,新区域不是相似区域,不能加入。
本文提出的基于纳什均衡的相似区域合并算法的具体实施过程如下:
1) 输入图像,将图像划分为N个区域,计算区域灰度的最大值,确定最大灰度值的区域Ni,以及该区域的相邻区域Nk;
2) 计算所有Ni相邻区域的14个纹理特征值的收益
3) 如果相邻区域的14个特征值的收益都最大,则达到纳什均衡,相邻区域和Ni是相似区域,并将两区域合并,Ni=Ni+1,Nk=Nk+1;否则,Nk=Nk+1;
4) 判断如果Nk < N,返回步骤2)查找合并区域的相邻区域;
5) 判断如果N=Nk,则u0i=Ni,将合并后的相似区域u0i输出至C-V模型中,用以确定图像分割线,算法结束。
2 改进的多纹理特征的C-V模型基于上述相似区域判断与合并,图像已经被分割成2个区域:相似区域和不相似区域,即目标区域和背景区域。为了获得光滑的图像目标区域的轮廓线,还要对轮廓线进行进一步的光滑处理。
目前比较典型的图像目标区域轮廓线光滑处理方法是主动轮廓模型(C-V模型)和它的改进方法。C-V模型的原理是采用一个逼近的方法,使得轮廓线和区域边缘足够地接近,进而使得区域边缘被光滑的轮廓线代替。为了使得轮廓线和区域边缘足够接近,文献[15]将纹理特征分为粗计算和精细计算等分步骤的C-V模型;而文献[16]则选取部分纹理特征,通过改进C-V模型中水平集的分段阈值设定,对图像轮廓线进行光滑处理。这些改进的C-V模型在实验过程中,都需要对Heaviside函数设定阈值。这个阈值大小的设定直接关系到轮廓线的光滑效果[17]。针对此问题,本文提出一种不用设定阈值的基于纳什均衡理论的改进的多纹理特征C-V模型。
本文提出基于纳什均衡的改进的多纹理特征:针对现有的C-V模型用水平集设定分段阈值的缺点,用纳什均衡理论的收益值作为曲线状态改变的依据,即:新的区域的收益值大于等于原来区域的收益值,轮廓曲线移动到新的区域边缘,否则曲线不动。这样就避免了分段阈值设定有可能带来的轮廓线移动位置不准确的问题。此外,纳什均衡中收益值是充分利用全图像14种纹理信息进行计算的,比只选取几种纹理特征计算结果要全面。
接下来,阐述本文改进方法实施过程。首先阐述没改进前的C-V模型的定义,然后给出本文改进后的C-V模型。
没改进之前的C-V模型的定义为[18]:
| $ \begin{array}{*{20}{c}} {F\left( {{c^ + },{c^ - },C} \right) = \mu \cdot {\rm{length}}\left( C \right) + }\\ {{\lambda _1} \cdot \int_{{\rm{inside}}\left( C \right)} {{{\left| {{u_0}\left( {x,y} \right) - {c^ + }} \right|}^2}{\rm{d}}x{\rm{d}}y} + }\\ {{\lambda _2} \cdot \int_{{\rm{outside}}\left( C \right)} {{{\left| {{u_0}\left( {x,y} \right) - {c^ - }} \right|}^2}{\rm{d}}x{\rm{d}}y} } \end{array} $ | (5) |
式中:μ、λ1和λ2是取值为正的权值常数,一般令λ1=λ2=1;c+和c-分别是轮廓曲线C内部和外部的图像灰度均值。第1项μ·length(C)轮廓曲线C长度约束函数,用以保证获得的是足够短的曲线;而第2项和第3项负责将轮廓曲线C吸引到轮廓线上来。
这里的轮廓曲线C,在实际操作中,通常是用水平集函数φ(x, y)来代替曲线C[19],且φ(x, y)值为点(x, y)与C的最小距离值;并定义如果点(x, y)在C的内部,则水平集函数φ(x, y) > 0;如果点(x, y)在C的外部时,则水平集函数φ(x, y) < 0;而如果点(x, y)恰好在C上面时,则φ(x, y)=0,于是:
| $ \begin{array}{*{20}{c}} {F\left( {{c^ + },{c^ - },\varphi } \right) = \mu \cdot \int_\mathit{\Omega } {\delta \left( {\varphi \left( {x,y} \right)} \right)\left| {\nabla \varphi \left( {x,y} \right)} \right|{\rm{d}}x{\rm{d}}y} + }\\ {{\lambda _1} \cdot \int_\mathit{\Omega } {{{\left| {{u_0}\left( {x,y} \right) - {c^ + }} \right|}^2}{H_\varepsilon }\left( {\varphi \left( {x,y} \right)} \right){\rm{d}}x{\rm{d}}y} + }\\ {{\lambda _2} \cdot \int_\mathit{\Omega } {{{\left| {{u_0}\left( {x,y} \right) - {c^ - }} \right|}^2}\left( {1 - {H_\varepsilon }\left( {\varphi \left( {x,y} \right)} \right)} \right.{\rm{d}}x{\rm{d}}y} } \end{array} $ | (6) |
内部和外部轮廓线灰度均值c+和c-为:
| $ \left\{ \begin{array}{l} {c^ + } = \frac{{\int_\mathit{\Omega } {{u_0}{H_\varepsilon }\left( \varphi \right){\rm{d}}x{\rm{d}}y} }}{{\int_\mathit{\Omega } {{H_\varepsilon }\left( \varphi \right){\rm{d}}x{\rm{d}}y} }}\\ {c^ - } = \frac{{\int_\mathit{\Omega } {{u_0}\left( {1 - {H_\varepsilon }\left( \varphi \right)} \right){\rm{d}}x{\rm{d}}y} }}{{\int_\mathit{\Omega } {\left( {1 - {H_\varepsilon }\left( \varphi \right)} \right){\rm{d}}x{\rm{d}}y} }} \end{array} \right. $ | (7) |
式(6)的函数δε是Heaviside函数Hε的微分形式,表示为δε=H′ε(z)。
式(6)中的Heaviside函数Hε的近似为分段阈值形式为[20]:
| $ \begin{array}{*{20}{c}} {{H_\varepsilon }\left( z \right) = f\left( x \right) = }\\ {\left\{ \begin{array}{l} 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;z > \varepsilon \\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;z > - \varepsilon \\ \frac{1}{2}\left[ {1 + \frac{2}{\varepsilon } + \frac{1}{{\rm{ \mathsf{ π} }}}\sin \left( {\frac{{{\rm{ \mathsf{ π} }}z}}{\varepsilon }} \right)} \right],\;\;\;\;\;\left| z \right| < \varepsilon \end{array} \right.} \end{array} $ | (8) |
式(8)中的ε就是预先设置的分段阈值,如果阈值ε的值设置大了,比ε小的数值变化,轮廓线是不会移动;反之,如果阈值ε设置小了,轮廓线不该移动的也动了,轮廓线的位置也一样不准确。
本文改进的多纹理特征的C-V模型定义如下:
首先,为了更全面地捕捉纹理特征的变化,本文将式(5)中的轮廓曲线C内部和外部的图像灰度均值c+和c-分别改进为不仅是灰度均值而且是包含全部14种纹理特征集合ci+和ci-。即:已知合并的相似区域为u0i,每个区域u0i中含有14种纹理特征。原来C-V模型中的一个纹理特征c+和c-改进为包含14种纹理特征的ci+和ci-的集合:ci+=(c1+, c2+…cM+)和ci-=(c1-, c2-….cM-),M=14。
其次,为了计算全部14种纹理特征值集合ci+和ci-,用来衡量曲线内部和外部区域纹理特征的变化,本文将式(5)中的|u0(x, y)-c+|2和|u0(x, y)-c-|2改为:
经过上述改进之后,式(5)的C-V模型的能量函数就被改进为基于纳什均衡理论的多纹理特征的C-V模型的能量函数F:
| $ \begin{array}{*{20}{c}} {F\left( {\overline {{c^ + }} ,\overline {{c^ - }} ,\varphi } \right) = \mu \cdot {\rm{length}}\left( C \right) + }\\ {\int {\frac{1}{N}\sum\limits_{i = 1}^N {\lambda _i^ + {{\left| {{u_{0i}}\left( {x,y} \right) - c_i^ + } \right|}^2}{\rm{d}}x{\rm{d}}y} } + }\\ {\int_{{\rm{outside}}\left( C \right)} {\frac{1}{N}\sum\limits_{i = 1}^N {\lambda _i^ - {{\left| {{u_{0i}}\left( {x,y} \right) - c_i^ - } \right|}^2}{\rm{d}}x{\rm{d}}y} } } \end{array} $ | (9) |
式(8)中的分段阈值函数Hε被改为纳什均衡收益函数为:
| $ \sigma \left( P \right) = \left\{ \begin{array}{l} 1,\;\;\;\;\;\sum {{{\left( {s_p^i} \right)}^ * }} > \sum {s_p^i} \\ 0,\;\;\;\;\sum {{{\left( {s_p^i} \right)}^ * }} \le \sum {s_p^i} \end{array} \right. $ | (10) |
这里没有分段阈值ε,也不需要对阈值的设定。当纳什均衡收益值大于原来的收益值时, 即:∑(spi)* > ∑spi,纳什均衡收益函数σ为1,说明达到了一个新的纳什均衡状态,轮廓线和区域边缘足够逼近。反之,当σ为0,即:∑(spi)*≤∑spi, 说明纳什均衡状态没有改变,轮廓线和区域边缘不接近。
定义函数δ(x)为纳什均衡收益函数为σ(P)的微分形式:δ(x)=
| $ \begin{array}{*{20}{c}} {F\left( {\overline {{c^ + }} ,\overline {{c^ - }} ,\phi } \right) = \mu \cdot \int_\mathit{\Omega } {\delta \left( {\phi \left( {x,y} \right)} \right)\left| {\nabla \phi \left( {x,y} \right)} \right|{\rm{d}}x{\rm{d}}y} + }\\ {\int_\mathit{\Omega } {\frac{1}{N}\sum\limits_{i = 1}^N {\lambda _i^ + {{\left| {{u_{0i}}\left( {x,y} \right) - c_i^ + } \right|}^2}\sigma \left( {\phi \left( {x,y} \right)} \right){\rm{d}}x{\rm{d}}y} } + }\\ {\int_\mathit{\Omega } {\frac{1}{N}\sum\limits_{i = 1}^N {\lambda _i^ - {{\left| {{u_{0i}}\left( {x,y} \right) - c_i^ - } \right|}^2}\left( {1 - \sigma \left( {\phi \left( {x,y} \right)} \right)} \right){\rm{d}}x{\rm{d}}y} } } \end{array} $ | (11) |
将原来C-V模型中分段阈值函数Hε被改为纳什均衡收益函数为σ(P),将原来的阈值设定改为不用阈值设定,减少了因为阈值设定可能带来的轮廓线不够光滑的问题。
3 实验验证为了检验本文提出的基于纳什均衡理论的改进的多纹理特征C-V模型的图像分割的效果,本文进行3个实验:1)本文改进的基于纳什均衡的改进的多纹理C-V模型的图像分割实验,目的是验证本文提出方法的实验效果。2)本文方法与改进的C-V模型[16]的对比实验,目的是验证本文提出的方法在同类的改进的C-V模型中的效果。3)本文方法与不用设定阈值的改进模糊c均值聚类算法[23]和混合高斯模型差异统计模型[24]的对比实验,目的是为了验证本文提出的方法在近似的方法中的效果。
运行实验程序的计算机硬件配置是:主机内存是8 GB,中央处理器是Intel(R) Xeon(R),CPU型号是E5-1603v3,CPU频率是2.80 GHz。实验图片采用的是典型纹理特征的脑瘤医学核磁共振(MRI)图片,其中3.1节的图片来自全国最大的放射科医生交流平台——放射沙龙[21],分别是:间变性星形细胞瘤、毛细管型星形细胞瘤、多行性肿瘤;3.2~3.3节采用的是与对比方法相同的图片。
实验结果的评价指标,采用常用的准确率(P), 召回率(R)还有综合评价指标(F)来进行评定[22]。
3.1 本文改进的多纹理C-V模型的实验在这个实验里,本文选择了3个典型的MRI脑瘤图像,用本文提出的基于纳什均衡理论的改进的多纹理C-V模型进行图像分割,结果如图 1所示。

|
Download:
|
| 图 1 本文改进的多纹理C-V图像分割结果 Fig. 1 Improved multi texture C-V image segmentation results | |
图 1中的第1列是3个MRI的原始图,第2列是经过相似区域合并后的图像,第3列是经过相似区域合并后输入到改进的多纹理C-V模型的图片,第4列是改进的多纹理C-V模型处理后输出图像分割的实验结果图片。
通过图 1第2列可以看出,相似区域合并的图片中目标区域的边缘有棱角,没有肉眼看到的原始图片的目标边缘光滑;但是通过把第3列的图片输入到第4列,经过多纹理特征C-V模型的处理,图片目标的边缘的轮廓线就变得光滑和精准了。从目视效果看本文改进的多纹理C-V模型的图像分割的准确度和光滑度都有较好的效果。
为了进一步说明本文方法的效果,将上述MRI肿瘤图片的实验过程参数和用程序测试的评价指标整理归纳,如表 1所示。
| 表 1 本文改进的多纹理C-V模型图像分割过程参数和分割结果评价指标 Table 1 The evaluation parameters of improved multi texture C-V image segmentation results |
numIter和timestep是程序运行的间隔区间和间隔时间,σ是改进的纳什均衡收益函数,T是算法的运行的时间。P、R和F是准确率、召回率还有综合评价指标等实验结果的评价指标。P、R和F的最大值是1,表示图像分割100%准确。
分析表 1中的数据可知,本文改进方法的准确率P值在0.949 4~0.981 8;召回率R在0.844 7~0.929 5,综合评价指标F值在0.916 0~0.954 9。P、R和F这3个评价指标都较最高的分割图片是毛细管型星形细胞瘤,其中准确率达0.981 8;指标高主要是因为这个图片中轮廓线内外的纹理特征值ci+和ci-分别是25和5,数值相差20,在3类图片中特征值相差最小;纳什均衡状态容易达到,因此容易区分。3个评价指标都较小的是间变性星形细胞瘤,其中准确率达0.949 4;因为这个图片中轮廓线内外的纹理特征值ci+和ci-分别是36和5,数值相差31,差别相对较大,纳什均衡状态不太容易达到,所以分割准确率会相对降低。从程序运行的效率角度来看,本文提出方法的运行时间T在0.078 0 s~0.1 248 s,这个时间效率比同类的纹理图像分割方法要高,下面实验会给出进一步数据对比分析。
3.2 本文方法与改进的C-V模型[16]的对比实验本部分实验是为了验证本文提出的基于纳什均衡理论的改进的多纹理C-V模型的方法与最新的改进的C-V模型的方法[16]对比效果。
本文实验选用的图片是来自参考文献[16]的脑胶质瘤MRI图片,分别为T1-w、T2-w和T1-w胶质瘤仿真实验图。
图像分割的实验结果如图 2所示,图 2中的第1列是原图,第2列是文献[16]的分割结果图,第3和第4列是本文方法的相似区域合并图和改进的多纹理C-V模型图像分割结果图。

|
Download:
|
| 图 2 文献[16]方法与本文改进的多纹理C-V模型的实验结果 Fig. 2 The experiment results of the literature [16] and the proposed improved C-V image segmentation | |
从图 2的目视效果来看,本文的分割区域接近目测的肿瘤区域和分割轮廓线都比文献[16]的位置准确和光滑。对比实验的结果评价指标如表 2所示。
| 表 2 本文改进的多纹理C-V方法与文献[16]方法对比实验结果评价指标 Table 2 The evaluation parameters of the our improved multi texture C-V method compared with the literature [16] |
从表 2可以看出,图像分割的3个指标P、R和F中,本文方法的准确率在0.988+0.011, 文献[14]方法的准确率在0.923+0.043, 准确率平均提高6.50%;本文方法与文献[16]方法相比,召回率R平均提高7%,综合评价指标F平均提高2%。在运行效率方面,文献[16]的运行时间在0.14 s左右,本文方法在0.046 8~0.0 93 6 s,平均提高约6%。对比实验结果验证了本文方法的有效性。
3.3 本文方法与文献[23-24]的对比实验除了在3.2节中和同类的其他的改进的C-V模型做对比实验外,本文提出的方法还要和近似的同样不用设置阈值的图像分割方法:模糊c均值聚类算法[23]和关于混合高斯模型差异统计模型[24]做对比实验。
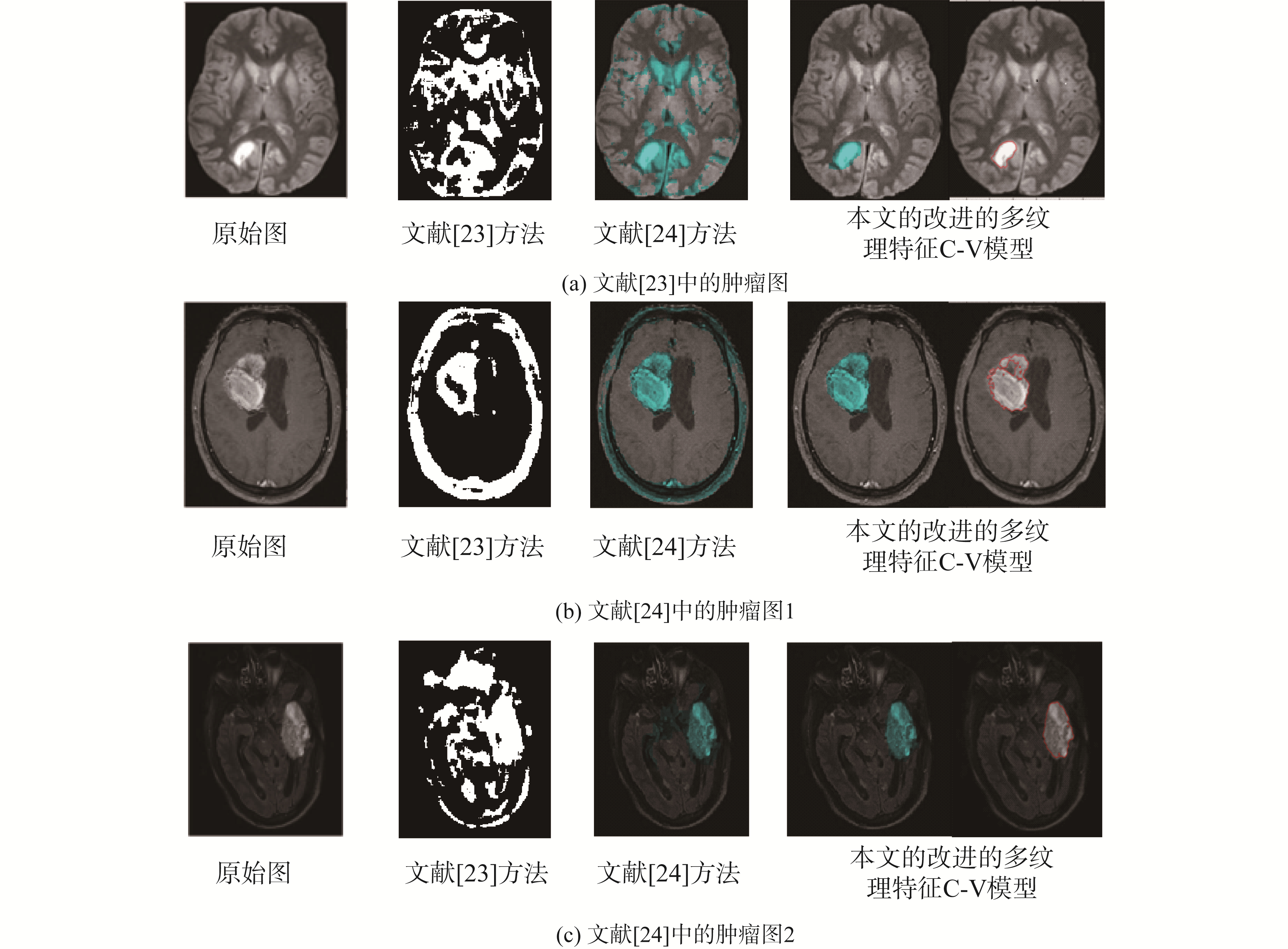
实验图片选用文献[23-24]的图片,图像分割的结果如图 3所示。
|
Download:
|
| 图 3 本文方法、文献[23]和[24]方法的图像分割实验结果 Fig. 3 Experimental results of literature methods [23], [24] and the proposed method | |
图 3中,第2列是改进的模糊c均值聚类算法的图片分割结果;第3列是混合高斯差异统计模型图片分割结果;最后一列是本文的改进的多纹理特征C-V模型分割的两个结果图。从目视效果来看,最后一列的本文方法的图像分割效果比第3和第4列的模糊c均值聚类算法和混合高斯模型差异统计模型算法的分割效果都要好。对比实验的结果评价指标如表 3所示。
由于文献[23-24]的评价指标中没有R、F和T项,因此,仅从准确率P值方面分析:本文方法的准确率P值在0.979 6~0.990 2,而参考文献[23-24]的准确率值在0.934 0~0.947 5。本文方法平均准确率为0.985,比文献[23]的脑瘤图分割准确率提高4.09%、比文献[24]的脑瘤图 1提高5.62%、比文献[24]的脑瘤图 2提高3.66%,3个图片分割准确率平均提高4.46%。对比实验结果,验证了本文提出的基于纳什均衡理论的改进的多纹理C-V模型方法的有效性。
归纳上述3个实验的结果,本文提出的基于纳什均衡理论的改进的多纹理C-V模型的方法,平均准确率达到0.985,比3个文献[16]、[23]和[24]方法提高了4.46%~6.50%,平均提高5%,本文方法的运行效率比文献[16]平均提高6%。实验结果验证了本文方法的有效性。
4 结论1) 本文方法与较典型的模糊c均值聚类方法相比脑肿瘤图像分割准确度平均提高5%,运行效率平均提高6%,验证了本文方法的有效性。
2) 本文提出的纳什均衡理论在多纹理图像分割领域中的计算公式和改进的多纹理C-V模型,为图像分割领域探索了一种解决问题的新思路。
| [1] |
董昱威.基于特征提取的纹理图像分割[D].西安: 长安大学, 2014: 19-21. DONG Yuwei. A research of texture image segmentation based on extracting features[D]. Xi'an: Chang'an University, 2014: 19-21. http://cdmd.cnki.com.cn/Article/CDMD-10710-1014070990.htm (  0) 0)
|
| [2] |
李中海.一种综合多种方法的纹理图像分割[D].大连: 大连理工大学, 2008: 12-13. LI Zhonghai. Texture image segmentation based on a synthetic approach[D]. Dalian: Dalian University of Technology, 2008: 12-13. http://cdmd.cnki.com.cn/Article/CDMD-10141-2009040788.htm (  0) 0)
|
| [3] |
胡永强, 宋良图, 张洁, 等. 基于稀疏表示的多特征融合害虫图像识别[J]. 模式识别与人工智能, 2014, 27(11): 985-992. HU Yongqiang, SONG Liangtu, ZHANG Jie, et al. Pest image recognition of multi-feature fusion based on sparse representation[J]. Pattern recognition and artificial intelligence, 2014, 27(11): 985-992. DOI:10.3969/j.issn.1003-6059.2014.11.005 (  0) 0)
|
| [4] |
张翔, 邓赵红, 王士同, 等. 极大熵Relief特征加权[J]. 计算机研究与发展, 2011, 48(6): 1038-1048. ZHANG Xiang, DENG Zhaohong, WANG Shitong, et al. Maximum entropy relief feature weighting[J]. Journal of computer research and development, 2011, 48(6): 1038-1048. (  0) 0)
|
| [5] |
ZHANG Kun, KONG Weiren, LIU Peipei, et al. Partition region-based suppressed fuzzy C-means algorithm[J]. Journal of systems engineering and electronics, 2017, 28(5): 996-1008. (  0) 0)
|
| [6] |
全卫澎, 李卫华, 李小春, 等. 基于统计与频谱模型特征融合的纹理图像分割[J]. 科学技术与工程, 2014, 14(19): 106-111. QUAN Weipeng, LI Weihua, LI Xiaochun, et al. A segmentation algorithm for texture based on statistical and spectrum model texture information weighting[J]. Science technology and engineering, 2014, 14(19): 106-111. DOI:10.3969/j.issn.1671-1815.2014.19.020 (  0) 0)
|
| [7] |
赵泉华, 高郡, 李玉. 基于区域划分的多特征纹理图像分割[J]. 仪器仪表学报, 2015, 36(11): 2519-2530. ZHAO Quanhua, GAO Jun, LI Yu. Multi-feature texture image segmentation based on tessellation technique[J]. Chinese journal of scientific instrument, 2015, 36(11): 2519-2530. DOI:10.3969/j.issn.0254-3087.2015.11.016 (  0) 0)
|
| [8] |
袁宝峰, 吴乐华, 曾伟. 基于纹理与灰度协同进化的图像分割算法[J]. 计算机应用, 2009, 29(1): 54-56. YUAN Baofeng, WU Lehua, ZENG Wei. Image segmentation algorithm based on coevolution with texture and gray scale[J]. Journal of computer applications, 2009, 29(1): 54-56. DOI:10.3969/j.issn.1001-3695.2009.01.014 (  0) 0)
|
| [9] |
黄宁宁, 贾振红, 杨杰, 等. 基于GLCM和EM算法的纹理图像分割[J]. 通信技术, 2011, 44(1): 48-49, 52. HUANG Ningning, JIA Zhenhong, YANG Jie, et al. Texture segmentation based on gray-level co-occurrence matrix features and EM algorithm[J]. Communications technology, 2011, 44(1): 48-49, 52. (  0) 0)
|
| [10] |
SINGH M, SINGH S, GUPTA S. An information fusion based method for liver classification using texture analysis of ultrasound images[J]. Information fusion, 2014, 19: 91-96. DOI:10.1016/j.inffus.2013.05.007 (  0) 0)
|
| [11] |
王亭, 王向阳. 基于纹理测度与自适应阈值的FCM图像分割算法[J]. 小型微型计算机系统, 2010, 31(6): 1209-1212. WANG Ting, WANG Xiangyang. New FCM image segmentation based on texture measure and adaptive threshold[J]. Journal of Chinese computer systems, 2010, 31(6): 1209-1212. (  0) 0)
|
| [12] |
张佳明, 张荣国, 赵建, 等. 基于纹理特征的主动轮廓模型图像分割[J]. 太原科技大学学报, 2017, 38(3): 190-195. ZHANG Jiaming, ZHANG Rongguo, ZHAO Jian, et al. Image segmentation of active contour model based on texture feasure[J]. Journal of Taiyuan university of science and technology, 2017, 38(3): 190-195. DOI:10.3969/j.issn.1673-2057.2017.03.005 (  0) 0)
|
| [13] |
林瑶, 田捷. 医学图像分割方法综述[J]. 模式识别与人工智能, 2002, 15(2): 192-113. LIN Yao, TIAN Jie. A survey on medical image segmentation methods[J]. Pattern recognition and artificial intelligence, 2002, 15(2): 192-113. DOI:10.3969/j.issn.1003-6059.2002.02.012 (  0) 0)
|
| [14] |
隗立涛, 修乃华. 基于启发搜索算法的纳什均衡计算[J]. 北京交通大学学报, 2007, 31(3): 58-62. WEI Litao, XIU Naihua. Computing Nash equilibria based on heuristic search methods[J]. Journal of Beijing Jiaotong University, 2007, 31(3): 58-62. DOI:10.3969/j.issn.1673-0291.2007.03.014 (  0) 0)
|
| [15] |
RESKA D, BOLDAK C, KRETOWSKI M. Towards multi-stage texture-based active contour image segmentation[J]. Signal, image and video processing, 2017, 11(5): 809-816. DOI:10.1007/s11760-016-1026-y (  0) 0)
|
| [16] |
NABIZADEH N, KUBAT M. Automatic tumor segmentation in single-spectral MRI using a texture-based and contour-based algorithm[J]. Expert systems with applications, 2017, 77: 1-10. DOI:10.1016/j.eswa.2017.01.036 (  0) 0)
|
| [17] |
卢芸.基于阈值分割的织物疵点检测方法研究与实现[D].石家庄: 河北科技大学, 2008: 22-24. LU Yun. Research and implementation of fabric defects detection method based on threshold segmentation[D]. Shijiazhuang: Hebei University of Science & Technology, 2008: 22-24. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1473656 (  0) 0)
|
| [18] |
徐玲凌, 肖进胜, 易本顺, 等. 改进的C-V水平集模型图像分割算法[J]. 计算机工程, 2009, 35(10): 209-210, 213. XU Lingling, XIAO Jinsheng, YI Benshun, et al. Improved C-V level set model image segmentation algorithm[J]. Computer engineering, 2009, 35(10): 209-210, 213. DOI:10.3969/j.issn.1000-3428.2009.10.069 (  0) 0)
|
| [19] |
付金明, 羿旭明, 檀伟伟, 等. 基于改进C-V水平集模型的SAR图像分割[J]. 数学杂志, 2016, 36(3): 649-654. FU Jinming, YI Xuming, TAN Weiwei, et al. SAR image segmentation based on improved level SET C-V model[J]. Journal of mathematics, 2016, 36(3): 649-654. (  0) 0)
|
| [20] |
王翠杰, 杨永红, 林明. 基于改进C-V模型的高分辨SAR图像分割[J]. 电子设计工程, 2017, 25(19): 161-164. WANG Cuijie, YANG Yonghong, LIN Ming. High-resolution SAR image segmentation based on improved C-V model[J]. Electronic design engineering, 2017, 25(19): 161-164. DOI:10.3969/j.issn.1674-6236.2017.19.040 (  0) 0)
|
| [21] |
DING W, WANG J, DONG J, et al. A quantum-inspired cooperative co-evolution based minimum attribute reduction algorithm and its application in medical MRI[J]. Journal of information and computational science, 2012, 9(5): 1125-1133. (  0) 0)
|
| [22] |
张石, 董建威, 佘黎煌. 医学图像分割算法的评价方法[J]. 中国图象图形学报, 2009, 14(9): 1872-1880. ZHANG Shi, DONG Jianwei, SHE Lihuang. The methodology of evaluating segmentation algorithms on medical image[J]. Journal of image and graphics, 2009, 14(9): 1872-1880. (  0) 0)
|
| [23] |
LI Changyang, WANG Xiuying, EBERL S, et al. Supervised variational model with statistical inference and its application in medical image segmentation[J]. IEEE transactions on biomedical engineering, 2015, 62(1): 196-207. (  0) 0)
|
| [24] |
BEEVI Z, SATHIK M. A robust segmentation approach for noisy medical images using fuzzy clustering with spatial probability[J]. International Arab journal of information technology, 2009, 9(1): 74-83. (  0) 0)
|
| [25] |
程旸, 蒋亦樟, 钱鹏江, 等. 知识迁移的极大熵聚类算法及其在纹理图像分割中的应用[J]. 智能系统学报, 2017, 12(2): 179-187. CHENG Yang, JIANG Yizhang, QIAN Pengjiang. A maximum entropy clustering algorithm based on knowledge transfer and its application to texture image segmentation[J]. CAAI transactions on intelligent systems, 2017, 12(2): 179-187. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


