认知无线电(cognitive radio,CR)被认为是一种可以提供频谱效率的颠覆性技术创新,广泛应用于军事、环境以及交通等各个领域。随着各种无线通信技术(如WiFi、蓝牙等)的兴起,ISM频段变得日益拥挤,现有的固定频谱分配方式必然会引起严重的频谱稀缺问题[1]。伴随认知无线网络的发展,利用动态频谱接入技术的认知无线传感网(cognitive radio sensor network,CRSN)得到广泛重视和发展,它允许次用户(SU)利用动态频谱访问(DSA)技术使用分配给主用户(PU)的空闲频谱。
在认知无线传感网中,当作为SU的传感器节点与其他节点之间进行控制信息交换和频谱管理等操作时,节点间以分布式的形式,根据系统时钟自动切换到同一频谱,建立通信链路以实现通信的过程被称为信道会合或信道相遇(channel rendezvous)。Rendezvous问题的研究对于CRSN中传感器节点的通信起到了重要作用,在IEEE 802.22中的MAC层协议虽然能够根据网络环境的动态变化合理利用频谱,但没有涉及到Rendezvous机制的研究。
目前,控制信息的传输大多采用集中式控制方法[2-3]或公共控制信道(common control channel,CCC)[4-5]。这些机制可以较好完成控制信息的处理,但是,当网络动态变化时极易造成公共控制信道缺失或瓶颈,难以适应网络动态变化,且极易受到攻击[6-7]。而Rendezvous机制不需要公共控制信道,也不需要目标节点感知信道集,可以更好适应网络动态变化,因此Rendezvous在实际应用中得到了广泛关注。
信道跳频(channel hopping,CH)技术是Rendezvous最具代表性的技术之一[8-9], 通过使用信道跳频技术,CRSN的每个用户在其可感知信道集中进行信道跳频,以便与其潜在的邻居进行Rendezvous。然而现有的Rendezvous有以下不足:1)不能提供的有保证的Rendezvous(guaranteed rendezvous); 2)只适用于时钟同步模型;3)无法适用于非对称模型;4)不适用于多用户和多跳系统。如ETCH算法[8]、较早的随机生成序列算法和时钟模块算法[10-11]均只能在对称模型下达到Rendezvous,而AMRCC算法尽管在仿真实验中得到较好结果,但由于AMRCC算法是随机的,因此理论分析中非对称模型下无法达到有保证的Rendezvous[12]。部分现有算法可以在对称和非对称模型下均达到有保证的Rendezvous,例如JS算法[9],但该算法在非对称模型下MTTR较大。
本文主要针对于CRSN中两用户提出一种新的Blind Rendezvous跳频算法,将节点状态按照发送状态和接收状态设置不同跳频序列,并引入信道使用概率设计逻辑信道和物理信道之间映射关系达到Full Rendezvous,较好达到了降低MTTR的目的。主要完成了以下研究问题:1)一种可以同时适用于对称模型和非对称模型的新的Rendezvous跳频算法,并且满足Rendezvous的有效执行(guaranteed rendezvous);2)适用于成对用户的Rendezvous算法;3)针对最大相遇时间(maximum time-to-rendezvous,MTTR)的相关分析和证明;4)实验比较算法的优劣。
1 系统模型本文主要讨论两个用户间的Rendezvous,假设在同一CRSN中,其中传感器节点i用Si表示,作为SU存在,每个节点均装有半双工无线电以感知其可用的授权频谱。授权频谱被划分为M(M≥1)个正交的非重叠信道,且这些信道下标独立且唯一,信道集合C={C1, C2, …, CM}。Gx, y定义为节点Sx和节点Sy的公共感知信道集合,即
当节点i处于发送状态下,信道x的发送概率记为Psi(x)(1≤x≤M),满足:
| $ P{s_i}\left( 1 \right) + P{s_i}\left( 2 \right) + P{s_i}\left( 3 \right) + \cdots + P{s_i}\left( x \right) = 1 $ | (1) |
当节点j处于接收状态下,信道y的接收概率为Prj(y)(1≤y≤M),满足:
| $P{r_j}\left( 1 \right) + P{r_j}\left( 2 \right) + P{r_j}\left( 3 \right) + \cdots + P{r_j}\left( y \right) = 1 $ | (2) |
本文SRP算法同时满足对称模型、非对称模型、时钟同步模型和时钟异步模型:
1) 对称模型:CRSN中所有用户感知信道集完全相同,即:Mr=MS。MS为发送状态下节点感知信道数目,Mr为接收状态下节点感知信道数目。
2) 非对称模型:CRSN中不同用户感知信道集不完全相同,即:Mr≠MS且GR, S≠0。Ux和Uy的公共感知信道集合。
3) 时钟同步模型:在CRSN中,所有用户开始跳频初始时间相同。本文假设时间被划分为长度相等的时间片。
4) 时钟异步模型:在分布式CRSN网络中,每个用户都可以在不同的时刻启动跳频序列,且该时刻是完全随机的,无法做到时钟同步。
相遇时间(time-to-rendezvous,TTR)是指用户达到Rendezvous所需要的时间片,是评估Rendezvous算法好坏的最重要的指标。由于跳频时间开始随机,所以TTR一般是不确定的。因此最大时间MTTR(maximum time-to-rendezvous)和平均时间ATTR(average time-to-rendezvous)是衡量SRP算法好坏的重要指标。
Rendezvous信道全覆盖(full Rendezvous)是指在感知信道集中的任意信道均可达到Rendezvous,本文将通过设置发送、接收概率阈值,调整逻辑跳频序列,避免某一信道使用频率过高的情况,有助于增强网络稳定性。
本文的重点工作是在满足Rendezvous的有效执行、Full Rendezvous的基础上,满足对称模型、非对称模型、时钟同步模型和时钟异步模型,并尽可能降低MTTR。
2 基于发送接收概率SRP算法 2.1 基本思想CRSN中传感器节点的分为两种状态:发送状态和接收状态,传感器节点分别在发送状态和接收状态下,维护2个信道跳频序列,基于收发概率SRP(sender-receiver-probability)算法(如下的算法1~4)来选择信道。通过调整步长生成循环的逻辑跳频序列,并根据在发送状态和接收状态下相应信道的使用概率Psi(x)和Prj(y)将逻辑信道映射到对应的物理信道,实现Rendezvous,降低MTTR。
节点根据其当前不同状态分别生成发送状态的和接收状态的逻辑跳频序列,序列长度由P决定,P是不小于信道M的最小质数[13],跳频步长L是[0, P-1]的整数,针对节点发送状态和接收状态将进行不同的处理。
1) 节点发送状态
当节点处于发送状态时,算法1用于构造发送方逻辑跳频序列,每Ps个时间片步长L改变一次,由Ps-1递减至0,每个循环将会持续Ps2个时间片长度,前Ps(Ps-1)个时间片用于跳频,最后Ps个时间片将一直停留在逻辑信道1用于补偿,保证在每个循环内至少达到一次Rendezvous。
发送状态逻辑跳频序列进一步通过发送概率控制算法(算法2)映射到对应的物理信道,节点使用物理信道进行实际的通信。首先,传感器节点根据发送状态下各信道使用概率进行排序,并将按照逻辑信道顺序映射到当前发送概率由高到低的物理信道。每当用户在某信道成功达到Rendezvous一次,其对应发送参数Psi(x)加1/Us,Us是发送状态下信道使用的总次数,其他信道发送参数减1/Us,反之亦然。当感知信道集中信道最大发送概率大于阈值λ,则将逻辑信道1切换至序号最大的逻辑信道,其余不变,以保证感知信道集中各信道使用概率均衡,增强网络稳定性,达到Full Rendezvous要求。
算法1 发送方逻辑序列构造算法(the sender logic sequence construction)
INPUT:Ms
OUTPUT: channel Cs[i]
Ps=the smallest prime number not less than Ms;
for L=Ps-1 to 0 do
for n=0 to Ps-1 do //每P个时间片步长减少一次
Csi=[(t×L)%Ps-L]%Ps+1;
End
End
2) 节点接收状态
当节点处于接收状态时,每Pr个时间片步长L改变一次,由0递增至Pr-1,每个循环将会持续Pr2个时间片长度,前Pr个时间片保持现有信道不变,处于等待状态,以增加Rendezvous成功概率,接下来Pr(Pr-1)个时间片用于跳频。生成的接收状态逻辑跳频序列通过接收概率控制(算法4),根据接收状态下各信道使用概率进行排序,并将按照逻辑信道顺序映射到当前发送概率由高到低的物理信道,进行接收。
算法2 发送方物理信道映射算法(the sender physical channel mapping)
INPUT: Psi[x],Csi[x], Us
//Csi[x]是用户i在发送状态下感知信道集合, Us是CRSN中用户数量
//输入各信道发送状态概率集、逻辑信道序列和信道使用总次数
OUTPUT: sender physical CH list Si(x)
sort Psi[x]
for (x=0;x < P; x++)
if Psi(x)max≤λ //最大发送概率≤阈值
Si(x)← Csi[x]//逻辑信道映射到物理信道
Else
Si(max)==Si(1)
//将逻辑信道1切换至序号最大信道
Si(x) ←Csi[x]
//逻辑信道按概率大小映射到对应物理信道
Psi(x)=Psi(x)+1/Us
//物理信道发送概率相应增加
Psi(k)=Psi(k)-
//其他信道发送概率相应减少
END
算法3 接收方逻辑序列构造算法(the receiver logic sequence construction)
INPUT:Mr OUTPUT: channel Cr[i]
Pr=the smallest prime number not less than Mr;
for L=0 to Pr-1 do
for n=0 to Pr-1 do //P个时间片步长增加一次
Cri=[(t×L)%Pr-L]%Pr+1;
End
End
算法4 接收方物理信道映射算法(the receiver physical channel mapping)
INPUT: Prj[y], Crj[y], Ur
//Crj[y]是用户j接收状态下感知信道集合, Ur是接收状态下信道使用的总次数
//各信道接收状态概率集、逻辑信道序列和信道使用总次数
OUTPUT: receiver physical CH list Rj(y)
sort Prj[y] //排序
for (y=0;y < P; y++)
if Prj(y)max≤λ//最大接收概率小于等于阈值
Rj(y)← Crj[y] //逻辑信道按概率大小映射到对应物理信道
Else
Rj(y)← Crj[y]//逻辑信道按概率大小映射到对应物理信道
Prj(y)=Prj(y)+1/Ur//物理信道发送概率增加
Rj(max)=Rj(1)//逻辑信道1切换至序号最大信道
Other channels Prj(k)=Prj(k)-1/Ur
End
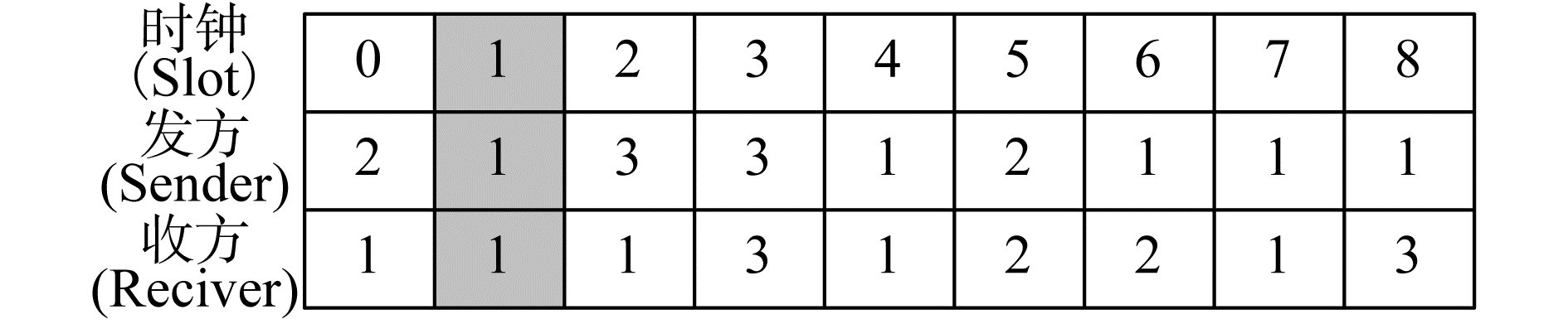
信道成功达到Rendezvous一次,对应发送参数Prj(y)加1/Ur,Ur接收状态下信道使用的总次数,其他信道发送参数减1/Ur,反之亦然。当感知信道集中信道最大发送概率大于阈值λ,则将逻辑信道1切换至序号最大的逻辑信道,其余不变,以保证感知信道集中各信道使用概率均衡,增强网络稳定性,达到Full Rendezvous要求。假设MS=Mr=3,Ps和Pr均为不小于3的最小质数,即Ps=Pr=3,则发送方和接收方均为每T=9个时间片重复一次。图 1表示根据算法1、算法3生成的发送方和接收方的逻辑调频序列(2 1 3 3 1 2 1 1 1)、(1 1 1 3 1 2 2 1 3),灰色部分表示在时间片1的位置双方达到Rendezvous。生成的逻辑跳频序列将根据算法2和算法4分别映射到当前所处状态下对应的物理信道,逻辑信道和物理信道对应关系将后续部分进行说明。
|
Download:
|
| 图 1 发送方和接收方逻辑跳频序列 Fig. 1 Sender and receiver logic hopping sequence | |
本节将分别对SRP算法在对称模型下以及非对称模型下的时钟同步、时钟异步的MTTR和ATTR进行理论分析。
定理1 对于成对节点i,j,有信道x和y,1≤x≤Ms,1≤y≤Mr,节点i与节点j通信过程中,Psi(x)表示节点i处于发送状态下信道x的使用概率,Prj(y)表示节点j处于接收状态下信道y的概率,Psi(x)max表示节点i处于发送状态下使用概率最大的信道,Prj(y)max表示节点j处于接收状态下使用概率最大的信道。若Psi(x)max=Psq,Prj(y)max= Prw,则有q=w。
证明 设发送方信道使用概率为Psi(1), Psi(2), Psi(3), …, Psi(x), 接收方信道使用概率为Prj(1), Prj(2), Prj(3), …, Prj(y),Psi(x)max=Psi(q),Prj(y)max=Prj(w)(q≤x, w≤y)时,q≠w,则发送方与接收方不在同一信道上Rendezvous,不符原则,因此必有q=w。证毕。
对于成对节点,发送概率最大的信道与接收概率最大信道必然相同,同理,发送概率的信道排序与接收概率信道排序必然相等。由此可得,发送方使用概率最大信道与接收方使用概率最大信道相同。
定理2 Csi(xt)表示t时刻发送方逻辑信道,假设发送方逻辑序列为Csi(xt),Csi(xt+1),Csi(xt+2), …, Csi(xt+z)(z≥P2),子序列Csi(xk),Csi(xk+1),…, Csi(xk+P+1)(1≤K≤t)必然有Csi(xk+f)=Csi(1)(1≤f≤Ps)。
证明 设t=nPs+1,(0≤n≤Ps-1), 则L=Ps-n+1,可得:Csi(xt)={[(nPs+1)*(Ps-n-1)] %Ps-(Ps-n-1)}%Ps+1,化简后:Csi(xt)=Csi(1)。可得t=1, Ps+1, …, nPs+1(0≤n≤Ps-1)时均有Csi(xk+f)=Csi(1),因此Csi(xt),Csi(xt+1),Csi(xt+2), …, Csi(xt+z)(z≥P2)的子序列Csi(xk),Csi(xk+1),…, Csi(xk+P+1)(1≤K≤t)必然有Csi(xk+f)=Csi(1)(1≤f≤Ps)。即发送方逻辑序列中任意一段长度为Ps的发送方子序列必然有逻辑信道1。证毕。
结论1 在对称模型下,即Mr=Ms=Gr,s,SRP算法的MTTR≤Ps
证明 当发送方和接收方满足时钟同步模型时,即Mr=Ms=Gr,s,则Pr=Ps。由定理2可知,发送方任意一段长度为Ps的子序列必然有逻辑信道1,根据算法3,接收方第0到Ps时间片内均在信道1等待,因此接收方从任意时间片开始进行跳频,必然在Ps个时间片内与发送方在逻辑信道1上完成Rendezvous,即MTTR≤Ps。
当发送方和接收方满足时钟异步模型时,发送方和接收方开始跳频时间片初始位置不同,同理可得MTTR≤Ps。证毕。
假设在时钟同步模型下,Mr=Ms=Gr, s=3,则有Pr=Ps=3,发送方和接收方初始时间片均为0,由算法1和算法3可得发送方和接收方逻辑跳频序列,其MTTR情况如图 2所示。

|
Download:
|
| 图 2 时钟同步模型逻辑信道示例(Mr=Ms=Gr, s=3) Fig. 2 Logic sequence illustration of the synchronization model(Mr=Ms=Gr, s=3) | |
假设Psi(1)=20%,Psi(2)=30%,Psi(3)=50%,Pri(1)=10%,Pri(2)=20%,Pri(3)=70%,由定理1可知,成对节点发送方和接收方各信道使用概率排序相同,根据算法2和算法4,图 2中生成的对应物理信道如图 3所示,发放和收方在信道3相遇。

|
Download:
|
| 图 3 时钟同步模型物理信道示例(Mr=Ms=Gr,s=3) Fig. 3 Physical sequence illustration of the synchronization model(Mr=Ms=Gr, s=3) | |
结论2 在非对称模型中,即Mr≠MS≠Gr,s,MTTR≤Ps2
证明 当Mr > MS, 即Pr > PS,由定理2可知,发送方逻辑序列中任意一段长度为Ps的子序列必然有逻辑信道1。因此在接收方处于等待阶段的Pr各时间片内一定达到Rendezvous,即MTTR≤Ps2。
当Mr < MS, 最坏情况为发送方和接收方在同一时间片开始跳频,但为达到Rendezvous,直到发送方补偿处达到Rendezvous,但最坏情况是在发送方补偿的Ps个时间片中的最后一个时间片处达到Rendezvous,即MTTR≤Ps2。
当发送方和接收方满足时钟异步模型时,发送方和接收方开始跳频时间片初始位置不同,同理可得MTTR≤Ps2。证毕。
下面将针对这2种情况分别示例说明:
1) 针对Mr>MS情况,假设在时钟同步模型下,Mr=5,MS=3,由此可得Pr=5,Ps=3,发送方和接收方初始时间片均为0,由算法1和算法3可得发送方和接收方逻辑跳频序列,其MTTR情况如图 4所示。

|
Download:
|
| 图 4 时钟同步模型逻辑信道示例(Mr=5,MS=3) Fig. 4 Logic sequence illustration of the synchronization model(Mr=5, MS=3) | |
进一步,关于物理信道映射问题,假设Psi(1)= 20%,Psi(2)=50%,Psi(3)=30%,Pri(1)=10%,Pri(2)=60%,Pri(3)=20%,Pri(4)=4%,Pri(5)= 6%,由定理1可知,成对节点发送方和接收方各信道使用概率排序相同,根据算法2和算法4,图 4中生成的对应物理信道如图 5所示

|
Download:
|
| 图 5 时钟同步模型物理信道示例(Mr=5,MS=3) Fig. 5 Physical sequence illustration of the synchronization model(Mr=5, MS=3) | |
2) 针对Mr < MS情况,假设在时钟同步模型下,Mr=3,MS=5,由此可得Pr=3,Ps=5.,发送方和接收方初始时间片均为0,由算法1和算法3可得发送方和接收方逻辑跳频序列,其MTTR情况如图 6所示。

|
Download:
|
| 图 6 时钟同步模型逻辑信道示例(Mr=3,MS=5) Fig. 6 Logic sequence illustration of the synchronization model(Mr=3, MS=5) | |
进一步,关于物理信道映射问题,假设Psi(1)= 10%,Psi(2)=20%,Psi(3)=60%,Psi(4)=4%,Psi(5)=6%,Pri(1)=20%,Pri(2)=30%,Pri(3)=50%,由定理1可知,成对节点发送方和接收方各信道使用概率排序相同,根据算法2和算法4,图 4中生成的对应物理信道如图 7所示。

|
Download:
|
| 图 7 时钟同步模型物理信道示例(Mr=3, MS=5) Fig. 7 Physical sequence illustration of the synchronization model(Mr=3, MS=5) | |
由上述例子可知,在对称模型中,最坏情况下MTTR为Ps2,由此可见算法的有效性。
3 实验为了验证SRP算法的有效性,本文用Matlab 2017实现了该算法,并给出了仿真结果。将SRP算法和最近提出的3种代表性算法,即JS[9]、ACH[14]、SR-JW[15],进行了比较。在仿真过程中,充分考虑了对称模型和非对称模型下的成对用户场景。对称模型下,每个用户的感知信道集完全相同,非对称模型下,随机生成每个用户的可用信道,并将u表s示为可用信道的比例,即每个用户平均有u×M个可用信道,在非对称模型下u是一个从0.1到1随机生成的十进制数。
为了模拟时钟异步环境,所有用户均随机启动跳频序列。由于JS、AHW、SR-JW均采用的时隙同步技术[16],允许多个分组在一个时间片传输,本文将JS]、AHW的一次时隙同步技术的持续时间设为2T。根据IEEE 802.22,T等于10 ms[17]。因此,这3种算法中的每一个时隙的持续时间为20 ms。此外,由于SR-JW一个时间片长度为10 ms,采用将SR-JW的一个时间片扩展到2T以建立相同的仿真环境。在不损失通用性的情况下,通过1 000次蒙特卡罗模拟得到了ATTR实验结果的平均值。
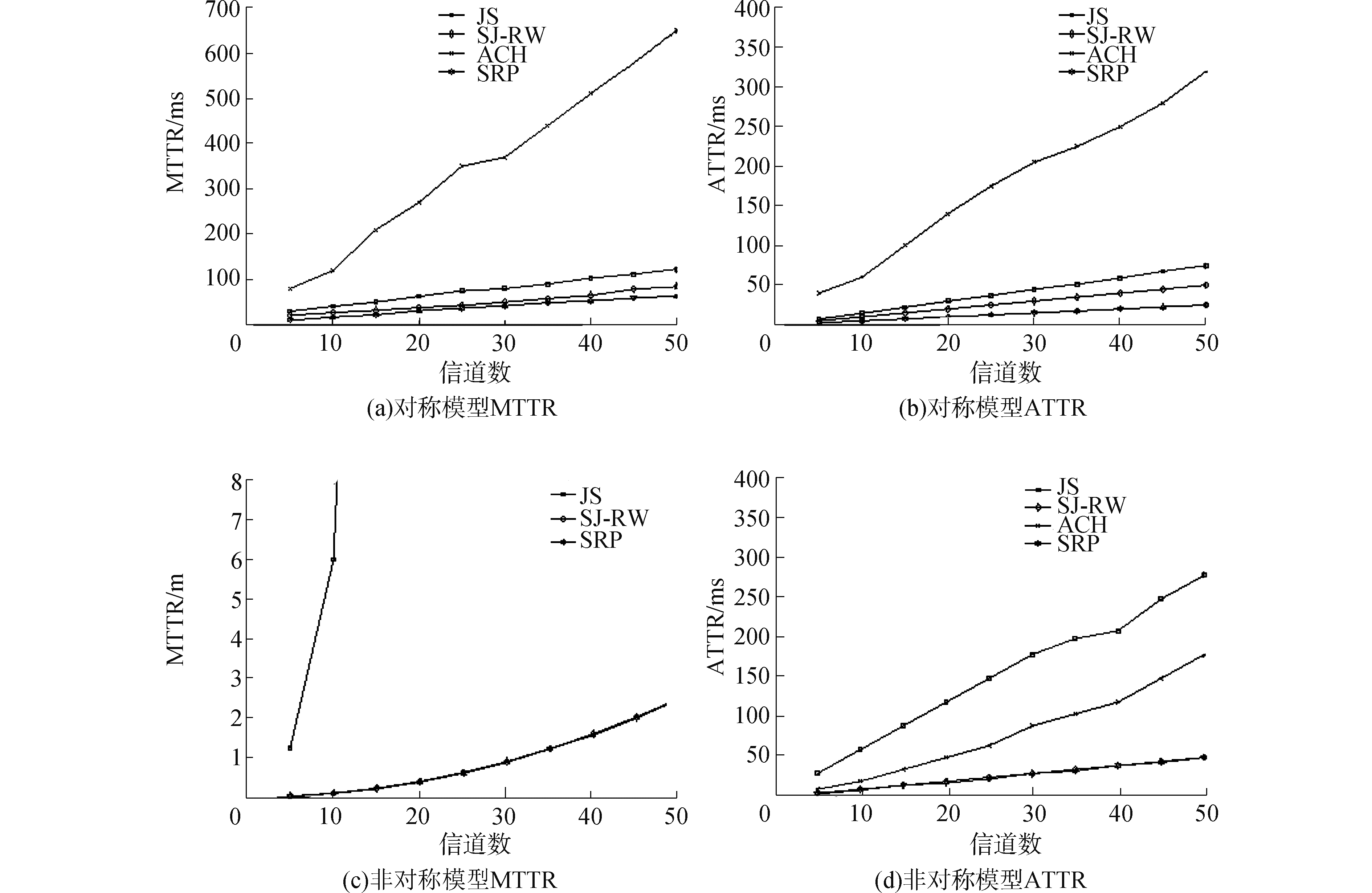
对称模型下两用户MTTR和ATTR如图 8(a)图 8(b)所示,由图可知对称模型下SRP算法的MTTR和ATTR均优于JS、ACH算法,远远小于AHW算法。非对称模型下成对用户MTTR和ATTR如图 8(c)、图 8(d)所示,由图可知非对称模型下SRP算法的MTTR和ATTR均较优于ACH算法,远远小于AHW和JS算法。
|
Download:
|
| 图 8 成对用户对称模型非对称模型的MTTR、ATTR Fig. 8 MTTR, ATTR under symmetric model and asymmetric model of 2-user | |
1) 该算法在信道集合对称、非对称模型,时钟同步、异步模型均实现了Rendezvous的有效执行;
2) 通过对比实验分析,SRP算法在信道集对称和非对称模型下的MTTR、ATTR均有明显的优化;
3) 通过引入信道使用概率,有效保证节点感知信道集中每一信道均具有Rendezvous可能性,解决了Rendezvous信道的整体均衡使用问题(Full Rendezvous),增强了网络的适应性。
综上所述,SRP算法有效解决CRSN中公共控制信道瓶颈问题,对提高动态网络稳定性和传输效率有重要意义。未来我们将对该方法进行进一步讨论,从成对用户扩展到多用户,在多源多跳Rendezvous问题上进一步进行研究,为认知无线传感器网络跨层传输提供新的思路。
| [1] |
DEBROY S, BHATTACHARJEE S, CHATTERJEE M. Spectrum map and its application in resource management in cognitive radio networks[J]. IEEE transactions on cognitive communications and networking, 2015, 1(4): 406-419. DOI:10.1109/TCCN.2016.2517001 (  0) 0)
|
| [2] |
BRIK V, ROZNER E, BANERJEE S, et al. DSAP: a protocol for coordinated spectrum access[C]//Proceedings of the 1st IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, 2005. Baltimore, MD, USA, 2005: 611-614. https://ieeexplore.ieee.org/document/1542680/
(  0) 0)
|
| [3] |
BUDDHIKOT M M, KOLODZY P, MILLER S, et al. DIMSUMnet: new directions in wireless networking using coordinated dynamic spectrum[C]//Proceedings of the 6th IEEE International Symposium on a World of Wireless Mobile and Multimedia Networks. Taormina-Giardini Naxos, Italy, 2005: 78-85. https://ieeexplore.ieee.org/document/1443488
(  0) 0)
|
| [4] |
CORDEIRO C, CHALLAPALI K, BIRRU D, et al. IEEE 802.22: the first worldwide wireless standard based on cognitive radios[C]//Proceedings of the 1st IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, 2005. Baltimore, MD, US, 2005. https://ieeexplore.ieee.org/document/1542649?reload=true&arnumber=1542649
(  0) 0)
|
| [5] |
JIA Juncheng, ZHANG Qian, SHEN Xuemin. HC-MAC:a hardware-constrained cognitive MAC for efficient spectrum management[J]. IEEE journal on selected areas in communications, 2008, 26(1): 106-117. DOI:10.1109/JSAC.2008.080110 (  0) 0)
|
| [6] |
MA Liangping, HAN Xiaofeng, SHEN C C. Dynamic open spectrum sharing MAC protocol for wireless ad hoc networks[C]//Proceedings of the 1st IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, 2005. Baltimore, MD, USA, 2005: 203-213. https://ieeexplore.ieee.org/document/1542636
(  0) 0)
|
| [7] |
PÉREZ-ROMERO J, SALLENT O, AGUSTÍ R, et al. A novel on-demand cognitive pilot channel enabling dynamic spectrum allocation[C]//Proceedings of the 2nd IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks. Dublin, Ireland, 2007: 46-54. https://ieeexplore.ieee.org/document/4221476
(  0) 0)
|
| [8] |
ZHANG Yifan, LI Qun, YU Gexin, et al. ETCH: efficient channel hopping for communication rendezvous in dynamic spectrum access networks[C]//Proceedings of 2011 IEEE INFOCOM. Shanghai, China, 2011: 2471-2479. https://ieeexplore.ieee.org/document/5935070
(  0) 0)
|
| [9] |
LIN Zhiyong, LIU Hai, CHU Xiaowen, et al. Jump-stay based channel-hopping algorithm with guaranteed rendezvous for cognitive radio networks[C]//Proceedings of 2011 IEEE INFOCOM. Shanghai, China, 2011: 2444-2452. https://ieeexplore.ieee.org/document/5935066
(  0) 0)
|
| [10] |
THEIS N C, THOMAS R W, DASILVA L A. Rendezvous for cognitive radios[J]. IEEE transactions on mobile computing, 2011, 10(2): 216-227. DOI:10.1109/TMC.2010.60 (  0) 0)
|
| [11] |
CORMIO C, CHOWDHURY K R. Common control channel design for cognitive radio wireless ad hoc networks using adaptive frequency hopping[J]. Ad hoc networks, 2010, 8(4): 430-438. DOI:10.1016/j.adhoc.2009.10.004 (  0) 0)
|
| [12] |
CHUANG I, WU H Y, LEE K R, et al. Alternate hop-and-wait channel rendezvous method for cognitive radio networks[C]//Proceedings of 2013 IEEE INFOCOM. Turin, Italy, 2013: 746-754. https://ieeexplore.ieee.org/document/6566861
(  0) 0)
|
| [13] |
SHIN J, YANG Dongmin, KIM C. A channel rendezvous scheme for cognitive radio networks[J]. IEEE communications letters, 2010, 14(10): 954-956. DOI:10.1109/LCOMM.2010.091010.100904 (  0) 0)
|
| [14] |
BIAN Kaigui, PARK J M. Maximizing rendezvous diversity in rendezvous protocols for decentralized cognitive radio networks[J]. IEEE transactions on mobile computing, 2013, 12(7): 1294-1307. DOI:10.1109/TMC.2012.103 (  0) 0)
|
| [15] |
LI Jiaxun, ZHAO Haitao, WEI Jibo, et al. Sender-jump receiver-wait:a simple blind rendezvous algorithm for distributed cognitive radio networks[J]. IEEE transactions on mobile computing, 2018, 17(1): 183-196. DOI:10.1109/TMC.2017.2703166 (  0) 0)
|
| [16] |
STEVENSON C R, CHOUINARD G, LEI Zhongding, et al. IEEE 802.22:the first cognitive radio wireless regional area network standard[J]. IEEE communications magazine, 2009, 47(1): 130-138. DOI:10.1109/MCOM.2009.4752688 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


