2. 上海交通大学 船舶海洋与建筑工程学院, 上海 200240;
3. 大连理工大学 工业装备结构分析国家重点实验室 船舶工程学院, 辽宁 大连 116024;
4. 高技术船舶与深海开发装备协同创新中心, 上海 200240;
5. 中国船舶科学研究中心 海洋防务技术创新中心, 江苏 无锡 214082
2. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;
3. School of Naval Architecture, State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, China;
4. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China;
5. Marine Defense Technology Innovation Center, China Ship Scientific Research Center, Wuxi 214082, China
部分充满液体的容器在外部激励下会引起自由液面的运动,这种现象就是晃荡。晃荡现象通常可以被理解为液面的自由波动,可分为驻波、行波、水跃和破波,甚至是几种运动的组合[1]。在外部激励频率接近液体的自振频率时,会产生共振现象,此时流体的运动极其复杂,呈现出非常强烈的非线性和随机性,与此同时,剧烈的液体运动会产生极大的局部抨击力,结构物将在瞬时承载巨大的冲击载荷,甚至造成结构的损坏以及船体稳性的丧失[1]。为了保障工程设计的安全性和船舶航行的稳定性,对于晃荡问题的研究就变得十分必要。
最早进行相关研究主要是在航空航天领域,Abramson等[2]研究了该问题并对前人的工作进行了梳理,主要采用势流理论分别对几种不同形状的液舱进行了研究,针对线性问题,不仅推导出了经典的解析解,还做了大量的实验予以验证;Faltinsen等[3-4]同样采用了不可压缩势流理论对该问题进行了研究,并得到了非线性的速度势公式,他的研究成果被许多人广泛使用,这其中就包括Nakayama等[5],以及Waterhouse等[6],但是其理论依然受到很大的限制,比如容器形状简单,内部光滑无其他结构物,且水深较高等;当水跃现象出现时,浅水波理论是有用的数学模型,这其中包括Verhagen等[7]以及Armenio等[8]对该理论和雷诺平均NS方程的比较;随着计算机的广泛运用,越来越多的人试图寻求计算机来求解流体力学问题,CFD的出现让晃荡问题的研究有了新的出路[9],事实上很多种数值方法都可以用来研究晃荡现象,这其中VOF方法因为其处理自由界面的优越性而得到了广泛的应用[10-11]。
本文采用一种将树形自适应网格与VOF方法相结合的并行算法[12]对几种情况下的晃荡问题进行了数值模拟,并将计算得到的几种工况下的自由表面升高,力和力矩同解析解,实验值进行了对比,验证了该数值方法对于此问题的有效性,并对计算结果进行了相应的分析。
1 液体晃荡数学模型 1.1 控制方程采用不可压变密度Navier-Stokes方程组作为控制方程:
| $ \rho \left( {\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial t}} + \mathit{\boldsymbol{u}} \cdot \nabla \mathit{\boldsymbol{u}}} \right) = \rho \mathit{\boldsymbol{F}}-\nabla p + \nabla \cdot \left( {2\mu \mathit{\boldsymbol{D}}} \right) $ | (1) |
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho \mathit{\boldsymbol{u}}} \right) = 0 $ | (2) |
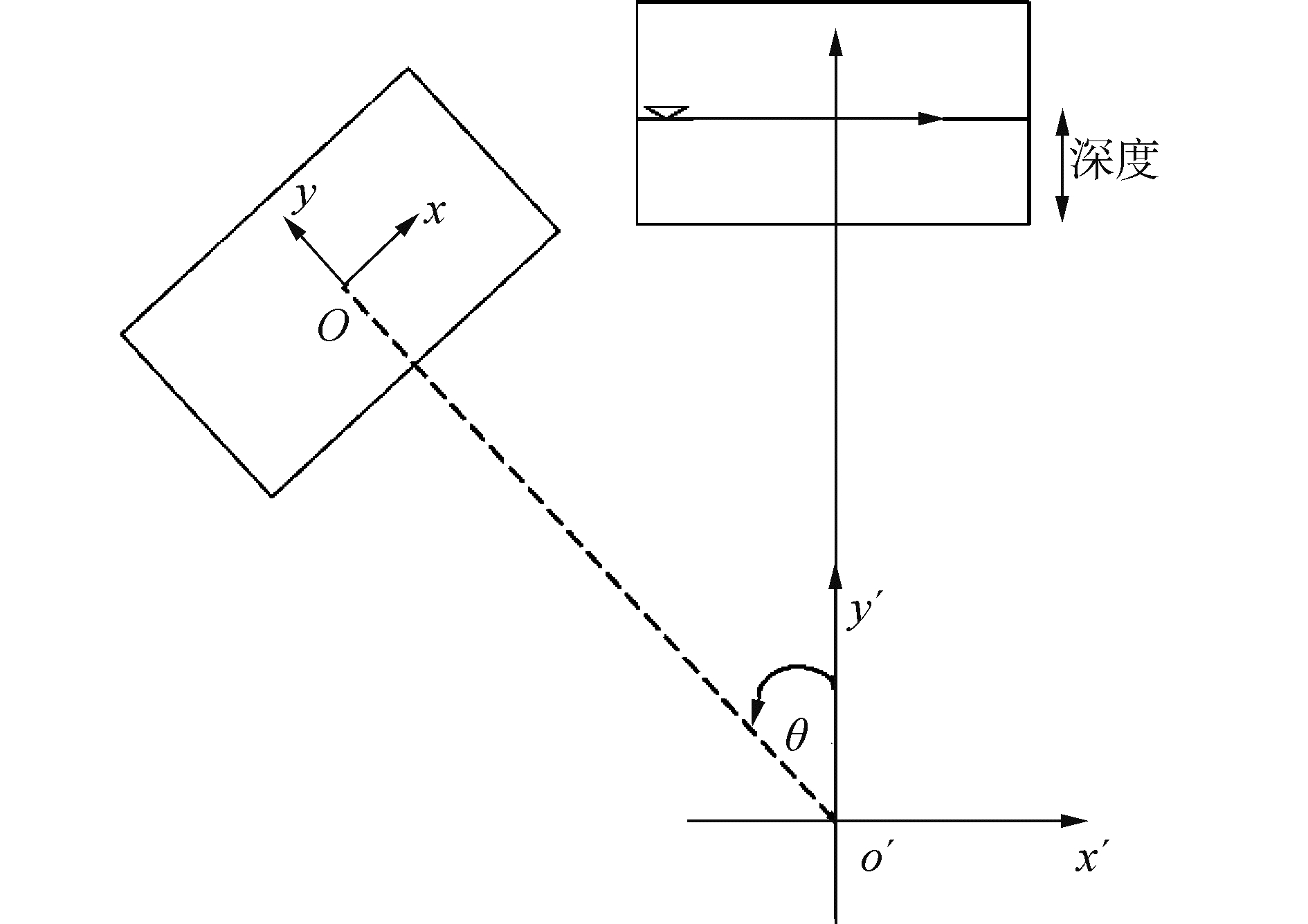
式中:u为速度向量;p为压力;D表示应变率对称张量,其各分量为Dij=(∂iuj+∂jui)/2;ρF代表体积力。晃荡问题坐标系如图 1所示,式(1)、(2)中各变量均在非惯性坐标系xoy上,故在该坐标系上的F各分量表示为[13-14]:
|
Download:
|
| 图 1 坐标系选取 Fig. 1 Definition sketch | |
| $ {F_i} =-g\sin \theta + {x_j}\ddot \theta + {x_i}{\dot \theta ^2} + 2\dot \theta {u_j}-\ddot A $ | (3) |
| $ {F_j} =-g\cos \theta-{x_i}\ddot \theta + {x_j}{\dot \theta ^2}-2\dot \theta {u_i} $ | (4) |
式中:g为重力加速度;xi为x轴坐标;xj为y轴坐标;ui为x方向速度标量;uj为y方向速度标量;θ和A(x′o′y′坐标系下)分别表示水槽外激励随时间变化的纵摇幅值和纵荡幅值(x′轴方向),且θ=0时为图中实线位置,它们的表达式为:
| $ A = {A_0}\sin \left( {{\omega _s}t + {\varepsilon _s}} \right) $ | (5) |
| $ \theta = {\theta _0}\sin \left( {{\omega _p}t + {\varepsilon _p}} \right) $ | (6) |
式中A0、θ0、ωs、ωp、εs、εp分别表示纵荡和纵摇的幅值、频率与相位差。
考虑到两相流问题VOF方法中体积分数T的引入,于是,密度ρ和动力粘性系数μ可表示为:
| $ \rho \left( T \right) = {\rho _1}T + {\rho _2}\left( {1-T} \right) $ | (7) |
| $ \mu \left( T \right) = {\mu _1}T + {\mu _2}\left( {1-T} \right) $ | (8) |
式中下标1、2分别代表 2种不同的流体。
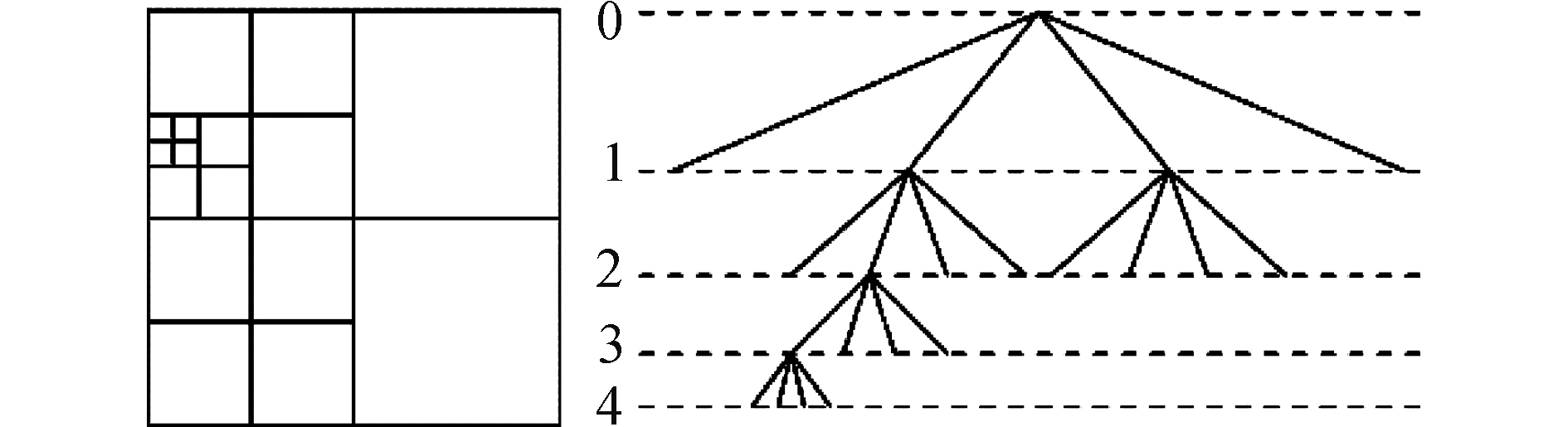
1.2 数值方法 1.2.1 空间离散整个计算域的离散采用的是若干正方形有限体积单元,它们之间具有如同数据结构中四叉树(Quadtree)(八叉树Octree)的继承关系,图 2给出了一个二维情况下计算域离散后的单元对应关系,定义每一个有限体积单元(cell)的边(Edge)的长度为h,每个单元都有可能是其4个子单元(Children)(三维情况下是8个)的父单元(Parent),需要注意的是根单元(Root cell)是结构树的根节点而叶节点处的叶单元(Leaf cell)则没有任何子单元,单元的水平(Level)是从根单元由零级开始每遇一级子单元则依次加1来确定的,每个单元C在同一水平时每个方向d(二维情况下为4个)上都有一个直接邻单元(Neighbour) Nd,它们之间通过单元的交界面(Face) Cd相连接,混合单元(Mixed cell)被用来处理嵌有固壁的计算域,控制方程中最初的变量都定义在各单元的中心位置。
|
Download:
|
| 图 2 四叉树空间离散及对应树形结构的图例 Fig. 2 Example of quadtreediscretisation and corresponding tree representation | |
为了方便在单元边界处的计算,以下约束需要注意,如图 2所示,首先,每个单元的直接邻单元的水平不能和其本身的水平相差超过1,其次,每个单元的对角线邻单元的水平不能和其本身的水平相差超过1。最后,所有和混合单元直接相邻的单元必须与混合单元具有同一水平。
目前所使用的满足数据结构算法需求的,是由Khokhlov等[16]提出的全线程树方法,它保证了对于给定的任意单元,得到它的临单元和其自身水平及空间坐标的时间复杂度为O(1)。对于遍历所有叶单元,所有给定水平的单元集以及所有混合单元使用的是标准的基于指针的树方法,其时间复杂度为O(NlogN)。
由于树型数据结构在空间离散中的应用,对于整个自适应的算法而言就变得相对易于操作了,它实际上分为2个部分,首先,所有满足给定自适应条件的叶单元需要被细分,其次,所有满足给定自适应条件的叶单元的父单元需要被重组为叶单元,即第一步的逆。
很多变量都可以作为自适应条件的依据,以涡量为例:
| $ \frac{{h\left\| {\nabla \times \mathit{\boldsymbol{U}}} \right\|}}{{\max \left\| \mathit{\boldsymbol{U}} \right\|}} > \tau $ | (9) |
式中:网格的大小用长度h来表示;自适应的阈值则用τ来表示(0 < τ < 1)。这样的话,一个基于局部涡量范数的自适应条件就定义了。
自适应算法较普通结构化均匀网格可以有效减少计算时所需的时间和存储空间,并且可以产生更加精确的计算结果,这是因为自适应算法可以在不需要高分辨率的网格计算区域做到网格自动加粗,而对于需要细化网格的地方进行加密,比如速度梯度较大,或者自由表面变形较大时,都需要较高的计算精度,从而保证计算的高效与准确。基于四叉树的自适应算法又继承了方形网格的优点,这样的有限体积单元形状方便对各点的变量进行插值计算和自由界面的重构,且计算精度较高。
1.2.2 时域离散对时域的离散,本文主要使用了分数步映射法[12],离散后的控制方程为:
| $ \begin{gathered} {\rho _{n + \frac{1}{2}}}\left[{\frac{{{u_*}-{u_n}}}{{\Delta t}} + {u_{n + \frac{1}{2}}} \cdot \nabla {u_{n + \frac{1}{2}}}} \right] = \hfill \\ \nabla \cdot \left[{{\mu _{n + \frac{1}{2}}}\left( {{D_n} + {D_{n + \frac{1}{2}}}} \right)} \right] + \rho \mathit{\boldsymbol{F}} \hfill \\ \end{gathered} $ | (10) |
| $ {u_{n + 1}} = {u_*}-\frac{{\Delta t}}{{{\rho _{n + \frac{1}{2}}}}}\nabla {p_{n + \frac{1}{2}}} $ | (11) |
| $ \nabla \cdot {u_{n + 1}} = 0 $ | (12) |
因为VOF方法中体积分数的引入,密度的对流方程(2)可等效地表示为体积分数T的对流方程,离散后的形式为:
| $ {T_{n + \frac{1}{2}}}-{T_{n-\frac{1}{2}}} + \nabla \cdot \left( {{T_n}{u_n}} \right) = 0 $ | (13) |
式中u*表示的是一个临时速度场,它实际体现的是以下的算法实质。
为和方程(11) ~(13)中变量区分,使用其他符号,读者可以近似地和控制方程的形式对比:
| $ \frac{{{U_*}-{U_n}}}{{\Delta t}} =-{A_{n + \frac{1}{2}}} $ | (14) |
| $ {U_*} = {U_{n + 1}} + \nabla \phi $ | (15) |
通过上面方程(14)和方程(15)将原来的速度场进行了分解得到了一个临时速度场U*,实质就是对U*运用了一个基于Hodge分解的映射法后得到的一个新的速度场Un+1和分数步压力场pn+1/2,注意到:
| $ \nabla \cdot \mathit{\boldsymbol{U}} = 0\;\;\;\;\;{\text{in}}\;\varOmega $ | (16) |
| $ \mathit{\boldsymbol{U}} \cdot n = 0\;\;\;\;\;\;\;\;{\text{on}}\;\;\partial \varOmega $ | (17) |
于是对方程(16)两边取散,就得到了压力Poisson方程:
| $ {\nabla ^2}\phi = \nabla \cdot {U_*} $ | (18) |
满足边界条件:
| $ \frac{{\partial \phi }}{{\partial n}} = {U_*} \cdot n\;\;\;\;\;\;\;\;\;在\partial \varOmega 上 $ | (19) |
通过求解压力Poisson方程得到无散速度场:
| $ \mathit{\boldsymbol{U}} = {U_*}-\nabla \phi $ | (20) |
需要指出的是方程(19)的求解对于不同水平的有限体积单元,特殊的插值格式是必要的,文献[12]中有详细的讨论。
1.2.3 自由界面处理自由界面的处理主要基于一种VOF和不可压缩四叉树自适应网格相结合的方法[17],其中经典的VOF几何格式被运用在树形自适应网格上,这是为了保证在自由界面上不同分辨率的空间网格可以被处理。
VOF是一种运用非常广泛且高效的处理自由表面的数值方法,最早由Debar等[18]提出,然后由Hirt等[19]进一步完成,VOF方法稳定且实用,其基本思想为:定义函数T和1-T,它们分别表示在计算域中水和空气的体积分数,对于每一个独立的网格单元,水和空气的体积分数之和必为1,于是存在以下3种情况:
1) T=1,网格单元内全部是水;
2) T=0,网格单元内全部是空气;
3) 0 < T < 1,网格单元内一部分是水,一部分为空气,于是水和空气之间就存在一个交界面,即自由界面或者自由表面。
这里使用的是拓展到树形空间网格的分段线性的几何VOF格式,传统的VOF主要分为2个步骤:1)界面重构;2)几何通量的计算及界面流动的处理。其主要思想[20]是运用体积分数的梯度来确定自由表面的法向,通过方程:
| $ \mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{x}} = \alpha $ | (21) |
来计算出自由表面的位置的近似值。式中:n为局部自由界面的法向;x为位置向量;α和T则满足一定的函数关系:T=V(n, α)。
VOF能够用来方便地描述自由界面的变化,所以在处理有自由界面的计算流体动力学问题时,VOF是一个理想的工具。
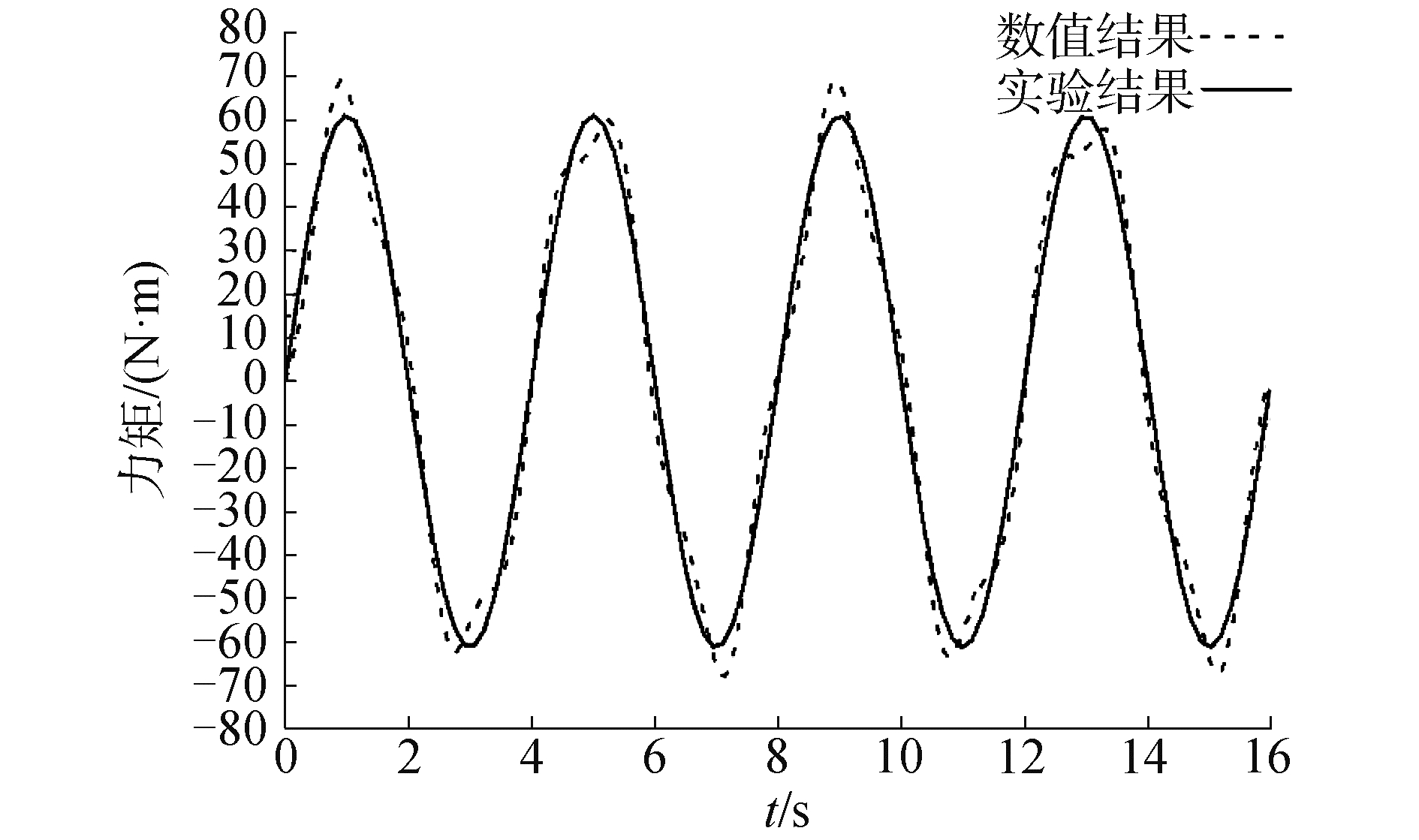
2 计算结果分析 2.1 算例1图 3给出了在方形容器内,宽为1 m,水深为0.7 m,纵摇幅值θ0=4°,频率ω0=0.5π rad/s时参考点为原点,力矩的计算结果,其中虚线为数值计算得到的数据,实线则为按照文献[2]中所给的解析解表达式得到的计算结果,从图中可以看出,计算值与解析解周期吻合,且波形也较为一致,考虑到势流理论得到的解析解的线性及刚性假设,幅值本身偏小,验证了该数值模拟对于晃荡问题力矩的计算是可靠的。
|
Download:
|
| 图 3 作用于原点的力矩 Fig. 3 Time history of pressure moment | |
如图 4所示的容器,对其施加一个相对于水槽中心的外部纵摇简谐激励,其中θ0分别为4°和8°,ωp=2.0 rad/s,图 5给出了压力的计算值和Akayildiz等[21]得到的实验值,通过对比发现,数值模拟的结果和实验测得的结果周期一致,波形大体一致,且激励幅值较小时计算值与实验值越接近,从图中数据可以看出,该数值模拟对于压力的计算也是较为准确的。

|
Download:
|
| 图 4 水槽模型1 Fig. 4 Tank dimensions and wave probe positions used in this simulation | |

|
Download:
|
| 图 5 压力的计算与实验曲线比较 Fig. 5 Comparison of pressure′s numerical and experimental values | |
如图 6所示一矩形水槽,距离左侧0.05 m的地方有探测器来输出液面高度,外部激励则为纵荡,通过数值计算得到图 7所示。根据Abramson[1]给出的晃荡问题一阶自然频率计算公式:

|
Download:
|
| 图 6 水槽模型2 Fig. 6 Tank dimensions and wave probe positions used in this simulation | |

|
Download:
|
| 图 7 液面升高曲线 Fig. 7 Free surface elevation at wave probe | |
| $ \omega _0^2 = \frac{{g\pi }}{l}\tanh \left( {\pi \frac{d}{l}} \right) $ | (23) |
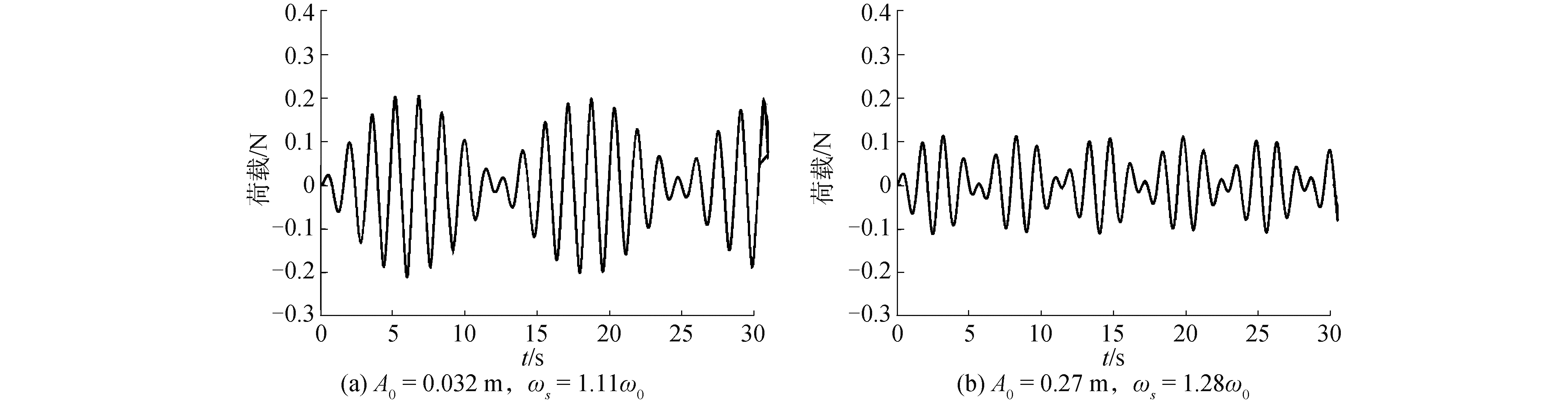
通过图 7数据,有ω0=3.767 4 rad/s。图 7 (a)和(b)为A0=0.032 m,ωs=1.11ω0时液面升高数值计算结果与Faltinsen[22]给出的解析解和实验值的比对,图 7(c)和(d)则为A0=0.27 m,ωs=1.28ω0时数值结果与Faltinsen[22]给出的解析解和实验值的对比。图 8(a)为A0=0.032 m,ωs=1.11ω0时水平方向合力的数值计算结果,图 8(b)为A0=0.27 m,ωs=1.28ω0时该工况下水平方向合力的数值计算结果。
|
Download:
|
| 图 8 沿水平方向力曲线 Fig. 8 Time history of horizontal forces | |
通过图 8的对比,数值结果明显较解析解更符合实验所得到的结果,首先解析解的周期要和实验值有一定的误差,图 8(c)、(d)在频率偏高,振幅较小时,Faltinsen[22]给出的理论计算方法的周期较实验值要偏小,而图 8(a)、(b)频率稍小,振幅稍微增大时,理论值的周期则又大于实验值,与此同时,无论何种情况,数值计算总能得到较为满意的结果,周期和实验完全吻合,波形上,数值方法的结果也和实验结果基本一致,外包络线基本相符,小波的峰值和周期也完全吻合,这充分说明了基于四叉树自适应网格的VOF方法具有处理二维强非线性晃荡问题的优势。
通过图 7和图 8的对比,发现水平激励下容器受到水平方向的合力与液面升高具有相同的周期,并且波形的时间历程相似,都属于拍振,是外在激励频率与自然频率相结合的结果,外包络线周期满足T=2π/|ω0-ωs|。
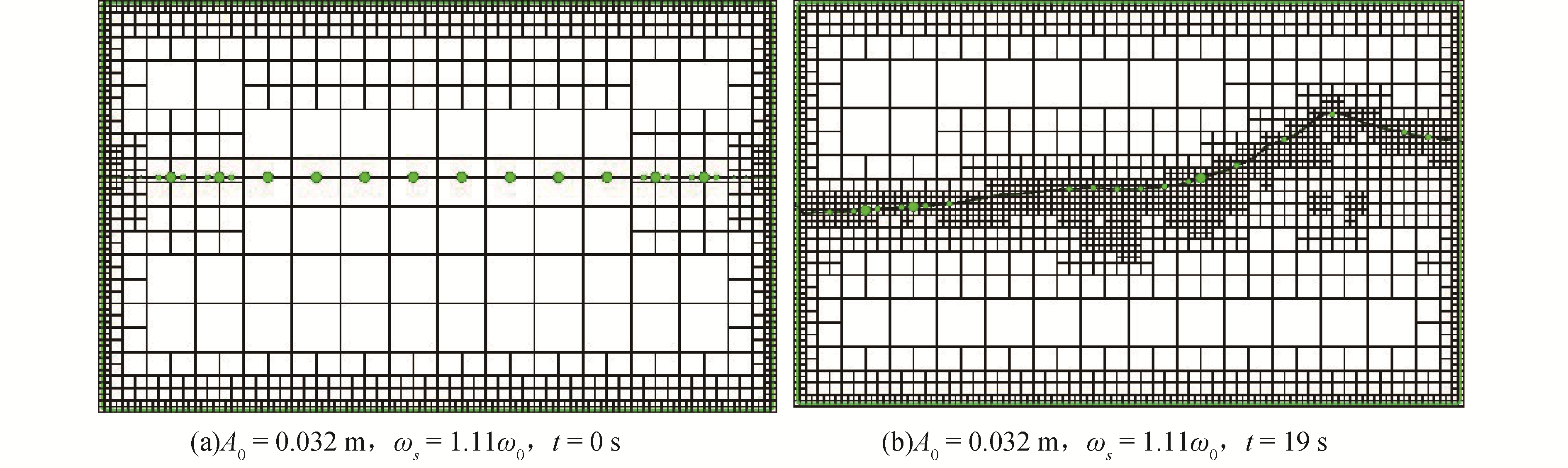
为考察自适应网格效果,图 9给出了此例计算网格模型,算例中采用了对速度、VOF函数梯度的自适应,网格此外对适应于该问题的边界层厚度进行了加密,通过图 9可以清楚的看到网格自适应的分布和变化情况。
|
Download:
|
| 图 9 自适应计算网格模型 Fig. 9 Grids adaption for validation | |
从网格模型可见,四叉树方法能够在自由液面附近自动进行加密,晃荡液面得到了精确捕捉,提高了计算精度,流场的其他区域采用大网格计算,有效提高了计算效率。
3 结论1) 基于四叉树自适应网格的VOF方法在处理晃荡问题时,通过对部分需要细化的网格加密自适应可以更加高效精确地得到相应的结果,从而有效地计算液面升高及力与力矩;
2) 纵摇时,对于压力的计算,数值计算结果同实验得到的数据基本一致,与此同时,激励幅值稍小时,得到的结果越符合实验结果;
3) 纵荡问题中,容器受到外部激励,当自然频率与激励频率相差不大时,水平方向的合力与液面升高具有相同的周期,且时间历程曲线都出现拍振,波形相似。
| [1] |
朱仁庆, 吴有生, 彭兴宁, 等. 船舶液体晃荡动力学的研究方法及进展[J]. 华东船舶工业学院学报, 1999, 13(1): 45-50. ZHU Renqing, WU Yousheng, PENG Xingning, et al. Research methods and progress of ship sloshing dynamics[J]. Journal of East China shipbuilding institute, 1999, 13: 45-50. DOI:10.3969/j.issn.1673-4807.1999.01.011 (  0) 0)
|
| [2] |
ABRAMSON H N. The dynamic behavior of liquids in moving containers[R]. Washington, DC: NASA, 1966.
(  0) 0)
|
| [3] |
VALTINSEN O M. A nonlinear theory of sloshing in rectangular tanks[J]. Journal of ship research, 1974, 18(4): 224-241. (  0) 0)
|
| [4] |
FALTINSEN O M. A numerical nonlinear method of sloshing in tanks with two-dimensional flow[J]. Journal of ship research, 1978, 22(3): 193-202. (  0) 0)
|
| [5] |
NAKAYAMA T, WASHIZU K. The boundary element method applied to the analysis of two-dimensional nonlinear sloshing problems[J]. International journal for numerical methods in engineering, 1981, 17(11): 1631-1646. DOI:10.1002/(ISSN)1097-0207 (  0) 0)
|
| [6] |
WATERHOUSE D D. Resonant sloshing near a critical depth[J]. Journal of fluid mechanics, 1994, 281: 313-318. DOI:10.1017/S0022112094003125 (  0) 0)
|
| [7] |
VERHAGEN J H G, VAN WIJNGAARDEN L. Non-linear oscillations of fluid in a container[J]. Journal of fluid mechanics, 1965, 22(4): 737-751. DOI:10.1017/S0022112065001118 (  0) 0)
|
| [8] |
ARMENIO V, LA ROCCA M. On the analysis of sloshing of water in rectangular containers:numerical study and experimental validation[J]. Ocean engineering, 1996, 23(8): 705-739. DOI:10.1016/0029-8018(96)84409-X (  0) 0)
|
| [9] |
朱仁庆, 吴有生, ATILLA I. 液体晃荡数值模拟研究综述(英文)[J]. 中国造船, 2004, 45(2): 14-27. ZHU Renqing, WU Yousheng, ATILLA I. Numerical simulation of liquid sloshing-a review[J]. Shipbuilding of China, 2004, 45(2): 14-27. DOI:10.3969/j.issn.1000-4882.2004.02.003 (  0) 0)
|
| [10] |
LIU Dongxi, TANG Wenyong, WANG Jin, et al. Hybrid RANS/LES simulation of sloshing flow in a rectangular tank with and without baffles[J]. Ships and offshore structures, 2017, 12(8): 1005-1015. DOI:10.1080/17445302.2017.1301341 (  0) 0)
|
| [11] |
邓棋, 尤云祥, 张新曙. 超谐共振横摇下液舱晃荡特性数值研究[J]. 水动力学研究与进展, 2016, 31(5): 525-534. DENG Qi, YOU Yunxiang, ZHANG Xinshu. Numerical study on tank sloshing characteristics under super-harmonic resonance rolling[J]. Journal of hydrodynamics, 2016, 31(5): 525-534. (  0) 0)
|
| [12] |
POPINET S. Gerris:a tree-based adaptive solver for the incompressible Euler equations in complex geometries[J]. Journal of computational physics, 2003, 190(2): 572-600. (  0) 0)
|
| [13] |
CELEBI M S, AKYILDIZ H. Nonlinear modeling of liquid sloshing in a moving rectangular tank[J]. Ocean engineering, 2002, 29(12): 1527-1553. DOI:10.1016/S0029-8018(01)00085-3 (  0) 0)
|
| [14] |
ALEMI ARDAKANI H, BRIDGES T J. Shallow-water sloshing in vessels undergoing prescribed rigid-body motion in two dimensions[J]. European journal of mechanics-B/fluids, 2012, 31: 30-43. DOI:10.1016/j.euromechflu.2011.08.004 (  0) 0)
|
| [15] |
BELL J B, COLELLA P, GLAZ H M. A second-order projection method for the incompressible navier-stokes equations[J]. Journal of computational physics, 1989, 85(2): 257-283. (  0) 0)
|
| [16] |
KHOKHLOV A M. Fully threaded tree algorithms for adaptive refinement fluid dynamics simulations[J]. Journal of computational physics, 1998, 143(2): 519-543. (  0) 0)
|
| [17] |
POPINET S. An accurate adaptive solver for surface-tension-driven interfacial flows[J]. Journal of computational physics, 2009, 228(16): 5838-5866. DOI:10.1016/j.jcp.2009.04.042 (  0) 0)
|
| [18] |
DEBAR R B. Fundamentals of the KRAKEN Code[R]. United States: LLNL, 1974.
(  0) 0)
|
| [19] |
HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of computational physics, 1981, 39(1): 201-225. (  0) 0)
|
| [20] |
GUEYFFIER D, LI Jie, NADIM A, et al. Volume-of-fluid interface tracking with smoothed surface stress methods for three-dimensional flows[J]. Journal of computational physics, 1998, 152(2): 423-456. (  0) 0)
|
| [21] |
AKYILDIZ H, VNAL N E. Sloshing in a three-dimensional rectangular tank:numerical simulation and experimental validation[J]. Ocean engineering, 2006, 33(16): 2135-2149. DOI:10.1016/j.oceaneng.2005.11.001 (  0) 0)
|
| [22] |
FALTINSEN O M, ROGNEBAKKE O F, LUKOVSKY I A, et al. Multidimensional modal analysis of nonlinear sloshing in a rectangular tank with finite water depth[J]. Journal of fluid mechanics, 2000, 407: 201-234. DOI:10.1017/S0022112099007569 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


