伞降空投是部队投送物资和人员的重要手段,能够极大增加军事行动的灵活度。随着我国自主研发的大型运输机逐步开始装备部队,这必然推动我国伞降空投平台的成熟化、系列化。因此有必要对以运输机为平台的物资空投过程中的一系列问题开展深入研究。
飞机在飞行过程中,机翼获得升力的同时对后方会有一个较强的下洗作用。这样的扰动对进入该下洗区域的飞行器都会产生较强的影响,甚至影响飞行安全。大型运输机的下洗流场很强,一些小型空投物资(100 kg级别)空投高度低、出仓即开伞、整体质量小,在空中运动时容易受到飞机尾流场的干扰,有必要对降落物资的运动轨迹进行仿真研究,这对于提高空投精度,提升空投效能具有重要意义。
目前,国内外对于使用降落伞的空投有很多研究。杨雪松等[1]通过计算仿真了超低空空投货物的过程,没有对降落伞进行建模仿真。王景志等[2]将降落伞空投的过程进行了全面的系统过程建模和仿真分析,并考虑了降落伞的开伞过程和物伞系统的双体动力学问题。张海妮等[3]从物理模型的角度对比了两种空投受力模型的建模方法,研究了结果和过程中的种种不同。刘日等[4]研究了三维空间风场下运输机空投货物舱内移动过程中的建模问题,主要研究了空投过程中的飞机响应情况。林轶群等[5]对空投的机-货物系统进行了建模,并对于在空投中影响飞机纵向动态特性的原因进行了分析。孙秀霞等[6]则建立了有牵引伞和货物滑轨的情况下,载运飞机的动力学模型,并提出了使飞机受到干扰减小的方法。马铭泽[7]借助MATLAB Simulink建立了简化的空投轨迹仿真模型,将空投物体抽象为刚体,模拟了空投物体在空中飞行的情况。Bolton[8]对一种用于超低空高速空投的降落伞进行了仿真,并用同一系统分析了实验结果,同时也给出了降落伞进行风洞测试时的一组数据。Dohher等[9]对于旋转伞进行了9自由度的动力学仿真,物体6自由度,伞3自由度,并将二者均抽象为刚体。文中指出双体模型的稳定性要低于单体模型,且旋转伞对于大气扰动极为敏感。Cuthbert等[10]的主要工作是将NASA的减速器系统模拟(decelerator system simulation,DSS)程序植入了桌面级计算机,移植后的程序易于使用,对计算资源的占用低,计算效率高。Neuhaus等[11]建立了一个多体动力学模型来模拟伞和物体组成的系统,不同的是挂伞对象是重于空气的飞行器。文中模拟了飞行器的全部飞行包线,可以用来分析飞行性能等。McQuilling等[12]则使用有限体积法模拟了在空投中装载货物的集装箱周围的空气流动状况。文中指出集装箱周围的空气流动是准定常的,讨论了气流方向对力和力矩的影响,并指出阻力在迎角正负变化时是不对称的。Moore等[13]建立了一个针对于NASA最新的猎户座飞船的降落伞系统的仿真环境,模拟飞船回收时的降落伞情况。
在现有的研究工作中,对于有扰动的、轻小货物的研究较少。因此本文针对大型运输机强尾流状态下小型空投物资运动轨迹进行了动力学仿真。采用涡格法计算飞机尾流场,建立空投物动力学模型计算下落轨迹和姿态。通过仿真计算,研究运输机尾流场对空投物下落轨迹和姿态的影响,并分析飞机速度和迎角对尾流场效应的间接影响。
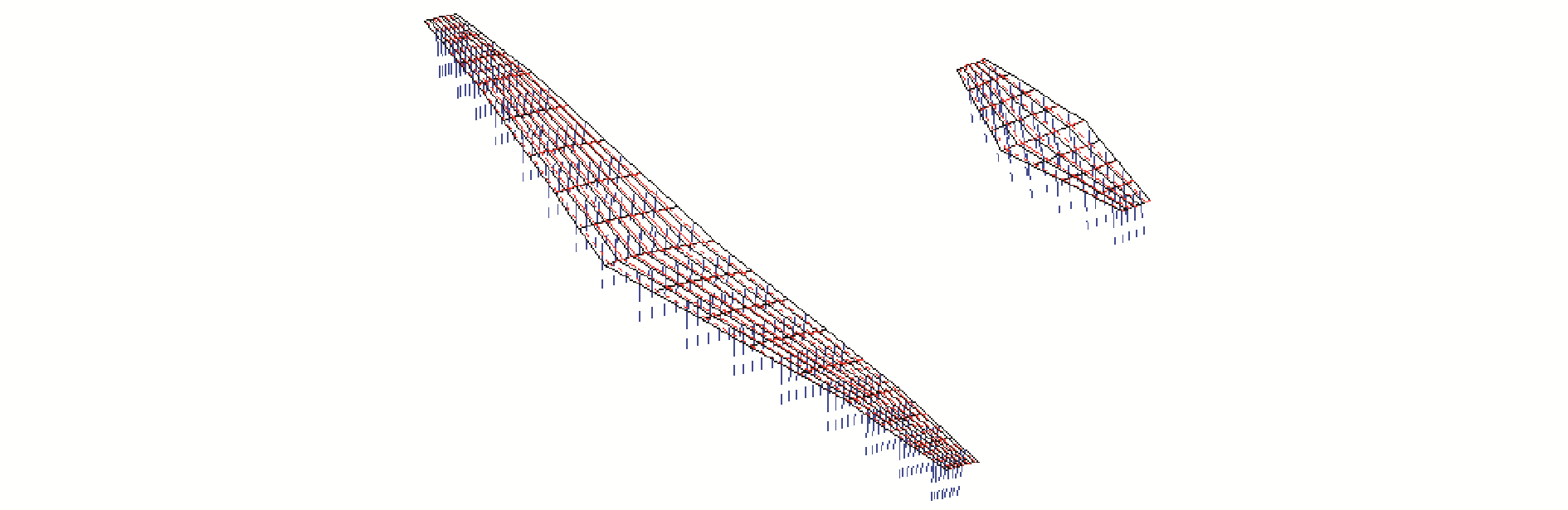
1 运输机尾流场求解为研究空投物离机后在全机流场扰动下运动轨迹,需首先完成全机下洗流场的求解。由于空投过程发生在空速较低的中低空高度,而下洗流场主要由机翼升力诱导产生,与空气粘性、压缩性均无太大关系,因此可应用基于位势流方程求解的涡格法[14]完成飞机附近流场解算。本文选取某中型运输机作为研究对象,该机翼展38 m,机长34 m,参考面积122 m2。由于下洗流场主要由机翼和尾翼产生,因此在本文中没有计算机身对流场的影响。全机计算涡格划分见图 1。
|
Download:
|
| 图 1 某运输机气动力计算网格 Fig. 1 Lattice layout for a certain transport aircraft aerodynamic prediction | |
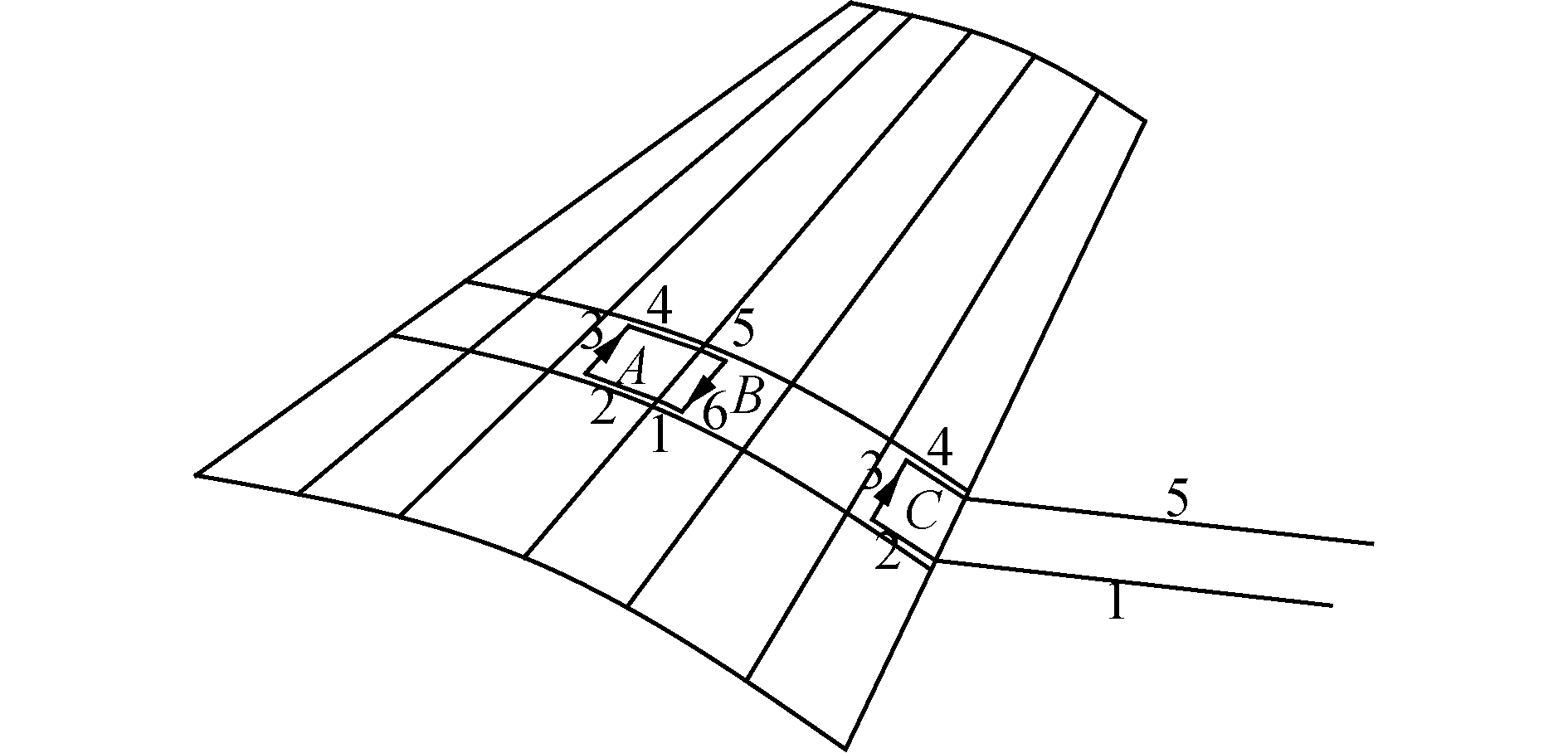
相对于传统涡格法将涡线全部布置在机翼弦平面的方法,为进一步提高翼型弯度对气动力影响的求解,本文采用机翼中弧面布置涡线的方法。对于一个已经将中弧面进行了网格划分的机翼而言,存在两种涡线布置方法,即后缘以前部分采用涡换模型,后缘部分采用Π形马蹄涡模型,如图 2所示。其中每个涡格中的展向涡段位于网格1/4弦长处,控制点取为3/4弦长处中点。
|
Download:
|
| 图 2 两种典型涡线布置形式 Fig. 2 Two typical vortex lattice layouts | |
闭合涡环与开放马蹄涡协调布置的方法,能够保证位势流方程的基本解没有违反亥姆霍兹定理。同时从数学上可以严格证明,这种涡线布置方法与传统涡格法中设置马蹄涡的方法完全等效[15]。由于采用了闭合涡环,使得程序运行中数据点数大大减少且程序结构更为紧凑,从而提升了软件的运行效率。
将全部网格上的所有涡线段对每个控制点处求解诱导速度,将诱导速度与来流速度叠加,为了满足控制点处表面不可穿透边界条件,则需求解线性方程组有:
| $ \left( {{\mathit{\boldsymbol{C}}_C} \times \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} + {\mathit{\boldsymbol{V}}_\infty }} \right) \cdot \mathit{\boldsymbol{N}} = 0 $ | (1) |
式中:CC为控制点处诱导速度项的系数矩阵;Γ为每个涡线涡强组成的列向量;V∞为每个控制点处的来流速度矩阵;N为控制点处单位法向量矩阵。通过在控制点处不可穿越边界条件,可求出每个涡格涡强组成的列向量Γ。对于空间中任意点处的相对气流速度,有:
| $ {\mathit{\boldsymbol{V}}_i} = {\mathit{\boldsymbol{C}}_{Vn}} \times \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} $ | (2) |
式中:Vi为空间某一点处的相对气流速度列向量;CVn为n个涡格上所有涡段对空间待求点处诱导系数组成的系数矩阵。在进行空投动态过程仿真时,可通过在迭代过程中将每一时刻坐标代入式(2),从而求出空投物在每一位置处所受到的来自飞机的扰动速度。
2 空投物资动力学建模 2.1 空投模型描述本文研究了一个小型空投物运动的情况。空投系统是由一个普通的半圆形伞体和正方形物资构成,伞体系统外形尺寸如图 3。其中伞体展开直径D为5.64 m2;伞体质心到系统质心的距离l1为7.83 m;物资质心到系统质心的距离l2为1.56 m。

|
Download:
|
| 图 3 空投系统外形 Fig. 3 Shape of airdrop system | |
空投系统的质量特性如表 2,表中的伞体质量和惯量假设均已经包含伞体的附加质量和附加质量力矩。由于本文仅研究飞行器尾流对下落轨迹的影响,因此空投系统的质量特性均为估计值。
| 表 1 空投系统质量特性 Table 1 Mass properties of airdrop system |
| 表 2 坐标系定义 Table 2 Definition of coordinate system |
本文的动力学建模中主要涉及2个坐标系,地面坐标系、降落伞系统坐标系。2个坐标系的定义和符号如表 2和图 3所示。
2.3 降落伞气动力求解由于物资体积较小,因此本文将其忽略,同时也忽略伞绳的气动力。气动力求解主要针对张开的伞体部分。
伞体的轴向力和法向力的表达式可以写为:
| $ \left\{ \begin{gathered} {F_A} = \frac{1}{2}\rho V_A^2{S_A}{C_A} \hfill \\ {F_N} = \frac{1}{2}\rho V_N^2{S_N}{C_N} \hfill \\ \end{gathered} \right. $ | (3) |
| $ \left\{ \begin{gathered} {V_A} = {w_1} \hfill \\ {V_N} = \sqrt {u_1^2 + v_1^2} \hfill \\ \end{gathered} \right. $ | (4) |
| $ {\mathit{\boldsymbol{V}}_1} = \mathit{\boldsymbol{V}} + \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{r}} = {\left( {\begin{array}{*{20}{c}} {{u_1}}&{{v_1}}&{{w_1}} \end{array}} \right)^{\text{T}}} $ | (5) |
式中:FN为法向力;FA为轴向力;CN为法向力系数;CA为轴向力系数;V为系统质心速度矢量;ω为系统角速度矢量;r为系统质心O到伞体压心O1的矢量(假设伞体压心和质心重合)。
2.4 动力学方程由于本文主要研究空投物资的下落轨迹,因此将伞体和悬挂物资视作一个刚性系统,建立刚体六自由度运动方程:
| $ \left\{ \begin{gathered} m\frac{{{\text{d}}V}}{{{\text{d}}t}} = {\mathit{\boldsymbol{F}}_{{\text{aero}}}} + \mathit{\boldsymbol{G}} \hfill \\ \frac{{{\text{d}}\mathit{\boldsymbol{H}}}}{{{\text{d}}t}} = {\mathit{\boldsymbol{M}}_{{\text{aero}}}} \hfill \\ \end{gathered} \right. $ | (6) |
式中:V为运动速度矢量;Faero为气动力矢量;G为重力矢量;H为惯量矩矢量;Maero为气动力矩矢量。
将矢量式(6)写成降落伞系统坐标系(ObXbYbZb)下的分量形式:
| $ \left\{ \begin{gathered} m{\left( {\frac{{{\text{d}}V}}{{{\text{d}}t}}} \right)_b} = {\mathit{\boldsymbol{F}}_{{\text{aero}}, b}} + {\mathit{\boldsymbol{G}}_b} \hfill \\ {\left( {\frac{{{\text{d}}\mathit{\boldsymbol{H}}}}{{{\text{d}}t}}} \right)_b} = {\mathit{\boldsymbol{M}}_{{\text{aero}}, b}} \hfill \\ \end{gathered} \right. $ | (7) |
根据转动坐标系求导法则,等式左侧可写为:
| $ \left\{ \begin{gathered} m\frac{{{\text{d}}{\mathit{\boldsymbol{V}}_b}}}{{{\text{d}}t}} + {\mathit{\boldsymbol{\omega }}_b} \times {\mathit{\boldsymbol{V}}_b} = \hfill \\ {\mathit{\boldsymbol{F}}_{{\text{aero}}, b}} + {\mathit{\boldsymbol{G}}_b} \hfill \\ \frac{{{\text{d}}{\mathit{\boldsymbol{H}}_b}}}{{{\text{d}}t}} + {\mathit{\boldsymbol{\omega }}_b} \times {\mathit{\boldsymbol{H}}_b} = {\mathit{\boldsymbol{M}}_{{\text{aero}}, b}} \hfill \\ \end{gathered} \right. $ | (8) |
代入惯性矩矩阵,得到
| $ \left\{ \begin{gathered} \frac{{{\text{d}}{\mathit{\boldsymbol{V}}_b}}}{{{\text{d}}t}} = \hfill \\ \frac{1}{m}\left( {{\mathit{\boldsymbol{F}}_{{\text{aero}}, b}} + {\mathit{\boldsymbol{G}}_b}-{\mathit{\boldsymbol{\omega }}_b} \times {\mathit{\boldsymbol{V}}_b}} \right) \hfill \\ \frac{{{\text{d}}{\mathit{\boldsymbol{\omega }}_b}}}{{{\text{d}}t}} = \hfill \\ \mathit{\boldsymbol{I}}_b^{-1}\left( {{\mathit{\boldsymbol{M}}_{{\text{aero}}, b}}-{\mathit{\boldsymbol{\omega }}_b} \times {\mathit{\boldsymbol{I}}_b}{\mathit{\boldsymbol{\omega }}_b}} \right) \hfill \\ \end{gathered} \right. $ | (9) |
式(9)中各个矢量和矩阵可表示为:
| $ \begin{gathered} {\mathit{\boldsymbol{V}}_b} = {\left[{\begin{array}{*{20}{c}} u&v&w \end{array}} \right]^{\text{T}}} \hfill \\ {\mathit{\boldsymbol{\omega }}_b} = {\left[{\begin{array}{*{20}{c}} p&q&r \end{array}} \right]^{\text{T}}} \hfill \\ {\left( \mathit{\boldsymbol{I}} \right)_b} = \left[{\begin{array}{*{20}{c}} {{I_x}}&{-{I_{xy}}}&{-{I_{zx}}} \\ {-{I_{xy}}}&{{I_y}}&{ - {I_{yz}}} \\ { - {I_{zx}}}&{ - {I_{yz}}}&{{I_z}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{I_x}}&0&0 \\ 0&{{I_y}}&0 \\ 0&0&{{I_z}} \end{array}} \right] \hfill \\ \end{gathered} $ | (10) |
采用某中型运输机作为空投平台,在水平定直飞行中进行物资空投作业。由于是小型物资空投,因此假设物资出舱后,降落伞已经打开。伞体以85°倾斜角出舱,与飞机的相对速度为10 m/s,初始下落高度为100 m。针对上述小型物资伞降空投模型,进行不同算例研究,获得以下计算结果。
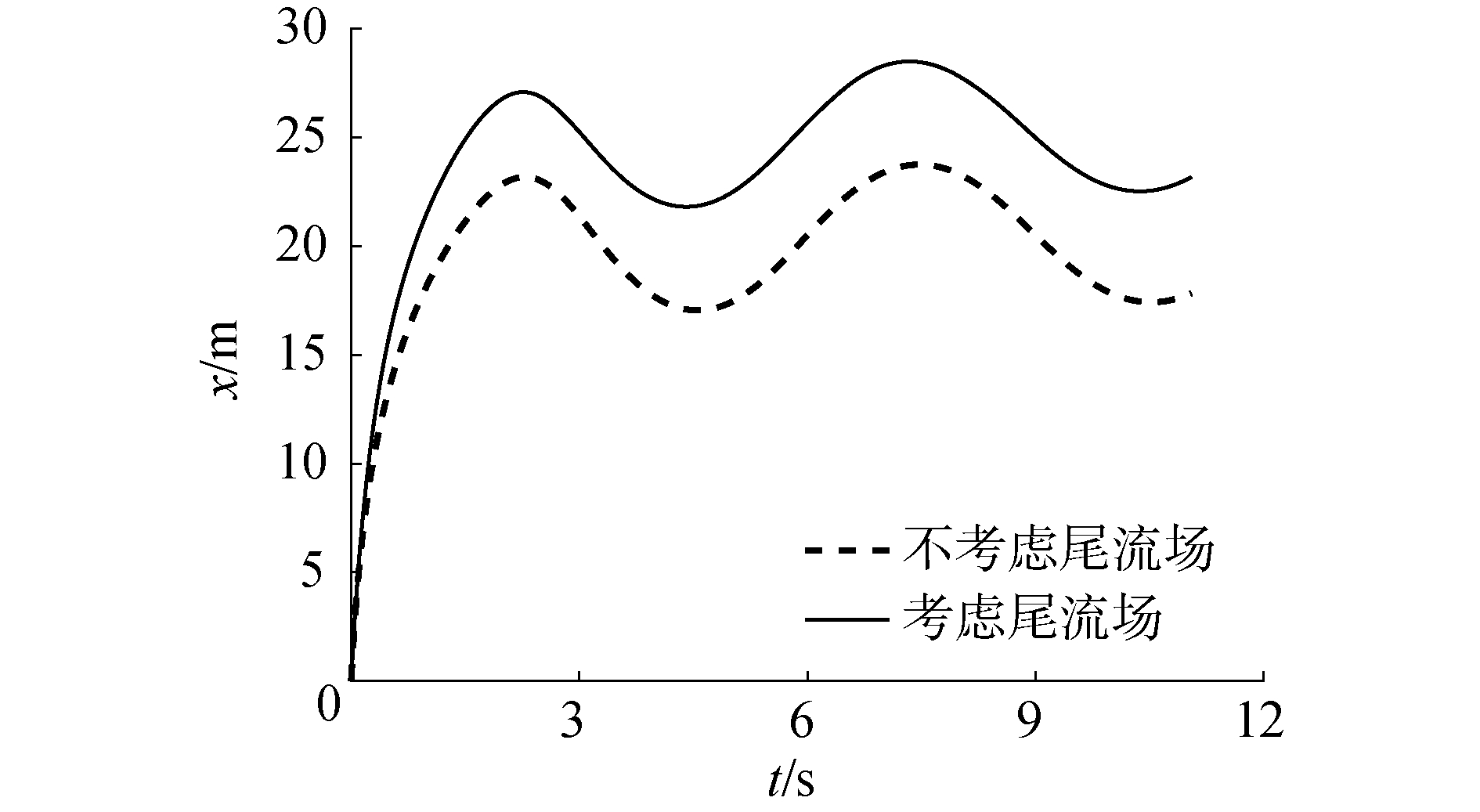
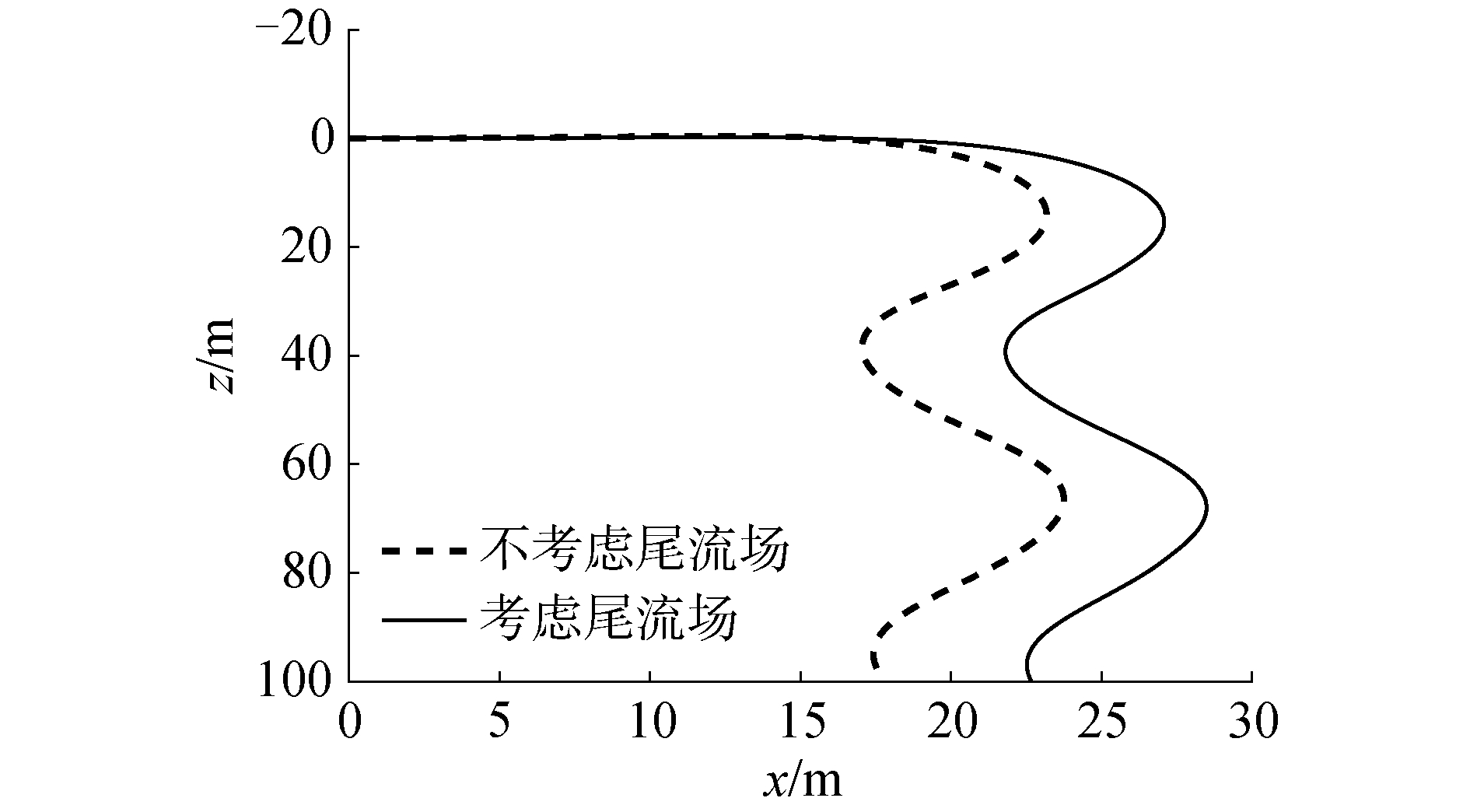
图 4为空投物资的质心在x方向上的位移变化情况,图 5为空投物资的质心在运动x-z平面上的轨迹。由图 4、5可以看出运输机的尾流场使空投物下落轨迹向运输机飞行方向偏移,但是下落轨迹的形状基本不变。
|
Download:
|
| 图 4 空投物资在x方向上的位移 Fig. 4 Displacement on x-axis of airdrop | |
|
Download:
|
| 图 5 空投物资运动平面的轨迹 Fig. 5 Path of airdrop on motion plane | |
图 6为物资俯仰角随时间的变化情况,可以得到这样的结论,即运输机尾流场对物资下落过程的姿态基本无影响。由于法向力主要受姿态影响,而法向力同时对下落轨迹的变化起着主要作用,因此也可以印证图 4、图 5中尾流场对下落轨迹的形状基本没有影响的现象。
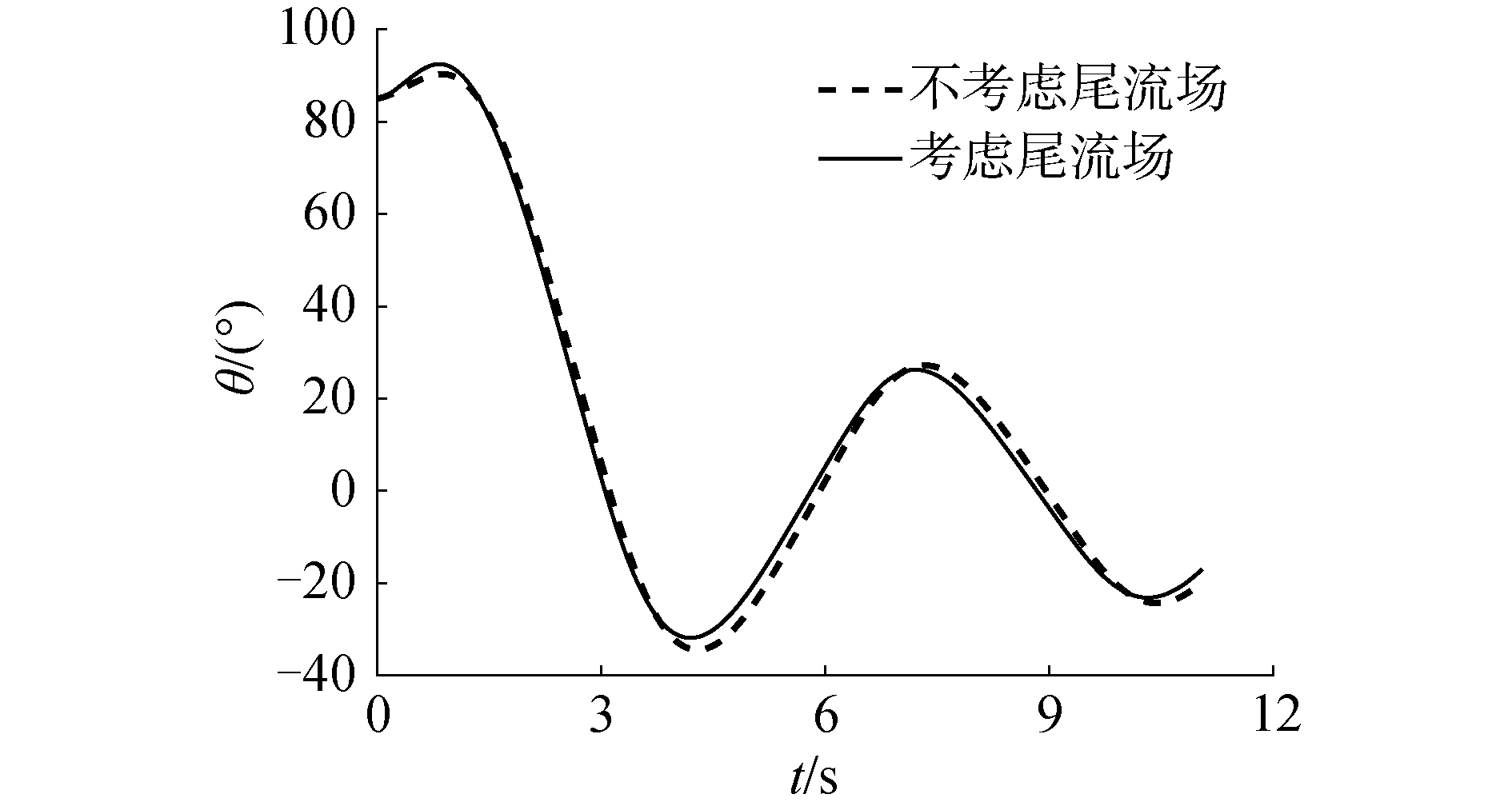
|
Download:
|
| 图 6 空投物资的俯仰角变化 Fig. 6 Change of airdrop pitch angle | |
图 7为尾流场存在前后物资x方向的位移差随时间的变化。位移差期初随着时间的增加而增加,在3~4 s后逐渐在一个值附加波动。造成种现象的原因在于,开始尾流场较大,对物资下落轨迹偏移量的影响不断叠加。一段时间后尾流场开始变弱,对物资下落轨迹的影响基本消失,因此偏移量就开始收敛于某个值。
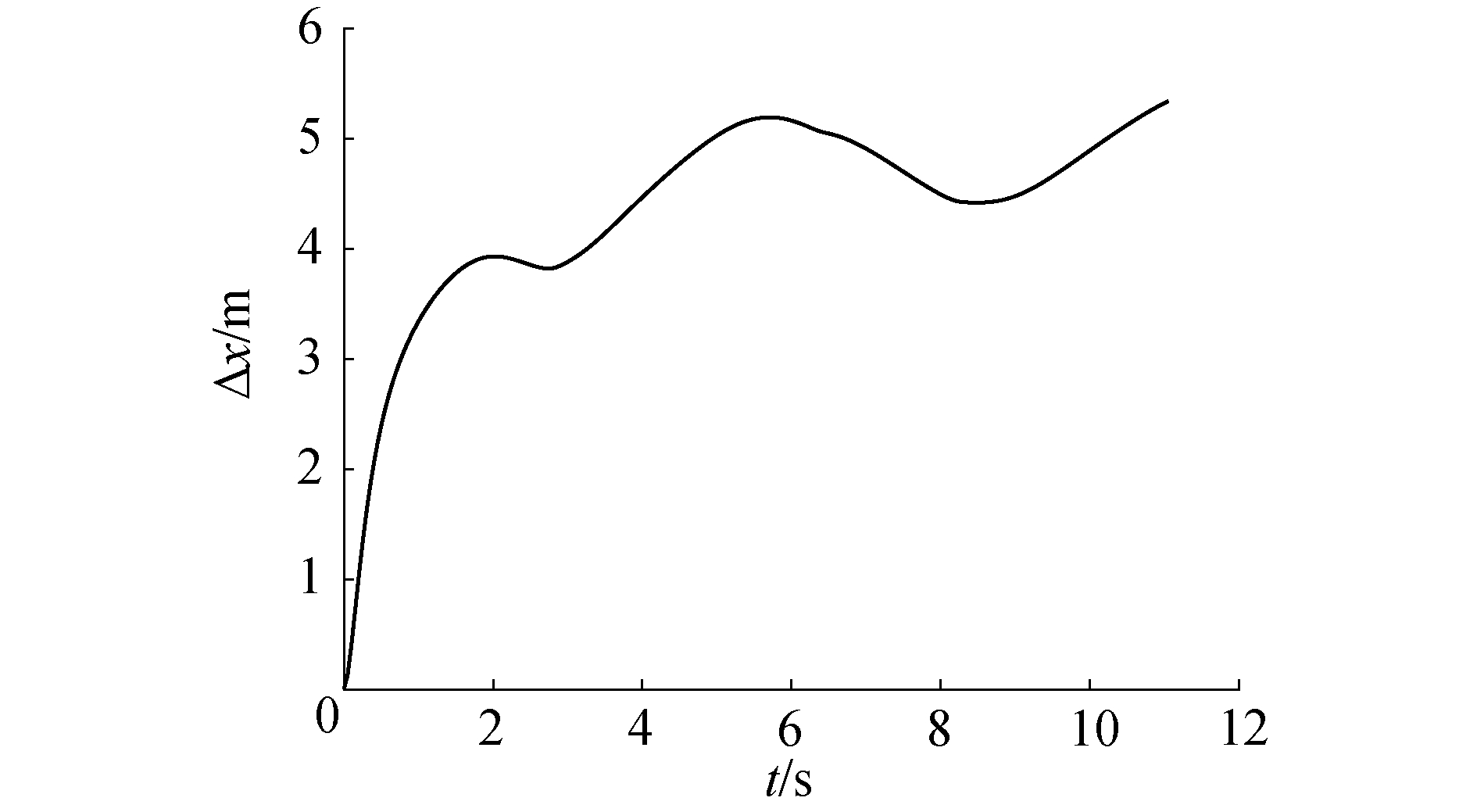
|
Download:
|
| 图 7 在考虑尾流场前后空投物资在x方向上的位移偏差 Fig. 7 Difference of displacement on x-axis between wake field on or off | |
为了研究不同尾流强度对空投物资下落轨迹的影响,在80 m/s的平飞速度下,分别在5°、7.3°、10°、15°迎角的情况下,进行空投仿真计算。比较不同迎角下的尾流场影响下的偏移量随时间的变化(如图 8)。可以看出迎角增加,下洗加强,偏移量就增加,同时最终的x方向偏移量基本和迎角大小成比例关系。

|
Download:
|
| 图 8 不同平飞迎角下空投物资的x方向的偏移量 Fig. 8 Displacement on x-axis with different angle of attack | |
| 表 3 不同平飞速度下的升力系数CL和迎角α Table 3 CL & α on different speeds |
在真实的飞行过程中,不同迎角下,飞机的平飞速度是不一样的。因此有必要研究在不同平飞速度条件下,飞机尾流对空投物资的运动偏移量的影响。假设运输机的飞行质量为60 t,翼面积113 m2,不同平飞速度下的升力系数和迎角如表4中所示。仿真获得不同平飞速度下的空投物资的x方向的偏移量如图 9所示。可以看出当运输机的平飞速度增加时,由于平飞迎角的较小,尾流场对空投物资x方向上的偏移量影响反而减小。
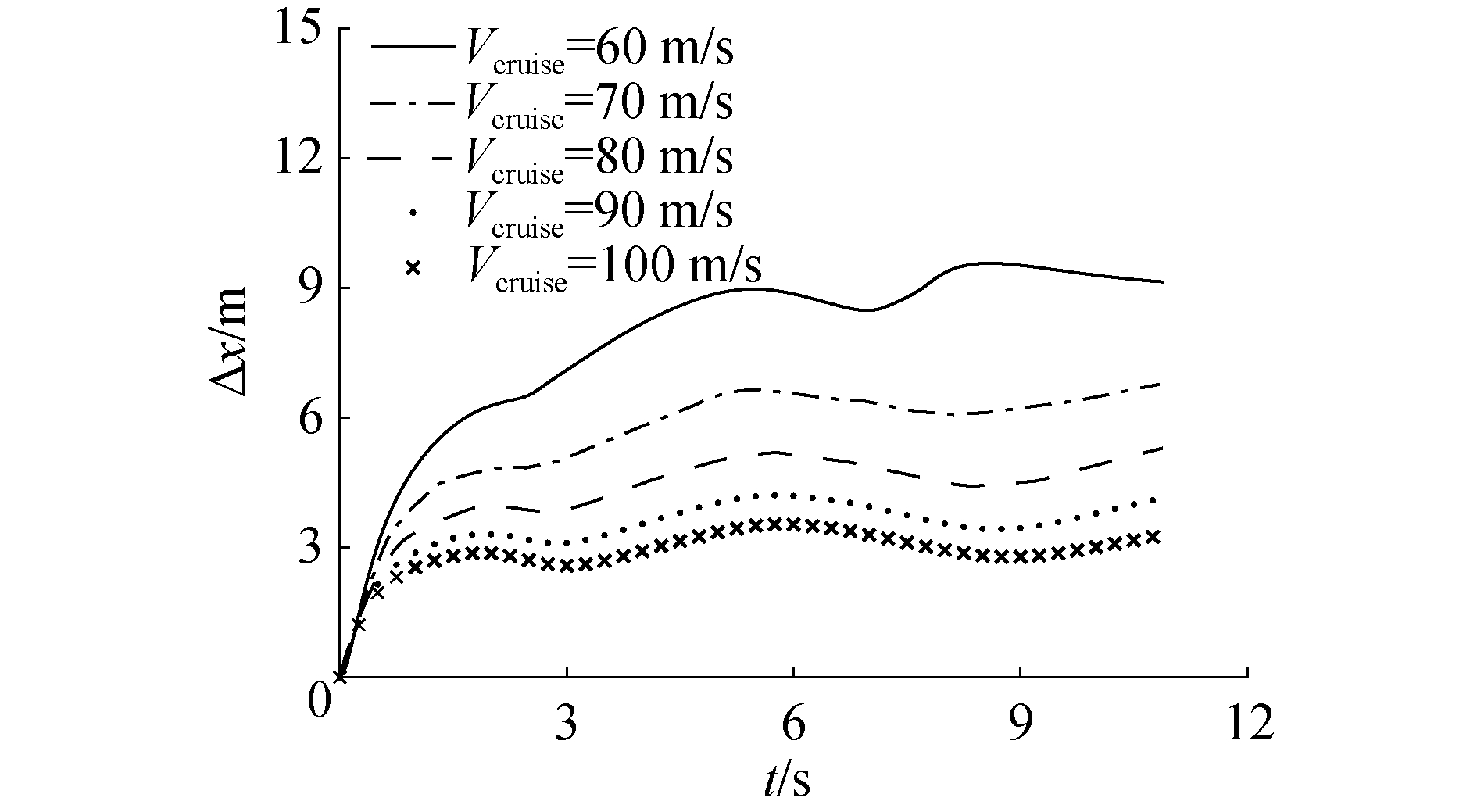
|
Download:
|
| 图 9 不同平飞速度下空投物资的x方向的偏移量 Fig. 9 Difference of displacement on x-axis between wake field on or off with different speed | |
1) 运输机尾流场对空投物资的质心下落轨迹影响较大,对下落过程中空投物资的姿态影响不大。
2) 运输机尾流场会使空投物资下落轨迹向飞机飞行方向整体偏移,这种偏移影响随着运输机平飞迎角的增加而增加。
3) 在运输机飞行重量一定的情况下,空投时的平飞速度越大,尾流场对空投物资下落轨迹的偏移量反而越小。
| [1] |
杨雪松, 王乘, 李振环. 超低空空投过程的仿真[J]. 华中科技大学学报(自然科学版), 2003, 31(4): 108-110. YANG Xuesong, WANG Cheng, LI Zhenhuan. Simulation of ultra -low air cast process[J]. Journal of Huazhong University of Science and Technology (nature science edition), 2003, 31(4): 108-110. DOI:10.3321/j.issn:1671-4512.2003.04.037 (  0) 0)
|
| [2] |
王景志, 陈红林. 基于龙格-库塔算法对降落伞空投的研究[J]. 现代电子技术, 2010(14): 124-126, 130. WANG Jingzhi, CHEN Honglin. Research for parachute airdrop based on Runge-Kutta algorithm[J]. Modern electronic technique, 2010(14): 124-126, 130. DOI:10.3969/j.issn.1004-373X.2010.14.041 (  0) 0)
|
| [3] |
张海妮, 张培田, 程伟豪. 两种空投建模方法的研究[J]. 科学技术与工程, 2012, 12(16): 3896-3900. ZHANG Haini, ZHANG Peitian, CHENG Weihao. Research of two different modeling methods of airdrop[J]. Science technology and engineering, 2012, 12(16): 3896-3900. DOI:10.3969/j.issn.1671-1815.2012.16.023 (  0) 0)
|
| [4] |
刘日, 孙秀霞, 董文瀚, 等. 大气扰动下运输机空投过程建模与仿真分析[J]. 飞行力学, 2013, 31(1): 24-28. LIU Ri, SUN Xiuxia, DONG Wenhan, et al. Modeling of flight dynamics and analyzing of simulation for airdrop in atmospheric disturbance[J]. Flight dynamics, 2013, 31(1): 24-28. (  0) 0)
|
| [5] |
林轶群, 张海妮, 方自立. 运输机重装空投系统仿真与分析[J]. 飞机设计, 2015, 35(2): 67-71. LIN Yiqun, ZHANG Haini, FANG Zili. Simulation and analysis of the transport-airplane heavy cargo airdrop[J]. Aircraft design, 2015, 35(2): 67-71. DOI:10.3969/j.issn.1674-9804.2015.02.018 (  0) 0)
|
| [6] |
孙秀霞, 徐光智, 刘日, 等. 航空运输物资空投过程动力学模型[J]. 交通运输工程学报, 2016, 16(2): 125-131. SUN Xiuxia, XU Guangzhi, LIU Ri, et al. Dynamics model of airdrop process for air transportation cargo[J]. Journal of traffic and transportation engineering, 2016, 16(2): 125-131. DOI:10.3969/j.issn.1671-1637.2016.02.015 (  0) 0)
|
| [7] |
MA Mingze. Simplified flight trajectory simulation based on MATLAB/SIMULINK[C]//IEEE CGNCC. Nanjing, China, 2016, 2016: 8.
(  0) 0)
|
| [8] |
BOLTON W R. Trajectory simulation of a parachute system[C]//Proceedings of the 6th Aerodynamic Decelerator and Balloon Technology Conference. Houston, TX, USA, 1979.
(  0) 0)
|
| [9] |
DOHERR K F, SCHILLING H. 9DOF-simulation of rotating parachute systems[C]//Proceedings of the 11th Aerodynamic Decelerator Systems Technology Conference. San Diego, CA, USA, 1991.
(  0) 0)
|
| [10] |
CUTHBERT P A, CONLEY G L, DESABRAIS K J. A desktop application to simulate cargo drop tests[C]//Proceedings of the 18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Munich, Germany, 2005.
(  0) 0)
|
| [11] |
NEUHAUSJ R, KENNEY P S. A Generic Multibody Parachute Simulation Model[C]//Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit. Keystone, Colorado, 2006.
(  0) 0)
|
| [12] |
MCQUILLING M, POTVIN J, RILEY J. Simulating the flows about cargo containers used during parachute airdrop operations[J]. Journal of aircraft, 2011, 48(4): 1405-1411. DOI:10.2514/1.C031299 (  0) 0)
|
| [13] |
MOORE J W, MORRIS A L. A hybrid parachute simulation environment for the Orion parachute development project[C]//Proceedings of the 21st AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Dublin, Ireland, 2011.
(  0) 0)
|
| [14] |
宋磊, 杨华, 解静峰, 等. 基于改进涡格法的飞翼布局飞机稳定性导数计算[J]. 南京航空航天大学学报, 2014, 46(3): 457-462. SONG Lei, YANG Hua, XIE Jingfeng, et al. Predicting stability derivatives of flying wing aircraft based on improved vortex lattice method[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2014, 46(3): 457-462. DOI:10.3969/j.issn.1005-2615.2014.03.019 (  0) 0)
|
| [15] |
徐华舫, 张炳暄, 朱自强. 亚、超音速定常位流的面元法[M]. 北京: 国防工业出版社, 1981: 5, 319-320. XU Huafang, ZHANG Bingxuan, ZHU Ziqiang. The surface method of subsonic and supersonic constant steady flow[M]. Beijing: National Defense Industry Press, 1981: 5, 319-320. (  0) 0)
|
| [16] |
徐华舫. 空气动力学基础[M]. 北京: 国防工业出版社, 1979. XU Huafang. Fundamentals of aerodynamics[M]. Beijing: National Defense Industry Press, 1979. (  0) 0)
|
| [17] |
KATZ J, PLOTKIN A. Low-speed aerodynamics[M]. Cambridge: Cambridge University Press, 2001.
(  0) 0)
|
| [18] |
CUMMING R M, MASON W H, MORTON S A, et al. Applied computational aerodynamics:a modern engineering approach[M]. Cambridge: Cambridge University Press, 1995.
(  0) 0)
|
| [19] |
徐华舫, 张炳暄, 朱自强. 亚、超音速定常位流的面元法[M]. 北京: 国防工业出版社, 1981: 319-320. XU Huafang, ZHANG Bingxuan, ZHU Ziqiang. The surface method of subsonic and supersonic constant steady flow[M]. Beijing: National Defense Industry Press, 1981: 319-320. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


