超大跨度桥梁地震作用下的安全性能是实现交通运输重要枢纽功能的保证,大跨度缆索支撑桥梁强震作用下的减震控制已是研究的热点工程问题之一[1-2]。随着悬索桥跨度的逐渐增大,采用全漂浮、缆索支撑等隔震体系尽管减小了桥塔地震作用下的内力,却也导致塔梁相对位移过大。强震作用下,主梁纵向位移超过允许值会引发诸多工程问题,如过大的塔梁相对位移会导致伸缩缝发生破坏、缆索的疲劳断裂、主梁与相邻跨引桥发生碰撞引起落梁等破坏[3-4]。作为一种新桥型,强震作用下的动力性能比双塔悬索桥更复杂。与此同时,行波效应是影响大跨度悬索桥地震响应的主要因素之一,会引起地震总持时发生改变,同时也会引起结构响应峰值的出现时间与峰值大小均发生改变,故大跨度悬索桥强震作用下的地震响应分析应考虑行波效应的影响[5-6]。针对考虑行波效应的大跨度结构的多点激励问题,国内外学者进行了大量研究[7-9],但有关三塔悬索桥的地震响应分析研究相对较少。因此,为解决强震作用下大跨度悬索桥主梁纵向位移超过允许值而引发碰撞及落梁等问题,采取合理有效的减震措施以约束塔梁相对位移具有重要意义。
为了有效控制强震作用下大跨度桥梁结构的地震响应,阻尼耗能装置得到了广泛的应用。如日本明港中大桥、广东汕头海湾二桥等采用弹性连接装置减小塔梁相对位移[10];金门大桥、苏通大桥等将黏弹性阻尼器用于控制地震作用下的塔梁相对位移[11];软钢阻尼器是一种新型耗能装置,在悬索桥中的应用尚不多见[12-13],南京江心洲大桥是我国首次采用软钢阻尼器作为减振元件的悬索桥[13]。上述的研究主要集中于单塔或两塔悬索桥[14-16],尽管软钢阻尼器在桥梁工程减震中得以应用,但在多塔悬索桥的减震控制中的应用较少,且强震作用下考虑行波效应的三塔悬索桥地震响应控制有待进一步研究。
本文以泰州大桥为研究对象,建立大跨度三塔悬索3D有限元模型,在分析其动力特性的基础上[10],考虑行波效应,对大跨度悬索桥进行强震作用下的地震响应分析,分别研究了采用弹性拉索、黏滞阻尼器、软钢阻尼器控制超大跨度悬索桥泰州大桥强震作用下结构地震响应的最优参数取值,并对比了3种减震装置取值最优参数对泰州大桥地震位移响应控制效果。
1 泰州大桥桥梁结构建模 1.1 工程背景泰州大桥横跨长江为大跨度三塔两跨悬索桥,主桥桥跨结构布置为(390+1 080+1 080+390) m。该桥于中塔处呈漂浮体系,主跨加劲梁采用封闭式流线型扁平钢箱梁,主缆矢跨比为1/9,两平行主缆横向间距为35.8 m,采用预制平行钢丝索股。主塔为门式框架结构,两边塔为174 m高的混凝土结构,中塔为钢结构桥塔,高194 m,两边塔在横桥向均呈单柱型,中塔采用倒Y型结构。
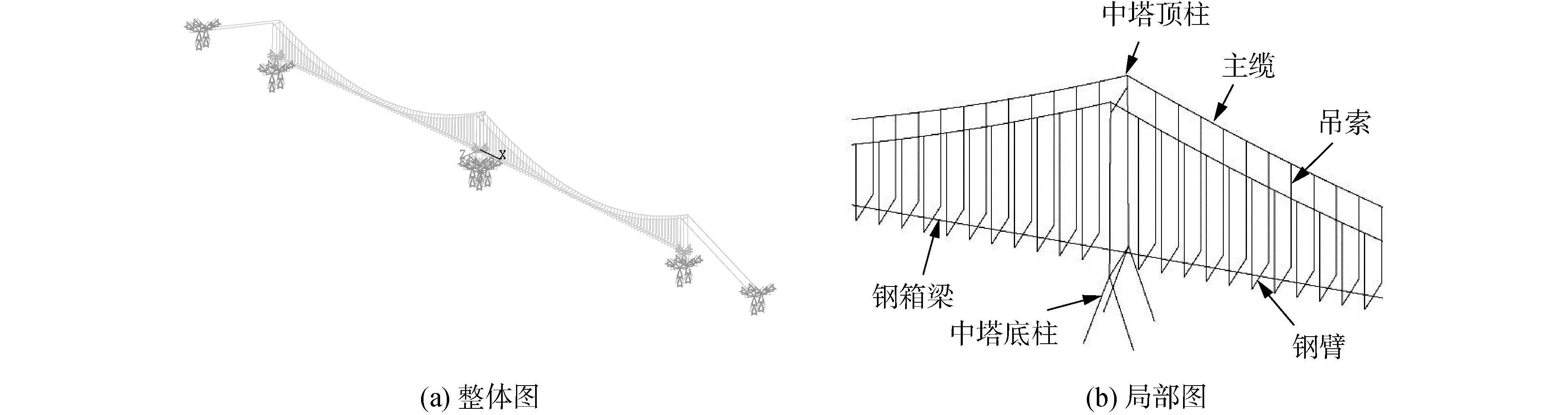
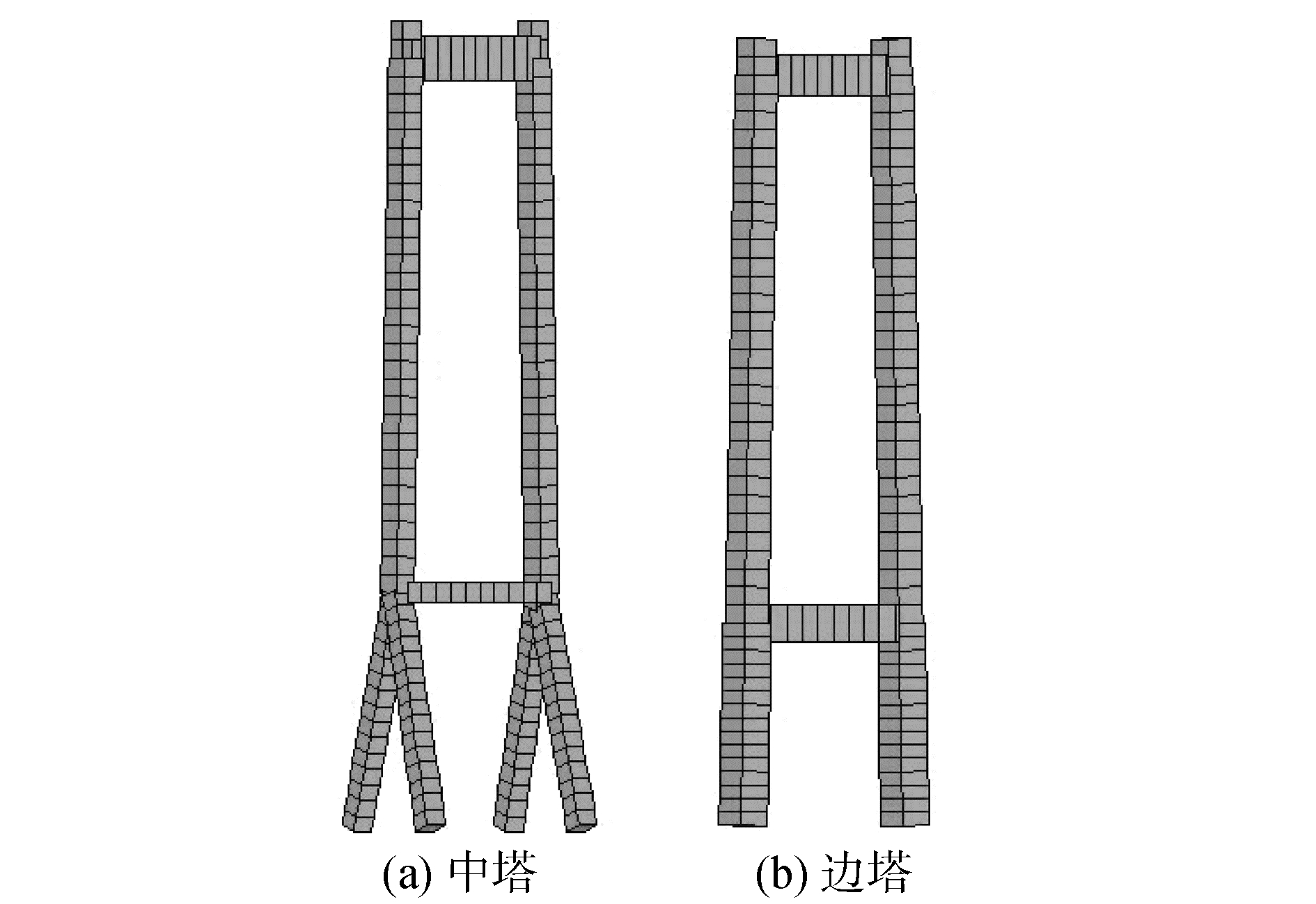
1.2 桥梁结构建模悬索桥主梁采用梁单元建模,采用空间梁单元Beam4模拟悬索桥的主梁与主塔,主梁刚度与质量分别以等效刚度与等效密度的形式予以考虑。采用空间杆单元Link10模拟主缆与吊杆,仅考虑抗拉强度。主梁和吊杆之间采用无质量刚性横梁连接,通过设置Link10的初应变并对其应力刚化来考虑成桥状态下主缆与吊杆在重力荷载下的几何刚度。主梁刚度按加劲梁的实际刚度考虑,但忽略桥面铺装、栏杆等的刚度。主梁为闭口箱形截面,截面翘曲刚度相对于自由扭转可以忽略不计。该桥有限元模型如图 1所示,主塔有限元模型如图 2所示。该模型可为本文强震作用下大跨度三塔悬索桥的减震控制研究提供可靠的模型基础[10, 17]。
|
Download:
|
| 图 1 三塔悬索桥有限元模型 Fig. 1 FE model of triple-tower suspension bridge | |
|
Download:
|
| 图 2 主塔有限元模型 Fig. 2 FE model of main tower | |
由于弹性拉索为单向受拉构件,且刚度不变,在ANSYS中常采用Combin14单元进行模拟。当用于模拟轴向“弹簧-阻尼器”单元时,该单元为单向压缩或拉伸单元,每个节点有3个自由度,可采用轴向Combin14单元模拟弹性拉索。单元阻尼实常数设置为0,改变单元刚度实常数即可模拟弹性拉索的刚度变化。
1.3.2 黏滞阻尼器根据桥梁用黏滞流体阻尼器,黏滞阻尼器的计算模型为[18]:
| $ {{F}_{d}}=c{{V}^{\alpha }} $ | (1) |
式中:Fd为阻尼力;c为阻尼常数,与阻尼器的具体构造有关;α为在0.3~1.0的阻尼速度指数。
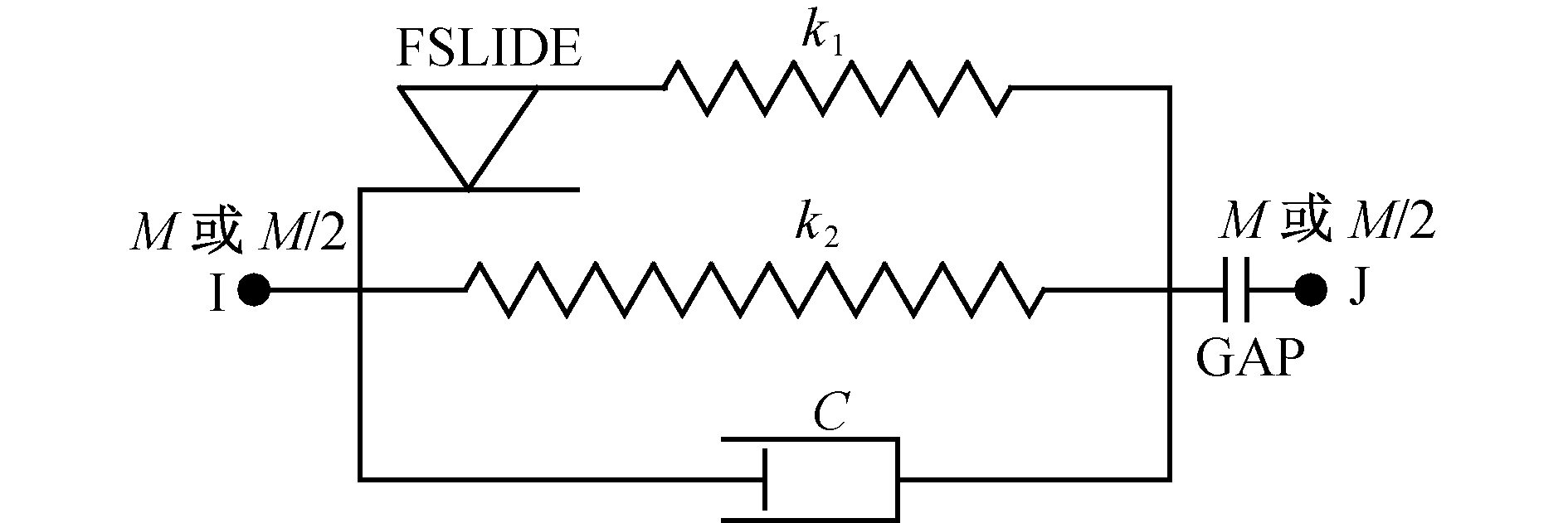
1.3.3 软钢阻尼器采用E型软钢阻尼器,软钢阻尼器的恢复力模型采用Ramberg-Osgood模型(RO模型)[19],该模型常用于模拟刚度退化,可简化为双线性模型。ANSYS中采用Combin40单元模拟软钢阻尼器,如图 3所示。为模拟软钢阻尼器,C、GAP和M均设置为0,k1设置为软钢阻尼器弹性刚度与屈服后刚度之差,即k1=K0-K1;k2取软钢阻尼器屈服后刚度K1,Fsl设置为软钢阻尼器的屈服力。
|
Download:
|
| 图 3 Combin40单元 Fig. 3 Combin40 element | |
为评价减震装置对塔梁相对位移的控制效果,定义减震系数
| $ \eta =\left| \frac{d-{{d}_{0}}}{d} \right| $ | (2) |
式中d、d0分别为减震前、减震后结构响应峰值。
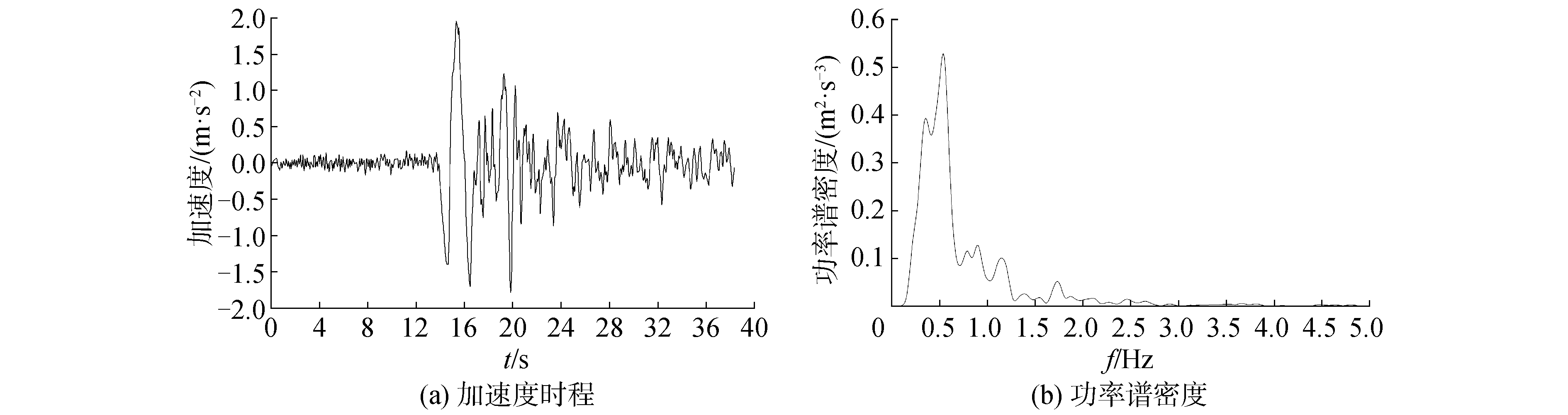
2 三塔悬索桥地震位移响应控制 2.1 地震记录选取根据《公路桥梁抗震设计细则》中的建议,选取3条典型地震波(Tianjin波、El-Centro波、Taft波)作为地震动输入,取计算结果的最大值。由于该悬索桥的空间对称性,仅考虑沿纵桥向的水平地震动输入。根据桥址区抗震设防烈度要求,将3条地震波峰值调整为0.2 g,Tianjin波时程及功率谱密度如图 4所示。
|
Download:
|
| 图 4 Tianjin波特性 Fig. 4 Characteristics of Tianjin ground motion | |
地震波输入点分别为左边缆底端锚碇、左边塔塔底、中塔塔底、右边塔塔底和右边缆底端锚碇。Tianjin波卓越频率为0.537 11 Hz,El-Centro波卓越频率为1.470 95 Hz,Taft波卓越频率为1.373 29 Hz,卓越频率较低的Tianjin波更能激发三塔悬索桥的低阶振型,因而Tianjin波作用下的地震响应最为显著。
2.2 行波效应视波速是大跨度悬索桥地震响应的重要影响因素之一。图 5以Tianjin波为例,列出了3组视波速下的中塔塔梁相对位移时程。

|
Download:
|
| 图 5 中塔塔梁相对位移时程 Fig. 5 Relative displacement time history between middle tower and main girder | |
由图 5可知,视波速对中塔塔梁相对位移时程峰值的出现时间和峰值大小均有影响,且对结构的地震总持时也有一定程度的影响,图中视波速取值区间范围为200~8 000 m/s,为了与一致输入的计算结果进行对比,视波速取值较大,最大达到8 000 m/s,以验证行波效应计算结果的准确性。当视波速小于等于2 000 m/s时,随视波速的增加,该桥的地震总持时急剧减少;当视波速介于2 000~8 000 m/s时,地震总持时变化趋于稳定,但仍不小于地震波持时。
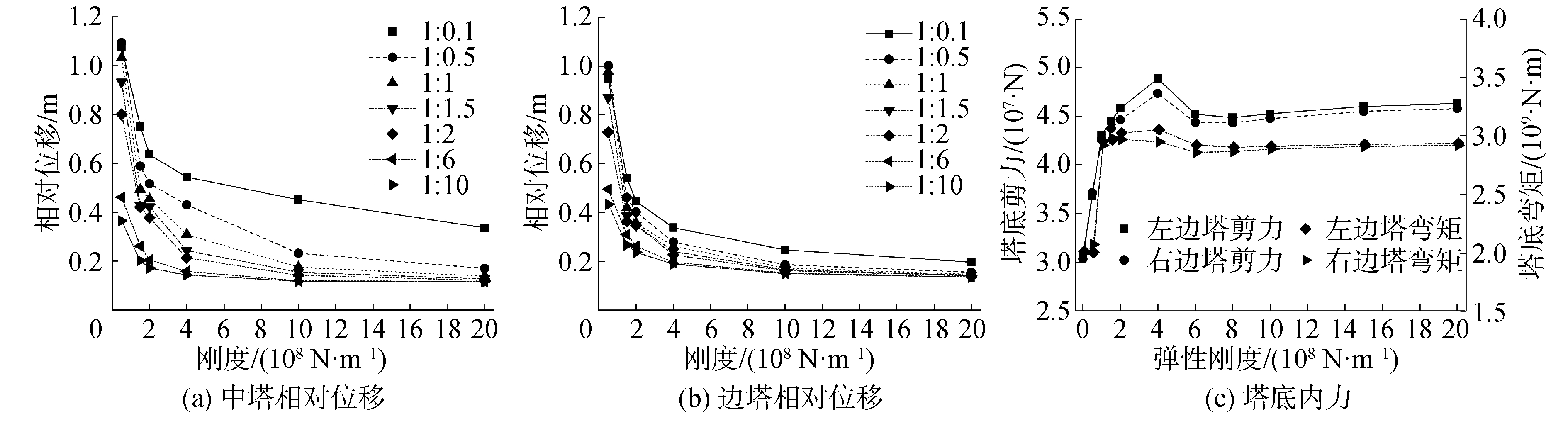
2.3 确定减震装置最优参数 2.3.1 弹性拉索最优参数地震作用下超大跨度悬索桥结构的内力分布状态受各塔弹性拉索分布的直接影响。考虑到结构的对称性,弹性拉索刚度的分布状态可由“边-中塔”弹性拉索刚度比α来反映。弹性拉索刚度比α在1 :0.1~1 :10变化时,以Tianjin波为例,分析不同弹性拉索刚度及不同刚度比下主塔关键位置的响应峰值如图 6所示。
|
Download:
|
| 图 6 弹性拉索刚度和结构响应峰值 Fig. 6 Cable stiffness vs. peak value of structural response | |
综合考虑经济预算、施工难度、减震率等多种因素,α建议取为1 :1。此外,当弹性拉索刚度小于6×108 N/m时,塔梁相对位移随拉索刚度的增加迅速减小;当拉索刚度大于6×108 N/m时,塔梁相对位移缓慢变小并逐渐趋于平缓,故取拉索刚度为6×108 N/m。
2.3.2 黏滞阻尼器最优阻尼系数Tianjin波输入下的三塔悬索桥地震位移响应随阻尼器阻尼系数的变化关系如图 7所示。对比塔梁相对位移峰值、塔顶位移峰值与黏滞阻尼器阻尼系数的关系,取阻尼系数为25×106 N ·s/m。

|
Download:
|
| 图 7 阻尼系数vs.结构位移峰值 Fig. 7 Damp coefficients vs. peak value of displacement | |
1) 屈服荷载最优值
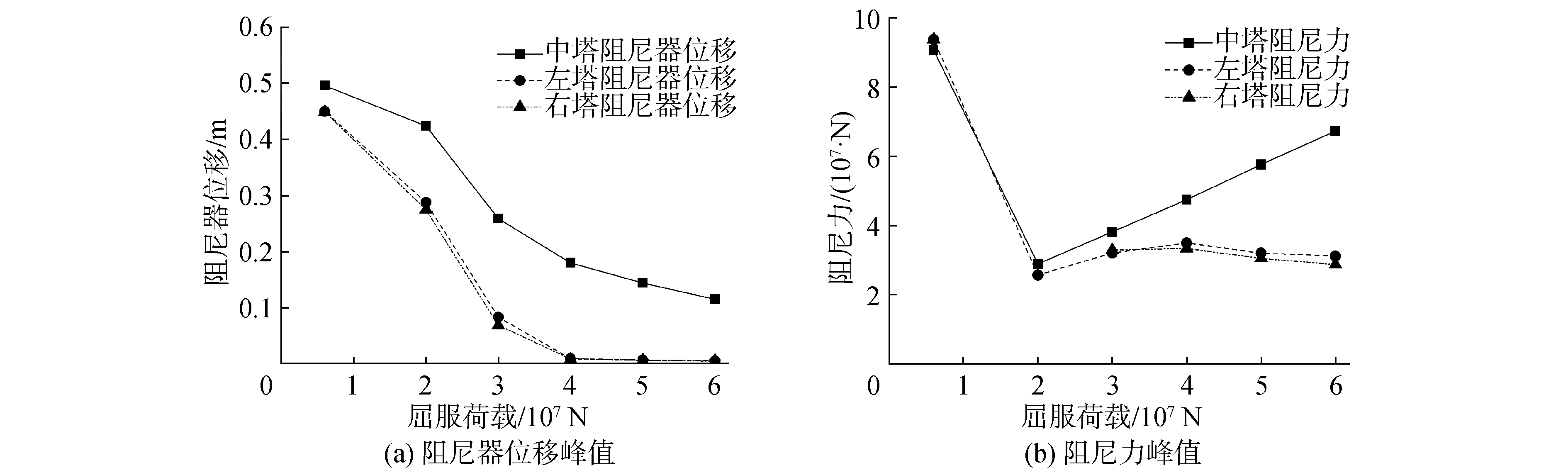
在塔梁连接处均设置相同参数的软钢阻尼器,软钢阻尼器的屈服位移Δy为10 mm,极限位移Δu为屈服位移的15倍,极限荷载Fu为屈服荷载Fy的1.15倍。Tianjin波作用下,不同屈服荷载时软钢阻尼器的位移峰值、阻尼力峰值如图 8所示。由图 8得屈服荷载最优值为4×107 N。
|
Download:
|
| 图 8 屈服荷载vs.阻尼器响应峰值 Fig. 8 Yield load vs. peak value of damper response | |
2) 最优弹性刚度
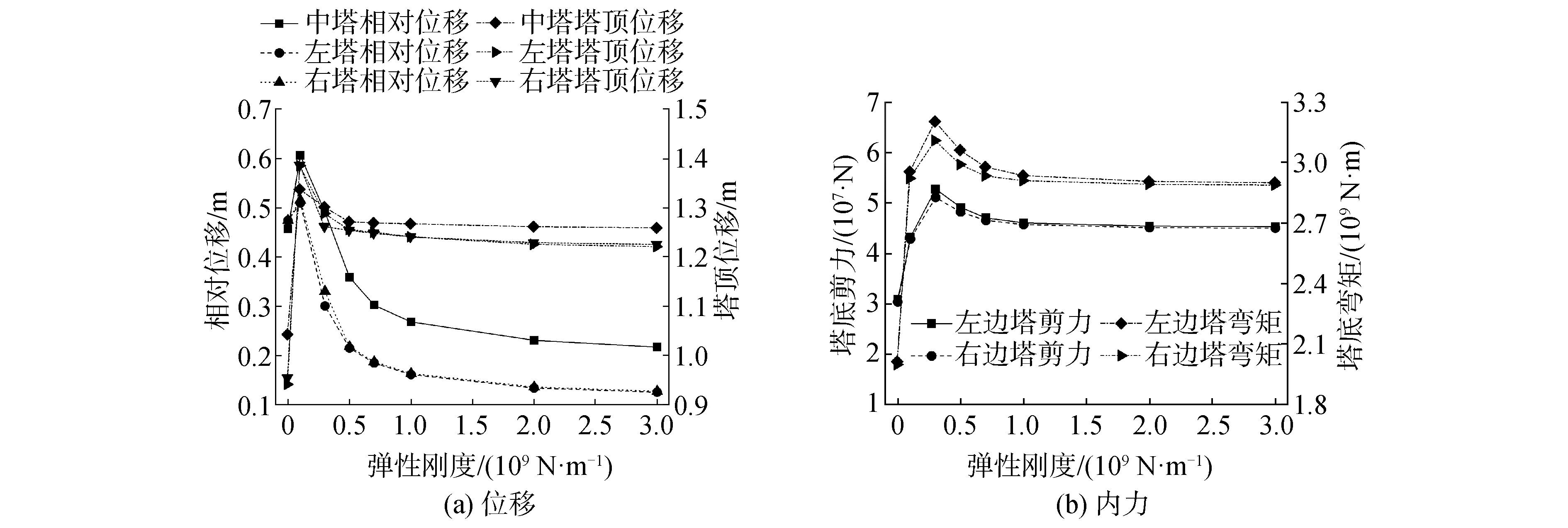
Tianjin波作用下,不同弹性刚度时软钢阻尼器的塔梁位移响应峰值、内力峰值如图 9所示。综合考虑塔梁相对位移和塔顶位移等因素,当软钢阻尼器弹性刚度大于1×109 N/m,结构地震响应变化很小。根据软钢阻尼器参数敏感性分析,得到软钢阻尼器的最优弹性刚度为1×109 N/m。
|
Download:
|
| 图 9 弹性刚度vs.结构响应峰值 Fig. 9 Elastic stiffness vs. peak value of structural response | |
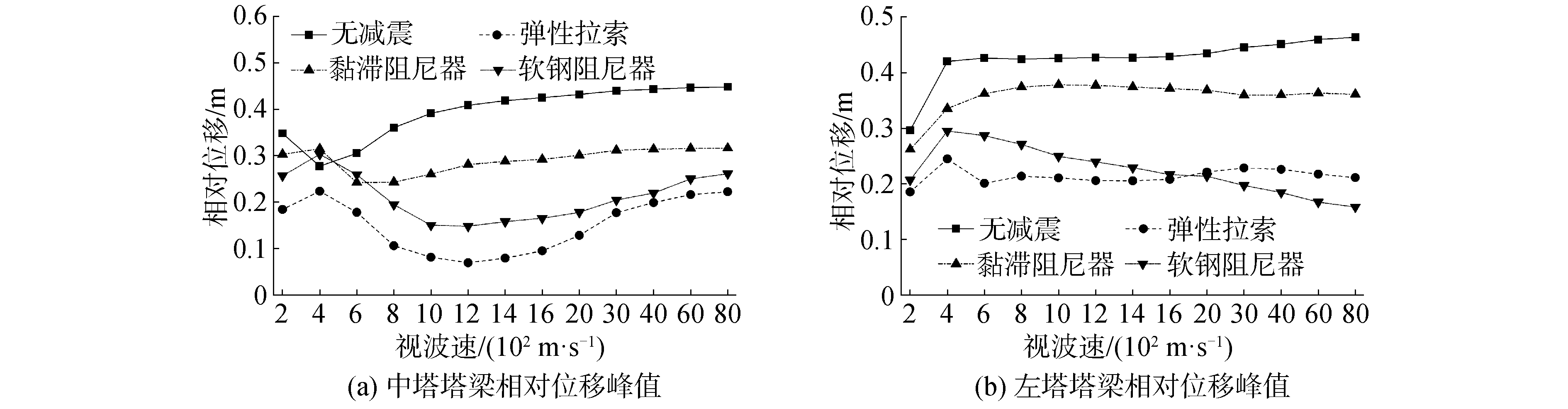
考虑行波效应的影响,重点分析对比了弹性拉索、黏滞阻尼器、软钢阻尼器对塔梁相对位移的控制效果。基于前述分析,3种减震装置,分别选取弹性拉索、黏滞阻尼器、软钢阻尼器的最优的参数分析其减震控制效果,不同视波速下,3种减震装置对塔梁相对位移的控制结果的对比如图 10所示,塔梁相对位移峰值减震率如图 11所示。
|
Download:
|
| 图 10 不同减震装置对塔梁相对位移控制效果 Fig. 10 Control effect of different devices on relative displacement between tower and main tower | |

|
Download:
|
| 图 11 塔梁相对位移峰值减震率 Fig. 11 Seismic mitigation ratio of relative displacement between tower and main tower | |
由图 10、图 11可知,在不同视波速下,弹性拉索、黏滞阻尼器、软钢阻尼器均能较好地控制塔梁相对位移。其中,采用弹性拉索进行减震控制时,中塔塔梁相对位移的减震效果基本保持在50%以上,最高可达83.1%;采用软钢阻尼器进行减震控制时,中塔塔梁相对位移的减震效果大都维持在40%以上,最高达到63.7%;而采用黏滞阻尼器进行减震控制时,对中塔塔梁相对位移的控制幅度约在30%左右。对于边塔塔梁相对位移,3种减震装置的控制效果基本与中塔塔梁相对位移一致。就阻尼器的控制效果而言,均表现出弹性拉索和软钢阻尼器优于黏滞阻尼器的规律。其中,弹性拉索在视波速小于2 000 m/s时其减震效果优于软钢阻尼器。
弹性拉索、黏滞阻尼器、软钢阻尼器的减震效果对比表明,3种减震装置均能较好的控制三塔悬索桥的塔梁相对位移。其中,弹性拉索与软钢阻尼器表现相对较优,但弹性拉索与软钢阻尼器的采用会显著增大主塔塔顶位移、主塔塔底剪力与弯矩。相比较而言,采用黏滞阻尼器进行三塔悬索桥减震控制时,主塔塔顶位移、主塔塔底剪力与弯矩变化均相对较小,增长幅度均在40%以内。
3 结论1) 对比一致输入下的结构地震响应,视波速对结构地震响应峰值影响很大。视波速会影响结构位移响应峰值的出现时刻,在低视波速区间时,结构地震位移响应峰值振荡明显;在高视波速区间时,结构地震位移响应峰值逐渐保持平稳。
2) 在最优参数取值条件下,弹性拉索对中塔塔梁相对位移的减震率最高可达80%以上,软钢阻尼器减震率最高可达40%以上,黏滞阻尼器减震率在30%左右。仅就位移控制效果而言,弹性拉索和软钢阻尼器优于黏滞阻尼器。
3) 3种减震装置均能较好的控制三塔悬索桥的塔梁相对位移,其中弹性拉索与软钢阻尼器的减震效果更优,但采用弹性拉索和软钢阻尼器会显著增大主塔塔顶位移、主塔塔底剪力与弯矩;采用黏滞阻尼器进行减震控制时,对主塔塔顶位移、主塔塔底剪力与弯矩的影响相对较小。
本文研究了3种不同的减震装置的最优取参数值及减震控制效果,可为大跨度三塔悬索桥的减震分析与设计提供参考,其普遍性仍需进一步在其他类型大跨度三塔悬索桥中进一步验证。后续工作中,课题组将进一步构造最优控制模型[15],开展大跨度三塔悬索桥综合最优控制研究。
| [1] |
MURPHY T P, COLLINS K R. Retrofitting suspension bridges using distributed dampers[J]. Journal of structural engineering, 2004, 130(10): 1466-1474. DOI:10.1061/(ASCE)0733-9445(2004)130:10(1466) (  0) 0)
|
| [2] |
FANG Youliang, YAN Guiping, HUANG Yan, et al. Active seismic response robustness control of cable-stayed-suspension bridges[J]. Progress in safety science and technology part A, 2002, 3: 513-518. (  0) 0)
|
| [3] |
ERKUS B, ABÉ M, FUJINO Y. Investigation of semi-active control for seismic protection of elevated highway bridges[J]. Engineering structures, 2002, 24(3): 281-293. DOI:10.1016/S0141-0296(01)00095-5 (  0) 0)
|
| [4] |
MEMISOGLU APAYDIN N. Earthquake performance assessment and retrofit investigations of two suspension bridges in Istanbul[J]. Soil dynamics and earthquake engineering, 2010, 30(8): 702-710. DOI:10.1016/j.soildyn.2010.02.011 (  0) 0)
|
| [5] |
ABDEL-GHAFFAR A M, RUBIN L I. Suspension bridge response to multiple-support excitations[J]. Journal of the engineering mechanics division, 1982, 108(2): 419-435. (  0) 0)
|
| [6] |
LI Jian, SPENCER B F JR, ELNASHAI A S, et al. Substructure hybrid simulation with multiple-support excitation[J]. Journal of engineering mechanics, 2012, 138(7): 867-876. DOI:10.1061/(ASCE)EM.1943-7889.0000394 (  0) 0)
|
| [7] |
潘旦光, 楼梦麟, 范立础. 多点输入下大跨度结构地震反应分析研究现状[J]. 同济大学学报, 2001, 29(10): 1213-1219. PAN Danguang, LOU Menglin, FAN Lichu. Status of seismic response analysis of long-span structures under multiple support excitations[J]. Journal of Tongji University, 2001, 29(10): 1213-1219. DOI:10.3321/j.issn:0253-374X.2001.10.016 (  0) 0)
|
| [8] |
何庆祥, 沈祖炎. 结构地震行波效应分析综述[J]. 地震工程与工程振动, 2009, 29(1): 50-57. HE Qingxiang, SHEN Zuyan. Review of structural seismic analysis of travelling wave effects[J]. Journal of earthquake engineering and engineering vibration, 2009, 29(1): 50-57. (  0) 0)
|
| [9] |
WANG Hao, LI Jian, TAO Tianyou, et al. Influence of apparent wave velocity on seismic performance of a super-long-span triple-tower suspension bridge[J]. Advances in mechanical engineering, 2015, 7(6): 1-14. (  0) 0)
|
| [10] |
WANG Hao, ZOU Keguan, LI Aiqun, et al. Parameter effects on the dynamic characteristics of a super-long-span triple-tower suspension bridge[J]. Journal of Zhejiang university-science A, 2010, 11(5): 305-316. DOI:10.1631/jzus.A0900496 (  0) 0)
|
| [11] |
CHARLES S P E.The seismic retrofit of the golden gate bridge[R].Shanghai: PRC-US Workshop on Seismic Analysis and Design of Special Bridges, 2002.
(  0) 0)
|
| [12] |
VADER T S, MCDANIEL C C. Influence of dampers on seismic response of cable-supported bridge towers[J]. Journal of bridge engineering, 2007, 12(3): 373-379. DOI:10.1061/(ASCE)1084-0702(2007)12:3(373) (  0) 0)
|
| [13] |
WANG Hao, ZHOU Rui, ZONG Zhouhong, et al. Study on seismic response control of a single-tower self-anchored suspension bridge with elastic-plastic steel damper[J]. Science China technological sciences, 2012, 55(6): 1496-1502. DOI:10.1007/s11431-012-4826-5 (  0) 0)
|
| [14] |
HE W L, AGRAWAL A K, MAHMOUD K. Control of seismically excited cable-stayed bridge using resetting semiactive stiffness dampers[J]. Journal of bridge engineering, 2001, 6(6): 376-384. DOI:10.1061/(ASCE)1084-0702(2001)6:6(376) (  0) 0)
|
| [15] |
王浩, 李爱群, 郭彤. 超大跨悬索桥地震响应的综合最优控制研究[J]. 湖南大学学报(自然科学版), 2006, 33(3): 6-10. WANG Hao, LI Aiqun, GUO Tong. Compositive optimal control of the seismic response for super-long-span suspension bridges[J]. Journal of Hunan University (natural sciences), 2006, 33(3): 6-10. DOI:10.3321/j.issn:1000-2472.2006.03.002 (  0) 0)
|
| [16] |
WANG Hao, LI Aiqun, JIAO Changke, et al. Damper placement for seismic control of super-long-span suspension bridges based on the first-order optimization method[J]. Science China technological sciences, 2010, 53(7): 2008-2014. DOI:10.1007/s11431-010-4009-1 (  0) 0)
|
| [17] |
SOONG T T, DARGUSH G F. Passive energy dissipation systems in structural engineering[M]. New York: John Wiley & Sons, 1997.
(  0) 0)
|
| [18] |
DARGUSH G F, SOONG T T. Behavior of metallic plate dampers in seismic passive energy dissipation systems[J]. Earthquake spectra, 1995, 11(4): 545-568. DOI:10.1193/1.1585827 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


