2. 桂林航天工业学院 广西高校机器人与焊接重点实验室, 广西 桂林 541004
2. Guangxi Key Laboratory of Robotics and Welding, Guilin University of Aerospace Technology, Guilin 541004, China
随着工业机器人在3C电子行业中的普及率猛增,人们对机器人运动速度、加速度和精度的要求越来越高。具体的性能指标表现在机器人的高重复定位精度、拾料节拍时TCP最大速度、TCP最大加速度以及短搬运周期等。由于机器人结构复杂、关节高度耦合以及控制的非线性并且时变等这些因素都会给机器人带来难以避免的动态响应迟滞及振荡等问题。尤其垂直六自由度工业机器人的关节普遍采用的是柔性特征较显著的同步传送带系统以及RV谐波减速器等元件,关节的柔性效应显著导致机械谐振,影响伺服系统的稳定性与跟踪精度。当今国内外专家学者针对“如何实现高速负载的机器人具有稳定的动态控制性能”这类课题展开深入研究。
机器人的控制方式分为2种:1)不考虑弹性变形的刚体机器人控制[1];2)考虑柔性因素的柔体机器人控制[2]。第1种类型常采用的是位置控制方法;而对于第2种类型针对机器人的柔性因素常采用振动的主动控制及被动控制等方法。Zhu等[3]在研究如何实现精确控制柔性关节机器人的问题上,提出了一种基于改进自适应控制算法的控制策略。建立了机器人结构和阻抗控制模型。然后,推导了间接自适应控制算法。提出了一种基于运动传感器的多连杆弹性关节机器人运动控制的识别与控制设计相结合的新方法。Makarov等[4]提出的基于模型的控制设计方法利用H∞框架与预期能设计一个二自由度控制器。输入命令整形法是柔性连杆机器人的开环控制常用的方法之一。Ahmad等[5]提出了一种基于输入整形技术的前馈控制来抑制振动。对于机器人的非线性控制,模糊控制方法也发挥着重要的作用。由于它不需要建立精确的数学模型,只需要建立一个大数据库,数据库中包含了使用者的操作数据、经验数据以及逻辑数据等。在对机器人进行控制时,计算机会根据判断条件做出对应较为准确的执行命令。该方法的优点在于可以实时获取信息,并通过模糊推理,解决通常方法很难处理的对象,比如非线性系统、不确定性系统等。目前严格单一的控制方法已不能满足工业上对于机器人的控制精度的要求。为保证生产质量、作业要求,专家学者们在未来的工作中都朝着柔性控制的方向展开深入研究。
本文则针对高速负载时机器人惯量时变性所带来的动态响应迟滞以及柔性传动环节导致的机械谐振的问题,研究柔体动力学模型的前馈力矩控制。该方法主要通过建立柔体动力学模型,并对柔性关节的刚度系数进行辨识,获取得到柔性参数,将期望轨迹的刚体位置信息改进为柔性因素下的位置信息,用于计算柔性因素下机器人的预设的前馈补偿力矩。
1 动力学建模 1.1 柔性关节动力学模型确定以具有六自由度垂直串联工业机器人作为实验平台,如图 1所示,根据Denavit-Hartenberg模型坐标系的构建原则对机器人进行连杆坐标系构建。{Ti}i=1, 2, …, 6为对应的6个关节的连杆坐标系,X、Y、Z对应的是旋转轴各个方向。构建连杆坐标系目的在于构建完整的动力学模型,准确表达出各个运动关节的位置、角速度、角加速度以及关节力矩之间的关系。

|
Download:
|
| 图 1 垂直六自由度工业机器人 Fig. 1 Vertical six degree of freedom industrial robot | |
根据Paul[6]的刚体动力学方程如式(1)所示,完全确定了机器人各个连杆的几何参数以及动力学参数。
| $ \tau_{i}=\sum\limits_{j=1}^{6} D_{i j} \ddot{q}_{j}+I_{a i} \ddot{q}_{i}+\sum\limits_{j=1}^{6} \sum\limits_{k=1}^{6} D_{i j k} \dot{q}_{j} \dot{q}_{k}+G_{i} $ | (1) |
式中:Dij为关节i和关节j的惯性项; Iai为关节i的惯量项; Dijk为哥氏力、向心力项; Gi为作用于关节i的重力项;
为实现基于柔体动力学模型的柔性前馈力矩控制目的,在建模过程中,利用文献[7]的柔体动力学建模思想,改进刚体动力学模型如式(1),增加机器人关节的柔性因素,建立实验平台的柔性关节的动力学方程,准确描述机器人在运动过程中的位置信息、关节的柔性信息与关节力矩之间的关系,则具有柔性关节的机器人动力学模型[8]为:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{M}}\left( {{\mathit{\boldsymbol{q}}_{{\mathop{\rm link}\nolimits} }}} \right)}&0\\ 0&{{\mathit{\boldsymbol{J}}_{{\rm{motor}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\ddot {q}}}_{{\rm{link}}}}}\\ {{\mathit{\boldsymbol{\ddot {q}}}_{{\rm{motor}}}}} \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{C}}\left( {{\mathit{\boldsymbol{q}}_{{\rm{link}}}},{{\dot q}_{{\rm{link}}}}} \right)}\\ {{\mathit{\boldsymbol{f}}_v} \cdot {{\dot q}_{{\rm{motor}}}} + {f_s} \cdot {\rm{sign}}\left( {{{\dot q}_{{\rm{motor}}}}} \right)} \end{array}} \right] + \mathit{\boldsymbol{K}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{q}}_{{\rm{link}}}} - \mathit{\boldsymbol{q}}}\\ {\mathit{\boldsymbol{q}} - {\mathit{\boldsymbol{q}}_{{\rm{link}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ \mathit{\boldsymbol{\tau }} \end{array}} \right]} \end{array} $ | (2) |
式(2)增加了柔性变量,使得动力学表达式精确度高,更符合工作场景下含有柔性因素的工业机器人。增加的变量有M(qlink)为n×n的惯性矩阵;C(qlink,
由于垂直六自由度工业机器人的每个关节均采用了电机与谐波减速器的结构形式,针对机器人单关节的柔性因素(柔性因素指刚度较高的构件如谐波减速器以及齿轮等,在高速运动中,构件的弹性变形增大,造成柔性),将这些柔性因素等价于电机-弹簧-质量的两惯量系统[9],如图 2所示,进行分析。电机端输出力矩为u,旋转角度为qm,电机转子旋转惯量为Jm,减速比为N;关节端关节旋转惯量为J1,旋转角度为q1。

|
Download:
|
| 图 2 电机-弹簧-质量的两惯量系统 Fig. 2 Two inertia system of motor-spring-mass | |
目前,针对垂直六自由度工业机器人存在着对刚度系数辨识困难的因素,如关节端未安装编码器设备,不能直接获取计算所需的关节角度;关节手腕处未安装力矩传感器,因而得不到计算所需的关节力矩。本文为了降低辨识刚度系数k的难度,采用单轴激励进行辨识的方法。先建立单自由度的柔性关节动力学模型,然后只运动第一轴,其余关节不做运动,进而获取实验数据,最后辨识得到关节刚度系数。单轴运动中减速比为N,重力项为G(q1);哥氏力、向心力项C(q1,
| $ J_{1} \ddot{q}_{1}+f_{v j}\left(\dot{q}_{1}\right)+f_{s j} \operatorname{sign}\left(\dot{q}_{1}\right)+G\left(q_{1}\right)-k\left(q-q_{1}\right)=0 $ | (3) |
| $ {J_m}{\ddot q_m} + {f_{vm}}\left( {{{\dot q}_m}} \right) + {f_{sm}}{\mathop{\rm sign}\nolimits} \left( {{{\dot q}_m}} \right) + k\left( {q - {q_1}} \right) = {\tau _m} $ | (4) |
| $ G\left(q_{1}\right)=M g X_{1} \cos q_{1}+M g Y_{1} \sin q_{1} $ | (5) |
式中:q=qm/N;fvj、fsj分别是关节端的粘性摩擦力系数和库伦摩擦力系数;fvm、fsm分别表示电机端的粘性摩擦力系数以及库伦摩擦力系数;sign(·)表示符号函数;X1、Y1表示关节的质心位置信息。为了实现刚度系数的辨识,需要对单轴动力学模型式(3)至式(5)进行线性形式的变换。则如式(6)所示的辨识的线性模型[9]:
| $ \boldsymbol{\tau}=\boldsymbol{D} \boldsymbol{X} $ | (6) |
式中:
| $ \mathit{\boldsymbol{\tau }} = {\left[ {\begin{array}{*{20}{c}} 0&{{T_{\rm{m}}}} \end{array}} \right]^{\rm{T}}},\mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{J_1}}&{{J_{vj}}}&{{f_{sj}}}&{M{X_1}}&{M{Y_1}}&k&{{J_m}}&{{f_{vm}}}&{{f_{sm}}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {{{\ddot q}_1}}&{{{\dot q}_1}}&{{\rm{sign}}\left( {{{\dot q}_1}} \right)}&{g\cos {q_1}}&{g\sin {q_1}}&{ - \left( {{q_1} - q} \right)}&0&0&0\\ 0&0&0&0&0&{\left( {q - {q_1}} \right)}&{{{\ddot q}_m}}&{{{\dot q}_m}}&{{\rm{sign}}\left( {{{\dot q}_m}} \right)} \end{array}} \right] $ |
由于机器人关节减速器输出端未安装编码器,因而不能直接获取关节端位置信息q1。针对式(6)中的关节角度q1未知,为了降低辨识难度,采用电机输出端的位置信息qm作为计算未知变量,将式(4)进行变换,得到柔性端位置角度计算公式为:
| $ {q_1} = \left( {{J_m}{{\ddot q}_m} + {f_{vm}}\left( {{{\dot q}_m}} \right) + {f_{sm}}{\mathop{\rm sign}\nolimits} \left( {{{\dot q}_m}} \right) + k{g_m}/N - {\tau _m}} \right)/k $ | (7) |
柔性端位置角速度与角加速度计算公式为:
| $ {\dot q_1} = \left( {{J_m}{{\ddot q}_m} + {f_{vm}}\left( {{{\ddot q}_m}} \right) + {k_m}/N - {{\dot \tau }_m}} \right)/k $ | (8) |
| $ {\ddot q_1} = \left( {{J_m}q_m^{(4)} + {f_{vm}}\left( {{{\ddot q}_m}} \right) + {{\ddot k}_m}/N - {{\ddot \tau }_m}} \right)/k $ | (9) |
考虑式(7)在代入式(5)时会造成计算困难,在设计激励轨迹时候尽量避免轨迹中重力项的影响,这里针对本实验平台的第一轴而言,重力项(5)为0。并将式(7)、(8)、(9)代入式(6)进行化简,得到最小惯性参数模型[9]为:
| $ \tau_{m}=\boldsymbol{W}_{s} \boldsymbol{X}_{s} $ | (10) |
式中:
| $ {{\boldsymbol{W}}_s} = \left[ {\begin{array}{*{20}{c}} { - {{\ddot \tau }_m}}&{ - {{\dot \tau }_m}}&{q_m^{(4)}}&{{{\dddot q}_m}}&{{{\ddot q}_m}}&{{{\dot q}_m}}&{\operatorname{sign} \left( {{{\dot q}_m}} \right)} \end{array}} \right] $ |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_s} = }\\ {\left[ {\frac{{{J_1}}}{k}\frac{{{f_{vj}}}}{k}\frac{{{J_1}{J_m}}}{k}\frac{{{J_1}{f_{vm}} + {J_m}{f_{vj}}}}{k}\frac{{k{J_m} + {f_{vj}}{f_{vm}} + {J_1}k/N}}{k}{f_{vm}} + \frac{{{f_{vj}}}}{N}{f_{sm}}} \right]} \end{array} $ |
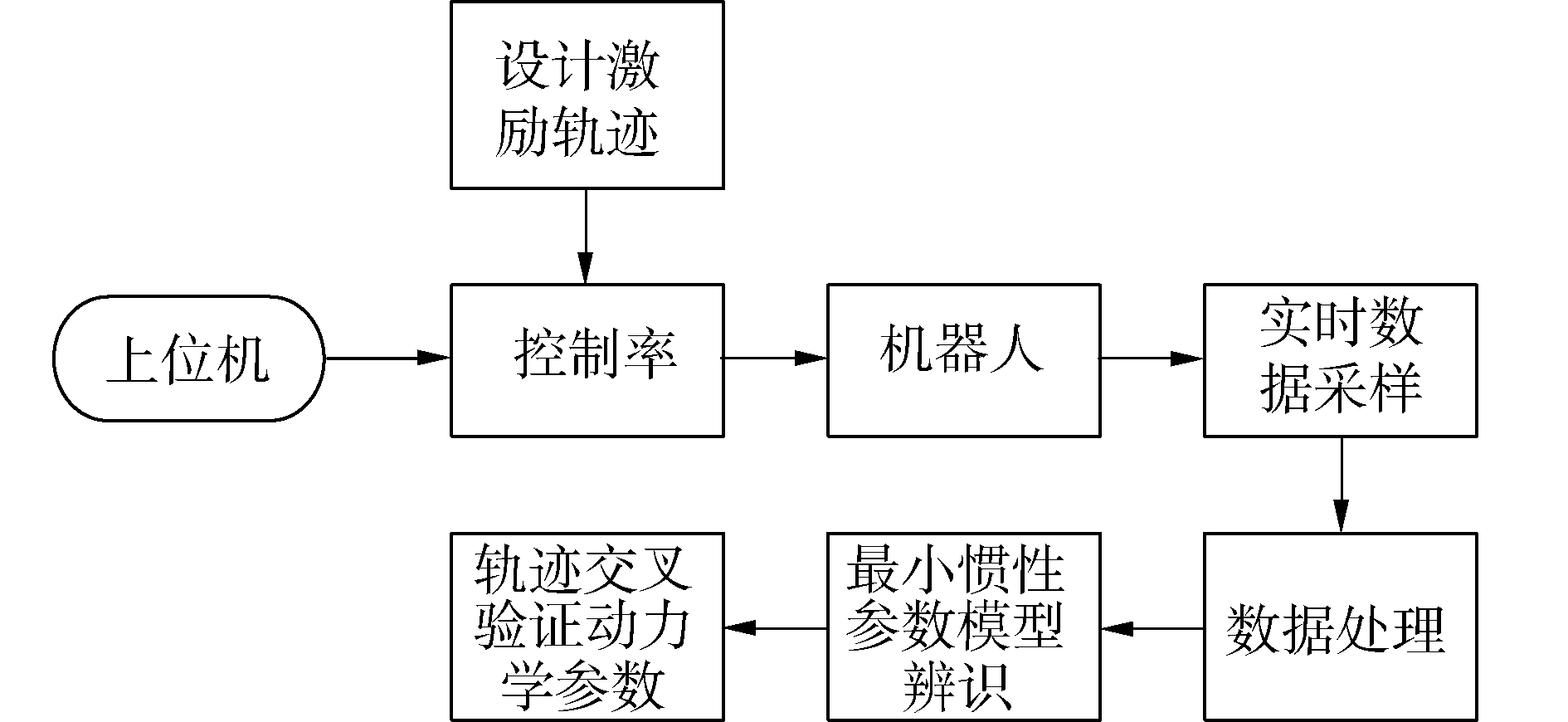
在辨识机器人动力学参数过程中,需考虑的要素有数据的采集形式以及数据的处理方式等。辨识参数流程如图 3所示,设计好激励轨迹,上位机发送指令,保证机器人在规划好的激励轨迹运动,并以采样周期为Ts实时对运动过程中的各个关节位置、速度、加速度和力矩信号进行数据采样。为了提高辨识精度,数据处理主要经过中心差分和低通滤波阶段,最终根据机器人的最小惯性参数模型,利用最小二乘辨识算法进行动力学参数的辨识。计算得到的理论结果与实际的力矩数据进行比对,以验证动力学参数的准确性。
|
Download:
|
| 图 3 参数辨识流程 Fig. 3 Flow chart of parameter identification | |
对于工业机器人而言,由于其关节并不具备直接测量关节角度、角速度、角加速度以及力矩的传感器,而需要间接通过测量电机的编码器值以及力矩反馈值来获取辨识所需要的位置信息以及力矩信息。在进行间接获取关节的角速度以及角加速度信息时,需要通过中心差分方法[9]获取关节的角速度和角加速度:
| $ \dot q\left( k \right) = \frac{{q\left( {k + 1} \right) - q\left( {k - 1} \right)}}{{2{T_s}}} $ | (11) |
| $ \ddot q\left( k \right) = \frac{{\dot q\left( {k + 1} \right) - \dot q\left( {k - 1} \right)}}{{2{T_s}}} $ | (12) |
由于电流环电流以及在进行中心差分数据处理时不可避免地引入高频噪声,高频噪声导致辨识精度下降,影响了实验结果的准确性,因此需要对采集回来的数字信号采取一些必要的处理措施,如低通滤波处理。一般的滤波方式有巴特沃斯法、平滑滤波法等。其中,巴特沃斯法设计的滤波器不考虑截止频率的坡度,通带内的幅频响应曲线能得到最大限度的平滑,能满足平滑振幅的滤波要求。由于关节角加速度通过二阶差分获得,在确定滤波器的阶数时,遵循滤波器阶数大于2的原则。由于差分引入的噪声和电流信号引入的噪声以高频噪声为主,应选择低通滤波器,而且截止频率满足关系[10]:
| $ {\omega _{{\rm{cutoff}}}} > 10{\omega _{{\rm{dyn}}}} $ | (13) |
式中:ωcutoff为滤波器截止频率;滤波器通带为[0,ωcutoff];ωdyn机器人动态频率ωdyn=2π/Ts。
根据式(13)的截止频率计算以及借助Matlab函数butter和filtfilt来构造零相位巴特沃斯低通数字滤波器,进行实验数据的滤波处理。流程如图 4所示。

|
Download:
|
| 图 4 滤波算法流程 Fig. 4 Flow chart of filtering algorithm | |
最小二乘估计法作为辨识参数最常用的方法之一:
| $ {\hat \chi _{{\rm{OLS}}}} = {\arg _{\rm{p}}}\min {\left\| {\mathit{\boldsymbol{\tau }} - D\mathit{\boldsymbol{\hat \chi }}} \right\|^2} $ | (14) |
将实验数据进行中心差分及低通滤波之后,代入式(14)中进行离线辨识与验证,结果如表 1所示。
| 表 1 动力学参数辨识结果 Table 1 Identification results of dynamic parameters |
对第一轴辨识回来的动力学参数进行交叉验证,即采用激励轨迹1进行动力学参数辨识,用激励轨迹2进行动力学参数的验证,验证效果如图 5所示。

|
Download:
|
| 图 5 动力学参数验证 Fig. 5 Dynamic parameter validation | |
从图 5可知,计算力矩和实际力矩重合度很高,误差在零刻度线附近波动,误差百分比最大为20%,误差在合理的范围内,可见建立的单轴的柔性关节动力学模型的准确性。
由于最小惯性参数为线性形式的,因此需要进一步对辨识回来的参数做表处理,并对关节刚度系数进行计算,如表 2参数辨识结果。
| 表 2 参数辨识结果 Table 2 Parameter identification results |
针对工业机器人第1、4、6关节运动过程中的无重力影响特性,因此侧重辨识这3个关节的刚度系数。在辨识第2、3关节的刚度系数时,则注意设计激励轨迹时候尽量使得重力影响最小,即可忽略重力项。用同样单轴激励的方法进行第1、4、6此3个关节的刚度系数的辨识,得到如表 3所示的刚度系数辨识结果。
| 表 3 刚度系数辨识结果 Table 3 Results of stiffness factor identification |
机器人在运动过程中,由于其手臂惯量随姿态而时变,惯量的大小随着速度而发生改变,使得关节受力不再恒定而出现有过冲现象。尤其对于高速负载的机器人而言,惯量时变性的影响性更突出。为了消除柔性抖动,采用基于柔体动力学模型的力矩前馈补偿控制[11-12]方式,将机器人视为柔性连接状态,计算出理想的各关节电机所需的转矩即可驱动系统,使其在高速中也能保持良好的动态性能。
如图 6所示的机器人控制系统,人机交互界面由C语言编程建立。采用实时控制系统实时拓展驱动,在Windows系统下,通过与之并行运行一个实时控制内核,利用标准的PC硬件资源,来构建一个实时子系统,工控机通过EtherCAT总线将控制量发送到伺服单元,系统控制周期为Ts=1 ms,能够满足对机器人控制的实时性能要求。

|
Download:
|
| 图 6 机器人控制系统 Fig. 6 Robot control system | |
根据此控制系统设计基于柔体动力学模型的力矩前馈控制律如图 7所示。设计控制率需要2步:1)离线刚度参数辨识以及最小惯性参数辨识;2)在线算法程序设计。首先对机器人进行柔体动力学模型的建立,其次设计激励轨迹进行数据的实时采样,最后通过辨识算法辨识得到最小惯性参数,辨识过程如式(2)~(13)所示,刚度系数的辨识步骤如表 2所示。离线辨识目的在于获取柔性因素下的关节刚度系数,为改进刚性关节的位置信息,从而计算柔性因素下的各个关节的实际位置信息,提高实际关节位置信息的准确性,使得预设的各关节力矩值更符合工作实际。

|
Download:
|
| 图 7 基于柔体动力学模型的力矩前馈控制律 Fig. 7 Torque feedforward control law based on flexible body dynamics model | |
在已经获得工业机器人精确的数学模型的基础上,提前规划好机器人的运动路径,并根据路径中的运动点获取期望的位置信息(如柔性因素下的各关节的角度、角速度及加速度),根据式(7)~(9),计算柔性因素下的关节的位置信息,再用动力学模型方程进行计算第1、4、6柔性关节所需要的前馈力矩,验证如图 8所示。

|
Download:
|
| 图 8 柔性各个关节前馈力矩补偿验证 Fig. 8 Verification diagram of feedforward torque compensation for flexible joints | |
在上位机程序中加入式(7)~(9)的柔性因素下的关节位置、角速度、角加速度算法,以及前馈力矩补偿算法。首先将柔性因素下的各关节的角度、角速度及角加速度的计算量代入动力学的最小惯性模型,计算得到前馈补偿力矩,工控机采用EtherCAT总线控制模式,每1 ms刷新计算柔性关节的力矩前馈值,并将前馈信号量发送给底层伺服驱动器,实时对伺服驱动的力矩进行实时补偿,从而达到提高机器人的响应速度目的。
由图 8的力矩对比图可以看出实际力矩与计算的柔性力矩的重合度很高,误差都是在零刻线处波动。柔性关节1中的力矩最大误差为25%,柔性关节4中的力矩最大误差为18%,柔性关节6中的力矩最大误差为10%。可得知该柔性位置信息对于此模型的适应性很高,与实际情况相符合。将计算得到的各柔性关节力矩作为前馈量,并以1 ms周期的形式发送到伺服驱动器的底层,实时刷新驱动器,采用补偿的形式与电流环输出量进行叠加,从而实现电机的实时力矩前馈补偿控制。
3 机器人动力学性能测试与实验面对垂直六自由度工业机器人在高速负载时关节的弹性变形的特性增加,使得结构发生变形与共振,导致任务实行的期望精度降低,采用的方法是基于柔体动力学模型的前馈补偿控制法。针对本实验平台的垂直六自由度工业机器人,通过拉格朗日方程建立柔体动力学模型,来实现基于柔体动力学模型的力矩前馈补偿控制方式。设计符合试验台的激励轨迹,让机器人手臂按照控制器下发的运动指令实时运动,通过实时操作系统每1 ms实时对运动数据采样。经过数据处理后利用辨识算法中的最小二乘法辨识动力学参数,以便完善动力学模型以及为力矩的前馈补偿提供模型依据。
在底层控制程序中,将柔性关节1、4、6的力矩前馈补偿的控制程序写入,采用C语言代码实现,通过预先估计机器人各个柔性关节在规划好的期望轨迹中各点所需的力矩值,将计算好的力矩估计值以脉冲电信号的形式送到底层控制器中,以每1 ms刷新控制器的周期,使得机器人在启动与运行过程中时刻保持平稳,实行柔性关节力矩前馈补偿。
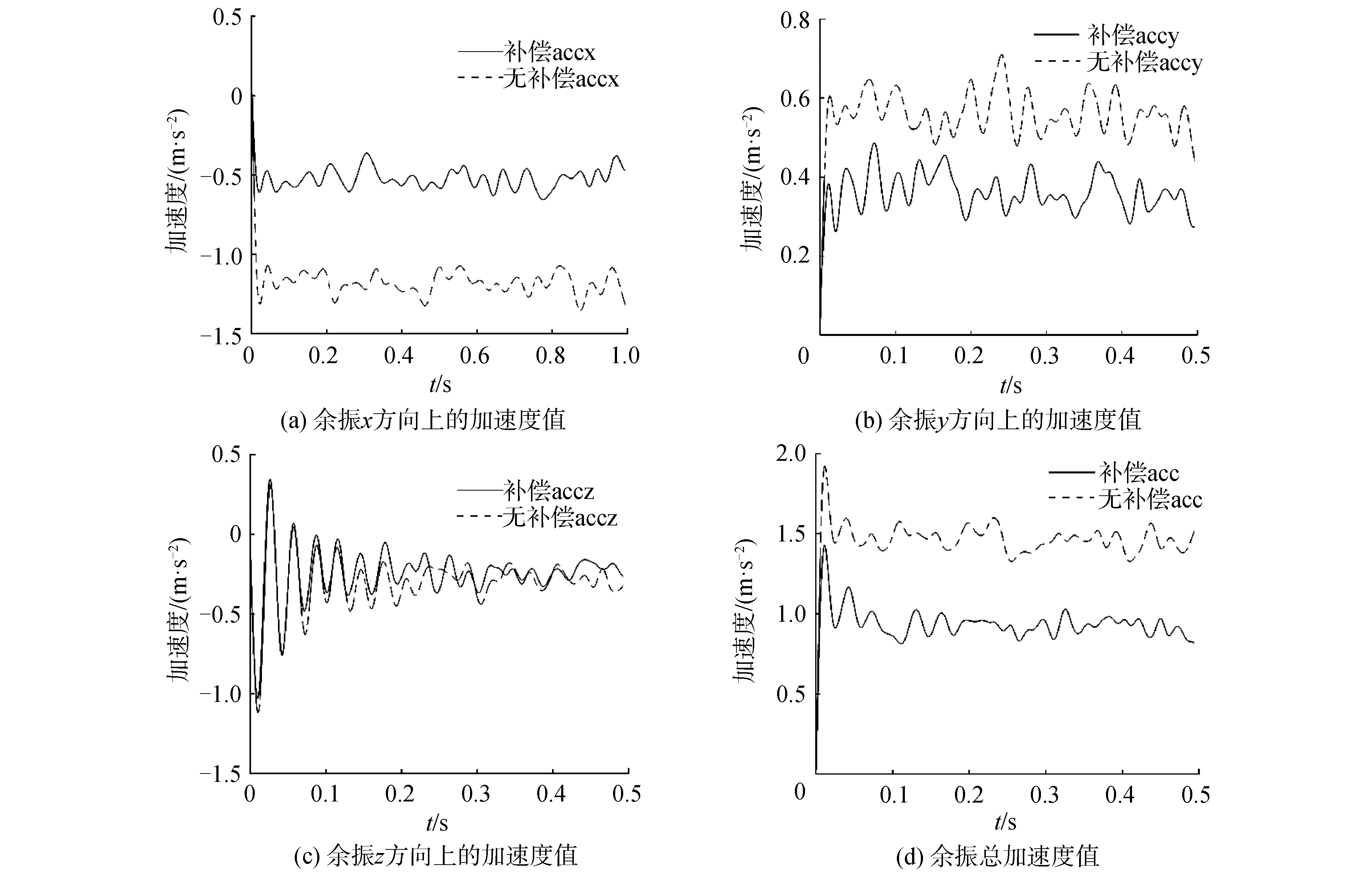
采用对照的形式,分别使用有无柔性关节前馈力矩补偿的控制方式。实验过程中,以1 kHz的采样频率采集机器人各个关节的位置信号与力矩数值以及加速度信号。通过分析加速度信号得到振动抑制效果。在规定的圆弧运动指令下,分别在有无柔性前馈力矩补偿条件下采集加速度信号,并进行加速度传感器实验数据的处理,比较末端余振上各方向加速度数值变化的影响,得到图 9速度段2 500 mm/s运动停止后末端余振加速度分析。
|
Download:
|
| 图 9 速度段2 500 mm/s运动停止后末端余振加速度分析 Fig. 9 Acceleration analysis of end residual vibration after velocity 2 500 mm/s stop motion | |
由图 9可知,圆弧运动指令速度分别为2 500 mm/s时,有无前馈力矩补偿与陷波滤波作用效果明显,余振振幅3个方向上都有所降低。如表 4所示,分析末端三维方向上的加速度下降的情况。
| 表 4 运动停止后末端余振加速度分析表 Table 4 The analysis table of the acceleration of the end residual vibration after the stop of motion |
在规定的圆弧运动指令下,分别在有无柔性力矩前馈补偿条件下采集加速度信号量。处理加速度传感器的实验数据,比较余振对末端各方向加速度数值变化的影响,如表 4所示,得到的加速度降幅最大的是60%,体现了基于柔体动力学模型的力矩前馈补偿控制方式的可行性。
4 结论1) 优化机器人的控制算法从而达到改善机器人动态特性的目的。根据机器人动力学特性进行机器人运动过程中的动态补偿,通过内控制回路使得机器人更易控制。
2) 将3 kg垂直六自由度工业机器人系统化为一个解耦的线性定常系统,柔体动力学模型的机器人柔性力矩前馈作为控制手段,即通过建立机器人柔性关节的动力学模型,辨识柔性关节的扭转刚度参数以及最小惯性参数,获取更为准确的柔性因素下的预设位置、速度、加速度信息。
3) 计算出柔性关节下所需的力矩值,最终实现机器人的柔性控制,使得机器人末端振动加速度幅值下降60%,提高了机器人末端的定位精度,满足了工业生产上对机器人的动态性能的要求。实验验证了柔体动力学模型的机器人柔性力矩前馈补偿控制具有一定的工程应用价值。
| [1] |
FENG Fei, LIU Yiwei, LIU Hong, et al. Design schemes and comparison research of the end-effector of large space manipulator[J]. Chinese journal of mechanical engineering, 2012, 25(4): 674-687. DOI:10.3901/CJME.2012.04.674 (  0) 0)
|
| [2] |
杨益波.柔性关节柔性臂杆机械臂动力学建模与振动抑制研究[D].哈尔滨: 哈尔滨工业大学, 2015. YANG Yibo. The dynamics modeling and vibration sup pression research off lexible joint-flex ible link manipulators[D]. Harbin: Harbin Institute of Technology, 2015. (  0) 0)
|
| [3] |
ZHU Yaguang, JIN Bo, LI Wei. Leg compliance control of a hexapod robot based on improved adaptive control in different environments[J]. Journal of Central South University, 2015, 22(3): 904-913. DOI:10.1007/s11771-015-2600-0 (  0) 0)
|
| [4] |
MAKAROV M, GROSSARD M, RODRÍGUEZ-AYERBE P, et al. Modeling and preview H∞ control design for motion control of elastic-joint robots with uncertainties[J]. IEEE transactions on industrial electronics, 2016, 63(10): 6429-6438. DOI:10.1109/TIE.2016.2583406 (  0) 0)
|
| [5] |
AHMAD M A, MOHAMED Z, ISMAIL Z H. Experimental investigation of feedforward control schemes of a flexible robot manipulator system[J]. Elektrika:journal of electrical engineering, 2008, 10(2): 28-35. (  0) 0)
|
| [6] |
PAUL R P. Robot manipulators:mathematics, programming, and control:the computer control of robot manipulators[M]. London: The MIT Press, 1981: 164-172.
(  0) 0)
|
| [7] |
OTT C. Cartesian impedance control of redundant and flexible-joint robots[M]. Berlin Heidelberg: Springer, 2008.
(  0) 0)
|
| [8] |
CHAN M L. Controller synthesis and vibration suppression techniques for industrial robotic manipulators with joint flexibilities[D]. Berkeley: University of California, 2013.
(  0) 0)
|
| [9] |
PHAM M T, GAUTIER M, POIGNET P. Identification of joint stiffness with bandpass filtering[C]//Proceedings of 2001 IEEE International Conference on Robotics and Automation. Seoul, South Korea, 2001: 2867-2872.
(  0) 0)
|
| [10] |
DING Li, WU Hongtao, YAO Yu, et al. Dynamic model identification for 6-DOF industrial robots[J]. Journal of robotics, 2015, 2015: 471478. (  0) 0)
|
| [11] |
CORKE P. Robotics, vision and control[M]. Berlin: Springer, 2011.
(  0) 0)
|
| [12] |
SOUSA C D, RUI C. Physical feasibility of robot base inertial parameter identification:A linear matrix inequality approach[J]. The international journal of robotics research, 2014, 33(6): 931-944. DOI:10.1177/0278364913514870 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


