2. 南京航空航天大学 能源与动力学院, 江苏 南京 210016;
3. 常州大学 机械工程学院, 江苏 常州 213164
2. College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;
3. School of Mechanical Engineering, Changzhou University, Changzhou 213164, China
轮胎是汽车行驶系的重要组成部分,是汽车与地面接触的唯一媒介。轮胎性能对整车的操纵稳定性、平顺性、通过性、安全性等具有重要的影响。轮胎的安全性是构成汽车行驶安全的重要组成。近年来,安全轮胎成为提高汽车行驶安全性的重要研究方向之一[1-3]。
安全轮胎按结构不同可分为双重内腔或多腔式、自密封式、内支撑式、自体支撑式和非充气安全轮胎等,根据装配的轮辋又可分为标准轮辋型和非标准轮辋型[4-5]。目前国内外学者对多种结构的安全轮胎进行了研究,如机械弹性车轮、自密封型安全轮胎、免充气安全轮胎等[6-11]。机械弹性车轮采用铰链连接车轮外圈和轮毂的非充气结构解决充气轮胎行驶过程中的刺破泄气、爆胎等问题[6]。免充气安全轮胎主要由胎面、支撑结构胎体和轮辋组成[7-8],支撑结构胎体可采用不同材料和结构以适应不同工况,如米其林公司的TWEEL车轮和美国Polaris公司的蜂窝结构轮胎[9-10]。自体支撑型安全轮胎主要是通过增强胎侧橡胶厚度的方法实现轮胎的泄气保用功能,故又称为胎侧补强型安全轮胎[11-14]。由于结构工艺复杂、抗刺扎、防爆能力有限等原因,多腔式、自密封式安全轮胎等技术的研究和应用空间日渐缩减。目前充气安全轮胎的研究主要集中在内支撑安全轮胎、自体支撑型安全轮胎以及2种方案的组合和优化等方面。
为提高内支撑安全轮胎的性能,本文提出了一种与标准轮辋装配的组合式内支撑安全轮胎结构,并对组合式内支撑安全轮胎进行了设计和仿真。
1 组合式内支撑安全轮胎 1.1 组合内支撑安全轮胎的结构与原理内支撑安全轮胎是一种基于普通充气轮胎结构的典型安全轮胎,通过在轮辋上安装辅助支撑体,再配备轮胎压力检测装置共同组成内支撑安全轮胎。内支撑结构的材料主要包括橡胶、金属、聚氨酯和高分子复合材料等。车辆在正常工况下行驶时,内支撑组件不参与轮胎系统的工作。当发生爆胎或者胎压降低到一定程度时,内支撑将作为承载汽车重量的主要部件,同时还与轮辋配合约束着轮胎,防止轮胎发生脱圈或碾胎,保证车辆能够继续安全行驶一定距离。由于该类型安全轮胎具有结构简单、零压承载能力强等优点,是一种具有发展前景的安全轮胎,采用传统辅助内支撑体的安全轮胎已经在军用越野车辆上得到了装车验证。零压续驶试验中失效的内支撑安全轮胎如图 1所示。

|
Download:
|
| 图 1 失效的的内支撑安全轮胎 Fig. 1 Failed inserts supporting run-flat tire | |
内支撑安全轮胎的轮辋分为标准轮辋和非标准轮辋。如图 1所示的失效的内支撑安全轮胎,内支撑组件采用装配在特制的对开式非标准轮辋上的整体聚氨酯结构。该型内支撑安全轮胎安装拆卸较为复杂,且轮辋需要特制,成本较高。除此之外,在零压行驶试验中发现该型安全轮胎的胎肩部位受损严重,胎面和胎肩处发生了撕裂。内支撑安全轮胎在零压工况下行驶时,内支撑作为承担汽车重量主要部件,受力较为复杂,存在胎面摩擦生热严重、胎圈易脱落等问题,不能满足车辆大负荷、高机动、长距离的使用要求。为提高内支撑安全轮胎零压行驶工况的性能,研究适用于乘用车的内支撑安全轮胎,在借鉴这种轮胎优点基础上提出了一种组合式内支撑安全轮胎,如图 2所示。

|
Download:
|
| 图 2 组合式内支撑安全轮胎三维模型 Fig. 2 The 3-D model of combined inserts supporting run-flat tire system | |
组合式内支撑安全轮胎采用标准轮辋进行设计,能够简化结构和降低成本。内支撑组件结构参数主要根据内支撑与轮胎轮廓、轮胎变形以及装配的关系进行设计。为解决零压行驶工况下胎面散热和轻量化设计的问题,在内支撑外表面增加了散热槽,并在内支撑两侧设计了减重槽。
1.2 轮辋及轮胎设计目前,国内乘用车一般使用深槽轮辋(DC)。组合式内支撑安全轮胎采用16×6.5J型的5°深槽轮辋,轮辋相关参数[15]为:轮辋标定宽度A为165 mm,胎圈座宽度P为19.5 mm,槽底宽度L为22 mm,槽的最大位置尺寸Mmax为45 mm,轮辋标定直径D为405.6 mm,平峰周长为1274.4 mm。
子午线轮胎与斜交轮胎相比具有生热少、耐磨性好、操纵稳定性好、滚动阻力小和噪声较小等优点[16],充气轮胎平衡轮廓曲线各点的曲率半径公式为[17]:
| $ \rho = \frac{{{r_k}\sin {\alpha _k}\left( {r_k^2 - r_m^2} \right){{\left( {r_k^2 - {r^2}{{\cos }^2}{\alpha _k}} \right)}^{1/2}}}}{{2r\left( {r_k^2 - {r^2}{{\cos }^2}{\alpha _k}} \right) - r\left( {r_k^2 - r_m^2} \right){{\cos }^2}{\alpha _k}}} $ | (1) |
式中:ρ为轮廓任意点的曲率半径,mm;rk为胎冠点半径,mm;rm为断面最宽点半径,mm;αkαk为胎冠点帘线角,rad;r为断面轮廓上任意点半径,mm。
对于子午线轮胎,其帘线角αk=90°,则公式简化为:
| $ \rho=\left(r_{k}^{2}-r_{m}^{2}\right) / 2 r $ | (2) |
根据式(2),可以算出轮廓任意点的曲率半径ρ,确定胎冠点的半径和断面最宽点的半径。组合式内支撑安全轮胎采用205/55R16子午线轮胎,参数如表 1[18]。
| 表 1 205/55R16轮胎参数 Table 1 205/55R16 tire parameters |
在设计内支撑时必须满足2个要求:1)车辆在胎压处于正常范围内行驶时,内支撑不能接触到轮胎;2)内支撑能够与轮辋正确配合。内支撑的内直径和轮辋标定直径要满足:
| $ D_{I 1}=D_{R} / 2-H_{r} $ | (3) |
式中:DI1为内支撑内直径,mm;DR为轮辋标定直径,mm;Hr为轮辋槽深,mm。
内支撑的外径和轮胎外径之间的关系为:
| $ D_{I 2}=D_{t 2}-2 t_{1}-2 X_{3} $ | (4) |
式中:DI2为内支撑外直径,mm;Dt2为轮胎外直径,mm;t1为轮胎胎面厚度,mm;X3为顶部放入内支撑的垂直余量,mm。
内支撑的断面高度满足关系式:
| $ H_{t}=\left(D_{r 2}-D_{T 1}\right) / 2 $ | (5) |
式中:Ht为内支撑断面高度,mm。
轮胎内部轴向和周向距离都影响着内支撑的断面高度,内支撑宽度可以在基于自然平衡轮廓的轮胎外形轮廓确定的基础上进行计算,内支撑宽度满足公式:
| $ \left\{ {\begin{array}{*{20}{l}} {{b_{I2}} = {A_R} - 2{k_T} - {X_1}}\\ {{b_{I3}} = {B_T} - 2{t_3} - {X_2}} \end{array}} \right. $ | (6) |
式中:bI2为基部总宽度,mm;AR为轮辋标定宽度,mm;kT为胎圈宽度,mm;X1为基部放入内支撑水平余量,mm;bI3为顶部宽度,mm;BT为轮胎断面宽度,mm;t3为轮胎胎侧厚度,mm;X2为顶部放入内支撑水平余量,mm。各空间余量X1、X2和X3如图 3所示。

|
Download:
|
| 图 3 安装内支撑后的空间余量 Fig. 3 Space allowance after mounting inserts supporting | |
轮胎在硬路面的变形特性一般用轮胎径向变形来表征,除此之外还包括侧偏变形以及外倾变形等[4]。轮胎径向变形可以由轮胎断面的高度参数确定,轮胎径向变形δT可表示为:
| $ {\delta _T} = {H_T} - {H_{TW}} $ | (7) |
式中:HT为轮胎空载断面高度,mm;HTW为轮胎加载断面高度,mm。
车辆在行驶时会受倾斜路面、侧向风或者曲线行驶时离心力的影响,此时地面会对轮胎产生侧向力FY[19],在FY的作用下轮胎所发生的变形为侧偏变形,如图 4(a)所示。当车辆受到限制时,车轮平面发生外倾,则轮胎接地印迹面向着弯道中心变形,如图 4(b)所示。

|
Download:
|
| 图 4 轮胎侧偏与外倾变形 Fig. 4 Tire cornering and extroversion deformation | |
假设轮胎此时不发生接地径向变形,则轮胎的侧偏变形量和外倾变形量可表示为:
| $ \left\{\begin{array}{l}{e_{T 1}=H_{T} \tan \beta} \\ {e_{T 2}=H_{T} \tan \gamma}\end{array}\right. $ | (8) |
式中:eT1为轮胎侧偏变形量,mm;eT2为轮胎外倾变形量,mm;β为轮辋标定直径位置和轮胎接地中心的连线与车轮中心面间的夹角,rad;γ为轮胎外倾角,rad。
内支撑的高度要保证内支撑在常载荷及常气压下不与轮胎内壁发生碰撞或摩擦,且内支撑顶部纵向空间余量X3仍能容纳轮胎径向变形,即:
| $ X_{3} \geqslant \delta_{T} $ | (9) |
同理,内支撑顶部横向余量X2在同条件下能够容纳轮胎侧偏和外倾变形,即:
| $ X_{2} \geqslant e_{T 1}+e_{T 2} $ | (10) |
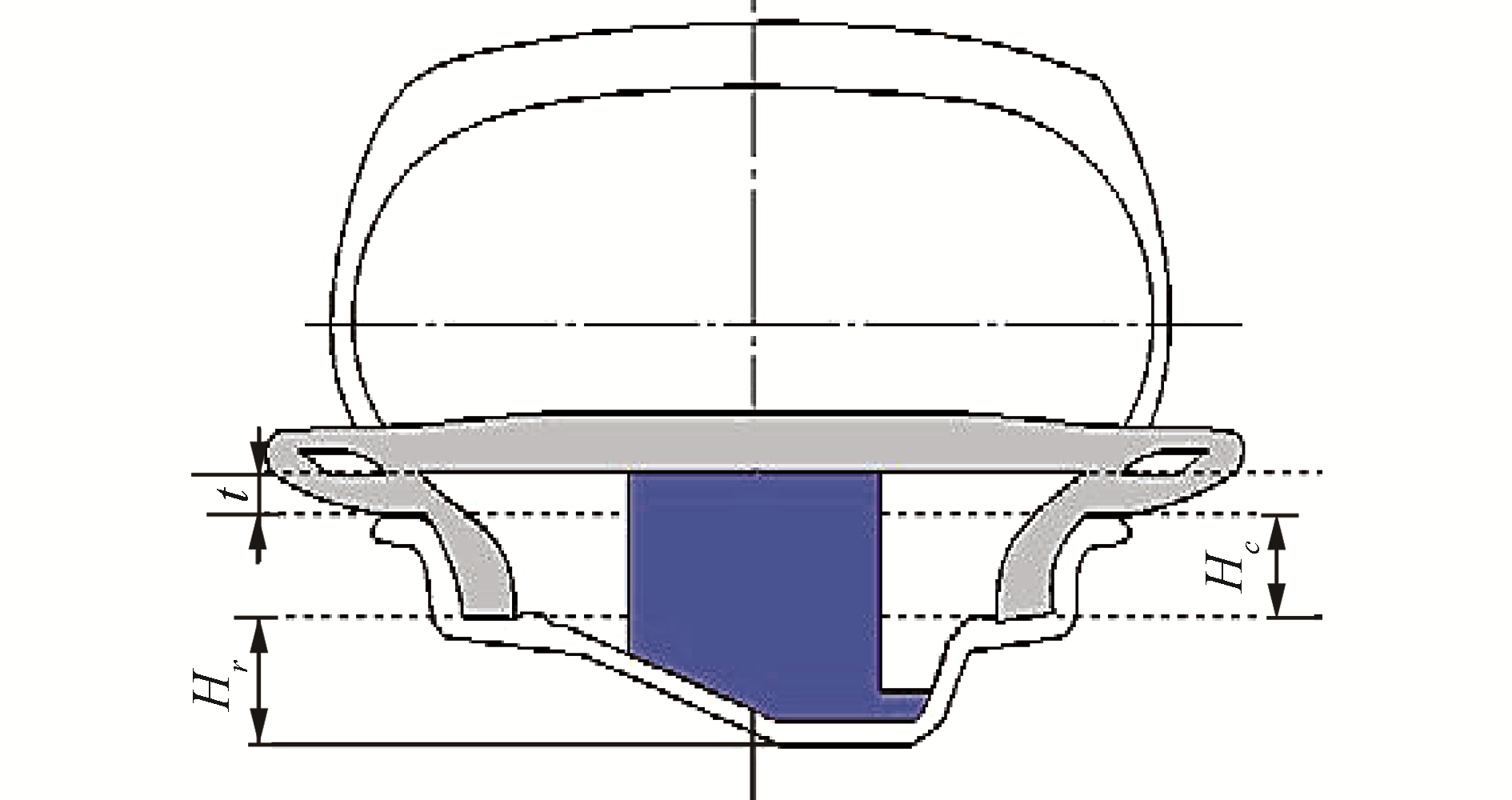
上述计算是基于轮胎正常充气状态讨论的,当轮胎失去行走能力时,内支撑最低高度必须保证轮胎胎体零压变形程度不足以达到胎体折叠的条件。假设轮胎处于零压无侧偏状态,其不脱圈的极限折叠情况如图 5所示。假设零压下轮胎不发生侧偏现象,内支撑的最低高度要足以支撑轮胎,使轮胎变形不足以达到脱圈的基本条件。由图 5可以确定内支撑的最低高度hmin满足公式:
| $ h_{\min }=H_{r}+H_{c}+t $ | (11) |
|
Download:
|
| 图 5 不发生脱圈的最小高度 Fig. 5 The minimum height does not occur | |
式中:Hr为轮辋槽底深度,mm;t为轮胎胎侧厚度,mm;Hc为轮缘高度,mm。
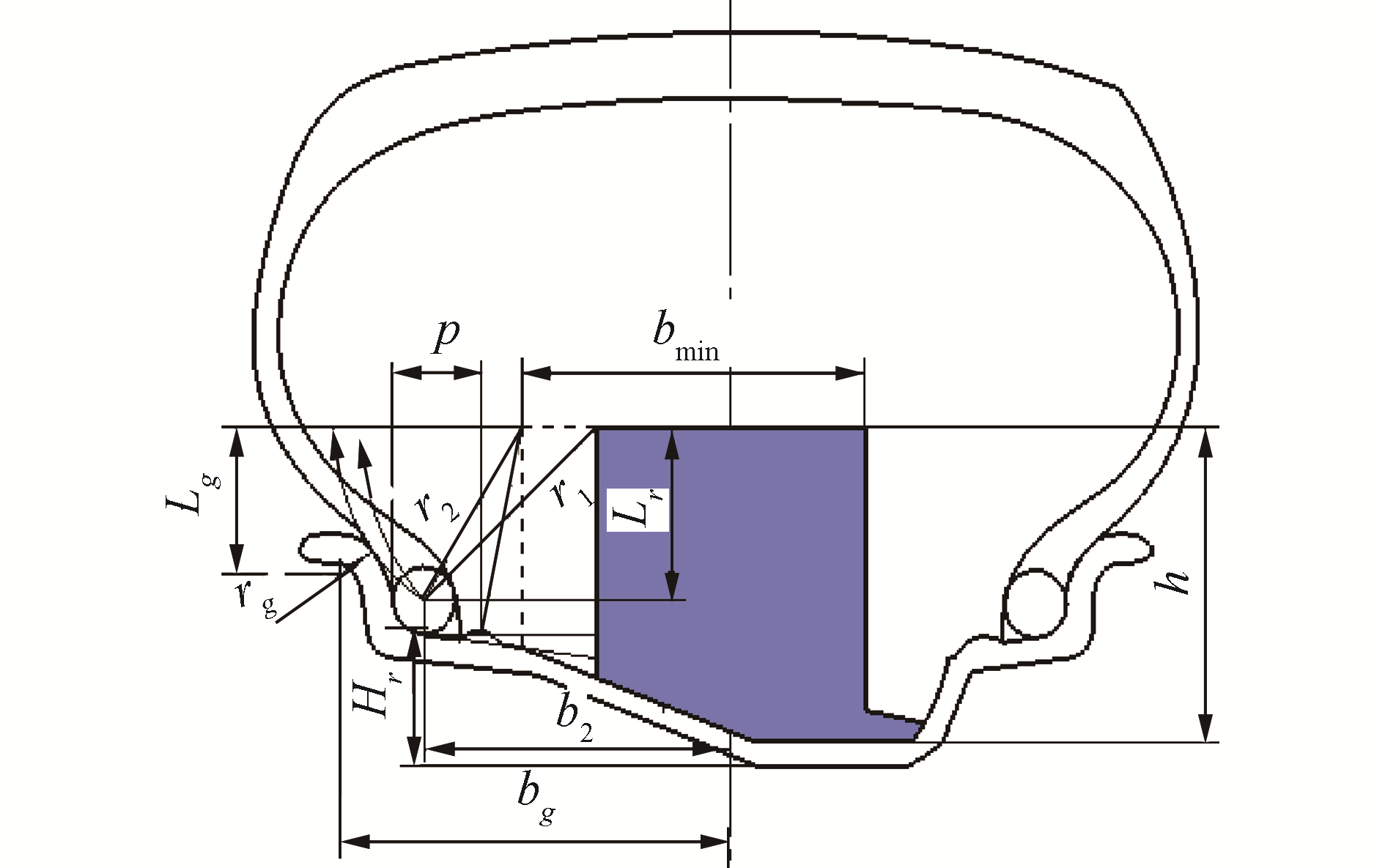
在内支撑安全轮胎在失压后,且受到很大的侧向力时,胎体就会向一侧偏移,因此内支撑宽度要保证胎圈不从轮辋槽中滑出。为防止胎圈滑出轮辋,内支撑宽度的最小极限位置如图 6中bmin所示,此时胎圈绕内支撑顶点的转动轨迹恰好与轮缘相切。当内支撑宽度小于该极限位置时,胎圈很容易从轮辋中翻出。
|
Download:
|
| 图 6 不发生脱圈的最小宽度 Fig. 6 The minimum width that does not occur | |
根据图 6中几何关系,列出下列方程组:
| $ \left\{\begin{array}{l}{\left(b_{2}-b_{\min } / 2\right)^{2}+L_{\mathrm{r}}^{2}=r_{r}^{2}} \\ {\left(b_{g}-b_{\min } / 2\right)^{2}+L_{g}^{2}=\left(r_{g}+r_{2}\right)^{2}}\end{array}\right. $ | (12) |
式中:rg为轮缘半径,mm;bg、b2为轮缘半径圆心和胎圈圆心到中心面的距离和到内支撑顶面的距离,mm;Lr、Lg已知,未知量为仅有bmin和r2,方程组可解。
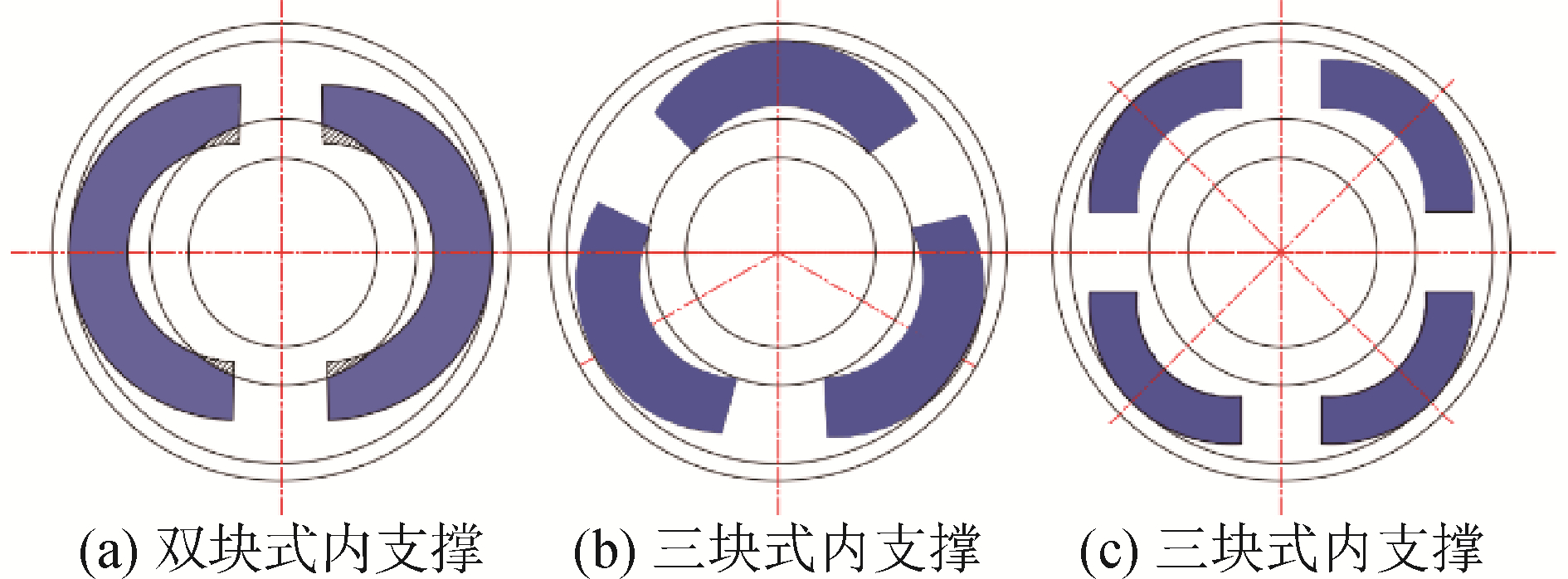
1.3.3 内支撑参数与安装工艺的关系假设轮胎充气轮廓不会变形,取前面分析的内支撑最低高度,可根据图 7来确定内支撑分块数量。由图 7可以看出2块内支撑装配时会与轮辋发生干涉,分3块和4块装配起来较为容易。考虑内支撑整体刚度和装卡锁紧装置数量,采用3块式结构比较合理[4]。
|
Download:
|
| 图 7 内支撑分块数量 Fig. 7 Block number of inserts supporting | |
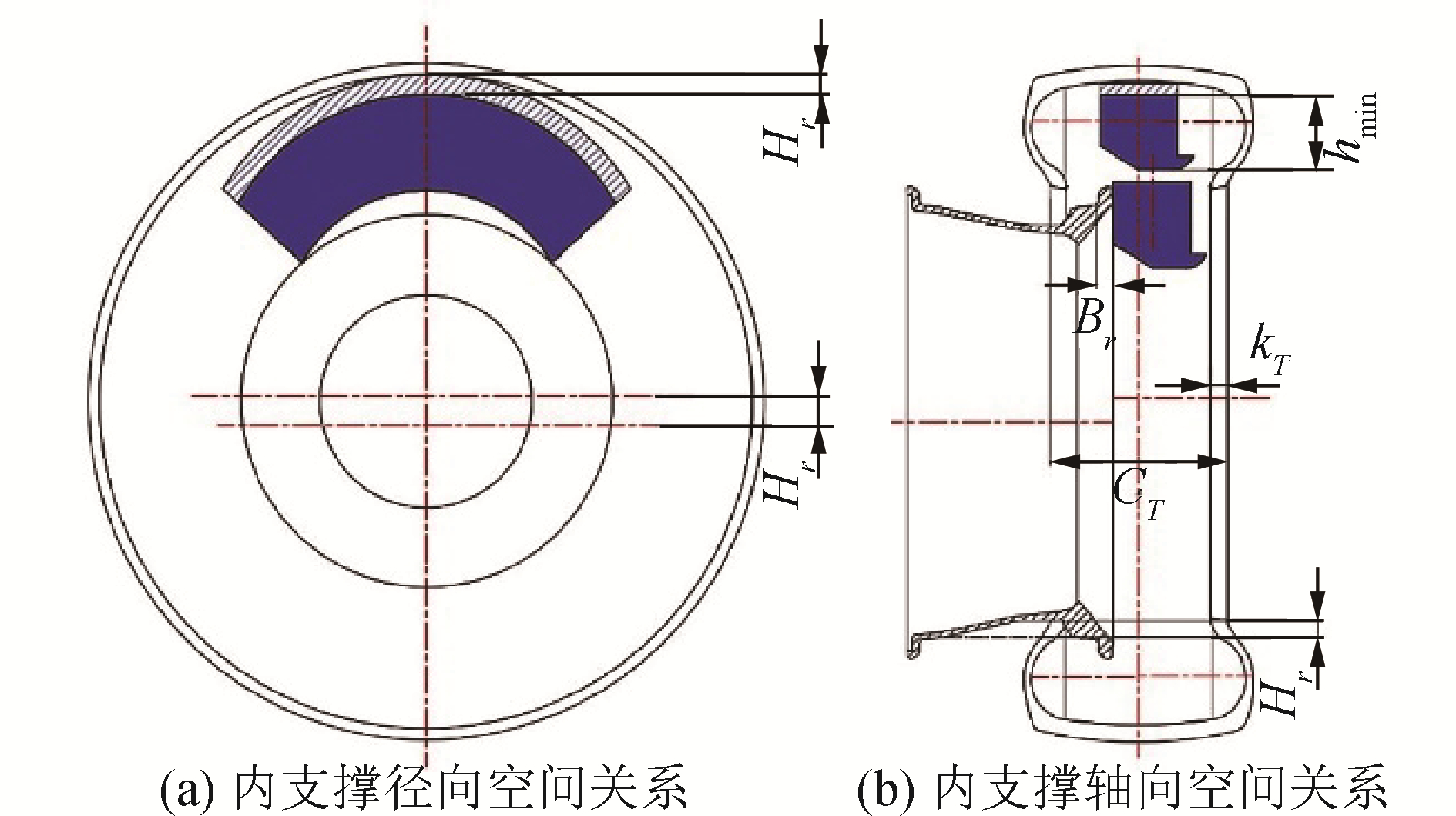
内支撑最大高度的计算需要考虑轮胎内侧胎圈进入轮辋槽的情况,如图 8所示。由于分块数量是通过内支撑最小高度所确定的最少分块数量,因此分块数为3块情况下,在最小高度的基础上加上轮辋槽深度得到的是内支撑高度上限,即:
| $ h_{\max }=h_{\min }+H_{r} $ | (13) |
|
Download:
|
| 图 8 内支撑与内部空间关系 Fig. 8 Relation of inserts supporting and inner space | |
考虑到轮胎承重时的径向变形以及遇到地面几何障碍时的变形,在高度方向应还留出一定的余量。
安装过程中对内支撑的最大宽度同样有限制,在胎圈未进入轮辋槽时,内支撑可达到最大宽度值bmax,从图 8中的几何关系可以得出:
| $ b_{\max }=C_{T}-B_{r}-2 k_{T} $ | (14) |
式中:Br为轮辋槽端点到轮辐边缘的距离,mm;kT为胎圈宽度,mm。
1.3.4 内支撑主要参数计算内支撑主要参数不但与轮辋和轮胎本身的几何尺寸有关,还与轮胎气压、负载、包容特性以及材料性能等因素相关。另外保证内支撑能够顺利的安装也是决定内支撑尺寸参数的关键因素。根据式(3)~(14)计算得到内支撑模型的主要参数,见表 2。
| 表 2 内支撑主要参数 Table 2 Main parameters of inserts supporting |
内支撑的内表面轮廓应和轮辋匹配,根据内支撑主要参数在SOLIDWORKS中创建内支撑三维模型,内支撑采用3块式结构,基于装配原理在装配体中将内支撑、轮胎以及轮辋进行装配,得到组合式内支撑安全轮胎的装配体模型。
2 组合式内支撑安全轮胎仿真 2.1 组合式内支撑安全轮胎有限元模型将组合式内支撑安全轮胎装配体模型导入HyperMesh中建立有限元模型。首先进行模型的网格划分,网格类型和数量直接影响结果精度和计算量,是有限元分析中关键的环节。倒角和小孔等特征会使模型结构复杂化,不能得到较规则的网格形式,且有可能导致无法计算结果。因此在划分网格时应尽量删除一些对结果影响不大的特征,以便获得便于计算的网格。
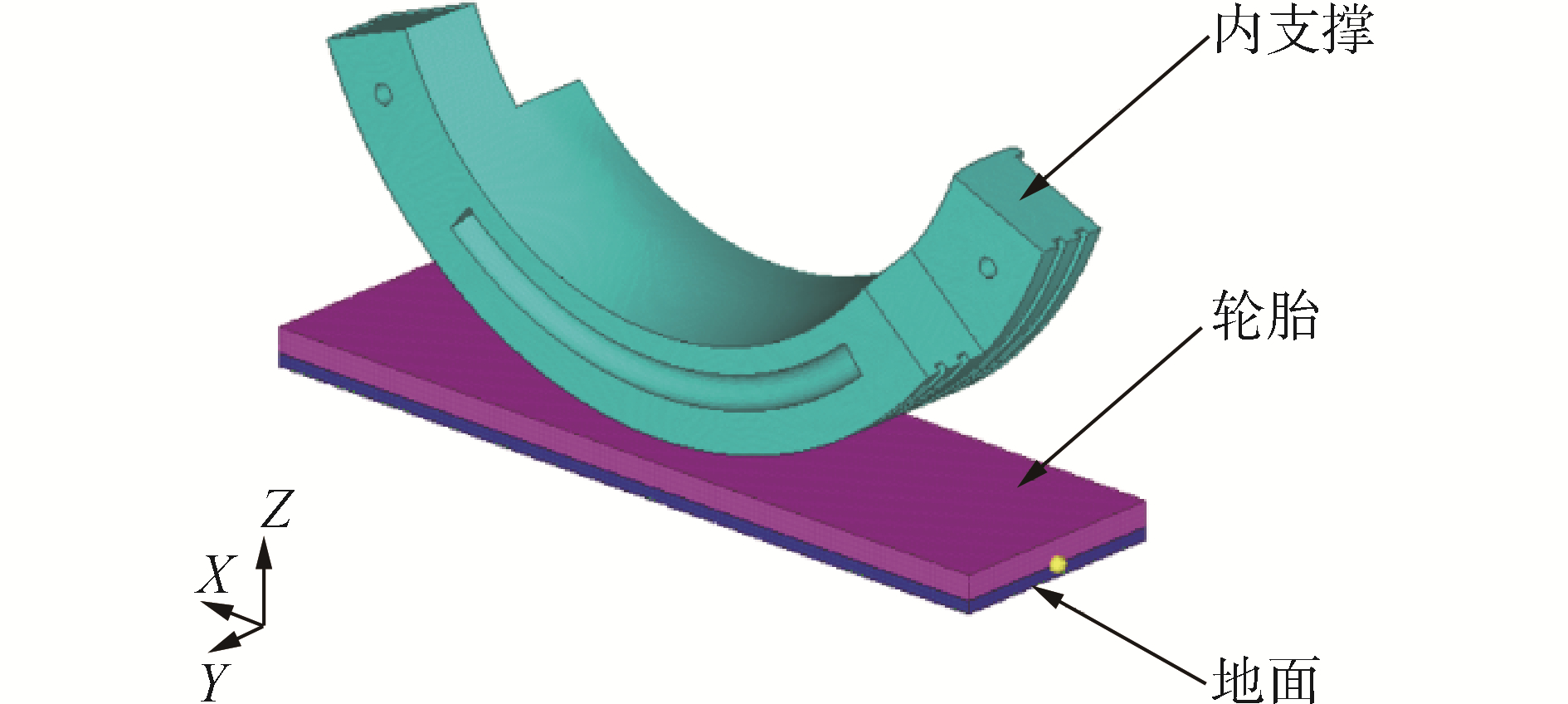
内支撑结构特征较为复杂,通过面网格生成体网格能够获得更好的网格质量,网格类型为四面体网格。为了便于模拟轮胎与内支撑的接触,将轮胎用平铺在地面上的一层弹性体代替,采用六面体网格划分。在零压工况下分析时,需固定轮辋,可以通过固定内支撑内表面来代替固定轮辋的方式进行仿真。模型网格划分结果如图 9所示。
|
Download:
|
| 图 9 内支撑有限元网格模型 Fig. 9 Finite element grids of inserts supporting | |
内支撑材料的选取需要考虑很多因素,比如材料密度、强度极限、泊松比、成本以及维护性等。选取Q235、ZL114以及PU(聚氨酯)3种材料作为内支撑的候选材料。
根据HyperMesh软件分析要求,需要定义材料的弹性模量、泊松比和密度等主要性能参数,所选3种材料的主要性能参数见表 3。
| 表 3 内支撑材料主要参数 Table 3 Main parameters of inserts supporting materials |
为了更准确地模拟内支撑与轮胎的接触对分析结果的影响,需要定义轮胎材料。轮胎橡胶并没有采用超弹性材料,而是用泊松比较大的弹性材料进行替代[20]。该材料弹性模量为6 895 MPa,泊松比为0.49,密度为2.768×10-6 kg/mm3。
目前大多数研究在进行内支撑静力学分析时,将内支撑内表面进行固定约束,在内支撑10°包角范围内施加均布载荷[21]。考虑到内支撑在不同工况以及不同材料的情况下,内支撑与轮胎的包角是不等的,所以都对内支撑的10°包角范围内施加均布载荷的方式进行分析计算,得到的结果会产生一定偏差。组合式内支撑安全轮胎有限元模型采用固定内支撑内表面,同时对地面施加垂直向上的载荷的方式进行内支撑的仿真分析。
在零压工况下,轮辋可视作固定,对内支撑与轮辋接触的表面施加固定约束。内支撑与轮胎之间进行接触设置,接触类型选择TIE。在地面上施加反力,根据轮胎最大负荷能力,通过轮胎传递给内支撑的作用力为6 150 N,内支撑自身所受重力对比负荷来说可忽略不计,地面定义为刚性面。
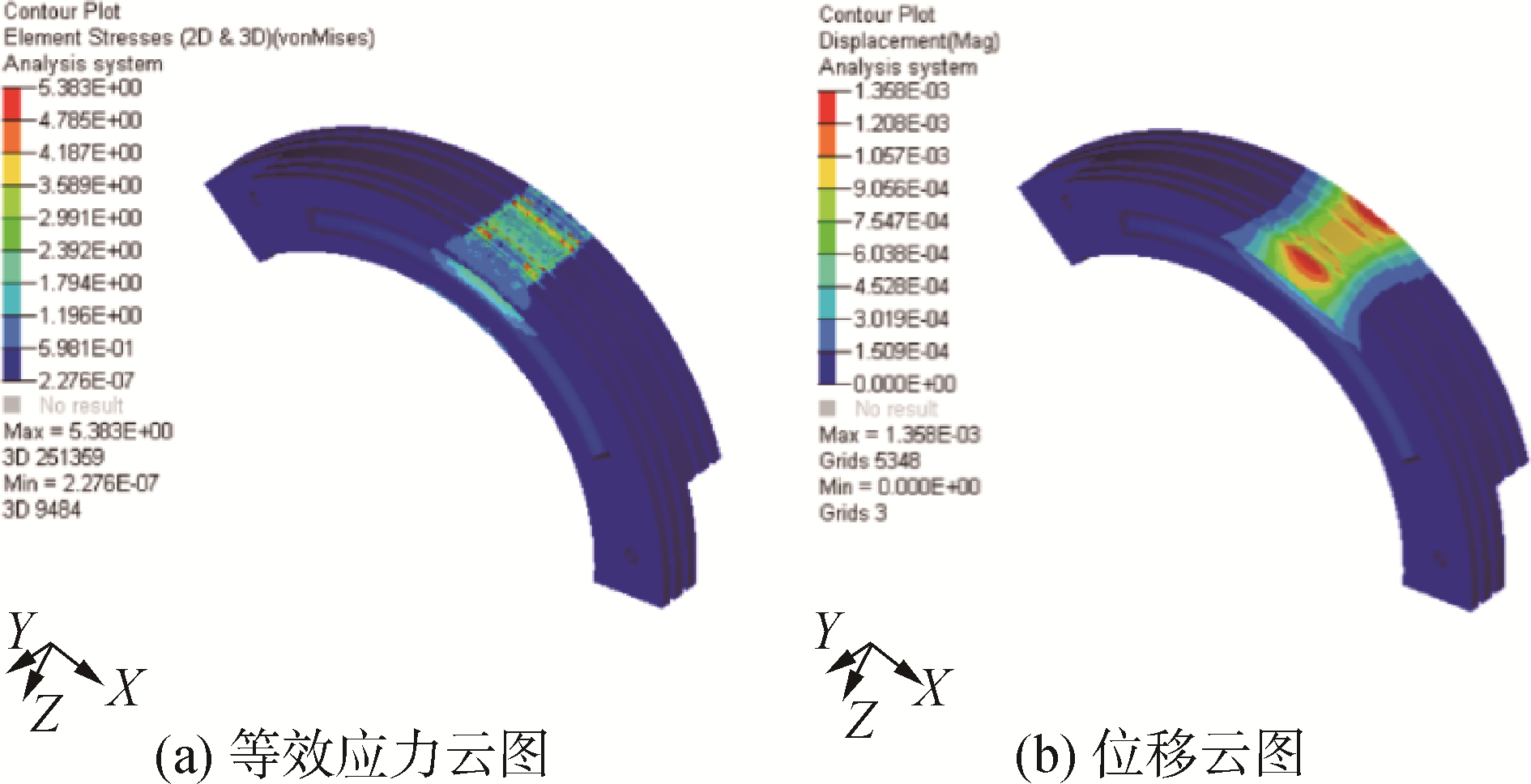
2.2 仿真结果与分析完成网格划分、材料属性赋予、约束和载荷施加等设置后,进行求解计算,得到3种不同材料的内支撑仿真结果。ZL114材料内支撑三维应力云图以及位移云图如图 10所示。
|
Download:
|
| 图 10 ZL114内支撑等效应力与位移云图 Fig. 10 Equivalent stress and displacement of ZL114 inserts supporting | |
从图 10可以看出,ZL114内支撑等效应力由接触区域中间向轴向两端递减,最大等效应力集中在接触区域中间两道散热槽处,最大等效应力为5.383 MPa;ZL114内支撑位移由接触区域中间向轴向两端递增,最大位移出现在接触区域轴向两端,最大位移为1.358×10-3 mm。
3种材料内支撑的最大等效应力及最大位移结果见表 4。
| 表 4 3种材料内支撑最大等效应力及最大位移 Table 4 Maximum equivalent stress and maximum displace-ment of inserts supporting with three materials |
根据3种不同材料内支撑的仿真分析结果,可以发现,3种材料内支撑按照最大等效应力从大到小顺序为Q235、ZL114、PU,按位移从大到小顺序为PU、ZL114、Q235。从3种材料内支撑的等效应力与位移分布规律来看,ZL114与Q235材料分布规律类似,等效应力由接触区域中间向轴向两端递减,位移由接触区域中间向轴向两端递增。PU材料内支撑等效应力分布规律为由接触区域中间向四周递增,位移分布规律为:在轴向上分布较为均匀,在轴向上由接触区域中间向周向递减。
为了能更加直观地判断内支撑与轮胎接触处材料是否发生永久变形,应用最大等效应力失效原理对可延展材料计算安全系数,即:
| $ S=[\delta] / \delta_{m} $ | (15) |
式中:S为安全系数;[δ]为材料最大许用应力,[δ]=δs/n,δs为材料屈服极限,n为屈服安全系数,取n=1.5;δm为最大等效应力。
根据式(15)可算出不同材料对应的安全系数,ZL114、Q235以及PU这3种材料安全系数分别为31、24、12。可以看出,这3种材料的安全系数均大于1,表明3种材料不会发生永久变形,都可作为内支撑材料。其中ZL114与Q235的抗变形能力好于PU。
内支撑作为车轮附加部件,其质量的大小对车轮转动惯量有所影响。为了减少内支撑对车轮转动惯量的影响,应选择质量较小的材料。通过计算单块内支撑的质量,Q235、ZL114以及PU这3种材料的内支撑质量分别为7.3、21.5、3.3 kg。从质量方面来看,ZL114以及PU这2种材料比Q235具有更大优势。
综合上述分析结果,从等效应力以及位移方面来看,ZL114以及Q235这2种材料较为理想;从安全系数方面来看,ZL114相比较来说最为优秀;从质量方面来看,PU以及ZL114这2种材料对比Q235来说有较大优势。所以综合比较这3种材料的各项性能,可以得出ZL114是较为理想的内支撑材料。
3 结论1) 组合式内支撑安全轮胎与标准轮辋装配,具有结构简单、拆卸方便、成本便宜等优点。组合式内支撑组件结构的主要设计参数由轮胎轮廓、轮胎变形以及装配的关系确定。
2) 由零压行驶工况下仿真分析可知,综合考虑内支撑受力和轻量化设计,Q235、PU和ZL114这3种材料中ZL114是较为理想的内支撑材料。
3) 为了获得性能更加优越的内支撑安全轮胎,应进一步研究内支撑材料以满足使用需求。此外,还可以对内支撑组件进行拓扑优化,在满足性能要求基础上减小内支撑质量。
| [1] |
赵又群, 付宏勋, 林棻, 等. 非充气车轮及其力学特性研究进展[J]. 江苏大学学报(自然科学版), 2016, 37(6): 621-627. ZHAO Youqun, FU Hongxun, LIN Fen, et al. Advancement of non-pneumatic wheels and mechanical characteristics[J]. Journal of Jiangsu University (natural science edition), 2016, 37(6): 621-627. (  0) 0)
|
| [2] |
庄继德. 现代汽车轮胎技术[M]. 北京: 北京理工大学出版社, 2001. ZHUANG Jide. Advanced technology of tire[M]. Beijing: Beijing Institute of Technology Press, 2001. (  0) 0)
|
| [3] |
臧利国, 赵又群, 李波, 等. 非充气机械弹性车轮接地特性试验研究[J]. 汽车工程, 2016, 38(3): 350-355. ZANG Liguo, ZHAO Youqun, LI Bo, et al. An experimental study on the ground contact characteristics of non-pneumatic mechanical elastic wheel[J]. Automotive engineering, 2016, 38(3): 350-355. (  0) 0)
|
| [4] |
杨欣. 安全轮胎设计理论与方法[M]. 北京: 清华大学出版社, 2015. YANG Xin. Design theory and method for run-flat tire[M]. Beijing: Tsinghua University Press, 2015. (  0) 0)
|
| [5] |
李波, 赵又群, 陈月乔, 等. 弹性车轮纵向力刷子模型分析[J]. 哈尔滨工程大学学报, 2015, 36(5): 662-665. LI Bo, ZHAO Youqun, CHEN Yueqiao, et al. Longitudinal force analysis for an elastic wheel based on the brush model[J]. Journal of Harbin Engineering University, 2015, 36(5): 662-665. (  0) 0)
|
| [6] |
臧利国, 赵又群, 李波, 等. 机械弹性车轮结构参数对牵引性能的影响[J]. 哈尔滨工程大学学报, 2014, 35(11): 1415-1421. ZANG Liguo, ZHAO Youqun, LI Bo, et al. Influence of mechanical elastic wheel configuration on traction performance[J]. Journal of Harbin Engineering University, 2014, 35(11): 1415-1421. (  0) 0)
|
| [7] |
解来卿, 高树新, 赵明, 等. 自封式安全轮胎与普通轮胎装车对比道路试验[J]. 汽车技术, 2008(8): 52-54. XIE Laiqing, GAO Shuxin, ZHAO Ming, et al. Road test comparison of self-sealing safety tire and ordinary tire[J]. Automobile technology, 2008(8): 52-54. (  0) 0)
|
| [8] |
黄京城, 王伟. 免充气轮胎与子午线轮胎的有限元分析对比[J]. 橡胶工业, 2016, 63(1): 31-35. HUANG Jingcheng, WANG Wei. Comparison of non-pneumatic tire and radial tire by finite element simulation[J]. China rubber Industry, 2016, 63(1): 31-35. (  0) 0)
|
| [9] |
RHYNE T B, CRON S M. Development of a non-pneumatic wheel[J]. Tire science and technology, 2006, 34(3): 150-169. DOI:10.2346/1.2345642 (  0) 0)
|
| [10] |
JU J, ANANTHASAYANAM B, SUMMERS J D, et al. Design of cellular shear bands of a non-pneumatic tire-investigation of contact pressure[J]. SAE international journal of passenger cars-mechanical systems, 2010, 3(1): 598-606. DOI:10.4271/2010-01-0768 (  0) 0)
|
| [11] |
ROBINETTE R D, FAY R J. Drag and steering effects from disablements of run flat tires. SAE Technical Paper 2000-01-1316[R]. New York: SAE, 2000.
(  0) 0)
|
| [12] |
杨欣, 许述财, 佟金, 等. 内支撑式RFT零压行走机理分析[J]. 清华大学学报(自然科学版), 2014, 54(7): 871-876. YANG Xin, XU Shucai, TONG Jin, et al. Runningmechanism of run-flat tire with inserts in zero pressure[J]. Journal of Tsinghua University (science & technology), 2014, 54(7): 871-876. (  0) 0)
|
| [13] |
BRAS B, COBERT A. Life-cycle environmental impact of michelin tweel? tire for passenger vehicles[J]. SAE international journal of passenger cars-mechanical systems, 2011, 4(1): 32-43. DOI:10.4271/2011-01-0093 (  0) 0)
|
| [14] |
CARDILE D, VIOLA N, CHIESA S, et al. Applied design methodology for lunar rover elastic wheel[J]. Acta Astronautica, 2012, 81(1): 1-11. DOI:10.1016/j.actaastro.2012.06.002 (  0) 0)
|
| [15] |
天津久荣车轮技术有限公司, 北京橡胶工业研究设计院, 山东玲珑轮胎股份有限公司. GB/T 3487-2015, 乘用车轮辋规格系列[S].北京: 中国标准出版社, 2016. Tianjin Jiurong Wheel Technology Co., Ltd., Beijing Research & Design Institute of Rubber Industry, Shandong Linglong Tyre Co., Ltd. GB/T 3487-2015, Rims for passenger car[S]. Beijing: Standards Press of China, 2016. (  0) 0)
|
| [16] |
薛梓晨, 贺建芸, 邓世涛, 等. 子午斜交轮胎力学性能有限元分析[J]. 轮胎工业, 2015, 35(3): 141-145. XUE Zichen, HE Jianyun, DENG Shitao, et al. Finite element analysis on mechanical properties of radial-bias tire[J]. Tire industry, 2015, 35(3): 141-145. (  0) 0)
|
| [17] |
俞淇, 丁剑平, 张安强, 等. 子午线轮胎结构设计与制造技术[M]. 北京: 化学工业出版社, 2006. YU Qi, DING Jianping, ZHANG Anqiang, et al. Radial tire structure design and manufacturing technology[M]. Beijing: Chemical Industry Press, 2006. (  0) 0)
|
| [18] |
三角轮胎股份有限公司, 广州市华南橡胶轮胎有限公司, 中策橡胶集团有限公司, 等. GB/T 2974-2014.轿车轮胎规格、尺寸、气压与负荷[S].北京: 中国标准出版社, 2015. Triangle Tire Co., Ltd., Guangzhou South China Rubber Tire Co., Ltd., Zhongce Rubber Co., Ltd. GB/T 2974-2014, Size designation, dimensions, inflation pressure and load capacity for passenger car tyres[S]. Beijing: Standards Press of China, 2015. (  0) 0)
|
| [19] |
詹特A N, 沃特J D.轮胎理论与技术[M].危银涛, 李勇, 冯希金, 等译.北京: 清华大学出版社, 2013. GENT A N, WALTER J D. The pneumatic tire[M]. WEI Yintao, LI Yong, FENG Xijin, et al trans. Beijing: Tsinghua University Press, 2013. (  0) 0)
|
| [20] |
杨守彬, 束长东, 束永平, 等. 带复杂花纹的轮胎有限元分析[J]. 华东理工大学学报(自然科学版), 2011, 37(5): 650-654. YANG Shoubin, SHU Changdong, SHU Yongping, et al. Finite element analysis of radial tire with complex tread pattern[J]. Journal of East China University of Science and Technology (natural science edition), 2011, 37(5): 650-654. (  0) 0)
|
| [21] |
程陆平. SUV轮胎内支撑系统设计与动力学分析[D].哈尔滨: 哈尔滨工程大学, 2014: 23-24. CHENG Luping. The design and dynamic analysis on internal support of the SUV tire[D]. Harbin: Harbin Engineering University, 2014: 23-24. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


