三维薄壁管件(简称管件)是工业生产中的重要零件,由于其壁厚较薄、长度较长,故管件的刚度很差,因此在薄壁长管与其他管件或法兰的装配过程中,当支撑位置和支撑角度选择不合理时,就会使管件在自身重力作用下产生较大的变形,进而改变其形状精度,使得管件与管件之间或管件与法兰之间接触处的中心线不重合,导致它们之间无法装配。因此,寻找管件的最佳支撑位置和支撑角度使其变形最小是很有必要、且很有实际意义的。
管件在不同支撑状态时,求取各点的挠度值大体上有2种方法:1)材料力学的相应公式;2)数值模拟方法。
由于三维管件的形状较为复杂,利用材料力学不能较为简便地推导计算出任意支撑点状态下的挠度计算模型;若用数值模拟结果(如ANSYS,ABAQUS等)寻找管件的最佳支撑位置,则由于商业有限元软件来分析管件变形是通过对实体模型进行一系列前处理后方能加载进行运算,且支撑位置或支撑方向及支撑位置的个数中某个参数的变化,都必须重新对其实体模型进行一系列的前处理,并进行仿真;变形最小的数据还必须将所有仿真结果进行比较后方能获得。上述过程凸显出计算量大和运算时间长的缺点,延长了求解最优支撑的时间。
本文提出一个既可以提高问题求解速度又能保证求解精度的方法,即基于粒子群优化算法(PSO)的三维薄壁空间管件支撑位置的优化方法。此方法首先利用有限元的思想把管件抽象分割成空间直线段,进而推导出任意管件的力学模型;之后利用建立的模型对管件进行变形量的计算,作为下一步优化方法的评价指标;最后采用PSO粒子群算法对管件的支撑位置进行优化。
1 空间管件数学模型的建立 1.1 三维管件轴线的提取在任意支撑位置的支撑状态下,管件截面的位置变动与其圆心的位置变动是一致的,而管件各点的挠度与其各点对应的轴线挠度也是一致的,故可通过计算管件轴线的挠度来代替管件的挠度,这样便可以大大简化模型。
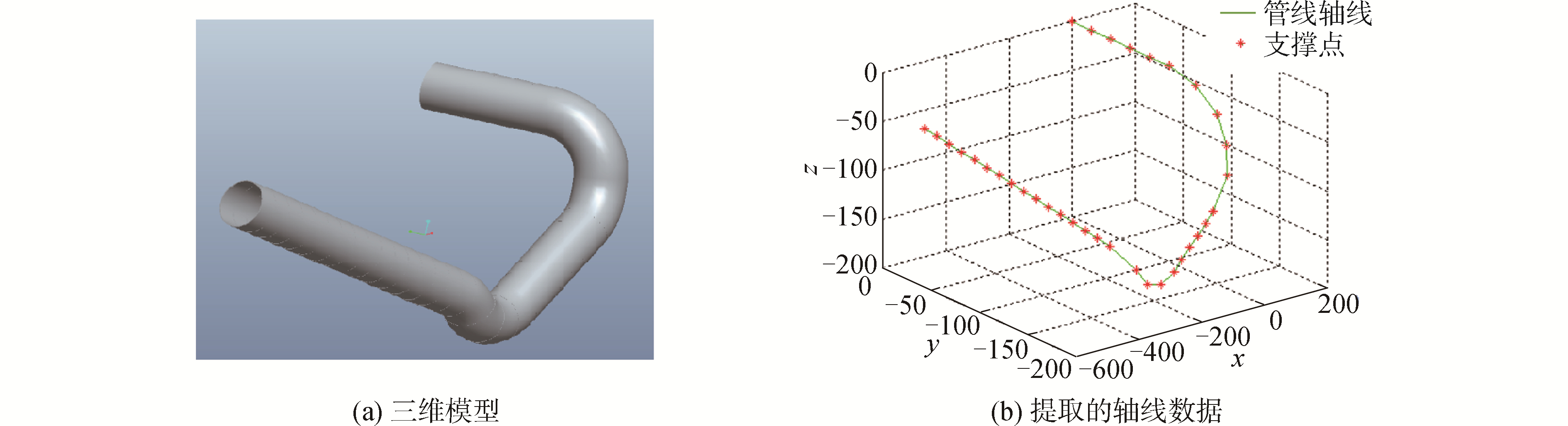
首先从管件三维模型中提取出管件的轴线特征,作为本文开发的有限元模型的基本数据[1]。例如某管件的三维模型如图 1(a)所示,提取的轴线数据如图 1(b)所示。
|
Download:
|
| 图 1 ProE二次开发提取的轴线与模型对比 Fig. 1 Comparison of the axis and model of the secondary development of ProE | |
由于本文所提出的方法必须满足任意形状的三维薄壁管件,因此无法用简便的力学公式计算其变形,故采用有限元的方式,将任意管件近似为一段段直管单元组成的空间折线管来推导其力学模型[2]。本节首先推导出单一直线单元的有限元刚度矩阵,在此基础上推导出任意空间管件模型,以便为获得不同支撑状态下管件的变形打下基础。
任意空间折线杆如图 2所示。

|
Download:
|
| 图 2 空间折线杆 Fig. 2 Space folding pole | |
在材料力学中,单元直杆的受力变形状态有轴向拉压变形、扭转变形、弯曲变形3种,见图 3。

|
Download:
|
| 图 3 单元杆受力变形情况 Fig. 3 Unit rod force deformation | |
在单元杆局部坐标系下,对于轴向拉压变形为:
| $ \gamma\left[\begin{array}{cc}{1} & {-1} \\ {-1} & {1}\end{array}\right]\left[\begin{array}{l}{u_{1}} \\ {u_{2}}\end{array}\right]=\left[\begin{array}{l}{f_{x 1}} \\ {f_{x 2}}\end{array}\right] $ | (1) |
式中:γ=EA/l;u1u2为2节点的位移;fx1、fx2为2节点的力。
对于扭转变形公式为:
| $ \delta\left[\begin{array}{cc}{1} & {-1} \\ {-1} & {1}\end{array}\right]\left[\begin{array}{c}{a_{x_{1}}} \\ {a_{x 2}}\end{array}\right]=\left[\begin{array}{c}{M_{x 1}} \\ {M_{x 2}}\end{array}\right] $ | (2) |
式中:δ=GJ/l;ax1、ax2为2节点的转角;Mx1、Mx2为2节点的力矩。
对于绕y轴弯曲变形公式为:
| $ \alpha \left[ {\begin{array}{*{20}{c}} {12}&{6l}&{ - 12}&{6l}\\ {6l}&{4{l^2}}&{ - 6l}&{2{l^2}}\\ { - 12}&{ - 6l}&{12}&{ - 6l}\\ {6l}&{2{l^2}}&{ - 6l}&{4{l^2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{V_1}}\\ {{v_{y1}}}\\ {{V_2}}\\ {{v_{y2}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{F_{y1}}}\\ {{M_{y1}}}\\ {{F_{y2}}}\\ {{M_{y2}}} \end{array}} \right] $ | (3) |
式中α=EIy/l3。
对于绕z轴弯曲变形公式为:
| $ \beta \left[ {\begin{array}{*{20}{c}} {12}&{ - 6l}&{ - 12}&{6l}\\ { - 6l}&{4{l^2}}&{6l}&{2{l^2}}\\ { - 12}&{6l}&{12}&{6l}\\ {6l}&{2{l^2}}&{6l}&{4{l^2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{W_1}}\\ {{v_{z1}}}\\ {{W_2}}\\ {{v_{z2}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{F_{z1}}}\\ {{M_{z1}}}\\ {{F_{z2}}}\\ {{M_{z2}}} \end{array}} \right] $ | (4) |
式中β=EIz/l3。
将上述各受力变形情况的材料力学刚度矩阵ki叠加成总的单元刚度矩阵k,且k关于对角线对称,则总的单元刚度矩阵k及单元杆力学公式为:
| $ \mathit{\boldsymbol{k}} \times \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{f}} $ | (5) |
其中:
| $ \mathit{\boldsymbol{k}} = \left[ {\begin{array}{*{20}{c}} \gamma &0&0&0&0&0&{ - \gamma }&0&0&0&0&0\\ {}&{12\alpha }&0&0&0&{6l\alpha }&0&{ - 12\alpha }&0&0&0&{6l\alpha }\\ {}&{}&{12\beta }&0&{ - 6l\beta }&0&0&0&{ - 12\beta }&0&{ - 6l\beta }&0\\ {}&{}&{}&\delta &0&0&0&0&0&{ - \delta }&0&0\\ {}&{}&{}&{}&{4{l^2}\beta }&0&0&0&{6l\beta }&0&{2{l^2}\beta }&0\\ {}&{}&{}&{}&{}&{4{l^2}\alpha }&0&{ - 6l\alpha }&0&0&0&{2{l^2}\alpha }\\ {}&{}&{}&{}&{}&{}&\gamma &0&0&0&0&0\\ {}&{}&{}&{}&{}&{}&{}&{12\alpha }&0&0&0&{ - 6l\alpha }\\ {}&{}&{}&{}&{}&{}&{}&{}&{12\beta }&0&{6l\beta }&0\\ {}&{}&{}&{}&{}&{}&{}&{}&{}&\delta &0&0\\ {}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{4{l^2}\beta }&0\\ {}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{4{l^2}\alpha } \end{array}} \right] $ |
| $ \mathit{\boldsymbol{d}} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{{u}}_1}}&{{\mathit{{V}}_1}}&{{\mathit{{W}}_1}}&{{a_{x1}}}&{{v_{y1}}}&{{v_{z1}}}&{{\mathit{{u}}_2}}&{{\mathit{{W}}_2}}&{{\mathit{{W}}_2}}&{{a_{x2}}}&{{v_{y2}}} \end{array}\;\;\;{v_{z2}}} \right]^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{f}} = {\left[ {\begin{array}{*{20}{c}} {{f_{x1}}}&{{F_{y1}}}&{{F_{z1}}}&{{M_{x1}}}&{{M_{y1}}}&{{M_{z1}}}&{{f_{x2}}}&{{F_{y2}}}&{{F_{z2}}}&{{M_{x2}}}&{{M_{y2}}}&{{M_{z2}}} \end{array}} \right]^{\rm{T}}} $ |
进一步整理单元刚度矩阵k得到:
| $ \mathit{\boldsymbol{k}} = \left[ {\begin{array}{*{20}{c}} {{h_1}}&0&0&0&0&0&{ - {h_1}}&0&0&0&0&0\\ {}&{{h_2}}&0&0&0&{{h_3}}&0&{ - {h_2}}&0&0&0&{{h_7}}\\ {}&{}&{{h_3}}&0&{ - {h_5}}&0&0&0&{ - {h_3}}&0&{ - {h_5}}&0\\ {}&{}&{}&{{h_4}}&0&0&0&0&0&{{h_4}}&0&0\\ {}&{}&{}&{}&{{h_6}}&0&0&0&{{h_1}}&0&{{h_9}}&0\\ {}&{}&{}&{}&{}&{{h_8}}&0&{{h_1}}&0&0&0&{{h_{10}}}\\ {}&{}&{}&{}&{}&{}&{{h_1}}&0&0&0&0&0\\ {}&{}&{}&{}&{}&{}&{}&{{h_2}}&0&0&0&{{h_7}}\\ {}&{}&{}&{}&{}&{}&{}&{}&{{h_3}}&0&{ - {h_5}}&0\\ {}&{}&{}&{}&{}&{}&{}&{}&{}&{{h_4}}&0&0\\ {}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{{h_6}}&0\\ {}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{{h_8}} \end{array}} \right] $ | (6) |
式(1)~(6)中参数含义为:E为材料的杨氏模量;G为材料剪切模量;A为管件截面面积;l为单元杆长度;b为刚度修正系数。
1.3 空间管件力学模型建立在实际情况中,单元杆会与总体坐标系下各个坐标轴有一定的角度。任意直管单元在总体坐标系下的受力情况如图 4所示。

|
Download:
|
| 图 4 空间单元杆受力变形情况 Fig. 4 Space unit rod force deformation situation | |
根据总体坐标系XYZ与局部坐标系xyz间的空间位置关系可得到坐标系XYZ下的力矢量F0与坐标系xyz下的力矢量f0间的关系为:
| $ \boldsymbol{F}_{0}=\lambda \boldsymbol{f}_{0} $ | (7) |
式中:
| $ \boldsymbol{\lambda}=\left[\begin{array}{ccc}{\cos \langle x, X\rangle} & {\cos \langle y, X\rangle} & {\cos \langle z, X\rangle} \\ {\cos \langle x, Y\rangle} & {\cos \langle y, Y\rangle} & {\cos \langle z, Y\rangle} \\ {\cos \langle x, Z\rangle} & {\cos \langle y, Z\rangle} & {\cos \langle z, Z\rangle}\end{array}\right] $ |
扩展得到总体坐标系下变形量和受力D, F与直杆单元坐标系下变形量和受力d,f的关系为:
| $ \boldsymbol{d}=\boldsymbol{R}^{\mathrm{T}} \boldsymbol{D} $ | (8) |
| $ \mathit{\boldsymbol{f}} = {\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{F}} $ | (9) |
总体坐标系下的刚度矩阵为:
| $ \boldsymbol{K}=\boldsymbol{R} \boldsymbol{k} \boldsymbol{R}^{\mathrm{T}} $ | (10) |
式中:
设总体坐标系下的单元杆负载向量为:
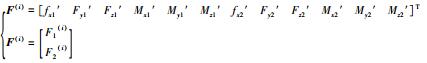
|
(11) |
在非支撑点的节点处,直管单元只受重力产生的均布载荷q。因而非支撑点处的载荷为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{F}}_1^{\left( i \right)} = {\left[ {\begin{array}{*{20}{c}} 0&0&{\frac{1}{2}{q_i}{l_i}}&0&0&{\frac{1}{{12}}{q_i}l_i^2} \end{array}} \right]^{\rm{T}}}\\ \mathit{\boldsymbol{F}}_2^{\left( i \right)} = {\left[ {\begin{array}{*{20}{c}} 0&0&{\frac{1}{2}{q_i}{l_i}}&0&0&{ - \frac{1}{{12}}{q_i}l_i^2} \end{array}} \right]^{\rm{T}}} \end{array} \right. $ | (12) |
当管件由n个直管单元组成时,管件在总坐标系XYZ下的总刚度矩阵Kt如式(13)。
将弯杆支撑近似为刚性约束,即各支撑点在各方向变形量均为零。因此,在计算时将各支撑点的变形矢量d置为零向量[3]。
总体坐标系下总载荷向量为:
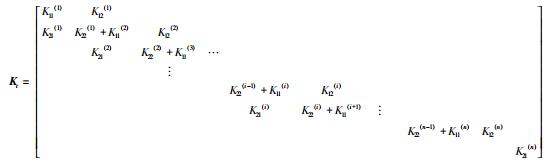
|
(13) |
| $ {\mathit{\boldsymbol{F}}_{{\rm{total}}}} = \left[ {\begin{array}{*{20}{c}} {F_1^{\left( 1 \right)}}\\ {F_2^{\left( 1 \right)} + F_1^{\left( 2 \right)}}\\ {F_2^{\left( 2 \right)} + F_1^{\left( 3 \right)}}\\ \vdots \\ {F_2^{\left( {i - 2} \right)} + F_1^{\left( {i - 1} \right)}}\\ {F_2^{i - 1} + F_1^{\left( i \right)}}\\ {F_2^{\left( i \right)} + F_1^{\left( {i + 1} \right)}}\\ \vdots \\ {F_2^{\left( {n - 2} \right)} + F_1^{\left( {n - 1} \right)}}\\ {F_2^{\left( {n - 1} \right)} + F_1^{\left( n \right)}}\\ {F_2^{\left( n \right)}} \end{array}} \right] $ | (14) |
式(13)、(14)即为所求解的最终模型,只需导入轴线点的信息以及支撑点信息即可通过刚度矩阵求解出各个点的变形量。
1.4 有限元模型的精度仿真验证为了验证利用本文所建立的弯管有限元模型计算三维管件变形的准确性,用ANSYS软件对同一管件、同一种支撑位置时的变形量进行仿真,采用相同的前处理进行设置,与本文所建立有限元模型的计算结果进行对比。以图 1(a)中的管件模型为研究对象,在本文建立的有限元模型中将管件分为35段进行分析,管件节点位置及旋转角度示意图如图 5所示,材料参数如表 2,单元杆参数如表 3。

|
Download:
|
| 图 5 管件节点位置及旋转方向示意 Fig. 5 Tube node location and direction of rotation diagram | |
| 表 2 空间管件的材料属性 Table 2 Material attribution of space poles |
| 表 3 单元杆参数表 Table 3 Unit bar parameters |
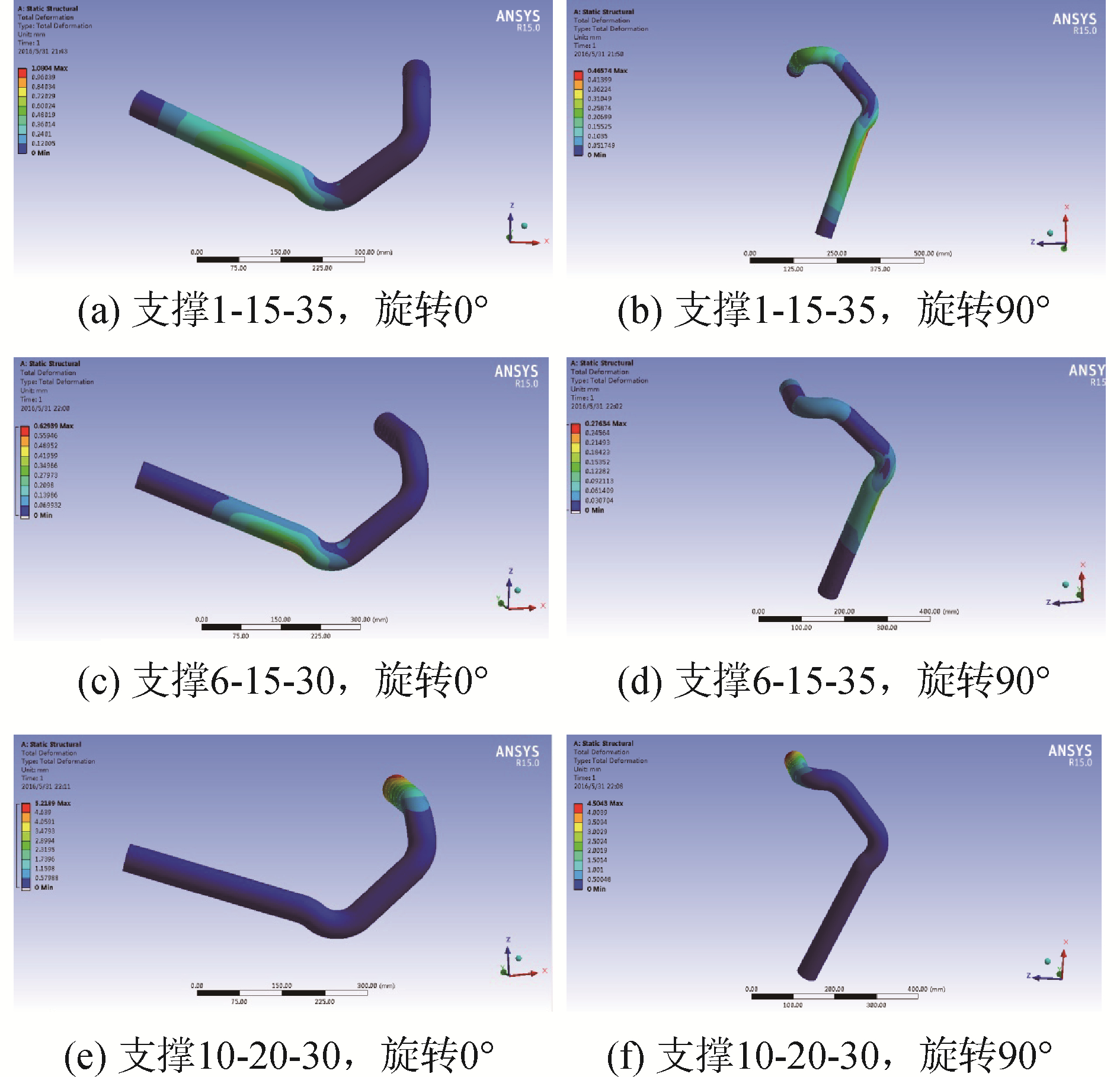
按照表 2设置材料参数,分别选取3种支撑条件下的2个角度,共6种情况, 在ANSYS中对管件进行模拟分析。仿真结果和仿真得到的最大变形量如图 6所示。
|
Download:
|
| 图 6 ANSYS管件变形量分析结果 Fig. 6 ANSYS pipe deformation analysis results | |
将各支撑情况下,ANSYS分析得到的管件的最大变形量与本文所建立的有限元模型计算结果进行对比,如表 4。可以看出,对用于验证的6种支撑情况,本文有限元模型计算出的管件最大变形量与ANSYS分析得到的最大变形量的平均偏差为0.07 mm,最大偏差为0.13 mm。
| 表 4 有限元结果与ANSYS仿真结果对比 Table 4 Comparison of finite element results with ANSYS simulation results |
为了实现三维管件支撑位姿的优选,首先,通过相应的二次开发技术从所给的三维模型中提取出管件轴线,作为PSO算法的原始数据;将本文2中所建立的模型计算出的最大变形量作为评价函数,计算每个可能为最优的支撑位置下的管件变形量;最后运行PSO粒子群算法,优选管件支撑位置。
2.1 粒子群优化算法基本原理PSO粒子群算法是一种模拟鸟类觅食的多目标优化算法。每个可能解都被看做为一个粒子,群体所有粒子信息共享。在本文中,弯管的每一种支撑位姿都可以看作一个粒子,包含弯管的支撑位置和弯管的旋转角度。所有粒子都有一个由适应函数fitness()决定的适应度,在本文中适应度是指每种弯管支撑位置组合下的弯管最大变形量。PSO算法首先初始化一群随机粒子,所有粒子组成一个群体,再通过迭代更新每个粒子的速度和位置。粒子个体自身找到的最优解,称为个体最优pbest,这可以看做粒子自身的经验。整个群体到目前为止找到的最优解,称为群体最优gbest,这可以看做粒子群体的经验。在每一次更新中,粒子通过跟踪个体最优pbest和群体最优gbest来更新自己的状态[4-8]。
对于第k次迭代,PSO中的第i个粒子是按照式(14)的方式更新的:
| $ \begin{array}{*{20}{c}} {v_i^{k + 1} = w \times v_i^k + {c_1} \times {\rm{rand}}\left( {\;\;} \right) \times \left( {{p_{{\rm{best}}}}_i^k - x_i^k} \right) + {c_2} \times }\\ {{\rm{rand}}\left( {\;\;} \right) \times \left( {{p_{{\rm{best}}}}^k - x_i^k} \right)x_i^{k + 1} = x_i^k + v_i^{k + 1}} \end{array} $ | (14) |
式中:i=1, 2, …, M,M为粒子群中粒子的总数;vik是粒子i第k-1次迭代的飞行速度矢量;xik是粒子i第k-1次迭代后的位置;pbestik是第k-1次迭代后,粒子i历史上最优位置;gbestk是第k-1次迭代后,所有子中的最优位置;c1, c2为权重因子;rand()为0~1内的随机数,w为惯性权重。
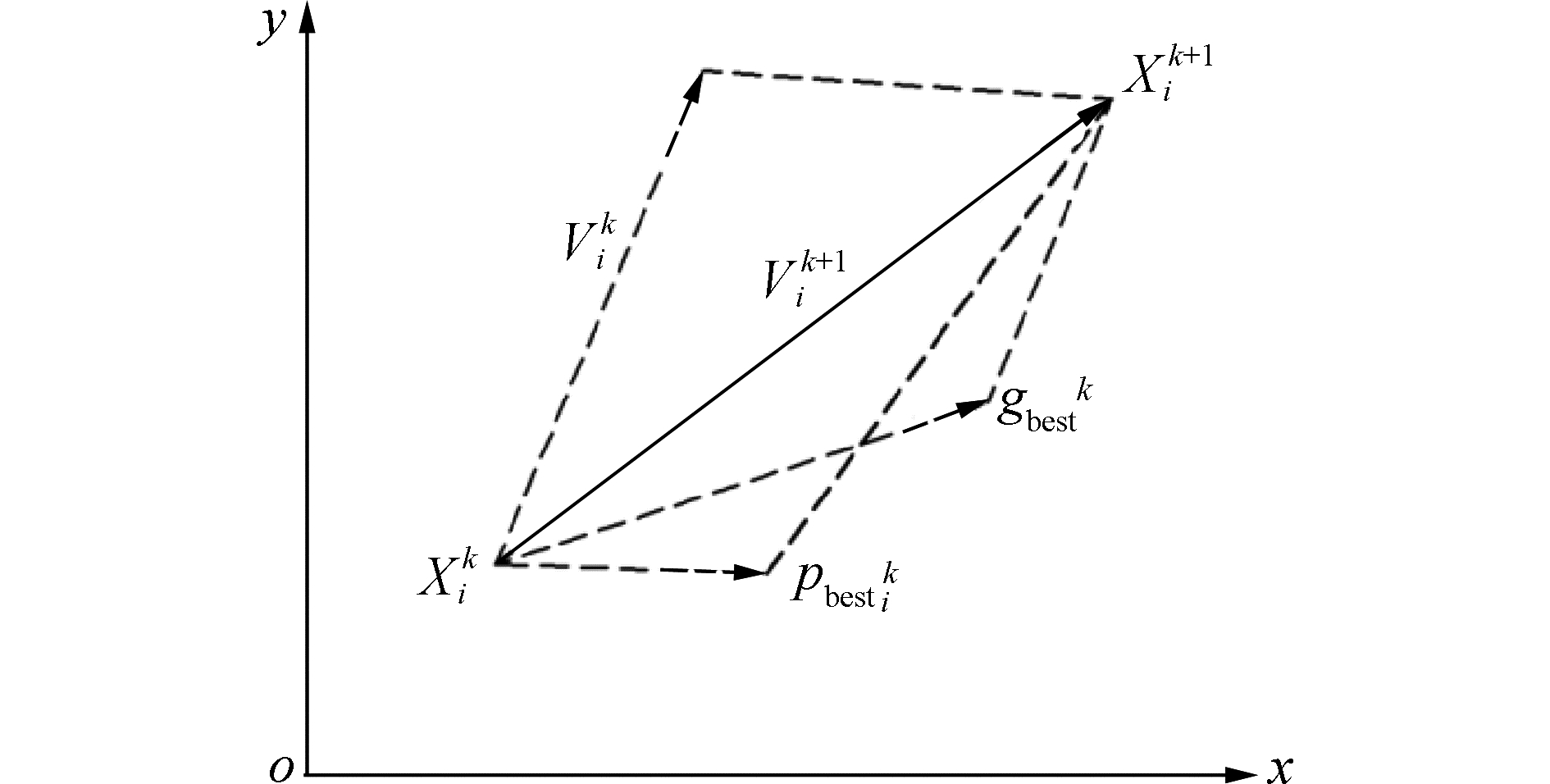
粒子速度vik+1的更新主要由3部分组成,分别为粒子i上次迭代的速度vik;粒子i当前位置与个体最优pbestik间的距离;粒子i当前位置与群体最优gbestk间的距离,如图 7所示。
|
Download:
|
| 图 7 粒子移动原理 Fig. 7 Particle movement schematic | |

|
Download:
|
| 图 8 粒子群优化算法流程 Fig. 8 Flow chart of PSO algorithm | |
本文以某一实际工程为例,以较为复杂的3个支撑来验证本文提出的整套基于粒子群优化算法(PSO)的三维薄壁空间管件支撑位置的优化方法的准确性和快速性。由于与管件一端连接的法兰轴线要保持水平,即整个管件可绕该法兰轴线360°旋转,因此可把管件的一个支撑位置看作粒子群中的一个粒子为:
| $ \boldsymbol{X}_{i}=\left[\begin{array}{llll}{n_{1}} & {n_{2}} & {n_{3}} & {a}\end{array}\right] $ | (15) |
式中:Xi表示第i个粒子; ni表示第i个支撑选取的位置; a表示管件的旋转角度。
本文粒子数取10,迭代上限50次。PSO算法最大变形量迭代过程如图 9。

|
Download:
|
| 图 9 PSO迭代曲线 Fig. 9 PSO iteration curve | |
从图 9中可以看出,迭代次数到达30次左右时,总变形量便不再减小,此时支撑位置参数已经收敛。得到的最优粒为(8,15,30,60),即选择8、15、30节点作为支撑点,旋转60°为最优支撑位姿。最优支撑位姿下的管件变形情况如图 10。变形量在z-x-y方向的分量沿管件轴线变化曲线分别如图 11所示。

|
Download:
|
| 图 10 PSO粒子群算法得到的最优支撑位置 Fig. 10 PSO to get the best support position | |

|
Download:
|
| 图 11 最优支撑位置在z-x-y方向的分量沿管件轴线变化曲线 Fig. 11 The component of the optimal support position in the z-x-y direction varies along the axis of the pipe | |
1) 文中所建立的空间管件有限元模型可应用于任意形状的管件;
2) 通过对比,本模型所得到的计算结果与ANSYS软件仿真的结果吻合的很好,误差在10%以内;
3) 有限元模型结合粒子群算法使寻找最优支撑位置的时间大大缩短,迭代30次以内即可找到最优支撑位置,计算时间上计算300次数学模型的时间少于商业软件计算1次的时间。
| [1] |
黄轶. PROE二次开发技术在装配干涉检查中的应用[J]. 山东工业技术, 2015(24): 216. HUANG Yi. Application of PROE secondary development technology in assembly interference inspection[J]. Shandong industrial technology, 2015(24): 216. (  0) 0)
|
| [2] |
许汉铮, 黄平明, 王宏博. 连续弯梁(刚构)桥的统一计算模式[J]. 中国公路学报, 2002, 15(4): 57-61. XU Hanzheng, HUANG Pingming, WANG Hongbo. Unified model for continuous curved girder bridges[J]. China journal of highway and transport, 2002, 15(4): 57-61. DOI:10.3321/j.issn:1001-7372.2002.04.016 (  0) 0)
|
| [3] |
侯丰, 陈亚军, 刘恩龙. 结构性土二元介质模型的有限元模拟[J]. 四川大学学报(工程科学版), 2016, 48(S1): 80-86, 93. HOU Feng, CHEN Yajun, LIU Enlong. FEM simulation of binary medium model for structured soils[J]. Journal of Sichuan University (engineering science edition), 2016, 48(S1): 80-86, 93. (  0) 0)
|
| [4] |
张海鹏, 韩端锋, 郭春雨. 改进PSO训练的BPNN方法的舰船主尺度建模[J]. 哈尔滨工程大学学报, 2012, 33(7): 806-810. ZHANG Haipeng, HAN Duanfeng, GUO Chunyu. Modeling of the principal dimensions of large vessels based on a BPNN trained by an improved PSO[J]. Journal of Harbin Engineering University, 2012, 33(7): 806-810. DOI:10.3969/j.issn.1006-7043.201108006 (  0) 0)
|
| [5] |
秦洪德, 石丽丽. PSO算法在油船双底结构优化设计中的应用研究[J]. 哈尔滨工程大学学报, 2010, 31(8): 1007-1011. QIN Hongde, SHI Lili. Optimizing the design of the double bottom structure of an oil tanker using a particle swarm optimization algorithm[J]. Journal of Harbin Engineering University, 2010, 31(8): 1007-1011. DOI:10.3969/j.issn.1006-7043.2010.08.003 (  0) 0)
|
| [6] |
张楠, 南敬昌, 高明明. 基于分组混沌PSO算法的模糊神经网络建模研究[J]. 计算机工程与应用, 2017, 53(9): 31-37. ZHANG Nan, NAN Jingchang, GAO Mingming. Fuzzy neural network for amplifier power modeling based on grouping parallel-chaotic particle swarm optimization[J]. Computer engineering and applications, 2017, 53(9): 31-37. (  0) 0)
|
| [7] |
马廉洁, 陈杰, 巩亚东, 等. 基于PSO算法改进BP神经网络的氟金云母点磨削工艺参数优化[J]. 中国机械工程, 2016, 27(6): 761-766. MA Lianjie, CHEN Jie, GONG Yadong, et al. Process parameter optimization based on PSO-BP neural network in point grinding fluorophlogopite[J]. China mechanical engineering, 2016, 27(6): 761-766. DOI:10.3969/j.issn.1004-132X.2016.06.010 (  0) 0)
|
| [8] |
宫华, 袁田, 张彪. 基于深度邻域搜索PSO算法的装配序列优化问题[J]. 控制与决策, 2016, 31(7): 1291-1295. GONG Hua, YUAN Tian, ZHANG Biao. Assembly sequence planning problem based on particle swarm optimization algorithm with depth local search[J]. Control and decision, 2016, 31(7): 1291-1295. (  0) 0)
|
| [9] |
陶泽南, 张丽杰. 基于粒子群算法的机械优化设计[J]. 军事交通学院学报, 2018, 20(10): 81-85. TAo Zenan, ZHANG Lijie. Mechanical optimization design based on particle swarm algorithm[J]. Journal of Military Transportation University, 2018, 20(10): 81-85. (  0) 0)
|
| [10] |
任志玲, 杨永伟, 孙雪飞. 基于PSO与模糊PI控制结合的最大风能捕获研究[J]. 计算机应用与软件, 2018, 35(11): 148-152, 167. REN Zhiling, YANG Yongwei, SUN Xuefei. Maximum wind energy capture based on PSO and fuzzy PI control[J]. Computer applications and software, 2018, 35(11): 148-152, 167. (  0) 0)
|
| [11] |
李烨, 郭子立, 郭奕杉. 基于PSO的轨道交通列车节能控制优化研究[J]. 控制工程, 2018, 25(10): 1911-1915. LI Ye, GUO Zili, GUO Yishan. Study on energy-saving control optimization for rail transit train based on PSO[J]. Control engineering of China, 2018, 25(10): 1911-1915. (  0) 0)
|
| [12] |
李磊, 张纯, 宋固全. 基于改进粒子群优化粒子滤波的结构损伤识别[J]. 应用力学学报, 2018, 35(5): 925-932, 1177. LI Lei, ZHANG Chun, SONG Guquan. An improved particle swarm optimized particle filter for structural damage identification[J]. Chinese journal of applied mechanics, 2018, 35(5): 925-932, 1177. (  0) 0)
|
| [13] |
陈建桥, 郭细伟, 葛锐.基于ANSYS-PSO方法的复合材料压力容器可靠性优化设计[C]//中国力学学会学术大会'2009论文摘要集.郑州: 中国力学学会, 2009: 1. CHEN Jianqiao, GUO Xiwei, GE Rui. Reliability optimization design of composite pressure vessels based on ANSYS-PSO method[C]//Chinese Society of Mechanics Academic Conference'2009 Abstracts Collection. Zhengzhou: Chinese Mechanics Learning, 2009: 1. (  0) 0)
|
| [14] |
朱剑宝, 张卫波. 基于PSO算法和ANSYS的变截面板簧优化仿真设计[J]. 福建工程学院学报, 2008, 6(S1): 74-78. ZHU Jianbao, ZHANG Weibo. Optimized simulation design of taper leaf spring based on particle swarm optimization algorithms and ANSYS[J]. Journal of Fujian University of Technology, 2008, 6(S1): 74-78. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


