2. 包头职业技术学院, 内蒙古 包头 014030
2. Baotou Vocational & Technical College, Baotou 014030, China
C80E型通用敞车是我国铁路货车第4次升级换代的代表车型,该车于2014年批量生产5 000辆在大秦线投入运用,经过2 a的运行考验后,在车体分解检查时发现部分车体在大横梁上盖板与地板焊缝连接处出现了疲劳裂纹,并结合现场调研可知,在该焊缝连接处出现裂纹的车辆颇多,属于批量性裂纹,说明产生裂纹的根本原因为车体局部结构设计不合理。目前我国对铁路货车车体的焊接接头疲劳强度评估主要参照北美铁路协会的AAR标准、国际焊接学会的IIW标准,以及英国的BS标准[1-3]。在对C80E型敞车的车体设计合理性验证时,分别参照以上标准对该焊缝进行了疲劳寿命评估,计算结果均符合625万km的寿命要求,但实际仅运用40万km已出现批量性疲劳裂纹,二者相差甚大。目前,对焊接结构件疲劳强度评估主要从产品的设计、工艺、制造、材料等方面进行评定,并通过相关试验进行验证[4-8]。车体静强度仿真提取的结点应力是疲劳寿命评估的输入,应力提取的精度直接影响疲劳强度评估的准确性。C80E型敞车车体疲劳寿命仿真结果与实际运用情况相差甚远,说明出现该现象的根本原因不是疲劳评定方法准确性的问题,而是对车体疲劳强度评估时在焊缝连接处提取的应力精度较差。
铁路货车车体属于薄板结构,在有限元分析时一般采用板壳单元对整车模型进行结构离散,后处理时为了克服结点上应力不连续的缺点,常采用结点周围几个单元的应力平均值作为结点应力,文献[9]指出在材料不同或厚度突变时不能以单元应力平均值作为结点应力,而焊缝连接处的板厚往往是突变的,但在有限元仿真计算的后处理分析过程中往往忽略了这一点。本文针对C80E型通用敞车车体疲劳寿命仿真结果与实际使用寿命相差较大的问题,提出了一种基于均方差加权应力修匀的疲劳损伤评估方法。根据1/4车体模型进行了静强度仿真结果,对比分析了网格大小对结点应力精度的影响,并对关键结点进行了均方差应力修匀;结合车体大横梁焊缝裂纹统计分析结果,提取大横梁焊缝在内补强座周围的结点应力最大值、均值、修匀值,计算了3种情况下各结点的应力损伤,并与实测损伤进行了对比分析。
1 基于均方差加权的应力修匀方法车体静强度仿真分析是对结构设计合理性的初始验证,同时也是模态、屈曲、疲劳等仿真分析的基础,因此提高静强度仿真结果应力解的精度,尤其是结点应力的精度具有较强的工程意义。目前改善有限元应力解的研究主要集中在2个方面:一方面为网格划分技术[10-11],目前的有限元分析软件均提供了较为全面的网格划分技术,选用合适的网格大小与单元类型基本可满足车体有限元仿真的要求,因此本文对网格划分技术不进行深入分析研究;另一方面为应力修匀技术[12-14],沿着单元边界的位移是连续的,但位移的导数往往是不连续的,所以在单元边界上的应力也是不连续的[9],而工程实际应用中通常感兴趣的是边缘和结点上的应力,因此需对结点应力进行修匀,但不同的应力修匀方法对修匀后的结点应力精度影响较大。本文根据围绕结点的单元应力离散性的特点,提出了基于均方差加权的应力修匀方法。
1.1 单元的最佳应力点弹性力学有限元的求解方程是通过最小势能原理建立的,近似解的位移u、应变ε、应力σ分别为:
| $ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{u}}^*} + \delta {\mathit{\boldsymbol{u}}^*}, \mathit{\boldsymbol{\varepsilon }} = {\mathit{\boldsymbol{\varepsilon }}^*} + \delta {\mathit{\boldsymbol{\varepsilon }}^*}, \mathit{\boldsymbol{\sigma }} = {\mathit{\boldsymbol{\sigma }}^*} + \delta {\mathit{\boldsymbol{\sigma }}^*} $ | (1) |
式中:u*、ε*、σ*分别为位移、应变、应力的精确解。
与近似解相对应的总势能为:
| $ \Pi (\mathit{\boldsymbol{u}}) = \frac{1}{2}\int\limits_V {{\mathit{\boldsymbol{\varepsilon }}^{\rm{T}}}} \mathit{\boldsymbol{\sigma }}{\rm{d}}v - \int\limits_V {{\mathit{\boldsymbol{u}}^{\rm{T}}}} f{\rm{d}}v - \int\limits_{{S_\sigma }} {{\mathit{\boldsymbol{u}}^{\rm{T}}}\bar f} {\rm{d}}s $ | (2) |
将式(1)代入式(2),并经整理后可得:
| $ \begin{array}{l} \prod {(\mathit{\boldsymbol{u}})} = \frac{1}{2}{\int\limits_V {\left( {{\mathit{\boldsymbol{\varepsilon }}^*}} \right)} ^{\rm{T}}}{\mathit{\boldsymbol{\sigma }}^*}{\rm{d}}v - \int\limits_V {{{\left( {{\mathit{\boldsymbol{u}}^*}} \right)}^{\rm{T}}}} f{\rm{d}}v - \\ \qquad\int\limits_{{S_\sigma }} {{{\left( {{\mathit{\boldsymbol{u}}^*}} \right)}^{\rm{T}}}} \bar f{\rm{d}}s + {\int\limits_V {\left( {{\mathit{\boldsymbol{\varepsilon }}^*}} \right)} ^{\rm{T}}}\delta {\sigma ^*}{\rm{d}}v - {\int\limits_V {\left( {\delta {\mathit{\boldsymbol{u}}^*}} \right)} ^{\rm{T}}}f{\rm{d}}v - \\ \qquad\int\limits_{{S_\sigma }} {{{\left( {\delta {\mathit{\boldsymbol{u}}^*}} \right)}^{\rm{T}}}} \bar f{\rm{d}}s + \frac{1}{2}{\int\limits_V {\left( {\delta {\mathit{\boldsymbol{\varepsilon }}^*}} \right)} ^{\rm{T}}}\delta {\sigma ^*}\mathit{\boldsymbol{d}}v = \\ \qquad\prod {\left( {{\mathit{\boldsymbol{u}}^*}} \right)} + \delta \prod {\left( {{\mathit{\boldsymbol{u}}^*}} \right)} + {\chi } \end{array} $ | (3) |
其中:
| $ \chi = \frac{1}{2}{\int\limits_V {\left( {\delta {\mathit{\boldsymbol{\varepsilon }}^*}} \right)} ^{\rm{T}}}\delta {\sigma ^*}{\rm{d}}v = \frac{1}{2}\int\limits_V {{{\left( {\mathit{\boldsymbol{\sigma }} - {\mathit{\boldsymbol{\sigma }}^*}} \right)}^{\rm{T}}}} \left( {\mathit{\boldsymbol{\varepsilon }} - {\mathit{\boldsymbol{\varepsilon }}^*}} \right){\rm{d}}v $ |
由于精确解对应的总势能的变分为0,即δ∏(u*)=0,则求式(3)的极小值可转换为求χ的极小值,即:
| $ \delta \chi = \int\limits_V {{{\left( {\mathit{\boldsymbol{\sigma }} - {\mathit{\boldsymbol{\sigma }}^*}} \right)}^{\rm{T}}}} \delta \varepsilon {\rm{d}}v = 0 $ | (4) |
将式(4)离散后,可得:
| $ \begin{array}{l} \delta \chi = \sum\limits_e {\int\limits_{Ve} {{{\left( {\mathit{\boldsymbol{\sigma }} - {\mathit{\boldsymbol{\sigma }}^*}} \right)}^{\rm{T}}}} } \delta \varepsilon {\rm{d}}v = \\ \qquad \sum\limits_e {\sum\limits_{i = 1}^p {{H_i}} } {\left( {\mathit{\boldsymbol{\sigma }} - {\mathit{\boldsymbol{\sigma }}^*}} \right)^{\rm{T}}}\delta {\varepsilon _i}|J| = 0 \end{array} $ | (5) |
式中
假如精确解σ*是p次多项式,则在p阶高斯积分点上,近似解应力σ在积分点上具有比本身高一次的精度,称这些积分点为单元的最佳应力点。
1.2 加权应力修匀方法应力修匀技术可以克服边缘和结点上应力不连续的缺点,目前比较常用应力修匀方法为加权应力修匀,其通用表达式为:
| $ {\sigma}_{j}=\sum\limits_{i=1}^{n} w_{i} {\sigma}_{j}^{i} / \sum\limits_{i=1}^{n} w_{i} $ | (6) |
式中:j为结点编号;i为围绕结点j的单元序号;n为围绕结点j的单元总数;wi为单元i的应力加权因子;σj为结点j修匀后的应力;σji为在结点j周围的单元i的单元应力。目前常用的加权方法具体形式主要有以下几种[15]:
1) 单元应力平均法。
当wi=1时,式(6)可简化为:
| $ {\sigma}_{j}=\sum\limits_{i=1}^{n} {\sigma}_{j}^{i} / n $ | (7) |
式(7)为单元应力平均法,即将围绕结点j周围的相关单元i的应力值进行平均,也是目前在有限元分析中比较常用的方法。
2) 面积加权平均法。
当wi=Si时,式(6)可转化为:
| $ {\sigma}_{j}=\sum\limits_{i=1}^{n} S_{i} {\sigma}_{j}^{i} / \sum\limits_{i=1}^{n} S_{i} $ | (8) |
式中Si为单元i的面积。
式(8)为面积加权平均法。在有限元分析时,对于薄板结构且形状较为规则的敞车车体,在网格划分时单元类型可采用四边形,则各单元的面积几乎一致。因此,在铁路敞车的有限元分析中该方法等同于应力平均法。
3) 质量导数加权平均法。
当wi=(mL-1)i时,可将式(6)简化为:
| $ \sigma_{j}=\sum\limits_{i=1}^{n}\left(m_{\mathrm{L}}^{-1}\right)_{i} \sigma_{j}^{i} / \sum\limits_{i=1}^{n}\left(m_{\mathrm{L}}^{-1}\right)_{i} $ | (9) |
式中(mL-1)i=1/(mL)i,(mL)i为单元i在结点j的团聚质量。而该方法主要应用于结构动力分析中,因结构动力分析与静力分析的主要区别为是否考虑惯性力,即质量的影响。
1.3 均方差加权的应力修匀方法根据1.2节给出的3种常用加权应力修匀方法的适用范围,并结合不同板厚的连接处或焊线上的结点周围各单元应力差别较大的特点,本文提出了均方差加权的应力修匀方法:
| $ \sigma_{j}=\overline{\sigma_{j}}\left(1+\sigma / \overline{\sigma_{j}}\right) $ | (10) |
式中,
| $ \sigma=\sqrt{\frac{\left[\left(\sigma_{j}^{1}-\overline{\sigma_{j}}\right)^{2}+\cdots+\left(\sigma_{n}^{1}-\overline{\sigma_{j}}\right)^{2}\right]}{n}} $ |
式中:
结合1.1节给出的最佳应力点,该方法首先通过有限元仿真计算各单元在高斯积分点上的单元应力,然后通过式(10)分别计算结点j的应力均值、应力均方差,最后得出修匀后的结点应力。
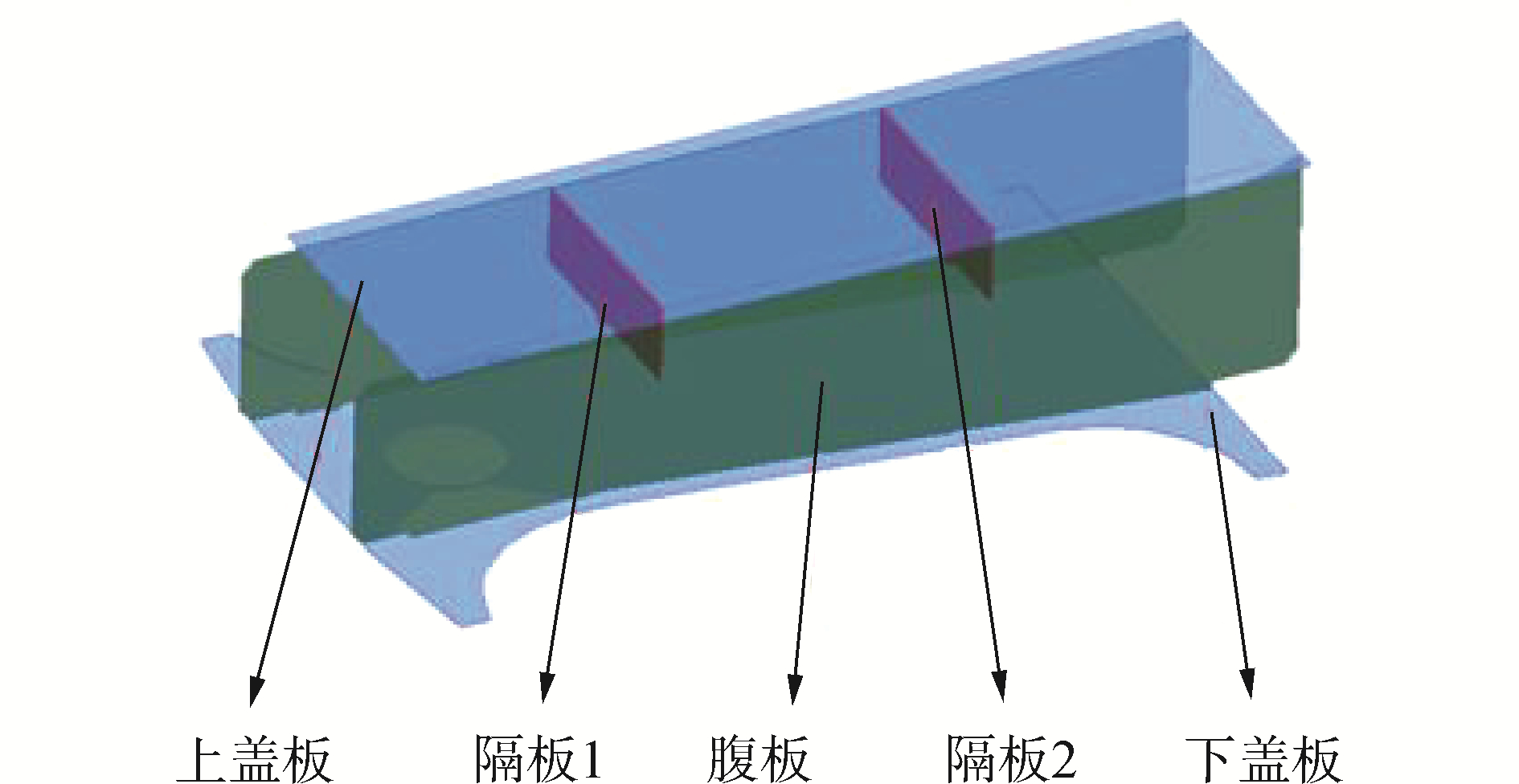
2 大横梁焊缝裂纹统计分析 2.1 C80E型通用敞车车体结构简介C80E型通用敞车车体为全钢焊接结构,由底架、侧墙、端墙、侧开门、下侧门等部件组成,底架由中梁、侧梁、枕梁、大横梁、端梁、纵向梁、小横梁以及钢地板等组焊而成,侧墙由上侧梁、侧柱、侧柱连铁、立柱、侧板以及内补强座等组焊而成。车体结构及本文研究涉及的关键零部件与关键焊缝名称如图 1所示,大横梁结构及各零件名称如图 2所示。

|
Download:
|
| 图 1 C80E型敞车车体结构 Fig. 1 The structure of C80E gondola car body | |
|
Download:
|
| 图 2 大横梁结构及其零件名称 Fig. 2 Cross bearer′s structure and its parts name | |
在运用考核结束后,对C80E型敞车进行解体检查时,发现部分车体在大横梁上盖板与地板焊缝连接处出现裂纹,见图 3所示。根据现场调研,车体裂纹主要发生在靠近车体中心的4个大横梁上盖板与地板的焊缝连接处,即图 1中的大横梁焊缝。

|
Download:
|
| 图 3 大横梁焊缝疲劳裂纹 Fig. 3 The fatigue crack of cross bearer weld | |
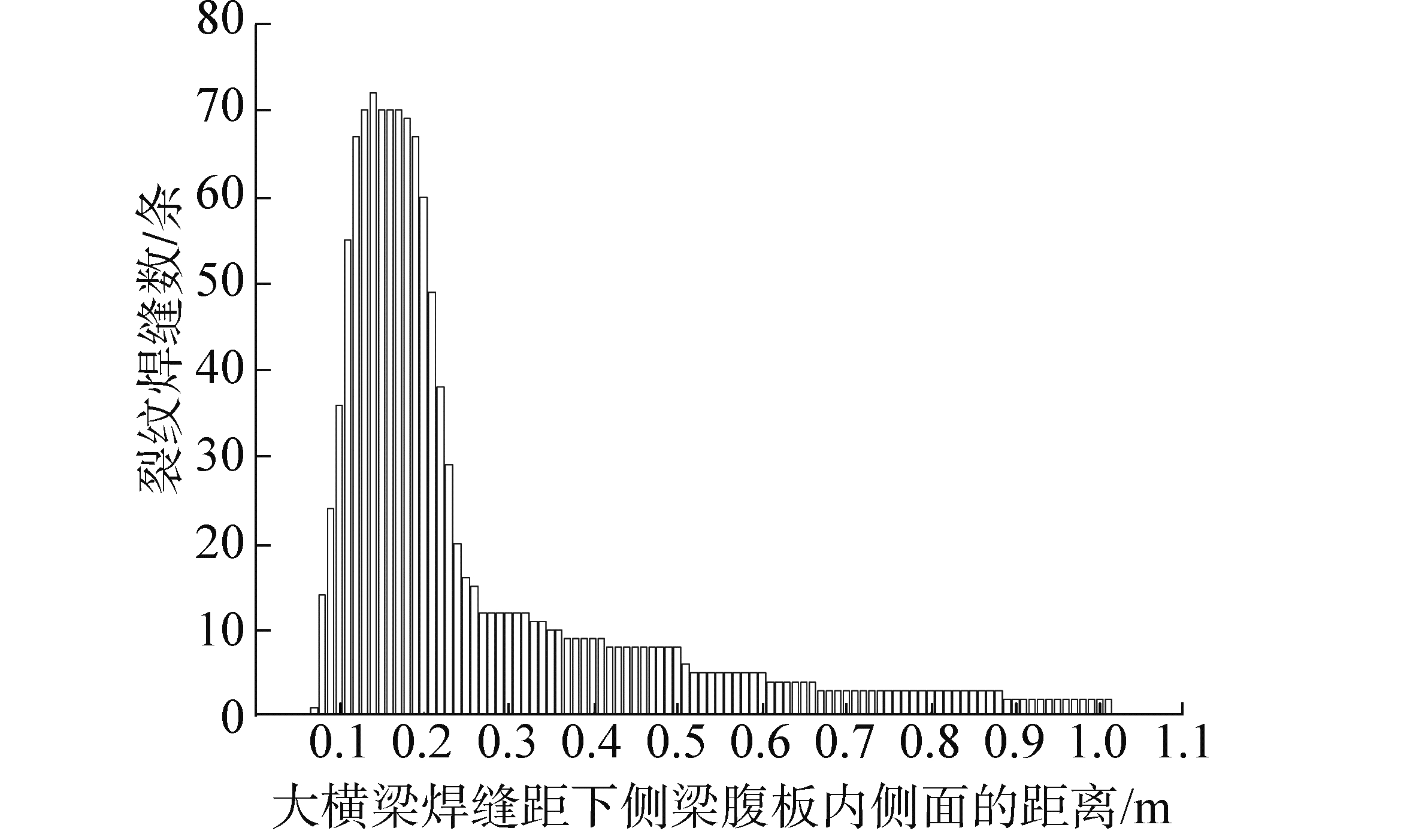
以下侧梁腹板内侧面为基准,对现场19辆C80E型通用敞车的大横梁焊缝裂纹长度进行测量,经统计分析后的结果如图 4所示。由图 4可知,裂纹焊缝数在130~170 mm最多,均在70条以上。而车体上内补强座的端面距下侧梁腹板内侧面的距离为149 mm,可初步推断大横梁焊缝在内补强座处的应力集中是裂纹产生的主要原因。
|
Download:
|
| 图 4 大横梁焊缝裂纹统计 Fig. 4 The statistics of cross bearer weld′s crack | |
C80E型通用敞车车体为薄板结构,可采用板壳单元对整车模型进行结构离散,且车体关于横向中心面与纵向中心面完全对称,因此可建立1/4车体模型进行研究,如图 5所示。

|
Download:
|
| 图 5 1/4车体有限元模型 Fig. 5 1/4 wagon body finite element modal | |
为了比较网格细化对大横梁焊缝应力的影响,按照是否细化大横梁焊缝相关部位的网格,形成2种网格模型,见表 1所示。
| 表 1 2种网格模型的区别 Table 1 The difference between two types of mesh models |
按照TB/T1335-1996《铁道车辆强度设计及试验鉴定规范》的规定,本文重点分析大横梁焊缝在垂向静载荷、第1工况纵向拉伸力以及第1工况纵向压缩力下的应力分布,后续分别简称为垂向工况、拉伸工况、压缩工况,结合表 1中的2种模型进行有限元计算,并采用单元应力平均法提取大横梁焊缝上的结点应力,结果如图 6所示。由图 6可知:

|
Download:
|
| 图 6 大横梁焊缝在不同工况下的结点应力分布 Fig. 6 The stress distribution of cross bearer weld under different condition | |
1) 网格细化的程度基本不影响大横梁焊缝在不同工况下应力极大值位置的体现,2种网格模型在各工况下均出现3个极大值,具体位置见表 2所示。车体模型中内补强座、隔板1、隔板2距下侧梁腹板的距离分别为149、410、850 mm,与3个应力极大点的位置基本一致,究其原因,内补强座、隔板1、隔板2导致与大横梁连接的相应位置刚度突变,导致不同程度的应力集中;
| 表 2 应力极大值的位置 Table 2 Location of stress maxima |
2) 2模型在不同工况下的结点应力基本一致,但在150 mm周围的应力差别较大,以压缩工况为例,模型1的最大值在153 mm处,应力为132.3 MPa,而模型2的最大值在150 mm处,应力为62.8 MPa,可以看出模型2未将应力最大点体现出来,说明刚度突变点周围的应力对网格的大小较为敏感,因此在有限元仿真分析时关键部位的网格细化尤为重要;
3) 在垂向、拉伸、压缩工况下,2种模型均在内补强座处应力梯度最大,在隔板1与隔板2处的应力梯度稍大,说明内补强座处的焊缝应力集中较为明显。
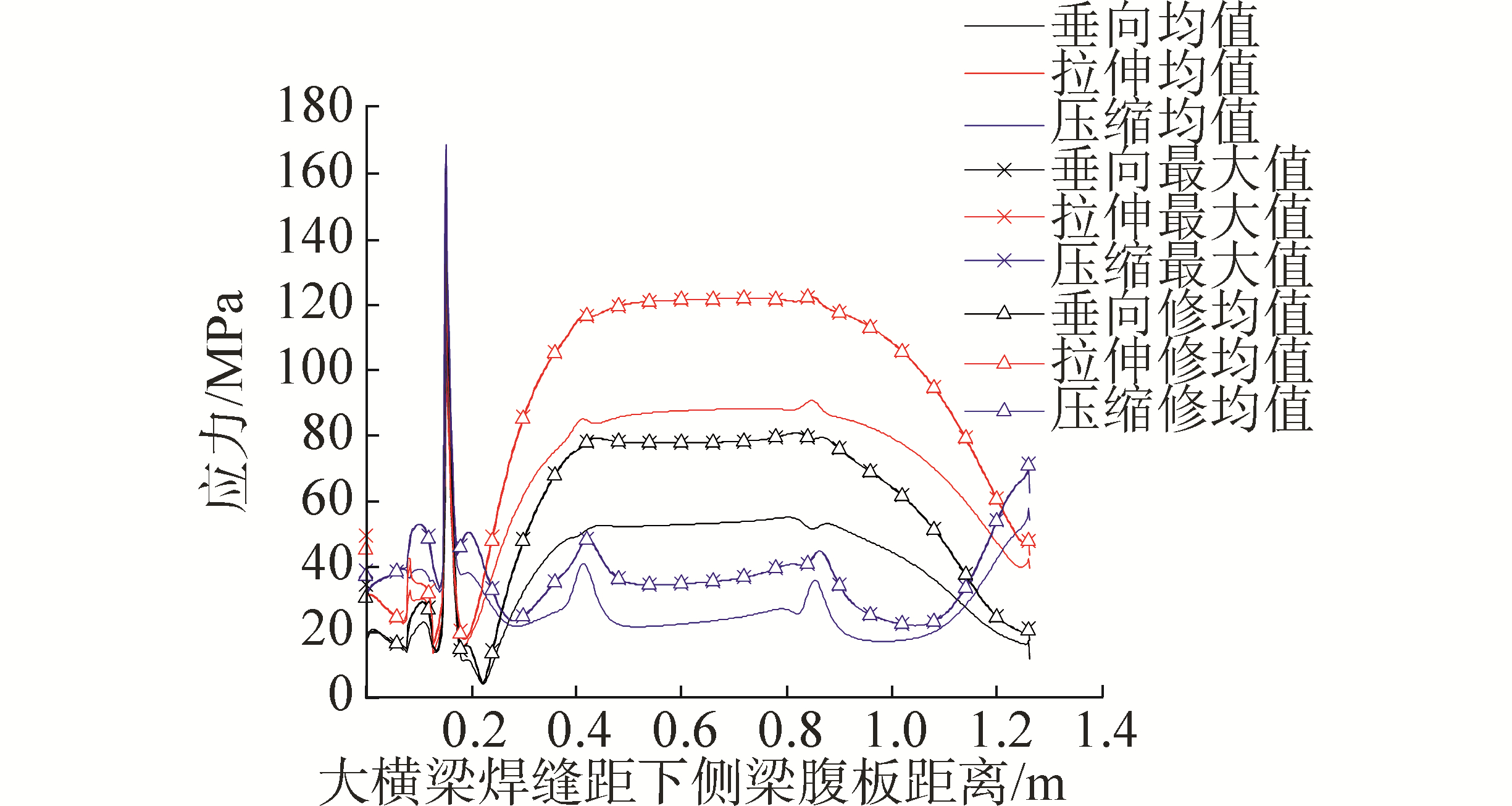
3.2 基于均方差加权的大横梁焊缝应力修匀根据3.1节分析结果可知,模型1的计算结果比模型2更准确,因此仅对模型1提取的大横梁焊缝结点应力进行修匀,并结合各应力修匀方法的特点,选用单元应力平均法与均方差加权应力修匀法进行修匀。本文为了进一步说明均方差加权应力修匀效果,同时也提取结点周围单元应力的最大值,与修匀后的应力进行对比分析。为了便于描述,将经单元应力平均法与均方差加权应力修匀法获得的结点应力分别简称为均值与修匀值,将结点周围最大值的单元应力简称为最大值,在各工况下通过不同的取值方法获得的大横梁焊缝应力如图 7所示。同时以150 mm处的结点应力为例,给出了采用均方差应力修匀方法计算后的修匀值。如表 3所示:1)总体来看,修匀值比均值大,且在150 mm附近时二者相差很大,因该位置为内补强座底座外沿与地板连接处,大横梁焊缝在该处的刚度变化较大,说明均方差应力修匀可较好的体现出刚度突变对应力影响的程度;2)150 mm附近的修匀值比最大值略小,其他位置的修匀值与最大值几乎完全一致。究其原因,可由式(10)可看出,在围绕结点的各单元应力差别较小时,修匀值与最大值基本相等,同时也说明式(10)更容易将刚度突变点的体现出来。
|
Download:
|
| 图 7 大横梁焊缝在不同取值方法下的结点应力分布图 Fig. 7 The stress distribution of cross bearer weld under different value method | |
| 表 3 150 mm处经均方差修匀的应力值 Table 3 The stresses after mean square deviation smoothing at 150 mm point |
根据3.1节与3.2节可知,应力最大点出现在150 mm附近,同时为了后续大横梁焊缝疲劳强度的评估,本节将150 mm周围的应力结点按垂向工况、拉伸工况、压缩工况分别进行修匀,为了说明不同的取值方法对应力的影响,列出了结点应力的最大值、均值,以及修匀值,见表 4所示。由表 4可以看出,150 mm与153 mm处的应力采用不同的取值方法提取的应力差别很大,但在其他位置应力受取值方法的影响较小,说明在刚度突变点附近的单元应力变化明显,选用较为合理的结点应力提取方法尤为重要。
| 表 4 在3种工况下的应力值 Table 4 The stresses of three conditions |
为了进一步分析大横梁裂纹产生原因,同时验证本文提出的均方差加权应力修匀新方法的合理性。结合以上的分析结果,本节采用大秦线实测载荷谱对大横梁焊缝在144、147、150、153 mm处的结点进行疲劳损伤评估,并与实测应力谱对应的疲劳损伤进行对比分析。
4.1 疲劳损伤计算方法根据Miner线性累积损伤理论,疲劳损伤的计算公式为:
| $ D^{\prime}=\sum\limits_{i=1}^{p} \frac{n_{i}}{N_{i}}=\frac{1}{C} \sum\limits_{i=1}^{p} n_{i} \sigma_{-1 a i}^{m} $ | (11) |
式中:σ-1ai为第i级应力水平;p为应力谱级数;ni为第i级应力水平作用下的实际循环次数;Ni为第i级应力水平作用下的循环次数;m、C为S-N曲线参数。
已知应力谱的运行公里数为L′,产生的相应损伤为D′;设结构设计时期望的安全运行里程L产生的相应损伤为D,则:
| $ \frac{D}{L}=\frac{D^{\prime}}{L^{\prime}} $ | (12) |
将式(11)代入式(12),可得在安全运行里程L产生的相应损伤D为:
| $ D=\frac{L}{L^{\prime} C} \sum\limits_{i=1}^{p} n_{i} {\sigma}_{-1 a i}^{m} $ | (13) |
C80E车体设计使用寿命期为625万km,根据大横梁各零件的材料及焊缝焊接接头形式,S-N曲线方程的相关参数取值可参照标准BS7608中焊缝F级的数据。
4.2 大横梁焊缝的疲劳损伤评估根据调研情况,并结合第3节车体有限元仿真分析结果,在内补强座周围的大横梁焊缝布置应力测点,具体位置分别为距下侧梁腹板内翼面144、147、150、153 mm,测点如图 8所示。

|
Download:
|
| 图 8 应力测点布置示意 Fig. 8 The schematic diagram of test point positions | |
试验采用SoMat eDAQ动态数据采集系统在大秦铁路湖东与京唐港区段往返进行线路运营测试,为了保证试验数据的完整性,设置采样频率为1 000 Hz。采用雨流计数法对应力-时间历程进行数理统计,并编制8级应力谱,4个测点的应力谱如图 9所示。

|
Download:
|
| 图 9 应力幅值谱 Fig. 9 The stress amplitude spectrum | |
采用4.1节的疲劳损伤计算方法,根据4个动应力测点的应力谱,计算后的疲劳损伤见表 5所示;同时采用大秦线实测心盘载荷谱和车钩载荷谱,对表 4中的数据进行疲劳损伤评估,因扭转工况对大横梁焊缝应力贡献很小,可忽略不计,与动应力测点相对应的4个结点疲劳损伤值见表 5所示。
| 表 5 各测点在不同取值方法下的疲劳损伤 Table 5 The fatigue damage of test point under different value method |
从表 5可以看出:各应力点的修正值对应的损伤与实测值基本相当;在结点150 mm与153 mm处均值对应的损伤比实测值小很多,说明应力均值方法不合理,未能真实的体现结点处的应力;最大值对应的损伤总体比实测值偏大,尤其在150 mm处偏差更大,说明对于应力突变点,最大值的取值方法偏离实际较大,对于疲劳损伤评估太过保守。
为了更进一步说明各取值方法的差别,本文列出了150 mm与153 mm处的寿命值,见表 6所示。
| 表 6 各测点在不同取值方法下的疲劳寿命 Table 6 The fatigue life of test point under different value method |
从表 6可以看出,在153 mm处各取值方法计算出的疲劳寿命均小于设计寿命的要求,而修正值接近40万km,符合实际。在150 mm处均值对应的疲劳寿命为665.61万km,大于设计寿命625万km,说明目前有限元分析时采用单元应力均值法修匀的结点应力不合理。同时若未细化网格,将不会体现153 mm处的结点应力,因此,在有限元分析时细化网格对刚度突变处的应力体现尤为重要。
5 结论1) 本文提出的基于均方差加权的应力修匀方法精度较高,获得的大横梁焊缝疲劳损伤值与实测值相近,说明经均方差应力加权修匀后的结点应力精度更高。
2) 与单元应力平均法相比,采用本文提出的均方差应力修匀方法获得的大横梁焊缝应力分布更有利于刚度突变点的体现,且与C80E车体大横梁焊缝裂纹统计分析得出的刚度突变点位置完全相符。
3) 通过对比分析网格大小分别为3 mm与20 mm时的关键部位结点应力,网格大小为20 mm时的仿真结果未能真实体现应力最大值的位置,说明对应力集中部位的网格细化尤为重要。
| [1] |
Association of American Railroads. Manual of standards and recommended practices section C-PartⅡ, design, fabrication, and construction of freight cars[S]. Washington: ARR, 2007.
(  0) 0)
|
| [2] |
British Standard Institute. BS 7608: 2014+A1: 2015, Guide to fatigue design and assessment of steel products[S]. London: BSI, 2015. https://shop.bsigroup.com/ProductDetail/?pid=000000000030329662
(  0) 0)
|
| [3] |
British Standard Institute. BS EN 1993-1-9: 2005, Eurocode 3: design of steel structures[S]. London: BSI, 2005. https://shop.bsigroup.com/ProductDetail/?pid=000000000030197059
(  0) 0)
|
| [4] |
YILDIRIM H C. Recent results on fatigue strength improvement of high-strength steel welded joints[J]. International journal of fatigue, 2017, 101: 408-420. DOI:10.1016/j.ijfatigue.2016.10.026 (  0) 0)
|
| [5] |
LU Yaohui, XIANG Penglin, DONG P, et al. Analysis of the effects of vibration modes on fatigue damage in high-speed train bogie frames[J]. Engineering failure analysis, 2018, 89: 222-241. DOI:10.1016/j.engfailanal.2018.02.025 (  0) 0)
|
| [6] |
HAN J W, KIM J D, SONG S Y. Fatigue strength evaluation of a bogie frame for urban maglev train with fatigue test on full-scale test rig[J]. Engineering failure analysis, 2013, 31: 412-420. DOI:10.1016/j.engfailanal.2013.01.009 (  0) 0)
|
| [7] |
李凡松, 邬平波, 曾京, 等. 构架三种常用疲劳强度校核方法对比研究[J]. 机械工程学报, 2014, 50(14): 170-176. LI Fansong, WU Pingbo, ZENG Jing, et al. Study on the differences between the three common fatigue strength analysis methods for bogie frame[J]. Journal of mechanical engineering, 2014, 50(14): 170-176. (  0) 0)
|
| [8] |
MADYIRA D M, KUMBAA T, KAYMAKCIA A. Influence of manufacturing conditions on fatigue life of welded joints[J]. Procedia manufacturing, 2017, 8: 665-672. DOI:10.1016/j.promfg.2017.02.085 (  0) 0)
|
| [9] |
朱伯芳. 有限单元法原理与应用[M]. 4版. 北京: 中国水利水电出版社, 2018. ZHU Bofang. Finite element method theory and applications[M]. 4th ed. Beijing: China Water & Power Press, 2018. (  0) 0)
|
| [10] |
李涛, 左正兴, 廖日东. 结构仿真高精度有限元网格划分方法[J]. 机械工程学报, 2009, 45(6): 304-308. LI Tao, ZUO Zhengxing, LIAO Ridong. Meshing method of high precision fem in structural simulations[J]. Chinese journal of mechanical engineering, 2009, 45(6): 304-308. (  0) 0)
|
| [11] |
LAI Yukun, MARTIN R R. Vertex location optimisation for improved remeshing[J]. Graphical models, 2012, 74(4): 233-243. DOI:10.1016/j.gmod.2012.04.011 (  0) 0)
|
| [12] |
PENG X, KULASEGARAM S, WU S C, et al. An extended finite element method (XFEM) for linear elastic fracture with smooth nodal stress[J]. Computers & structures, 2017, 179: 48-63. (  0) 0)
|
| [13] |
IVIRMA L, VERGARA M, PROVENZANO S, et al. Artificial neural networks application for stress smoothing in hexaedrons[J]. WSEAS transactions on information science and applications, 2009, 6(5): 872-883. (  0) 0)
|
| [14] |
徐小明, 张盛, 姚伟岸, 等. 基于辛弹性力学解析本征函数的有限元应力磨平方法[J]. 计算力学学报, 2012, 29(4): 511-516. XU Xiaoming, ZHANG Sheng, YAO Weian, et al. A stress recovery method based on the analytical eigenfunctions of symplectic elasticity[J]. Chinese journal of computational mechanics, 2012, 29(4): 511-516. (  0) 0)
|
| [15] |
王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003. WANG Xucheng. Finite element method[M]. Beijing: Tsinghua University Press, 2003. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


