2. 水电机械设备设计与维护湖北省重点实验室, 湖北 宜昌 443002
2. Hubei Key Laboratory of Hydroelectric Machinery Design & Maintenance, Yichang 443002, China
由于配合间隙不可避免地存在于各种活动铰连接处,而多间隙机械臂实质是一个强耦合非线性系统,表现出非常复杂的动力学特性,且间隙的存在会导致机械臂位姿精度的降低、动力学行为的恶化,同时,由于机械臂运行过程中存在冲击与振动,极大地降低机械臂的使用寿命,所以研究含铰间隙机械臂的振动抑制,对精密机械和工业机械臂等的设计研究与发展,具有重要的理论意义和工程实际价值。
王铁成等[1]建立了同时含旋转副间隙和移动副间隙的多体系统动力学模型, 以曲柄滑块机构为研究对象, 分析了混合间隙对该系统动力学特性的影响。白争锋等[2]以四杆机构为对象,研究了运动副间隙对机构系统动态特性的影响。侯甜甜[3]以含铰间隙的二自由度空间机械臂为研究对象, 考虑不同重力环境, 通过建立含铰间隙机构动力学模型, 设计间隙补偿控制器, 在不同重力环境下都能够使空间机械臂达到理想的轨迹跟踪精度。刘志全等[4]针对空间机械臂辅助对接任务中的复杂关节力矩控制问题, 建立了含间隙、非线性刚度及啮合阻尼的多级行星齿轮传动复杂关节精细动力学模型。娄军强等[5]提出一种结合遗传优化算法和多项式函数插值的抑振轨迹规划方法抑制柔性臂的弹性振动。文献[6-10]对含间隙机械臂的动力学特性进行了研究,文献[11-18]在机器人运行稳定性及抑振方面进行了研究并取得了成果。
以上研究只考虑了做单间隙或双间隙情况,而很少分析多间隙耦合下机械臂动力学行为及其抑振方法,且只研究了间隙大小、重力因素等对动力学的影响,未对其他参数进行综合分析。本文重点考虑在关节铰间隙大小和杆件质量的双重耦合作用影响下,串联机械臂含间隙关节的动力响应特征,并在此基础上展开抑振优化研究。
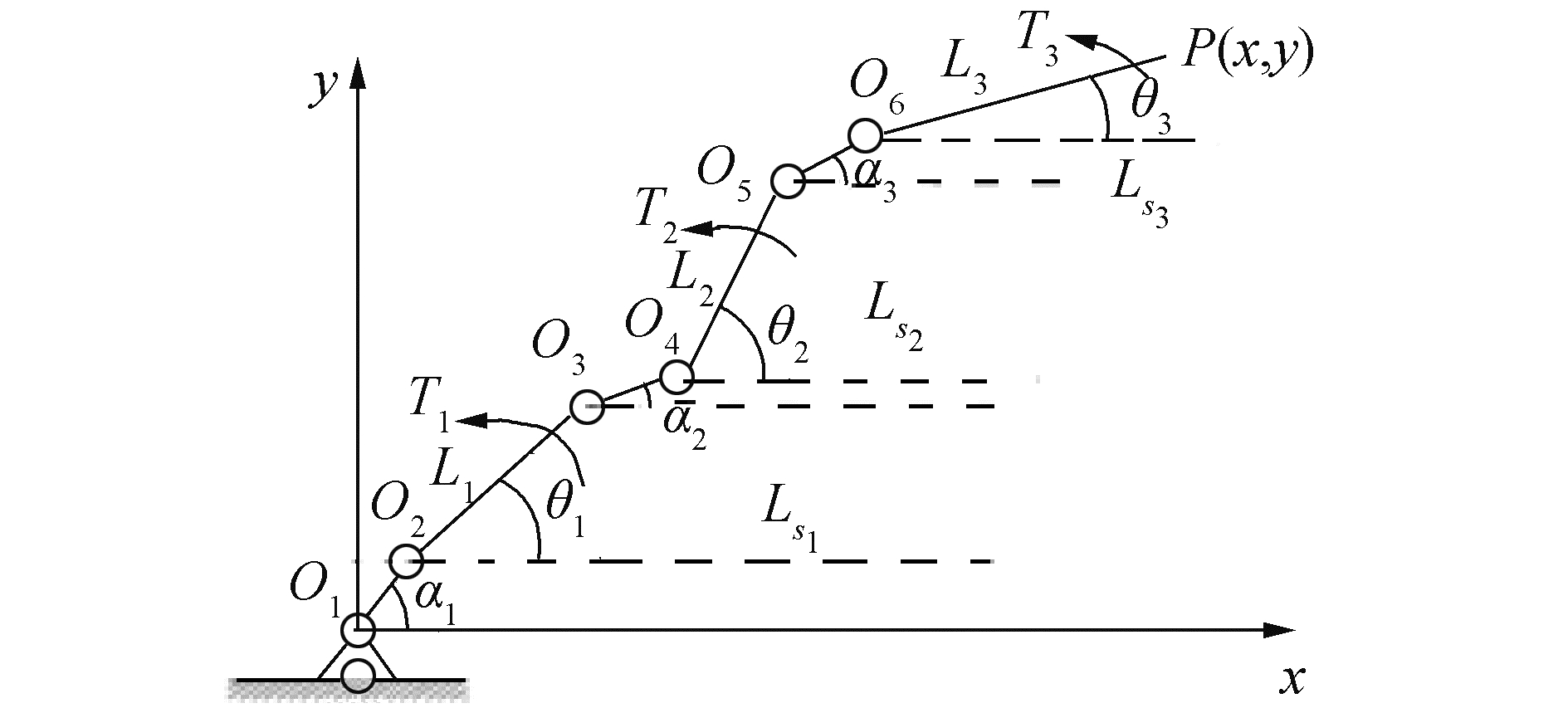
1 多间隙机械臂动力学建模由于铰间隙的存在导致了机械臂关节处均存在偏心,即机械臂关节处连杆n的轴颈轴心与连杆n-1的轴套轴心不重合,在x和y方向均存在一个偏心量enx、eny。由此可知,每增加一个间隙,机械臂系统会增加2个自由度,考虑各个关节铰的结构相似性,仅以3R关节铰链为研究对象,含间隙3R串联机械臂的等效示意图如图 1所示。
|
Download:
|
| 图 1 含间隙3R串联机械臂等效示意图 Fig. 1 Equivalent schematic diagram of 3R series manipulator with clearances | |
由图 1几何关系有等式:
| $ {\alpha _1} = \arctan \frac{{{e_{1y}}}}{{{e_{1x}}}}, {\alpha _2} = \arctan \frac{{{e_{2y}}}}{{{e_{2x}}}}, {\alpha _3} = \arctan \frac{{{e_{3y}}}}{{{e_{3x}}}} $ |
在多间隙机械臂进行运动过程中,连杆1质心S1的位置坐标方程为:
| $ \left[ {\begin{array}{*{20}{l}} {{x_{{S_1}}}}\\ {{y_{{S_1}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{e_{1x}}}\\ {{e_{1y}}} \end{array}} \right] + {L_{{S_1}}}\left[ {\begin{array}{*{20}{c}} {\cos {\theta _1}}\\ {\sin {\theta _1}} \end{array}} \right] $ | (1) |
将式(1)进行一次求导可得连杆1质心S1的线速度为:
| $ \left[ {\begin{array}{*{20}{c}} {{{\dot x}_{{S_1}}}}\\ {{{\dot y}_{{S_1}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\dot e}_{1x}}}\\ {{{\dot e}_{1y}}} \end{array}} \right] + {L_{{S_1}}}{{\dot \theta }_1}\left[ {\begin{array}{*{20}{c}} { - \sin {\theta _1}}\\ {\cos {\theta _1}} \end{array}} \right] $ | (2) |
再将式(2)进行一次求导可得连杆1质心S1的加速度方程为:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{l}} {{{\ddot x}_{S1}}}\\ {{{\ddot y}_{S1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\ddot e}_{1x}}}\\ {{{\ddot e}_{1y}}} \end{array}} \right] + {L_{{S_1}}}{{\ddot \theta }_1}\left[ {\begin{array}{*{20}{c}} { - \sin {\theta _1}}\\ {\cos {\theta _1}} \end{array}} \right] + \\ \;\;\;\;\;\;\;\;\;\;{L_{{S_1}}}\dot \theta _1^2\left[ {\begin{array}{*{20}{l}} { - \cos {\theta _1}}\\ { - \sin {\theta _1}} \end{array}} \right] \end{array} $ | (3) |
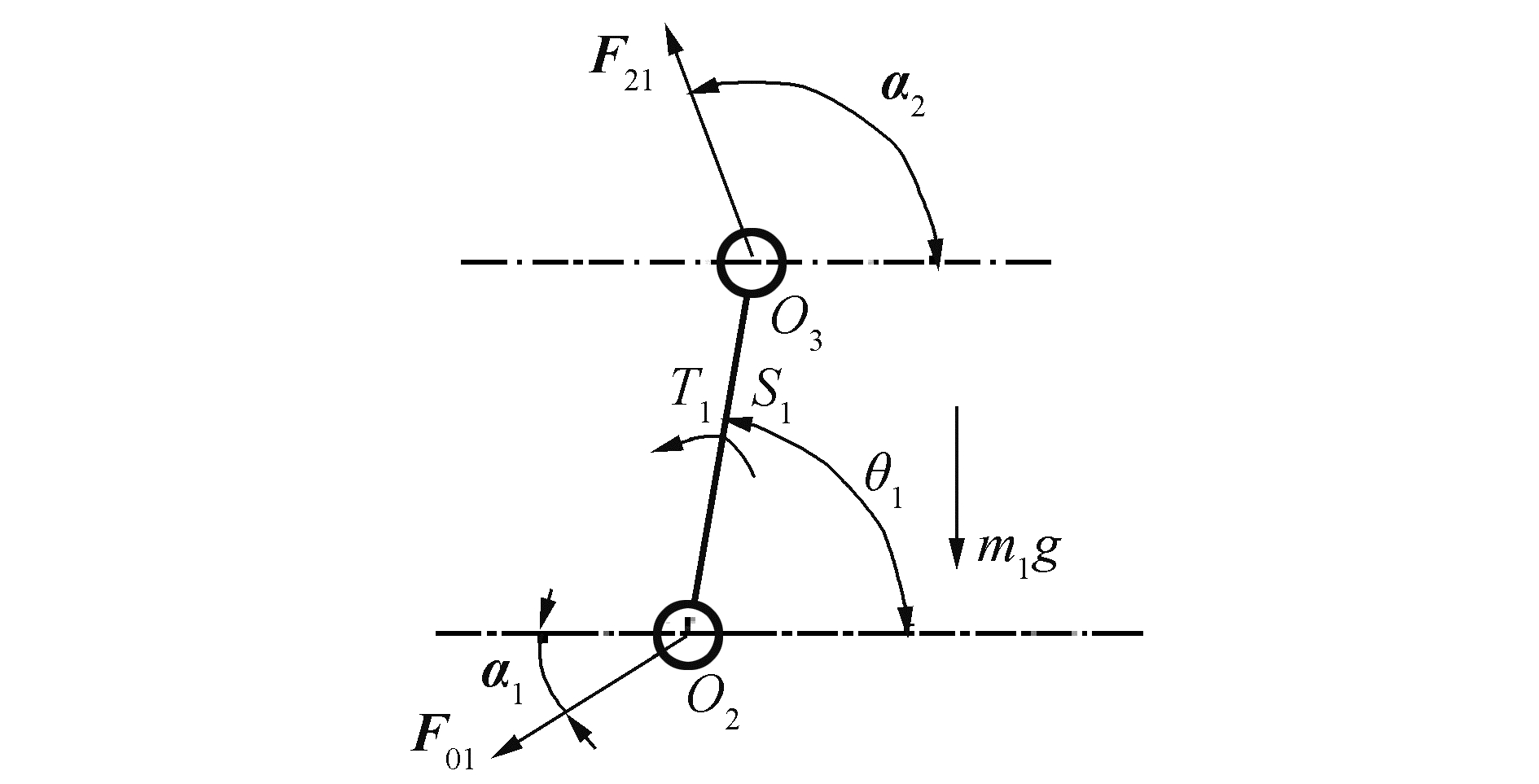
根据达朗贝尔原理,对连杆1进行动力学分析,连杆1的受力分析如图 2所示。
|
Download:
|
| 图 2 连杆1受力分析图 Fig. 2 Force analysis of connecting bar 1 | |
由于间隙的存在,连杆与基座、连杆与连杆之间均存在碰撞,图 2中F01为基座对连杆1的碰撞力,F21为连杆2对连杆1的碰撞力。利用达朗贝尔原理,对连杆1进行分析可得:
| $ \left\{ \begin{array}{*{35}{l}} {{\mathit{\boldsymbol{F}}}_{21}}\sin {{\alpha }_{2}}-{{\mathit{\boldsymbol{F}}}_{01}}\sin {{\alpha }_{1}}-{{m}_{1}}g={{m}_{1}}{\overset{..}{{\mathit{\boldsymbol{y}}}}}_{{{S}_{1}}}\, \\ {{\mathit{\boldsymbol{F}}}_{21}}\cos {{\alpha }_{2}}-{{\mathit{\boldsymbol{F}}}_{01}}\cos {{\alpha }_{1}}={{m}_{1}}{\overset{..}{{\mathit{\boldsymbol{x}}}}}_{{{S}_{1}}}\, \\ {{J}_{1}}{{{\ddot{\theta }}}_{1}}={{T}_{1}}+{{\mathit{\boldsymbol{F}}}_{01}}\sin {{\alpha }_{1}}{{R}_{2}}-{{\mathit{\boldsymbol{F}}}_{01}}\cos {{\alpha }_{1}}{{R}_{2}}+ \\ \begin{array}{*{35}{l}} \ \ \ \ \ \ \ \ \ {{\mathit{\boldsymbol{F}}}_{21}}\left( {{R}_{3}}\sin {{\alpha }_{2}}+{{L}_{1}}\sin {{\theta }_{1}} \right)- \\ \ \ \ \ \ \ \ \ \ {{\mathit{\boldsymbol{F}}}_{21}}\left( {{R}_{3}}\cos {{\alpha }_{2}}+{{L}_{1}}\cos {{\theta }_{1}} \right)-{{m}_{1}}g{{L}_{{S1}}}\cos {{\theta }_{1}} \\ \end{array} \\ \end{array} \right. $ | (4) |
同理,利用运动学方程求导以及达朗贝尔原理对连杆2、3进行分析可得:
| $ \left\{ \begin{array}{*{35}{l}} \begin{array}{*{35}{l}} {{\mathit{\boldsymbol{F}}}_{32}}\sin {{\alpha }_{3}}-{{\mathit{\boldsymbol{F}}}_{12}}\sin {{\alpha }_{2}}-{{m}_{2}}g={{m}_{2}}{{\overset{..}{\mathop{\mathit{\boldsymbol{y}}}}\,}_{{{S}_{2}}}} \\ {{\mathit{\boldsymbol{F}}}_{32}}\cos {{\alpha }_{3}}-{{\mathit{\boldsymbol{F}}}_{12}}\cos {{\alpha }_{2}}-{{m}_{2}}g={{m}_{2}}{{\overset{..}{\mathop{\mathit{\boldsymbol{x}}}}\,}_{{{S}_{2}}}} \\ \end{array} \\ {{J}_{2}}{{{\ddot{\theta }}}_{2}}={{T}_{2}}+{{\mathit{\boldsymbol{F}}}_{12}}\sin {{\alpha }_{2}}{{R}_{4}}-{{\mathit{\boldsymbol{F}}}_{12}}\cos {{\alpha }_{2}}{{R}_{4}}+ \\ \begin{array}{*{35}{l}} \ \ \ \ \ \ \ \ \ \ {{\mathit{\boldsymbol{F}}}_{32}}\left( {{R}_{5}}\sin {{\alpha }_{3}}+{{L}_{2}}\sin {{\theta }_{2}} \right)- \\ \ \ \ \ \ \ \ \ \ \ {{\mathit{\boldsymbol{F}}}_{32}}\left( {{R}_{5}}\cos {{\alpha }_{3}}+{{L}_{2}}\cos {{\theta }_{2}} \right)-{{m}_{2}}g{{L}_{S2}}\cos {{\theta }_{2}} \\ \end{array} \\ \end{array} \right. $ | (5) |
| $ \left\{ \begin{array}{*{35}{l}} -{{\mathit{\boldsymbol{F}}}_{23}}\sin {{\alpha }_{3}}-{{m}_{3}}g={{m}_{3}}{{\overset{..}{\mathop{\mathit{\boldsymbol{y}}}}\,}_{{{S}_{3}}}} \\ {{\mathit{\boldsymbol{F}}}_{23}}\cos {{\alpha }_{3}}={{m}_{3}}{{\overset{..}{\mathop{\mathit{\boldsymbol{x}}}}\,}_{{{S}_{3}}}} \\ {{J}_{3}}{{{\ddot{\theta }}}_{3}}={{\bf{T}}_{3}}+{{\mathit{\boldsymbol{F}}}_{23}}\sin {{\alpha }_{3}}{{R}_{6}}-{{\mathit{\boldsymbol{F}}}_{23}}\cos {{\alpha }_{3}}{{R}_{6}}-{{m}_{3}}g{{L}_{{{{S}}_{3}}}}\cos {{\theta }_{3}} \\ \end{array} \right. $ | (6) |
式中:F21为连杆1对连杆2的碰撞力,F32为连杆3对连杆2的碰撞力,F23为连杆2对连杆3的碰撞力,其中F21与F12、F32与F23为两对相互作用力;R1、R3、R5分别为基座、连杆1、连杆2关节处轴套半径,R2、R4、R6分别为连杆1、连杆2、连杆3关节处轴颈的半径;J1、J2和J3分别为连杆1、连杆2、连杆3的转动惯量。
将运动学方程及其求导后方程结合式(4)~(6)整理后可得多间隙机械臂动力学模型:
| $ \overset{..}{\mathop{\mathit{\boldsymbol{x}}}}\,={{\mathit{\boldsymbol{M}}}^{-1}}\mathit{\boldsymbol{F}} $ | (7) |
式中:
由以上各式可以看出,不仅间隙大小对机械臂动力学有影响,杆件质量及其分布也对机械臂动力学有不可忽视的作用。由此可知,通过3个关节处合适的精度组合以及杆件质量的调整会对多间隙机械臂的抑振起到积极作用。
2 单间隙下杆件质量对碰撞的影响本文研究以含间隙串联机械臂为研究对象。在仿真模型中,基座固接于平台,连杆1、连杆2长度均为330 mm,连杆3长度为360 mm,轴颈直径为40 mm,轴套直径为40 mm,3个关节处间隙大小由各关节处轴与轴颈的配合精度决定。
在SolidWorks/Motion中对4种模型进行动力学仿真,机械臂初始位置为:连杆1与水平面呈30°夹角,连杆2与水平面呈60°夹角,连杆3与水平面水平。在关节处均设置电机,关节1处电机5 s内逆时针转动90°,关节2处电机5 s内均顺时针转动30°,关节3处电机5 s内均逆时针转动30°。动力学仿真均在重力环境下进行。机械臂初始位置与最终位置及各臂转动方向如图 3所示。
|
Download:
|
| 图 3 机械臂位置示意 Fig. 3 Schematic diagram of the position of the manipulator | |
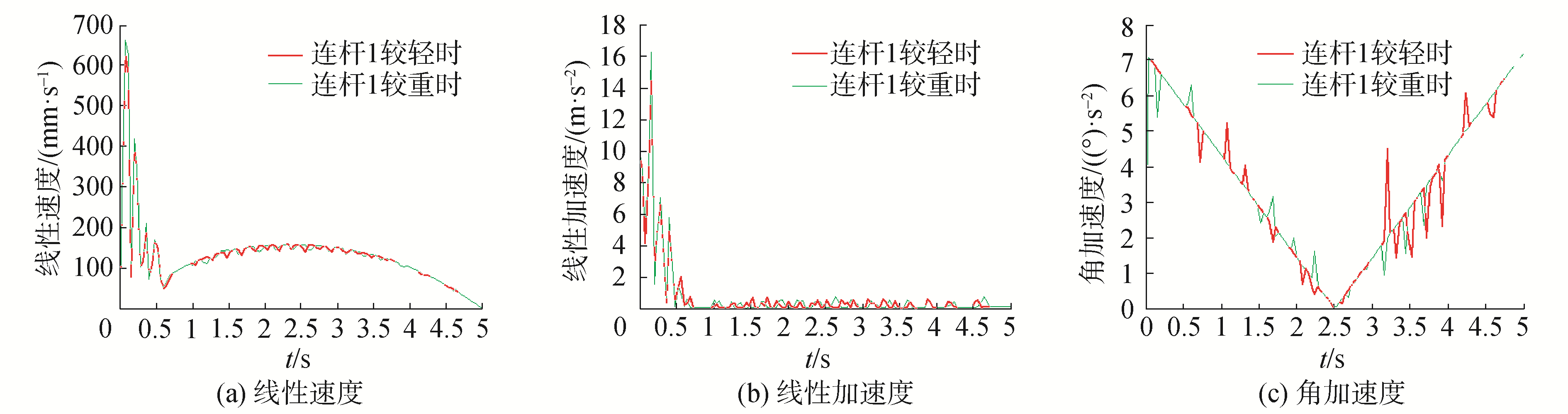
为了研究各杆件对质量的敏感性,分别只考虑远关节和基关节单间隙情况下杆件质量对运动学和动力学参数的影响。当只考虑基关节处间隙时,杆件1分别用铸钢和铝合金2种材料来改变杆件1的质量,利用铸钢时杆件1较重,利用铝合金时杆件1较轻,取间隙为0.5 mm, 通过仿真可得出在只考虑基关节处间隙时,杆件1较轻和较重2种情况下线性速度对比图、线性加速度对比图和角加速度对比图,如图 4所示。
|
Download:
|
| 图 4 只考虑基关节处间隙时速度对比 Fig. 4 Velocity contrast diagram only considering the clearance between the base joint | |
通过以上仿真结果可以看出,仿真启动0.6 s左右后,机械臂开始平稳运行,在仿真开始时由于间隙的存在以及重力原因,机械臂末端执行器存在较大冲击,主要体现在速度和加速度的平稳性方面,只考虑基关节处间隙时运动参数对比图可以得出,当连杆1较轻时最大速度出现在0.08 s,速度值为629.969 mm/s, 最大线性加速度出现在0.16 s,线性加速度值为15 164.566 mm/s2,角加速度10个较大冲击,其中3.92 s处冲击最大为1.855(°)/s2。当连杆1较重时最大速度出现在0.08 s,速度值为662.264 mm/s, 最大线性加速度出现在0.16 s,线性加速度值为16 216.268 mm/s2,角加速度13个较大冲击,其中3.64 s处冲击最大为2.073(°)/s2,从角加速度对比图可以明显看出,在基关节处存在间隙且杆件1重量较轻时,碰撞较多,冲击与振动情况严重,当无间隙时连杆1作纯转动,当有间隙时连杆1由于碰撞而作平面运动,由式(4)可知,当杆1较重时,其在x、y方向上的加速度会较小,此时机械臂在杆1处的稳定性较好,当杆1较轻时,这种影响较大,所以杆1较轻时,振动较大。
当只考虑远关节处间隙时,杆件3分别用铸钢和铝合金2种材料来改变杆件3的质量,利用铸钢时杆件3较重,利用铝合金时杆件3较轻,取间隙为0.5 mm, 机械臂仿真模型以及各关节处驱动参数与前面所述相同,通过仿真可得出在只考虑远关节处间隙时,杆件3较轻和较重2种情况下线性速度对比、线性加速度对比图和角加速度对比图,如图 5所示。

|
Download:
|
| 图 5 只考虑远关节处间隙时速度对比 Fig. 5 Velocity contrast diagram only considering the clearance between the distal joint | |
通过以上仿真结果可以看出,仿真启动后0.4 s左右,机械臂开始时平稳运行,在运动开始时由于间隙的存在以及重力原因,机械臂末端执行器存在较大冲击,主要体现在速度和加速度的不平稳方面,从仅考虑远关节处间隙时运动参数对比图可以得出,当连杆3较轻时最大速度出现在0.08 s,速度值为586.802 mm/s, 最大线性加速度出现在0.12 s,线性加速度值为14 412.171 mm/s2,角加速度9个较大冲击,其中0.48 s处冲击最大为4.839 (°)/s2。当连杆3较重时最大速度出现在0.08 s,速度值为662.264 mm/s, 最大线性加速度出现在0.16 s,线性加速度值为23 543.289 mm/s2,角加速度12个较大冲击,其中0.12 s处冲击最大为10.056 (°)/s2,从线性速度、线性加速度以及角加速度,图 5可以明显看出,在远关节处存在间隙且杆件3重量较重时,碰撞较多,冲击与振动的幅值较大,运动平稳性很差,连杆3处于最末端,由式(6)可知,其他连杆对其无重量上的叠加作用的影响,其碰撞力的大小仅与连杆3的质量有关,其质量越大碰撞力越大,反之碰撞力越小,所以在运行过程中,杆件质量较重时冲击与振动较大,而杆件质量较轻时冲击与振动较小。
由以上分析可知,当间隙处于不同位置时,杆件重量对碰撞的影响也不同,当间隙越靠近基座时,杆件质量对碰撞的影响较小,但考虑到机械臂整体平衡性问题,此时杆件质量较重时,机械臂具有较好的动力学特性,当间隙远离基座时,杆件质量对碰撞的影响较大,间隙对杆件质量的敏感性较强,此时杆件质量较轻时可以很好的抑制由间隙带来的振动。
3 优化模型参数变量及其仿真文献[9]中对2R含间隙机械臂质量不变时不同间隙的振动情况分析方法进行了研究和说明,将其应用至3R含间隙机械臂上可确定多间隙机械臂的精度分布,结合优化后多间隙机械臂模型,其优化前后模型参数为基关节、中关节及远关节7级精度优化后变为8级精度,间隙大小由0.039 mm分别变为0.025、0.039及0.062 mm;连杆3材料由铸面变为铝合金,质量由36.161 kg变为12.517 kg。
由于本文只考虑抑振,故以线性速度、线性加速度和角加速度作为能否达到抑振效果的评判指标,得到优化前后多间隙机械臂模型线性速度、线性加速度和角加速度曲线后,优化前后工作行程中得出对比图如图 6所示。

|
Download:
|
| 图 6 优化前后3种速度对比 Fig. 6 Comparison of the three speeds before and after optimization | |
由图 6(a)可知优化后机械臂在0.5 s之后稳定运行后线性速度最大值出现在0.08 s,最大值为583.663 mm/s, 而优化前在0.7 s之后才稳定运行, 线性速度最大值出现在0.08 s,最大值为663.476 mm/s。由图 6(a)可以看出振动与冲击主要集中在仿真开始后前1 s,对前1 s所采集的线性速度得出优化前后线性速度如表 1所示。
| 表 1 仿真实验前1 s内优化前后线性速度 Table 1 Linear velocity before and after optimization in 1 s |
由图 6(a)以及表 2可以明显看出,优化后的机械臂可以很快的进入平稳运行阶段,而且最大冲击从663.476 mm/s降低到了583.663 mm/s,降低12.03%,在冲击集中阶段冲击幅度比优化前大大降低。优化前后工作行程中的线性加速度对比如图 6(b)所示。由图 6(b)所示的优化前后线性加速度对比图可以看出,优化后的机械臂可以很快的进入平稳运行阶段,而且线性加速度最大冲击出现在0.12 s,最大幅度为14 211.816 mm/s2, 优化前的机械臂末端执行器线性加速度最大冲击出现在0.15 s,最大幅度为23 608.294 mm/s2,由此可以计算出线性加速度最大冲击降低百分比为39.80%。优化前后工作行程中的角加速度对比如图 6(c)所示。
由图 6(c)所示的角加速度对比图可以看出:优化后在角加速度上存在7个较大冲击,最大冲击出现在3.84 s, 最大冲击幅值为8.651 (°)/s2, 优化前在角加速度上存在10个较大冲击,最大冲击出现在1.5 s左右, 最大冲击幅值为12.437 (°)/s2, 经优化后角加速度冲击幅值降低了30.44%。
从线性速度、线性加速度和角加速度3种对比图均可得出:优化后在机械臂动态工作行程中,振动得到了明显抑制,达到了优化效果。
4 结论1) 利用达朗贝尔原理以及运动学方程对多间隙耦合下串联机械臂动力学方程进行了推导,此方法建立的动力学模型较为精确,且过程相对简单。
2) 利用多间隙耦合下串联机械臂动力学方程对关节间隙大小以及杆件质量分布进行了分析,得出了不同关节部位不同大小间隙时,杆件质量不同分布对多关节间隙机械臂动力学行为的影响。
3) 针对关节精度和杆件质量,对机械臂进行合理优化,即靠近基座关节处使用较高精度,远离基座关节处精度可适当放低,且在高精度处使用较重杆件,精度较低处使用较轻杆件可以对机械臂的抑振起到明显作用。
| [1] |
王铁成, 陈国平, 马方, 等. 含混合间隙多体系统动力学分析[J]. 振动与冲击, 2016, 35(9): 178-183. WANG Tiecheng, CHEN Guoping, MA Fang, et al. Dynamic analysis of multibody systems with mixed clearance[J]. Journal of vibration and shock, 2016, 35(9): 178-183. (  0) 0)
|
| [2] |
白争锋, 赵阳, 赵志刚. 考虑运动副间隙的机构动态特性研究[J]. 振动与冲击, 2011, 30(11): 17-20, 41. BAI Zhengfeng, ZHAO Yang, ZHAO Zhigang. Dynamic characteristics of mechanisms with joint clearance[J]. Journal of vibration and shock, 2011, 30(11): 17-20, 41. DOI:10.3969/j.issn.1000-3835.2011.11.005 (  0) 0)
|
| [3] |
侯甜甜.考虑铰间间隙和重力效应的空间机械臂轨迹跟踪控制[D].秦皇岛: 燕山大学, 2016. HOU Tiantian. The study of space manipulator trajectort tracking control considering the joint clearance and gravity[D]. Qinhuangdao: Yanshan University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10216-1016764061.htm (  0) 0)
|
| [4] |
刘志全, 危清清, 王耀兵. 空间机械臂关节精细动力学模型的建立及关节力矩控制[J]. 宇航学报, 2014, 35(6): 663-668. LIU Zhiquan, WEI Qingqing, WANG Yaobing. Detailed joint dynamics modeling and joint torque control system of space manipulators[J]. Journal of astronautics, 2014, 35(6): 663-668. DOI:10.3873/j.issn.1000-1328.2014.06.007 (  0) 0)
|
| [5] |
娄军强, 魏燕定, 李国平, 等. 基于遗传优化算法的柔性机械臂抑振轨迹规划研究[J]. 振动与冲击, 2016, 35(11): 1-6, 40. LOU Junqiang, WEI Yanding, LI Guoping, et al. Optimal trajectory planning of a flexible manipulator for its vibration suppression using genetic algorithm[J]. Journal of vibration and shock, 2016, 35(11): 1-6, 40. (  0) 0)
|
| [6] |
张发军, 朱鑫, 李林子, 等. 铰间隙对采摘机械臂动态扰动的响应分析[J]. 中国农机化学报, 2016, 37(6): 47-53. ZHANG Fajun, ZHU Xin, LI Linzi, et al. Dynamic disturbance response of the picking manipulator with joints clearance[J]. Journal of Chinese agricultural mechanization, 2016, 37(6): 47-53. (  0) 0)
|
| [7] |
任武, 吴运新, 张赵威. 计及铰间隙的多柔体机械臂动力学特性[J]. 振动、测试与诊断, 2015, 35(3): 563-567. REN Wu, WU Yunxin, ZHANG Zhaowei. Dynamic characterization analysis of flexible multibody manipulator with joint clearance[J]. Journal of vibration, measurement & diagnosis, 2015, 35(3): 563-567. (  0) 0)
|
| [8] |
WANG Xupeng, LIU Geng, MA Shangjun. Dynamic analysis of planar mechanical systems with clearance joints using a new nonlinear contact force model[J]. Journal of mechanical science and technology, 2016, 30(4): 1537-1545. DOI:10.1007/s12206-016-0308-1 (  0) 0)
|
| [9] |
张发军, 张烽, 杨晶晶, 等. 串联机械臂关节铰间隙配合精度的设计方法[J]. 组合机床与自动化加工技术, 2017(4): 38-42. ZHANG Fajun, ZHANG Feng, YANG Jingjing, et al. The precision design method on hinge joints clearance fit in series robot[J]. Modular machine tool & automatic manufacturing technique, 2017(4): 38-42. (  0) 0)
|
| [10] |
RAHMANIAN S, GHAZAVI M R. Bifurcation in planar slider-crank mechanism with revolute clearance joint[J]. Mechanism and machine theory, 2015, 91: 86-101. DOI:10.1016/j.mechmachtheory.2015.04.008 (  0) 0)
|
| [11] |
SUN Dongyang, CHEN Guoping, Wang Tiecheng, et al. Wear prediction of a mechanism with joint clearance involving aleatory and epistemic uncertainty[J]. Journal of tribology, 2014, 136(4): 041101. DOI:10.1115/1.4027607 (  0) 0)
|
| [12] |
张发军, 张烽, 佘奕, 等. 考虑杆件自重影响含间隙铰机械臂的抑振策略[J]. 华中科技大学学报(自然科学版), 2008, 46(3): 75-79. ZHANG Fajun, ZHANG Feng, SHE Yi, et al. A. Vibration suppression strategy of manipulator with clearances under consideration of member bar's weight[J]. Journal of huazhong University of Science and Technology (natural science edition), 2008, 46(3): 75-79. (  0) 0)
|
| [13] |
董楸煌, 陈力. 柔性空间机械臂捕获卫星碰撞动力学分析、镇定运动神经网络控制及抑振[J]. 机械工程学报, 2014, 50(9): 34-42. DONG Qiuhuang, CHEN Li. The impact dynamics analysis of flexible space manipulator capturing a satellite and neural network calming motion control and vibration suppression[J]. Journal of mechanical engineering, 2014, 50(9): 34-42. (  0) 0)
|
| [14] |
XU Lixin, LI Yonggang. Investigation of joint clearance effects on the dynamic performance of a planar 2-DOF Pick-and-place parallel manipulator[J]. Robotics and computer-integrated manufacturing, 2014, 30(1): 62-73. DOI:10.1016/j.rcim.2013.09.002 (  0) 0)
|
| [15] |
JAWALE H P, THORAT H T. Comparison of open chain and closed chain planar two degree of freedom manipulator for positional error[J]. Journal of mechanisms and robotics, 2014, 6(2): 024501. DOI:10.1115/1.4026329 (  0) 0)
|
| [16] |
韩金华, 王海龙, 王刚, 等. 仿蟹机器人横行步态运动稳定性及能耗分析[J]. 哈尔滨工程大学学报, 2017, 38(6): 898-906. HAN Jinhua, WANG Hailong, WANG Gang, et al. Stability and energy consumption of laterally walking gait in crablike robots[J]. Journal of Harbin Engineering University, 2017, 38(6): 898-906. (  0) 0)
|
| [17] |
LI Yuanyuan, CHEN Guoping, SUN Dongyang, et al. Dynamic analysis and optimization design of a planar slider-crank mechanism with flexible components and two clearance joints[J]. Mechanism and machine theory, 2016, 99: 37-57. DOI:10.1016/j.mechmachtheory.2015.11.018 (  0) 0)
|
| [18] |
ZHAO Bo, ZHANG Zhinan, DAI Xudong. Modeling and prediction of wear at revolute clearance joints in flexible multibody systems[J]. Proceedings of the institution of mechanical engineers, Part C:Journal of mechanical engineering science, 2014, 228(2): 317-329. DOI:10.1177/0954406213486384 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


