2. 西安航天精密机电研究所, 陕西 西安 710100
2. Xi'an Aerospace Precision Mechatronics Institute, Xi'an 710100, China
凹凸半球是半球型动压陀螺电机的核心部件,其精密程度和品质优劣直接影响到半球动压陀螺电机的整体精度。凹凸半球由形状的对称性、加工误差、加工应力引起的变形,会导致气体轴承气膜间隙不均匀,影响轴承转子的回转精度,最终造成气体动压轴承刚度和承载力变低[1-2],导致产品的可靠性变差。基于球面展成原理的定心变角旋转加工法是半球超精密加工[3-4]的最佳方法之一,目前对半球研磨轨迹的研究较少,主要集中在对全球研磨均匀性的研究。程相文[5]通过坐标转换法对四轴球体研磨机研磨轨迹进行了研究,文献[6-7]基于数值模拟的方法研究了双自转研磨方式下研磨盘转速曲线对研磨轨迹的影响,郑斌[8]采用正交实验对研磨参数进行优化组合实现提高球体表面质量的目的,Liang等[9]利用一种近似球面的自由曲面近似算法在半精加工中得到近似球面,文献[10]通过建立自转角和轨迹的关系模型对单转盘变曲率槽球面磨削进行研究。因此,关于半球研磨均匀性评价方法和设计参数对均匀性的研究很有必要,本文利用材料去除理论对定心变角旋转加工法的加工原理进行研究, 开展了半球研磨均匀性三维运动和加工仿真, 且进行试验验证。
1 定心变角旋转加工原理及结构模型 1.1 半球加工原理文献[11-15]通过实验建立起研磨过程中材料去除量与研具摩擦做功的联系:
| $ \mathrm{d} H / \mathrm{d} t=k p v $ | (1) |
式中:dH/dt是单位时间内材料去除量;k是与半球材料、研具材料、研料粒度相关的系数;p是研具与半球之间的压强;v是研具与半球之间的相对速度。
定心变角旋转加工法的研具与半球相对运动关系如图 1所示,半球的半径是r1,研具的半径是r2,半球的转动速度是w1,研具的摆动速度是w2,研具的自转速度是w3,研具与半球的夹角是θ,其中w1、w2、w3全部为角速度。
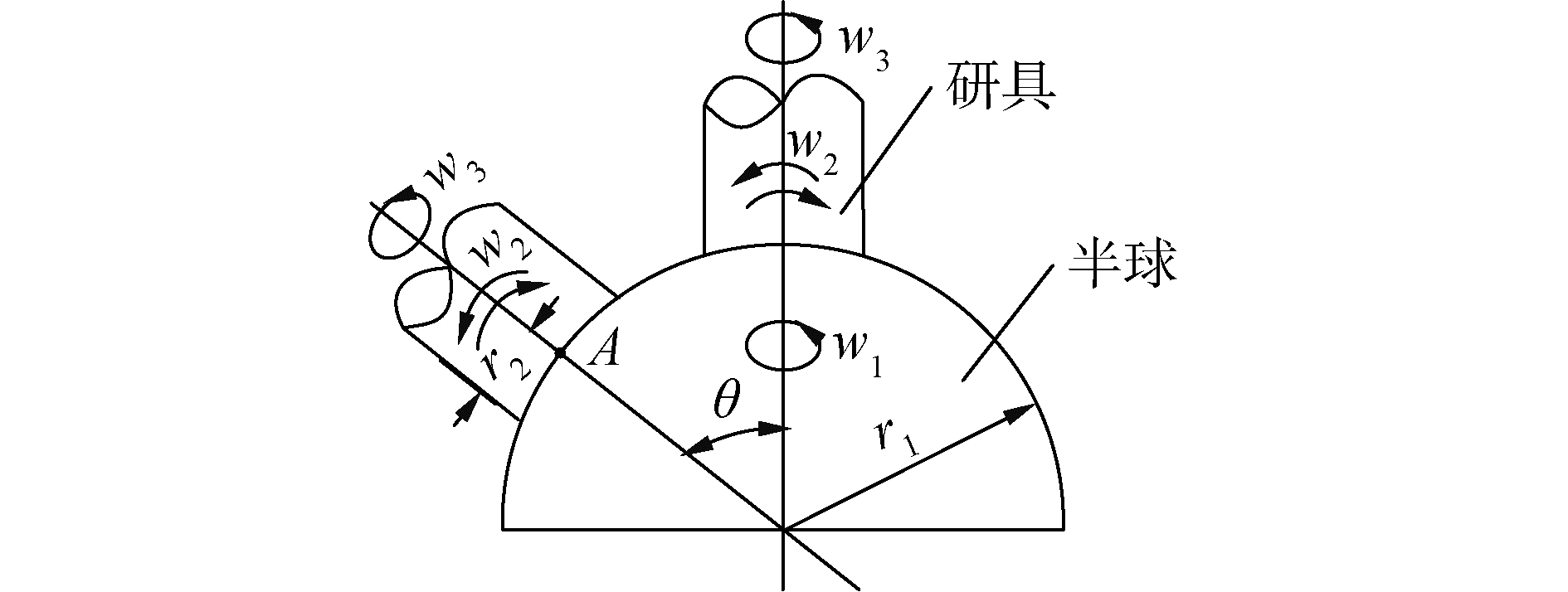
|
Download:
|
| 图 1 研具与半球相对运动关系示意 Fig. 1 Diagram of relative motion relation between tool and hemisphere | |
研具与半球的相对速度v主要由3部分组成,半球的转动速度v1、研具的摆动速度v2和研具的自转速度v3,其中v、v1、v2、v3全部为线速度。研具摆动角度为θ时,其与半球的接触点是A,半球上A点的转动速度v1为:
| $ {\mathit{\boldsymbol{v}}_1} = {\mathit{\boldsymbol{w}}_1}{\mathit{\boldsymbol{r}}_1}\sin \theta $ | (2) |
研具的摆动速度v2为:
| $ \boldsymbol{v}_{2} =\boldsymbol{w}_{2} \boldsymbol{r}_{1} $ | (3) |
研具的自转速度v3为:
| $ \boldsymbol{v}_{3}=\boldsymbol{w}_{3} \boldsymbol{r}_{2} $ | (4) |
速度v由v1、v2和、v3合成,工件带动研具旋转,v1与v3同向,方向与纸面垂直,相对速度为二者之差,v2位于纸面内,所以速度v可表示为:
| $ \mathit{\boldsymbol{v}} = \sqrt {{{\left( {{\mathit{\boldsymbol{v}}_1} - {\mathit{\boldsymbol{v}}_3}} \right)}^2} + \mathit{\boldsymbol{v}}_2^2} $ | (5) |
将式(5)代入式(1)中,得出材料去除率dH/dt与速度v的关系为:
| $ {\rm{d}}H/{\rm{d}}t = kp\mathit{\boldsymbol{v}} = kp\sqrt {{{\left( {{\mathit{\boldsymbol{v}}_1} - {\mathit{\boldsymbol{v}}_3}} \right)}^2} + \mathit{\boldsymbol{v}}_2^2} $ | (6) |
式中:压强p是定值,可以测出; 系数k也是定值,所以对分析没有影响。可以看出材料去除率与半球的转动速度、研具的摆动速度和自转速度有关,而研具的自转速度相对于半球的转动速度很小,所以在忽略研具自转速度的情况下,只需要通过调整半球的转动速度和研具的摆动速度就可以控制研磨的均匀性。
1.2 半球研磨机结构模型图 2所示为研磨机运动原理图,研磨机研磨时的运动主要是由2部分组成:1)主轴电机通过主动齿轮和从动齿轮带动主轴,从而带动安装于工作台上的半球的旋转运动;2)摇摆电机通过曲柄、连杆和摇杆带动研磨主轴的摇摆运动。研磨棒安装于研磨主轴的下方,且下部涂有研磨膏,研磨棒带动研磨膏一起运动,通过研磨机的旋转运动和摇摆运动实现半球的精密加工。
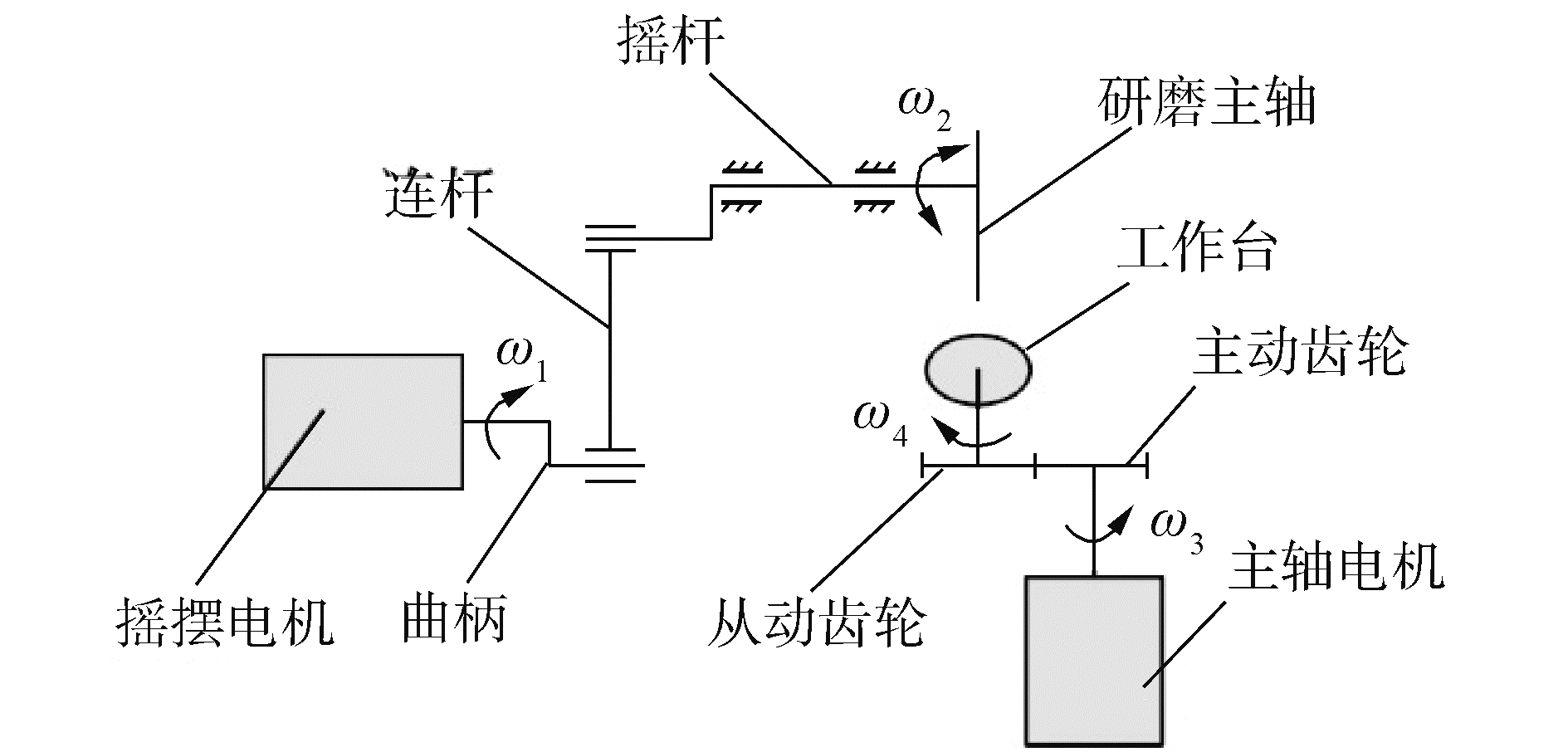
|
Download:
|
| 图 2 研磨机运动原理 Fig. 2 Motion schematic diagram of grinding machine | |
为了更好的研究研磨机的运动规律,应用三维软件UG对研磨机的运动机构进行三维建模,其整体结构如图 3所示。
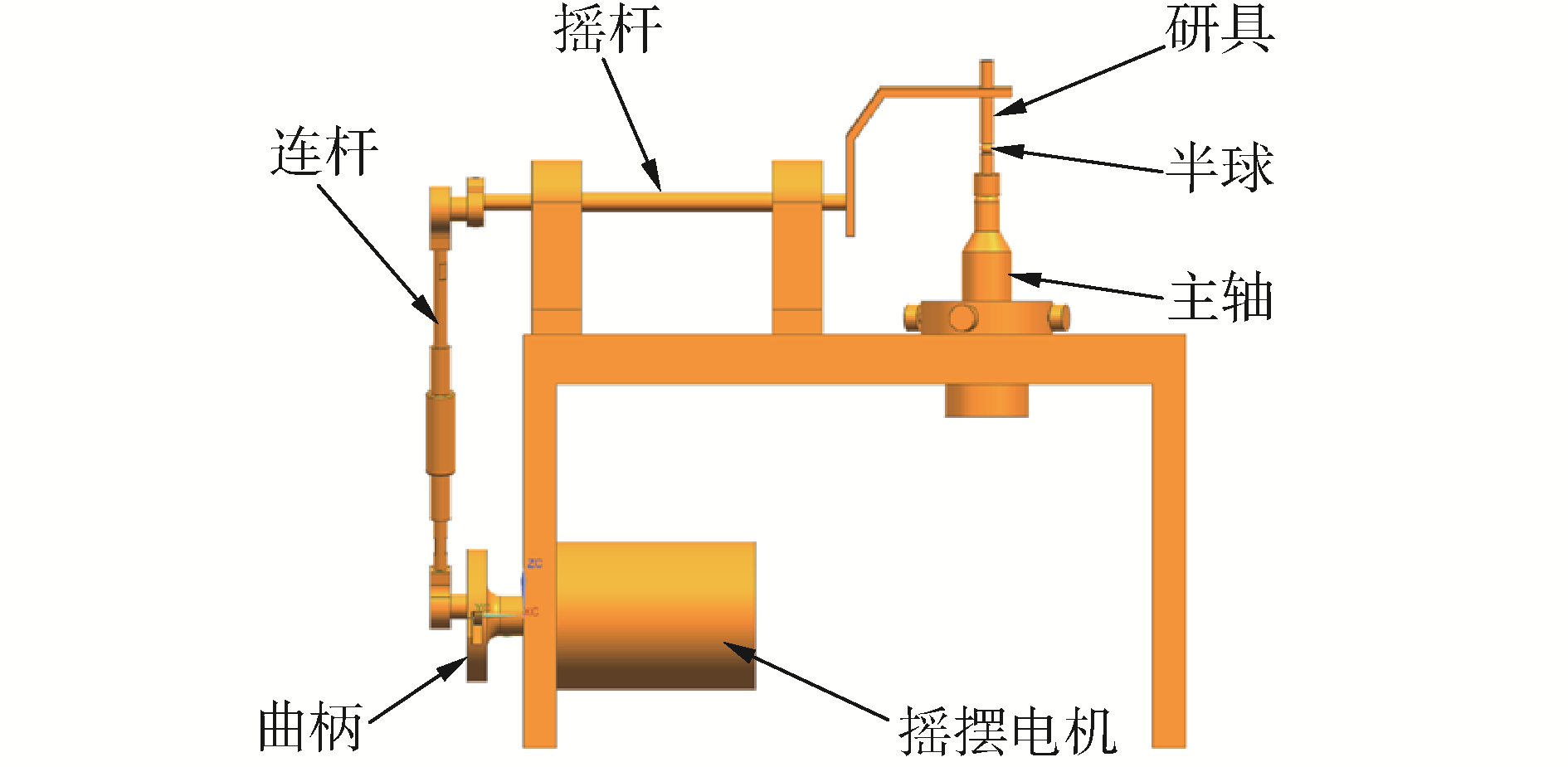
|
Download:
|
| 图 3 研磨机三维示意 Fig. 3 3D diagram of grinding machine | |
应用UG的运动仿真模块对研磨机进行运动仿真,设置主轴电机和摇摆电机的初始转速都是60 r/min。通过运动仿真,得到研磨棒运动的速度和加速度图,可以作为后续加工运动仿真的输入,研磨仿真的输入必须给出研磨棒的角速度—位置曲线图和角加速度—位置曲线图,分别如图 4、图 5所示。
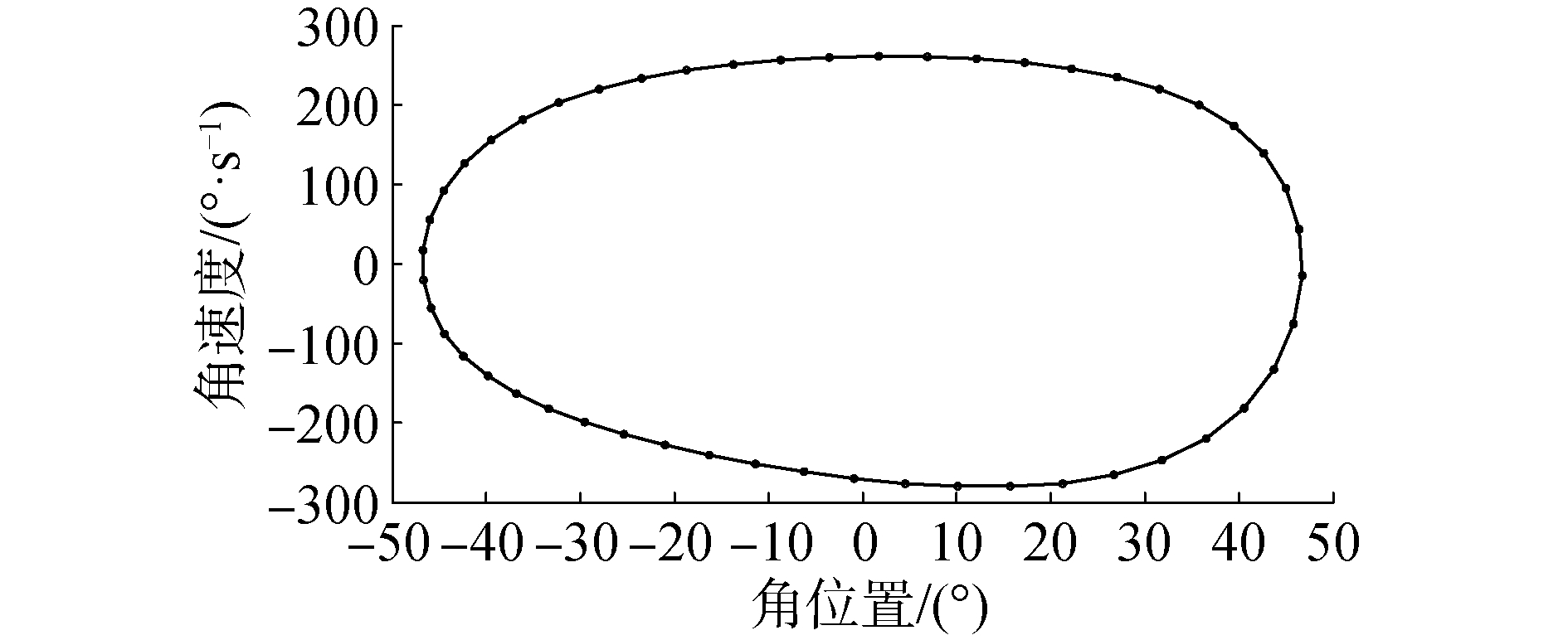
|
Download:
|
| 图 4 研磨棒角速度—位置曲线 Fig. 4 Angular velocity and displacement curve of grinding tool | |

|
Download:
|
| 图 5 研磨棒角加速度—位置曲线 Fig. 5 Angular acceleration and displacement curve of grinding tool | |
角速度—位置曲线和角加速度—位置曲线都是光滑且连续封闭的,说明研磨棒的摆动是平稳的。研磨棒的摆动角度是-46.74°~46.74°,每一个位置对应的角速度和角加速度是不同的,顺时针旋转时速度先增大后减小,逆时针旋转时速度先减小后增大,在2个极限位置(±46.74°)对应的角速度最小。角速度呈不严格对称分布,顺时针旋转时最大值是261.2(°)/s,出现在4.35°处,逆时针旋转时最大值是280.5(°)/s,出现在12.95°处,加速度曲线的不完全重合也证明了这一点。
2.2 轨迹仿真本文应用数字化加工仿真和模拟软件Vericut对研磨机的研磨过程进行仿真,以得到的研磨棒角速度—位置曲线和角加速度—位置曲线作为输入,通过调整摆动角度、摆动速度和旋转速度得到最佳结果。
图 6所示为研磨机加工仿真截图,按照1:1的比例开展机床、夹具、工装和毛坯全方位加工仿真,对实际的加工情况进行完美模拟。
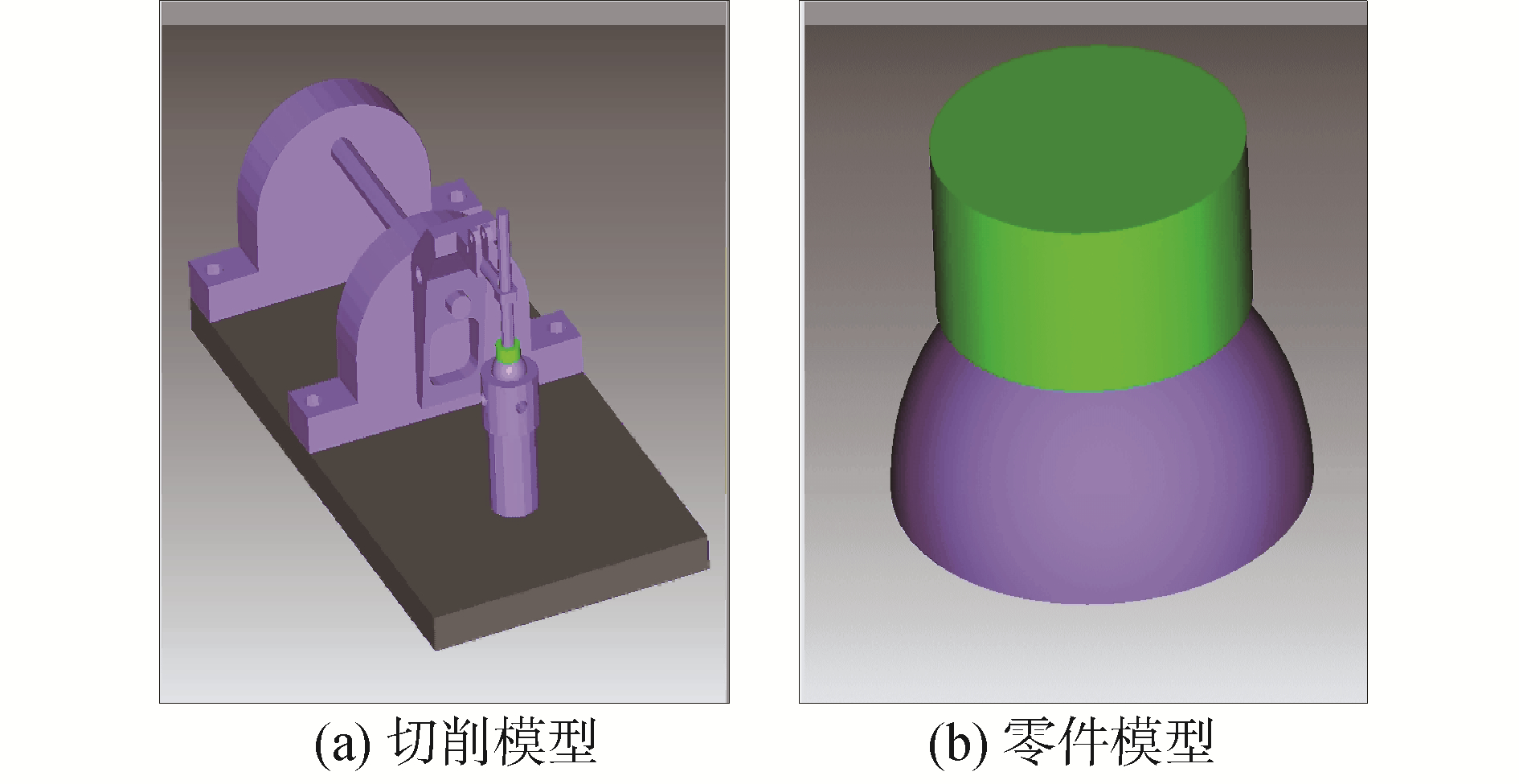
|
Download:
|
| 图 6 研磨机加工仿真 Fig. 6 Machining simulation of grinding machine | |
为了验证摆动角度对研磨均匀性的影响,寻找合理的角度值,只调整摆动角度观察其最终加工效果。
图 7分别是摆动角度为30°、33°和36°时的最终加工效果,验证在无限长的时间内,摆动角度对球面加工的影响,深色区域为研具与半球的接触区域,可以看出图 7(a)中半球顶部和根部存在波浪形未覆盖区域,即加工盲区,图 7(b)中半球根部存在狭窄环形加工盲区,图 7(c)中不存在加工盲区,可见摆动角度设置的不合理会造成加工盲区的出现。

|
Download:
|
| 图 7 摆动角度对球面加工的影响 Fig. 7 Influence of swing angle on machining | |
通过仿真发现,摆动角度的临界数值为36°,小于此角度时存在加工不到的情况,大于此角度时则存在空刀的现象,所以最佳摆动角度为36°。
摆动速度和旋转速度的比值对研磨也有影响,值设置的太小的话严重影响加工效果,设置的太大的话结构运动的不平衡性将成倍的增加,且存在加工均匀性的问题,所以也必须设置一个合理的摆动速度和旋转速度。
通过调整摆动速度,保证旋转速度(60 r/min)不变,验证其对研磨均匀性的影响。图 8分别是摆动速度和旋转速度的比值为1、1.5和2时的最终加工效果,验证在一定的时间内,调整摆动速度与旋转速度的比例关系来观察最后的加工效果,可以看出图 8(a)、(b)中单位时间内研具未实现与球面的全接触,且存在重复加工的区域,影响研磨速度,从而证明速度比率对于加工质量有很大影响。

|
Download:
|
| 图 8 速度比值对球面加工的影响 Fig. 8 Influence of velocity rate on machining | |
图 9是将研磨时间设置为无限长,将摆动速度与旋转速度的比值设置为2/3时的最终加工图,存在始终加工不到的区域,由此可见,速度比率关系设置的不合理会造成研磨盲区的出现。

|
Download:
|
| 图 9 研磨盲区效果 Fig. 9 Effect of grinding blind area | |
通过仿真发现,将研磨棒的摆动角度设置成36°,且将摆动速度与主轴旋转速度的比值调整为2时,就可以有效避免加工盲区的出现,也能使得研磨的均匀性更好,可以在最短的时间内实现研磨轨迹在球面的全部覆盖。
3 半球研磨试验验证试验以GT35材料凹半球为加工对象,分别在摆动速度与旋转速度的比值为1和2的条件下研磨,在相同的研磨环境下,设置加工载荷为15 N,研磨时间为60 min,旋转速度为60 r/min,摆动角度为36°。对半球进行半精研,分别使用W14碳化硼研磨膏和W5、W1金刚石研磨膏研磨20 min。
共进行了3组对比试验,并从中随机选取一组半球在200倍的显微照相机下照相,如图 10所示。图 10(a)是速度比值为1的条件下的加工效果图,可以看出半球的光洁度较差,且球面亮度不一致,说明该半球存在没有研磨到位的点,研磨均匀性较差。图 10(b)是速度比值为2的条件下的加工效果图,半球表面质量则刚好相反,球面研磨的均匀性较好,这点恰好与图 8中的轨迹仿真相符。

|
Download:
|
| 图 10 不同速度比值下半球的研磨效果 Fig. 10 Hemisphere grinding effects of different velocity rate | |
使用三坐标测量仪分别测量3组半球的球径、球心距和3个方向的圆度,如表 1所示,155#~157#和158#~160#半球分别是在摆动速度与旋转速度的比值为1和2的条件下研磨的。
| 表 1 半球研磨数据对比表 Table 1 Hemisphere grinding data contrast |
半精研的要求是:圆度小于等于0.3 μm,球径小于等于Sϕ15.6°—0.0030,球心距小于等于0.01~0.1,而表 3中155#~157#半球的0°水平圆度和±15°倾斜圆度均存在超差,这点与数值仿真的结果相吻合(图 8(a)所示),说明155#~157#半球在底部存在不均匀分布的高点,相反158#~160#半球的圆度都在偏差范围内,进一步说明了158#~160#半球的均匀性更好,从而验证了数值模拟的正确性。
球心距是指球心到半球端面的距离,球径是通过测量半球一周上的点的数据再取平均值获得的,二者的数量级都是毫米级的,而研磨属于超精密加工,其数量级是微米的,所以研磨对球心距与球径的影响不大。
以上试验数据与仿真结果相一致,表明数值模拟的结论能够指导生产,通过调整摆动速度与旋转速度的比值,可以达到均匀研磨的目的。
4 结论1) 研磨棒摆动角度主要影响加工区域,角度小时存在研磨盲区,角度大时存在空走刀,36°为最佳的摆动角度。
2) 摆动速度和旋转速度比值影响加工区域的覆盖均匀性,当比值为2时,研磨棒覆盖球面的均匀性最好。
3) 半球研磨均匀性不仅包括加工区域的全覆盖,还包括研磨棒覆盖加工区域频率的一致性,必须同时满足前两条的最优,才能实现半球研磨均匀性的最优。
本文采用了全新的三维运动分析与加工仿真的研究方法,研究过程易于理解,为后续球面均匀性研究提供了一种新思路。
| [1] |
王京锋, 刘景林, 闫亚超, 等. 半球型动压气体轴承陀螺电机设计及性能测试[J]. 哈尔滨工业大学学报, 2017, 49(9): 144-150. WANG Jingfeng, LIU Jinglin, YAN Yachao, et al. Design and performance testing of hemispheric aerodynamic bearing gyro motor[J]. Journal of Harbin Institute of Technology, 2017, 49(9): 144-150. (  0) 0)
|
| [2] |
YUAN J L, WANG Z W, LYU B H, et al. Simulation study on the developed eccentric V-grooves lapping mode for precise ball[J]. Key engineering materials, 2005, 304-305: 300-304. (  0) 0)
|
| [3] |
纪宏波, 刘成刚. 高精度球体研磨加工技术的现状和发展[J]. 机械研究与应用, 2016, 29(3): 205-207. JI Hongbo, LIU Chenggang. The situation and development of high-precision ball lapping technique[J]. Mechanical research & application, 2016, 29(3): 205-207. (  0) 0)
|
| [4] |
YAN Jiwang, TAMAKI J, SYOJI K, et al. Single-point diamond turning of CaF2 for nanometric surface[J]. International journal of advanced manufacturing technology, 2004, 24(9/10): 640-646. (  0) 0)
|
| [5] |
程相文, 王凌霄. 四轴球体研磨机研磨轨迹的研究[J]. 制造业自动化, 2013, 35(20): 98-100, 107. CHENG Xiangwen, WANG Lingxiao. Research on lapping trace of four cup lapping machine[J]. Manufacturing automation, 2013, 35(20): 98-100, 107. DOI:10.3969/j.issn.1009-0134.2013.20.028 (  0) 0)
|
| [6] |
张坤领, 韦建军. 基于Matlab的数控磨削球面粗糙度分析及仿真[J]. 组合机床与自动化加工技术, 2010(3): 16-21. DOI:10.3969/j.issn.1001-2265.2010.03.005 (  0) 0)
|
| [7] |
ZHANG Kunling, WEi Jianjun. Analysis and simulation of numerical control grinding spherical roughness based on Matlab[J]. Combined machine tool and automatic machining technology, 2010(3): 16-21. (  0) 0)
|
| [8] |
郁炜, 吕冰海, 姚蔚峰, 等. 基于ADAMS的球体双自转研磨方式下研磨盘转速优化研究[J]. 中国机械工程, 2013, 24(7): 866-872, 881. YU Wei, LYU Binghai, YAO Weifeng, et al. Speed optimization for lapping plates in RDP lapping mode based on ADAMS[J]. China mechanical engineering, 2013, 24(7): 866-872, 881. DOI:10.3969/j.issn.1004-132X.2013.07.004 (  0) 0)
|
| [9] |
YU W, LIU D, YUAN J L, et al. Processing of lapping track in dual rotated plates eccentric lapping mode[J]. Key engineering materials, 2011, 487: 248-252. DOI:10.4028/www.scientific.net/KEM.487 (  0) 0)
|
| [10] |
郑斌, 袁巨龙, 赵萍, 等. 变曲率沟槽精密球研磨加工优化实验研究[J]. 表面技术, 2017, 46(2): 214-219. ZHENG Bin, YUAN Julong, ZHAO Ping, et al. Experiment of optimized grinding of precision ball with variable-radius groove[J]. Surface technology, 2017, 46(2): 214-219. (  0) 0)
|
| [11] |
刘伟, 邓朝晖, 万林林, 等. 基于正交试验-遗传神经网络的陶瓷球面精密磨削参数优化[J]. 中国机械工程, 2014, 25(4): 451-455. LIU Wei, DENG Zhaohui, WAN Linlin, et al. Parameter optimization on precision grinding of ceramic sphere using orthogonal experiment and genetic neural network[J]. China mechanical engineering, 2014, 25(4): 451-455. DOI:10.3969/j.issn.1004-132X.2014.04.005 (  0) 0)
|
| [12] |
LIANG Fusheng, ZHAO Ji, JI Shijun, et al. Spherical approximation of free-form surface closed to a sphere in semi-finishing[J]. Key engineering materials, 2016(679): 199-206. (  0) 0)
|
| [13] |
郭伟刚, 袁巨龙, 项震, 等. 基于单转盘变曲率沟槽研磨方法的球体加工试验研究[J]. 表面技术, 2018, 47(7): 252-258. GUO Weigang, YUAN Julong, XIANG Zhen, et al. Spheroidal machining test based on variable turning curvature grinding method with single turntable[J]. Surface technology, 2018, 47(7): 252-258. (  0) 0)
|
| [14] |
PRESTON F W. The theory and design of plate glass polishing machines[J]. Journal of the society of glass technology, 1927(11): 214-256. (  0) 0)
|
| [15] |
周芬芬, 袁巨龙, 姚蔚峰, 等. 陶瓷球成球过程的建模与仿真[J]. 华中科技大学学报(自然科学版), 2016, 44(2): 128-132. ZHOU Fenfen, YUAN Julong, YAO Weifeng, et al. Modeling and simulation on sphere-shaping of ceramic balls[J]. Journal of Huazhong University of Science and Technology (natural science edition), 2016, 44(2): 128-132. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


