2. 高新船舶与深海开发装备协同创新中心, 上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
声强指的是在某点上单位时间通过的垂直于指定方向的单位面积的平均声能,可用于识别振动结构表面的声辐射热区。倏逝波是结构振动带来的亚声速(Subsonic)波形成的非辐射波,传播会沿着和结构表面相切的方向进行,幅值则会随着传播距离的改变而沿着结构表面的法线方向呈现出按指数衰减的趋势,所以该波只会贡献于近场声压。但是传播波指的是结构振动带来的超声速波而形成的辐射波,无论是远场声压还是近场声压都能够作出贡献,远场仅可测出传播波。所以,在振动结构表面的远场声辐射热区使用声强来进行识别时,应使用一定的方法过滤掉倏逝波,得到只包含传播波成分的超声速声强[1]。超声速声强是与傅里叶声学和角谱理论相联系的[1-2]。稳态声场可表示为平面波(传播波和倏逝波)的叠加[1];在波数域中以波数为半径的辐射圆中的平面波都是传播波,在辐射圆外的都是倏逝波;传播波即为超声速波,倏逝波即为亚声速波;超声速波和亚声速波并不是指声波实际的传播速度超过或低于声速,而是指声波在空间直角坐标轴上投影的迹波速度大于或小于声速;通过超声速声强能够有效识别出结构声辐射表面对远场声辐射有贡献的热点区域,如板声辐射的角辐射模态和边辐射模态等。近年来,除超声速声强[3-4]外,表面贡献方法、非负声强和有用声强等[5-8]被提出和应用于结构振动表面远场声辐射热区的识别。
表面阻尼处理[9]是一种常用的减振降噪方法,其通过在结构表面敷设阻尼来抑制结构共振和辐射噪声。局部阻尼处理一般是将阻尼敷设在结构的一些减振降噪关键位置,这样就会导致结构阻尼的不均匀分布,进而导致结构的复模态振动[10]。在实模态情况下,各点只有2个振动相位差,要么是0°,要么是180°,从结构中的各点来看,振动速度取极值是同时的,从平衡位置经过也是同时的;但是就复模态情况而言,考虑到阻尼会带来一定影响,结构中的各点取极值是不同时的,同样从平衡位置经过也不是同时的,都是存在先后之分的,和实模态振型不同,并无稳定节线或者是节点。Unruh[11]对非均匀敷设阻尼板的复模态进行了分析,指出所有类型的板振动复模态都是耦合的,尤其是存在非对称敷设阻尼时,复模态会存在较为明显的耦合作用并会带来非常显著的影响。张鑫等[12]对非均匀阻尼板不同构型的阻尼效果进行了分析。目前还未看到非均匀阻尼敷设导致的复模态对超声速声强影响的研究,本文探讨了不同的阻尼敷设型式、不同面积的阻尼、不同的阻尼比等情况下,阻尼板复模态对超声速声强的影响。
由于阻尼层材料的厚度、覆盖面积和形状等分布方式会导致其复模态有较大不同。Koruk等[13]对使用模态振型复杂度指标(mode shape complexity,MSC)、模态相位共线指标(modal phase collinearity,MPC)、平均相位偏差指标(mean phase deviation,MPD)、模态复杂因子(mode complexity factor,MCF)、模态相关因子(modal correlation coefficient,MCC)等对复模态振型存在的复杂性进行描述的各大指标进行了比较,指出MSC是较可靠的复模态复杂性指标。Unruh[11]基于声辐射效率采用复模态辐射指数(complex mode radiation index,CMRI)来表征复模态结构声辐射的复杂性。
综上所述,本文以非均匀阻尼板为研究对象,以MSC为复模态复杂性指标,分析了不同复模态的对应的超声速声强,而后对辐射声功率和复模态复杂度存在何种关系进行了探讨,指出可用复模态声辐射复杂度指标CMRC表示复模态声辐射的复杂程度及其相应特性。
1 理论 1.1 非均匀阻屁和复模态对于多自由系统而言,其振动方程为:
| $ \mathit{\boldsymbol{M\ddot x}} + \mathit{\boldsymbol{C\dot x}} + \mathit{\boldsymbol{Kx}} = \mathit{\boldsymbol{f}}\left( t \right) $ | (1) |
式中:x表示的是位移向量;M表示质量阵;C表示阻尼阵;K表示刚度阵;f(t)是激励力向量。
如果利用的是比例阻尼模型,那么可用式(2)来表征阻尼阵C:
| $ \mathit{\boldsymbol{C}} = \alpha \mathit{\boldsymbol{M}} + \beta \mathit{\boldsymbol{K}} $ | (2) |
式中α和β均是比例系数。本文为对非均匀阻尼会如何影响到板超声速声强展开探讨,针对板的各个部位设定的阻尼比也会各不相同,其阻尼阵为:
| $ \mathit{\boldsymbol{C}} = \sum\limits_{i = 1}^n {{\alpha _i}{\mathit{\boldsymbol{M}}_i}} + \sum\limits_{i = 1}^n {{\beta _i}{\mathit{\boldsymbol{K}}_i}} $ | (3) |
式中n为不同阻尼区域的数量。由式(3)可见,阻尼阵C已经不是比例阻尼,其对应的特征值问题为:
| $ \left( {\mathit{\boldsymbol{M}}{\lambda ^2} + \mathit{\boldsymbol{C}}\lambda + \mathit{\boldsymbol{K}}} \right)\psi = 0 $ | (4) |
它具有N对复共轭特征值λi, λi*和相对应的特征向量ψi、ψi*[14]:
| $ {\lambda _i} = {\sigma _i} + {\rm{i}}{w_i} $ | (5) |
| $ {\mathit{\boldsymbol{\psi }}_i} = {\left[ {\begin{array}{*{20}{l}} {{r_{i1}}{{\rm{e}}^{ - i{\varphi _{i1}}}}}&{{r_{i2}}{{\rm{e}}^{ - i{\varphi _{i2}}}}}&\mathit{\boldsymbol{K}}&{{r_{{\rm{in}}}}{{\rm{e}}^{ - i{\varphi _{{\rm{i}}n}}}}} \end{array}} \right]^{\rm{T}}} $ | (6) |
式中σi、wi、rik和φik均是实数。
1.2 复模态的模态复杂度指标Koruk等[13]采用振动周期内的系统应变能的最大值除最小值所得到的值MSC代表复模态复杂度。第r阶复模态的复杂度定义为:
| $ {\rm{MSC}} = \min \left( {{U_r}} \right)/\max \left( {{U_r}} \right) $ | (7) |
式中Ur是振动结构在第r阶复模态时的应变能,可以表示为:
| $ {U_r}(t) = \mathit{\boldsymbol{X}}_r^{\rm{T}}(t) \cdot \mathit{\boldsymbol{K}} \cdot {\mathit{\boldsymbol{X}}_r}(t)/2 $ | (8) |
式中Xr(t)是结构在第r阶复模态振动时的位移向量;K是结构的刚度矩阵;Xr(t)可以表示为:
| $ {X_{rk}}(t) = {\psi _{rk}}\cos \left( {2{\rm{ \mathsf{ π} }}t/{T_r} + {\varphi _{rk}}} \right) $ | (9) |
式中φrk表示的是复模态振型ψr内第k个元素对应的相角;Tr是第r阶复模态的周期。
按照MSC的定义,其值为0~1,实模态时MSC值为0,MSC值越大其复模态复杂程度越高,完全复模态时MSC值为1。
Unruh利用实模态振型的声辐射效率和复模态振型的声辐射效率定义了一个声辐射的评价指标复模态辐射指数CMRI来衡量同等振型复杂程度下复模态的声辐射能力,计算公式为:
| ${\rm{CMRI}} = \int_0^{{f_i}} {\frac{{|10{\rm{lg}}\left( {\left| {{\sigma _r}(f) - {\sigma _n}(f)} \right|} \right)|}}{{{\rm{MCI}}}}} {\rm{d}}f $ | (10) |
式中:σr是振动结构未敷设阻尼以实模态振动时的声辐射效率;σn是振动结构敷设阻尼之后以复模态振动时的声辐射效率;fi是这阶复模态的固有频率;MCI是模态共线性指数,其计算式定义为:
| ${\rm{MCI}} = 1 - \frac{{\left| {{\mathop{\rm Re}\nolimits} {{\left( {{{\tilde V}_n}} \right)}^{\rm{T}}}{\mathop{\rm Im}\nolimits} \left( {{{\tilde V}_n}} \right)} \right|}}{{\sqrt {\left[ {{\mathop{\rm Re}\nolimits} {{\left( {{{\tilde V}_n}} \right)}^{\rm{T}}}{\mathop{\rm Re}\nolimits} \left( {{{\tilde V}_n}} \right)} \right]\left[ {{\mathop{\rm Im}\nolimits} {{\left( {{{\tilde V}_n}} \right)}^{\rm{T}}}{\mathop{\rm Im}\nolimits} \left( {{{\tilde V}_n}} \right)} \right]} }} $ | (11) |
| $ {{\tilde V}_n} = \left( {{V_n}/\max \left( {\left| {{V_n}} \right|} \right)} \right){{\rm{e}}^{j{\rm{ \mathsf{ π} }}/4}} $ | (12) |
式中:Vn是结构表面的法向振速;MCI表示的是复模态振型的复杂程度;CMRI的数值越大则代表在单位模态共线性指标下,实模态与复模态声辐射效率的相对偏差越大。
复模态复杂性指标MSC是从结构振动角度表征复模态振型复杂性。复模态辐射指数CMRI同样把振型的复杂程度考虑进去,其表征结果和MSC类似。为了准确描述复模态的声辐射特性和复杂程度,直接基于辐射声功率定义复模态声辐射复杂度指标(complex mode radiation complexity, CMRC)为:
| $ {\rm{CMRC}} = \left( {{W_{{\rm{sr}}}} - {W_{{\rm{cr}}}}} \right)/{W_{{\rm{sr}}}} $ | (13) |
式中:Wsr代表结构在阻尼不予考虑时的阶数为r的实模态振动声辐射的声功率级;Wcr代表结构在有阻尼敷设时阶数为r的复模态振动声辐射的声功率级。不难发现,CMRC表征在阶数为r时振动结构在辐射声功率级上实模态和复模态之间的相对误差,该值越大就代表复模态有更弱的声辐射能力,相应地声辐射也会更加复杂。
1.3 波数域计算超声速声强的方法空间稳态声场的控制方程为Helmholtz方程:
| $ {\nabla ^2}p + {k^2}p = 0 $ | (14) |
式中:p为频域声压;k=ω/c为波数;ω=2πf为角频率。Helmholtz方程的平面波解为:
| $ p(\omega ) = A(\omega ){{\rm{e}}^{{\rm{i}}\left( {{k_x}x + {k_y}y + {k_z}z} \right)}} $ | (15) |
式中:kx、ky、kz分别为x、y、z3个方向的波数分量,满足:
| $ k_x^2 + k_y^2 + k_z^2 = {k^2} $ | (16) |
从式(16)可以推出:
| $ {k_z} = \sqrt {{k^2} - \left( {k_x^2 + k_y^2} \right)} $ | (17) |
若kx2+ky2 < k2,则kz为实数,此时对应的是传播波,传播波是普通的平面波,可以传播到远场;若kx2+ky2>k2,则kz为虚数,此时对应的是倏逝波。
z=0平面的声场可以表示为:
| $ p\left( {x,y,0} \right) = \frac{1}{{4{{\rm{ \mathsf{ π} }}^2}}}\int {\int_{ - \infty }^{ + \infty } {P\left( {{k_x},{k_y},0} \right){{\rm{e}}^{ - {\rm{i}}\left( {{k_x}x + {k_y}y} \right)}}{\rm{d}}{k_x}{\rm{d}}{k_y}} } $ | (18) |
式中:P(kx, ky, 0)为声压角谱。可以看到,式(18)给出的是傅里叶逆变换的定义式,也就是说p(x, y, 0)为P(kx, ky, 0)的傅里叶逆变换。同样,P(kx, ky, 0)也可以表示为:
| $ P\left( {{k_x},{k_y},0} \right) = \int {\int_{ - \infty }^{ + \infty } {p\left( {x,y,0} \right){{\rm{e}}^{ - {\rm{i}}\left( {{k_x}x + {k_y}y} \right)}}{\rm{d}}x{\rm{d}}y} } $ | (19) |
即P(kx, ky, 0)为p(x, y, 0)的傅里叶变换。同理:
| $ v(x,y,0) = \frac{1}{{4{{\rm{ \mathsf{ π} }}^2}}}\int {\int_{ - \infty }^{ + \infty } {V\left( {{k_x},{k_y},0} \right){{\rm{e}}^{ - {\rm{i}}\left( {{k_x}x + {k_y}y} \right)}}{\rm{d}}{k_x}{\rm{d}}{k_y}} } $ | (20) |
| $ V\left( {{k_x},{k_y},0} \right) = \int {\int_{ - \infty }^{ + \infty } {v\left( {x,y,0} \right){{\rm{e}}^{ - {\rm{i}}\left( {{k_x}x + {k_y}y} \right)}}{\rm{d}}x{\rm{d}}y} } $ | (21) |
式中:v(x, y, 0)表示z=0平面的法向速度;V(kx, ky, 0)则表示其法向速度角谱。
将声压角谱仅在波数圆内积分得到超声速声压为:
| $p^{(s)}(x, y, 0)=\frac{1}{4 {\rm{\pi }}^{2}} \iint_{S_{r}} P\left(k_{x}, k_{y}, 0\right) \mathrm{e}^{-\mathrm{i}\left(k_{x} x+k_{y}\right)} \mathrm{d} k_{x} \mathrm{d} k_{y} $ | (22) |
在波数圆内对法向振速进行积分得到超声速声压为:
| $ {v^{\left( s \right)}}\left( {x,y,0} \right) = \frac{1}{{4{{\rm{\pi }}^2}}}\iint_{{{{S}}_r}} {V\left( {{k_x},{k_y},0} \right){{\text{e}}^{ - {\text{i}}\left( {{k_x}x + {k_y}y} \right)}}{\text{d}}{k_x}{\text{d}}{k_y}} $ | (23) |
式(22)、(23)内的Sr代表的是波数圆内部区域,其内是传播波,上标(s)代表超声速波。求得超声速的声压及其法向速度之后,可知超声速声强和声功率为:
| ${p^{(s)}}(x,y,0) = \frac{1}{2}{\rm{Re}}\left\{ {{p^{(s)}}(x,y,0){v^{(s)}}{{(x,y,0)}^*}} \right\} $ | (24) |
| $ \prod {{\Pi _s}} = \iint\limits_{{S_s}} {{I^{(s)}}(x,y){\text{d}}x{\text{d}}y} $ | (25) |
式中Ss为声源表面。
2 不同复模态复杂度下非均匀阻尼对超声速声强的影响对阻尼层结构的振动声辐射计算,本文使用的是有限元方法,采用商用有限元软件ANSYS进行建模和计算,对结构选用shell63单元进行模拟,并通过定义材料特性(MP)来设置不同部位的不同阻尼比,得到不同复模态复杂度下非均匀阻尼板上各个节点的位移(速度),再通过上节介绍的理论,自编程序计算辐射声压,并进行滤波处理,最后计算出超声速声强。以四边简支的矩形薄板为例进行计算,薄板长0.9 m,宽0.6 m,厚度0.005 m,密度2 700 kg/m3,弹性模量72 GPa,泊松比0.3。声速是343 m/s,空气密度则为1.21 kg/m3。在计算时,无论是边界元还是有限元选用的都是线性四边形单元,开始计算后会对薄板进行划分,使之变成40×24个计算网格,节点总数为1 025,单元总数为960。板的一般区域的阻尼比设置为0.01。
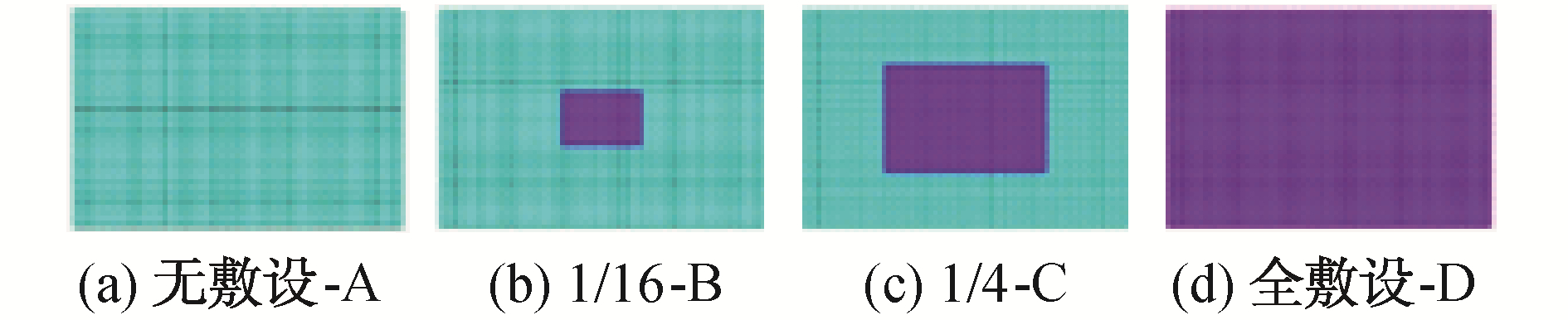
2.1 阻尼敷设面积对超声速声强的影响如图 1所示,(a)、(b)、(c)、(d)为是4种不同面积比例的阻尼构型,其中浅色区域代表阻尼板的一般阻尼区域,深色区域代表高阻尼区域,阻尼比设置为0.2。高阻尼区域的面积逐渐增大,依次为不敷设构型A,1/16中心敷设构型B,1/4中心敷设构型C以及全敷设构型D这4种情况。分析并且计算了如上各种情形,表 1列举出了不同阻尼敷设面积阻尼构型的复模态复杂度,图 2列举出的依次是位移振型的实部、虚部、相位和超声速声强。
|
Download:
|
| 图 1 不同面积比例的阻尼构型 Fig. 1 Damping configuration with different area ratios | |
| 表 1 不同阻尼敷设面积的复模态复杂度 Table 1 Modal complexity of different damping laying area |

|
Download:
|
| 图 2 不同阻尼面积比例构型的计算结果 Fig. 2 Calculation results for different damping area ratio configurations | |
上面的A和D构型,由于整个板结构使用的是同一种比例阻尼,其振型为实模态振型,复模态复杂度也接近于零。从中心敷设部分高阻尼的振型图可以看出,位移振型中的各个元素是复数,且各点的相位差不再是实模态中同相或反相状态,会呈现出一定的坡度变化,属于复模态,但复模态复杂度也不是很高。上述4种情形的超声速声强均能够清晰地看出是角辐射模态。
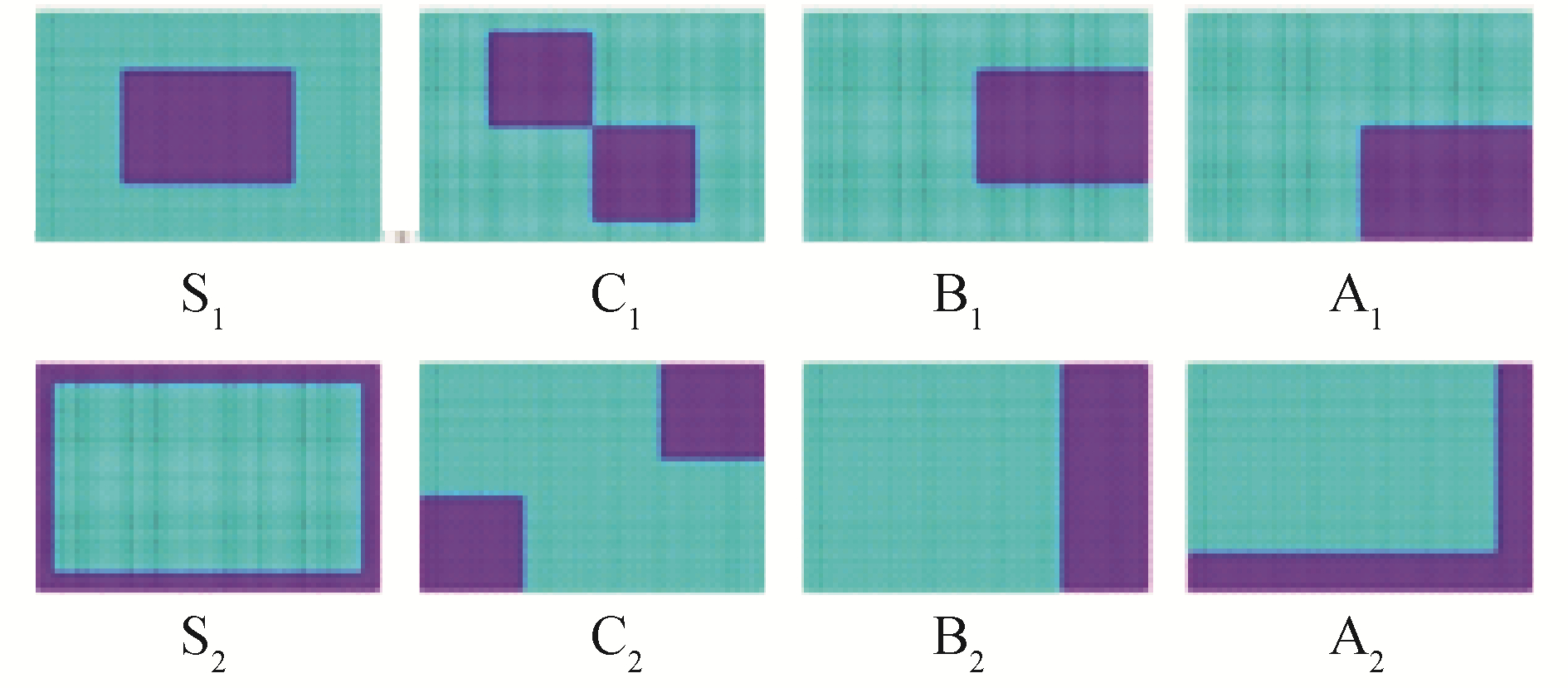
2.2 不同的阻尼分布型式对超声速声强的影响如图 3所示,根据对称性的不同,文献[11]定义了的8种不同的阻尼分布型式,其中对称形式共有4种,分别是完全对称型S、中心对称型C、左右对称型B以及不对称型A,而这4种对称形式又能够分成2种,其一是集中型,其二是分散型。出于方便分析以及比较的目的,在建立阻尼模型的过程中,各种不同的阻尼分布型式的高阻尼敷设面积在薄板面积中的占比为1/4,而且高阻尼比选定为0.2。表 2给出了各种阻尼分布型式阻尼构型的复模态复杂度,位移振型和超声速声强的计算结果可见图 4。
|
Download:
|
| 图 3 不同阻尼分布型式的构型 Fig. 3 Different configurations of damping distributions | |
| 表 2 不同阻尼分布型式的复模态复杂度 Table 2 Modal complexity of different damping distributions |

|
Download:
|
| 图 4 不同阻尼分布型式的计算结果 Fig. 4 Calculation results for different damping distributions | |
图 4显示的是位移振型所得到的结果,不难发现,由于对称性以及敷设位置的区别导致阻尼效果也各不相同,也就是说(5, 3)模态图像所列示出相位以及虚部是各不相同的。就复模态复杂度而言,A2、A1 2种不对称阻尼分布型式无疑是最高的。但是单从超声速声强得到的结果图像可知,对于阻尼分布型式而言,不管是在对称性上存在不同还是在布置方式上呈现出分散或者是集中,超声速声强都可以清晰地指明辐射到远场的声能量来自非均匀阻尼板的4个角落,所以,阻尼分布型式各不相同的简支板复模态并不会给超声速声强带来很大的影响。
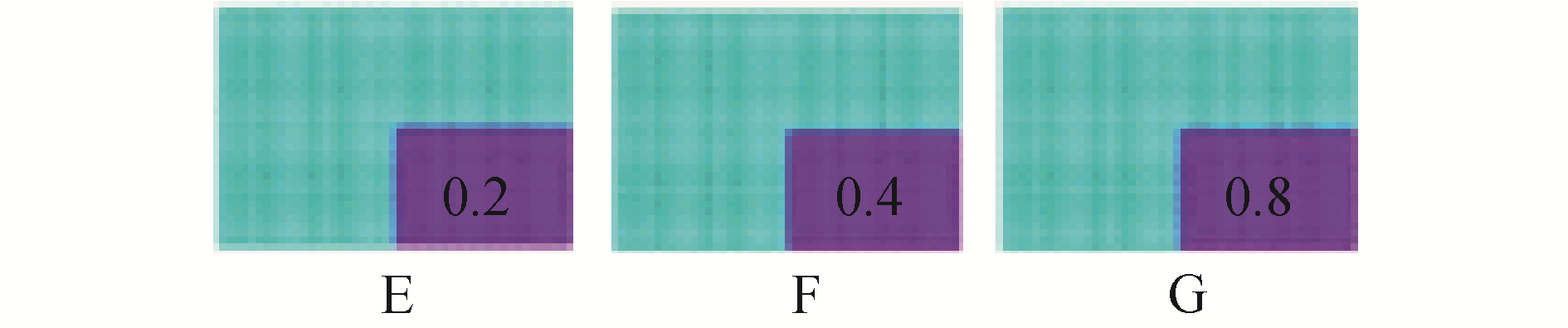
2.3 不同的附加阻尼比对超声速声强的影响如图 5所示,以2.2中复模态复杂度最高的A1作为基础模型,以高阻尼区域为对象,依次将其阻尼比设定成0.2、0.4与0.8,而且敷设面积依旧为薄板结构总面积的1/4。表 3列举出了不同附加阻尼比A1构型的复模态复杂度,位移振型和超声速声强的计算结果如图 6所示。
|
Download:
|
| 图 5 不同附加阻尼比的A1构型 Fig. 5 A1 configuration with different additional damping ratios | |
| 表 3 不同附加阻尼比A1模型的复模态复杂度 Table 3 Modal complexity of A1 configuration with different additional damping ratios |
|
Download:
|
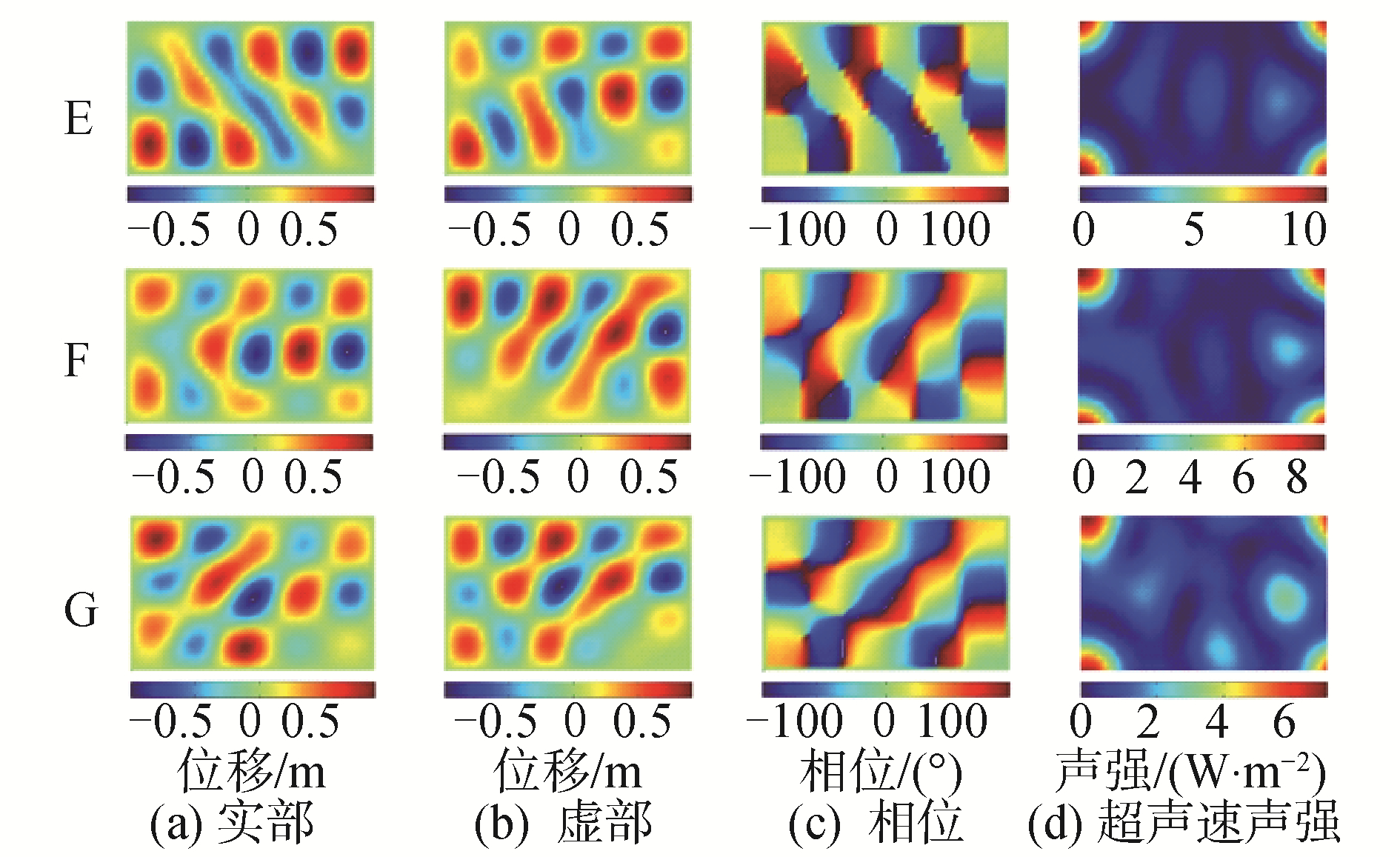
| 图 6 不同附加阻尼比构型的计算结果 Fig. 6 Calculation results of different additional damping ratio configurations | |
从复模态复杂度的角度来看,复模态复杂度会随着附加阻尼比的增大而明显增高,从超声速声强的结果图会发现,当该阶复模态复杂度很高的时候,辐射到远场的声能量热点区域并不能与低模态复杂度一样有着足够清晰且均匀的表现,同时图像中部还会有未被抵消的强度较低的热点区域出现,但依旧能够识别出该构型对远场声辐射有贡献的区域是角辐射模态。
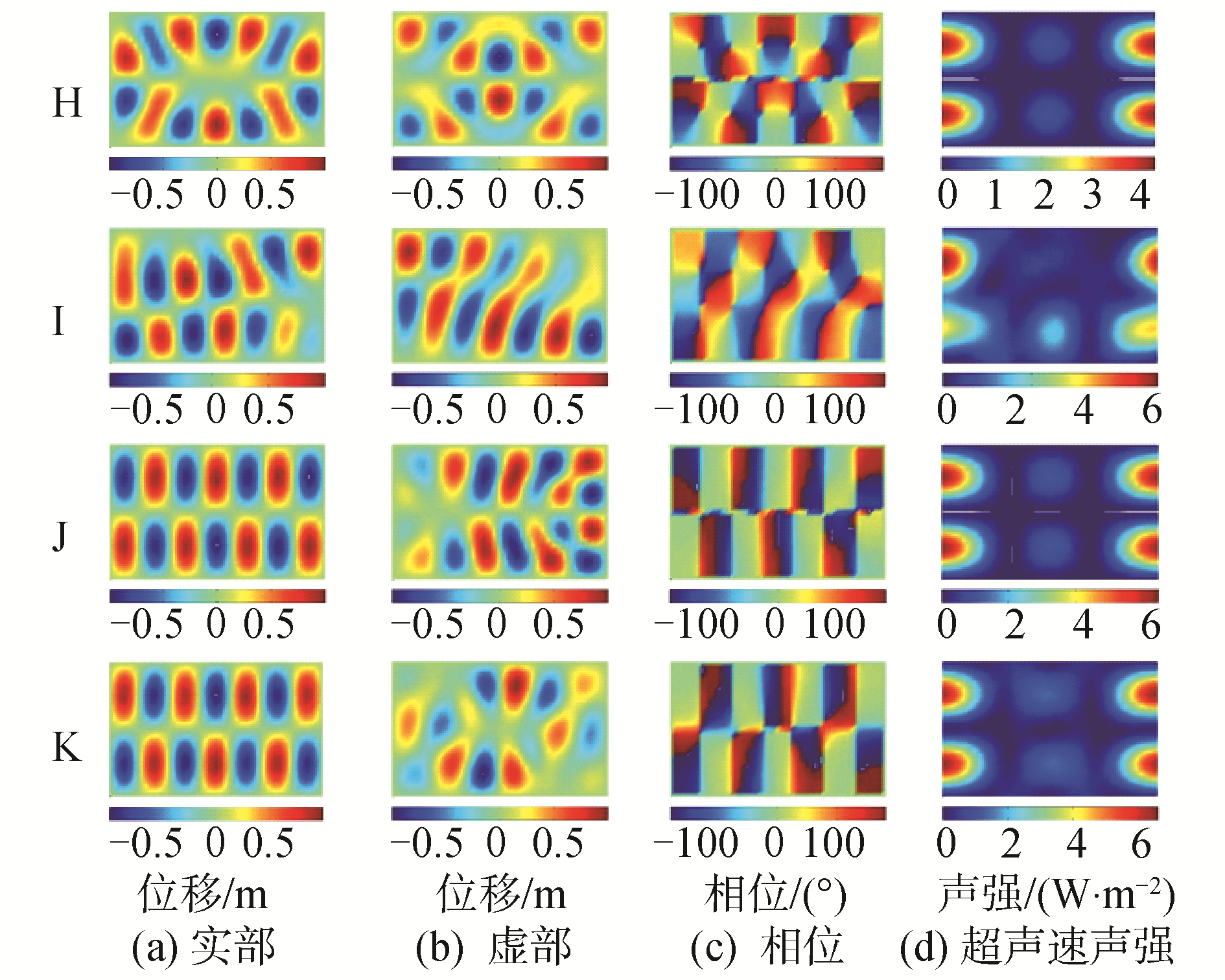
2.4 非均匀阻尼板对超声速声强的影响——边辐射模态如所知,根据Gideon Maidanik提出的辐射模态分类理论不难发现,板存在3种辐射模态,即为面辐射模态、角辐射模态和边辐射模态,本节围绕着边辐射模态展开。假设非均匀阻尼板的振动频率等于800 Hz,振型选用的是(7, 2)振型,选取2.2小节中较具代表性的S1、A1、B1、C1这4种非均匀阻尼板构型展开了分析,同时在表 4中给出了这4种阻尼构型对应的复模态复杂度,位移振型和超声速声强的计算结果如图 8所示。
| 表 4 H、I、J、K的复模态复杂度 Table 4 Modal complexity of H, I, J, K damping configuration |
|
Download:
|
| 图 8 不同构型的计算结果 Fig. 8 Calculation results of different damping configurations | |
根据超声速声强的图像不难看出,在复模态复杂度不是很大的情况下,如H、J、K情况下超声速声强能够清晰地显示远场声辐射热区位于薄板结构的边缘处,属于边辐射模态,当复模态复杂度足够高的时候(如I),超声速声强指示的热点区域就不像低复模态复杂度那么清晰均匀,2个热点区域会变小且稍显模糊,此外还出现了除边热点外的强度较低的热点区域,但依旧能够识别出该阻尼构型对远场声辐射有贡献的区域是边辐射模态。

|
Download:
|
| 图 7 阻尼构型 Fig. 7 Damping configurations | |
本节的计算模型为上节的非均匀阻尼板A1、A2、B1、B2、C1、C2、S1、S2,高阻尼敷设面积均为薄板面积的1/4,高阻尼比取为0.4。表 5则对不同阻尼分布型式的(3, 3)模态对应的固有频率进行了列示。
| 表 5 各阻尼分布型式(3, 3)模态的固有频率 Table 5 Natural frequency of (3, 3) mode of each damping distribution type |
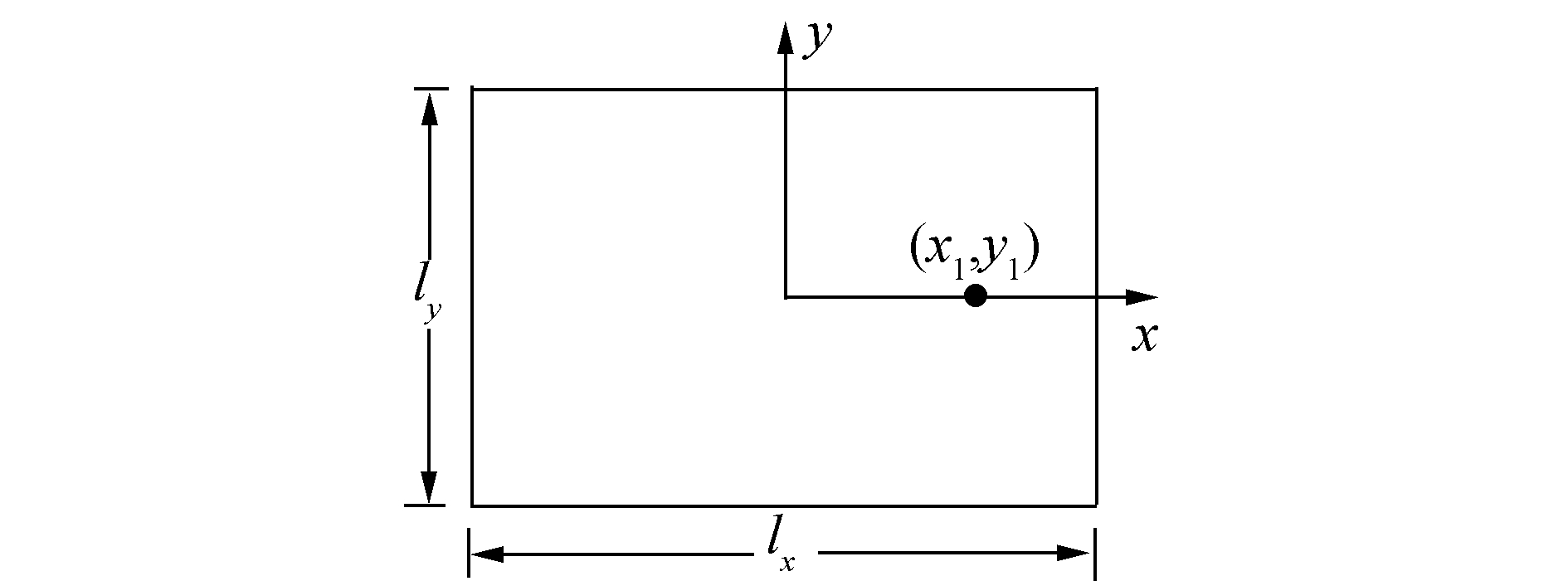
如图 9所示,假设该四边简支的薄板结构受到一个垂向的点激励作用,激励力的大小为1 N,作用位置为(3, 3)模态的波峰处,即(x1, y1)=(0.3, 0),激励频率为各阻尼分布型式(3, 3)模态的固有频率,参考声功率取为10-12 W。表 6对所有阻尼板的辐射声功率及其复模态复杂度进行了列示。表 7对所有阻尼板的辐射声功率及其复模态辐射指数进行了列示。表 8列举出了上述各阻尼板的复模态声辐射复杂度与辐射声功率。
|
Download:
|
| 图 9 激励力作用位置示意 Fig. 9 Excitation force position diagram | |
| 表 6 各阻尼板的复模态复杂度与辐射声功率 Table 6 Mode complexity and radiated sound power of different damping plates |
| 表 7 各阻尼板的复模态辐射指数与辐射声功率 Table 7 Complex mode radiation index and radiated sound power of different damping plates |
| 表 8 各阻尼板的复模态声辐射复杂度与辐射声功率 Table 8 Complex mode radiation complexity and radiated sound power of different damping plates |
由表 6中可以看到,当复模态复杂度低时,如A2、C1、S1、S2的情况,辐射声功率则在67 dB左右,当复模态复杂度高时,如B1、B2、C2的情况,辐射声功率在62 dB左右,2种情况的声功率级相差5 dB左右,可以说复模态复杂度会极大地影响到声辐射。在共振的情况下,结构辐射声功率会因为复模态复杂度的加大而变小。当然也会存在特殊情况,就拿表 6列示的A1来说,复模态复杂度是非常之高的,但是辐射声功率级为66 dB。原因在于MSC测算的是系统在1个周期内的应变能的最大值除最小值所得到的比值,表示的是复模态振型所对应的复杂度,尽管该指标能够充当复模态声辐射的参照之一,但是并非绝对准确。由表 7内的数据不难发现,对于非均匀阻尼板而言,复模态声辐射指数会因为复模态复杂度的加大而减小,得到了与复模态复杂度相类似的结果,这说明虽然复模态辐射指数CMRI计算的是实模态与复模态声辐射效率的偏差,但是把复模态复杂度考虑进去并不合理,所以复模态辐射指数也不能很好地来衡量复模态声辐射的复杂程度。
从表 8可以看出,复模态声辐射复杂度越高,共振时结构辐射声功率就会越小,意味着复模态声辐射复杂度指标CMRC能够让复模态声辐射对应的复杂度及其相应特性得到较为精准的表达:某阶结构振动复模态的声辐射复杂度指标CMRC越高,该复模态的声辐射能力相对就越弱。
4 结论1) 以非均匀阻尼板为对象,利用复模态复杂性指标对其复模态的复杂度进行了表示,对各种复模态复杂度之下对应的超声速声强进行了测算分析。当复模态复杂度增大时,超声速声强显示的声辐射热区会变小或模糊,还可能出现未被抵消的强度较低的热点区域,但从总体上来看,阻尼板复模态超声速声强显示的板表面对远场声辐射有贡献的热点区域与无阻尼板实模态超声速声强显示的角模态和边模态是一致的。
2) 研究了复模态复杂度与辐射声功率的关系,提出可以利用复模态声辐射复杂度指标CMRC来描述复模态声辐射对应的复杂程度及其相应特性:某阶结构振动复模态的声辐射复杂度指标CMRC越高,该复模态的声辐射能力相对就越弱。
| [1] |
WILLIAMS E G. Fourier acoustics:sound radiation and nearfield acoustical holography[M]. San Diego: Academic Press, 1999.
(  0) 0)
|
| [2] |
WILLIAMS E G. Supersonic acoustic intensity[J]. The journal of the acoustical society of America, 1995, 97(1): 121-127. DOI:10.1121/1.412991 (  0) 0)
|
| [3] |
FERNANDEZ-GRANDE E, JACOBSEN F, LECL È RE Q. Direct formulation of the supersonic acoustic intensity in space domain[J]. The journal of the acoustical society of America, 2012, 131(1): 186-193. DOI:10.1121/1.3662052 (  0) 0)
|
| [4] |
FERNANDEZ-GRANDE E, JACOBSEN F. Conservation of power of the supersonic acoustic intensity[J]. The Journal of the acoustical society of America, 2014, 136(2): 461-465. DOI:10.1121/1.4887446 (  0) 0)
|
| [5] |
MARBURG S, LÖSCHE E, PETERS H, et al. Surface contributions to radiated sound power[J]. The journal of the acoustical society of America, 2013, 133(6): 3700-3705. DOI:10.1121/1.4802741 (  0) 0)
|
| [6] |
LIU Daipei, PETERS H, MARBURG S, et al. Supersonic intensity and non-negative intensity for prediction of radiated sound[J]. The journal of the acoustical society of America, 2016, 139(5): 2797-2806. DOI:10.1121/1.4948567 (  0) 0)
|
| [7] |
WILLIAMS E G. Convolution formulations for non-negative intensity[J]. The journal of the acoustical society of America, 2013, 134(2): 1055-1066. DOI:10.1121/1.4812262 (  0) 0)
|
| [8] |
JUNIOR C A C, TENENBAUM R A. Useful intensity:a technique to identify radiating regions on arbitrarily shaped surfaces[J]. Journal of sound and vibration, 2013, 332(6): 1567-1584. DOI:10.1016/j.jsv.2012.10.031 (  0) 0)
|
| [9] |
孙庆鸿, 张启军, 姚慧珠. 振动与噪声的阻尼控制[M]. 北京: 机械工业出版社, 1993. SUN Qinghong, ZHANG Qijun, YAO Huizhu. Vibration and noise damping control[M]. Beijing: Machinery Industry Press, 1993. (  0) 0)
|
| [10] |
傅志方, 华宏星. 模态分析理论与应用[M]. 上海: 上海交通大学出版社, 2000. FU Zhifang, Hua Hongxing. Modal analysis theory and application[M]. Shanghai: Shanghai Jiaotong University Press, 2000. (  0) 0)
|
| [11] |
UNRUH O. Influence of inhomogeneous damping distribution on sound radiation properties of complex vibration modes in rectangular plates[J]. Journal of sound and vibration, 2016, 377: 169-184. DOI:10.1016/j.jsv.2016.05.009 (  0) 0)
|
| [12] |
张鑫, 黎胜, 王博涵. 非均匀阻尼板的复模态与声辐射特性[J]. 噪声与振动控制, 2018, 38(2): 36-41. ZHANG Xin, LI Sheng, WANG Bohan. Complex modes and sound radiation properties of inhomogeneous damping plates[J]. Noise and vibration control, 2018, 38(2): 36-41. DOI:10.3969/j.issn.1006-1355.2018.02.008 (  0) 0)
|
| [13] |
KORUK H, SANLITURK K Y. A novel definition for quantification of mode shape complexity[J]. journal of sound and vibration, 2013, 332(14): 3390-3403. DOI:10.1016/j.jsv.2013.01.039 (  0) 0)
|
| [14] |
MORZFELD M, MA F. The decoupling of damped linear systems in configuration and state spaces[J]. journal of sound and vibration, 2011, 330(2): 155-161. DOI:10.1016/j.jsv.2010.09.005 (  0) 0)
|
| [15] |
MAIDANIK G. Response of ribbed panels to reverberant acoustic fields[J]. The journal of the acoustical society of America, 1962, 34(6): 809-826. DOI:10.1121/1.1918200 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


