一定速度的海流流经立管时，边界层的分离在尾流场产生漩涡，漩涡的泄放使立管表面产生时变的压差力，从而产生涡激振动，同时在波浪的作用下引起与立管相连的上部浮体的升沉运动，升沉运动会给立管一个时变的顶部张力，引起立管轴向的张力波动，浮体对立管的影响可以看成一个参量激励，这将引起立管的涡激-参激耦合振动。Joost Brugmans^[1]考虑时变的轴向张力，采用富洛开理论对立管不稳定性进行分析，计算表明一阶不稳定区对立管影响更大，增加阻尼对减小不稳定区域效果显著; Zhang^[2]基于马修不稳定性理论推导了TTR基于欧拉梁的马修方程，探究了涡激振动造成TTR张力波动频率等于泄涡频率2倍这一现象，杨和振^[3]运用富洛开理论的数值算法探究了阻尼对立管马修稳定性的影响，结果表明当参数处于不稳定区域时，阻尼可以在一定范围内减小不稳定区域的大小。

本文考虑到沿立管轴向的自重影响，变轴力引起系统复杂的振动响应。基于复杂梁弯曲理论和尾流振子方程提出深海TTR的涡激-参激联合振动模型，通过数值方法对四阶振动方程求解，研究了不同流动形式和不同参数对立管振动的影响。

1 TTR涡激-参激耦合振动模型的建立 1.1 基于范德波尔方程的尾流振子模型

本文采用经典的范德波尔方程来刻画双自由度上的涡激力计算精度满足工程实际要求，且计算相对简便。描述涡激振动时流体力的范德波尔方程为^[4]:

$ \frac{{{{\rm{d}}^2}q}}{{{\rm{d}}{t^2}}} + \varepsilon {\omega _{st}}\left( {{q^2} - 1} \right)\frac{{{\rm{d}}q}}{{{\rm{d}}t}} + \omega _{st}^2q = F $

(1)

式中:F表示立管对流场的反作用力，体现了流场和结构的耦合; $q=\frac{2 C_{L}}{C_{L 0}}$表示时变的升力系数C_L和静止立管的升力系数C_L0之比; ω_st为漩涡泄放的频率，ω_st=2πS_t$\frac{U}{D}$。立管横流向的涡激力可以表示为:

$ {f_y} = \frac{1}{2}{\rho _w}D{U^2}\frac{{{C_{L0}}}}{2}q $

(2)

在横向上立管由于运动会受到莫里森力的作用:

$ {f_{{\rm{yMorison}}}} = \frac{1}{2}{\rho _w}D{C_D}\dot y\left| {\dot y} \right| $

(3)

任意时刻立管横流向上的载荷为:

$ f\left( {z,t} \right) = \frac{1}{2}{\rho _w}D{U^2}\frac{{{C_{L0}}}}{2}q - \frac{1}{2}{\rho _w}D{C_D}\dot y\left| {\dot y} \right| $

(4)

为达到双向耦合形式，结构对尾流场反作用力可以表示为:

$ F = \frac{A}{D}\ddot x $

(5)

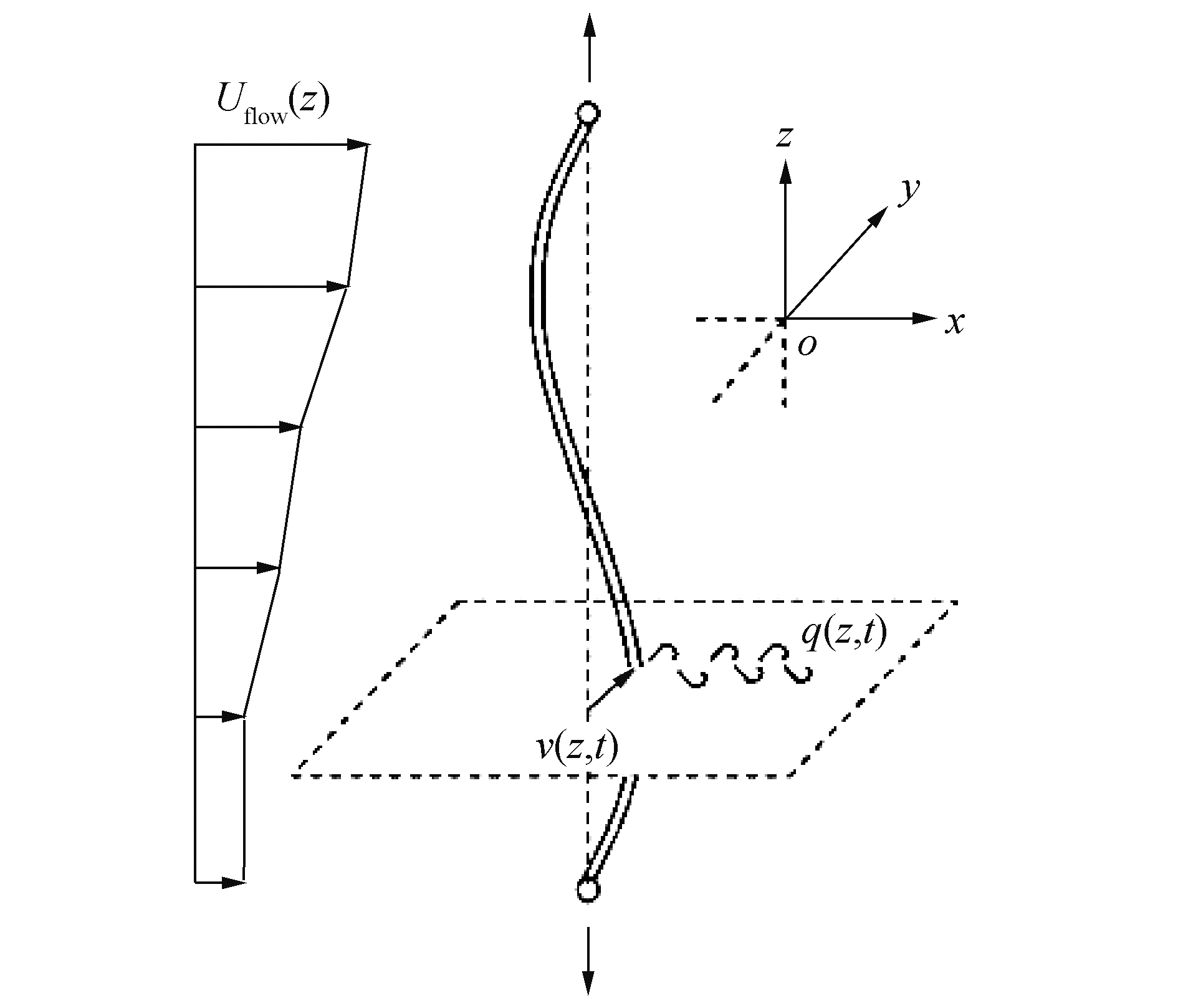
参照立管涡激-参激载荷示意(图 1)，建立立管横流向运动方程为:

$ \left\{ \begin{array}{l} \bar m\frac{{{\partial ^2}y\left( {z,t} \right)}}{{\partial {t^2}}} + EI\frac{{{\partial ^4}y\left( {z,t} \right)}}{{\partial {z^4}}} - \\ \;\;\;\;\;\frac{\partial }{{\partial z}}\left( {\left( {{T_z} - {w_z} + Ka\cos \mathit{\Omega }t\frac{{\partial y(x,t)}}{{\partial z}}} \right) = } \right.\\ \;\;\;\;\;\frac{1}{4}{\rho _w}D{C_{L0}}q{U^2} - \frac{1}{2}{\rho _w}D{C_D}q\dot y\left| {\dot y} \right|\\ \frac{{{{\rm{d}}^2}q}}{{{\rm{d}}{t^2}}} + \varepsilon {\omega _{st}}\left( {{q^2} - 1} \right)\frac{{{\rm{d}}q}}{{{\rm{d}}t}} + \omega _{st}^2q = \frac{A}{D}\ddot y \end{array} \right. $

(6)

立管顺流向运动方程为:

$ \left\{ \begin{array}{l} \bar m\frac{{{\partial ^2}x\left( {z,t} \right)}}{{\partial {t^2}}} + EI\frac{{{\partial ^4}x\left( {z,t} \right)}}{{\partial {z^4}}} - \\ \;\;\;\;\;\frac{\partial }{{\partial z}}\left( {\left( {{T_z} - {w_z} + Ka\cos \mathit{\Omega }t\frac{{\partial x(x,t)}}{{\partial z}}} \right) = } \right.\\ \;\;\;\;\;\frac{1}{4}{\rho _w}D{C_D}q{U^2}\\ \frac{{{{\rm{d}}^2}q}}{{{\rm{d}}{t^2}}} + \varepsilon {\omega _{st}}\left( {{q^2} - 1} \right)\frac{{{\rm{d}}q}}{{{\rm{d}}t}} + \omega _{st}^2q = \frac{A}{D}\ddot x \end{array} \right. $

(7)

式中:m=m_a+m_f+m_r, ${m_f} = \frac{1}{4}{\rho _f}{\rm{ \mathsf{ π} }}{d^2}$表示立管单位长度管内油气质量; ${m_r} = \frac{1}{4}{\rho _s}{\rm{ \mathsf{ π} }}{(D - d)^2}$表示单位长度立管的质量; ${m_a} = \frac{1}{4}{C_a}{\rho _\omega }{\rm{ \mathsf{ π} }}{D^2}$表示单位长度附加水质量; ρ_ω表示立管外部海水的密度; ρ_f表示管内油的密度; ρ_s表示钢质立管的密度; EI为抗弯刚度; D为立管外径，d为内径; C_a为附加水质量系数; T_{(z, t)}表示立管顶部施加的张力，T_{(z, t)}=T_t-w_z+kacos(Ωt), T_t为顶端的初始静张力，k为顶端张紧器的等效弹簧刚度，a为张力变化幅值，A为结构与流体的耦合动力参数，一般取12^[5-6]。

1.2 耦合模型的数值求解

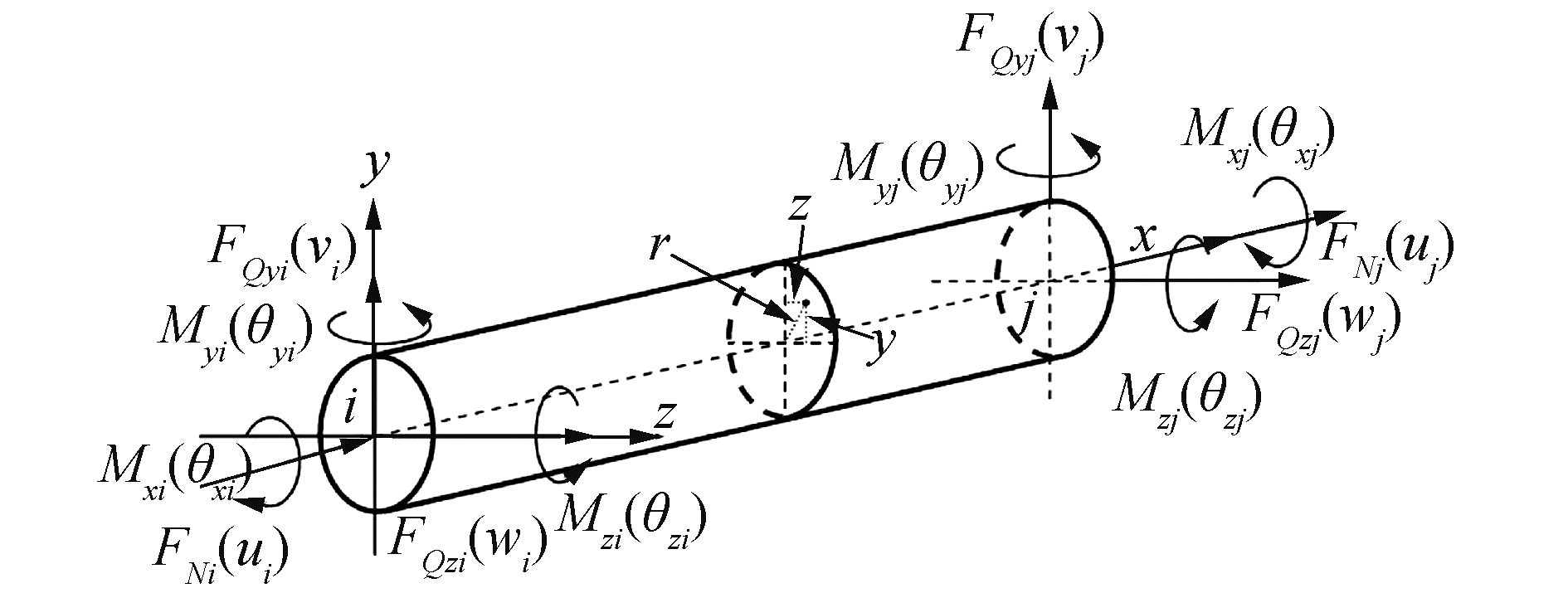
本文选用有限元法对立管的振动方程在时域内进行离散求解。沿立管长度方向将结构分成n等份，水面处z坐标为零，海底立管连接处z坐标为1 600，将立管分成n个梁单元，n+1个节点，每个单元的长度为dl。从图 2、3中的立管单元受力分析可知，任意一个单元的广义位移可以用相邻节点的插值函数表示^[7]:

$ {\mathit{\boldsymbol{\delta }}_i} = {\left[ {\begin{array}{*{20}{l}} {{u_i}}&{{v_i}}&{{w_i}}&{{\theta _{xi}}}&{{\theta _{yi}}}&{{\theta _{zi}}} \end{array}} \right]^{\rm{T}}} $

(8)

$ {\mathit{\boldsymbol{\delta }}_j} = {\left[ {\begin{array}{*{20}{l}} {{u_i}}&{{v_i}}&{{w_i}}&{{\theta _{xj}}}&{{\theta _{yj}}}&{{\theta _{zj}}} \end{array}} \right]^{\rm{T}}} $

(9)

$ {\mathit{\boldsymbol{\delta }}^e} = {\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\delta }}_i^{\rm{T}}}&{\mathit{\boldsymbol{\delta }}_j^{\rm{T}}} \end{array}} \right]^{\rm{T}}} $

(10)

该单元两端的受力为:

$ {\mathit{\boldsymbol{f}}_i} = {\left[ {\begin{array}{*{20}{l}} {{F_{Ni}}}&{{F_{Oyi}}}&{{F_{Qzi}}}&{{M_{xi}}}&{{M_{yi}}}&{{M_{zi}}} \end{array}} \right]^{\rm{T}}} $

(11)

$ {\mathit{\boldsymbol{f}}_j} = {\left[ {\begin{array}{*{20}{l}} {{F_{Nj}}}&{{F_{Oyj}}}&{{F_{Qzj}}}&{{M_{xj}}}&{{M_{yj}}}&{{M_{zj}}} \end{array}} \right]^{\rm{T}}} $

(12)

$ {\mathit{\boldsymbol{f}}^e} = {\left[ {\mathit{\boldsymbol{f}}_i^{\rm{T}}\mathit{\boldsymbol{f}}_j^{\rm{T}}} \right]^{\rm{T}}} $

(13)

式中:F_Qyi、F_Qzi、F_Qyj、F_Qzj表示在局部坐标系下单元两端2个方向的剪力，F_Ni、F_Nj为两端的张力，M_xi、M_yi、M_zi和M_xj、M_yj、M_zj表示2个节点在相应方向上的扭矩和弯矩。节点3个方向位移和θ_x可以用x线性的表示:

$ u = {a_0} + {a_1}x,v = {b_0} + {b_1}x + {b_2}{x^2} + {b_3}{x^3} $

(14)

$ w = {c_0} + {c_1}x + {c_2}{x^2} + {c_3}{x^3}{\theta _x} = {e_0} + {e_1}x $

(15)

从而节点位移可以表示成如下形式:

$ u = {N_u}{\delta _u},{\theta _x} = {N_\theta }{\delta _\theta },v = {N_v}{\delta _v},w = {N_w}{\delta _w} $

(16)

式中:N_u、N_θ、N_v、N_w为相邻节点的位移插值函数:

$ {\mathit{\boldsymbol{H}}_u}\left( x \right) = \left[ {\begin{array}{*{20}{l}} 1&0&0&0&0&0&x&0&0&0&0&0 \end{array}} \right] $

(17)

$ {\mathit{\boldsymbol{H}}_v}\left( x \right) = \left[ {\begin{array}{*{20}{c}} 0&1&0&0&0&x&0&{{x^2}}&0&0&0&{{x^3}} \end{array}} \right] $

(18)

$ {\mathit{\boldsymbol{H}}_w}\left( x \right) = \left[ {\begin{array}{*{20}{c}} 0&0&1&0&x&0&0&0&{{x^2}}&0&{{x^3}}&0 \end{array}} \right] $

(19)

$ {\mathit{\boldsymbol{H}}_\theta }\left( x \right) = \left[ {\begin{array}{*{20}{c}} 0&0&0&1&0&0&0&0&0&x&0&0 \end{array}} \right] $

(20)

基于伽辽金(Galerkin)方法可推导得出如下的方程^[7]:

$ \begin{array}{l} \left( {EI\int_0^l {N_{(z)}^{\prime \prime \prime \prime }} {\rm{d}}z - {T_{(z,t)}}\int_0^l {N_{(z)}^{\prime 2}} {\rm{d}}z - \omega \int_0^l {N_{(z)}^\prime } {\rm{d}}z} \right){x_{(z,t)}} + \\ m\int\limits_0^l {N_{(z)}^2{\rm{d}}z{{\ddot x}_{(z,t)}}} = \int\limits_0^l {{N_{(z)}}{f_{x(z,t)}}{\rm{d}}z} \end{array} $

(21)

$ \begin{array}{l} \left( {EI\int_0^l {N_{(z)}^{\prime \prime \prime \prime }} {\rm{d}}z - {T_{(z,t)}}\int_0^l {N_{(z)}^{\prime 2}} {\rm{d}}z - \omega \int_0^l {N_{(z)}^\prime } {\rm{d}}z} \right){y_{(z,t)}} + \\ m\int\limits_0^l {N_{(z)}^2{\rm{d}}z{{\ddot y}_{(z,t)}}} = \int\limits_0^l {{N_{(z)}}{f_{y(z,t)}}{\rm{d}}z} \end{array} $

(22)

$ \int\limits_0^l {\frac{{{\partial ^2}q}}{{\partial {t^2}}}w{\rm{d}}z} = \int_0^l {{\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{N}}{\rm{d}}z\ddot r_q^e} $

(23)

$ \int\limits_0^l {\varepsilon {\omega _{st}}\left( {{q^2} - 1} \right)\frac{{\partial q}}{{\partial t}}\omega {\rm{d}}z} = \int_0^l {\varepsilon {\omega _{st}}\left( {{q^2} - 1} \right){\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{N}}{\rm{d}}z\dot r_q^e} $

(24)

式中:x(z, t)、y(z, t)代表单元梁在2个自由度上的位移; f_x(z, t)和f_y(z, t)分别代表单元在2个自由度上的载荷。

已知:

$ K_X^e = K_Y^e = EI\int\limits_0^l {{N^{\prime \prime }}^2(z){\rm{d}}z} - T\int_0^l {{N^{\prime 2}}} (z){\rm{d}}z $

(25)

$ M_X^e = M_Y^e = \left( {m + {m_a}} \right)\int\limits_0^l {{N^2}(z){\rm{d}}z} $

(26)

F_X^e为立管顺流向节点单元的载荷矩阵:

$ \mathit{\boldsymbol{F}}_X^e = \int\limits_0^l {N(z){f_x}(z,t){\rm{d}}z} $

(27)

F_Y^e为立管横流向节点单元的载荷矩阵:

$ \mathit{\boldsymbol{F}}_Y^e = \int\limits_0^l {N(z){f_y}(z,t){\rm{d}}z} $

(28)

将沿立管长度方向的所有单元的相应矩阵通过矩阵拼凑法组装到一起，得到系统整体的质量矩阵，刚度矩阵，同时系统整体的运动方程的矩阵形式为^[8]:

$ \mathit{\boldsymbol{Ku}} + \mathit{\boldsymbol{M\ddot u}} = {\mathit{\boldsymbol{F}}_x}(t) $

(29)

$ \mathit{\boldsymbol{Kv}} + \mathit{\boldsymbol{M\ddot v}} = {\mathit{\boldsymbol{F}}_y}(t) $

(30)

式中:K表示立管系统整体刚度矩阵: K=$\sum\limits_0^l {\mathit{\boldsymbol{G}}_e^{\rm{T}}} {\mathit{\boldsymbol{K}}_e}{\mathit{\boldsymbol{G}}_e}$; M表示立管系统整体质量矩阵: M=$\sum\limits_0^l {\mathit{\boldsymbol{G}}_e^{\rm{T}}} {\mathit{\boldsymbol{M}}_e}{\mathit{\boldsymbol{G}}_e}$; F_x表示立管系统顺流向的载荷向量: ${\mathit{\boldsymbol{F}}_x} = \sum\limits_0^l {\mathit{\boldsymbol{G}}_e^{\rm{T}}} {\mathit{\boldsymbol{F}}_x}{(t)_e}$; F_y表示立管系统横流向的载荷向量:

$ {\mathit{\boldsymbol{F}}_y} = \sum\limits_0^l {\mathit{\boldsymbol{G}}_e^{\rm{T}}} {\mathit{\boldsymbol{F}}_y}{(t)_e} $

式中G表示由立管单元到整体的扩展矩阵，为了计算简便，立管的阻尼采用瑞利阻尼(Rayleigh)替代，瑞利阻尼矩阵满足正交条件也被称为经典阻尼^[9]:

$ \mathit{\boldsymbol{C}} = {a_0}\mathit{\boldsymbol{M}} + {a_1}\mathit{\boldsymbol{K}} $

(31)

式中:系数a₀和a₁是对应的比例系数，a₀=$\frac{{2\xi {\omega _m}{\omega _n}}}{{{\omega _m} + {\omega _n}}}, {a_1} = \frac{{2\xi }}{{{\omega _m} + {\omega _n}}}$，量纲为s^-1和s; ξ取值为0.08;ω_n为结构的第三阶固有频率; ω_m为系统的基频。

立管的两端用铰支模型处理，由于立管单元组装的系统整体刚度矩阵不具有非奇异性，立管的位移解有无数个，需要对立管边界进行处理，本文采用划行划列法。同时采用Newmark-β法求解系统响应^[10]，采用Matlab软件编制程序DRPVR。

2 深海立管涡激-参激联合振动响应 2.1 模型验证

为验证深海TTR立管涡激-参激耦合振动响应程序DRPVR的正确性和适用性，对比Chaplin^[11]进行的经典立管试验结果。Chaplin选用一根长度为13.12 m的圆截面立管放置在水槽中，水槽长度为230 m，深度为6.5 m，立管外径为0.028 m，长细比达468。选取工况的主要参数:流速取0.5 m/s，顶部张力为670 N, 雷诺数Re为12 290，斯特劳哈尔数St为0.17。

图 4为模型结果和试验结果的对比图，包括横流向振幅包络图、横流向振幅标准差，顺流向振幅标准差。从图中可以看出横向振幅的第6阶模态被激发，和模型结果相比，趋势相同。横流向和顺流向振幅标准差和实验结果相一致，顺流向11阶模态被激发，幅值大约是横流向的2倍。通过对比Chaplin的试验数据，发现本模型结果吻合度较高。

2.2 不同来流速度下的立管响应

本文选用来流类型为均匀流，流速范围取0.1~ 0.9 m/s，取计算步长为0.002 s，张力变化幅值为0.1 T，张力变化频率为0.5 rad/s时，计算50 s下不同流速下立管的响应。

如图 5所示为不同流速下参激、涡激分别作用下的振幅曲线，左侧一列从上往下依次为立管节点L/4处、L/2处和3L/4处的横向振幅，右侧则为顺流向振幅。整个流速区域内，参激使得节点响应明显变化，低流速时振幅增大，随着流速的增加，参激的作用减弱，相同流速下立管底部节点受参激影响大于顶部。

2.3 不同流动形式下的立管振动响应

本文选用剪切流和阶梯流2种流动形式，流速取0.1、0.3和0.5 m/s，根据现场测量统计数据可知，Spar平台垂荡幅值范围约为0.43~1.56 m，均值0.61 m^[12]，即使在百年一遇的风浪下，Spar平台垂荡极值也仅在2 m左右^[13]，则根据Spar平台垂荡运动特点，确定立管参数激励范围:0≤a≤2 m，参数激励频率0.4≤Ω≤1.6 rad/s。本文选取参激振动频率为0.5 rad/s。图 6为不同流动形式下，L/4处、L/2处和3L/4立管节点处涡激-参激耦合特性响应曲线。可以看出参数激励使得节点振幅增大，阶梯流在横流向和顺流向的振动频率均高于剪切流。

2.4 参激频率对立管轨迹的影响

本节选取不同顶部激励频率来探究在整个立管长度方向横向和顺流向的振幅随时间和空间的演化，计算工况如表 1所示。

图 7为立管横流向各节点振幅变化曲线，图 8为立管顺流向各节点振幅变化曲线，图中每一条曲线为某一时刻立管各节点的位置，时间间隔为50个时间步，从25 s开始取, 一直取到50 s结束。

从图 7中可以看出，对于横流向振幅，当参激频率由0.6 rad/s增大到1.0 rad/s时，横向振幅最大值由1.23 m减小0.66 m。此外工况1存在1个节点，表明立管激发二阶模态，工况2不存在节点，但有二阶模态的趋势，立管振型较为发散，工况3的节点最大振幅又增加到0.85 m，振型又回归到二阶模态。

从图 8可以看出工况1存在1个节点，二阶模态被激发，工况2表现为类四阶模态，立管振幅变大且底部振幅增加明显，工况3三阶模态被激发，振幅较工况2小。

3 结论

1) 通过与Chaplin试验中试验数据对比表明本模型和试验吻合的很好，可以用于计算立管的涡激振动。

2) 在整个流速区域内，参激使得节点响应明显变化，低流速时振幅增大，随着流速的增加，参激的作用减弱，相同流速下立管底部节点受参激影响大于顶部，当流速为0.3 m/s时顺流向振动频率约为横流向的2倍，表明此时该立管节点进入锁振状态。

3) 在流速不变的情况下参数激励频率的变化会导致横流向振幅和振型的改变，且参激对立管底部的作用更加明显，参数激励的作用是较为显著的。

本文所考虑的是规则波作用下平台垂荡运动引发的简谐参数激励的影响，而对于耦合随机波浪下所产生的随机参数激励的影响则需要今后进一步研究。