2. 河海大学 水利水电学院, 江苏 南京 210098;
3. 河海大学 水文水资源学院, 江苏 南京 210098
2. College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China;
3. College of Hydrology and Water Resources, Hohai University, Nanjing 210098, China
随着水资源供需矛盾日趋尖锐,水资源变化已经成为国家发展和人民生活最关心的问题之一。作为陆地淡水资源的总括,陆地水储量(terrestrial water storage,TWS)包括地表水、地下水、土壤含水量、冰雪和生物体含水量。TWS会由于降水入渗而增加,随着土壤水分蒸发、植被蒸腾、河流输送以及向深层地下的渗透等过程而减少。研究陆地水储量的变化对进一步掌握地区水文循环现状,规划区域未来水资源发展具有重要意义。美国宇航局(NASA)和德国宇航中心(DLR)于2002年3月联合发射的GRACE重力卫星为陆地水储量变化研究提供了方法[1]。
目前,大量研究表明GRACE重力卫星数据在估算不同尺度的陆地水储量变化上具有极高的实用价值,能够精确估算大尺度地区厘米级陆地水储量变化[2]。GRACE数据反演的陆地水储量与全球尺度下水文模型模拟的陆地水储量在年尺度上一致性较好,且能更精确反应水储量季节性变化波动较为显著的干旱区情况[3-4],但在反演过程中,受到目标区域的地理信息影响[5]。通过GRACE卫星轨道观测值为初值的线性化方法能够建立反演地球重力场的改进动力学法理论模型[6]。
结合多源水文数据研究流域陆地水储量已经成为新的研究趋势。近十年,我国内陆十大流域陆地水储量与降水年际变化大多呈正相关,在不同频段和尺度的时空变化一致性较好[7-8]。长江上游陆地水储量与降雨、径流和土壤水蓄量无明显变化,中游水库蓄量与陆地水储量都有显著性增加,反映出人类活动影响中游地区陆地水储量变化[9]。利用逐月GRACE数据、同期GLDAS模型中土壤水和实测地下水埋深数据推算淮河流域地下水储量的时空变化,发现淮河流域地下水储量呈递增趋势[10]。
本文以黄河流域高村水文站控制断面以上范围为研究对象,通过GRACE卫星数据计算2003-2016年期间黄河流域陆地水储量变化,并利用GLDAS水文模型模拟的水储量与其结果进行对比,验证GRACE卫星数据在黄河流域的适用性; 分析流域陆地水储量变化的时空变化规律及其变化的主要影响因子。
1 数据与方法 1.1 数据来源 1.1.1 GRACE重力卫星数据研究人员利用GRACE卫星监测到的时变重力场变化推求地球表面质量的变化,继而得到影响地表质量变化的主要因素陆地水储量的质量变化,进一步转化为等效水高变化。数据处理过程中去除了潮汐(海潮、固体潮、地球自转带来的极潮等)、非潮汐大气及海洋的的影响,排除了冰后期反弹的信号,并利用高斯滤波平滑和球谐滤波器进行数据处理以增大其精度。美国德克萨斯大学空间研究中心(CSR)、美国喷气推进实验室(JPL)及德国地学研究中心(GFZ)3个机构发布全球空间分辨率为1°×1°的逐月等效水高变化值(TWSA),其值为各月陆地水储量相对于2004年1月-2009年12月陆地水储量均值的变化值。本文选用3个机构发布数据的平均值。根据流域地形图,进行面积加权计算平均数,得到流域各月平均陆地水储量变化。
以月为时段的流域陆地水储量变化TWSA可表示为:
| $ {\rm{TWSA}} = \sum\limits_{i = 1}^n h (i, t)\frac{{{A_i}}}{A} $ | (1) |
式中:n为流域所占栅格个数; h(i, t)为第i个栅格的等效水深; Ai是第i个栅格与流域相交的面积; A为流域总面积。
1.1.2 GLDAS水文模型数据美国宇航局哥达航空中心与海洋大气局环境预报中心联合开发的GLDAS全球陆面数据同化系统,可以驱动4个不同的陆面模型(CLM、NOAH、MOS和VIC),模拟生成22个不同的陆地水文变量。本文选用GLDAS-NOAH陆面模式Version l的2003年1月-2016年12月份地表径流、土壤含水量、地下径流、雪水当量和生物含水量数据(来自https://earthdata.nasa.gov/),时间分辨率为1个月,空间分辨率为1°×1°。为保持与GRACE卫星数据一致,采用与GRACE卫星数据相似处理方式,将利用GLDAS-NOAH各分量数据模拟所得的陆地水储量数据减去其2004-2009年的平均值,得到陆地水储量逐月变化量,进而估算陆地水储量变化。
1.1.3 实测降雨、气温、径流数据降雨、气温数据来源于国家气象信息中心,数据系列为1961年迄今、分辨率为0.25°×0.25°的月值格点数据,个别缺损数据采用样条法插值。径流选用黄河高村水文站的月径流资料,来自2003-2016年《黄河流域水文资料》中高村站逐月平均流量。
1.2 方法原理 1.2.1 Mann-Kendall检验法Mann-Kendall检验法(M-K检验法)是一种非参数统计检验方法,对所用样本序列的分布无要求,不受少数异常值干扰。因其能够实现高效率定量化操作,且检测范围广,受人为影响小,已在预测气温、降水、径流等水文气象时间序列资料的长期变化趋势中得到广泛应用[11]。
假定x1, x2, …, xn为时间序列变量,n为时间序列的长度, 确定时间序列全部对偶值(xi, xj)(j>i)中xi<xj出现的个数p,再根据p值确定τ,从而得出Var(τ)和U,计算公式为:
| $ \begin{array}{l} \;\tau = \frac{{4p}}{{n(n - 1)}} - 1\\ {\mathop{\rm Var}\nolimits} (\tau ) = \frac{{2(2n + 5)}}{{9n(n - 1)}}\\ \;\;U = \frac{\tau }{{{\mathop{\rm Var}\nolimits} {{(\tau )}^{1/2}}}} \end{array} $ |
当τ>0,表示序列有上升趋势,当τ < 0,表示序列有下降趋势; 当|U|>U0.05=1.96时,表示序列趋势变化显著,反之没有显著趋势(在0.05显著性水平下)。
1.2.2 皮尔逊相关系数法皮尔逊相关系数法是一种能够准确度量2个计算变量间关系密切程度的统计学方法[12]。变量x、y通过实验可获得若干组数据,记为(xi, xj) (i=1, 2, …, n),则相关系数的数学表达式为:
| $ r = \frac{{\sum\limits_{i = 1}^n {\left( {{x_i} - \bar x} \right)} \left( {{y_i} - \bar y} \right)}}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} \sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} } }} $ | (2) |
式中:x、y分别为n个试验值的均值; 相关系数r的取值范围在-1~+1,即|r|≤1。|r|越逼近于1,则表明x与y线性相关程度越高[13]。
1.2.3 快速傅里叶变换水文时序数据普遍存在周期性。频谱分析法可以利用傅里叶级数将时序数据分解为有限个不同频率的正弦函数和余弦函数的组合,将时域水文数据转化至频域,进而分析水文数据的周期性。由于水文时序数据的采集是不连续的,其周期分析应采用离散傅里叶变换算法,快速傅里叶变换是离散傅里叶变换中最为常用的快速算法。
2 区域概况和陆地水储量变化分析 2.1 黄河流域概况黄河流域面积79.5万km2,水量约占全国河川的2%。黄河流域年降雨量少,空间上呈现下游多,中上游少的趋势,中上游部分干旱地区年降雨量小于400 mm,分布极不均匀。降水年内分布也不均匀,夏季和秋季降水多。黄河流域面积大,测站分布不均,观测难度大,研究陆地水循环特征的水文模型不够完善。相较之下,GRACE卫星全球观测分布均匀,观测尺度统一,从而弥补了传统观测和研究方法的不足,有利于黄河流域陆地水储量变化的定量研究。
2.2 黄河流域多年陆地水储量空间变化分析由于轨道调整等原因,部分月份的GRACE数据缺失,为保证数据在每个季节均具有完整性以及数据的准确性,选用2003年1月-2016年12月的GRACE数据,缺失数据采用三次样条法插值补充。如图 1所示,GRACE反演的黄河流域多年平均陆地水储量变化分布连续性较好。春季黄河流域水储量较低,流域水储量整体处于亏损状态,南部干旱程度高于北部。夏季黄河处在汛期,陆地水储量较春季有明显增加,特别是黄河上游地区,陆地水储量盈余状态十分显著。流域陆地水储量整体呈现从上游向下游逐步递减的规律。秋季陆地水储量整体处于盈余状态,且分布较为均衡。扎陵湖及鄂陵湖水域范围为最丰地带,内蒙地区为最枯区,整体从西南向东北递减。冬季黄河流域陆地水储量变化较为均匀,上下游较中游丰,水储量亏损区域的面积远远超过盈余的面积。

|
Download:
|
| 图 1 黄河流域2003-2016年平均四季水储量变化空间分布 Fig. 1 Spatial distribution of average seasonal TWSA in the Yellow River basin from 2003 to 2016 | |
2003-2016年,经计算,黄河流域水储量逐年四季变化情况:春夏秋冬四季均值分别为-3.57、-1.72、0.05、-2.51 cm,秋季平均陆地水储量最大,夏季次之,春季最小。流域春季、夏季和冬季的水储量常年处于亏损状态,而秋季水储量整体为盈余状态。流域各季水储量变化规律各有不同,但是总体来讲春、夏、秋、冬四季水储量变化均呈现下降趋势,线性拟合后下降速率分别为-0.47、-0.46、-0.68、-0.57 cm/a,其中秋季降幅最大。
2.3 GRACE反演与GLDAS模拟结果比较选用2003年1月-2016年12月GRACE与GLDAS的数据作为分析对象,黄河流域陆地水储量多年变化过程如图 2所示。黄河流域陆地水储量变化具有季节性周期,在秋季达到峰值,在年际尺度上两者的多年变化规律基本一致。总体来看,GLDAS模拟的陆地水储量变化振幅小于GRACE,主要原因是前者估算结果只包括雪水和地表及以下0~2 m深度的土壤水,GRACE涵盖面更广,如湖泊、湿地、部分大气水等。GLDAS模拟结果与GRACE反演结果相较存在时间上的滞后性。GLDAS反演结果与前一个月GRACE反演结果的相关系数最大,GLDAS结果滞后于GRACE结果一个月。

|
Download:
|
| 图 2 GRACE反演与GLDAS模拟的黄河流域水储量变化对比 Fig. 2 Comparison of GRACE data with GLDAS simulation results of the Yellow River basin | |
GRACE卫星数据反演陆地水储量变化与GLDAS模拟的陆地水储量变化显著相关,二者的皮尔逊相关系数为0.59(P < 0.01)。采用M-K检验法对黄河流域GRACE反演与GLDAS模拟的陆地水储量变化的年变化数据分别进行趋势性分析。如表 1所示,GRACE反演的水储量变化数据存在显著下降趋势(在0.05显著性水平下),GLDAS模拟的水储量则无明显趋势,下降幅度极小。纵观整个系列年份,黄河水储量呈现整体下降趋势。相比GLDAS数据,GRACE数据对陆地水储量的变化更为敏感,本文采用GRACE反演的陆地水储量变化数据作进一步分析。
| 表 1 黄河流域TWSA数据的M-K检验结果 Table 1 Mann-Kendall test results of TWSA in the Yellow River basin |
选取M-K法检验黄河流域月尺度陆地水储量变化及降水、径流、气温等水文气象因子的趋势性,结果见表 2。
| 表 2 黄河流域主要水文气象要素M-K检验结果 Table 2 The Mann-Kendall trend analysis results of main hydrological and meteorological elements |
流域陆地水储量变化呈显著下降性趋势,径流有显著上升的趋势(在0.05显著性水平下),降水和气温存在微弱上升趋势。
对于确定的降雨过程,径流的显著增加会导致陆地水储量的显著下降。因为径流显著上升,出境水量显著增大,所以流域陆地水储量减少。虽然地表径流渗入可变成地下水,形成水储量的增加,但较为缓慢,存在滞后性,且影响较小。流域气温升高,蒸发增大,将导致陆地水储量下降。虽然黄河流域降水有微弱上升趋势,但对流域陆地水储量的补充不及蒸发和径流增大对流域陆地水储量削减作用,因此黄河流域陆地水储量呈显著下降趋势。
降水、蒸发和径流是陆地水文循环过程中最重要的3个环节,由其构成的水循环决定了一个地区的水储量总量。但陆地水储量的形成是由多项因素作用的复杂过程,因此,水储量的变化趋势与各项影响因子的变化趋势并不完全一致。
3.2 滞后性分析对整个黄河流域2003-2016年月尺度降水、径流、气温数据与陆地水储量变化间的滞后性进行分析,结果见表 3。水储量变化滞后于降水和径流2个月,对气温的迟滞时间达到3个月。黄河流域陆地水储量变化与2个月前的降水和径流的相关系数最大,与3个月前的气温变化相关系数最大。
| 表 3 黄河流域陆地水储量变化与各水文气象要素的滞后时间及相关系数 Table 3 The time lag and coherence of the TWSA and meteorological factors in the Yellow River |
降水到径流、土壤水、地下水进而完成水储量的转换需要一定的时间,蒸散发作为循环中重要的环节之一也需要一定的过程,气温是影响流域蒸散发量的主要因素,因此流域陆地水储量变化相对降水和气温变化必然存在一定的滞后时间。黄河流域为超渗产流,降水先转化为径流,再向土壤中入渗。
3.3 相关性分析陆地水储量变化与同期径流、气温及降水的相关系数呈递减趋势,其受同期径流的影响最直接。由表 3可见,对各研究要素滞后相关处理后,陆地水储量变化与降水和气温的相关性较高,与径流的相关性较低。
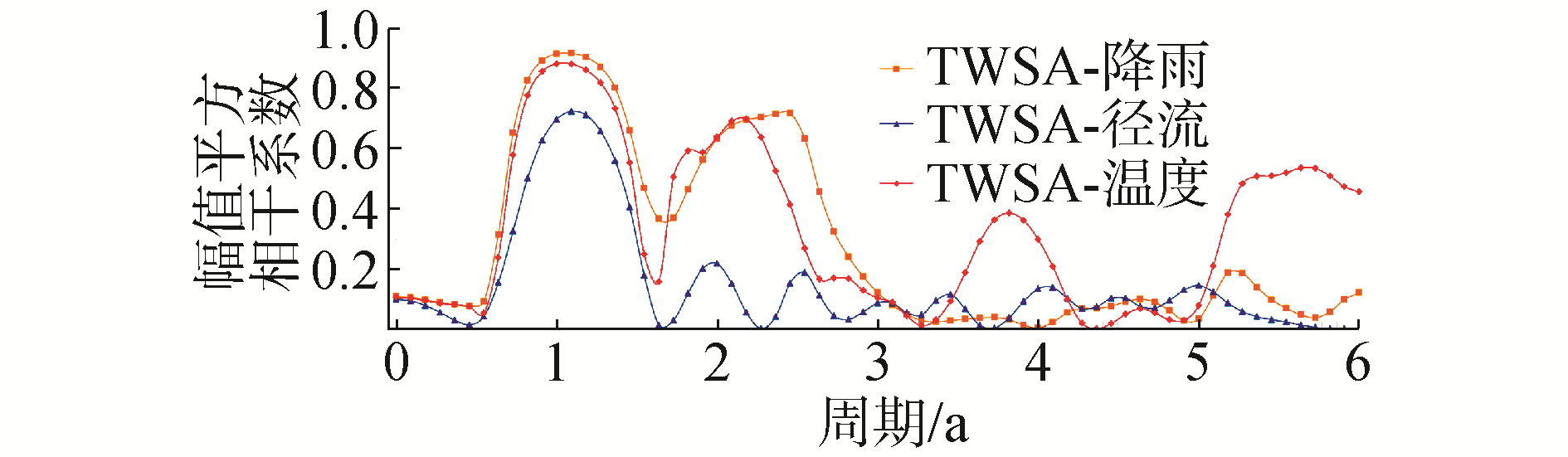
运用快速傅里叶变换将其从时域转换为频域,如图 3所示,黄河流域陆地水储量变化与降水、径流、气温在周期为一年时均达到最大值。在一年左右的低频存在明显的同周期,周期性随周期长度增长而变小。在周期为一年的短周期部分,陆地水储量变化与三者的相关性较高,与降水、气温的相关性整体高于径流。短周期部分陆地水储量变化与降水间的相关性接近1,而对于长周期部分,由于受高频固有噪声等因素的影响,其相关性较差。图 4中可以明显看出陆地水储量变化对气温的响应弱于降水,但持续时间最长。

|
Download:
|
| 图 3 黄河流域陆地水储量变化与降水、径流、气温频谱图 Fig. 3 Spectrum of the TWSA and precipitation, runoff and temperature in the Yellow River basin | |
|
Download:
|
| 图 4 黄河流域陆地水储量变化与降水、径流、气温幅值平方相干图 Fig. 4 Amplitude square coherence map between the TWSA and the precipitation, runoff and temperature | |
1) GRACE的反演结果与GLDAS的模拟结果相关性较好,在时间变化上,都显示黄河流域陆地水储量变化具有明显的季节性周期,验证了GRACE反演陆地水储量变化的能力。
2) 黄河流域水储量夏秋季呈现从上游向下游递减的明显趋势。黄河流域陆地水储量在扎陵湖及鄂陵湖水域范围水储量最丰,内蒙地区水储量常年较枯。黄河流域陆地水储量多年季节变化均呈下降趋势,秋季降幅最大。
3) 相较降水和气温,径流对陆地水储量变化同期影响最直接。但考虑迟滞性,影响陆地水储量变化的主要水文气象因素是降水和气温,其中降水的影响程度最大,气温影响的持续时间最长。
本文在研究黄河流域陆地水储量变化时,相较年、月分析更着重于流域陆地水储量的季节性空间变化特征分析,研究了陆地水储量变化与相关多源水文气象因素的响应关系,研究成果可为未来流域水资源规划提供科学依据。未来在研究陆地水储量变化影响时可进一步考虑人类活动对陆地水储量的影响,探讨陆地水储量与水文气象灾害间的相互作用机制。
| [1] |
RIEGGER J, TOURIAN M J. Characterization of runoff-storage relationships by satellite gravimetry and remote sensing[J]. Water resources research, 2014, 50(4): 3444-3466. DOI:10.1002/2013WR013847 (  0) 0)
|
| [2] |
SWENSON S, WAHR J, MILLY P C D. Estimated accuracies of regional water storage variations inferred from the gravity recovery and climate experiment (GRACE)[J]. Water resources research, 2003, 39(8): 1223. (  0) 0)
|
| [3] |
SCHMIDT R, SCHWINTZER P, FLECHTNER F, et al. GRACE observations of changes in continental water storage[J]. Global and planetary change, 2006, 50(1/2): 112-126. (  0) 0)
|
| [4] |
STRASSBERG G, SCANLON B R, RODELL M. Comparison of seasonal terrestrial water storage variations from GRACE with groundwater-level measurements from the high plains aquifer (USA)[J]. Geophysical research letters, 2007, 34(14): L14402. DOI:10.1029/2007GL030139 (  0) 0)
|
| [5] |
SEO K W, WILSON C R, FAMIGLIETTI J S, et al. Terrestrial water mass load changes from gravity recovery and climate experiment (GRACE)[J]. Water resources research, 2006, 42(5): W05417. (  0) 0)
|
| [6] |
陈秋杰, 沈云中, 张兴福, 等. 基于GRACE卫星数据的高精度全球静态重力场模型[J]. 测绘学报, 2016, 45(4): 396-403. CHEN Qiujie, SHEN Yunzhong, ZHANG Xingfu, et al. GRACE data-based high accuracy global static earth's gravity field model[J]. Acta geodaetica et cartographica sinica, 2016, 45(4): 396-403. (  0) 0)
|
| [7] |
严家宝, 贾绍凤, 吕爱锋, 等. 近十年中国陆地水储量变化及其时空分布规律[J]. 南水北调与水利科技, 2016, 14(4): 21-28. YAN Jiabao, JIA Shaofeng, LYU Aifeng, et al. Spatial-temporal variation characteristics of China terrestrial water storage in the last ten years[J]. South-to-North water transfers and water science & technology, 2016, 14(4): 21-28. (  0) 0)
|
| [8] |
尼胜楠, 陈剑利, 李进, 等. 利用GRACE卫星时变重力场监测长江、黄河流域水储量变化[J]. 大地测量与地球动力学, 2014, 34(4): 49-55. NI Shengnan, CHEN Jianli, LI Jin, et al. Terrestrial water storage change in the Yangtze and Yellow river basins from GRACE time-variable gravity measurements[J]. Journal of geodesy and geodynamics, 2014, 34(4): 49-55. (  0) 0)
|
| [9] |
王文, 王鹏, 崔巍. 长江流域陆地水储量与多源水文数据对比分析[J]. 水科学进展, 2015, 26(6): 759-768. WANG Wen, WANG Peng, CUI Wei. A comparison of terrestrial water storage data and multiple hydrological data in the Yangtze River basin[J]. Advances in water science, 2015, 26(6): 759-768. (  0) 0)
|
| [10] |
周志才, 王卫平, 李冰瑶. 基于GRACE卫星时变重力场的淮河流域地下水储量变化规律研究[J]. 水电能源科学, 2017, 35(10): 37-41. ZHOU Zhicai, WANG Weiping, LI Bingyao. Research on groundwater reserve variation regulations in Huaihe basin based on GRACE temporal gravity field[J]. Water resources and power, 2017, 35(10): 37-41. (  0) 0)
|
| [11] |
于延胜, 陈兴伟. 基于Mann-Kendall法的径流丰枯变化过程划分[J]. 水资源与水工程学报, 2013, 24(1): 60-63. YU Yansheng, CHEN Xingwei. Division of variation process of high and low runoff based on Mann-Kendall method[J]. Journal of water resources & water engineering, 2013, 24(1): 60-63. (  0) 0)
|
| [12] |
LEE RODGERS J, NICEWANDER W A. Thirteen ways to look at the correlation coefficient[J]. The American statistician, 1998, 42(1): 59-66. (  0) 0)
|
| [13] |
董永权, 王占民. 关于相关系数ρ的几点注释[J]. 大学数学, 2008, 24(2): 182-186. DONG Yongquan, WANG Zhanmin. Some notes about correiation coefficient ρ[J]. College mathematics, 2008, 24(2): 182-186. DOI:10.3969/j.issn.1672-1454.2008.02.042 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


