2. 工业装备结构分析国家重点实验室, 辽宁 大连 116024;
3. 高技术船舶与深海开发装备协同创新中心, 上海 200240
2. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian 116024, China;
3. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
随着人类对海洋资源的不断勘测与开发,海底管道将成为海底资源运输的重要途径。为了保护海底管道不受人为和自然的破坏,需要将管道进行挖沟掩埋。根据挖沟掩埋和铺设管道的顺序不同,将挖沟方法分为3种:预挖沟法、同步挖沟法和后挖沟法。其中后挖沟法应用最广泛[1],该方法是当海底管道沉放在海床上之后将挖沟机骑在海底管道上进行挖沟,随着挖沟机的前进,管道自动沉入沟底,沟两侧沙土以及悬浮的泥沙在水流和波浪作用下自然回积到沟内[2-4]。喷射式挖沟机就是后挖沟法中应用最多的挖沟机,其工作原理是利用从喷嘴喷出高压水射流冲刷海管两侧下部海床,破除海床土层或将土体液化,在海管下方形成沟槽。目前成熟产品主要有SMD等公司研制的ROV型喷射式挖沟机和自行走喷射式挖沟机[5]。喷射式挖沟机设计有2根对称的喷射臂,分别骑在管道的两侧。喷射臂上安装一系列喷嘴,喷嘴参数设计是挖沟机设计中的关键技术之一[6],并且对冲刷沟形起到决定性影响。国内外研究者对于喷嘴的参数设计与优化做了大量研究,其中高溦通过数值模拟对喷嘴不同的收缩段长度、圆柱段长度、扩散段长度以及收缩角度进行了研究[7]; 吴强[8]从实验和数值2个方面对喷嘴的形式及组合方式进行分析; Leach等[9]分别从最大冲击力的角度和射流紧密性入手研究了冲刷效果最佳的锥形收缩角; Barker等[10]运用射流实验, 分析了最佳入口收缩角和圆柱段长度之间的联系; YangGeunyoung[11]运用实验方法得到了射流在轴心方向上的速度衰减与喷嘴内部流道型线相关。过去的研究主要集中于喷嘴形式、各段长度、收缩角度等参数,针对喷嘴直径大小的设计却没有提出合理且普适的方法,尤其是对于斜向喷嘴直径大小与其倾斜角度之间的关系没有进行系统性的研究。因此本文结合喷嘴的直径和喷嘴倾斜角度这2个参数提出了一种应用较为广泛的设计方法,并利用数值模拟进行了验证,对今后的挖沟机喷嘴优化设计有重要意义。
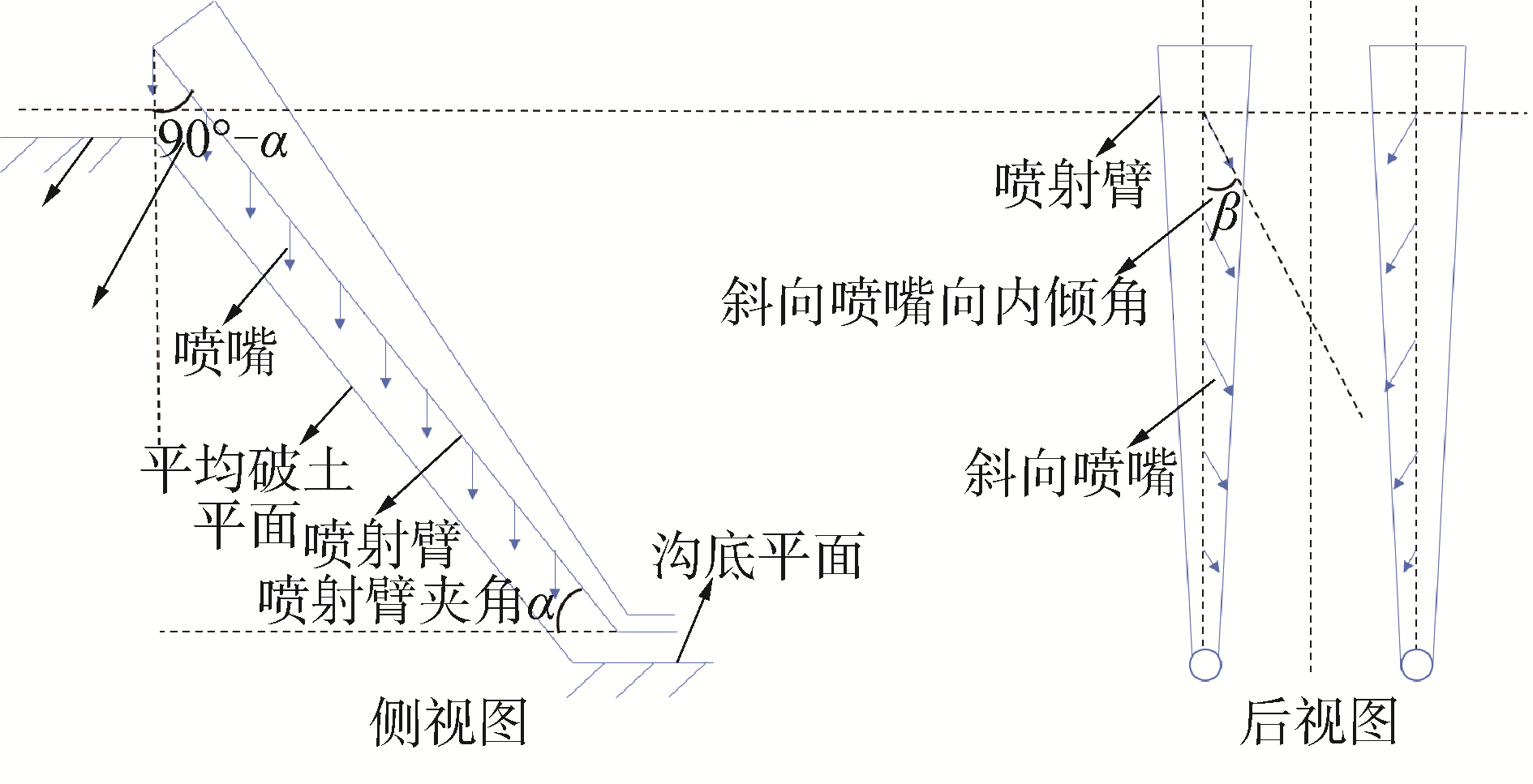
1 喷嘴参数设计 1.1 喷嘴形式目前投入生产的喷射式挖沟机喷嘴形状以及排布都各不相同,但喷射式挖沟机都会在2个对称的喷射臂上布置一排喷嘴。如图 1所示,喷射臂与水平面成一定夹角α,喷嘴分为2种型式,型式1喷嘴即垂向喷嘴,铅垂于水平面,与喷射臂夹角为α的余角; 型式2喷嘴即斜向喷嘴,在侧视图中与垂向喷嘴平行或重合,而从后视图可以看出其是在与喷射臂夹角为α的余角的基础上,再向沟内侧倾斜角度β。垂向喷嘴喷出高压流体主要用于破土,形成一定的沟深; 而斜向内侧喷嘴喷出流体主要用于将沟内的液化沙土冲走,同时形成一定的沟宽,使管道沉入。垂向喷嘴与斜向喷嘴交替排列,能使管道随着沟逐渐变深同时自动沉降到沟底。
|
Download:
|
| 图 1 挖沟机喷嘴示意 Fig. 1 Schematic diagram of trencher nozzle | |
根据文献[12]中提出的理论公式,距离喷嘴x处即靶距的冲击面上的射流有效冲击压强F可根据下式计算:
| $ \bar F = \frac{{p{R^2}}}{{0.00127{x^2}}} $ | (1) |
式中:R为喷嘴半径; p为喷嘴出口动压,即p=0.5ρu2,ρ为水体密度,u为喷嘴出口流速。
由图 1可知向内倾斜β的斜向喷嘴与垂向喷嘴出口垂向高度几乎相等且冲击面相同。则斜向喷嘴靶距xo为垂向喷嘴靶距xv的
| $ {x_o} = \frac{1}{{\cos \beta }}{x_v} $ | (2) |
再结合式(1),为在使用同样的出口动压下,2种型式喷嘴的射流在同一冲击面上达到同样有效冲击压强,半径应满足:
| $ {R_o} = \frac{1}{{\cos \beta }}{R_v} $ | (3) |
由式(3)得出垂向喷嘴和斜向喷嘴的半径大小关系,以口径参数为例说明设计过程:Rv=1 cm,Ro=
斜向喷嘴向内倾斜角度的大小主要取决于设计冲刷沟的形状,理想的冲刷沟形需要达到设计的管道掩埋深度,并具有足够的宽度让管道沉入底部。因此根据不同的管道尺寸,理想的沟形也将会不同。如果向内倾斜角度过大,则斜向喷嘴和垂向喷嘴将会在移动过程中冲刷出两道沟,沟内的泥沙不能被有效的冲走,破土管道将不会沉到沟最深的位置; 而且若倾斜角度过大,两侧喷射臂上的斜向喷嘴将有可能会产生射流对冲,尤其是在两侧斜向喷嘴向内倾斜角度超过45°时,导致射流动能损失,无法在冲击面上形成足够的破土压强。如果向内倾斜角度过小,沟的宽度将会过小,两侧喷射臂之间的土层没有射流作用,不会形成共同的沟,管道无法下沉。在以往的设计及模型实验中,斜向喷嘴倾斜角度设计一般都大于10°。根据以上分析以及国内外成型产品的喷嘴设计,斜向喷嘴倾斜角度应在10°~45°。本文选取实际作业工况和实验中常用的倾斜角度15°、30°和一个临界倾斜角度45°进行3组数值模拟并研究沟形的变化情况。
1.3 数值工况设计参照成型产品的设计经验,设定喷射臂的倾斜角度α为45°,喷嘴出口压力为0.6 MPa,喷嘴设为收缩式,其中收缩段长度为150 mm, 圆柱段长度为20 mm,收缩角度为7°。
有效冲击压强取为射流破土临界压力值,假设临界压力F=50 kPa。则由式(1)知靶距:
| $ {x_{\rm{v}}} = 30.62\;{\rm{cm}} $ |
因此,为了能冲出一定深度的沟形,数值模拟靶距应不大于30.62 cm,则靶距为:
| $ {x_{\rm{v}}} = 30\;{\rm{cm}}, {x_{\rm{o}}} = \frac{{30}}{{\cos \beta }}\;{\rm{cm}} $ |
根据以上关系式设定参数,并拟定以下3组数值模拟工况,如表 1所示。
| 表 1 数值模拟工况 Table 1 Conditions of numerical simulation |
| $ \begin{array}{l} {V_F}\frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {\rho u{A_x}} \right) + R\frac{\partial }{{\partial y}}\left( {\rho v{A_y}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{\partial }{{\partial z}}\left( {\rho w{A_z}} \right) + \xi \frac{{\rho u{A_x}}}{x} = {R_{{\rm{DIF}}}} + {R_{{\rm{SOR}}}} \end{array} $ | (4) |
式中:VF为流体的体积分数; ρ为流体密度; RDIF为湍流扩散项,RSOR为质量源项。u、v和w是流体速度的3个方向上的分量; Ax、Ay、Az分别为3个方向上的流体面积分数。
2.1.2 动量方程将流体速度分解为3个方向(u、v、w)分量,使用N-S方程:
| $ \begin{array}{l} \frac{{\partial u}}{{\partial t}} + \frac{1}{{{V_F}}}\left\{ {u{A_x}\frac{{\partial u}}{{\partial x}} + v{A_y}\frac{{\partial u}}{{\partial y}} + w{A_z}\frac{{\partial u}}{{\partial z}}} \right\} - \xi \frac{{{A_y}{v^2}}}{{x{V_F}}} = \\ \;\;\;\;\;\;\;\;\; - \frac{1}{\rho }\frac{{\partial \rho }}{{\partial x}} + {G_x} + {f_x} - {b_x} - \frac{{{R_{{\rm{SOR}}}}}}{{\rho {V_F}}}\left( {u - {u_w} - \delta {u_s}} \right)\\ \frac{{\partial v}}{{\partial t}} + \frac{1}{{{V_F}}}\left\{ {u{A_x}\frac{{\partial v}}{{\partial x}} + v{A_y}\frac{{\partial v}}{{\partial y}} + w{A_z}\frac{{\partial v}}{{\partial z}}} \right\} + \xi \frac{{{A_y}uv}}{{x{V_F}}} = \\ \;\;\;\;\;\;\;\;\; - \frac{1}{\rho }\left( {R\frac{{\partial \rho }}{{\partial x}}} \right) + {G_y} + {f_y} - {b_y} - \frac{{{R_{{\rm{SOR}}}}}}{{\rho {V_F}}}\left( {v - {v_w} - \delta {v_s}} \right)\\ \frac{{\partial w}}{{\partial t}} + \frac{1}{{{V_F}}}\left\{ {u{A_x}\frac{{\partial w}}{{\partial x}} + v{A_y}\frac{{\partial w}}{{\partial y}} + w{A_z}\frac{{\partial w}}{{\partial z}}} \right\} = - \frac{1}{\rho }\frac{{\partial \rho }}{{\partial z}} + \\ \;\;\;\;\;\;\;\;\;{G_z} + {f_z} - {b_z} - \frac{{{R_{{\rm{SOR}}}}}}{{\rho {V_F}}}\left( {w - {w_w} - \delta {w_s}} \right) \end{array} $ | (5) |
式中:G为重力加速度; f为粘滞加速度; b为流体在流经多孔介质受到阻力时能量损失。
2.1.3 湍流模型Liang等[13]研究了近海管道在恒定流下的局部冲刷二维数值模拟问题,比较亚格子尺度模型(Smagorinsky subgrid scale,SGS)湍流模型和k-ε湍流模型计算结果,发现后者好于前者。Lu等[14]采用基于有限元方法和非结构化三角网格系统的重整化群(renormalization group,RNG)湍流模型研究了海底管线的局部冲刷。CFD计算软件提供了2种k-ε模型:标准k-ε模型及RNG k-ε模型,标准k-ε模型中对于雷诺应力的各个分量,假定粘性系数相同,而在弯曲流线的情况下,粘性系数是各向异性的,因此标准k-ε模型对于强旋流、弯曲壁面流动或曲线流动时会产生一定失真[6]。RNG k-ε模型是由标准k-ε修正而来,考虑了平均流动中的旋转和旋流,并在耗散率方程中增加了可反映主流时均应变率的项[15],能更好地计算具有剪切力的流体区域,适用于水流对泥沙造成局部冲刷的模拟运算。本研究采用RNG k-ε模型,其包含湍流动能k方程及湍流动能消散率ε方程。
湍流动能k方程:
| $ \begin{array}{l} \frac{{\partial k}}{{\partial t}} + {u_j}\frac{{\partial k}}{{\partial {x_j}}} = {v_t}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)\frac{{\partial {u_i}}}{{\partial {x_j}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{\partial }{{\partial {x_j}}}\left( {{\alpha _k}{v_{{\rm{eff}}}}\frac{{\partial k}}{{\partial {x_j}}}} \right) - \varepsilon \end{array} $ | (6) |
湍流动能消散率ε方程:
| $ \begin{array}{l} \frac{{\partial \varepsilon }}{{\partial t}} + {u_j}\frac{{\partial \varepsilon }}{{\partial {x_j}}} = {C_{\varepsilon 1}}\frac{\varepsilon }{k}{v_t}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)\frac{{\partial {u_i}}}{{\partial {x_j}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{\partial }{{\partial {x_j}}}\left( {{\alpha _\varepsilon }{v_{{\rm{eff}}}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right) - {C_{\varepsilon 1}}\frac{{{\varepsilon ^2}}}{k} - R \end{array} $ | (7) |
其中:
| $ \begin{array}{l} R = \frac{{{C_\mu }{\eta ^3}\left( {1 - \frac{\eta }{{{\eta _0}}}} \right){\varepsilon ^2}}}{{\left( {1 + {C_\mu }{\eta ^3}} \right)k}}, {v_{{\rm{eff}}}} = {v_t}{(1 + \sqrt {\frac{{{C_\mu }k}}{{\mu \sqrt \varepsilon }}} )^2}, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\eta = \sqrt {\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)\frac{{\partial {u_i}}}{{\partial {x_j}}}} \frac{k}{\varepsilon } \end{array} $ |
数值模拟采用的泥沙模型可用于计算泥沙的运输、冲刷和沉降过程。模型通过预测泥沙的侵蚀、对流和沉积来模拟泥沙的运动[16]。该模型判断泥沙起动的条件是:当床面受到的剪切应力大于床面临界剪切应力时,泥沙开始运动。模型分别计算2种状态的泥沙:悬沙和底沙,泥沙在射流的作用下运动状态也就分为悬沙运动和底沙推移2种类型[17]。悬沙浓度低,直径较小,悬浮于运动流体中,通过与流体对流而运动; 而推移质沙粒一般直径较大,在沙床表面低速运动,并会与床面静止沙粒交换。泥沙模型通过跟踪悬沙和底沙的含沙浓度(Cs和Cp),来计算泥沙体积分数,总泥沙体积分数αs是网格中悬沙和底沙的总体积分数,表达式为:
| $ {\alpha _s} = \frac{{{C_s} + {C_p}}}{{{\rho _s}}} = 1 - {\alpha _f} $ | (8) |
式中:αf为网格中流体的体积分数; ρs为泥沙颗粒密度。底沙体积分数的表达式为αs, p=Cp/ρs,悬沙体积分数的表达式为αs, s=Cs/ρs, 临界泥沙体积分数为αcr, 总泥沙体积分数αs≤αcr。
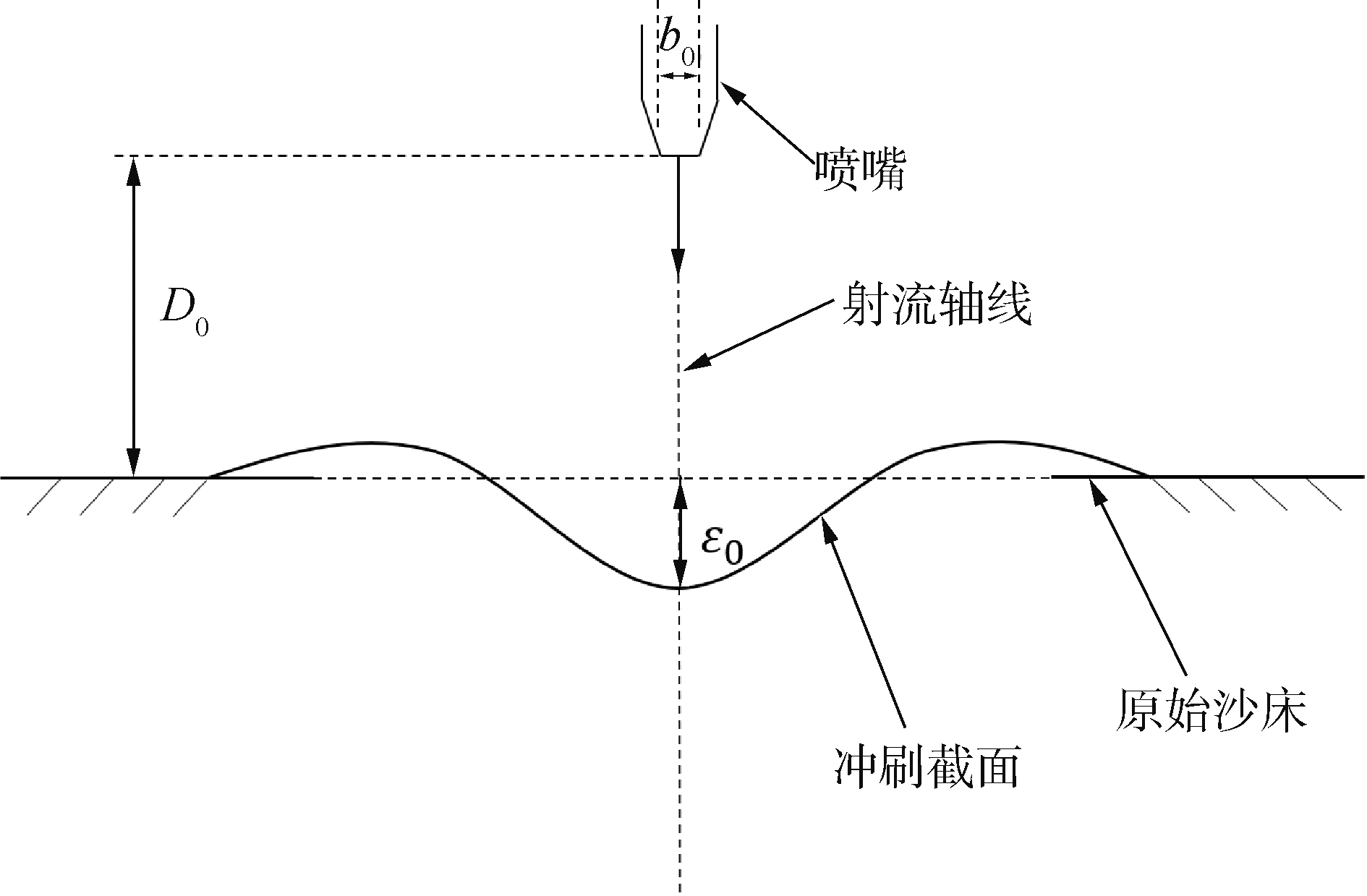
2.2 模型验证应用文献[18]中的二维射流冲刷实验进行数学模型验证,试验在宽300 mm,长1 300 mm的小型透明水槽中进行,喷嘴截面宽度b0为2.5 mm,靶距D0为150 mm,沙粒中值粒径d50为1.8 mm,沙粒中孔隙度为50%,泥沙密度为2 650 kg/m3,原始沙床高度为400 mm。一共进行了3组试验,每组试验设计喷嘴出口流速不同,其余参数不变。3组试验的喷嘴出口流速分别设为3.12、5.10、7.04 m/s。
|
Download:
|
| 图 2 射流冲刷实验示意 Fig. 2 Jet scouring experiment schematic | |
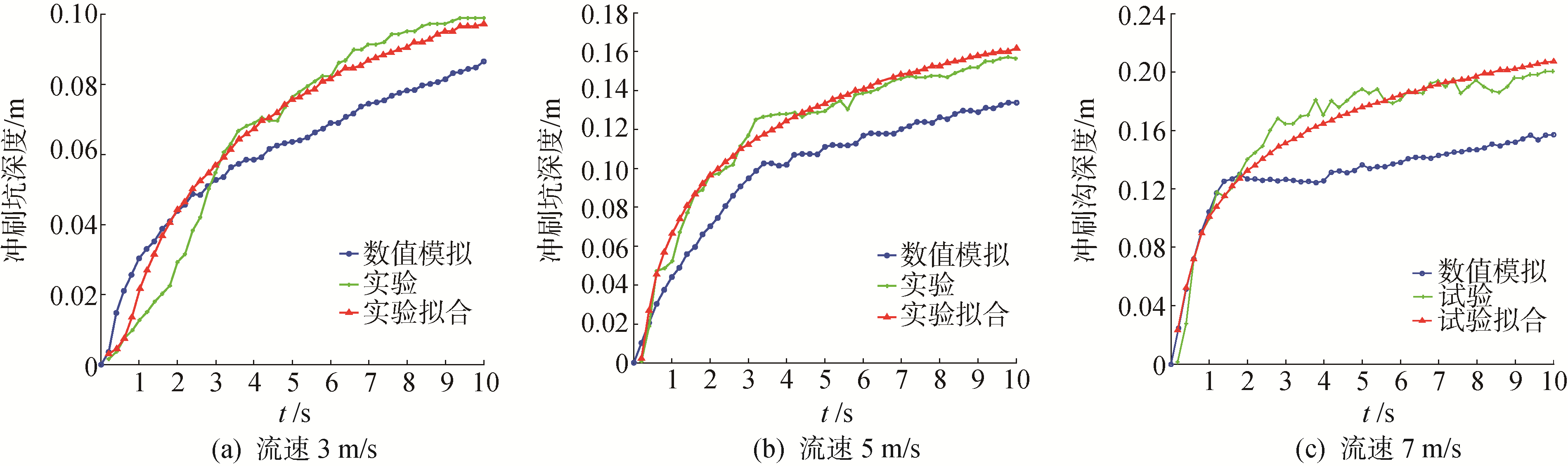
数值模拟的计算区域与试验一致,设置与试验相同的沙床条件,并激活重力模型,黏性和湍流模型(RNG k-ε)。图 3给出了3组试验10 s内坑深变化曲线的试验结果和数值结果的对比。通过对比结果可以发现数值模拟冲刷坑深的变化趋势与试验一致,初始阶段,冲刷坑在很短的时间内迅速变深; 随后进入缓慢发展阶段,冲坑在深度方向增加缓慢; 最后冲坑达到动态平衡状态,坑的深度几乎不随时间发生变化,在10 s后坑深增加速度逐渐趋于平缓。由图可以发现达到动态平衡时的数值结果冲刷坑深要略小于试验结果,尤其体现在试验3结果中,这是因为喷嘴出口流速增大,冲刷坑两侧的沙丘将会大量堆积; 试验水槽宽度过小,沙丘的高度将会受到明显的壁面作用影响而进一步增大,同时试验测量的是壁面处的结果,比实际上的坑要深[19]。而数值模拟采用的是真正意义上的二维试验,坑的两侧没有壁面边界条件。通过对比可以发现,CFD软件的数学模型计算准确,符合实际的物理情况。
|
Download:
|
| 图 3 试验与数值结果对比 Fig. 3 Comparison of experimental and numerical results | |
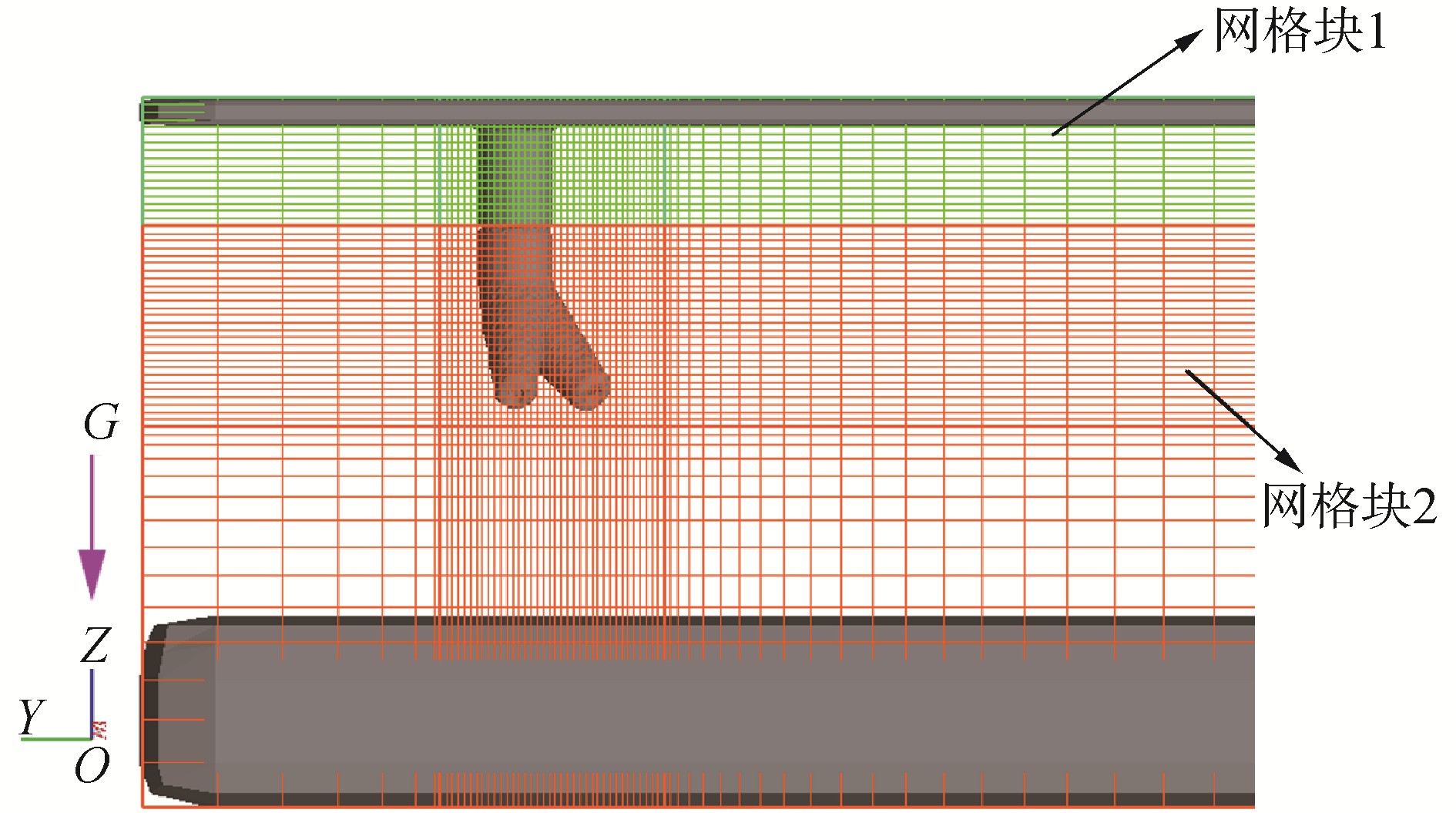
喷射臂上一般都布置有10~20只喷嘴,垂向喷嘴和斜向喷嘴交替布置。由于喷嘴数量过多带来网格数量的庞大,将会使计算时间大大增加。因此本文建立1组喷嘴(1只垂向喷嘴和1只斜向喷嘴组合)模型进行计算模拟。根据工况设计的斜向喷嘴倾角不同分别建立了3个模型,图 4为预处理后的计算模型,模型由4个部件组成,即上部挡板、垂向喷嘴、斜向喷嘴、泥沙底质。为了方便建模和模型运动,此处以水平板代替喷射臂,即喷射臂角度设为水平,同时破土面也设置为水平,因此垂向喷嘴设为向下倾斜α的余角45°,斜向喷嘴则在向下倾斜45°的基础上再向内倾斜β。建模完成后进行网格的划分,为了合理的控制网格数量,只需对图中中间区域进行加密,加密区域3个方向上的网格尺寸都为0.01 m,计算域内两侧网格较为稀疏,网格尺寸为0.01~0.1 m渐变,网格总量在100万左右。模型预处理能在模拟前对网格中的几何模型进行计算,从而直观的观察计算模型,以检查网格质量,从图中可以明显看出,计算模型完整,说明网格划分不存在缺陷。
|
Download:
|
| 图 4 组合喷嘴模型 Fig. 4 The model of combined nozzles | |
如图 4所示,将整个计算区域分成2个区块(Mesh block)。区块1四周的边界(Xmax、Xmin、Ymax、Ymin)都设置为压力边界,压力值设置为0,这使溢流的流体从区块1的四周边界流出,使计算域内液体保持在固定的高度。Zmax边界设置为压力边界,压力值设为0.6 MPa, 即喷嘴入口压力0.6 MPa。由于上部是一块被喷嘴贯通的挡板,流体被阻止之后只能从通孔进入到喷嘴。区块1的Zmin与区块2的Zmax连接,因此将Zmin设置为默认边界,这样在前处理时软件将自动与区块2的Zmax边界进行连接。区块2的四周边界(Xmax、Xmin、Ymax、Ymin)都设置为墙边界,Zmin由于是泥沙底质,因此也设置为墙边界。而为Zmax设置为默认边界,与区块1的Zmin边界进行连接。
3.3 物理模型1) 重力模型
泥沙的冲刷与沉淀都需要考虑重力的作用,数值模拟要激活重力模型,这里设置重力加速度为Z方向,值为-9.8 m/s2。
2) 移动和变形体模型
数值工况中喷嘴移动冲刷,需要激活该模型,并定义几何体过程中设置运动速度为200 m/h,运动方向为X方向。
3) 湍流模型
湍流模型选择RNG k-ε湍流模型。
4) 沉积物冲刷模型
沉积物冲刷模型即泥沙模型,CFD软件中,泥沙模型设置的参数有:泥沙中值粒径0.000 8 m,泥沙密度2 650 kg/m3,临界希尔兹参数,夹带系数α为0.001 8,推移质系数为8,休止角为45°,泥沙临界体积分数为0.64。其中临界希尔兹参数由软件内置的希尔兹方程自动计算得出。根据文献[20]中的射流破土临界压力公式:
| $ {F_{cr}} = \alpha \tau _f^2{\left( {\frac{{{d_{60}}}}{k}} \right)^{ - 2}}\gamma _d^{ - 1} $ | (9) |
计算出泥沙的临界破坏压力约为42.45 kPa, 小于作用到泥沙表面压力F=50 kPa, 说明设计压力能完成冲刷破土。
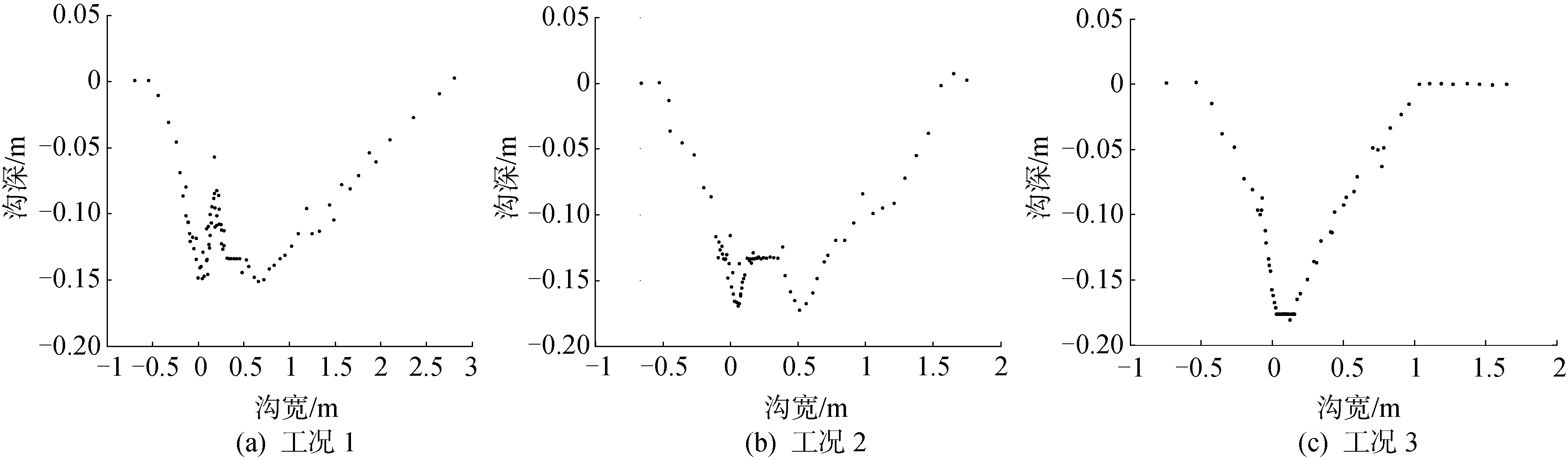
4 结果分析3个数值模拟工况在达到动态平衡时的计算结果冲刷剖面如图 5所示。图 5(a)是由工况1计算结果得到的沟形稳定时冲刷剖面散点图,由图可以看出,垂直喷嘴与斜向喷嘴冲刷出两道沟,斜向喷嘴冲刷剖面的右侧与垂向喷嘴相比则要平缓。冲刷剖面的最大沟深都在0.15 m左右,这说明从2个喷嘴出口的射流作用到泥沙表面上的有效冲击压强也几乎相等; 冲刷剖面最大直径在3.35 m左右。两道沟的中间有明显的凸起,说明泥沙在沟内堆积,不能被有效的冲出,管道不能沉入到沟底最深位置。
|
Download:
|
| 图 5 冲刷剖面 Fig. 5 Trench profiles | |
图 5(b)由工况2的计算结果得到的沟形稳定时冲刷剖面散点图,由图可以看出,垂直喷嘴与斜向喷嘴能冲刷出接近一道共同的沟,沟的底部有较大的平整区域,沟形剖面左侧相比右侧更陡峭,倾斜角度更大。冲刷剖面的最大沟深为0.169 m,这说明分别从2个喷嘴出口的射流作用到泥沙床面上的有效冲击压强保持一致; 冲刷剖面的最大直径为2.18 m。沟的中间有稍微的凸起,说明沟内大部分泥沙都已经被冲刷到沟外。
图 5(c)由工况3的计算结果得到的沟形稳定时冲刷剖面散点图,由图可以看出,垂直喷嘴与斜向喷嘴能冲刷出同一道沟,两侧沟形相似且倾斜角度几乎相等。最大沟深0.177 m,这说明从2个喷嘴出口的高压水流作用到沙质表面上的有效冲击压强相等; 冲刷剖面的最大直径为1.57 m。沟底区域平整,不存在凸起部分,说明沟内泥沙已被全部冲出,合适尺寸的管道将会顺利沉入沟底最深处。
5 结论1) 垂向喷嘴与斜向喷嘴冲刷出的最大沟深相等,证明了满足关系式(3)的2个喷嘴冲击面位置处于同一垂向高度时能达到同样有效冲击压强,体现了该设计方法合理可行,为以后的2种喷嘴半径大小设计提供了一种重要的思路。
2) 若喷嘴长度和靶距固定且垂向喷嘴和斜向喷嘴冲刷剖面有重叠区域,当斜向喷嘴倾斜角度在15°~45°范围内变化时,垂向喷嘴和斜向喷嘴冲刷出的最大沟深将会随着倾斜角度的增大而稍有减小。
3) 若喷嘴长度和靶距固定且垂向喷嘴和斜向喷嘴冲刷剖面有重叠区域,斜向喷嘴倾斜角度的变化对冲刷剖面直径的影响远大于对沟深的影响,当倾斜角度在15°~45°范围内变化时,冲刷剖面最大直径随着倾斜角度的增加明显的增大。
4) 定性分析了当喷嘴长度和靶距固定时,随着斜向喷嘴倾斜角度增大会出现冲刷出两道沟的可能性,这为以后的斜向喷嘴倾斜角度设计提供了一定的参考。
| [1] |
杜喜军, 赵杰, 王艳涛, 等. 海底管道挖沟方法的选择[J]. 管道技术与设备, 2015(5): 52-54. DU Xijun, ZHAO Jie, WANG Yantao, et al. Contrast of subsea pipeline trenching methods[J]. Pipeline technique and equipment, 2015(5): 52-54. DOI:10.3969/j.issn.1004-9614.2015.05.017 (  0) 0)
|
| [2] |
王佐祥, 高学仕, 王路林. 喷射式水下挖沟机地基承载力计算分析[J]. 中国海洋平台, 2005, 20(5): 32-34. WANG Zuoxiang, GAO Xueshi, WANG Lulin. Compute and analysis of groundwork bearing capacity for jet underwater ditch digger[J]. China offshore platform, 2005, 20(5): 32-34. DOI:10.3969/j.issn.1001-4500.2005.05.007 (  0) 0)
|
| [3] |
刘润, 闫澍旺, 田英辉, 等. 喷射式挖沟机机体的稳定性分析[J]. 海洋技术, 2005, 24(2): 93-97. LIU Run, YAN Shuwang, TIAN Yinghui, et al. Stability analysis on a designed jet trencher for ocean pipeline installation[J]. Ocean technology, 2005, 24(2): 93-97. DOI:10.3969/j.issn.1003-2029.2005.02.024 (  0) 0)
|
| [4] |
Trenching Technology, International Construction, 1991(10): 60-64.
(  0) 0)
|
| [5] |
王喆, 马洪新, 李翔, 等. 新型喷冲式挖沟机总体设计与结构安全性评估[J]. 哈尔滨工程大学学报, 2015, 36(5): 600-605. WANG Zhe, MA Hongxin, LI Xiang, et al. Evaluation on the overall design and structural safety of a new type of jet trencher for subsea oil pipelines[J]. Journal of Harbin Engineering University, 2015, 36(5): 600-605. (  0) 0)
|
| [6] |
戴必林.射流助推式ROV型开沟机喷射臂及其冲刷过程研究[D].杭州: 浙江大学, 2016. DAI Bilin. Research on the jetting arm of jetting propelled ROV trencher and its jetting process[D]. Hangzhou: Zhejiang University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10335-1016042281.htm (  0) 0)
|
| [7] |
高溦.水力冲射海底开沟机的参数优化[D].大连: 大连理工大学, 2008. GAO Wei. Parameter optimization of seabed hydraulic jet trenching machine[D]. Dalian: Dalian University of Technology, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10141-2009116392.htm (  0) 0)
|
| [8] |
吴强.用于喷射式挖沟机的喷嘴结构及喷嘴组合的研究[D].北京: 中国石油大学, 2011. WU Qiang. Study on nozzle configuration and nozzle combination used on jet trencher[D]. Beijing: China University of Petroleum, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10425-1011287024.htm (  0) 0)
|
| [9] |
LEACH S J, WALKER G L. The application of high speed liquid jets to cutting[J]. Philosophical transactions of the royal society of London, 1965, 260: 295-308. (  0) 0)
|
| [10] |
BARKER C R, SELBERG B P. Water jet nozzle performance tests[C]//4th International Symposium on Jet Cutting Technology. Canterbury, UK, 1979.
(  0) 0)
|
| [11] |
YANG G, CHOI M, LEE J S. An experimental study of slot jet impingement cooling on concave surface:effects of nozzle configuration and curvature[J]. International journal of heat and mass transfer, 1999, 42(12): 2199-2209. DOI:10.1016/S0017-9310(98)00337-8 (  0) 0)
|
| [12] |
马飞, 宋志辉. 水射流动力特性及破土机理[J]. 北京科技大学学报, 2006, 28(5): 413-416. MA Fei, SONG Zhihui. Dynamic property and breaking soil mechanism of water jet[J]. Journal of University of Science and Technology Beijing, 2006, 28(5): 413-416. DOI:10.3321/j.issn:1001-053X.2006.05.002 (  0) 0)
|
| [13] |
LIANG Dongfang, CHENG Liang, LI Fangjun. Numerical modeling of flow and scour below a pipeline in currents:part Ⅱ. Scour simulation[J]. Coastal engineering, 2005, 52(1): 43-62. (  0) 0)
|
| [14] |
LU Lin, LI Yucheng, QIN Jianmin. Numerical simulation of the equilibrium profile of local scour around submarine pipelines based on renormalized group turbulence model[J]. Ocean engineering, 2005, 32(17/18): 2007-2019. (  0) 0)
|
| [15] |
王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2004. WANG Fujun. Computational fluid dynamics analysis[M]. Beijing: Tsinghua University Press, 2004. (  0) 0)
|
| [16] |
孟然.海底管道后挖沟技术实验研究及数值模拟[D].天津: 天津大学, 2012. MENG Ran. Experimental study and numerical simulation on post trenching of submarine pipelines[D]. Tianjin: Tianjin University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10056-1012022255.htm (  0) 0)
|
| [17] |
彭勃.基于淹没射流的前混合磨料回收系统优化设计[D].徐州: 中国矿业大学, 2014. PENG Bo. Optimal design of recycle system in ASJ based on submerged jet[D]. Xuzhou: China University of Mining and Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10290-1014075002.htm (  0) 0)
|
| [18] |
张浩, 倪福生, 顾磊. 某靶距下射流垂直冲刷坑深的实验研究[J]. 科学技术与程, 2014, 14(2): 238-240. ZHANG Hao, NI Fusheng, GU Lei. An experimental study of depth of dynamic scour by vertical water jets at a height[J]. Science technology and engineering, 2014, 14(2): 238-240. (  0) 0)
|
| [19] |
王建军, 倪福生. 二维垂向淹没射流冲刷粗砂砂床的数值模拟[J]. 科学技术与工程, 2014, 14(3): 108-111. WANG Jianjun, NI Fusheng. Numerical simulation of coarse sandy bed scour by 2D vertical submerged jet[J]. Science technology and engineering, 2014, 14(3): 108-111. DOI:10.3969/j.issn.1671-1815.2014.03.022 (  0) 0)
|
| [20] |
李范山, 杜嘉鸿, 施小博, 等. 射流破土机理研究及其工程应用[J]. 流体机械, 1997, 25(2): 26-29. LI Fanshan, DU Jiahong, SHI Xiaobo, et al. Study on the mechanism of jet breaking soil and its engineering application[J]. Fluid machinery, 1997, 25(2): 26-29. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


