2. 水沙科学与水灾害防治湖南省重点实验室, 湖南 长沙 410004;
3. 美国麻省大学 海洋科学与技术学院, 美国马萨诸塞州 新贝德福德 02744;
4. 国家海洋局 南海调查技术中心, 广东 广州 510300
2. Hu'nan Provincial Key Laboratory of Water, Sediment Sciences & Flood Hazard Prevention, Changsha 410004, China;
3. School for Marine Science and Technology, University of Massachusetts Dartmouth, New Bedford, MA 02744, USA;
4. Key Laboratory of Technology for Safeguarding of Maritime Rights and Interests and Application, State Oceanic Administration, Guangzhou 510300, China
波浪和水流(潮流、径流、波生流、风生流)是河口、近岸地区最重要的动力要素,波流相互作用关系非常复杂,目前相关作用机理仍不明确。为研究近岸海区的动力过程,诸多学者开展了大量波流耦合相关工作[1-3]。研究表明,水流对波浪传播和运动过程会产生显著影响,甚至可能导致波浪破碎;同样,波浪对水流运动的内部结构也会有非常复杂的影响,Longuet-Higgins等[4]提出了辐射应力的概念,阐述了波浪对水流的驱动效应,该理论被广泛应用于海洋模式中[1, 5]。
波流耦合研究初期,学者们在利用水动力模型研究波流耦合作用时,主要采用沿水深方向均匀分布的辐射应力公式[6],未考虑辐射应力的分层效应[7],分析水深平均的二维波流耦合关系,而忽视了三维水流结构的影响。近年来,Xia等[8]和Zheng等[9]等提出了基于σ坐标系、笛卡尔坐标系的三维辐射应力计算公式,王平等[10]将随水深变化的辐射应力想加入到水动力模型中,建立了波生流三维数值模型。
本文利用MCT耦合器,将第3代海浪模型SWAN与海洋模型ROMS进行耦合,建立了三维波流双向实时耦合计算模型,并将其应用于理想潮汐通道的模拟中,计算分析波流耦合模式下的波流和潮流模拟结果。
1 数学模型简介 1.1 区域海洋模式区域海洋模型(regional ocean model system,ROMS)是目前国际上最为先进的海洋模式系统之一。ROMS模式在垂向上采用地形追随的S坐标系,在温跃层和底边界层等层面上可以具有更高的解析度。ROMS在水平压力梯度上相比以往传统的地形追随坐标而言也采用了新的算法,使其在地形变化大的区域对水平压力梯度的计算误差累计有明显改善[11]。
在水平笛卡尔坐标系,垂向σ坐标系下,ROMS的动量方程为:
| $ \begin{array}{*{20}{c}} {\frac{{\partial \left( {{H_z}u} \right)}}{{\partial t}} + \frac{{\partial \left( {u{H_z}u} \right)}}{{\partial x}} + \frac{{\partial \left( {v{H_z}u} \right)}}{{\partial y}} + \frac{{\partial \left( {w{H_z}u} \right)}}{{\partial s}} - }\\ {f{H_z}v = - \frac{{{H_z}}}{{{\rho _0}}}\frac{{\partial p}}{{\partial x}} - {H_z}g\frac{{\partial \eta }}{{\partial x}} - \frac{\partial }{{\partial s}}\left( {\overline {u'w'} - \frac{v}{{{H_z}}}\frac{{\partial u}}{{\partial s}}} \right) - }\\ {\frac{{\partial \left( {{H_z}{S_{xx}}} \right)}}{{\partial x}} - \frac{{\partial \left( {{H_z}{S_{xy}}} \right)}}{{\partial y}} + \frac{{\partial {S_{px}}}}{{\partial s}}} \end{array} $ | (1) |
| $ \begin{array}{*{20}{c}} {\frac{{\partial \left( {{H_z}v} \right)}}{{\partial t}} + \frac{{\partial \left( {u{H_z}v} \right)}}{{\partial x}} + \frac{{\partial \left( {v{H_z}v} \right)}}{{\partial y}} + \frac{{\partial \left( {w{H_z}v} \right)}}{{\partial s}} - }\\ {f{H_z}u = - \frac{{{H_z}}}{{{\rho _0}}}\frac{{\partial p}}{{\partial y}} - {H_z}g\frac{{\partial \eta }}{{\partial y}} - \frac{\partial }{{\partial s}}\left( {\overline {v'w'} - \frac{v}{{{H_z}}}\frac{{\partial v}}{{\partial s}}} \right) - }\\ {\frac{{\partial \left( {{H_z}{S_{yx}}} \right)}}{{\partial x}} - \frac{{\partial \left( {{H_z}{S_{yy}}} \right)}}{{\partial y}} + \frac{{\partial {S_{py}}}}{{\partial s}}} \end{array} $ | (2) |
| $ - \frac{1}{{{\rho _0}}}\frac{{\partial p}}{{\partial s}} - \frac{g}{{{\rho _0}}}{H_z}\rho = 0 $ | (3) |
连续性方程为:
| $ \frac{{\partial \eta }}{{\partial t}} + \frac{{\partial \left( {{H_z}u} \right)}}{{\partial x}} + \frac{{\partial \left( {{H_z}v} \right)}}{{\partial y}} + \frac{{\partial \left( {{H_z}w} \right)}}{{\partial s}} = 0 $ | (4) |
对流扩散方程为:
| $ \begin{array}{*{20}{c}} {\frac{{\partial \left( {{H_z}C} \right)}}{{\partial t}} + \frac{{\partial \left( {u{H_z}C} \right)}}{{\partial x}} + \frac{{\partial \left( {v{H_z}C} \right)}}{{\partial y}} + \frac{{\partial \left( {w{H_z}C} \right)}}{{\partial s}} = }\\ { - \frac{\partial }{{\partial s}}\left( {\overline {c'w'} - \frac{{{v_\theta }}}{{{H_z}}}\frac{{\partial C}}{{\partial s}}} \right) + {C_{{\rm{source}}}}} \end{array} $ | (5) |
海水状态方程为:
| $ \rho = f\left( C \right) $ | (6) |
式中:u、v和w分别代表x、y和z 3个方向上的流速;垂向σ坐标s=(z-η)/(h+η),-1 < s < 0。
1.2 第3代海浪模式SWAN基于能量平衡方程的海浪模型是可以用于大范围、长时序的波浪计算模拟。目前,通过发展和改进动谱方程,能量平衡方程模型已经经历了第1代和第2代模式,发展为相对完善的以SWAN模型为代表的第3代模式,本文采用第3代风浪模型SWAN开展波流耦合作用模拟。
第3代海浪模型SWAN由荷兰Delft University of Technology(代尔夫特理工大学)开发,其前身是WAM模式,该模式具有较好的近岸浪模拟精度,并得到广泛应用。SWAN模型通过在谱波浪能量平衡方程源、汇项中综合考虑了波浪浅水变形、折射、绕射、反射等传播变形过程,能够模拟底摩擦、破碎、白浪、风能输入以及波浪非线性效应等影响,可以准确描述复杂的潮流、地形、风场环境下风浪从生成、成长直至大风过后衰减的全过程。关于海浪模型SWAN的控制方程和求解方法在前人研究中已有详细阐述[12],本文中不再赘述。
1.3 三维辐射应力计算方法区域海洋模式ROMS通过在控制方程中加入了三维辐射应力项,用于模拟近岸海域内的波流相互作用的模拟。在动量方程(1)、(2)中,Sxx、Sxy、Syx和Syy为水平辐射应力项,Spx和Spy为垂向辐射应力项,忽略了表面风压变化和波面倾斜产生的动量输运。
水平辐射应力为:
| $ \left\{ \begin{array}{l} {S_{xx}} = kE\left( {\frac{{{k_x}{k_x}}}{{{k^2}}}{F_{CS}}{F_{CC}} + {F_{CC}}{F_{CS}} - {F_{SS}}{F_{CS}}} \right) + \frac{{{k_x}{k_x}}}{k}\frac{{{c^2}}}{L}{A_R}{R_z}\\ {S_{xy}} = {S_{yx}} = kE\left( {\frac{{{k_x}{k_y}}}{{{k^2}}}{F_{CS}}{F_{CC}}} \right) + \frac{{{k_x}{k_y}}}{k}{A_R}{R_z}\\ {S_{yy}} = kE\left( {\frac{{{k_y}{k_y}}}{{{k^2}}}{F_{CS}}{F_{CC}} + {F_{CS}}{F_{CC}} - {F_{SS}}{F_{CS}}} \right) + \frac{{{k_y}{k_y}}}{k}\frac{{{c^2}}}{L}{A_R}{R_z} \end{array} \right. $ | (7) |
式中:c、k分别为波速和波数; E=gHs2/16为波能,括号中是波浪水质点运动产生的动量流; 最后一项是由波浪破碎产生的波生流,它含有一个垂向分布函数Rz:
| $ R_{z}=1-\tanh (2 s / \gamma)^{4} $ | (8) |
式中:γ是波高与水深的比,γ=Hs/D; Hs是有效波高; AR是波浪水滚面积,可以由波浪模型提供,也可以计算得出:
| $ A_{\mathrm{R}}=\alpha H_{s} L Q_{b} / \sqrt{2} $ | (9) |
式中:α参数通常取为0.06;Qb为破波系数。
垂向辐射应力为Spx和Spy:
| $ \left\{ \begin{array}{l} {S_{px}} = \left( {{F_{CC}} - {F_{SS}}} \right)\left[ {\frac{{{F_{SS}}}}{2}\frac{{\partial E}}{{\partial x}} + {F_{CS}}(1 + s)E\frac{{\partial (kD)}}{{\partial x}} - } \right.\\ \;\;\;\;\;\;\;\;\;\left. {E{F_{SS}}\coth (kD)\frac{{\partial (kD)}}{{\partial x}}} \right]\\ {S_{py}} = \left( {{F_{CC}} - {F_{SS}}} \right)\left[ {\frac{{{F_{SS}}}}{2}\frac{{\partial E}}{{\partial y}} + {F_{CS}}(1 + s)E\frac{{\partial (kD)}}{{\partial y}} - } \right.\\ \;\;\;\;\;\;\;\;\;\left. {E{F_{SS}}\coth (kD)\frac{{\partial (kD)}}{{\partial y}}} \right] \end{array} \right. $ | (10) |
式(9)和式(10)中的垂向结构函数分别为:
| $ \left\{ \begin{array}{l} {F_{SS}} = \frac{{\sinh \left[ {kD\left( {1 + s} \right)} \right]}}{{\sinh \left( {kD} \right)}},{F_{CS}} = \frac{{\cosh \left[ {kD\left( {1 + s} \right)} \right]}}{{\sinh \left( {kD} \right)}}\\ {F_{SC}} = \frac{{\sinh \left[ {kD\left( {1 + s} \right)} \right]}}{{\cosh \left( {kD} \right)}},{F_{CC}} = \frac{{\cosh \left[ {kD\left( {1 + s} \right)} \right]}}{{\cosh \left( {kD} \right)}} \end{array} \right. $ | (11) |
ROMS在解方程时使用了内外模式分别求解的方法,这种方法需要求解垂向平均的动量方程。包含辐射应力项的垂向平均动量方程为:
| $ \begin{array}{*{20}{c}} {\frac{{\partial (D\bar u)}}{{\partial t}} + \frac{{\partial (\bar uD\bar u)}}{{\partial x}} + \frac{{\partial (\bar vD\bar v)}}{{\partial y}} - fD\bar v = - D\frac{{\partial p}}{{\partial x}} + }\\ {{\tau _{sx}} - {\tau _{bx}} - \frac{{\partial {{\bar S}_{xx}}}}{{\partial x}} - \frac{{\partial {{\bar S}_{xy}}}}{{\partial y}}} \end{array} $ | (12) |
| $ \begin{array}{*{20}{c}} {\frac{{\partial (D\bar v)}}{{\partial t}} + \frac{{\partial (\bar vD\bar v)}}{{\partial x}} + \frac{{\partial (\bar vD\bar v)}}{{\partial y}} - fD\bar u = - D\frac{{\partial p}}{{\partial y}} + }\\ {{\tau _{sy}} - {\tau _{by}} - \frac{{\partial {{\bar S}_{xy}}}}{{\partial x}} - \frac{{\partial {{\bar S}_{yy}}}}{{\partial y}}} \end{array} $ | (13) |
连续性方程为:
| $ \frac{{\partial \eta }}{{\partial t}} + \frac{{\partial \left( {D\bar u} \right)}}{{\partial x}} + \frac{{\partial \left( {D\bar v} \right)}}{{\partial y}} = 0 $ | (14) |
方程(12)和方程(13)中的水平辐射应力项也包含了表面波浪水滚的贡献,表达式为:
| $ \left\{ \begin{array}{l} {{\bar S}_{xx}} = E\frac{{{c_g}}}{c}\frac{{{k_x}{k_x}}}{{{k^2}}} + E\left( {\frac{{{c_g}}}{c} - \frac{1}{2}} \right) + \frac{{{k_x}{k_x}}}{k}\frac{{{c^2}{A_R}}}{L}\\ {{\bar S}_{xy}} = {{\bar S}_{yx}} = E\frac{{{c_g}}}{c}\frac{{{k_x}{k_y}}}{{{k^2}}} + \frac{{{k_x}{k_y}}}{k}\frac{{{c^2}{A_R}}}{L}\\ {{\bar S}_{yy}} = E\frac{{{c_g}}}{c}\frac{{{k_y}{k_y}}}{{{k^2}}} + E\left( {\frac{{{c_g}}}{c} - \frac{1}{2}} \right) + \frac{{{k_y}{k_y}}}{k}\frac{{{c^2}{A_R}}}{L} \end{array} \right. $ | (15) |
式(15)中的cg为波群速度为:
| $ c_{g}=\frac{\partial \sigma}{\partial k}=\frac{c}{2}\left[1+\frac{2 k D}{\sinh (2 k D)}\right] $ | (16) |
垂向平均流速也是在拉格朗日坐标系统下推导的,可以通过垂向平均的斯托克斯流速转换到欧拉坐标系统,垂向平均的斯托克斯流速为:
| $ {\bar u_s} = \frac{{{k_x}E}}{{ckD}} + \frac{{{k_x}}}{k}\frac{{g{A_R}}}{{cL}},{\bar v_s} = \frac{{{k_y}E}}{{ckD}} + \frac{{{k_y}}}{k}\frac{{g{A_R}}}{{cL}} $ | (17) |
同样,用拉格朗日坐标系统下的平均流速减去斯托克斯平均流速就可以获得与ROMS模型一致的欧拉坐标系统下的平均流速。
1.4 波流实时双向耦合方法在进行波流耦合计算时,早期的研究主要是将波浪辐射应力作为条件引入到海洋模式中,而海洋模式对波浪模式无反馈作用,这种耦合被称为单向耦合[13]。从20世纪90年代开始,随着对海浪和海洋数值模式理解的深入,广大学者开始同时考虑海浪对海洋的影响以及海洋模式对海洋模式的反馈作用[14-15],这种耦合模式称之为海浪-海洋的双向耦合模式。
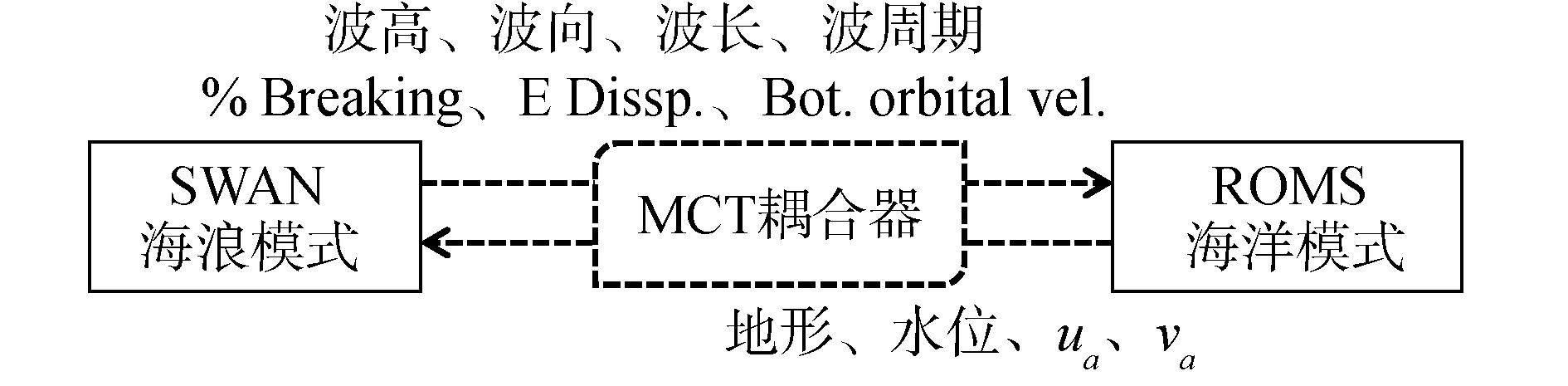
为进行波流实时双向耦合计算,本文将SWAN海浪模式和ROMS海洋模式通过MCT耦合器(the model coupling toolkit)[16]进行耦合,综合考虑海浪和海洋之间的相互影响,建立海浪-海洋耦合模型系统,该模型系统的耦合机制见图 1所示。MCT耦合器是时下最流行的耦合工具之一,是一个基于Fortran语言编译的高度模块化的开源程序包,能够支持多模型接入,支持并行运行,有很高的耦合效率。
|
Download:
|
| 图 1 海浪—海洋耦合机制及数据传递示意图 Fig. 1 Diagrammatic sketch of coupling mechanism and data switching in wave and ocean model | |
从图 1中可以看出,海浪-海洋模型系统通过MCT耦合器将SWAN与ROMS之间的数据进行实时传递,实现实时双向耦合。SWAN模型将计算得到的波高、波向、波长、波周期、碎波比、能量耗散率,底部运动轨迹速度通过MCT耦合器传递给ROMS模型;ROMS将海洋模型计算得到的地形、水位、水深平均流速(ua、va)通过MCT耦合器反馈给海浪模型SWAN。
图 2为SWAN-ROMS耦合模型的计算流程示意图,主要包括5个部分:耦合模型计算主程序Master;并行程序MPI的初始化;耦合模式在各个子模式内的MCT初始化;耦合模式的运行;MCT的终止化。在各个子程序内部,在初始时刻t=0,模式获得初始场,并通过MCT耦合器与耦合模式交换初始数据,在各自的时间步长内进行积分求解,当计算时长达到设置的MCT时间步长时,将各自的求解结果通过MCT耦合器与耦合模式进行数据传递和交换,循环往复至计算结束。

|
Download:
|
| 图 2 基于MCT耦合的SWAN-ROMS模式计算流程示意图 Fig. 2 Diagrammatic sketch of calculation process in coupled SWAN-ROMS model | |
理想潮汐通道算例为波流耦合经典算例[14],本文利用其进行SWAN-ROMS耦合模型的波流实时耦合计算分析。如图 3所示即为理想潮汐通道水深分布,通道北侧为开敞式海域,在模型中设置为开边界,潮汐、波浪等动力强迫由北往南传播,外侧水深最深为15 m,由南往北依线性关系减小至通道位置,潮汐通道及内侧水位为4 m,总计算范围为东西宽15 km,南北长14 km,潮汐通道宽2 km,如图 3所示,其中P点为潮汐通道中心位置。模型将计算区域划分为150×140个网格,格距为10 m,垂向分为10层。计算总时长为一个周期,即12 h,时间步长设置为10 s。

|
Download:
|
| 图 3 理想潮汐通道算例水深分布 Fig. 3 Topography of the idealized tidal inlet | |
在模型开边界处设置为潮汐强迫,为规则半日潮S2分潮,振幅为1 m、潮差为2 m,周期为12 h;在开边界设置规则波,波高为1 m,周期为10 s,由开边界向内部传递。本文设置2组数值试验:1)Exp1为SWAN模式单独运行,仅考虑波浪作用;2)Exp2为SWAN-ROMS模式实时耦合计算,考虑波流耦合作用,ROMS模式将水流流速、水位等传递给SWAN模式,SWAN将波高、波周期和波长与ROMS模式进行实时反馈,数据交换时间步长设置为300 s。
2.2 波高模拟结果分析 2.2.1 无潮流影响下的波高分布图 4给出了没有潮流影响条件下,仅采用SWAN模式计算,得到的潮汐通道波高分布。没有潮流影响时,模型在计算到t=2 h时即形成稳定的波浪场,如图 4所示。

|
Download:
|
| 图 4 无潮流影响下波高分布(t=6 h) Fig. 4 Distribution of wave height in the Exp1 (t=6 h) | |
波浪由北向南传播,在传播过程中逐渐减小,在通过潮汐通道后波高急剧减小。在潮汐通道外侧,即通道以北区域,其波高基本分布在0.7 m以上;而在潮汐通道内侧,波浪等高线呈抛物线型分布,波高由0.6 m递减至小于0.1 m;而在通道内东西两侧,其波高接近为零。
2.2.2 潮流对波高分布的影响图 5给出了潮汐通道中心位置P1的潮位、流速和流向随时间的变化关系,本文后续关于该算例的分析中考虑涨急、落急均以P1点为参照,从图 5可以看出,t=6 h时为涨急时刻、t=12 h为落急时刻,同时对潮位最低t=3 h和潮位最高t=9 h进行分析,对4个特征时刻的波高分布开展进一步分析。

|
Download:
|
| 图 5 潮汐通道中间P1点潮位、流速及流向过程 Fig. 5 Tidal level, velocity and direction of P1 in the inlet | |
图 6为上述4个特征时刻的波高分布结果,展现了通过SWAN-ROMS模式进行波流实时耦合计算,在涨、落急等不同时刻的波高分布及流速矢量场。从图 6可以看出,在波流耦合作用下,由于潮流的周期性运动,受潮流流速和水位变化的影响,波浪分布也呈现周期性的变化。

|
Download:
|
| 图 6 波流耦合模式下不同时刻波高及流速矢量分布 Fig. 6 Distribution of wave height and flow field in the Exp2 | |
从波高等值线分布来看,潮流影响下,在t=9 h时的波高等值线分布(图 6(c))与无潮流影响时形成的稳定波浪场波高等值线(图 4)较为相似,在通道以北,即潮汐通道外侧,等值线分布较为规整;在潮汐通道内侧,波高等值线也基本保持抛物线型分布,但由于潮流的影响,抛物线分布范围更广。
在涨急时刻,波浪传播方向与水流方向一致,潮汐通道处(P1点)的波高在0.7 m左右,潮汐通道外侧的波高分布在0.8~1.0 m,波高等深线在潮汐通道外侧形成了双峰状等值线。在潮汐通道内侧,波浪在传入通道后,波高逐渐减小,波高值由0.7 m向内侧逐渐衰减,与无潮流影响下的波高分布相似,在近乎封闭的东西两侧,波高接近于零。与无潮流影响下的波高分布对比,可以发现在潮流影响下,波浪在潮汐通道内传播到更广的水域。
在落急时刻,波浪传播方向与水流运动方向相反,潮汐通道及潮汐通道北侧的波高值接近1.0 m,在外侧同样形成双峰状等值线,波高范围在0.8 m以上。在潮汐通道以南,由于退潮的影响,波高也达到了0.6 m左右。在潮汐通道内侧,波高逐渐减小,对于近乎封闭的东西两侧,波高值接近于零。比较涨急与落急时刻的波高等值线,潮汐通道在涨急时刻的波高值为0.7 m,而落急时刻的波高值为0.95 m,明显高于涨急时刻。
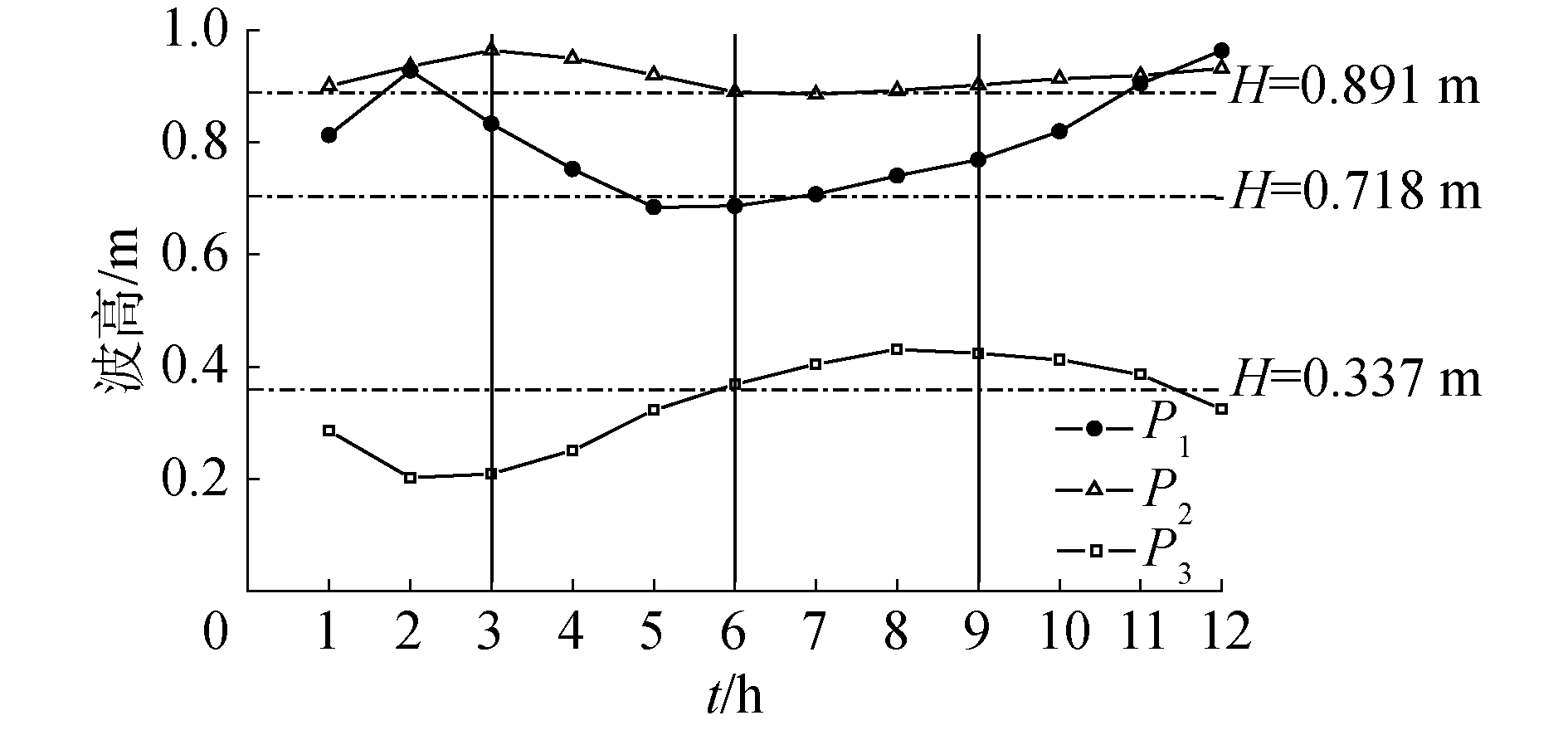
图 7给出了潮汐通道附近3个特征点(见图 3所示)在潮流影响下波高随时间的变化曲线,图中实线为潮流影响下波高的变化曲线,点画线为无潮流影响下形成稳定波浪场后该位置的波高值,该值在图 7右侧已给出。从图 7可以看出,由于潮流的影响,除涨急时刻外,潮汐通道外侧(P1、P2)的波高值明显大于无潮流影响下该位置形成的稳定波高,而在潮汐通道内侧(P3),潮流影响下的波高在无潮流影响下该位置形成的稳定波高附近变化。
|
Download:
|
| 图 7 各特征点波高随时间变化关系 Fig. 7 The impact-time history curves of wave height in three characteristic positions | |
因而,从上述分析中可以看出,在潮流影响下,波流传播方向相反时,同一位置的波高大于波流同向传播时的波高;在潮汐通道及附近,潮流的影响更为显著,涨、落急时刻形成的波高等高线之差可达25 cm。潮流的影响使得波浪在潮汐通道内侧的传播范围更广,但在内侧对波高大小的影响较为有限。
2.3 潮流模拟结果分析前一部分论述了潮流的存在对波高的影响,本节阐述波流耦合作用下,波浪对潮汐的影响情况。图 8中给出了潮汐通道附近3个特征点(见图 3所示)的潮位、波高随时间的变化关系。从图中可以看出,从3个位置潮位随时间的变化来看,规则半日潮的特征明显,无论是振幅、潮差,还是潮周期,都与理论潮位曲线相似。不同位置的潮位过程除存在相位差外,潮差、周期都相近,与同时期的波高变化规律不同,这反映出在本文理想潮汐通道的算例中,波浪作用对潮流运动的影响较小,潮流收波浪的影响不明显。究其原因,波浪主要通过波浪辐射应力对潮流产生影响,而波浪辐射应力的大小与波高的平方成正比,但在本文算例中,入射波高为1 m,因此波浪辐射应力较小,对潮流运动的影响非常有限。王世澎等[17]针对潮流对波浪的影响开展了相似研究,其结论与本文成果相似。

|
Download:
|
| 图 8 各特征点水位、波高随时间变化关系 Fig. 8 The impact-time history curves of tidal level and wave height in three characteristic positions | |
对特征点的潮位过程进行分析后,下文针对计算域内的流场进行探讨。选取前文中叙述的涨急、落急等4个特征时刻,分别对表层和底层流场进行分析,如图 9和图 10所示。

|
Download:
|
| 图 9 波流耦合模式下不同时刻表层流速分布 Fig. 9 Distribution of flow field in surface in the Exp2 | |

|
Download:
|
| 图 10 波流耦合模式下不同时刻底层流速分布 Fig. 10 Distribution of flow field in bottom in the Exp2 | |
潮汐强迫由北往南传播,t=6 h时刻,在传播到潮汐通道附近时,从图 9(b)和图 10(b)中可以看出,由于水流通道突然变小,造成水位壅高,因此在潮汐通道内流速急剧增大,潮汐通道附近表层流速超过了1.5 m/s,底层流速也达到1.0 m/s左右。在t=9 h时,潮汐通道水位达到最高值,从图 9(c)和图 10(c)中可以看出,无论是表层水体还是底层水体,流速都在0.2 m/s范围内。在t=12 h时,潮汐通道内水流运动速度再达极值,与涨急时相似,同样是由于水体在达到潮汐通道时由于口门突然减小,通道内侧造成壅水,潮汐通道附近流速急剧增大,表层最大流速达到1.8 m/s左右,底层流速也接近1.5 m/s。
垂向来看,对比图 9和图 10可以发现,在整个潮位过程中,不同时刻下,各层流态基本一致,表层流速大于底层流速。为更确切反映同一位置分层流速的关系,图 11中给出了潮汐通道附近3个特征点(图 3所示)不同分层流速随时间的变化曲线。从图中可以看出,潮汐通道(P1)处的流速无论是表层还是底层均明显大于其他位置,这从图 9和图 10中已能直观反映。各特征点底层流速较中层流速和表层流速都小,中层和表层流速较为接近。

|
Download:
|
| 图 11 各特征位置分层流速随时间的变化关系 Fig. 11 The impact-time history curves of current velocity on the different vertical location in three characteristic positions | |
1) 基于区域海洋模型ROMS和第3代海浪模型SWAN,基于MCT耦合器,建立了波流实时双向耦合模型。SWAN模型将计算得到的波高、波向、波长、波周期、碎波比、能量耗散率,底部运动轨迹速度通过MCT耦合器传递给ROMS模型;ROMS将海洋模型计算得到的地形、水位、水深平均流速通过MCT耦合器反馈给海浪模型SWAN。
2) 通过将SWAN和ROMS进行耦合,针对理想潮汐通道的典型算例进行波流耦合计算分析,分别对仅采用SWAN模型和采用SWAN与ROMS耦合模型进行了数值试验,通过对照两者的结果,分析波流相互作用条件下对波浪和潮流的影响。
3) 潮流的存在对波浪影响较为明显,周期性的潮流运动使得稳定的波浪场也产生了周期性变化,潮流与波浪向同一方向传播时,会导致波高减小,而相对运动则会导致波高增加。
| [1] |
UCHIYAMA Y, MCWILLIAMS J C, SHCHEPETKIN A F. Wave-current interaction in an oceanic circulation model with a vortex-force formalism:application to the surf zone[J]. Ocean modelling, 2010, 34(1/2): 16-35. (  0) 0)
|
| [2] |
FENG Xingru, YIN Baoshu, YANG Dezhou. Development of an unstructured-grid wave-current coupled model and its application[J]. Ocean modelling, 2016, 104: 213-225. (  0) 0)
|
| [3] |
LIM H S, CHUN I, SHIM J S, et al. Wave-induced current simulated by wave-current coupled model in Haeundae[J]. Journal of coastal research, 2016, 2: 1392-1396. (  0) 0)
|
| [4] |
LONGUET-HIGGINS M S, STEWART R W. Radiation stress and mass transport in gravity waves, with application to 'surf beats'[J]. Journal of fluid mechanics, 1962, 13(4): 481-504. (  0) 0)
|
| [5] |
SABATINO A D, MCCAIG C, O'HARA MURRAY R B, et al. Modelling wave-current interactions off the east coast of Scotland[J]. Ocean science, 2016, 12(4): 875-897. (  0) 0)
|
| [6] |
GODA Y. Examination of the influence of several factors on longshore current computation with random waves[J]. Coastal engineering, 2006, 53(2/3): 157-170. (  0) 0)
|
| [7] |
刘磊, 费建芳, 章立标, 等. 台风条件下一种新的浪流相互作用参数化方法在耦合模式中的应用[J]. 物理学报, 2012, 61(5): 059201. LIU Lei, FEI Jianfang, ZHANG Libiao, et al. New parameterization of wave-current interaction used in a two-way coupled model under typhoon conditions[J]. Acta physica sinica, 2012, 61(5): 059201. (  0) 0)
|
| [8] |
XIA Huayong, XIA Zongwan, ZHU Liangsheng. Vertical variation in radiation stress and wave-induced current[J]. Coastal engineering, 2004, 51(4): 309-321. (  0) 0)
|
| [9] |
ZHENG Jinhai. Depth-dependent expression of obliquely incident wave induced radiation stress[J]. Progress in natural science, 2007, 17(9): 1067-1073. (  0) 0)
|
| [10] |
王平, 张宁川. 近岸波生环流的三维数值模拟研究[J]. 哈尔滨工程大学学报, 2015, 36(1): 34-40. WANG Ping, ZHANG Ningchuan. Three-dimensional numerical simulation of the wave-induced nearshore circulation[J]. Journal of Harbin Engineering University, 2015, 36(1): 34-40. (  0) 0)
|
| [11] |
伍志元, 蒋昌波, 邓斌, 等. 基于海气耦合模式的南中国海北部风暴潮模拟[J]. 科学通报, 2018, 63(33): 3494-3504. WU Zhiyuan, JIANG Changbo, DENG Bin, et al. Simulation of the storm surge in the South China Sea based on the coupled sea-air model[J]. China science bulletin, 2018, 63(33): 3494-3504. (  0) 0)
|
| [12] |
SWAN Team. SWAN implementation manual[R]. Delft: Delft University of Technology, 2013.
(  0) 0)
|
| [13] |
DENG Zeng'an, XIE Li'an, HAN Guijun, et al. The effect of Coriolis-Stokes forcing on upper ocean circulation in a two-way coupled wave-current model[J]. Chinese journal of oceanology and limnology, 2012, 30(2): 321-335. (  0) 0)
|
| [14] |
WARNER J C, SHERWOOD C R, SIGNELL R P, et al. Development of a three-dimensional, regional, coupled wave, current, and sediment-transport model[J]. Computers & geosciences, 2008, 34(10): 1284-1306. (  0) 0)
|
| [15] |
AKAN Ç, MOGHIMI S, ÖZKAN-HALLER H T, et al. On the dynamics of the mouth of the Columbia River:results from a three-dimensional fully coupled wave-current interaction model[J]. Journal of geophysical research:oceans, 2017, 122(7): 5218-5236. (  0) 0)
|
| [16] |
LARSON J, JACOB R, ONG E. The model coupling toolkit:a new Fortran90 toolkit for building multiphysics parallel coupled models[J]. The international journal of high performance computing applications, 2005, 19(3): 277-292. (  0) 0)
|
| [17] |
王世澎, 梁书秀, 孙昭晨. 二维情况下波浪对潮流场作用的数值分析[J]. 海洋学报, 2007, 29(2): 173-178. WANG Shipeng, LIANG Shuxiu, SUN Zhaochen. The numerical analysis of wave effects on a tidal current in two dimensions[J]. Acta oceanologica sinica, 2007, 29(2): 173-178. DOI:10.3321/j.issn:0253-4193.2007.02.023 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


