2. 广州船舶及海洋工程设计研究院, 广东 广州 119077;
3. 中山大学 海洋科学学院, 广东 广州 119077
2. Guangzhou Marine Engineering Corporation, Guangzhou 119077, China;
3. College of Marine Science, Sun Yat-sen University, Guangzhou 119077, China
海洋流体和工程结构物相互作用的相关数值模拟研究中,准确且能够保证数值稳定性的数值计算方法一直是当今研究的热点。在此类数值模拟中,结构会在受到流体力的作用下产生运动或变形,这就是流固耦合问题。流固耦合的数值计算方法中,由于理论来源和应用范围的不同,导致了不同的空间离散需求,这种需求在海洋工程领域深海立管、系泊管线、港湾振动的流固耦合应用中十分常见。此类需求往往会对计算资源,计算手段和计算方法提出许多必需且困难的问题,例如大规模计算资源、数值算法的精度、守恒性和稳定性、网格划分技术等众多问题。
在当前流固耦合数值计算方法的进展中,由于上述空间离散的不同需求,在网格划分层面提出了网格非匹配的要求,这种要求衍生出了和多重网格技术与自适应网格技术不同的非匹配网格技术,并逐渐受到了研究者的关注[1-2]。非匹配网格技术中,需要对网格两侧的数据对另一方进行插值和投影。插值和投影方式的不同,会对计算结果的守恒性和稳定性产生非常大的影响。在非定常计算中,如果采用较低精度的插值或投影方式,其带来的误差会随着时间积累并放大,导致最终计算结果的不准确或者发散;反之,若采用较高精度的插值方式,其误差不会随时间不断积累,保证了数值计算的稳定性和精度。
Common-Refinement方法是一种精度很高,并能够保证数值计算稳定性和守恒性的非匹配网格技术。由于其数据结构的困难性和复杂程度,只有部分学者在一维和二维假设下对此进行了精度和稳定性的分析与研究[3-5]。研究表明,常规的节点投影,以及单元投影方法产生的非匹配网格两侧的局部误差会非常大,且会随着时间不断放大,并且对网格两侧的空间划分比例的依赖性很高,进而影响数值计算的稳定性。
在Common-Refinement方法中,其生成的新的网格数据结构包含了在两侧区域的面网格的所有节点,并依赖于此生成了新的网格数据结构。Common-Refinement方法的数据结构可以对某一侧网格节点的空间位置在另一侧网格的附近的节点信息进行查询并导出,进而基于有限元法,使用两侧网格单元的形函数对当前投影单元进行积分和加权,然后传输到另一侧。由于两侧面网格均采用了有限元法进行插值,因此可以保证两侧积分的一致性并且在单元内部保证了连续性,因此在加权后能够保证插值和投影的精度[6-9]。在实际操作中,对于低维度的Common-Refinement方法形成的数据结构还较为简单,但是生成全三维的Common-Refinement数据结构是一项非常具有挑战性的工作。原因在于:不同的流固耦合问题是由不同属性的介质相互作用而组成,而介质的不同和问题背景的不同,对网格的空间划分的要求非常多样,且结构的一侧几何结构的复杂度直接决定了交界面的几何形状与网格划分时采用的单元类型。Common-Refinement方法的几何实现可以参照[10-11]。
采用Common-Refinement方法分析深海立管涡激振动问题中,流体附加质量对求解过程的稳定性有着较大的影响。前期学者的工作中,采用可压缩流体介质。而在涡激振动问题中,流体介质需采用不可压缩假设。两者的区别在于附加质量随时间的变化。前者往往依赖于时间,而后者会逐渐趋近于某一恒定值。不可压缩流动和可压缩流动的控制方程以及相应数值算法的差别,对流固耦合分区域求解方法的设计有着重要的帮助,且两者所带来的数值稳定性的证明方法也有着明显的不同[12]。
本文的第1个目标是采用伽辽金有限元统一处理流体区域和结构区域,并且流体方面采用不可压缩介质,采用连续Galerkin(CG)有限元离散化方法对非线性超弹性体结构模型进行离散,采用Petrov-Galerkin有限元离散求解不可压缩流动,进而构成本文的分区域求解流固耦合方法)。本文的第2个目标是将三维Common-Refinement方法应用于不可压缩流体和立管结构的交界面,对流体和结构两侧的网格进行不同尺寸的空间划分,对实际海洋工程的立管的涡激振动问题进三维非定常计算模拟,得到了令人满意的结果。
1 控制方程首先给出流固耦合系统的控制方程。对于结构区域采用拉格朗日形式,而对于流体区域采用拉格朗日欧拉形式。流固耦合问题中,流体结构相互作用采用贴体边界方法处理。假设
| $ \begin{array}{*{20}{c}} {{\rho ^{\rm{f}}}\frac{{\partial {{\mathit{\boldsymbol{\bar u}}}^{\rm{f}}}}}{{\partial t}}\left| {_{\hat x}} \right. + {\rho ^{\rm{f}}}\left( {{{\mathit{\boldsymbol{\bar u}}}^{\rm{f}}} - {{\mathit{\boldsymbol{\bar w}}}^{\rm{f}}}} \right) \cdot \nabla {{\mathit{\boldsymbol{\bar u}}}^{\rm{f}}} = \nabla \cdot {{\mathit{\boldsymbol{\bar \sigma }}}^{\rm{f}}} + }\\ {\nabla \cdot {\mathit{\boldsymbol{\sigma }}^{{\rm{sgs}}}} + {\mathit{\boldsymbol{b}}^{\rm{f}}},{\rm{on}}\;{\mathit{\Omega }^{\rm{f}}}\left( t \right)} \end{array} $ | (1) |
| $ \nabla \cdot {\mathit{\boldsymbol{\bar u}}^{\rm{f}}} = 0,{\rm{on}}\;{\mathit{\Omega }^{\rm{f}}}\left( t \right) $ | (2) |
式中:
| $ {\mathit{\boldsymbol{\bar \sigma }}^{\rm{f}}} = - {\bar p^{\rm{f}}}I + {\mu ^{\rm{f}}}\left( {\nabla {{\mathit{\boldsymbol{\bar u}}}^{\rm{f}}} + {{\left( {\nabla {{\mathit{\boldsymbol{\bar u}}}^{\rm{f}}}} \right)}^{\rm{T}}}} \right) $ | (3) |
式中:在经过滤波后的流体应力表示为
| $ \begin{array}{*{20}{c}} {\int_{{\mathit{\Omega }^{\rm{f}}}\left( t \right)} {{\rho ^{\rm{f}}}\left( {{\partial _t}{{\mathit{\boldsymbol{\bar u}}}^{\rm{f}}} + \left( {{{\mathit{\boldsymbol{\bar u}}}^{\rm{f}}} - {\mathit{\boldsymbol{w}}^{\rm{f}}}} \right) \cdot \nabla {{\mathit{\boldsymbol{\bar u}}}^{\rm{f}}}} \right) \cdot {\phi ^{\rm{f}}}\left( x \right){\rm{d}}\mathit{\Omega }} + }\\ {\int_{{\mathit{\Omega }^{\rm{f}}}\left( t \right)} {\left( {{{\mathit{\boldsymbol{\bar \sigma }}}^{\rm{f}}} + {\mathit{\boldsymbol{\sigma }}^{{\rm{sgs}}}}} \right):\nabla {\phi ^{\rm{f}}}\left( x \right){\rm{d}}\mathit{\Omega }} = }\\ {\int_{{\mathit{\Omega }^{\rm{f}}}\left( t \right)} {{\mathit{\boldsymbol{b}}^{\rm{f}}} \cdot {\phi ^{\rm{f}}}\left( x \right){\rm{d}}\mathit{\Omega }} + \int_{\mathit{\Gamma }_{\rm{h}}^{\rm{f}}\left( t \right)} {{h^{\rm{f}}} \cdot {\phi ^{\rm{f}}}\left( x \right){\rm{d}}\mathit{\Gamma }} } \end{array} $ | (4) |
| $ \int_{{\mathit{\Omega }^{\rm{f}}}\left( t \right)} {\nabla \cdot {{\mathit{\boldsymbol{\bar u}}}^{\rm{f}}}q\left( x \right){\rm{d}}\mathit{\Omega }} = 0 $ | (5) |
式中:
采用虚功原理处理结构一侧的动力学方程及其应力平衡。对于流固耦合系统中,立管在流体作用下随时间产生的大幅变形采取非线性超弹性体来进行描述[13]。结构体的密度假设为, 其中的每个节点都需要采用其位置的矢量进行表达。假设固体的密度为ρs,固体的每一个点都由各自位置的矢量来描述,采用xs∈Ω0s表示立管的空间节点的初始位置,采用ds(xs, t)∈Ωs(t)表示空间节点xs在某一时刻t下的位移。基于虚功原理的弱形式的控制方程为:
| $ \begin{array}{*{20}{c}} {\int_{\mathit{\Omega }_0^{\rm{s}}} {\tau _{ij}^{\rm{s}}\delta L_{ij}^{\rm{s}}{\rm{d}}\mathit{\Omega }} - \int_{\mathit{\Omega }_0^{\rm{s}}} {{\rho ^{\rm{s}}}b_i^{\rm{s}}\delta v_i^{\rm{s}}{\rm{d}}\mathit{\Omega }} + \int_{\mathit{\Omega }_0^{\rm{s}}} {\frac{{\partial u_i^{\rm{s}}}}{{\partial t}}\delta v_i^{\rm{s}}{\rm{d}}\mathit{\Omega }} - }\\ {\int_{\mathit{\Gamma }_2^{\rm{s}}} {t_i^{\rm{s}}\delta v_i^{\rm{s}}{\eta ^{\rm{s}}}{\rm{d}}\mathit{\Gamma }} = 0} \end{array} $ | (6) |
式中:τijs=Jsσijs是Kirchhoff应力;Js=det(Fs)是雅克比变形梯度张量;σijs是超弹性体的柯西应力;δLijs=∂δvis/∂φjs是虚速度梯度;bis是体积力;δvis=δvis(xs)是虚速度场。柯西应力σijs的表达式为:
| $ \sigma _{ij}^{\rm{s}} = \frac{{{\mu ^{\rm{s}}}}}{{{{\left( {{J^{\rm{s}}}} \right)}^{5/3}}}}\left( {B_{ij}^{\rm{s}} - \frac{1}{3}B_{kk}^{\rm{s}}{\delta _{ij}}} \right) + {K^{\rm{s}}}\left( {{J^{\rm{s}}} - 1} \right){\delta _{ij}} $ | (7) |
式中:Bijs=FiksFjks是柯西-格林张量;μs是剪切模量。变形梯度张量为:
| $ F_{i j}^{\mathrm{s}}=\delta_{i j}+\partial d_{i}^{\mathrm{s}} / \partial x_{j} $ | (8) |
这里进而给出立管涡激振动问题中耦合交界面的数学描述。流体域采用Ω0f表示,结构域采用Ω0s表示,耦合边界Γfs(t)=∂Ωf(t)∩∂Ωs(t),且其上的应力和速度矢量必须保持连续,因此耦合界面边界条件可表示为:
| $ {\mathit{\boldsymbol{\bar u}}^{\rm{f}}}\left( {{\mathit{\boldsymbol{\varphi }}^{\rm{s}}}\left( {{\mathit{\boldsymbol{x}}^{\rm{s}}},t} \right),t} \right) = {\mathit{\boldsymbol{u}}^{\rm{s}}}\left( {{\mathit{\boldsymbol{x}}^{\rm{s}}},t} \right) $ | (9) |
| $ \int_{{{\rm{ \mathsf{ φ} }}^s}\left( {\gamma ,t} \right)} {{\mathit{\boldsymbol{\sigma }}^{\rm{f}}}\left( {{\mathit{\boldsymbol{x}}^{\rm{f}}},t} \right)} \cdot \mathit{\boldsymbol{n}}{\rm{d}}\mathit{\Gamma }\left( {{x^{\rm{f}}}} \right) + \int_\gamma {{t^{\rm{s}}}{\rm{d}}\mathit{\Gamma }} = 0 $ | (10) |
式中:位置矢量表示为φs;ts是作用在结构边界上的流体应力矢量;us为弹性体在时间t的速度;n为耦合边界的外法线矢量。以上的边界条件保证了流体在耦合界面的速度完全等于立管的运动速度,并且立管的运动受到了流体产生的压力和剪切应力的影响。
2 流固耦合系统的离散化基于有限元法,采用互不重叠的三维有限单元Ωe去离散流体空间Ωf,e=1, 2, …, nel, 总的单元数为nel。generalized-alpha方法被用来处理时间相关项t∈[tn, tn+1],这种方法对于线性问题是无条件稳定,且能保证时间上的二阶精度。generalized-alpha的参数(αf, αmf)的选取参见文献[14]。经过generalized-alpha处理后的变分形式的控制方程可以写作:
| $ \begin{array}{*{20}{c}} {\int_{\mathit{\Omega }_{\rm{h}}^{\rm{f}}\left( {{t^{n + 1}}} \right)} {{\rho ^{\rm{f}}}} \left( {{\partial _t}\mathit{\boldsymbol{\overline u}} _h^{{\rm{f}},n + \alpha _m^{\rm{f}}} + \left( {\mathit{\boldsymbol{\overline u}} _h^{{\rm{f}},n + {\alpha ^{\rm{f}}}} - \mathit{\boldsymbol{w}}_h^{{\rm{f}},n + {\alpha ^{\rm{f}}}}} \right) \cdot \nabla \mathit{\boldsymbol{\overline u}} _h^{{\rm{f}},n + {\alpha ^{\rm{f}}}}} \right) \cdot }\\ {{\phi ^{\rm{f}}}{\rm{d}}\mathit{\Omega } + \int_{\mathit{\Omega }_h^{\rm{f}}\left( {{t^{n + 1}}} \right)} {\left( {\mathit{\boldsymbol{\bar \sigma }}_h^{{\rm{f}},n + {\alpha ^{\rm{f}}}} + \mathit{\boldsymbol{\sigma }}_h^{{\rm{sgs}},n + {\alpha ^{\rm{f}}}}} \right):\nabla {\phi ^{\rm{f}}}{\rm{d}}\mathit{\Omega }} - }\\ {\int_{\mathit{\Omega }_h^{\rm{f}}\left( {{t^{n + 1}}} \right)} {\nabla \cdot \mathit{\boldsymbol{\overline u}} _h^{{\rm{f}},n + {\alpha ^{\rm{f}}}}q{\rm{d}}\mathit{\Omega }} + \sum\limits_{e = 1}^{{n_{{\rm{el}}}}} {\int_{{\mathit{\Omega }^{\rm{e}}}} {\tau _m^{\rm{f}}\left( {{\rho ^{\rm{f}}}\left( {\mathit{\boldsymbol{\overline u}} _h^{{\rm{f}},n + {\alpha ^{\rm{f}}}} - \mathit{\boldsymbol{w}}_h^{{\rm{f}},n + {\alpha ^{\rm{f}}}}} \right) \cdot } \right.} } }\\ {\nabla {\phi ^{\rm{f}}} + \nabla q) \cdot \left( {{\rho ^{\rm{f}}}{\partial _t}\mathit{\boldsymbol{\overline u}} _h^{{\rm{f}},n + {\alpha ^{\rm{f}}_{\rm{m}}}} + {\rho ^{\rm{f}}}\left( {\mathit{\boldsymbol{\overline u}} _h^{{\rm{f}},n + {\alpha ^{\rm{f}}}} - \mathit{\boldsymbol{w}}_h^{{\rm{f}},n + {\alpha ^{\rm{f}}}}} \right)} \right. \cdot }\\ {\nabla \mathit{\boldsymbol{\overline u}} _h^{{\rm{f}},n + {\alpha ^{\rm{f}}}} - \nabla \cdot \mathit{\boldsymbol{\overline \sigma }} _h^{{\rm{f}},n + {\alpha ^{\rm{f}}}} - \nabla \cdot \mathit{\boldsymbol{\sigma }}_h^{{\mathop{\rm sgs}\nolimits} ,n + {\alpha ^{\rm{f}}}} - {\mathit{\boldsymbol{b}}^{\rm{f}}}\left( {{t^{n + {\alpha ^{\rm{f}}}}}} \right)){\rm{d}}{\mathit{\Omega }^e} + }\\ {\sum\limits_{e = 1}^{{n_{{\rm{el}}}}} {\int_{{\mathit{\Omega }_{\rm{e}}}} {\nabla \cdot {\phi ^{\rm{f}}}\tau _c^{\rm{f}}{\rho ^{\rm{f}}}\nabla \cdot \mathit{\boldsymbol{\overline u}} _h^{{\rm{f}},n + {\alpha ^{\rm{f}}}}{\rm{d}}{\mathit{\Omega }^{\rm{e}}}} } = \int_{\mathit{\Omega }_h^{\rm{f}}\left( {{t^{n + 1}}} \right)} {{b^{\rm{f}}}\left( {{t^{n + {\alpha ^{\rm{f}}}}}} \right)} \cdot }\\ {{\phi ^{\rm{f}}}{\rm{d}}\mathit{\Omega } + \int_{\mathit{\Gamma }_h^{\rm{f}}\left( {{t^{{\rm{n}} + 1}}} \right)} {{\mathit{\boldsymbol{h}}^{\rm{f}}} \cdot {\phi ^{\rm{f}}}{\rm{d}}\mathit{\Gamma }} } \end{array} $ | (11) |
式中:第3、4和5行表示局部稳定项;τmf和τcf为稳定参数;τmf定义为:
| $ \begin{array}{*{20}{c}} {\tau _m^{\rm{f}} = \left[ {{{\left( {\frac{{2{\rho ^{\rm{f}}}}}{{\Delta t}}} \right)}^2} + {{\left( {{\rho ^{\rm{f}}}} \right)}^2}\left( {\mathit{\boldsymbol{\bar u}}_h^{\rm{f}} - \mathit{\boldsymbol{w}}_h^{\rm{f}}} \right) \cdot \mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{\bar u}}_h^{\rm{f}} - \mathit{\boldsymbol{w}}_h^{\rm{f}}} \right) + } \right.}\\ {{{\left. {{C_I}{{\left( {{\mu ^{\rm{f}}} + {\mu ^{\rm{t}}}} \right)}^2}\mathit{\boldsymbol{G}}:\mathit{\boldsymbol{G}}} \right]}^{ - 1/2}}} \end{array} $ | (12) |
式中:CI是常数,来自于元素的逆向估计;G是元素逆变度量张量的大小;μt是湍流粘性;上面其他各参数定义为:
| $ \mathit{\boldsymbol{G}} = \frac{{\partial {\mathit{\boldsymbol{\xi }}^{\rm{T}}}}}{{\partial {\mathit{\boldsymbol{x}}^{\rm{f}}}}}\frac{{\partial \mathit{\boldsymbol{\xi }}}}{{\partial {\mathit{\boldsymbol{x}}^{\rm{f}}}}},\;\;\;\;\tau _c^{\rm{f}} = \frac{1}{{\left( {{\rm{tr}}\mathit{\boldsymbol{G}}} \right)\tau _m^{\rm{f}}}} $ | (13) |
式中:x和ξ分别是空间坐标及其对应参数;tr G表示逆变度量张量的迹。稳定项的作用是对于流固耦合问题中的对流占优区域的速度场的稳定性提供帮助。
基于式(6),能够得到基于伽辽金有限元法的立管大幅变形的控制方程,并采用超弹性体描述立管的大幅变形。对于具有n个节点的单元,使用xia表示每个节点的坐标,其上标a表示节点范围,下标i表示空间范围(1~3),dis, a表示每个节点的位移矢量,位移场和虚速度场分别表示为:
| $ \mathit{\boldsymbol{d}}_i^{\rm{s}}\left( {{\mathit{\boldsymbol{x}}^{\rm{s}}}} \right) = \sum\limits_{a = 1}^n {{N^a}\left( {{\mathit{\boldsymbol{x}}^{\rm{s}}}} \right)\mathit{\boldsymbol{d}}_i^{{\rm{s}},a}} ,\delta v_i^{\rm{s}}\left( {{\mathit{\boldsymbol{x}}^{\rm{s}}}} \right) = \sum\limits_{a = 1}^n {{N^a}\left( {{\mathit{\boldsymbol{x}}^{\rm{s}}}} \right)\delta v_i^{{\rm{s,}}a}} $ | (14) |
式中:xs表示任意网格节点的坐标;Na表示形函数。将其代入式(6),离散后的立管的控制方程可以表示为:
| $ \begin{array}{*{20}{c}} {\int_{\mathit{\Omega }_0^{\rm{s}}} {{\rho ^{\rm{s}}}{N^b}{N^a}\frac{{{\partial ^2}d_i^{{\rm{s}},b}}}{{\partial {t^2}}}{\rm{d}}\mathit{\Omega }} + \int_{\mathit{\Omega }_0^{\rm{s}}} {\tau _{ij}^{\rm{s}}\left[ {F_{pq}^{\rm{s}}\left( {d_k^{{\rm{s}},b}} \right)} \right]\frac{{\partial {N^a}}}{{\partial {x_m}}}F_{mj}^{{\rm{s}}, - 1}{\rm{d}}\mathit{\Omega }} - }\\ {\int_{\mathit{\Omega }_0^{\rm{s}}} {{\rho ^{\rm{s}}}b_i^{\rm{s}}{N^a}{\rm{d}}\mathit{\Omega }} - \int_{{\mathit{\Gamma }^{{\rm{fs}}}}} {t_i^{\rm{s}}{N^a}{\eta ^{\rm{s}}}{\rm{d}}\mathit{\Gamma }} = 0} \end{array} $ | (15) |
虚功方程(15)给出了n个非线性方程,包含了n个未知量。为Kirchhoff应力与变性梯度之间的函数关系。这组非线性方程在每个时间步内可以用Newton-Raphson迭代求解,时间推进使用标准Newmark方法处理,同样具有时间方向的二阶精度。需要注意的是方程组中的弹性矩阵需要在每个时间步内重构。
离散后的立管的控制方程中包含了n个非线性方程和n个未知量。Kirchhoff应力与变形梯度之间的关系可以表示为τijs[Fpqs(dis, a)]。此非线性方程组在每个时间步内采用Newton-Raphson迭代法进行求解,并采用Newmark-Beta方法处理时间项。在立管产生大幅变形时,方程组中的弹性矩阵需要在每个时间步内进行重构。
3 Common-Refinement方法本章节给出基于非匹配网格的三维流固耦合问题的Common-Refinement方法。流固耦合问题中,流体与结构的控制方程在求解时,流体应力和结构位移在保证流体区域和结构区域的耦合界面的连续性的前提下进行数据交换,进而构成了另一侧求解时的边界条件。在求解过程中,流体与结构单元的插值多项式的次数与耦合界面网格单元的插值多项式的次数保持一致。
为了保证牵引力在流体和结构区域的平衡条件,在物理上,流体一侧产生的动量通量以应力形式传输到结构区域的表面。采用Nif和Njs表示各自的有限元形函数,下标i表示在流体区域,下标j表示在结构区域,tf和ts表示流体区域和结构区域的应力矢量,在本文中可以写作:
| $ t^{\mathrm{f}}\left(x^{\mathrm{f}}\right) \approx \sum\limits_{i=1}^{m_{f}} N_{i}^{\mathrm{f}} t_{i}^{\mathrm{f}}, t^{\mathrm{s}}\left(x^{\mathrm{s}}\right) \approx \sum\limits_{j=1}^{m_{s}} N_{j}^{\mathrm{s}} t_{j}^{\mathrm{s}} $ | (16) |
式中:mf和ms分别是耦合界面上流体域和固体域的节点数目。一旦得到了tf、Nif和Njs,进而便能够得到
| $ \int_{{\varGamma ^{{\rm{fs}}}}} {N_i^{\rm{s}}} {\mathit{\boldsymbol{t}}^{\rm{s}}}{\rm{d}}\mathit{\Gamma } = \int_{{\varGamma ^{{\rm{fs}}}}} {N_i^{\rm{s}}} {t^{\rm{f}}}{\rm{d}}\mathit{\Gamma } $ | (17) |
使用有限元近似后的牵引力平衡条件为:
| $ \int_{{\mathit{\Gamma }^{{\rm{fs}}}}} {N_i^{\rm{s}}N_j^{\rm{s}}\mathit{\boldsymbol{\tilde t}}_j^{\rm{s}}{\rm{d}}\mathit{\Gamma }} = \int_{{\mathit{\Gamma }^{{\rm{fs}}}}} {N_i^{\rm{s}}N_j^{\rm{f}}\mathit{\boldsymbol{\tilde t}}_j^{\rm{f}}{\rm{d}}\mathit{\Gamma }} $ | (18) |
结构一侧的牵引力
| $ \tilde{\boldsymbol{t}}_{j}^{\mathrm{s}}=\boldsymbol{M}_{i j}^{\mathrm{s}-1} \boldsymbol{f}_{i}^{\mathrm{s}} $ | (19) |
式中:Ms表示耦合界面结构一侧的质量矩阵,表示为:
| $ \mathit{\boldsymbol{M}}_{ij}^{\rm{s}} = \int_{{\mathit{\Gamma }^{{\rm{fs}}}}} {N_i^{\rm{s}}} N_j^{\rm{s}}{\rm{d}}\mathit{\Gamma } $ | (20) |
节点力的矢量fjs为:
| $ \mathit{\boldsymbol{f}}_i^{\rm{s}} = \sum\limits_{j = 1}^{{m_f}} {\mathit{\boldsymbol{\widetilde t}}_j^{\rm{f}}} \int_{{\mathit{\Gamma }^{{\rm{fs}}}}} {N_j^{\rm{f}}} N_i^{\rm{s}}{\rm{d}}\mathit{\Gamma } $ | (21) |
采用结构区域的形函数去构造质量矩阵,此时应力矢量的积分是由两侧的形函数共同构成。在流体和结构区域的网格划分一致时,这种做法不会产生误差。而对于非匹配网格,不同的形函数会导致两侧数据传输的不连续性。Common-Refinement方法所构造的耦合边界由流体区域和结构区域的边界网格进行拓扑交叉后生成的复杂的多边形进行构造。基于有限元法,流体区域和结构区域的空间节点的位置可以表示为:
| $ {x^{\rm{f}}} \approx \sum\limits_{i = 1}^{{m_f}} {N_i^{\rm{f}}\left( x \right)x_i^{\rm{f}}} \;\;\;{\rm{on}}\;\;\;\;\mathit{\Gamma }_h^{\rm{f}} $ | (22) |
| $ {x^{\rm{s}}} \approx \sum\limits_{j = 1}^{{m_s}} {N_j^{\rm{s}}\left( x \right)x_j^{\rm{s}}} \;\;\;{\rm{on}}\;\;\;\;\mathit{\Gamma }_h^{\rm{s}} $ | (23) |
在本文中,Common-Refinement方法构造的耦合界面中的单元拓扑是由流体一侧和结构一侧的单元的交线来构成,生成的新的单元被称为子单元。在本文中,子单元上的应力矢量的计算方法为:
| $ \mathit{\boldsymbol{f}}_j^{\rm{s}} = \sum\limits_{i = 1}^{{e_c}} {\int_{\sigma _i^c} {N_j^{\rm{s}}{{\mathit{\boldsymbol{\tilde t}}}^{\rm{f}}}{\rm{d}}\mathit{\Gamma }} } $ | (24) |
式中:ec表示为匹配界面中子单元的总量;σic表示第i个单元。本文采用高斯积分来进行子单元中的数值积分。综上所述,Common-Refinement方法的实现过程为:首先,根据生成的流体一侧和结构一侧在耦合边界上的边界网格生成新的匹配界面上的子单元;进而,在每个子单元中遍历所有积分点并计算子单元的面积;随后,将积分点和包含其单元的周边的单元进行联立,对应力矢量按照式(24)进行数值积分;最后,得到传输后的应力矢量数值。
在具体实现过程中,本文采用C语言,同时采用OpenMP结合MPI进行并行编程,编写了流固耦合的完整的计算代码。Common-Refinement方法同样通过C语言实现。立管产生的位移通过Common-Refinement方法传输至流体区域作为流体区域N-S方程求解和网格运动的边界条件,而流体产生的应力载荷同样通过Common-Refinement方法传输至立管,作为结构动力学方程求解的边界条件。
4 深海立管的涡激振动海洋立管涡激振动的预测是预防在深海工程作业运行故障的关键问题。在这里用一个实际的深海立管为算例,说明基于共同细化方案的三维流固耦合求解器能够准确地预测立管的动态特性。为了达到这一点,选取了文献[15]中深海作业立管在均匀流动下的物理实验来开展数值研究。
数值计算采用立管的直径为D,轴心距离入流Γin和出流Γout边界的距离分别为10D和30D,距离侧边界的距离10D。立管Z方向展长L为481.5D。流速矢量为
在耦合界面上,流体和结构沿周向的网格划分数目分别为120和96,沿立管布置多层边界层网格,保证在壁面法向上y+ < 1。流域被划分为9×105个节点连同1.2×106非结构六面体网格,立管被划分为8.7×104个节点连同9.7×104非结构六面体网格。数值计算无量纲时间步为ΔtU/D=0.1,采用LES求解湍流。数值模拟用无量纲参数如下:
| $ \mathit{Re} = \frac{{{\rho ^{\rm{f}}}UD}}{{{\mu ^{\rm{f}}}}} = 4\;000 $ | (25) |
| $ EI/\left( {{\rho ^{\rm{f}}}{U^2}{D^{\rm{4}}}} \right) = {\rm{2}}{\rm{.115}}\;{\rm{8}} \times {\rm{1}}{{\rm{0}}^{\rm{7}}} $ | (26) |
| $ T/\left( {{\rho ^{\rm{f}}}{U^2}{D^2}} \right) = 5.1062\;5 \times {10^4} $ | (27) |
| $ {\mathit{\boldsymbol{m}}^ * } = {\mathit{\boldsymbol{m}}^{\rm{s}}}\left( {\frac{{\rm{ \mathsf{ π} }}}{4}{D^2}L{\rho ^{\rm{f}}}} \right) = 2.23 $ | (28) |
式中:I是横截面面积的二阶矩;ms是立管质量。给出了立管的动态响应结果,并与实验结果做了比较。
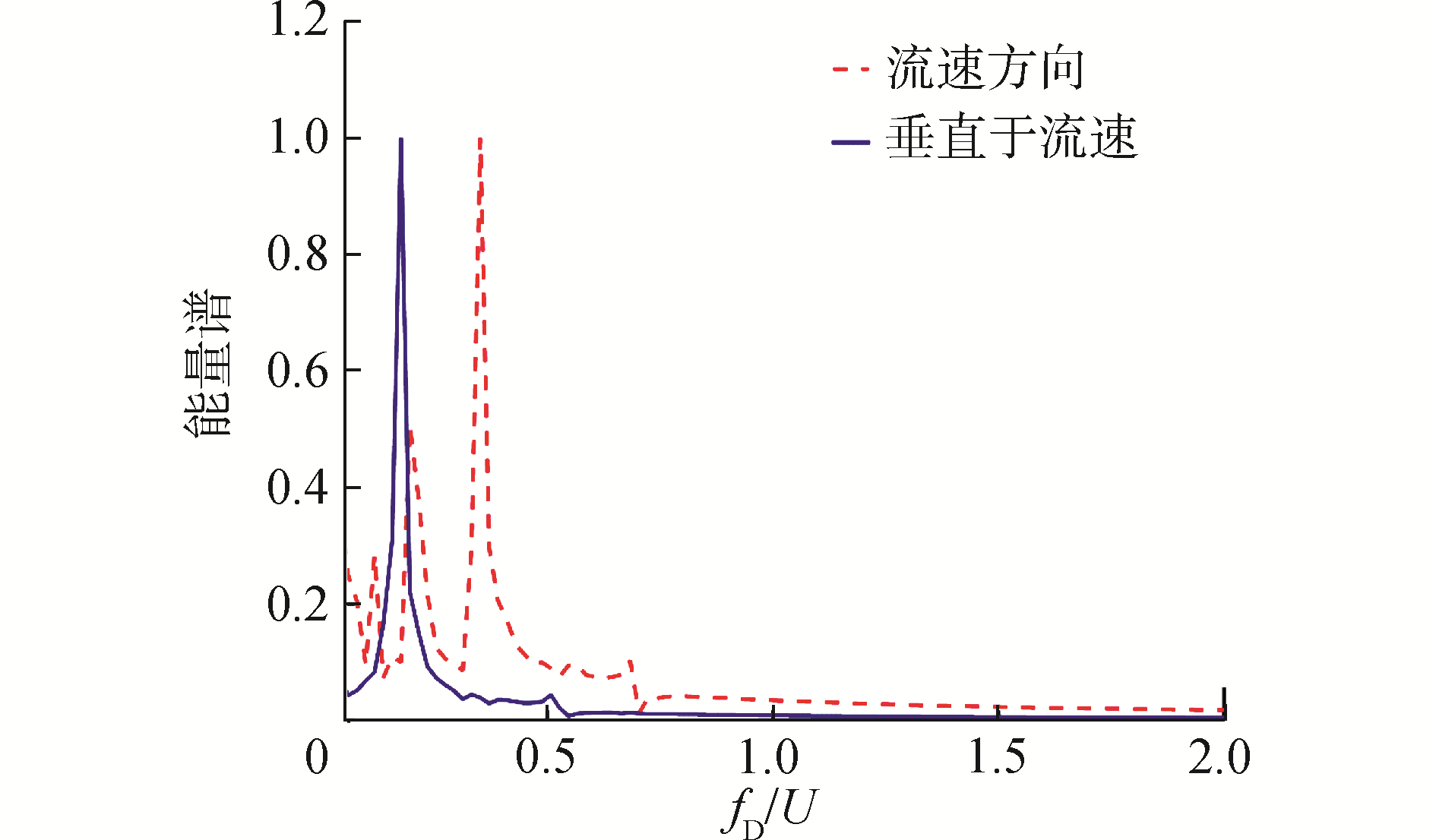
从谱分析的结果图 1中能够观察到,流速方向上立管的响应频率fD/U=0.351 6正好是垂向于流速方向上的响应频率fD/U=0.175 8的2倍。
|
Download:
|
| 图 1 立管动态响应谱分析结果 Fig. 1 Spectral analysis of riser motion response | |
同时比较立管响应的均方根值。假设Ax和Ay分别为立管在和流速同向和垂向的位移幅度,对应的平均位移幅度分别为
| $ \left\{ \begin{array}{l} {A_{x,{\rm{rms}}}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{A_{x,i}} - {{\bar A}_x}} \right)}^2}} } \\ {A_{y,{\rm{rms}}}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{A_{y,i}} - {{\bar A}_y}} \right)}^2}} } \end{array} \right. $ | (29) |
式中:N为时间方向采样点的数目。均方根值的结果见表 1。
| 表 1 计算结果和模型试验结果对比 Table 1 Resule comparison between numerical and experiment results |
从表 1中能够看出,尽管在垂向于流速方向的结果吻合良好,在流速同向的幅度有过高估计的趋势。参照文献[15],虑及总均方根峰值A/D,其中
以上计算结果能够说明所采取的基于非匹配网格和Common-Refinement方法的流固耦合求解器能够很好地捕捉到深海柔性立管的物理特性和动态响应。
5 结论1) Common-Refinement方法可以准确地对流体和结构区域的计算数据进行传输,并同时保证流固耦合问题的计算精度与准确性。
2) 通过将提出的基于三维Common-Refinement方法的流固耦合有限元求解器应用于实际大尺度海洋立管问题,能够看出三维Common-Refinement方法提供了稳定且准确的模拟方式,立管的物理特性和动态响应捕捉良好,更进一步说明了这种方法的在海洋工程领域的实用价值。
目前需要更进一步对结构动力学的的非线性特性以及沿立管变张力,以及粗糙度对立管表面流动分离的影响做出更细致的研究工作。
为了改进这种方法的效率,值得进一步去开发和研究自适应三维非匹配网格在流固耦合问题中的运用。
| [1] |
FARHAT C, VAN DER ZEE K G, GEUZAINE P. Provably second-order time-accurate loosely-coupled solution algorithms for transient nonlinear computational aeroelasticity[J]. Computer methods in applied mechanics and engineering, 2006, 195(17/18): 1973-2001. (  0) 0)
|
| [2] |
DE BOER A, VAN ZUIJLEN A, BIJL H. Review of coupling methods for non-matching meshes[J]. Computer methods in applied mechanics and engineering, 2007, 196(8): 1515-1525. (  0) 0)
|
| [3] |
DE BOER A, VAN ZUIJLEN A H, BIJL H. Comparison of conservative and consistent approaches for the coupling of non-matching meshes[J]. Computer methods in applied mechanics and engineering, 2008, 197(49/50): 4284-4297. (  0) 0)
|
| [4] |
JAIMAN R K, JIAO X, GEUBELLE P H, et al. Conservative load transfer along curved fluid-solid interface with non-matching meshes[J]. Journal of computational physics, 2006, 218(1): 372-397. (  0) 0)
|
| [5] |
JAIMAN R K, JIAO X, GEUBELLE P H, et al. Conservative load transfer along curved fluid-solid interface with non-matching meshes[J]. Journal of computational physics, 2006, 218(1): 372-397. (  0) 0)
|
| [6] |
FARHAT C, VAN DER ZEE K G, GEUZAINE P. Provably second-order time-accurate loosely-coupled solution algorithms for transient nonlinear computational aeroelasticity[J]. Computer methods in applied mechanics and engineering, 2006, 195(17/18): 1973-2001. (  0) 0)
|
| [7] |
DE BOER A, VAN ZUIJLEN A, BIJL H. Review of coupling methods for non-matching meshes[J]. Computer methods in applied mechanics and engineering, 2007, 196(8): 1515-1525. (  0) 0)
|
| [8] |
DE BOER A, VAN ZUIJLEN A H, BIJL H. Comparison of conservative and consistent approaches for the coupling of non-matching meshes[J]. Computer methods in applied mechanics and engineering, 2008, 197(49/50): 4284-4297. (  0) 0)
|
| [9] |
JAIMAN R K, JIAO X, GEUBELLE P H, et al. Conservative load transfer along curved fluid-solid interface with non-matching meshes[J]. Journal of computational physics, 2006, 218(1): 372-397. (  0) 0)
|
| [10] |
JIAO Xiangmin, HEATH M T. Common-Refinement-based data transfer between non-matching meshes in multiphysics simulations[J]. International journal for numerical methods in engineering, 2004, 61(14): 2402-2427. (  0) 0)
|
| [11] |
JIAO Xiangmin, HEATH M T. Overlaying surface meshes, part Ⅰ:Algorithms[J]. International journal of computational geometry & applications, 2004, 14(6): 379-402. (  0) 0)
|
| [12] |
JIAO Xiangmin, HEATH M T. Overlaying surface meshes, part Ⅱ:Topology preservation and feature matching[J]. International journal of computational geometry & applications, 2004, 14(6): 403-419. (  0) 0)
|
| [13] |
JANDRON M A, HURD R C, BELDEN J L, et alModeling of hyperelastic water-skipping spheres using abaqus/explicit[C]//SIMULIA Community Conference, 2014.
(  0) 0)
|
| [14] |
JANSEN K E, WHITTING C H, HULBERT G M. A generalized-α method for integrating the filtered Navier-Stokes equations with a stabilized finite element method[J]. Computer methods in applied mechanics and engineering, 2000, 190(3/4): 305-319. (  0) 0)
|
| [15] |
JOSHI V, JAIMAN R K. A variationally bounded scheme for delayed detached eddy simulation:Application to vortex-induced vibration of offshore riser[J]. Computers & fluids, 157: 84-111. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


