2. 湖南省高速公路建设开发有限公司, 湖南 长沙 410001;
3. 中南大学 重载铁路工程结构教育部重点实验室, 湖南 长沙 410075
2. Hu'nan Expressway Construction and Development Co., Ltd., Changsha 410001, China;
3. Key Laboratory of Engineering Structure of Heavy Railway, Ministry of Education, Central South University, Changsha 410075, China
隧道施工一般采用两端对向开挖以加快施工进度。当开挖面小于一定间距时,一端施工将对另一端产生影响,此时隧道贯通前开挖面稳定性、地层失稳形态及范围是关注重点。
目前,关于隧道单向开挖面稳定性分析的研究报道很多,一些学者采用模型试验[1-2]、数值计算[3-5]、理论分析[6-7]等多种手段开展了相关研究。在理论分析与计算方面,塑性极限分析方法是研究隧道开挖面稳定性的特色手段[8-13]。Zhang等[8]运用极限分析方法研究了非均质黏土隧道工作面支护反力上限值;Huang等[9]提出一种上限分析数值算法并研究了不排水条件下隧道工作面稳定性问题;而针对砂土地层,杨峰等[10-11]构造浅埋隧道工作面破坏模式求解极限支护反力,随后应用塑性变形单元和刚性运动单元上限有限元研究了隧道工作面稳定性;阳军生等[12]应用六节点三角形单元以网格加密方式得到工作面稳定性临界值上限解。
上述隧道开挖面稳定性理论与数值计算研究多侧重于极限支护反力的确定。采用矿山法施工时,隧道开挖面为自由表面,此时评价土体自重作用下的稳定性并研究临界失稳状态下精细破坏模式变得更为重要。基于此,本文针对隧道对向施工开挖面稳定性和失稳破坏模式问题,采用刚体平动运动单元上限有限元法[13](the upper bound finite element method with rigid translatory moving element, UBFEM-RTME)开展计算分析,获得稳定系数图表和有效间断线网破坏模式及其演变规律。
1 对向开挖面稳定性问题 1.1 力学模型隧道对向开挖面稳定性实际是复杂的三维问题。从保守角度出发,将计算模型简化为沿隧道纵向中心线剖开的二维平面应变问题考虑(如图 1所示)可降低计算难度,所得结果仍可反映隧道稳定性及破坏形态等诸多有益信息[6, 10-12]。特别是当隧道跨度较大时,此假定也是合理的。

|
Download:
|
| 图 1 隧道对向施工开挖面稳定性力学模型 Fig. 1 The stability mechanics model of the tunnel faces on the opposite direction | |
隧道对向开挖面稳定性力学模型如图 1,为使研究目标清晰,进一步作如下简化:1)隧道埋深为H,高度为D,对向开挖面间距为S,地表为水平自由面;2)隧道开挖面为竖向自由面,其后方上下部均为紧跟的刚性支护;3)地层为均质土体,服从相关联流动法则的摩尔-库伦材料,内摩擦角为φ,黏聚力为c,容重为γ;4)仅考虑按体积力(土体自重)增加法使隧道开挖面发生失稳破坏,不考虑地下水的作用。这些简化虽与实际工程存在差异,但从理论计算方面系统开展对向开挖面稳定性规律研究仍是有意义的。需要指出,当内摩擦角φ较大时,假定土体服从相关联流动法则将夸大剪胀效应,计算结果将偏于保守。
1.2 稳定性系数Ncr定义对于二维平面应变条件下隧道开挖面稳定性评价指标,Broms等[14]提出黏土不排水条件下的稳定系数为:
| $ N = \left( {{\sigma _{\rm{s}}} - \gamma H - {\sigma _{\rm{T}}}} \right)/{S_{\rm{u}}} $ | (1) |
式中:N为开挖面稳定系数;σs为地表超载;σT为开挖面均布荷载;H为隧道埋深;γ为黏土容重;Su为隧道轴心处土体的不排水抗剪强度。
参考式(1)的形式,不考虑σs和σT,引入无量纲稳定系数Ncr=γcrH/c评价土体自重作用下隧道对向开挖面稳定性。Ncr能够反映极限状态下开挖面地层临界容重γcr的规律。Ncr是对向开挖面间距比S/D、隧道埋深比H/D和内摩擦角φ的函数,定义为:
| $ {N_{{\rm{cr}}}} = {\gamma _{{\rm{cr}}}}H/c = f(S/D, H/D, \phi ) $ | (2) |
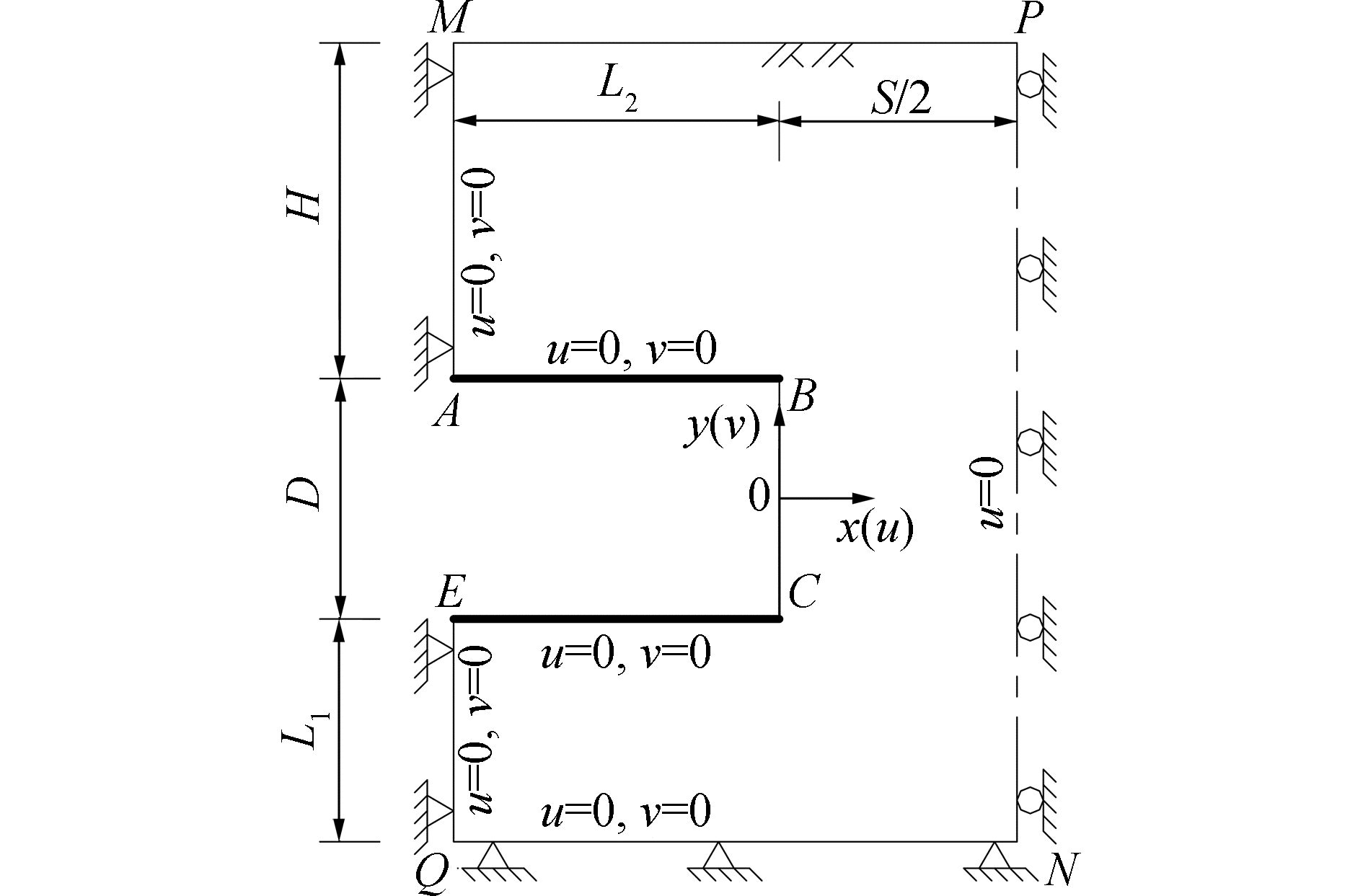
隧道对向开挖面稳定性上限有限元模型如图 2所示,利用对称性取完整模型(见图 1)右侧的一半。坐标原点取为开挖面中点,x和y正方向分别为向右和向上,速度正方向与此一致。开挖面到对称轴PN距离为S/2,隧道下方EQ段长度L1、AB和EC段长度L2的取值与隧道埋深H相关,取足够大的数值以消除边界效应的影响。
|
Download:
|
| 图 2 隧道对向施工开挖面稳定性上限有限元模型 Fig. 2 The upper bound finite element stability analysis model of tunnel faces on the opposite direction | |
由于模型只承受地层自重荷载,按容重增加法对应的稳定性分析思路,施加自重体力约束:
| $ \sum\limits_{i = 1}^{{n_e}} {{A_i}} {v_i} = - 1, - {A_i} < 0, \quad i = 1, 2, \cdots , {n_e} $ | (3) |
式中:Ai为单元i的面积,需始终大于零;vi为单元i的竖向速度分量;ne为单元总数。
根据上限定理,将模型中所有间断线耗散能最小化,可得到UBFEM-RTME非线性规划目标函数,即为极限状态对应的土体临界容重γcr:
| $ {\gamma _{{\rm{cr}}}} = \sum\limits_{i = 1}^{{n_d}} {{P_{d, i}}} = c\sum\limits_{i = 1}^{{n_d}} {\xi _i^\prime } $ | (4) |
式中:Pd, i是第i条速度间断线上耗散能;c为土体粘聚力,在计算中取单位值;nd为间断线总数;ξi′为第i条速度间断线的过程变量,计算如下:
| $ \begin{array}{l} \xi _i^\prime = 1/\tan \phi \left[ {{u_{r, i}}\left( {{y_{f, i}} - {y_{s, i}}} \right) + {v_{r, i}}\left( {{x_{s, i}} - {x_{f, i}}} \right) + } \right.\\ \;\;\;\;\;\;\left. {{u_{l, i}}\left( {{y_{s, i}} - {y_{f, i}}} \right) + {v_{l, i}}\left( {{x_{f, i}} - {x_{s, i}}} \right)} \right] \end{array} $ | (5) |
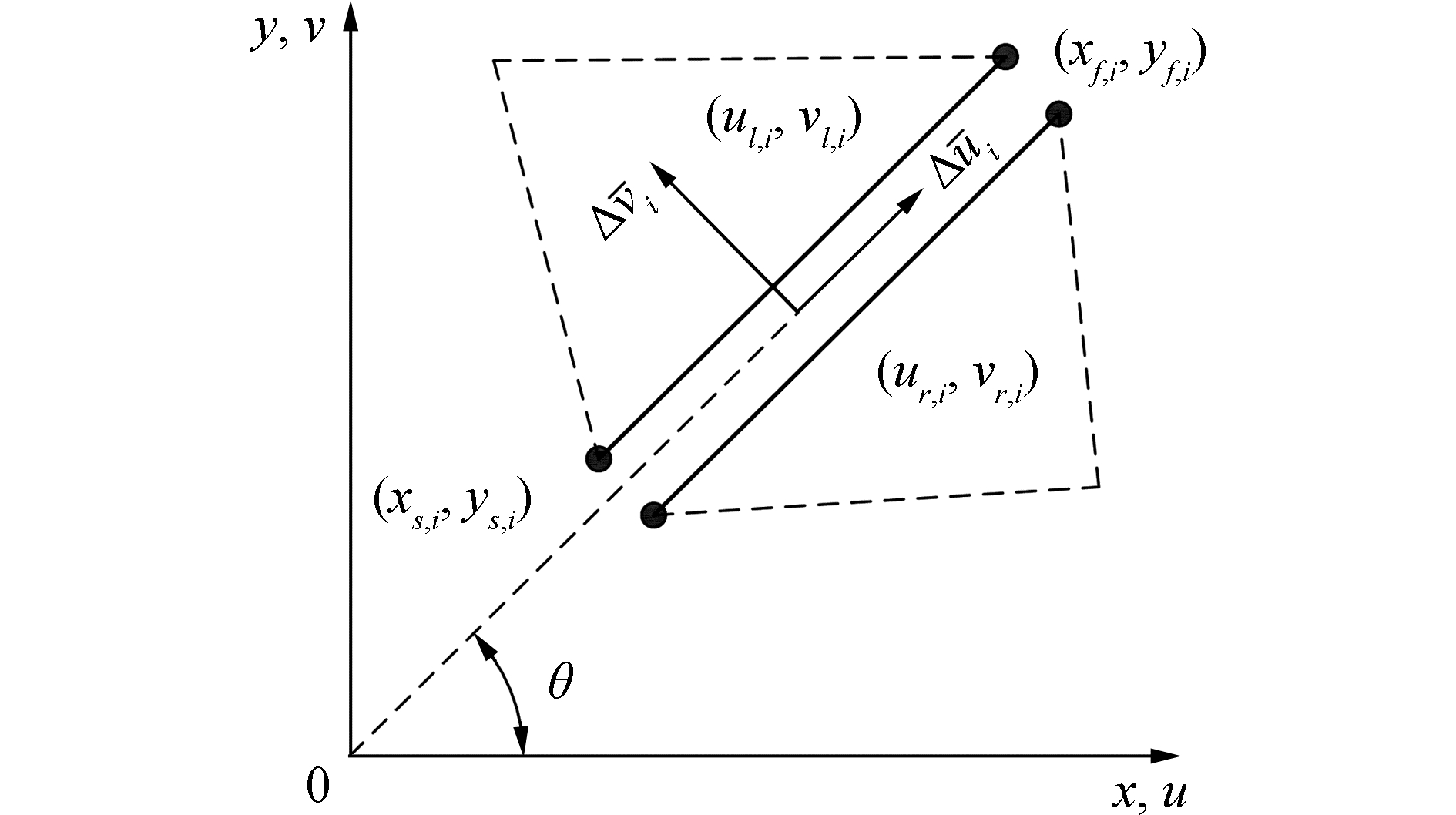
式中:ur, i和vr, i为第i条速度间断线顺时针方向一侧单元速度分量;ul, i和vl, i为逆时针方向一侧单元速度分量;xs, i和ys, i为第i条速度间断线起点坐标;xf, i和yf, i为终点坐标。其余符号说明见图 3。
|
Download:
|
| 图 3 刚体平动运动单元上限有限元速度间断线说明 Fig. 3 The illustration of velocity discontinuityin UBFEM-RTME | |
速度间断线的另一个过程变量ξi″表达如下:
| $ \begin{array}{l} \xi _i^{\prime \prime } = {u_{r, i}}\left( {{x_{s, i}} - {x_{f, i}}} \right) + {v_{r, i}}\left( {{y_{s, i}} - {y_{f, i}}} \right) + \\ \;\;\;\;\;\;{u_{l, i}}\left( {{x_{f, i}} - {x_{s, i}}} \right) + {v_{l, i}}\left( {{y_{f, i}} - {y_{s, i}}} \right) \end{array} $ | (6) |
对2个过程变量施加如下不等式约束:
| $ - \xi _i^{\prime \prime } - \xi _i^\prime \le 0, \xi _i^{\prime \prime } - \xi _i^\prime \le 0, i = 1, 2, \cdots , {n_d} $ | (7) |
则式(7)相当于非线性规划计算中对间断线施加相关联流动法则约束
对于模型各条边界,还需施加如图 2所示的速度约束与几何约束,以保证各边界上的节点均仅在该边界上移动。UBFEM-RTME具体求解过程可参见文献[13]。
2.2 参数选取为展开系统分析,考虑隧道对向开挖计算参数取值合理性,选取计算参数如下:内摩擦角φ为10°~30°;隧道高度D为10 m,埋深H和对向开挖面间距S均为D的倍数,即H/D为1~4,S/D为0.5、0.625、0.75、…、8.75、9.0等,S/D依H/D值的不同而不同。为反映一些变化规律的细节,部分S/D间隔值取为0.125。
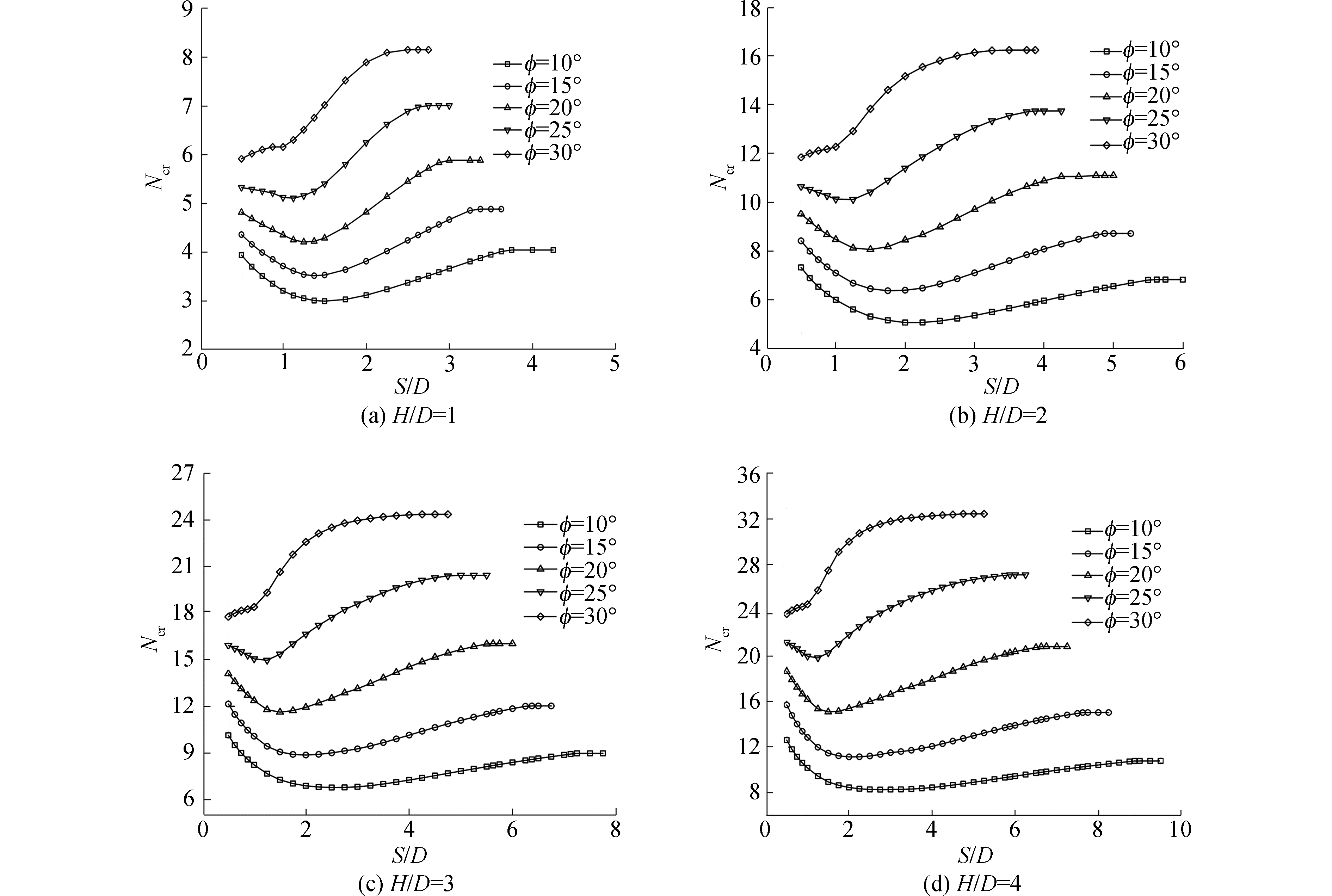
3 稳定性系数Ncr上限有限元分析 3.1 稳定性系数Ncr与开挖面间距比S/D针对隧道对向开挖面稳定性开展大量的上限有限元计算分析,获得稳定性系数Ncr结果曲线如图 4所示。需要说明的是,本文对于Ncr的求解实际暗含了在极限状态下,地层发生塑性流动且充分发挥了自身强度,进一步认为地层变形并未引起强度的任何损失。这与实际地层可能存在的强度降低或者局部破坏情况有一定差异。在工程应用中,可依据具体工程条件获得现场稳定性参数,与图 4的Ncr结果对比即可作出初步评判。
|
Download:
|
| 图 4 隧道对向施工开挖面稳定系数Ncr Fig. 4 The stability factor Ncr of tunnel faces on the opposite direction | |
下面分析对向开挖面间距比S/D对稳定性系数Ncr的影响规律。由图 4可知,S/D对Ncr有显著影响,大致规律为:随着S/D增加,Ncr先减小再增大,最终趋于某一定值并不再变化,此时对应的S/D称之为转换间距比Str/D。如图 4(a)中H/D=1,φ=20°所对应曲线,当S/D=0.5时,对应Ncr=4.82;随着S/D逐渐增加,Ncr值呈减小趋势;当S/D=1.25时,Ncr=4.21为曲线极小值;而后Ncr随着S/D增加近似线性增长,达到转换间距比Str/D=3后趋于定值(Ncr=5.89)并不再变化。
该规律可解释如下:1)模型假定隧道支护结构紧贴开挖面且刚度与承载力足够大,当S/D较小时“拱效应”现象明显,上覆地层荷载大多转移至隧道刚性支护上,因此稳定性系数Ncr有所增加。2)随着S/D增加,“拱效应”逐渐减弱,Ncr减小即对向开挖面稳定性变差,期间存在Ncr某一最小值;3)S/D继续增加,对向开挖面间的相互影响逐步减弱,Ncr值逐渐增长并最终趋于某一定值,此时(即S/D>Str/D)认为对向开挖面间的互相影响消失,等同于单向开挖情形。
除上述规律外,当土体内摩擦角较大时(如φ=30°),随着S/D增加,稳定系数Ncr未出现局部极小值。原因可能是φ较大情况下,地层能够较好发挥其自承能力,此时开挖面更趋向于局部破坏,转移至隧道支护荷载的效应不再明显。
3.2 稳定性系数Ncr演化规律除对向开挖面间距比S/D外,隧道埋深比H/D和土体内摩擦角φ对稳定性系数Ncr也有影响。如图 4,其他条件不变时,随着H/D增加,Ncr均顺势增加且曲线形态特征一致。如图 5,φ相同时,H/D越大,转换间距比Str/D也越大,表明此时对向开挖面存在相互影响的距离越远。需说明的是,随着H/D增加,Ncr值相应增加,但不意味着开挖面稳定性变好。例如H/D=1、S/D=1、φ=10°时,Ncr=3.21,此时的γcrD/c=3.21;当H/D=4、S/D=1、φ=10°时,Ncr=10.17较前者的增加216.8%,而此时γcrD/c=2.38反而较前者减少25.9%。这表明随着埋深增加,对向开挖面稳定性有所变差,原因是采用容重增加法使对向开挖面达到极限失稳状态,上覆土体自重对于维持隧道开挖面稳定是不利的。为分析土体内摩擦角φ的影响,保持H/D和S/D不变,此时φ越大Ncr也越大,开挖面稳定性变好。由图 4可知,φ越大,Ncr由局部极小值上升到恒定值的增长趋势会越快。

|
Download:
|
| 图 5 转换间距Str/D Fig. 5 The transition spacing Str/D | |
为验证本文结果的可靠性,将UBFEM-RTME计算得到的单向开挖情形下(即S/D>Str/D)对应的稳定系数Ncr,与已有文献[11-12]数据对比如图 6所示。需要指出的是,Yang等[11]上限有限元模型中开挖面以扁平椭圆曲线近似代替,地表存在超载且接触面粗糙,通过线性插值转换为本文所定义的稳定性系数Ncr;而阳军生等[12]上限有限元模型中开挖面为竖向直线,按容重增加法使地层达到临界失稳状态,将其获得的γD/c上限解转换为本文所定义的稳定性系数Ncr。

|
Download:
|
| 图 6 稳定系数Ncr对比分析图 Fig. 6 The comparison of stability factor Ncr | |
从图 6可知,本文稳定性系数Ncr均小于H/D相同情况下文献[11]三节点三角形单元上限解,并与文献[12]高阶六节点三角形单元上限解结果十分接近。本文结果与图中文献[11]结果的最大相对误差为4.4%,对应于H/D=1、φ=10°情况,而与阳军生等[12]结果的最大相对误差为0.43%,对应于H/D=2、φ=20°情况。还注意到,当H/D=2、φ=10°时,本文稳定系数Ncr与文献[12]均为6.82,但文献[12]六节点三角形单元数目为6 341,而UBFEM-RTME采用的刚性单元数目为260,仅有前者的4.1%。
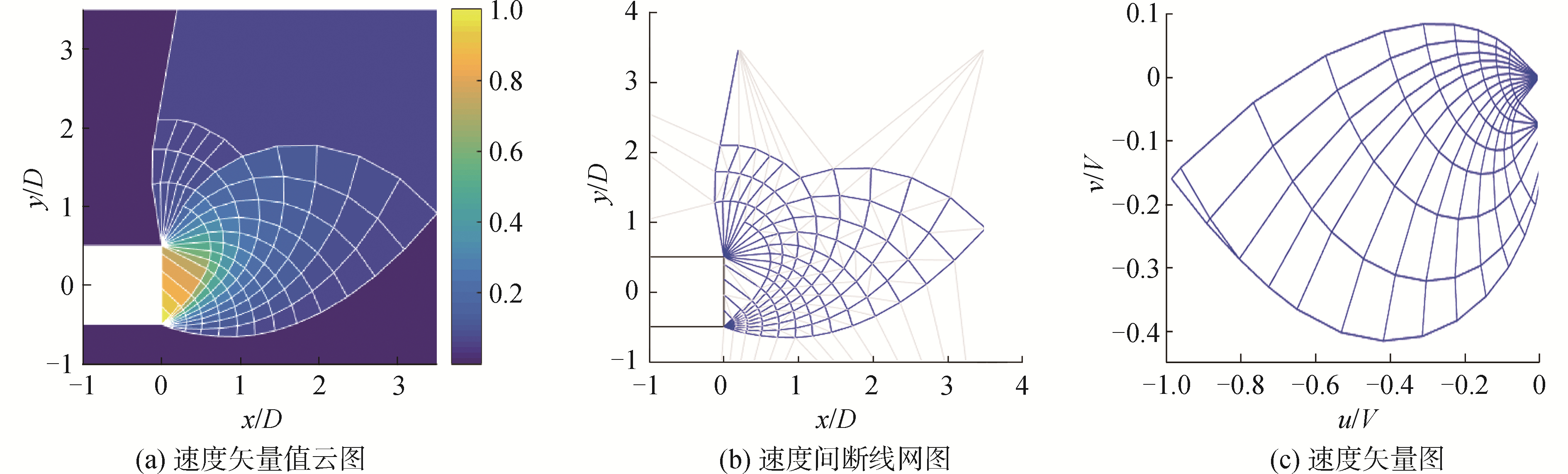
4 对向开挖面破坏模式及演化规律 4.1 典型破坏模式形态特征除稳定性系数Ncr外,UBFEM-RTME方法还可获得以有效间断线网表达的隧道对向开挖面临界失稳破坏模式,为工程中可能采用的地层预加固措施提供一定理论支撑。选取H/D=3,S/D=7,φ=10°对应的开挖面临界失稳破坏模式,以单元速度矢量值云图、速度间断线网和速度矢量图形式呈现如图 7所示。
|
Download:
|
| 图 7 对向开挖面典型破坏模式形态特征分析(H/D=3,S/D=7,φ=10°,Ncr=8.88) Fig. 7 The characteristic failure mode analysis of tunnel faces on the opposite direction(H/D=3, S/D=7, φ=10°, Ncr=8.88) | |
图 7(a)为单元速度矢量值云图,速度矢量值进行了归一化处理。可以看出,隧道开挖面特别是其下方区域速度矢量值很大,而开挖面前方直至地表大范围速度矢量值均较小。图中还给出了有效间断线网。
图 7(b)为对向开挖面临界状态下速度间断线网图,其中实线部分显示的是有效间断线网,表明这些间断线两侧单元速度不相等;同时,浅色部分显示为无效间断线网,它能保证UBFEM-RTME模型的拓扑结构,在计算过程中不可或缺,不过可在网格更新时尽量予以减少。
图 7(c)为速度矢量图,反映了有效间断线两侧单元相对速度。该图可与图 7(a)和(b)对照分析。即图 7(c)中的每一条线段均对应于图 7(a)和(b)中某一条有效间断线上的相对速度。图中原点与任意交叉点的连线代表图 7(a)和(b)中某一单元的速度矢量。如原点与最左侧交叉点的连线,实际上对应于开挖面下方位置的速度,此处速度最大且方向接近水平向。需要说明的是,速度矢量图中数据同样进行了归一化处理,因为对于上限理论而言,速度的相对大小才是有意义的。
4.2 对向开挖面破坏模式演化规律为讨论多参数的综合影响,选取φ=15°,H/D=1, 2, 3,S/D取不同值时,隧道对向开挖面破坏模式演变规律进行分析。图 8为隧道对向开挖面典型破坏模式选取示意图。图中所标示出的曲线特征点a~o均对应于特定的破坏模式,以有效间断线网格的方式绘制破坏模式如图 9所示。图 9中x/D和y/D反映了2个坐标轴方向的无量纲尺度,可用来判断破坏模式范围大小。

|
Download:
|
| 图 8 隧道对向开挖面典型破坏模式选取示意 Fig. 8 Typical failure mechanism selection of tunnel faces on the opposite direction | |

|
Download:
|
| 图 9 隧道对向开挖面破坏模式(φ=15°) Fig. 9 Failure mechanisms of tunnel faces on the opposite direction(φ=15°) | |
由图 9(a)、(f)、(k)可知,S/D较小时(如S/D=0.5),破坏模式主要由开挖面前方刚性楔形块体、靠近地表的整体刚性下沉区、开挖面顶部角点延伸出的类似滑移线的网状破坏区组成。埋深比H/D增加将使得开挖面顶部破坏区向后方扩散。
由图 9(b)、(g)、(l)可知,随着S/D增加,开挖面顶部和底部延伸出的交错网状滑移线范围逐渐扩大,而上方直至地表大范围网状破坏区减小,此时稳定性系数Ncr达到极小值(如图 8)。进一步分析图 9(c)、(h)、(m),随着S/D增加对向开挖面间网状破坏区域明显增加,且有向地表延伸趋势。
图 9(d)、(i)、(n)进一步反映了上述随着S/D增大对应破坏模式的变化规律。不同的是,图 9(d)、(i)、(n)均为临近转换间距Str/D时的对向开挖面破坏模式。当S/D达到Str/D后,对向开挖面间的相互影响消失,破坏模式变为对称的单向开挖情形,其特征可从图 9(e)、(j)、(o)看出。
结合图 8、9还可发现,尽管破坏模式形态和范围差异明显,图 9(d)、(i)、(n)和图 9(e)、(j)、(o)对应的稳定性系数Ncr差异并不大。例如图 9(n)与图 9(o),稳定系数Ncr值由17.80变化为17.83,仅增加0.17%,而破坏模式却变化显著,开挖面前方的网状破坏区域宽度由4.5D变化为2.7D,减少达40%。还注意到,开挖面失稳破坏随S/D增加的演变特征对于不同埋深H/D情况下基本相似,只是破坏范围有所增加。
除S/D和H/D外,土体内摩擦角φ对隧道开挖面破坏模式亦有影响。限于篇幅,这里不再绘图说明。一般情况下,内摩擦角φ较大时网状滑移线相互交错更为密集(相关联流动法则高估了土体剪胀效应的影响),破坏范围进一步减小。
5 结论1) 对向开挖面间距比S/D对稳定性系数Ncr有显著影响。随着S/D增加,稳定性系数Ncr先减小再增大,当S/D达到转换间距比Str/D后,Ncr不再变化,对向开挖面间的互相影响消失,等同于单向开挖情形。
2) 隧道埋深比H/D和土体内摩擦角φ对稳定性系数Ncr也有影响。随着H/D增加,Ncr均增加且曲线形态特征一致;φ相同时,H/D越大对应Str/D也越大,表明同等情况下对向开挖面存在相互影响的范围越远。而φ越大Ncr也越大,开挖面稳定性变好。
3) 在转换间距比Str/D附近,稳定系数Ncr值差别不大,但破坏模式形态范围差异明显。对向开挖面临界失稳破坏特征对于不同埋深比H/D情况下基本相似,破坏范围有所增加。内摩擦角φ较大时网状滑移线交错更为密集,破坏范围进一步减小。研究结论可为对向施工隧道贯通前的稳定性评价、预加固方案制定等提供一定理论支撑。
| [1] |
汤旅军, 陈仁朋, 尹鑫晟, 等. 密实砂土地层盾构隧道开挖面失稳离心模型试验研究[J]. 岩土工程学报, 2013, 35(10): 1830-1838. TANG Lyujun, CHEN Renpeng, YIN Xinsheng, et al. Centrifugal model tests on face stability of shield tunnels in dense sand[J]. Chinese journal of geotechnical engineering, 2013, 35(10): 1830-1838. (  0) 0)
|
| [2] |
吕玺琳, 周运才, 李冯缔. 粉砂地层盾构隧道开挖面稳定性离心试验及数值模拟[J]. 岩土力学, 2016, 37(11): 3324-3328, 3335. LYU Xilin, ZHOU Yuncai, LI Fengdi. Centrifuge model test and numerical simulation of stability of excavation face of shield tunnel in silty sand[J]. Rock and soil mechanics, 2016, 37(11): 3324-3328, 3335. (  0) 0)
|
| [3] |
UKRITCHON B, YINGCHALOENKITKHAJORN K, KEA-WSAWASVONG S. Three-dimensional undrained tunnel face stability in clay with a linearly increasing shear strength with depth[J]. Computers and geotechnics, 2017, 88: 146-151. DOI:10.1016/j.compgeo.2017.03.013 (  0) 0)
|
| [4] |
石钰锋, 阳军生, 杨峰, 等. 软弱围岩大断面隧道相向施工围岩稳定性分析与掌子面加固研究[J]. 公路交通科技, 2013, 30(5): 82-88, 111. SHI Yufeng, YANG Junsheng, YANG Feng, et al. Study of stability of surrounding rock due to approaching of two excavation faces and face reinforcement in a large cross-section tunnel in weak stratum[J]. Journal of highway and transportation research and development, 2013, 30(5): 82-88, 111. DOI:10.3969/j.issn.1002-0268.2013.05.014 (  0) 0)
|
| [5] |
王俊, 何川, 王闯, 等. 砂土地层土压盾构隧道施工掌子面稳定性研究[J]. 岩土工程学报, 2018, 40(1): 177-185. WANG Jun, HE Chuan, WANG Chuang, et al. Face stability analysis of EPB shield tunnel in sand[J]. Chinese journal of geotechnical engineering, 2018, 40(1): 177-185. (  0) 0)
|
| [6] |
张箭, 杨峰, 刘志, 等. 浅覆盾构隧道开挖面挤出刚性锥体破坏模式极限分析[J]. 岩土工程学报, 2014, 36(7): 1344-1349. ZHANG Jian, YANG Feng, LIU Zhi, et al. Three-dimensional limit analysis of blow-out failure modes of shallow shield tunnels[J]. Chinese journal of geotechnical engineering, 2014, 36(7): 1344-1349. (  0) 0)
|
| [7] |
赵明华, 毛韬, 牛浩懿, 等. 上硬下软地层盾构隧道开挖面极限支护力分析[J]. 湖南大学学报(自然科学版), 2016, 43(1): 103-109. ZHAO Minghua, MAO Tao, NIU Haoyi, et al. Analysis of limit supporting force of tunnel excavation face for shield machine in upper-hard lower-soft ground[J]. Journal of Hunan University (Natural Sciences), 2016, 43(1): 103-109. DOI:10.3969/j.issn.1674-2974.2016.01.014 (  0) 0)
|
| [8] |
ZHANG F, GAO Y F, WU Y X, et al. Upper-bound solutions for face stability of circular tunnels in undrained clays[J]. Géotechnique, 2018, 68(1): 76-85. DOI:10.1680/jgeot.16.T.028 (  0) 0)
|
| [9] |
HUANG Maosong, LI Sen, YU Jian, et al. Continuous field based upper bound analysis for three-dimensional tunnel face stability in undrained clay[J]. Computers and geotechnics, 2018, 94: 207-213. DOI:10.1016/j.compgeo.2017.09.014 (  0) 0)
|
| [10] |
杨峰, 阳军生, 赵炼恒. 浅埋隧道工作面破坏模式与支护反力研究[J]. 岩土工程学报, 2010, 32(2): 279-284. YANG Feng, YANG Junsheng, ZHAO Lianheng. Collapse mechanism and support pressure for shallow tunnel face[J]. Chinese journal of geotechnical engineering, 2010, 32(2): 279-284. (  0) 0)
|
| [11] |
YANG Feng, ZHANG Jian, ZHAO Lianheng, et al. Upper-bound finite element analysis of stability of tunnel face subjected to surcharge loading in cohesive-frictional soil[J]. KSCE journal of civil engineering, 2016, 20(6): 2270-2279. DOI:10.1007/s12205-015-0067-z (  0) 0)
|
| [12] |
阳军生, 张箭, 杨峰. 浅埋隧道掌子面稳定性二维自适应上限有限元分析[J]. 岩土力学, 2015, 36(1): 257-264. YANG Junsheng, ZHANG Jian, YANG Feng. Stability analysis of shallow tunnel face using two-dimensional finite element upper bound solution with mesh adaptation[J]. Rock and soil mechanics, 2015, 36(1): 257-264. (  0) 0)
|
| [13] |
杨峰, 赵炼恒, 张箭, 等. 基于刚体平动运动单元的上限有限元研究[J]. 岩土力学, 2014, 35(6): 1782-1786, 1808. YANG Feng, ZHAO Lianheng, ZHANG Jian, et al. Investigation on finite element upper bound solution based on rigid translatory moving element[J]. Rock and soil mechanics, 2014, 35(6): 1782-1786, 1808. (  0) 0)
|
| [14] |
BROMS B B, BENNERMARK H. Stability of clay at vertical openings[J]. Journal of soil mechanics & foundations division, 1967, 193: 71-94. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


