2. 江苏省土木工程防震技术研究中心, 江苏 南京 210009
2. Civil Engineering and Earthquake Disaster Prevention Center of Jiangsu Province, Nanjing 210009, China
剪切波速Vs或小应变剪切模量Gmax=ρVs2,(ρ为土的质量密度)是表征土体动力特性的最基本参数,在预测土体的地震变形、液化势和场地反应特性方面具有重要的作用[1]。Gmax通常指剪应变水平1×10-6的土体剪切模量。现有的研究成果表明,Gmax与土的孔隙比、颗粒特征(如粒径与颗粒形状)、结构性、沉积特性(颗粒排列与层理)、应力历史与应力状态、加载速率密切相关[2]。不同研究者利用各种方法探讨了Gmax的主要影响因素,发现Gmax主要取决于孔隙比e和初始有效围压σ′3c的大小[3]。
大多数天然沉积的砂并非纯砂粒土,而是具有不同细粒含量FC(粒径小于0.075 mm的土颗粒质量百分比)的砂类土[4]。根据粒径的大小,细粒分为粉粒和黏粒;且随着FC的增加,砂类土分为砂、含细粒土砂和细粒土质砂[5]。FC对砂类土的基本物理属性以及静/动力学特性影响显著[6],这使得越来越多的学者开始关注FC对砂类土Gmax或Vs的影响。Iwasaki等[7]利用共振柱仪较早开展了类砂类土的Gmax的影响因素研究,分析表明:各类砂类土的归准化小应变剪切模量Gmax/F(e)随初始有效围压的增大基本呈线性增加,且两者的相关性与土性和孔隙比无关,其中F(e)=(2.17-e)2/(1+e),当σ′c0确定后,Vs随e的增大呈线性降低;当σ′c0和e相同时,Gmax随不均匀系数或FC的增大而减小。Huang等[8]试验结果表明:当e一致时,台湾麦寮砂类土的Vs随FC的增加而减小,而当FC相同时,Vs随e的增大呈线性减小,这与Oka等[9]的试验结果基本一致。Carraro等[10]利用弯曲元研究了塑性细粒和非塑性细粒对饱和渥太华砂类土Gmax的影响,发现细粒的塑性、σ′c0以及FC对Gmax都有显著影响。砂类土的Gmax随σ′c0的增大呈指数函数形式增大,塑性细粒的增加并没有引起Gmax明显的变化;而非塑性细粒的增加将显著降低砂类土的Gmax。Salgado等[11]通过砂类土弯曲元试验阐述了细粒增大导致砂类Gmax降低的机理,指出细粒的增加并没有完全参与土体骨架的组成,而是部分参与力链传递,部分填充砂粒间的孔隙,使得剪切波速不能完全通过细粒传递,从而降低土体刚度,最终导致Gmax的减小。Choo等[12]利用弯曲元测量了4种具有不同细粒级配的渥太华砂类土Vs,系统研究了σ′c0、有效粒径比(砂粒有效粒径与细粒平均粒径比)、e以及FC对Vs的影响。分析表明:Vs与压σ′c0呈幂函数关系;4类砂类土的Vs都随FC的增大而减小,且FC对Vs的影响随有效粒径比的增大而显著增强;具有不同Vs和e的4类Vs随esk的增大呈线性降低。由文献可知,学者们尝试建立Gmax或Vs与FC的关系,但结论不尽相同,仍具争议。
压电弯曲元剪切波速测试技术由于原理简明、操作便捷以及具有无损检测等特点,被广泛地应用在各类试验设备中进行土样Gmax的测量研究。因此,本文通过一系列的弯曲元试验,综合考虑级配特性,固结应力和密实状态对Gmax的影响,研究了具有不同FC的饱和砂类土的Gmax,并基于砂类土的二元介质模型,建立具有不同FC、e以及σ′c0的砂类土Gmax的预测模型,并分析了该模型的普适性。
1 弯曲元试验 1.1 测试设备及测试方法砂类土的剪切波速由安装在GCTS HCA-300静动三轴仪上的一对弯曲元系测试系统测量获得,设备参数见文献[13]。弯曲元由2片压电陶瓷片和中心铜加劲层组合而成。在试验中,弯曲元插入试样中,与试样完全耦合。激发元在脉冲电压的刺激下,在试样的一端激发剪切波;剪切波经过试样传播后到达接收元,通过示波器上显示的激发信号和接受信号可以计算出剪切波或压缩波的传播时间,再结合剪切波的传播距离,就可以计算出土体剪切波速Vs为:
| $ {V_{\rm{s}}} = d/t $ | (1) |
式中:d为波的有效传播距离,即弯曲元发射和接受段部距离;t为波的传播时间。确定波的传播时间的方法包括:时域法和频域法2种,然而Brignoli等[14]和陈云敏等[15]的研究成果表明:时域初达波法能简单而准确的确定波传播时间。因此本次试验采用“时域初达波”法确定t。
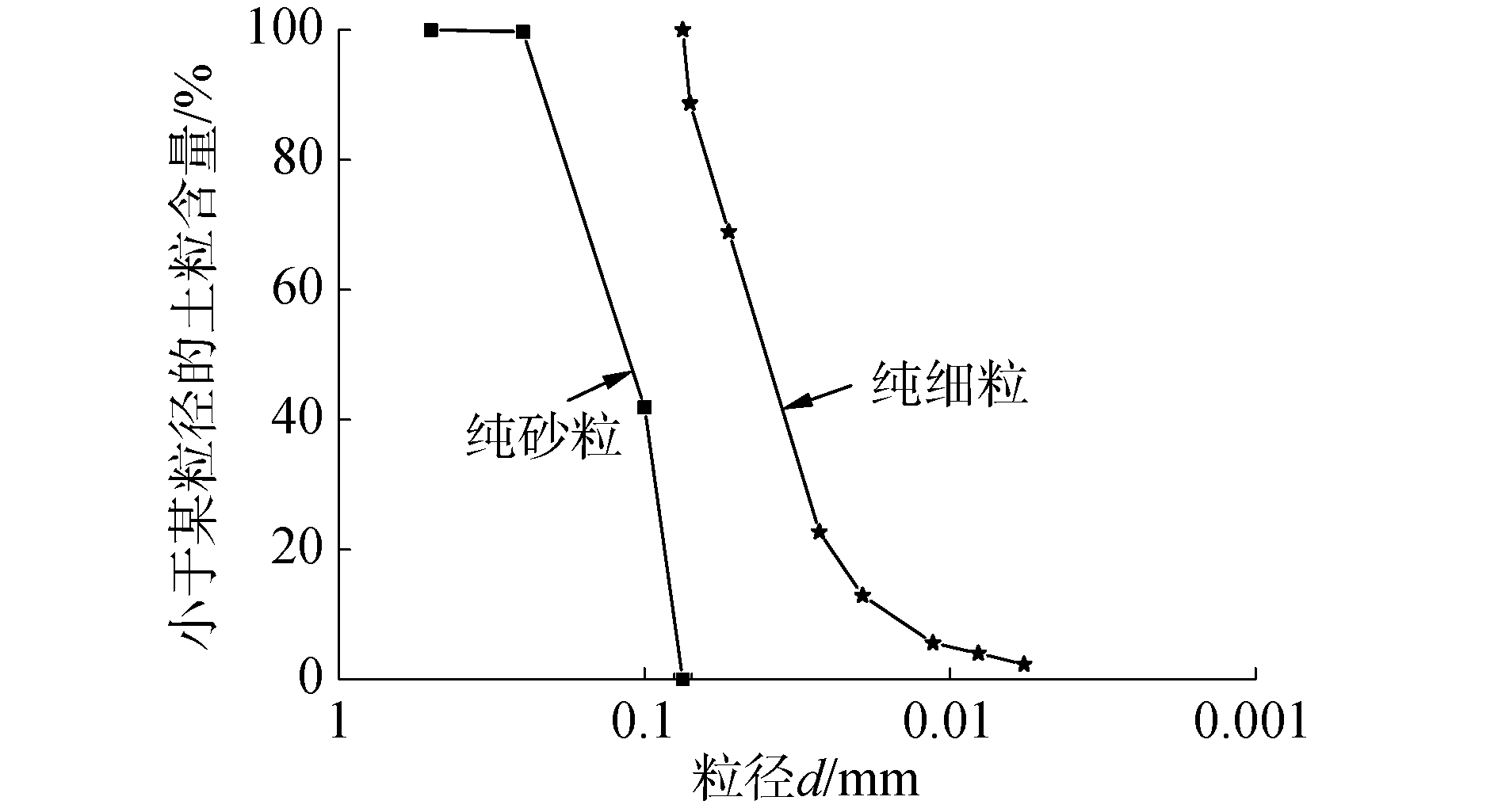
1.2 试验砂类土选取南通砂类土作为研究对象。南通砂类土取自南通沿海滩涂,烘干后呈灰色,松散,分选性较好,颗粒呈次角状。其砂粒和细粒的基本物理属性指标依据《土工试验规程》[16]获得:砂粒的平均粒径d50为0.1 134 mm,有效粒径d10为0.080 mm,不均匀系数Cu为1.672,密度G为2.672 g/cm3,最大孔隙比emax和最小孔隙比emin分别为1.262和0.662;细粒的d50为0.1 134 mm,d10为0.080 mm,Cu为1.672,G为2.672 g/cm3,emax和emin分别为1.262和0.662。级配曲线如图 1所示。
|
Download:
|
| 图 1 砂类土的砂粒和细粒的级配曲线 Fig. 1 Grain size distributions of sand grains and fine grains for sandy soils | |
试样为100 mm×200 mm的实心圆柱样。由于湿击法具有适用范围广且可较精准的控制试样e[18],因此,采用湿击法制样具有不同级配特征和密实状态的砂类土试样,制备时将试样分成4层,每层所需各粒径颗粒的质量按级配单独配制以保证各层试样的均匀性。
试样的饱和分为3步:1)通15 min的CO2以除去试样中空气;2)从试样底部到顶部通无气水直到顶部没有气体排出;3)进行分级反压饱和。对分级反压饱和后的试样进行孔压系数B值测定,若B>0.95,认为试样达到饱和[13]。对完全饱和的试样进行均等固结。
1.4 试验方案为探讨级配组成,密实状态和固结应力条件对砂类土Gmax的影响,依次取FC为0%、10%、20%和30%,以研究FC对砂类土Gmax的影响。表 2给出了FC不同的砂类土的基本物理属性,对特定FC的砂类土,选取3个差别较大的e作为制样的密实状态控制指标,而对FC和e相同的试样,依次施加5个等级的σ′3c:100、200、250、300和400 kPa。综合考虑级配组成,密实状态以及固结应力条件12组共60个试验工况汇总于表 2。
| 表 1 FC不同的砂类土的最大、最小孔隙比及比重 Table 1 Maximum, minimum void ratio and specific gravity of sandy soils with various FC |
| 表 2 砂-粉混合料的弯曲元试验工况 Table 2 Schemes of bender element tests for sand-silt mixtures |
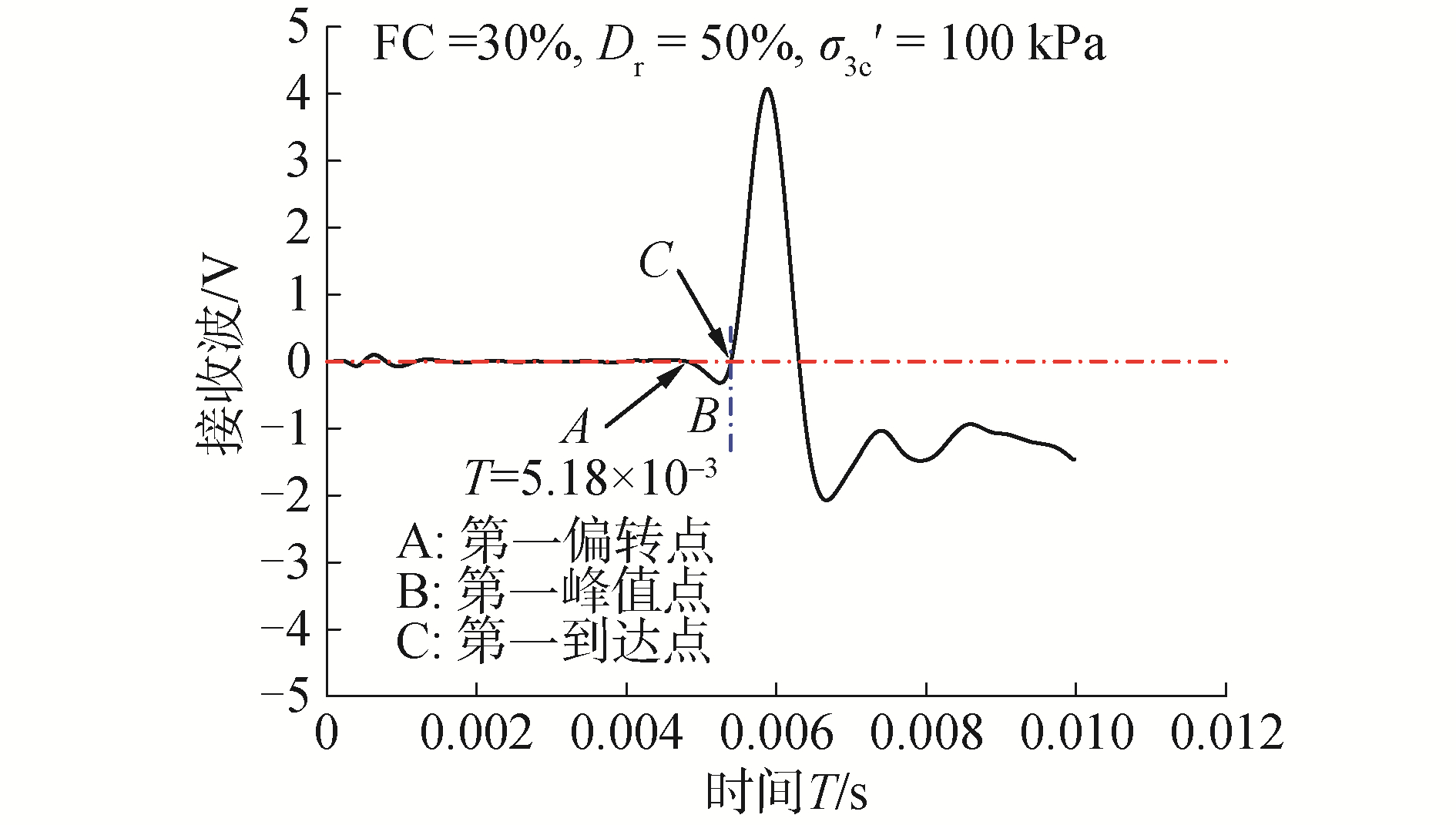
图 2为FC=30%,Dr=50%且σ′c0=100 kPa的弯曲元接收信号图,图中A、B和C点分别表示弯曲元接收信号的第一偏转点、第一峰值点和第一到达点,将C点作为剪切波初次到达的时间以确定剪切波的传播时间t[8-9]。由图可知,利用“时域初达波”法获得的T=5.18 ms。
|
Download:
|
| 图 2 典型的弯曲元接收端时程曲线 Fig. 2 Typical time history of output signal from bender element tests | |
图 3为各FC的砂类土Gmax与e的关系曲线。由图可知,具有不同FC和σ′3c的砂类土Gmax与e呈现较强的函数关系,且FC、e和σ′3c对Gmax影响显著。在每幅图中有5条拟合线描述e对Gmax的影响,而每条线的分布差异呈现了σ′3c对Gmax的影响。当控制其他试验条件相同时,Gmax随e或FC的增大而减小,但随σ′3c的增大而增大。产生该现象的可能原因是:当e增大时,砂类土的密实状态变得更加松散,这使得颗粒间的力链减少,从而引起砂类土刚度下降,Gmax随之降低;当e相同时,随着细颗粒的增多,部分组成骨架颗粒的砂粒由细粒所替代,这使得砂类土骨架组构改变,颗粒接触面积减小,从而导致Gmax的降低。此外,Gmax随e增大而减小的速率对σ′3c呈现较低的敏感性,但对FC呈现较强的敏感性。Yang等[18]发现:丰浦砂类土的Gmax与e基本呈线函数关系,且两者的相关性与FC基本无关,这表明,Gmax随e增大而减小的速率对砂类土的土性有较强的敏感性,具体的影响规律需要更完善的试验数据加以论证,此处不再赘述。

|
Download:
|
| 图 3 Gmax与e的关系曲线 Fig. 3 The relationship between Gmax and e | |
当砂类土的FC为定值时,鉴于Gmax值同时依赖于σ′3c和e,在量化σ′3c对Gmax的影响时,必须综合考虑e的影响,因此引入孔隙方程F(e)统一描述e对Gmax的影响:
| $ F(e) = \frac{{{{(c - e)}^2}}}{{1 + e}} $ | (2) |
式中:c为与土粒形状相关的参数,Hardin等[3]建议取2.97。以往研究表明,无粘性土的Gmax和σ′3c与e的经验关系为[6]:
| $ {G_{\max }} = A{P_{\rm{a}}}F(e){\left( {\frac{{\sigma _{3{\rm{c}}}^\prime }}{{{P_{\rm{a}}}}}} \right)^n} $ | (3) |
式中:A为拟合参数;Pa为标准大气压,n为应力指数,对一般砂土,其值一般分布于0.4 ~ 0.6,Hardin等建议n可取为0.5[3];因此预测Gmax的Hardin模型表示为:
| $ {G_{\max }} = A\frac{{{{(c - e)}^2}}}{{1 + e}}{\left( {\frac{{\sigma _{3{\rm{c}}}^\prime }}{{{P_{\rm{a}}}}}} \right)^{0.5}} $ | (4) |
一般采用Pa≈100 kPa进行规准化。
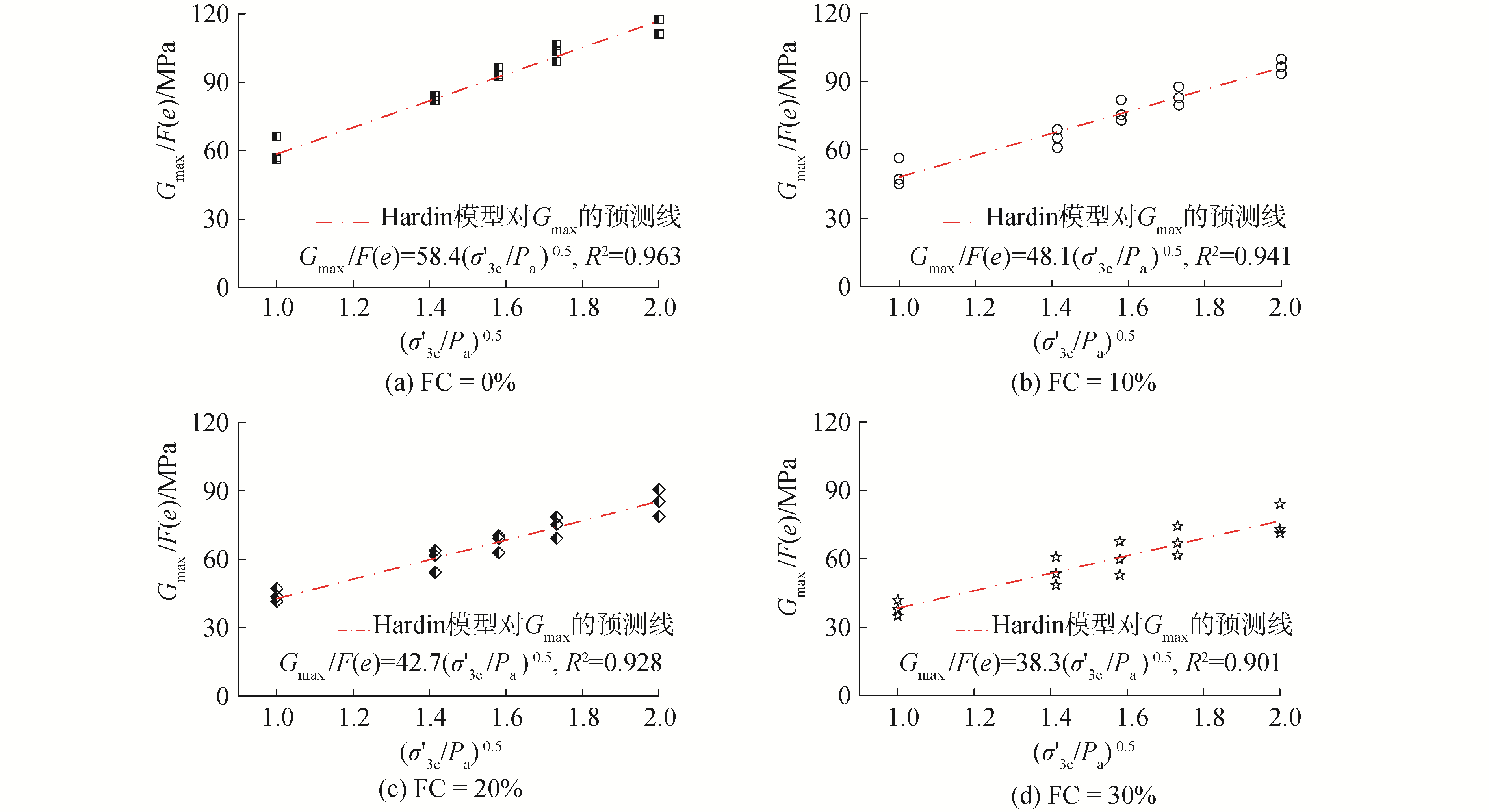
图 4给出了各FC对应的孔隙修正小应变剪切模量Gmax/F(e)与归准化有效围压(σ′3c/Pa)0.5的分布关系。由图可知,Gmax/F(e)随(σ′3c/Pa)0.5的增加呈线性增大,这表明,Hardin模型可以很好的描述砂类土的σ′3c和e对Gmax的影响。此外,不同FC的砂类土的R2都大于0.9,这说明Hardin模型可以合理预测给定FC的砂类土Gmax。此外,由对比可知,反应Gmax/F(e)线性增长速率的拟合参数A随FC的增大而减小,两者呈幂函数关系,如图 5所示。A与FC可描述为如下函数形式:
|
Download:
|
| 图 4 FC不同的砂类土的Gmax/F(e)与(σ′3c/Pa)0.5的关系曲线 Fig. 4 The relationship between Gmax/F(e) and (σ′3c/Pa)0.5 for sandy soils with different FC | |

|
Download:
|
| 图 5 Hardin模型参数A与FC的关系 Fig. 5 The relationship between A of Hardin model and FC for sandy soils | |
| $ A({\rm{FC}}) = {A_0}\exp (nFC) $ | (5) |
式中:n为拟合参数,A0为纯砂粒(FC=0%)的Hardin模型拟合参数A,对于本试验所用的砂类土,n=-1.52。
综合考虑e和σ′3cHardin模型无法统一描述FC对砂类土Gmax的影响。
2.2 修正Hardin模型对Gmax的评价土颗粒通过不同方式的排列与咬合,形成具有抵抗外部荷载能力的骨架结构,称之为土结构。土结构的破坏总是发生在骨架颗粒之间咬合薄弱的部位。为了描述天然砂类土的聚集条件,引入二元介质模型。理想化的二元介质模型存在3个基本假设:1)由2种区别明显的大、小颗粒组成;2)大、小颗粒粒径的比值较大;3)大颗粒的聚集不受小颗粒的影响,反之也然。根据二元介质聚集模型,土体由土骨架和骨架间的孔隙组成:组成土骨架的颗粒称为骨架颗粒,充填于骨架间的孔隙但不影响土骨架结构强度的颗粒称之为填充颗粒。
Thevanayagam等[20]细颗粒的增加会明显改变砂类土的骨架颗粒组成,从而改变颗粒接触状态,当FC较小时,砂类土的颗粒处于“细粒填充砂粒”状态,砂粒组成土体骨架,其力学特性主要由砂粒组构决定。而当FC较大时,砂类土的颗粒处于“砂粒悬浮于细粒”状态,细粒组成土体骨架,此时力学特性主要由细粒组构决定。因此,对于不同颗粒接触状态的砂类土,必然存在着一个阈值细粒含量FCth(threshold fines content)[20]以区分“细粒填充砂粒”与“砂粒悬浮于细粒”2种完全不同的颗粒接触状态。Rahman等[19]基于9种砂类土的力学特性试验结果建立了预测FCth的经验公式:
| $ {\rm{F}}{{\rm{C}}_{{\rm{th}}}} = 0.40 \times \left( {\frac{1}{{1 + \exp (0.50 - 0.13\chi )}} + \frac{1}{\chi }} \right) $ | (6) |
式中:χ=d10s/d50f,d10s为砂粒有效粒径;d50f为细粒平均粒径。
随着FC的增加,细粒会逐渐参与砂类土骨力链的组成,因此,引入等效骨架孔隙比esk*表征细粒含量对砂类土颗粒接触状态的影响,esk*定义为组成砂类土骨架颗粒间的孔隙体积与砂类土骨架颗粒体积之比:
| $ e_{{\rm{sk}}}^* = \frac{{e + (1 - b){\rm{FC}}}}{{1 - (1 - b){\rm{FC}}}} $ | (7) |
式中:b的物理含义为描述细粒参与土体骨架颗粒组成程度,0≤b≤1且满足FC<FCth。Mohammadi等[21]验证了Rahman等[19]的b值经验公式的适用性,并建立了b值的简化经验公式:
| $ b = \left[ {1 - \exp \left( { - \frac{{0.3}}{k}} \right)} \right]{\left( {r \times \frac{{{\rm{FC}}}}{{{\rm{F}}{{\rm{C}}_{{\rm{th}}}}}}} \right)^r} $ | (8) |
现有研究表明,与e相比,esk*可以更合理的描述FC不同的砂类土的颗粒密实状态[22-23],将esk*代替e代入孔隙比函数中,可以获得等效骨架孔隙比函数:
| $ F\left( {e_{{\rm{sk}}}^*} \right) = {\left( {c - e_{{\rm{sk}}}^*} \right)^2}/\left( {1 + e_{{\rm{sk}}}^*} \right) $ | (9) |
随即,可建立基于二元介质模型的修正Hardin模型:
| $ {G_{\max }} = AF\left( {e_{{\rm{sk}}}^*} \right){\left( {\sigma _{3{\rm{c}}}^\prime /{P_{\rm{a}}}} \right)^{0.5}} $ | (10) |
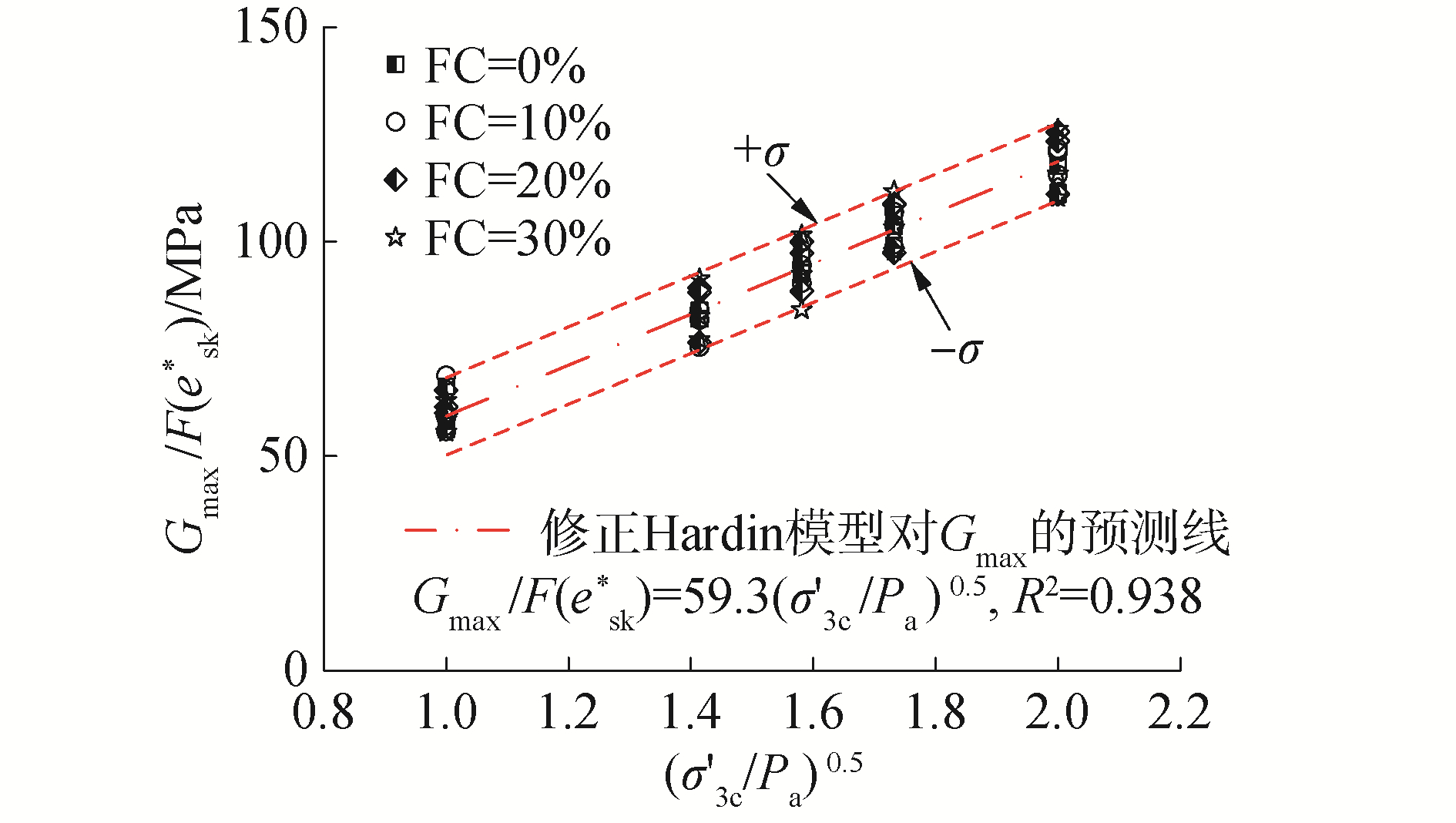
图 6给出了基于二元介质模型的孔隙修正小应变剪切模量Gmax/F(esk*)与归准化有效围压(σ′3c/Pa)0.5的关系曲线,综合考虑级配组成和密实状态的Gmax/F(esk*)随(σ′3c/Pa)0.5的增大呈线性增大,且不同FC、e或σ′3c对且两者的相关性基本没有影响。对于南通砂类土,A=59.3,可决系数R2=0.938。
|
Download:
|
| 图 6 FC不同的砂类土的Gmax/F(esk*)与(σ′3c/Pa)0.5的关系曲线 Fig. 6 The relationship between Gmax/F(esk*) and (σ′3c/Pa)0.5 for sandy soils with different FC | |
为评价上述预测砂类土Gmax预测模型的合理性,将弯曲元试验获得Gmax的试验值与基于二元介质模型的修正Hardin模型预测值进行对比,如图 7所示。对于不同e、σ′3c和FC的砂类土,预测值与试验值基于均匀的分布在45°线两侧,修正Hardin模型的Gmax预测值的误差基本小于10%。这说明修正Hardin模型可以合理预测具有不同固结条件、密实状态及颗粒接触状态的砂类土的Gmax。

|
Download:
|
| 图 7 Gmax的修正Hardin模型预测值与测试值的比较 Fig. 7 Comparison of the measured values and the predicted values using the modified Hardin model for the Gmax | |
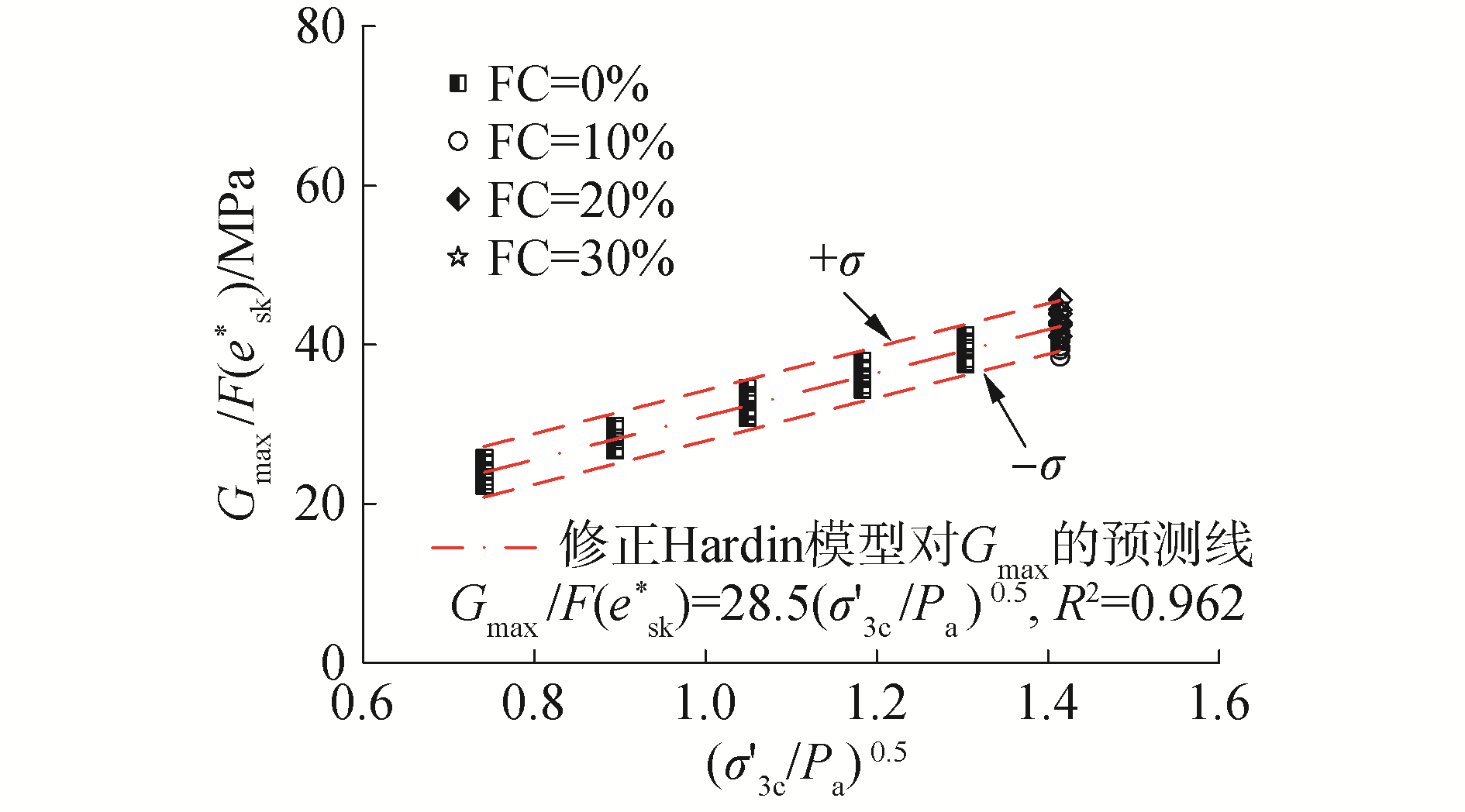
为进一步验证修正Hardin模型对的砂类土的Gmax预测的普适性,对Goudarzy等[24]Gmax试验数据进行重新整理,并基于二元介质模型,利用esk*重新评价了文献所述砂类土的Gmax,如图 8所示。与本试验砂类土类似,文献所述的砂类土的Gmax/F(esk*)也呈现出随(σ′3c/Pa)0.5的增大线性增大现象,且试验数据处于一条窄带内,并与σ′3c、FC、或e的大小基本无关。图 9给出了Goudarzy等[24]的试验值与修正Hardin模型预测值的对比。可以看出,修正Hardin模型仍能合理的预测其Gmax,且误差也基本小于10%。
|
Download:
|
| 图 8 修正Hardin模型对文献[21]所述砂类土Gmax的评价 Fig. 8 Gmax evaluation for sandy soils in the literature [21] using the modified Hardin model | |

|
Download:
|
| 图 9 修正Hardin模型对文献[21]所述砂类土Gmax预测值与测试值的比较 Fig. 9 Comparison of the measured values and the predicted values using the modified Hardin model for the Gmax of sandy soil in the literature [21] | |
1) 当其他条件相同时,Gmax随e的增大而减小;Gmax随σ′3c的增大而增大,且σ′3c对Gmax随e增大而减小的速率没有明显影响,而FC对Gmax随e增大而减小的速率有显著影响。
2) 对于特定FC,Hardin模型对砂类土的Gmax有良好的预测效果,但拟合参数A随FC的增大呈指数函数形式减小,这表明,随FC的增大,砂类土的颗粒接触面积减小,使得归准化Gmax/F(e)逐渐降低。Hardin模型无法统一描述FC对砂类土Gmax的影响。
3) 综合考虑砂1类土固结条件、密实状态及颗粒接触状态的修正Hardin模型能较好的预测FC、σ′3c和e不同的砂类土的Gmax,且其预测误差小于10%。此外,该修正模型可以适用于不同砂类土。
| [1] |
YANG J, YAN X R. Site response to multi-directional earthquake loading:a practical procedure[J]. Soil dynamics and earthquake engineering, 2009, 29(4): 710-721. (  0) 0)
|
| [2] |
CLAYTON C R I. Stiffness at small strain:research and practice[J]. Géotechnique, 2011, 61(1): 5-37. DOI:10.1680/geot.2011.61.1.5 (  0) 0)
|
| [3] |
HARDIN B O, BLACK W L. Sand stiffness under various triaxial stresses[J]. Journal of soil mechanics & foundations division, 1966, 92(SM2): 27-42. (  0) 0)
|
| [4] |
GOUDARZY M, RAHEMI N, RAHMAN M M, et al. Predicting the maximum shear modulus of sands containing nonplastic fines[J]. Journal of geotechnical and geoenvironmental engineering, 2017, 143(9): 06017013. DOI:10.1061/(ASCE)GT.1943-5606.0001760 (  0) 0)
|
| [5] |
范明桥, 藤延京. GB/T 50145-2007, 土的工程分类标准[S].北京: 中国计划出版社, 2008. FAN Mingqiao, TENG Yanjing. GB/T 50145-2007, Standard for engineering classification of soil[S]. Beijing: China Planning Press, 2008. (  0) 0)
|
| [6] |
HSIAO D H, PHAN V T A, HSIEH Y T, et al. Engineering behavior and correlated parameters from obtained results of sand-silt mixtures[J]. Soil dynamics and earthquake engineering, 2015, 77: 137-151. DOI:10.1016/j.soildyn.2015.05.005 (  0) 0)
|
| [7] |
IWASAKI T, TATSUOKA F. Effects of grain size and grading on dynamic shear moduli of sands[J]. Soils and foundations, 1977, 17(3): 19-35. DOI:10.3208/sandf1972.17.3_19 (  0) 0)
|
| [8] |
HUANG Yaotao, HUANG Anbin, KUO Yuchen, et al. A laboratory study on the undrained strength of a silty sand from Central Western Taiwan[J]. Soil dynamics and earthquake engineering, 2004, 24(9/10): 733-743. (  0) 0)
|
| [9] |
OKA L G, DEWOOLKAR M, OLSON S M. Comparing laboratory-based liquefaction resistance of a sand with non-plastic fines with shear wave velocity-based field case histories[J]. Soil dynamics and earthquake engineering, 2018, 113: 162-173. DOI:10.1016/j.soildyn.2018.05.028 (  0) 0)
|
| [10] |
CARRARO J A H, PREZZI M, SALGADO R. Shear strength and stiffness of sands containing plastic or nonplastic fines[J]. Journal of geotechnical and geoenvironmental engineering, 2009, 135(9): 1167-1178. DOI:10.1061/(ASCE)1090-0241(2009)135:9(1167) (  0) 0)
|
| [11] |
SALGADO R, BANDINI P, KARIM A. Shear strength and stiffness of silty sand[J]. Journal of geotechnical and geoenvironmental engineering, 2000, 126(5): 451-462. DOI:10.1061/(ASCE)1090-0241(2000)126:5(451) (  0) 0)
|
| [12] |
CHOO H, BURNS S E. Shear wave velocity of granular mixtures of silica particles as a function of finer fraction, size ratios and void ratios[J]. Granular matter, 2015, 17(5): 567-578. DOI:10.1007/s10035-015-0580-2 (  0) 0)
|
| [13] |
吴琪, 杨文保, 朱雨萌, 等. 砂-粉混合料小应变剪切模量弯曲元试验研究[J]. 东南大学学报(自然科学版), 2018, 48(6): 1059-1067. WU Qi, YANG Wenbao, ZHU Yumeng, et al. Experimental study on small-strain shear modulus of sand-silt mixtures by bender element testing[J]. Journal of Southeast University (natural science edition), 2018, 48(6): 1059-1067. (  0) 0)
|
| [14] |
BRIGNOLI E G M, GOTTI M, STOKOE K H. Measurement of shear waves in laboratory specimens by means of piezoelectric transducers[J]. Geotechnical testing journal, 1996, 19(4): 384-397. DOI:10.1520/GTJ10716J (  0) 0)
|
| [15] |
陈云敏, 周燕国, 黄博. 利用弯曲元测试砂土剪切模量的国际平行试验[J]. 岩土工程学报, 2006, 28(7): 874-880. CHEN Yunmin, ZHOU Yanguo, HUANG Bo. International parallel test on the measurement of shear modulus of sand using bender elements[J]. Chinese journal of geotechnical engineering, 2006, 28(7): 874-880. DOI:10.3321/j.issn:1000-4548.2006.07.013 (  0) 0)
|
| [16] |
南京水利科学研究院. SL 237-1999, 土工试验规程[S].北京: 中国水利水电出版社, 1999. Nanjing Hydraulic Research Institute. SL 237-1999, Specification of soil test[S]. Beijing: China Water Power Press, 1999. (  0) 0)
|
| [17] |
ISHIHARA K. Liquefaction and flow failure during earthquakes[J]. Géotechnique, 1993, 43(3): 351-451. DOI:10.1680/geot.1993.43.3.351 (  0) 0)
|
| [18] |
YANG J, LIU X, RAHMAN M M, et al. Shear wave velocity and stiffness of sand:the role of non-plastic fines[J]. Géotechnique, 2018, 68(10): 931-934. DOI:10.1680/jgeot.16.D.006 (  0) 0)
|
| [19] |
RAHMAN M M, LO S R, GNANENDRAN C T. On equivalent granular void ratio and steady state behaviour of loose sand with fines[J]. Canadian geotechnical journal, 2008, 45(10): 1439-1456. DOI:10.1139/T08-064 (  0) 0)
|
| [20] |
THEVANAYAGAM S, SHENTHAN T, MOHAN S, et al. Undrained fragility of clean sands, silty sands, and sandy silts[J]. Journal of geotechnical and geoenvironmental engineering, 2002, 128(10): 849-859. DOI:10.1061/(ASCE)1090-0241(2002)128:10(849) (  0) 0)
|
| [21] |
MOHAMMADI A, QADIMI A. A simple critical state approach to predicting the cyclic and monotonic response of sands with different fines contents using the equivalent intergranular void ratio[J]. Acta geotechnica, 2015, 10(5): 587-606. DOI:10.1007/s11440-014-0318-z (  0) 0)
|
| [22] |
POLITO C P, MARTIN Ⅱ J R. Effects of nonplastic fines on the liquefaction resistance of sands[J]. Journal of geotechnical and geoenvironmental engineering, 2001, 127(5): 408-415. DOI:10.1061/(ASCE)1090-0241(2001)127:5(408) (  0) 0)
|
| [23] |
吴琪, 陈国兴, 朱雨萌, 等. 基于等效骨架孔隙比指标的饱和砂类土抗液化强度评价[J]. 岩土工程学报, 2018, 40(10): 1912-1922. WU Qi, CHEN Guoxing, ZHU Yumeng, et al. Evaluating liquefaction resistance of saturated sandy soils based on equivalent skeleton void ratio[J]. Chinese journal of geotechnical engineering, 2018, 40(10): 1912-1922. (  0) 0)
|
| [24] |
GOUDARZY M, RAHMAN M, KÖNIG D, et al. Influence of non-plastic fines content on maximum shear modulus of granular materials[J]. Soils and foundations, 2016, 56(6): 973-983. DOI:10.1016/j.sandf.2016.11.003 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


