2. 哈尔滨工程大学 船舶与海洋工程学院, 黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学 理学院, 黑龙江 哈尔滨 150001
2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China;
3. College of Science, Harbin Engineering University, Harbin 150001, China
近年来海上风机发展迅速,截至2016年底世界海上风机装机容量达14 384 MW,其中中国海上风机装机容量1 627 MW,比2015年增长57%,为世界海上风能发展做出了重要贡献[1]。目前商业运行的海上风场多集中在水深50 m内,其桩基础以单桩或三角桩底部固定式为主。受近岸用地日益紧张影响和对海上高品质风资源开发需求的驱动下,浮式风机的研发成为海上风机发展的热点领域,以张力腿平台(TLP)[2]、单筒平台(spar)[3-4]、半潜式平台(semi-submersible)[5-8]为深水平台载体支撑水平轴风机的研究工作已广泛开展。垂直轴风机在叶片加工、制造和整机维护具有成本优势,如用于海上风力发电其发电机可以直接安装在平台载体上,不仅可以提高系统稳性而且易于维护[5],因此垂直轴浮式风力机近年来重新受到了人们的关注。Hang等[6]研究了俯仰运动对Spar型直叶片垂直轴风机的气动载荷影响进行了分析,指出与没有俯仰运动相比,垂直轴风机的俯仰运动可以增大风机的功率输出,同时增大叶片的载荷。王凯等[7]将广泛用于海洋油气开发的工具Simo-Riflex结合双盘面流管模型(DMS)开发了一种全耦合数值模拟工具Simo-Riflex-DMS,用于分析半潜式φ型垂直轴风机空气动力载荷、流体载荷、运动响应和锚链受力,给出了该型风机不同风速下整体运动响应在统计意义下的随方位角的变化。由于DMS气动模型计算大密实度轮机时动量方程易发散是其固有缺陷,因此只适用于小密实度轮机[8];Simo模块采用势流理论计算平台的水动力和力矩忽略了粘性效应,研究表明粘性影响与规则波周期有关[9]。浮式海上风机在气动力、波浪力和锚链力共同耦合作用下的各自由度的运动响应和载荷分析在初选型后的设计阶段至关重要,有关垂直轴海上风机这方面的特性与规律研究较少。为了研究直叶片垂直轴半潜式风机纵荡运动对风机气动载荷的影响,本文采用计算流体力学URANS求解器计算非定常气动载荷和波浪载荷;锚链力由求解悬链线方程得到;整体平台的运动由锚链力、波浪力和气动力结合6自由度求解器迭代给出。风机、平台等刚体的运动采用了动态流体固体交互方法(dynamic fluid body interaction, DFBI)模拟,在风机、平台、波浪与空气交界面采用了重叠网格技术以处理平台大幅运动问题。
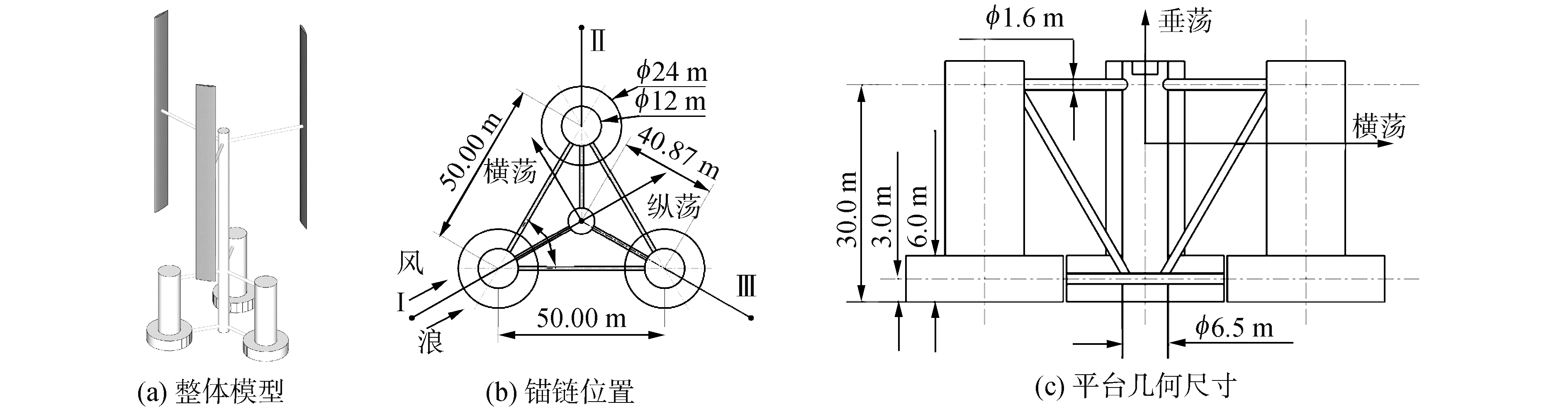
1 系统整体设计 1.1 半潜型浮式基础整个直叶片风机-平台系统模型如图 1所示,其中浮式平台为DeepCwind浮式风机半潜型平台[10],平台由3个平板立柱、1个风机的支撑柱和一系列支撑杆构成,3个立柱底部采用混凝土压载以降低基础重心并提高平台稳性。建模时这些部件均可由圆柱代替,3个立柱底面圆心构成等边三角形,该等边三角形外接圆心与风机支撑柱底部中心在三角形所在平面投影点重合,上圆柱、基圆柱和支撑柱的底面圆半径分别为24、12、6.5 m,横撑截面圆直径为1.6 m,平台的重力中心(CG)在海平面(SWL)下14.4 m。平台的设计参数见表 1。
|
Download:
|
| 图 1 浮式平台几何示意图 Fig. 1 Floating platform geometrical sketch | |
| 表 1 平台主要设计参数 Table 1 Platform gross properties |
锚泊系统主要由标号为Ⅰ、Ⅱ、Ⅲ锚链构成,用于提供平台回复力矩以约束各自由度的运动。如图 1(b)所示,相邻两条锚链线的夹角为120°,锚链Ⅰ与风向和波浪推进方向平行,即平台纵荡正向,垂荡和横荡如图 1(b)、图 1(c)所示,锚链主要属性见表 2。
| 表 2 锚链主要参数 Table 2 Mooring system properties |
美国可再生能源实验室设计的5 MW水平轴风机[11]是目前海上浮式风机研究热点之一,为了匹配单机5 MW额定功率,首先需要对直叶片垂直轴风机几何尺寸进行设计。设垂直轴风机在自由来流速度V下以恒定角速度ω转动,为了分析方便定义如下无量纲参数:
| $ \lambda = \frac{{R\omega }}{V} $ | (1) |
| $ \sigma = \frac{{ZC}}{R} $ | (2) |
| $ {C_P} = \frac{{Q\omega }}{{0.5\rho {V^3}DH}} $ | (3) |
| $ {C_q} = \frac{Q}{{0.5\rho {V^2}{D^2}H}} $ | (4) |
| $ {C_{tx}} = \frac{{{t_x}}}{{0.5\rho {V^2}DH}} $ | (5) |
式中:R为风机半径;λ为叶尖速比;σ为轮机密实度;CP为轮机能量利用率系数;Cq为轮机转矩系数;Q为叶片对轴转矩;tx为单个叶片推力;Ctx为单个叶片推力系数;ρ为当地空气密度。若要达到同样的功率P,要求风轮迎风面积S满足:
| $ {S_{\rm{h}}}{C_{{\rm{p}}, {\rm{h}}}} = {S_{\rm{v}}}{C_{p, {\rm{v}}}} $ | (6) |
式中下标“h”、“v”分别代表水平轴风机和垂直轴风机。假设垂直轴风机的直径和5 MW水平轴风机相同,可以得到叶片高度H,接着估计叶片雷诺数值确定能量利用率较大的密实度范围,根据密实度计算得到弦长C,叶片数Z取3,风机主要属性见表 3。
| 表 3 风机主要参数 Table 3 Wind turbine properties |
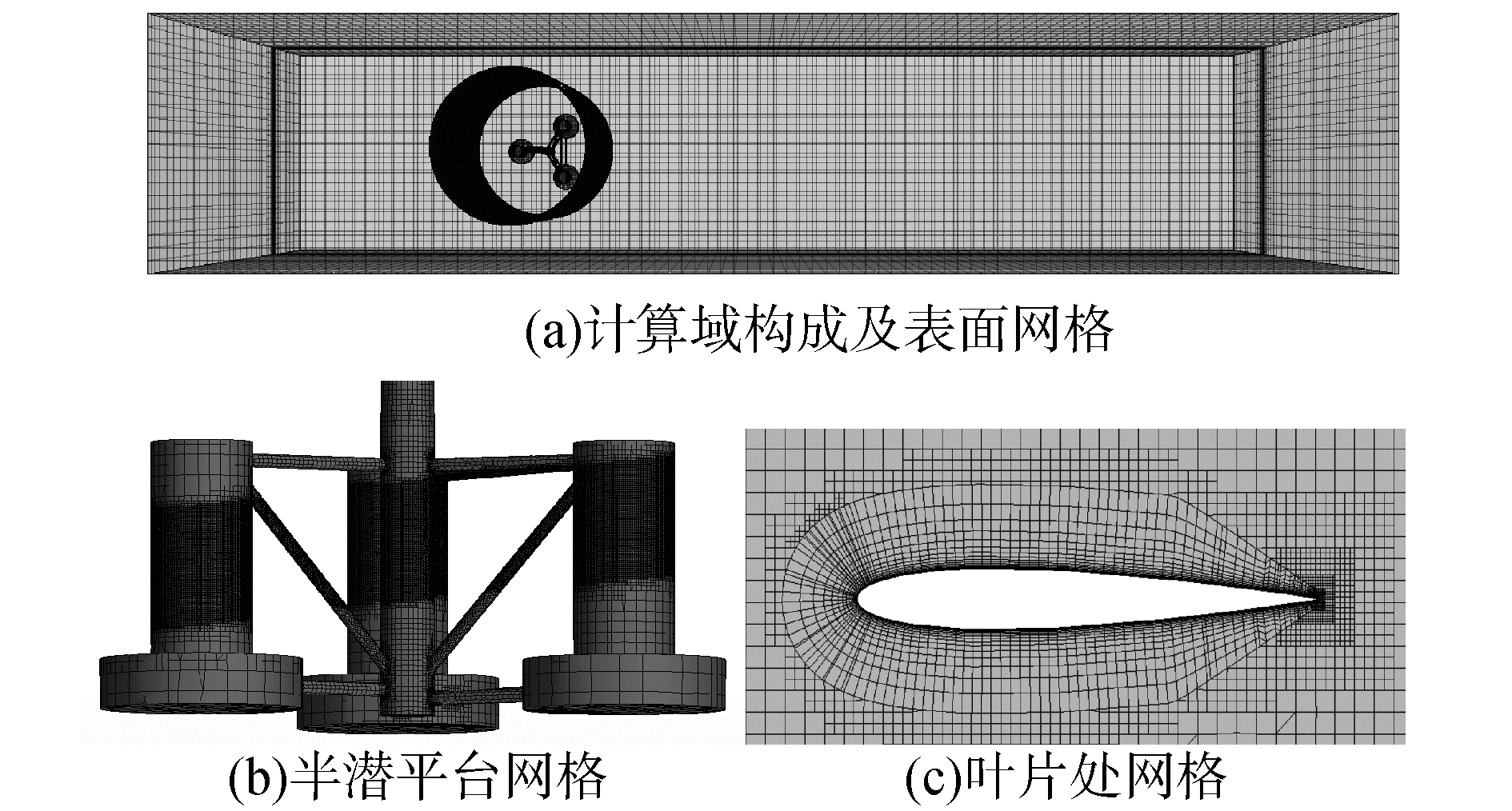
整个计算域尺寸为950 m×250 m×270 m,如图 2(a)所示。计算需要同时模拟风机的旋转、平台的纵荡运动,因此将整个计算域分为旋转域、运动域和静止域。叶片的运动通过叠加域旋转技术实现,即在3个叶片外包一个圆环柱体令其旋转,为旋转域;运动域用于实现风机和平台的运动。计算域除去旋转域和运动域为静止域。
|
Download:
|
| 图 2 计算域和网格划分 Fig. 2 Computational domain and mesh model | |
整个计算域网格划分采用非结构化网格方式,网格模型具体为六面体模型和边界层网格模型,半潜平台和叶片表面网格如图 2(b)、图 2(c)所示。边界层总厚度0.06 m,边界层网格增长率为1.5,一共10层网格,第1层网格厚度为0.8 mm,网格总数量约为600万。
2.3 计算参数设置进口边界设定为速度进口,出口边界采用压力出口边界条件;流体设定为自由滑动墙面;旋转域给定恒定转速。计算模型中选取了欧拉多相流模型[12]、、SST k-ω湍流模型[13]、分离流模型[14]。自由液面生成采用了VOF波模型[15],由于波浪集中在自由液面交界处,该处网格质量直接影响波浪数值模拟精度,因此首先针对2.1节所述计算域研究网格精细度对造波精度的影响。为简化计算,仅考虑沿波浪传播方向的二维截面,水深为1 m,消波区长度为30 m,波浪形式为一阶波,波浪周期为2.85 s,波高Hw为0.04 m。沿波浪传播方向布置若干监测点,图 3给出了3种不同网格划分方式对波浪生成的影响,具体网格划分方式见表 4,综合考虑计算精度与时间,后续模拟取网格2的划分方式。图 4给出了距离速度入口处25 m的造波时历曲线与解析值的比较,当时间大于10 s时,计算趋于稳定。

|
Download:
|
| 图 3 网格划分方式对数值造波的影响 Fig. 3 Effect of mesh type on numerical wave generation | |
| 表 4 自由表面网格划分方式 Table 4 Details of free surface mesh generation |

|
Download:
|
| 图 4 数值造波时历曲线与解析值对比 Fig. 4 Comparison of wave generation with analytical result | |
求解器采用了隐式非定常方法,对流项采用了二阶迎风格式离散,时间步长为0.02 s。
锚链在计算时简化为悬链线,平台的运动由锚链力、VOF波浪力和气动力结合6自由度求解器(6-DOF)得到。
3 算例与分析参照Jonkman计算水平轴半潜式浮式风机的工况[11],额定风速V=11.2 m/s,波浪周期T=7.5 s,波高3.96 m。取风机转速ω为0.711、1.156、1.267 rad/s,对应工作速比λ为4、6.5、7.12,分别代表低速比、中等速比、高速比工况。
3.1 纵荡运动响应规律图 5给出在这3种速比下平台纵荡响应(surge RAO)随时间的变化规律,可以看出平台纵荡频率随风机速比增大而增大,纵荡幅值随速比增大而减小,但纵荡均值随速比增大而增大,说明相对于低速比运动,高速比运动时平台在一个较大的位置高频小幅振荡。

|
Download:
|
| 图 5 不同速比下平台纵荡时历曲线 Fig. 5 Surge RAO of semi- submerged platform on the different TSRs | |
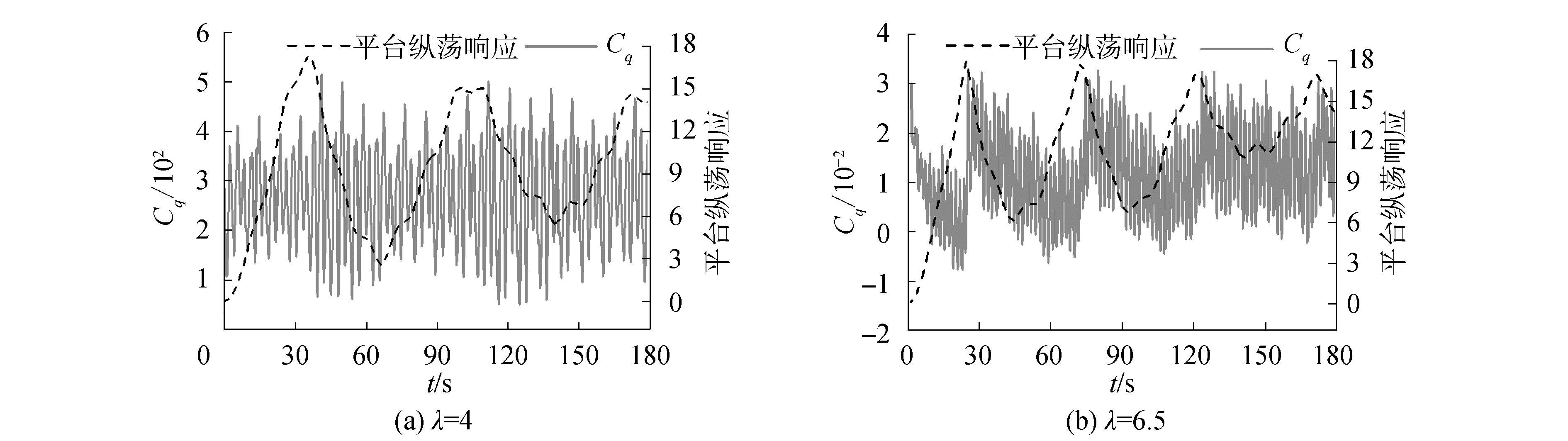
图 6给出了速比分别为4和6.5下风机瞬时转矩系数Cq和纵荡运动随时间的变化曲线。可见风机瞬时转矩的峰值出现在平台受锚链力作用做回复运动时刻附近,如图 6(b)中t为25、73、122 s时。平台运动速度和自由来流速度的叠加构成叶片的迎流速度,当平台纵荡运动与风向、浪向同向时,叶片迎流速度小于自由来流速度;反之,叶片迎流速度大于自由来流速度,由式(3)知转矩正比于风速的立方,因此纵荡沿浪向运动的风机平均转矩(Q+)小于回复运动的转矩均值(Q-)。图 7给出了速比4、6.5、7.12下这两者的比较,可以看出纵荡对转矩的影响随着速比增大而增大:在速比4时Q-比Q+提升1.28%,当速比7.12时Q-是Q+的2.76倍。
|
Download:
|
| 图 6 不同速比下转矩与纵荡时历曲线 Fig. 6 Time history of torque and surge motion on the different TSRs | |

|
Download:
|
| 图 7 沿风浪向运动与回复运动转矩比较 Fig. 7 Comparison of torque along and in opposite wind and wave motion | |
图 8给出了相同速比下浮式平台纵荡运动时风机的能量利用率Cp_s和平台静止只有风机旋转时的能量利用率Cp的比较。与陆地风机相比,本算例中海上浮式半潜垂直轴风机在一个纵荡周期内的平均能量利用率在中低速比下(λ=4, 5)有所提高,在高速比时(λ=6.5, 7.2)降低,能量利用率峰值提高约10%。

|
Download:
|
| 图 8 纵荡运动能量利用率比较 Fig. 8 Power coefficient comparison between wind turbine in steady and surge motion | |
因为受纵荡运动影响,风机上游迎风面入流速度动态变化,入流速度为定常风速与平台纵荡运动速度的叠加,改变了叶片的气动攻角最终影响轮机的能量利用率。纵荡周期内每时刻的时变叠加速度都对风机能量利用率有贡献,由图 5平台纵荡运动时历曲线看出,低速比下(λ=4)平台往复运动平均速度 l和高速比(λ=7.12)的平台往复平均速度uh相同,约为0.3 m/s,可以计算得到,低速比下叶轮瞬时速比区间为[3.16, 4.11],高速比下叶轮瞬时速比区间为[6.8, 7.48], 低速比下瞬时速比变化范围Δλl=0.95,高速比下瞬时速比变化范围Δλh=0.685,由于能量利用率曲线在中低速比范围更加饱满,曲率也较大,因此Δλl对应的能量利用率收益大于Δλh的能量利用率收益,这可以简单解释平台纵荡对风机能量利用率的影响规律。
3.4 纵荡运动对叶片推力系数的影响单个叶片推力系数Ctx在速比4和6.5下的变化规律如图 9所示,可以看出推力系数的变化规律与转矩同频变化,在高速比时幅值较大且波动激烈,这对于叶片载荷是不利的,因此在设计时应当选取合适的锚链减少纵荡运动的幅度。

|
Download:
|
| 图 9 不同速比叶片推力系数变化 Fig. 9 Variation of trust force coefficient at two TSRs | |
1) 当垂直轴风机、半潜式浮式平台和系泊系统在风和波浪双激励作用时,平台纵荡的频率和均值随着叶片工作速比的增大而增大;
2) 叶轮转矩系数受纵荡运动影响在高速比下较为明显,总的说来当平台运动为纵荡正向时叶轮转矩减少,平台做回复运动时转矩增大,转矩的峰值在平台回复运动时刻附近,这个规律对于分析叶片疲劳较为重要;
3) 一个纵荡周期内的同型海上垂直轴直叶片风机的能量利用率在小速比下高于同型陆地风机,在大速比下低于同型陆地风机且峰值略高,这对于统计全年发电量有重要意义;
4) 单个叶片的推力系数变化规律和叶轮转矩系数一致。
接下来将进一步研究系统在不同波浪和风参数组合下进行多自由度耦合运动时的运动响应和载荷变化规律,得到简化的解析载荷表达。
| [1] |
Lauha Fried. Global wind statistics 2016[EB/OL]. Belgium: Global Wind Energy Council.[2017-12-11]. http://www.gwec.net/wp-content/uploads/vip/GWEC_PRstats2016_EN_WEB.pdf.
(  0) 0)
|
| [2] |
BACHYNSKI E E, MOAN T. Design considerations for tension leg platform wind turbines[J]. Marine structures, 2012, 29(1): 89-114. DOI:10.1016/j.marstruc.2012.09.001 (  0) 0)
|
| [3] |
尚景宏, 赵玉娜, 张亮, 等. Spar型海上浮式风力机系统运动耦合计算方法[J]. 哈尔滨工程大学学报, 2016, 37(9): 1163-1171. SHANG Jinghong, ZHAO Yuna, ZHANH Liang, et al. Coupled method for predicting motions of Spar-type offshore floating wind turbine systems[J]. Journal of Harbin Engineering University, 2016, 37(9): 1163-1171. (  0) 0)
|
| [4] |
焦忠虎, 肖纪升. 海上风力发电基础形式及关键技术分析[J]. 中国高新技术企业, 2016(1): 145-146. JIAO Zhonghu, XIAO Jisheng. Analysis on the floating foundation type and key technology of offshore wind turbine[J]. China high-tech enterprises, 2016(1): 145-146. (  0) 0)
|
| [5] |
吴海涛, 张亮, 马勇, 等. 半潜式海上浮式风力机平台随机响应特性分析[J]. 华中科技大学学报(自然科学版), 2014, 42(5): 111-115, 121. WU Haitao, ZHANG Liang, MA Yong, et al. Stochastic response characteristics analysis of semisubmersible platform for floating offshore wind turbine[J]. Journal of Huazhong University of Science and Technology (natural science edition), 2014, 42(5): 111-115, 121. (  0) 0)
|
| [6] |
刘中柏, 唐友刚, 王涵, 等. 半潜型风电浮式基础运动特性试验研究[J]. 哈尔滨工程大学学报, 2015, 36(1): 51-56. LIU Zhongbai, TANG Yougang, WANG Han, et al. Experimental study of motion behaviors for semi-submersible floating foundation of wind power[J]. Journal of Harbin Engineering University, 2015, 36(1): 51-56. (  0) 0)
|
| [7] |
TARN T T, KIM D H. The coupled dynamic response computation for a semi-submersible platform of floating offshore wind turbine[J]. Journal of wind engineering and industrial aerodynamics, 2015, 147: 104-119. DOI:10.1016/j.jweia.2015.09.016 (  0) 0)
|
| [8] |
TARN T T, KIM D H. Fully coupled aero-hydrodynamic analysis of a semi-submersible FOWT using a dynamic fluid body interaction approach[J]. Renewable energy, 2016, 92: 244-261. DOI:10.1016/j.renene.2016.02.021 (  0) 0)
|
| [9] |
BORG M, SHIRES A, COLLU M. Offshore floating vertical axis wind turbines, dynamics modelling state of the art. PartⅠ:aerodynamics[J]. Renewable and sustainable energy reviews, 2014, 39: 1214-1225. DOI:10.1016/j.rser.2014.07.096 (  0) 0)
|
| [10] |
LEI Hang, ZHOU Dai, LU Jiabao, et al. The impact of pitch motion of a platform on the aerodynamic performance of a floating vertical axis wind turbine[J]. Energy, 2017, 119: 369-383. DOI:10.1016/j.energy.2016.12.086 (  0) 0)
|
| [11] |
WANG Kai, MOAN T, HANSEN M O L. Stochastic dynamic response analysis of a floating vertical-axis wind turbine with a semi-submersible floater[J]. Wind energy, 2016, 19(10): 1853-1870. DOI:10.1002/we.v19.10 (  0) 0)
|
| [12] |
姜劲.竖轴叶轮的流体动力分析与性能优化方法的改进与应用[D].哈尔滨: 哈尔滨工程大学, 2012: 37-39. JIANG Jin. Fluid dynamic analysis and optimization method for vertical-axis turbine: improvement and application[D]. Harbin: Harbin Engineering University, 2012: 37-39. http://cdmd.cnki.com.cn/Article/CDMD-10217-1014134017.htm (  0) 0)
|
| [13] |
KVITTEM M I, BACHYNSKI E E, MOAN T. Effects of hydrodynamic modelling in fully coupled simulations of a semi-submersible wind turbine[J]. Energy procedia, 2012, 24: 351-362. DOI:10.1016/j.egypro.2012.06.118 (  0) 0)
|
| [14] |
COULLING A J, GOUPEE A J, ROBERTSON A N, et al. Validation of a FAST semi-submersible floating wind turbine numerical model with deepcwind test data[J]. Journal of renewable and sustainable energy, 2013, 5(2): 023116. DOI:10.1063/1.4796197 (  0) 0)
|
| [15] |
JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development. NREL/TP-500-38060[R]. Golden, Colorado, US: National Renewable Energy Laboratory, 2009.
(  0) 0)
|
| [16] |
张珅榕, 蔡卫军, 闵景新. 基于欧拉多相流模型的空泡数值模拟[J]. 船海工程, 2015, 44(1): 103-106, 111. ZHANG Shenrong, CAI Weijun, MIN Jingxin. Numerical simulation of cavity based on Eulerian multiphase model[J]. Ship & ocean engineering, 2015, 44(1): 103-106, 111. DOI:10.3963/j.issn.1671-7953.2015.01.027 (  0) 0)
|
| [17] |
胡国玉, 孙文磊, 曹莉. 风力机三维旋转叶片非定常气动特性数值模拟研究[J]. 可再生能源, 2016, 34(6): 867-871. HU Guoyu, SUN Wenlei, GAO Li. Numerical simulation of unsteady aerodynamic characteristics of wind turbine rotational blade[J]. Renewable energy resources, 2016, 34(6): 867-871. (  0) 0)
|
| [18] |
ELGAMMI M, SANT T. Integrating a new flow separation model and the effects of the vortex shedding for improved dynamic stall predictions using the Beddoes-Leishman method[J]. Wind energy, 2016, 19(11): 2089-2112. DOI:10.1002/we.v19.11 (  0) 0)
|
| [19] |
高慧, 张照刚, 熊高涵. 粘性流体数值波浪水池研究[J]. 舰船科学技术, 2017, 39(11): 44-47. GAO Hui, ZHANG Zhaogang, XIONG Gaohan. Study of numerical wave tank for viscous fluid[J]. Ship science and technology, 2017, 39(11): 44-47. DOI:10.3404/j.issn.1672-7649.2017.11.009 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


