2. 海军大连舰艇学院 海洋测绘工程军队重点实验室, 辽宁 大连 116018
2. Key Laboratory of Hydrographic Surveying and Mapping of PLA, Dalian Naval Academy, Dalian 116018, China
电子海图是海上活动的基础,航线的自动生成是电子海图应用的重要内容[1]。最优航线是在保证舰船航行安全的前提条件下,使航线达到某种指标上的最佳[2]。为了使舰船能够安全、快速地到达目的地,最短距离航线设计一直受到国内外学者的广泛关注。Chang等[3]提出了基于改进迷宫的最短距离航线生成算法。王德春等[4]应用A*算法,进行了最短路径的研究。文献[5-8]分别针对不同应用需求特点,改进Dijkstra算法,对最短距离航线问题展开了研究。Rafal[9]通过分析转向和避碰容差条件,进行了航线优化选取研究。但上述方法所得出的航线都是针对已知航路点库的最优航线,实际上并不是任何海区事先都建有非常合理的航路点库,同时也并非只有这些航路点之间可以航行[10]。近年来,不少学者开始探索基于矢量电子海图的航线自动生成。张立华等[1]建立了自动、高效绕行碍航区的机制和准则,提出了矢量电子海图平台下的计算机智能设计航线方法。汪柱等[10]针对航线自动生成中存在的贪婪性的弱点,提出了基于航路二叉树的航线自动生成方法。曹鸿博等[2]对航路二叉树方法进行了改进,采用碍航区路径的递归搜索、绕行优化以及动态求解等策略,提高了航线自动生成的质量和效率。王涛等[11-12]针对航路二叉树方法未考虑舰船转向限制、航道宽度的问题,分别提出了考虑转向限制和顾及航道宽度的最短距离航线自动生成方法。但上述方法仅能对单幅海图数据来构建碍航区,并在此基础上自动规划最短距离航线。由于海图尺寸大小的限制,一幅海图往往很难覆盖舰船航行经过的整个海区,通常需要多幅海图才能满足[13]。此时,现有方法为了能够事先完成航线的自动规划,只能使用一幅比例尺较小的海图,以确保海图所表达的地理范围能够覆盖航行区域。显然,海图比例尺越小,其数据表达真实海洋地理信息的精度就越低,由此规划出的航线的安全可靠性也会随之降低。针对当前基于电子海图数据的航路二叉树方法求解最短距离航线时仅能考虑单幅海图的不足,本文提出一种基于多幅海图碍航区融合的舰船航线自动生成改进方法。通过定量分析海图的精度和现势性,融合多幅海图碍航区,设计增量更新机制,为航线自动生成提供更为丰富的海洋地理信息数据。同时考虑融合碍航区数据量对航线自动生成效率的影响,以航路二叉树算法为基础,采用航路窗口、改进R树索引等方式提升航线自动生成的效率,并通过实验验证了所提方法的可行性。
1 二叉树最短距离航线自动生成改进方法 1.1 现有方法的理论基础 1.1.1 现有方法的基本思想在现有航线自动生成研究中,基于单一海图的航路二叉树算法是其中较有代表性的一种。其基本思想是:首先,利用海图数据,从海图数据的定义出发,通过分析与建模,构建威胁舰船航行安全的碍航区;然后,根据所构建的碍航区,设计自动规避碍航区的算法,生成可行的航线。
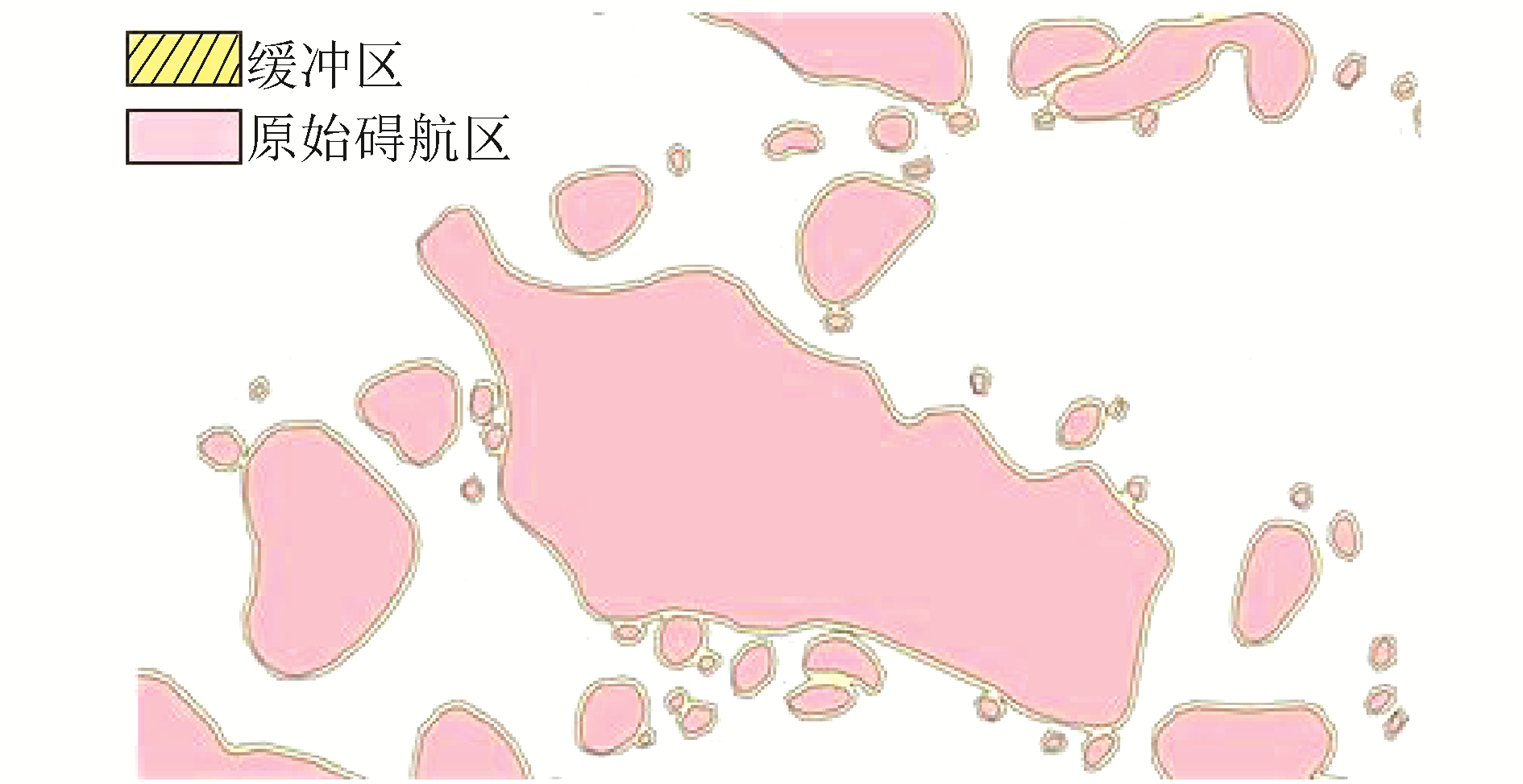
1.1.2 单幅海图的碍航区表达为了自动生成安全、可靠的航线,学者大多采用碍航区这一概念来描述舰船无法通过的海域,以区分可航渡区域的界限。综合前人研究,本文所述碍航区集合主要包括浅水碍航区、人工碍航区和点状碍航区。分别对应影响船只航行安全的浅水区域(如大陆、岛礁、干出滩等)、人工区域(如禁航区、沉船区、渔业养殖区等)和点状碍航物(如暗礁、干出礁、沉船等)[14-16]。本文中碍航区主要按如下方式表达:首先,对于浅水碍航区,主要针对水深及海底地形、岸线岛礁等相关地理信息共同构建三角网,依据舰船吃水深度追踪安全等深线,完成安全水域的提取[17];其次,对于人工碍航区,则依据海图在数据定义时人为划定的特殊区域进行提取和归类。最后,对于点状碍航区,则以碍航物点状几何体为中心,扩展成为具有一定航行安全半径的圆形区域。海上航行环境复杂多变,舰船的回旋半径、定位系统精度等因素都会对航行安全造成一定的影响[16]。为保证自动生成出的航线在实际运用中的安全性,对碍航区范围进行一定的扩充,建立碍航区的缓冲区,扩充入原始碍航区中。某海域的碍航区表达如图 1所示。
|
Download:
|
| 图 1 某海域碍航区表达 Fig. 1 The expression of obstacle areas in one area | |
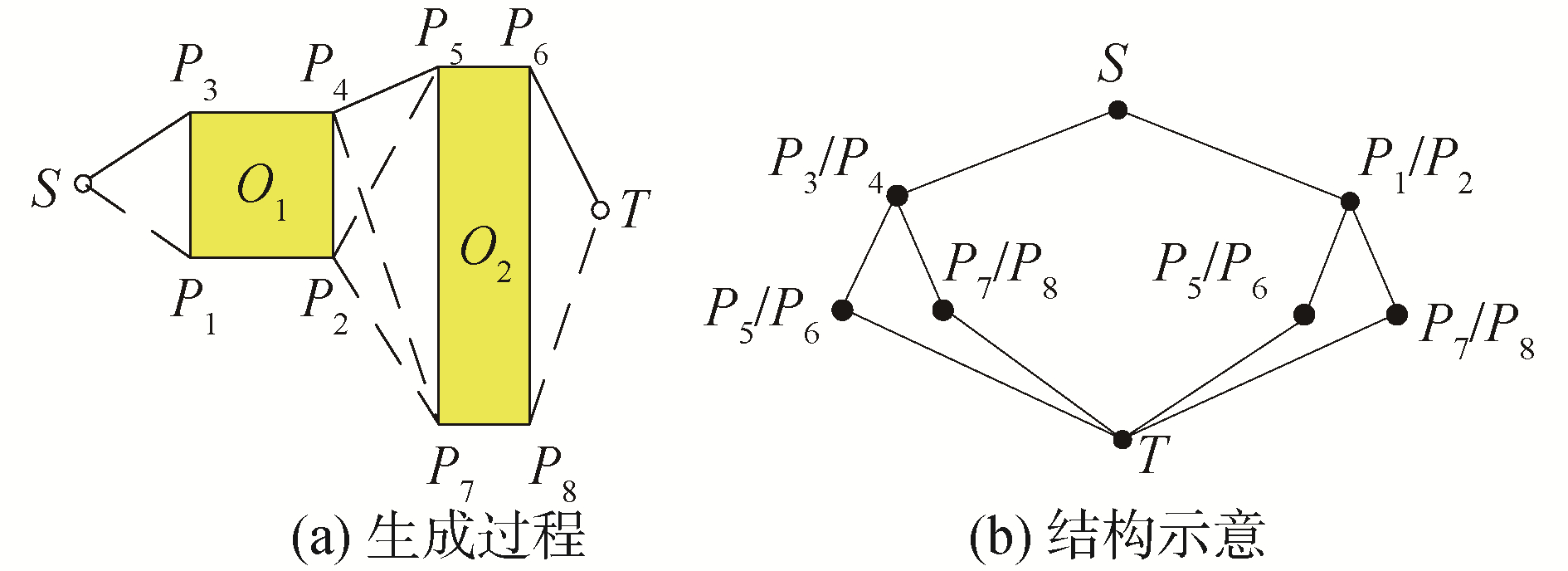
最短距离航线的自动生成,实际上就是找出一条能够避开所有碍航区,从起点至终点的最短路径。如图 2(a)所示,起点为S,终点为T,碍航区为O1、O2,航路二叉树算法的基本原理是:把起点作为当前测试点,搜索当前测试点的最近绕行碍航区,根据航路绕行碍航区二分性的特点,确定左、右子结点并建立航路子二叉树;以子结点作为当前测试点,重复上述步骤得到各航路子二叉树,循环计算直至所有子结点与终点T之间没有碍航区为止。然后,将各航路子二叉树有序组织起来,建立可行的航路二叉树(如图 2(b)所示)。最后,在所有可行的航路二叉树中提取出最短距离航线。
|
Download:
|
| 图 2 航路二叉树生成过程及二叉树结构示意 Fig. 2 The process of route binary tree generation and structure of route binary tree | |
现有的航路二叉树算法实现了单幅海图上任意2点的最短距离航线规划。然而,实际海上航行过程中往往要经过多个海区,使用多幅海图,现有技术无法实现。为实现基于多幅海图的航线自动生成,采用以下思路:
1) 多幅海图碍航区数据融合。通过对比同区域不同精度的单幅海图数据,构建多幅海图碍航区数据融合模型,对不同海图的碍航区进行融合;
2) 碍航区数据库建立及增量更新。考虑海图小改正及更新等因素的影响,建立碍航区空间数据库并设计增量更新机制;
3) 效率优化。考虑融合后碍航区数据量激增对算法效率的影响,通过构建航路窗口和改进R树,对碍航区数据进行快速提取、查询,提高航路二叉树算法的运行效率。
1.3 多幅海图碍航区数据融合海图的载负量总是有限的,大比例尺海图中的数据,不可能不加任何化简和概括,直接转换到小比例尺海图中[18]。必须要对其进行制图综合,牺牲数据精度以调和海图图幅与复杂现实之间的矛盾。这就造成不同海图在同一海域内的碍航区表达往往存在较大差别。
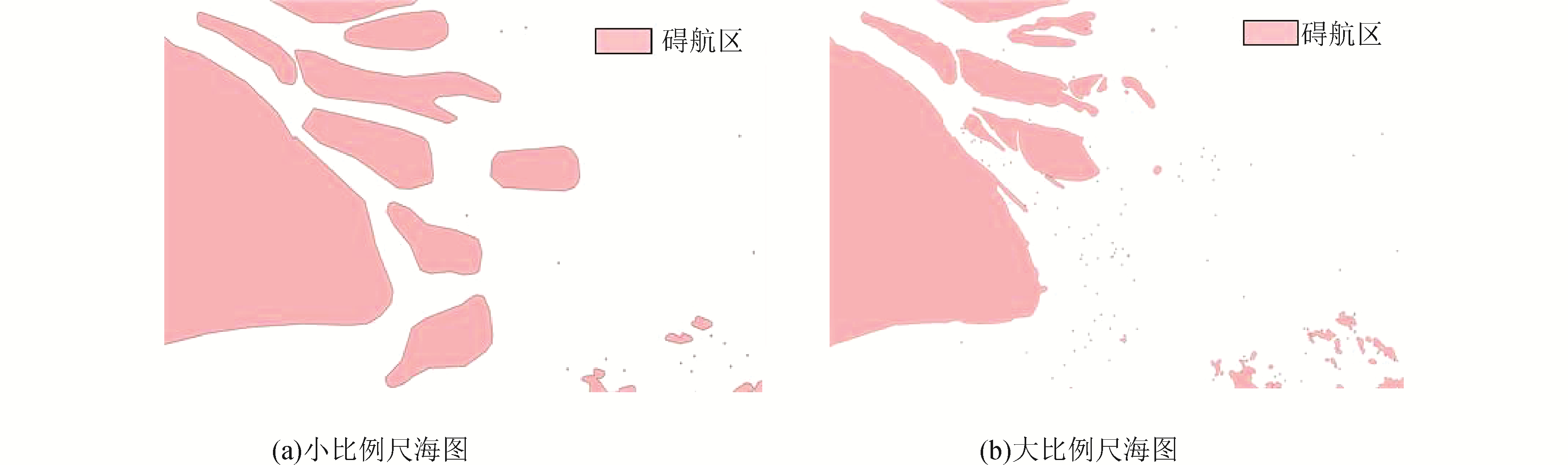
基于图 1碍航区表达方式,可以实现对单幅海图的碍航区构建。如图 3所示。可以看出,2幅海图在碍航区的表示精细程度上存在差异显著。通常情况下,大比例尺海图覆盖地理区域小,但精度较高;小比例尺海图覆盖地理区域大,但精度低。当前航线自动生成方法只能基于单幅海图碍航区进行计算。当航线跨出图幅时,只能采用覆盖航线范围的小比例尺海图所构建的碍航区,由此规划出的航线的准确程度和可靠性也会随之降低。
|
Download:
|
| 图 3 不同海图在同一海域内的碍航区表达结果 Fig. 3 The expression of different chart′s obstacle areas in the same area | |
为解决这一问题,实现2幅及以上海图的碍航区数据融合,使之成为兼顾精度和范围的碍航区数据,本文设计了海图碍航区的数据融合机制。具体思路如下:
1) 为定量分析海图的精度,定义海图精度指数μ,对海图的精细化程度进行评估。海图精度指数μ在数值上同海图比例尺呈正相关关系。比例尺越大,精度越高:
| $ \left\{ {\begin{array}{*{20}{l}} {{S_{({\rm{A}})}} = {F_{\left( {{\varepsilon _1}, {\mu _1}} \right)}} = \left\{ {{a_0}, {a_1}, {a_2}, \cdots , {a_m}} \right\}}\\ {{S_{({\rm{B}})}} = {F_{\left( {{\varepsilon _2}, {\mu _2}} \right)}} = \left\{ {{b_0}, {b_1}, {b_2}, \cdots , {b_n}} \right\}} \end{array}} \right. $ | (1) |
式中:S(A)、S(B)分别为A、B海图所表示的海域的碍航区集合;F(ε, μ)为碍航区的表达函数,其参数ε、μ分别代表海图图幅区域和海图精度指数;ai、bj分别代表A、B海图中的第i、j个碍航区地理实体。
2) 海图图幅相交区域是指在2幅或多幅海图区域内,有2幅及以上海图同时包含某海域,形成的海域重叠,需要对其进行提取以便下一步进行融合:
| $ \left\{ \begin{array}{l} {\varepsilon _0} = {\varepsilon _1} \cap {\varepsilon _2}\\ {S_{\left( {{{\rm{A}}_0}} \right)}} = {F_{\left( {{\varepsilon _0}, {\mu _1}} \right)}} = {S_{({\rm{A}})}} \cap {\varepsilon _0} = \left\{ {{a_i}, {a_{i + 1}} \cdots {a_{i + k}}} \right\}\\ {S_{\left( {{{\rm{B}}_0}} \right)}} = {F_{\left( {{\varepsilon _0}, {\mu _2}} \right)}} = {S_{({\rm{B}})}} \cap {\varepsilon _0} = \left\{ {{a_j}, {a_{j + 1}}, \cdots {a_{j + h}}} \right\} \end{array} \right. $ | (2) |
式中:S(A0)、S(B0)分别为A、B海图重叠表示的海域的碍航区集合;ε0代表 2幅海图图幅的交叠海域;ax(x∈Z, i≤x≤i+k)、by(y∈Z, j≤y≤j+h)分别代表A、B海图中的第x/y个碍航区地理实体,均在A、B海图的交叠海域内。若存在碍航区与交叠海域相交的情况,则在碍航区表达过程中对其进行裁剪。
3) 获取到交叠海域后,计算非交叠海域的碍航区集合,在航线生成过程中,这部分海域只有某一精度的碍航物数据,不能将其随意舍去:
| $ \left\{ \begin{array}{l} {S_{\left( {{{\rm{A}}^\prime }} \right)}} = {F_{\left( {{\varepsilon _1}, {\mu _1}, {t_1}} \right)}} - {F_{\left( {{\varepsilon _0}, {\mu _1}, {t_1}} \right)}} = \\ \;\;\;\;\;\;\;\;\left\{ {{a_0}, {a_1} \cdots {a_{i - 1}}, {a_{i + k + 1}} \cdots {a_m}} \right\}\\ {S_{\left( {{{\rm{B}}^\prime }} \right)}} = {F_{\left( {{\varepsilon _2}, {\mu _2}, {t_2}} \right)}} - {F_{\left( {{\varepsilon _0}, {\mu _2}, {t_2}} \right)}} = \\ \;\;\;\;\;\;\;\;\;\left\{ {{b_0}, {b_1} \cdots {b_{j - 1}}, {b_{j + h + 1}} \cdots {b_n}} \right\} \end{array} \right. $ | (3) |
式中:S(A′)、S(B′)分别为A、B海图非重叠表示的海域的碍航区集合。
4) 依精度对交叠海域内的碍航区集合进行替换,值得注意的是,2幅或多幅海图之间的交叠区域可能不存在,这时需要将其都纳入碍航物集合范围内:
| $ {S_{({\rm{C}})}} = \left\{ \begin{array}{l} {S_{\left( {{{\rm{A}}^\prime }} \right)}} + {S_{\left( {{{\rm{B}}^\prime }} \right)}} + {S_{\left( {{{\rm{A}}_0}} \right)}} = {F_{\left( {{\varepsilon _1}, {\mu _1}} \right)}} + {F_{\left( {{\varepsilon _2}, {\mu _2}} \right)}} - \\ \;\;\;\;\;\;\;\;\;\;\;{F_{\left( {{\varepsilon _0}, {\mu _2}} \right)}}, {\varepsilon _0} \ne 0, {\mu _1} \ge {\mu _2}\\ {S_{\left( {{{\rm{A}}^\prime }} \right)}} + {S_{\left( {{{\rm{B}}^\prime }} \right)}} + {S_{\left( {{{\rm{B}}_0}} \right)}} = {F_{\left( {{\varepsilon _1}, {\mu _1}} \right)}} - {F_{\left( {{s_0}, {\mu _1}} \right)}} + \\ {F_{\left( {{s_2}, {\mu _2}} \right)}}, {\varepsilon _0} \ne 0, {\mu _2} > {\mu _1}\\ {S_{\left( {{{\rm{A}}^\prime }} \right)}} + {S_{\left( {{{\rm{B}}^\prime }} \right)}} = {F_{\left( {{\varepsilon _1}, {\mu _1}} \right)}} + {F_{\left( {{\varepsilon _2}, {\mu _2}} \right)}}, {\varepsilon _0} = 0 \end{array} \right. $ | (4) |
式中S(C)为A、B海图融合生成的碍航区集合。
将上述思想进一步扩展至多幅海图,从而实现多幅海图的碍航区空间数据融合。
1.4 碍航区数据库建立及增量更新海图是基于测绘资料编制而成的,反应的是测量时的海域客观实际。而海域状态变化频繁,海图表示的地理信息会逐渐同实际产生差异。为保证现势性,海图需要定期进行更新。采用文件存储碍航区数据的传统方式占用空间大、效率低,且数据更新难以实现。为此,本文建立碍航区空间数据库,并设计碍航区增量更新机制,实现对碍航区空间数据的高效组织与管理,满足数据增量更新的需求。
为了定量分析海图的现势性,将式(1)进一步扩充,引入海图现势性的影响:
| $ S = F(\varepsilon , \mu , t) $ | (5) |
式中:t为海图现势性指数。海图现势性指数在数值上同海图出版时间及版本号呈正相关关系。出版时间越晚、版本号越大,现势性指数越高。
考虑采用顾及现势性的原则来对碍航区数据进行增量更新,其流程可如图 4所示,设计思路如下:

|
Download:
|
| 图 4 碍航区数据融合更新流程 Fig. 4 The flow-diagram of obstacle data fusion and update | |
1) 在现有海图数据的基础上,将海图数据存入空间数据库中。
2) 按图幅对空间数据库中的海图进行读取,依据1.1.2节中所述方式对其进行单幅海图的碍航区表达,同时剔除数据库中与航行无关的要素以减少数据冗余。
3) 依据1.3节中所述方式进行多幅海图的碍航区融合,获取海图图幅范围,提取叠幅海域的碍航区数据,依精度对其进行替换,保留高精度数据,将低精度数据从数据库中删除。形成顾及精度和范围的海图数据。
4) 若存在新的海图数据,则定量分析其版本号、出版时间等现势性要素,判断其是否优于现有海图数据。对更新海图完成表达后重复步骤2)、3),对空间数据库中的碍航区数据进行更新,保证数据的现势性。
1.5 航路二叉树算法的效率优化文献[2, 10-12]采用的航路二叉树生成算法,本质上是对空间数据进行的欧式几何拓扑计算。但在航路二叉树的生成过程中,需要多次遍历当前所有的碍航区,逐个进行计算。随着多幅海图碍航区数据的融合和异步更新,碍航区数据量越发增大,航线生成的效率受到严重影响。为此,提出面向航路窗口的碍航区快速提取和基于改进R树索引的碍航区快速查询方法,提高算法效率。
1.5.1 面向航路窗口的碍航区快速提取本文在生成航线时所使用的碍航区数据,均基于1.3、1.4节中所述多幅海图碍航区数据融合、更新而来。其具有数据量大、拓扑关系复杂、表示范围广等多种特点。假如能将调用航路二叉树生成算法时数据的搜索范围限定在一定的区域内,就能减少计算的数据量,从而提升航线生成的效率[19]。
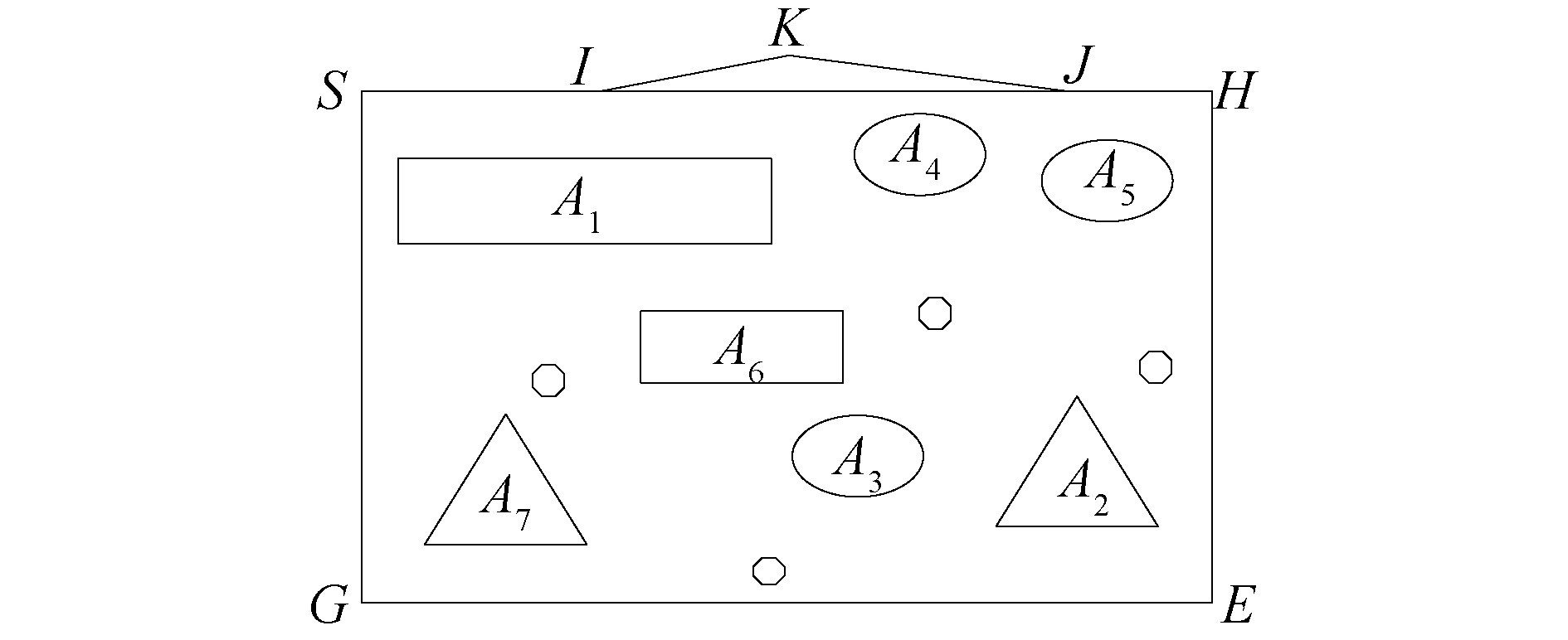
本文对航路窗口及所含碍航区给出如下定义:建立航路起点、终点之间的连线,将该线段看作空间中某一矩形的对角线,由该对角线所确定的唯一矩形称之为航路窗口;若存在与航路窗口拓扑相交的碍航区,则将航路窗口进行扩展,将此碍航区放入航路窗口中。如图 5所示,起点为S,终点为E,则航路窗口为矩形SHEG,航路窗口下的碍航区为A1、A2、…、A7。航路窗口具有如下性质:通过航路二叉树生成的航线,必定在航路窗口下的碍航区之间。可以用反证法得出证明结论:以图 5为例,设起终点分别为点S、点E,矩形SHGE为以SE为对角线确定出的航路窗口,若生成的航线经过航路窗口外一点K,且与航路窗口交与点I、J。根据几何性质易得IK+KJ>IJ,而IJ是可通航路径,这与最短航线经过点K互相矛盾,假设不成立,性质得证。在复杂海区内,利用航路窗口可以减少纳入计算的碍航区数量,提升算法效率。
|
Download:
|
| 图 5 航路窗口及其所含碍航区 Fig. 5 Route window and its obstacle areas | |
R树索引是目前应用非常广泛的一种空间数据索引,实践证明相对于其他空间索引,R树索引对于大量空间数据有更加出色的表现[20]。常规的R树索引由根节点、中间节点和叶节点组成,中间节点代表空间数据中的一个矩形,该矩形是其所有叶节点的最小外接矩形(MBR),并不是实际世界中的地理对象,叶节点则是具有现实意义的地理实体。
但是,基于R树索引的空间查询效率同所构建的MBR交叠面积呈现正相关关系,MBR的交叠情况则随着数据的更新和插入而越发严重。航线生成过程中,所进行的空间查询操作具有极大的线性性质,MBR的交叠面积越大,进行空间查询时所返回的子节点就越多,需要进行查找的范围也越广。如图 6所示,在进行空间查询时与线SE相交的MBR包括a、b、c、d,依照查询算法,需要遍历这4棵子树中的所有子节点。然而当中a、b、d子树都不包含最终需要的真实地物所在的叶节点,极大影响空间查询的时间开销。为解决MBR的交叠问题,本文尝试通过分裂子节点的方式,提高MBR中的地物密度,对常规R树进行改进。

|
Download:
|
| 图 6 传统R树中的空间查询示意 Fig. 6 The diagram of spatial query in traditional R-tree | |
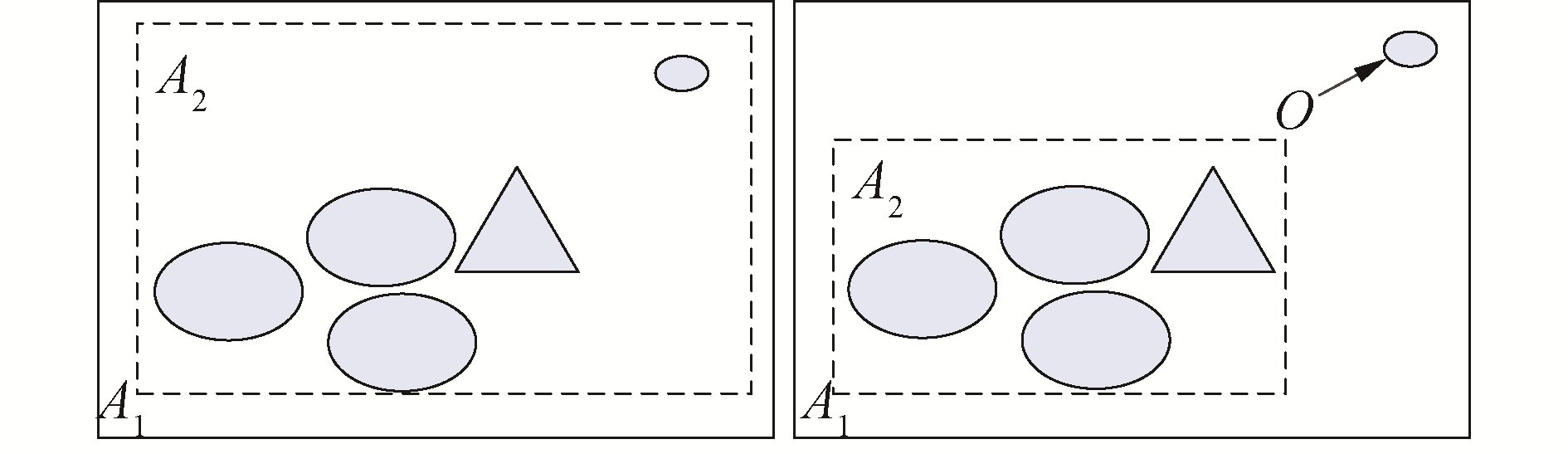
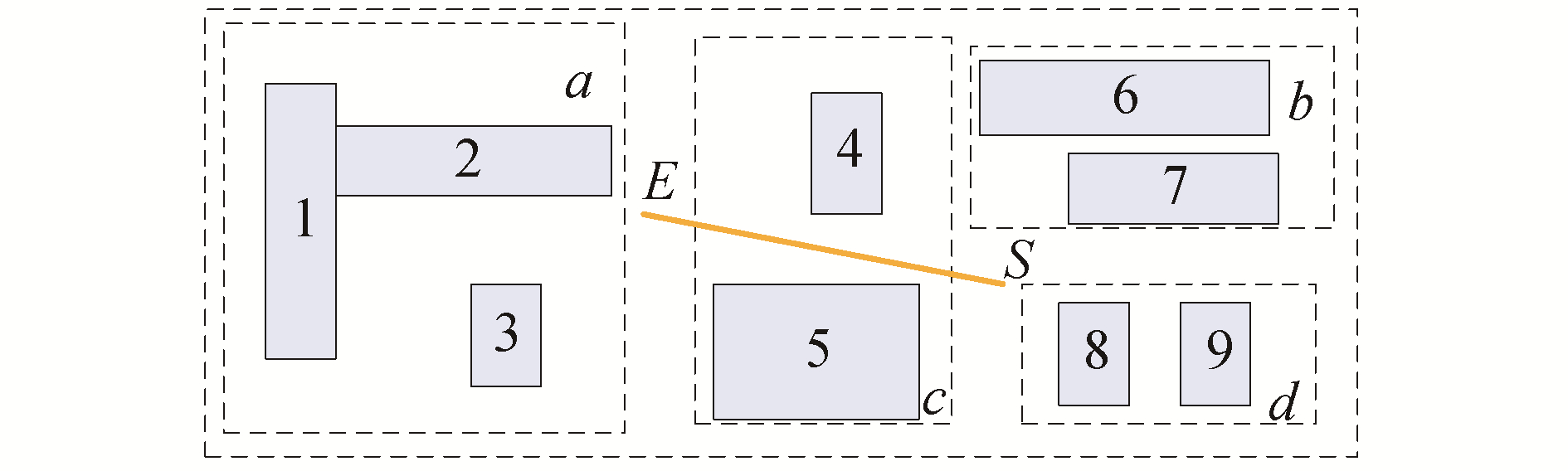
在节点分裂的过程中,主要思想是将子节点中的可划分边界对象存储到其父节点中。图 7为进行节点分裂前后的模型示意图。节点分裂前,想要查询对象O时,需要查询A1和A2才能得到结果,而节点分裂后只查询节点A1,减少了MBR的面积,提高了空间查询的效率。当然,实际运用中不可能一味地分裂节点,这样形成的R树和遍历数据没有差别。结合海图数据的特点,规定分裂后的新节点所存储的真实地物不能少于M/4,这里M指节点的最大空间(即MBR)。以图 6所示区域为例,进行空间分裂后,空间查询示意图如图 8所示,只经过矩形c,大大减少了搜索的子树个数,提升了查询效率。
|
Download:
|
| 图 7 节点分裂模型 Fig. 7 Node splitting model | |
|
Download:
|
| 图 8 改进后的R树空间查询示意 Fig. 8 The diagram of space query in improved R tree | |
为验证现有的航路二叉树算法与本文所提算法在碍航区表达上的差异,选取(31.47°N, 121.24°E)~ (30.26°, 123.35°E)范围作为试验区域,采用上述2种方法来构建试验区域内的碍航区。使用海图的基本信息如表 1所示。
| 表 1 碍航区测试电子海图 Table 1 Electronic charts used to make obstacle areas |
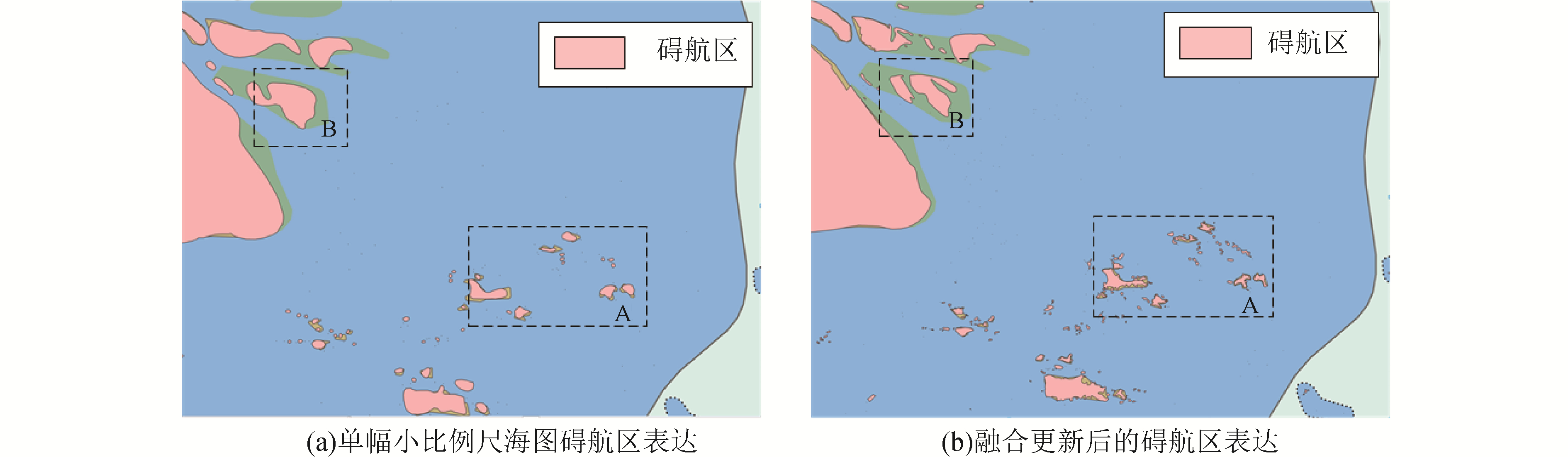
试验结果如图 9所示。其中,现有的航路二叉树算法由于找不到一幅合适的大比例尺海图能够覆盖试验区域,因此只能利用小比例尺海图(图号C1100103,比例尺1:2 300 000)来构建碍航区,如图 9(a)所示;本文所提算法首先通过对所有海图的碍航区数据进行融合,然后根据试验区域航路窗口提取相应的碍航区数据,生成结果如图 9(b)所示。
|
Download:
|
| 图 9 碍航区生成结果 Fig. 9 Result of obstacle areas expression | |
如图 9所示,现有的航路二叉树方法所使用的小比例尺海图由于图幅载负量限制,对图中各要素进行了大量的制图综合,构建出的碍航区也就较为粗略。以虚线框A中所示的海区为例,小比例海图中一些事实上存在的碍航区没有在图中表达,这就会威胁到舰船的航行安全;海域左侧的虚线框B中,则存在着经过制图综合后,碍航区堵塞航道的情况,生成出的航线不再是事实上的最短航线。
与现有的航路二叉树方法相比,本文所提算法在碍航区的构建与表达上更为精细,如图 9(b)所示。这是由于本文所提算法通过对不同比例尺海图所建碍航区进行数据融合,既能准确表达实际碍航区(如图 9(b)中区域A所示),又能合理显示出可以航行的航道(如图 9(b)中区域B所示)。
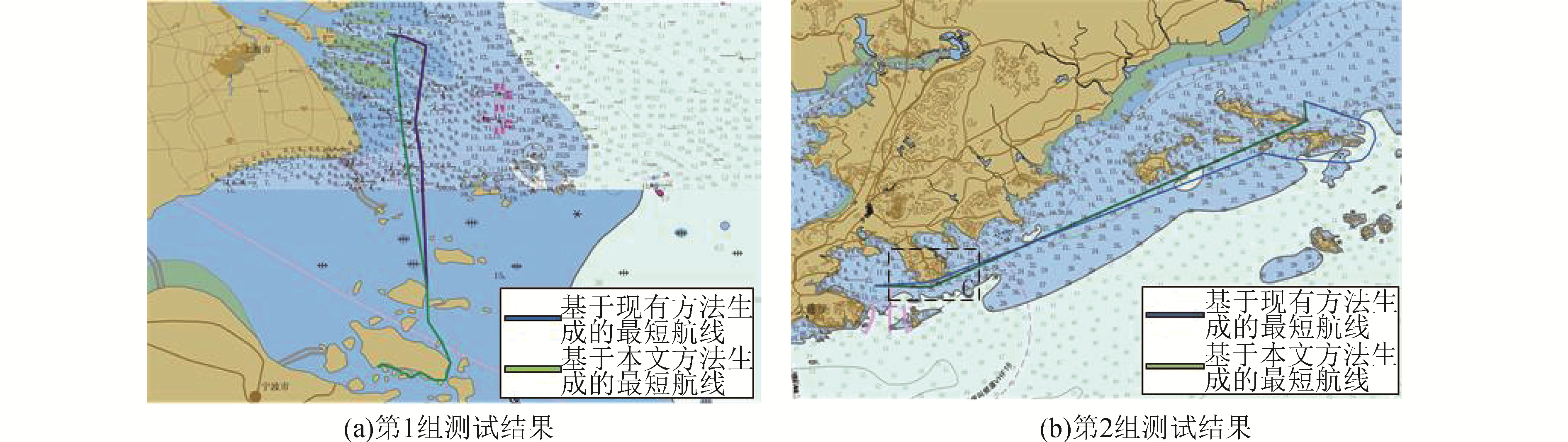
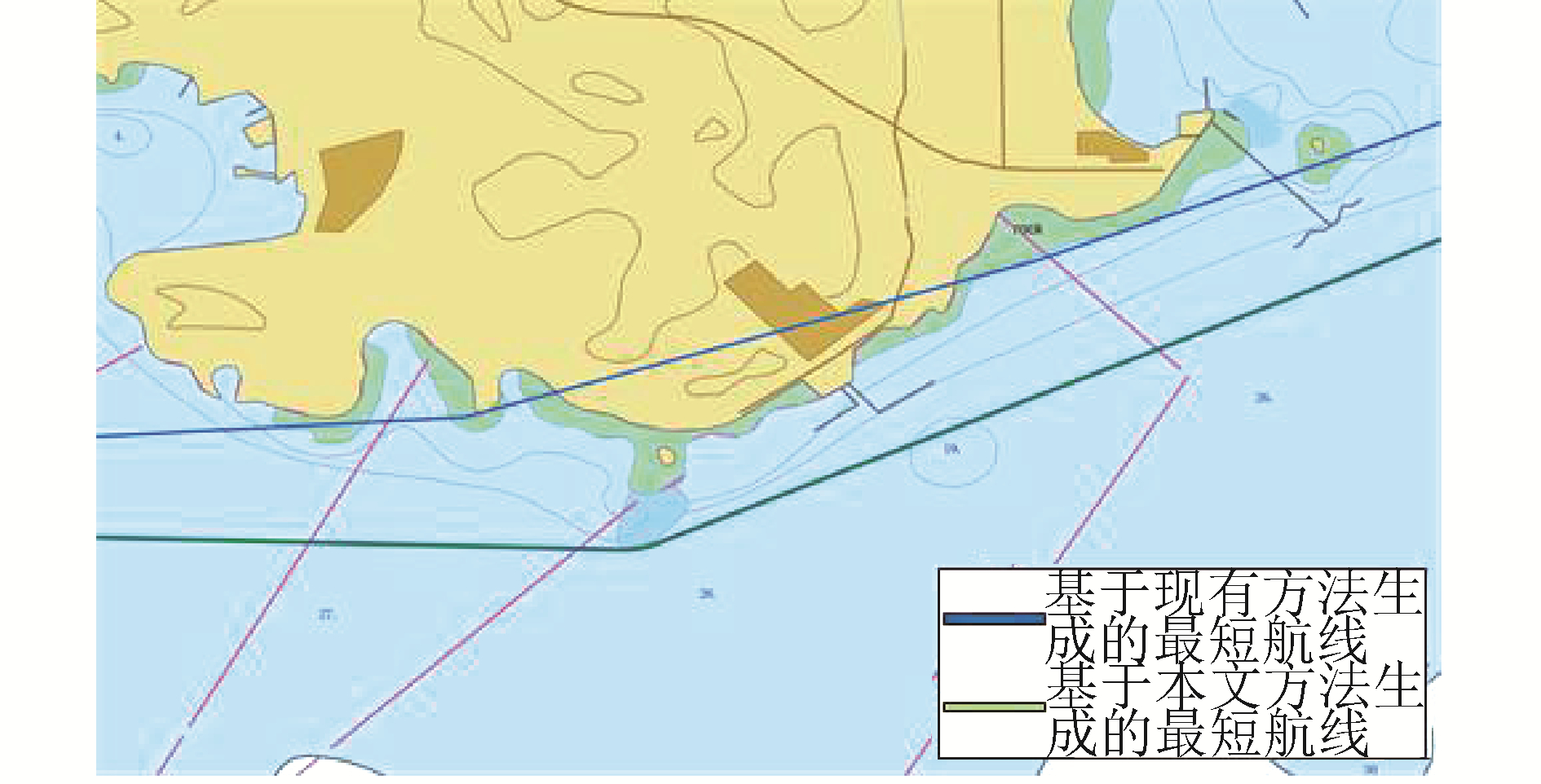
2.2 航线生成质量比对分析进一步比对分析现有的航路二叉树方法与本文所提方法在航线生成中的差异。选取表 2所示的2组电子海图数据,分别采用上述2种方法来规划航线,试验结果如图 10所示。为便于比较,对图 10(b)的局部区域C进行放大显示,如图 11所示。
| 表 2 航线生成测试电子海图 Table 2 Electronic charts used for route making |
|
Download:
|
| 图 10 航线自动生成结果 Fig. 10 Results of route making | |
|
Download:
|
| 图 11 某海域航线对比 Fig. 11 The comparison of routes in one area | |
从图 10的实验结果来看,与现有的航路二叉树算法相比,本文所提方法生成航线的距离明显短于现有的航路二叉树算法生成的航线。这是由于本文所提方法是在表达更为精细的碍航区基础上规划最短距离航线,能够更为充分地利用可航渡空间。
通过对图 10(b)中区域C进行放大显示的图 11中可以进一步看出,现有航路二叉树方法由于采用小比例尺海图来生成航线,其航线在大比例尺海图上显示时出现了穿越碍航区的情况。这在实际应用中将对航行安全带来极大隐患。
综合实验结果,与现有的航路二叉树算法相比,本文所提方法生成的最短距离航线无论是在距离上还是安全程度上都有了极大的提高,其可行性及可靠性情况如表 3所示。
| 表 3 不同方法可行性及可靠性比对 Table 3 Feasibility and reliability comparison of different methods |
进一步比较现有的航路二叉树算法与本文所提方法在航线生成效率上的差异。选取图 10中所示的2组最短距离航线,在测试PC上进行比对实验,配置为Intel core i5-3 230 M 2.60 GHz处理器、8 GB内存、1 TB硬盘、AMD 7 400 M/1 GB显卡/显存、Windows7 X64操作系统,其效率测试结果如表 4所示。
| 表 4 不同方法算法效率情况 Table 4 The comparison of different methods in efficiency |
从表 4可以看出,与经典的航路二叉树算法相比,本文所提方法明显缩短了航线生成的时间。这是由于在航路窗口对碍航区数据进行有效筛选的基础上,改进R树索引实现了碍航区数据的高效空间查询,效率得到提升。
3 结论1) 与现有基于单幅海图的碍航区表达方式相比,本文所提通过分析不同海图的精度、现势性差异,对多幅海图的碍航区进行数据融合、所构建的碍航区对真实地理环境表达的准确程度高。
2) 与现有航路二叉树方法的应用局限于单幅海图相比,本文所提方法能够实现跨海图图幅的航线自动生成论在航程上还是可靠程度上,都得到长足提升。在航程和可靠性上都有了明显的提高。
3) 同现有航路自动生成方法相比,在大量碍航区数据下,本文所提航路窗口、改进R树方式对航路自动生成效率进行了极大改进,航线生成时间大大缩短。
本文碍航区数据融合只是考虑了精度和现势性2个基本要素,对于更多复杂情况(如不同国家发行的海图)下的碍航区数据融合,还有待于进一步分析。对于更长距离、海量碍航区数据下的航线自动生成,如何提高效率,这些都有待于今后进一步研究。
| [1] |
张立华, 朱庆, 刘雁春, 等. 电子海图平台下的航线自动设计方法[J]. 大连海事大学学报, 2007, 33(3): 109-112. ZHANG Lihua, ZHU Qing, LIU Yanchun, et al. A method for automatic routing based on ECDIS[J]. Journal of Dalian Maritime University, 2007, 33(3): 109-112. DOI:10.3969/j.issn.1006-7736.2007.03.024 (  0) 0)
|
| [2] |
曹鸿博, 张立华, 贾帅东, 等. 电子海图最短距离航线自动生成的改进方法[J]. 武汉大学学报(信息科学版), 2011, 36(9): 1107-1110. CAO Hongbo, ZHANG Lihua, JIA Shuaidong, et al. An Improved method for automatically building shortest route based on electronic chart[J]. Geomatics and Information Science of Wuhan University, 2011, 36(9): 1107-1110. (  0) 0)
|
| [3] |
CHANG K Y, JAN G E, PARBERRY I. A method for searching optimal routes with collision avoidance on raster charts[J]. The journal of navigation, 2004, 56(3): 371-384. (  0) 0)
|
| [4] |
王德春, 陈利敏, 张孝芳. 基于A*算法的舰船最佳航线选择[J]. 青岛大学学报(自然科学版), 2005, 18(4): 10-13. WANG Dechun, CHEN Limin, ZHANG Xiaofang. Selecting ship's optimum route using A* algorithm[J]. Journal of Qingdao University (natural science edition), 2005, 18(4): 10-13. DOI:10.3969/j.issn.1006-1037.2005.04.003 (  0) 0)
|
| [5] |
叶清, 郁振伟. 改进最短路径算法在最佳航线选择中的应用[J]. 中国航海, 2003(2): 15-17. YE Qing, YU Zhengwei. The improved shortcut algorithm and it's application in selecting ship's optimum route[J]. Navigation of China, 2003(2): 15-17. DOI:10.3969/j.issn.1000-4653.2003.02.005 (  0) 0)
|
| [6] |
王科.基于电子海图的航线设计研究[D].大连: 海军大连舰艇学院, 2004. WANG Ke. A study for designing navigation route based on ECDIS[D]. Dalian: Dalian naval Academic, 2004. (  0) 0)
|
| [7] |
ANEL A M. Network shortest path application for optimum track ship routing[D]. California: Naval Postgraduate School, 2005.
(  0) 0)
|
| [8] |
李源惠, 潘明阳, 吴娴. 基于动态网格模型的航线自动生成算法[J]. 交通运输工程学报, 2007, 7(3): 34-39. LI Yuanhui, PAN Mingyang, WU Xian. Automatic creating algorithm of route based on dynamic grid model[J]. Journal of traffic and transportation engineering, 2007, 7(3): 34-39. DOI:10.3321/j.issn:1671-1637.2007.03.008 (  0) 0)
|
| [9] |
SZLAPCZYNSKI R. A new method of ship routing on raster grids, with turn penalties and collision avoidance[J]. The journal of navigation, 2006, 59(1): 27-42. (  0) 0)
|
| [10] |
汪柱, 李树军, 张立华, 等. 基于航路二叉树的航线自动生成方法[J]. 武汉大学学报(信息科学版), 2010, 35(4): 407-410. WANG Zhu, LI Shujun, ZHANG Lihua, et al. A method for automatic routing based on route binary tree[J]. Geomatics and Information Science of Wuhan University, 2010, 35(4): 407-410. (  0) 0)
|
| [11] |
王涛, 张立华, 彭认灿, 等. 顾及航道宽度的最短距离航线自动生成方法[J]. 海洋测绘, 2016, 36(3): 29-31, 36. WANG Tao, ZHANG Lihua, PENG Rencan, et al. A method for automatically generating the shortest distance route based on electronic navigational chart considering channel width[J]. Hydrographic surveying and charting, 2016, 36(3): 29-31, 36. DOI:10.3969/j.issn.1671-3044.2016.03.007 (  0) 0)
|
| [12] |
王涛, 张立华, 彭认灿, 等. 考虑转向限制的电子海图最短距离航线自动生成方法[J]. 哈尔滨工程大学学报, 2016, 37(7): 923-929. WANG Tao, ZHANG Lihua, PENG Rencan, et al. Automatic generation of the shortest route of an electronic navigational chart considering turning restrictions[J]. Journal of Harbin Engineering University, 2016, 37(7): 923-929. (  0) 0)
|
| [13] |
张莉, 金一丞, 汪柱, 等. 电子海图的航线多尺度生成方法[J]. 测绘科学, 2011, 36(5): 197-199. ZHANG Li, JIN Yichen, WANG Zhu, et al. A method for multi-scale routing based on ECDIS[J]. Science of surveying and mapping, 2011, 36(5): 197-199. (  0) 0)
|
| [14] |
张莉, 王义涛. 一种基于海图水深的碍航区自动提取方法[J]. 海洋技术, 2010, 29(3): 69-72. ZHANG Li, WANG Yitao. A method for automatic acquisition of obstacle areas based on the depth in a chart[J]. Ocean technology, 2010, 29(3): 69-72. DOI:10.3969/j.issn.1003-2029.2010.03.016 (  0) 0)
|
| [15] |
张浩, 栾俊, 纪宏宇, 等. 一种碍航区自动提取的方法[J]. 海洋测绘, 2015, 35(6): 55-57. ZHANG Hao, LUAN Jun, JI Hongyu, et al. A method for constructing obstacle areas[J]. Hydrographic surveying and charting, 2015, 35(6): 55-57. DOI:10.3969/j.issn.1671-3044.2015.06.014 (  0) 0)
|
| [16] |
张立华, 朱庆, 张安民, 等. 一种智能的最短航线构建方法[J]. 测绘学报, 2008, 37(1): 114-120. ZHANG Lihua, ZHU Qing, ZHANG Anmin, et al. An intelligent method for the shortest routing[J]. Acta geodaetica et cartographica sinica, 2008, 37(1): 114-120. DOI:10.3321/j.issn:1001-1595.2008.01.020 (  0) 0)
|
| [17] |
贾帅东, 张立华, 彭认灿, 等. 确保水深模型航海安全性的深度保证率控制方法[J]. 交通运输工程学报, 2015, 15(5): 101-109. JIA Shuaidong, ZHANG Lihua, PENG Rencan, et al. Control method of probability of adequate depth ensuring navigation safety of depth model[J]. Journal of traffic and transportation engineering, 2015, 15(5): 101-109. DOI:10.3969/j.issn.1671-1637.2015.05.013 (  0) 0)
|
| [18] |
陈惠荣.海图设计自动化关键技术研究[D].大连海事大学, 2011. CHEN Huirong. Research on key techniques of chart design automation[D]. Dalian: Dalian Maritime University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10151-1012261155.htm (  0) 0)
|
| [19] |
汤青慧.基于电子海图的航线规划方法研究[D].中国海洋大学, 2011. TANG Qinghui. Research on route planning method based on electronic chart[D]. Qingdao: Ocean University of China, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10423-1011231344.htm (  0) 0)
|
| [20] |
邓红艳, 武芳, 翟仁健, 等. 一种用于空间数据多尺度表达的R树索引结构[J]. 计算机学报, 2009, 32(1): 177-184. DENG Hongyan, WU Fang, ZHAI Renjian, et al. R-tree index structure for multi-scale representation of spatial data[J]. Chinese journal of computers, 2009, 32(1): 177-184. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


