2. 天津中德应用技术大学 智能制造学院, 天津 300350
2. Intelligent Manufacturing College, Tianjin Sino-German University of Applied Science, Tianjin 300350, China
动力翼伞系统又称伞翼无人机,是一种由动力装置与冲压式翼伞相结合的无人飞行器,具有飞行安全可靠、操作简单易行和性价比高等特点[1-4]。动力翼伞系统是在传统翼伞的基础上发展而来,它不仅继承了传统翼伞的优势,还弥补了由于高度不足造成的空投误差,并且更多地应用到航拍无人机等民用领域,具有更加广阔的发展前景[5]。
近年,国内外学者对动力翼伞系统进行了研究。Watanabe等[6]建立了伞翼无人机系统的八自由度(degree of freedom,DOF)非线性动力学模型。Zhu等[7]提出了一种基于模糊逻辑的翼伞导航控制算法,在翼伞空投系统上取得了精确效果。Hattis等[8]将PID和低通滤波器相结合,设计了翼伞系统的轨迹跟踪控制器。Slegers等[9]将模型预测控制应用于伞翼无人机的轨迹跟踪控制,控制方法利用简化的动力翼伞模型进行求解。Liang等[10]提出基于灵敏度分析的优化算法,该方法提高了翼伞系统的落地精度并降低了控制能耗。谢亚荣[11]设计了翼伞姿态控制系统,引入模糊干扰观测器对翼伞飞行过程中所受的复合干扰进行逼近和控制。Grignion等[12]设计了鲁棒干扰力矩观测器,实现了对直流电机负载扰动的精确估计。通过以上研究发现,由于柔性材料结构,动力翼伞系统对风场干扰及其敏感,风场的不可预测性和多变性加大了控制难度。同时,这些研究大都忽略了舵机负载扰动的存在,将控制器输出的单侧下偏量直接应用到偏航角度变化上。实际上,舵机负载转矩是必然存在的时变不确定扰动输入,且左右舵机负载是不平衡的,负载转矩的特性直接影响了运动系统控制策略的选择,系统的动态性能和稳定性。因此,实现复杂扰动环境下的轨迹跟踪问题,是动力翼伞系统建模和控制中的重要研究方向。
自抗扰控制(active disturbance rejection control, ADRC)是由韩京清提出的一种面向工程应用的控制算法[13-14],它不依赖具体的数学模型,可以将系统建模误差和非线性不确定扰动通过扩张状态观测器(extended state observer,ESO)进行估计和补偿,适合动力翼伞这类柔性系统[15]。本文的自抗扰控制器分为横纵向2个通道,横向通道采用串级自抗扰控制器,外环回路完成系统飞行方向的跟踪,内环回路实现单侧下偏量的精确控制,由舵机调节操控绳长度。纵向通道中,将交叉耦合和系统内外部扰动看作总扰动量,利用线性ESO实时观测系统状态,由动力装置来提供推力。
本文从实际环境出发,充分考虑风场和舵机负载的影响,将直流电机模型引入动力翼伞系统的8-DOF数学模型,优化系统建模。设计了动力翼伞系统的轨迹跟踪控制器。通过半实物仿真平台,完成了动力翼伞系统飞行仿真实验,验证了改进模型和控制策略的可行性和有效性。
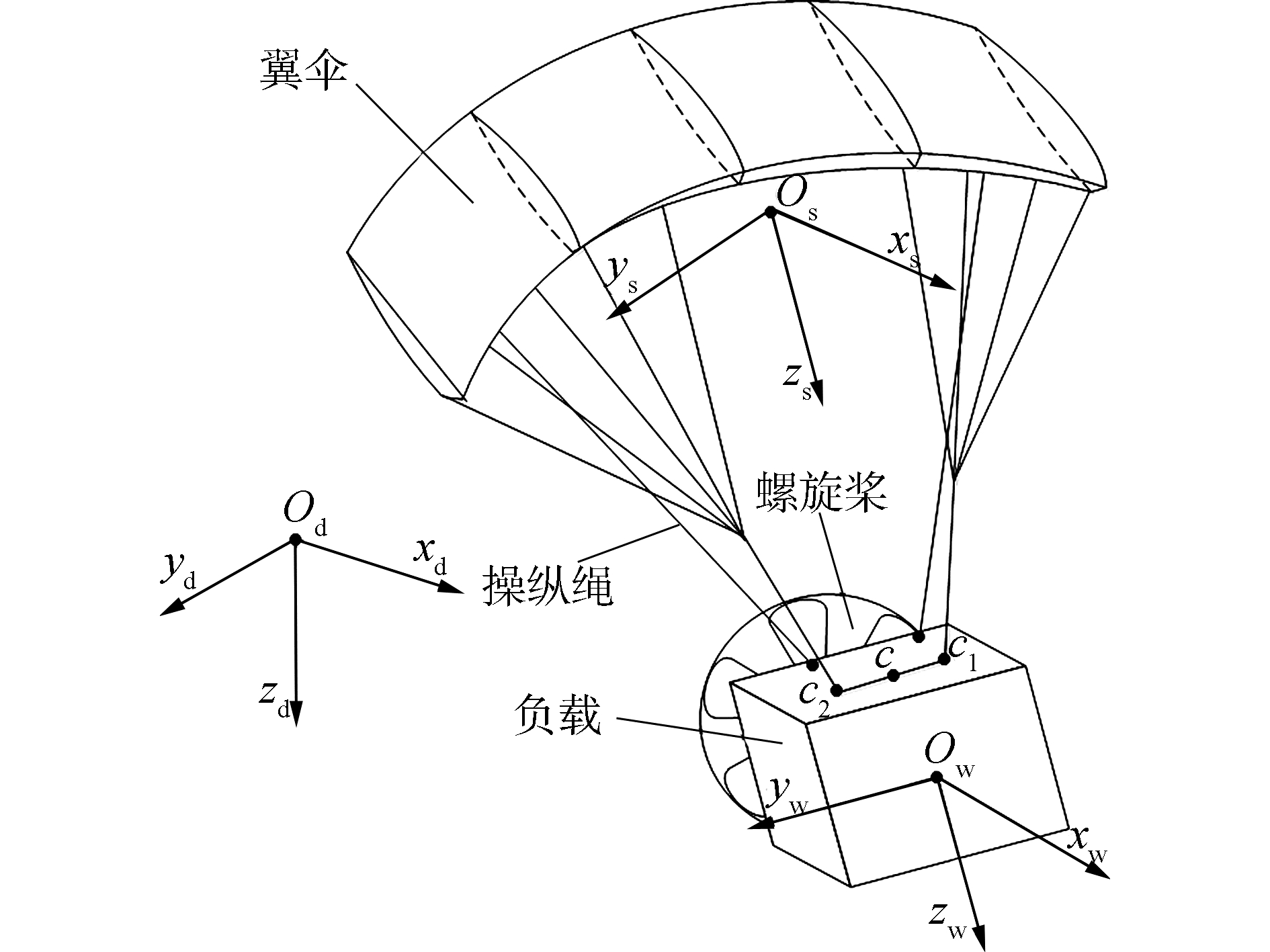
1 数学模型 1.1 动力翼伞系统模型在动力翼伞系统中,考虑了翼伞与负载物之间的相对偏航和相对俯仰运动,建立了8-DOF数学模型。图 1所示为动力翼伞系统结构图。
|
Download:
|
| 图 1 动力翼伞系统结构 Fig. 1 Structure of powered parafoil system | |
动力翼伞系统共用到了3个坐标系:大地坐标系Odxdydzd、翼伞坐标系Osxsyszs和负载物坐标系Owxwywzw。翼伞和负载物之间通过柔性的伞绳连接,两体之间存在相对运动,在连接点处存在运动约束关系:
| $ {\mathit{\boldsymbol{V}}_{\rm{w}}} + {\mathit{\boldsymbol{W}}_{\rm{w}}} \times {\mathit{\boldsymbol{L}}_{{\rm{wc}}}} = {\mathit{\boldsymbol{V}}_{\rm{s}}} + {\mathit{\boldsymbol{W}}_{\rm{s}}} \times {\mathit{\boldsymbol{L}}_{{\rm{sc}}}} $ | (1) |
| $ {\mathit{\boldsymbol{W}}_{\rm{w}}} = {\mathit{\boldsymbol{W}}_{\rm{s}}} + {\mathit{\boldsymbol{\tau }}_{\rm{s}}} + {\mathit{\boldsymbol{\kappa }}_{\rm{w}}} $ | (2) |
式中:V=[u v w]T和W=[p q r]T分别为速度和角速度;下标w、s分别为负载物坐标系和翼伞坐标系;
施加在负载物和翼伞上的作用力包括气动力、自身重力、伞绳之间的拉力以及动力装置提供的推力。利用动量定理和动量矩定理进行分析,可得:
| $ \frac{{\partial {\mathit{\boldsymbol{P}}_{\rm{w}}}}}{{\partial t}} + {\mathit{\boldsymbol{W}}_{\rm{w}}} \times {\mathit{\boldsymbol{P}}_{\rm{w}}} = \mathit{\boldsymbol{F}}_{\rm{w}}^{{\rm{aero}}} + \mathit{\boldsymbol{F}}_{\rm{w}}^{\rm{G}} + \mathit{\boldsymbol{F}}_{\rm{w}}^{\rm{t}} + \mathit{\boldsymbol{F}}_{\rm{w}}^{{\rm{th}}} $ | (3) |
| $ \frac{\partial \boldsymbol{H}_{\mathrm{w}}}{\partial t}+\boldsymbol{W}_{\mathrm{w}} \times \boldsymbol{H}_{\mathrm{w}}=\boldsymbol{M}_{\mathrm{w}}^{\mathrm{exro}}+\boldsymbol{M}_{\mathrm{w}}^{\mathrm{f}}+\boldsymbol{M}_{\mathrm{w}}^{\mathrm{t}} $ | (4) |
| $ \frac{\partial \boldsymbol{P}_{\mathrm{s}}}{\partial t}+\boldsymbol{W}_{\mathrm{s}} \times \boldsymbol{P}_{\mathrm{s}}=\boldsymbol{F}_{\mathrm{s}}^{\mathrm{aero}}+\boldsymbol{F}_{\mathrm{s}}^{\mathrm{G}}+\boldsymbol{F}_{\mathrm{s}}^{\mathrm{t}} $ | (5) |
| $ \frac{\partial \boldsymbol{H}_{\mathrm{s}}}{\partial t}+\boldsymbol{W}_{\mathrm{s}} \times \boldsymbol{H}_{\mathrm{s}}+\boldsymbol{V}_{\mathrm{s}} \times \boldsymbol{P}_{\mathrm{s}}=\boldsymbol{M}_{\mathrm{s}}^{\mathrm{ero}}+\boldsymbol{M}_{\mathrm{s}}^{\mathrm{G}}+\boldsymbol{M}_{\mathrm{s}}^{\mathrm{t}}+\boldsymbol{M}_{\mathrm{s}}^{\mathrm{f}} $ | (6) |
式中:P和H分别代表动量和动量矩;上标aero、t、G、f和th分别为气动力、伞绳拉力、重力、摩擦力和推力;F和M分别为力和力矩。考虑到翼伞所受附加质量影响,负载物和翼伞的动量和动量矩可表示为:
| $ \left\{\begin{array}{l}{\boldsymbol{P}_{\mathrm{w}}=m_{\mathrm{w}} \boldsymbol{V}_{\mathrm{w}}} \\ {\boldsymbol{H}_{\mathrm{w}}=\boldsymbol{J}_{\mathrm{w}} \boldsymbol{W}_{\mathrm{w}}}\end{array}\right. $ | (7) |
| $ \left[\begin{array}{c}{\boldsymbol{P}_{\mathrm{s}}} \\ {\boldsymbol{H}_{\mathrm{s}}}\end{array}\right]=\left[\boldsymbol{A}_{\bf{a}}+\boldsymbol{A}_{\mathrm{r}}\right]\left[\begin{array}{c}{\boldsymbol{V}_{\mathrm{s}}} \\ {\boldsymbol{W}_{\mathrm{s}}}\end{array}\right] $ | (8) |
式中:mw为负载物质量;Jw为负载转动惯量矩阵;Ar和Aa分别为翼伞真实质量和附加质量矩阵。
联立式(1)~(8),即可建立动力翼伞系统的8-DOF模型,详细过程可参考文献[5]。动力翼伞系统横向控制是通过拉动伞体后侧边缘的伞绳,改变单侧下偏角度,进而改变翼伞襟翼的气动外形和气动力进行转弯或雀降。确定翼伞气动力和单侧下偏角的动态关系,对于横向轨迹跟踪至关重要。
翼伞气动力可由伞体主体和襟翼表示为:
| $ \mathit{\boldsymbol{F}}_{\rm{s}}^{{\rm{aero}}} = \mathit{\boldsymbol{F}}_{\rm{b}}^{{\rm{aero}}} + \mathit{\boldsymbol{F}}_{{\rm{lf}}}^{{\rm{aero}}} + \mathit{\boldsymbol{F}}_{{\rm{rf}}}^{{\rm{aero}}} $ |
| $ \mathit{\boldsymbol{M}}_{\rm{s}}^{{\rm{aero}}} = \mathit{\boldsymbol{M}}_{\rm{b}}^{{\rm{aero}}} + \mathit{\boldsymbol{M}}_{{\rm{lf}}}^{{\rm{aero}}} + \mathit{\boldsymbol{M}}_{{\rm{rf}}}^{{\rm{aero}}} $ |
式中:下标b、lf和rf分别为伞体主体、左侧襟翼和右侧襟翼。襟翼偏转带来的翼伞气动力的变化是最主要的,因此忽略伞体主体的影响。
襟翼气动力由升力和阻力组成[16],可表示为:
| $ {\mathit{\boldsymbol{F}}_{{\rm{Lf}}}} = {k_{\rm{f}}}{C_{{\rm{Lf}}}}0.5\rho {S_{\rm{f}}}\sqrt {u_{\rm{f}}^2 + w_{\rm{f}}^2} {\left[ {\begin{array}{*{20}{c}} {{w_{\rm{f}}}}&0&{ - {u_{\rm{f}}}} \end{array}} \right]^{\rm{T}}} $ |
| $ {\mathit{\boldsymbol{F}}_{{\rm{Df}}}} = - {C_{{\rm{Df}}}}0.5\rho {S_{\rm{f}}}\sqrt {u_{\rm{f}}^2 + v_{\rm{f}}^2 + w_{\rm{f}}^2} {\left[ {\begin{array}{*{20}{c}} {{u_{\rm{f}}}}&{{v_{\rm{f}}}}&{{w_{\rm{f}}}} \end{array}} \right]^{\rm{T}}} $ |
式中:下标L和D代表升力和阻力;kf为乘积因子;Sf为襟翼面积;
| $ \begin{array}{l} {C_{{\rm{Lf}}}} = {k_{{\rm{Ls}}}}\left( {{\theta _{\rm{d}}} - {\theta _{{\rm{a0}}}}} \right)\cos a + \\ \;\;\;\;\;\;\;\;{\theta _{{\rm{AR}}}}{\sin ^2}\left( {{\theta _{\rm{d}}} - {\theta _{{\rm{a0}}}}} \right)\cos \left( {{\theta _{\rm{d}}} - {\theta _{{\rm{a0}}}}} \right) \end{array} $ |
| $ \begin{array}{l} {C_{{\rm{Df}}}} = {C_{{\rm{Df0}}}} + k_{{\rm{Ls}}}^2\left( {{\theta _{\rm{d}}} - {\theta _{{\rm{a0}}}}} \right)2{k_{\rm{c}}}/\left( {{\rm{ \mathit{ π} }} \times {R_{\rm{A}}}} \right) + \\ \;\;\;\;\;\;\;\;{\theta _{{\rm{AR}}}}{\sin ^3}\left( {{\theta _{\rm{d}}} - {\theta _{{\rm{a0}}}}} \right) \end{array} $ |
式中:kLs为升力线斜率; θa0是升力为0时的攻角;RA为展弦比;θAR是由RA决定的系数;CDf0为初始阻力系数;kc为权重值。θd为翼伞的实际单侧下偏角度,由系统初始安装角、当前状态的攻角和控制器输出的单侧下偏量来确定。即:
| $ {\theta _{\rm{d}}} = {\theta _{\rm{c}}} + {\theta _{\rm{a}}} - {\theta _{\rm{I}}} $ |
式中:θa为攻角;θI为初始安装角;θc为横向控制器输出量。
控制量θc在仿真中是直接加到翼伞的单侧下偏角度变化中,没有考虑舵机负载变化对于执行机构的作用。而在实际飞行实验中,执行机构跟踪参考角度时,需考虑转速、负载转矩和电枢电压等因素影响,单侧下偏角度无法做到直接到位的变化,将会削弱控制效果。因此,需要在动力翼伞系统8-DOF模型的基础上,引入舵机的数学模型。
1.2 舵机模型舵机系统是由电动机主体和驱动器组成。电动机主体由直流电机、减速器和舵盘组成。直流电机调速范围广、转速快、过载能力强,适合动力翼伞这种存在变负载的动态系统。
首先,需要得到单侧下偏角度和下拉伞绳长度的关系,从而得到舵机转动的参考角度。通过分析动力翼伞系统的结构特性,得到关系如下:
| $ {\theta _{\rm{c}}} = \arctan \left( {\frac{{y\frac{L}{R}}}{{{c_{{\rm{o}} - {\rm{y}}}}\left( {1 - \frac{L}{R}} \right)}}} \right) $ | (9) |
| $ L = {\rm{ \mathit{ π} }}d\frac{A}{{360}} $ | (10) |
式中:y为操纵绳的垂直分量;L为下拉伞绳长度;R为伞绳全长;
根据直流电机的结构和工作原理,直流电机的电压平衡方程式可表示为:
| $ {U_{\rm{a}}} = E + {I_{\rm{a}}}{R_{\rm{a}}} + {L_{\rm{a}}}\frac{{{\rm{d}}{I_{\rm{a}}}}}{{{\rm{d}}t}} $ | (11) |
| $ U_{\mathrm{f}}=I_{\mathrm{f}} R_{\mathrm{f}}+L_{\mathrm{f}} \frac{\mathrm{d} I_{\mathrm{f}}}{\mathrm{d} t} $ | (12) |
式中:下标a和f分别为电枢和励磁;E为感应电动势;U、I、R和L分别为电压、电流、电阻和电感。
其中感应电动势E可表示为:
| $ E = {C_{\rm{e}}}\mathit{\Phi }n = {C_{\rm{e}}}\mathit{\Phi }\frac{{30{\omega _{\rm{m}}}}}{{\rm{ \mathit{ π} }}} $ | (13) |
式中:Ce表示由电动机结构决定的电动势常数;Φ表示励磁磁通;n和ωm代表电动机的转速, n=30ωm/π。
若忽略阻尼转矩和扭转弹性转矩,则直流电机的基本运动方程式可简化为:
| $ J\frac{{{\rm{d}}{\omega _{\rm{m}}}}}{{{\rm{d}}t}} = {T_{\rm{e}}} - {T_{\rm{L}}} $ | (14) |
式中:J为机械转动惯量;TL为负载转矩;Te为电磁转矩。
电磁转矩Te可表示为:
| $ {T_{\rm{e}}} = \frac{{30}}{{\rm{ \mathit{ π} }}}{C_{\rm{e}}}\mathit{\Phi }{I_{\rm{a}}} $ | (15) |
结合式(11)~(15),直流电机的微分方程表达式为:
| $ \begin{array}{*{20}{c}} {\frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} {{I_{\rm{a}}}}\\ {{I_{\rm{f}}}}\\ {{\omega _{\rm{m}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{{{R_{\rm{a}}}}}{{{L_{\rm{a}}}}}}&0&{ - \frac{{\frac{{30}}{{\rm{ \mathit{ π} }}}{C_{\rm{e}}}\mathit{\Phi }}}{{{L_{\rm{a}}}}}}\\ 0&{ - \frac{{{R_{\rm{f}}}}}{{{L_{\rm{f}}}}}}&0\\ {\frac{{\frac{{30}}{{\rm{ \mathit{ π} }}}{C_{\rm{e}}}\mathit{\Phi }}}{J}}&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{I_{\rm{a}}}}\\ {{I_{\rm{f}}}}\\ \omega \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} {\frac{1}{{{L_{\rm{a}}}}}}&0&0\\ 0&{\frac{1}{{{L_f}}}}&0\\ 0&0&{ - \frac{1}{J}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{U_{\rm{a}}}}\\ {{U_{\rm{f}}}}\\ {{T_{\rm{L}}}} \end{array}} \right]} \end{array} $ | (16) |
由式(11)、(13)可知,直流电机的稳态转速可表示为:
| $ n = \frac{{U - IR}}{{{C_{\rm{e}}}\mathit{\Phi }}} $ | (17) |
对于要求在一定范围内无级平滑调速的动力翼伞系统来说,采用改变电枢电压的方法来调节转速,实现左右舵机的单侧下偏动作。
由此,建立了引入舵机的动力翼伞系统数学模型。针对动力翼伞系统存在不平衡且时变非线性的舵机负载转矩问题,改进的系统模型将改善舵机执行到位的快速性和准确性,减小因负载变化引起的舵机振荡和死区的影响,提高系统的控制精度。
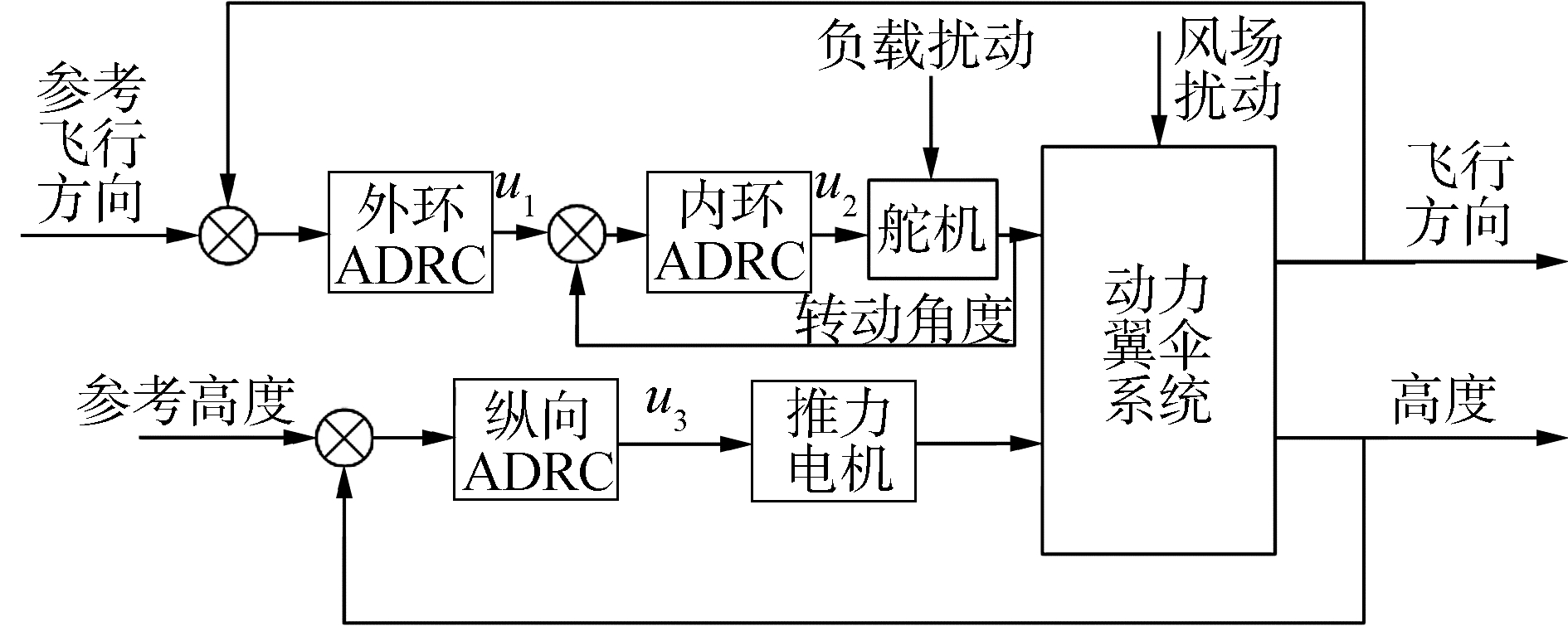
2 轨迹跟踪控制器设计 2.1 横向轨迹控制器由于舵机模型的加入,横向轨迹通道需要设计为串级控制器结构。根据图 2轨迹跟踪控制器结构可知,内环回路的给定输入为舵机的参考角度,外部干扰为左右舵机上的负载转矩。外环回路的给定输入为系统的参考飞行偏航角度,外部干扰为风场扰动。串级控制器对内环回路的负载扰动有很强的克服能力,能做到敏捷的微调控制,加快横向轨迹控制的响应速度,并且提高系统的自适应能力。
|
Download:
|
| 图 2 轨迹跟踪控制器结构 Fig. 2 Structure of trajectory tracking controller | |
根据动力翼伞系统模型的特点,将系统当前偏航角φ表示为二阶微分形式:
| $ \ddot \varphi = f\left( {\dot \varphi , \varphi } \right) + {b_1}{u_1} + {w_{{\rm{dis}}}} $ | (18) |
式中:
将式(18)转化为扩张状态方程的形式为:
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = {x_3} + {b_1}{u_1}\\ {{\dot x}_3} = \dot f\\ y = {x_1} \end{array} \right. $ | (19) |
式中:x1为偏航角φ;x2为偏航角速度
建立三阶线性ESO,将ESO的扩张状态z3看作为f,当参数调为最优时,扰动项的观测误差将会收敛为0,即:
| $ {z_3} \approx f $ |
三阶线性ESO表示为:
| $ \left\{\begin{array}{l}{e_{1}=z_{1}-\varphi} \\ {\dot{z}_{1}=z_{2}-\beta_{1} e_{1}} \\ {\dot{z}_{2}=z_{3}+b_{1} u_{1}-\beta_{2} e_{1}} \\ {\dot{z}_{3}=-\beta_{3} e_{1}}\end{array}\right. $ | (20) |
式中:e1为观测值与系统实际输出的观测误差;zi为各阶xi的观测状态值;
增益矩阵可表示为:
| $ \mathit{\boldsymbol{L}} = {\left[ {\begin{array}{*{20}{l}} {3{\omega _{\rm{o}}}}&{3\omega _{\rm{o}}^2}&{\omega _{\rm{o}}^3} \end{array}} \right]^{\rm{T}}} $ |
为消除扰动项,令控制量u1为:
| $ u_{1}=\frac{u_{0}-z_{3}}{b_{1}}=\frac{k_{\mathrm{p}}\left(r-z_{1}\right)+k_{\mathrm{d}}\left(\dot{r}-z_{2}\right)-z_{3}}{b_{1}} $ |
式中:r和
式(18)表示的二阶被控对象简化为:
| $ \ddot{\varphi}=u_{0} $ |
因此,非线性的系统被转化为更便于控制的积分串联型对象。
2.1.2 内环控制器横向通道的内环回路输入由外环的输出量决定,即参考单侧下偏量,由式(9)、(10)可转化为给定舵机旋转角度。舵机当前旋转角度二阶形式表示为:
| $ \ddot{a}=f(\dot{a}, a)+b_{2} u_{2}+w_{\mathrm{dis}} $ |
式中:a为舵机的当前角度;f(
构建类似于式(20)的三阶扩张状态观测器,表示为:
| $ \left\{\begin{array}{l}{e_{1}=z_{1}-a} \\ {\dot{z}_{1}=z_{2}-\beta_{1} e_{1}} \\ {\dot{z}_{2}=z_{3}+b_{2} u_{2}-\beta_{2} e_{1}} \\ {\dot{z}_{3}=-\beta_{3} e_{1}}\end{array}\right. $ |
令控制量u2为:
| $ u_{2}=\frac{u_{0}-z_{3}}{b_{2}}=\frac{k_{\mathrm{p}}\left(r-z_{1}\right)+k_{\mathrm{d}}\left(\dot{r}-z_{2}\right)-z_{3}}{b_{2}} $ |
由此,设计了横向通道的串级自抗扰控制器。内环回路控制舵机完成对参考角度的快速粗调,实时估计和补偿舵机上的负载扰动项,进行前导区控制。外环回路完成水平轨迹的单侧下偏,进行惰性区的细调控制。
2.2 纵向轨迹控制器纵向轨迹控制器是为了完成动力翼伞系统跟踪参考高度任务,系统当前高度的二阶形式为:
| $ \ddot h = f(\dot h, h) + {b_3}{F_{{\rm{th}}}} + {w_{{\rm{dis}}}} $ |
式中:h为系统高度;f(
同样设计了三阶线性ESO,推力输出根据误差反馈控制律得到:
| $ F_{\mathrm{th}}=\frac{u_{0}-z_{3}}{b_{3}}=\frac{k_{\mathrm{p}}\left(r-z_{1}\right)+k_{\mathrm{d}}\left(\dot{r}-z_{2}\right)-z_{3}}{b_{3}} $ |
由此,动力翼伞系统轨迹跟踪控制器已经设计完成,双通道分别对飞行方向和高度进行控制。扩张状态观测器通过零阶保持器法进行离散化[18],在采样周期较大时,此类方法的观测效果更加精确,满足控制性能要求。
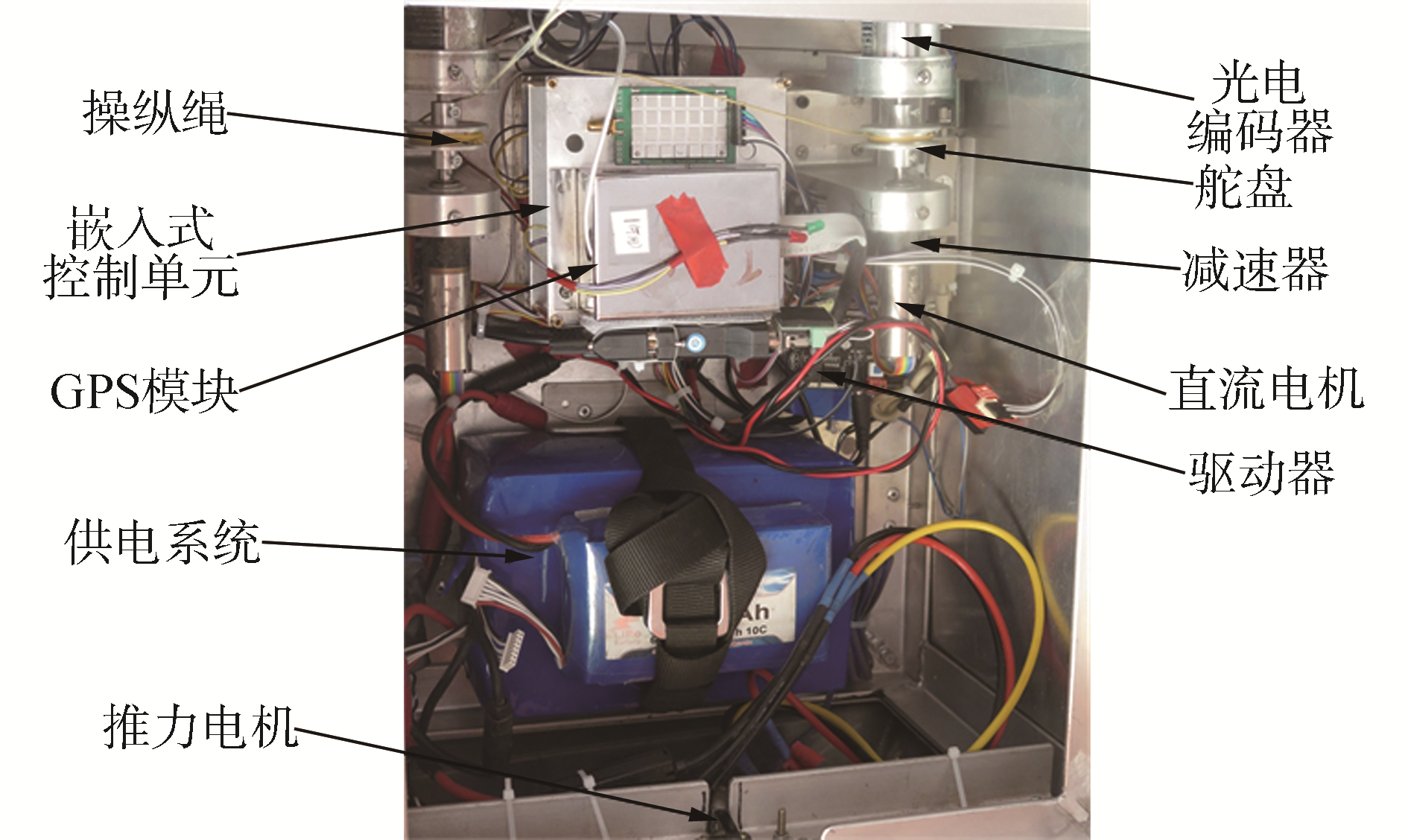
3 半实物仿真实验为验证系统模型和控制策略的有效性,搭建了半实物仿真平台,平台中用到的所有硬件设备均和实际飞行实验相同。半实物仿真便于参数调节,还可以很大程度上代替空投实验,是评估动力翼伞系统性能的有效手段。半实物仿真平台如图 3所示。
|
Download:
|
| 图 3 半实物仿真平台 Fig. 3 Semi-physical simulation platform | |
通过半实物仿真平台,可检测内环控制器在舵机中的控制效果,验证内环回路的必要性。舵机和负载如图 4所示,伞绳和重物通过固定架上方的定滑轮连,其中直流电机额定电压24 V,额定转速10 400 r/min,空载转速12 900 r/min,额定电流1.4 A,额定转矩22.7 mN·m,最大效率76 %。将ADRC控制器、PID控制器和固定转速控制分别应用到内环回路。控制器参数整定通过理论计算和工程试验方法相结合来确定,ADRC控制器首先通过系统数学模型来估算输入增益b0,然后调节ESO带宽ωo使其观测误差能够收敛为0;比例微分系数通过控制器带宽ωc来大致确定,再通过工程试验来进行微调。PID控制器参数通过工程经验法获得,遵循“先比例,再积分,后微分”的原则进行整定。经过多次半实物仿真实验后,ADRC控制器参数设置为:ωo=2.2,kp=2.22,kd=0.19,b0=2.3;PID控制器:kp=0.65,kd=0.2,ki=0.01;固定转速控制为占空比40%的PWM信号。以上参数均已调为最优。

|
Download:
|
| 图 4 舵机与负载 Fig. 4 Rudder and load | |
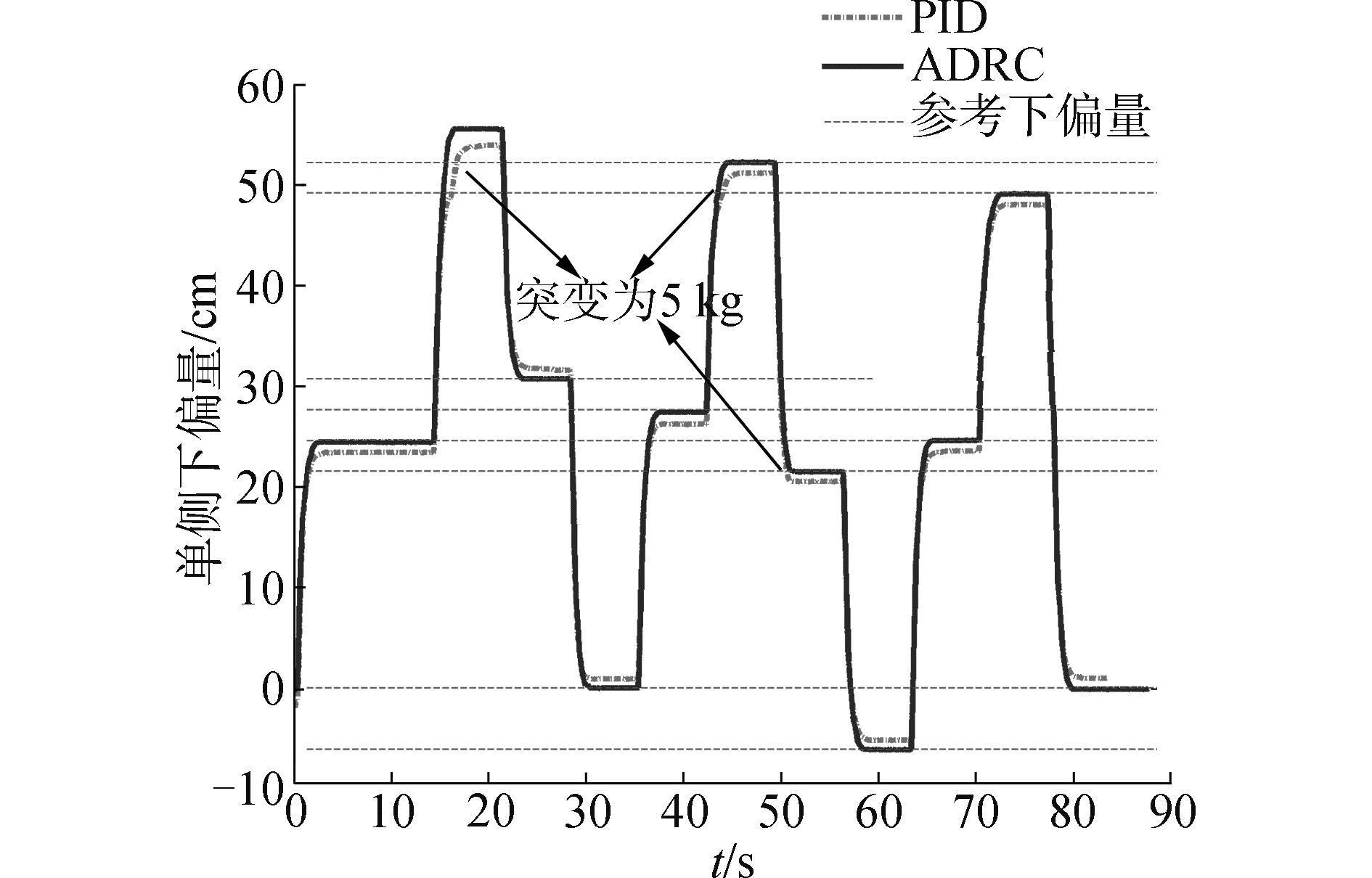
设定参考单侧下偏量,并设置不同的工况。工况1:舵机伞绳上不悬挂重物,模拟理想环境下的飞行; 工况2:悬挂3 kg重物,并在第14、42和49 s时重物突变为5 kg,突变时间持续7 s,模拟系统不稳定的负载扰动变化。
由图 5看出,相对于PID控制器和固定转速控制,ADRC控制器表现了更高的到位精度,且比PID控制器反应敏捷,超调更小,最大误差为0.2 cm。固定转速控制虽然反应较快,但是存在1.1 cm的死区空间。在图 6中,舵机加入了固定和突变的负载扰动,固定转速控制已经失效,舵机震荡严重。ADRC控制器能够抑制负载扰动的影响,在负载突变时迅速响应,使系统恢复稳定,误差控制在0.2 cm以内。而PID控制器对突变负载应对能力不足,跟踪误差达到了1.5 cm,稳定时间较长。所以,ADRC控制器对扰动的补偿和消除优势更加明显,控制精度高,表现出更好的稳定性和鲁棒性。

|
Download:
|
| 图 5 舵机无负载时控制效果 Fig. 5 Rudder control effect without load | |
|
Download:
|
| 图 6 舵机受负载时控制效果 Fig. 6 Rudder control effect with load | |
通过实验结果对比,说明内环控制器提高了舵机转动精度,减小了死区误差,有效抑制负载扰动影响,系统无明显震荡,减轻了横向通道外环控制器的压力。
3.2 半实物仿真分析为验证轨迹跟踪控制策略的有效性,结合动力翼伞系统模型,在半实物仿真平台上进行了仿真实验。动力翼伞系统模型参数设置为:展长4.5 m,弦长1.3 m,展弦比3.4,翼伞面积6.5 m2,质量1.7 kg,绳长3 m,安装角10°,负载质量20 kg。
为检验轨迹跟踪控制效果,将飞行过程的状态进行记录对比。定义l(i)为在第i次采样时刻目标位置和当前位置的距离;lh(i)为参考高度和当前高度的距离,并以此定义:
动力翼伞系统的初始值设定为:初始位置(0 m, 0 m, 500 m),初始速度Vs=(14.9 m/s, 0 m/s, 2.1 m/s),纵向跟踪高度为450 m,水平方向跟踪目标正方形,水平轨迹可以检测动力翼伞这类惯性较大系统的大角度转弯能力。仿真时间350 s,步长0.025 s。将串级ADRC、传统ADRC和PID控制器分别应用到半实物仿真中,其中传统ADRC为未引入舵机模型的单环结构。参数整定方法和3.1节中类似,但是串级ADRC控制器需要先调整内环,再调整外环,并选择适当的控制量更新频率。控制器参数设定为:串级ADRC,内环控制器:ωo=2.1,kp=2.35,kd=0.4,b0=2,控制量更新频率10 Hz;外环控制器:ωo=2,kp=0.195,kd=0.85,b0=0.3,控制量更新频率0.5 Hz;纵向通道:ωo=3.5,kp=0.032,kd=0.6,b0=0.05。传统ADRC除了不具备内环控制器之外,其余参数和串级ADRC相同;PID控制器,横向通道:kp=0.61,kd=1,ki=0.11;纵向通道:kp=2.3,kd=0.9,ki=0.032。以上参数均已调为最优状态。
外界干扰设置为:舵机负载变化在2.5~3.5 kg随机扰动;风场环境为常值风和突风混合作用,速度分别为3 m/s和5 m/s,方向分别为沿着大地坐标系下x轴负方向和正方向。常值风始终存在,突风采用NASA经典离散突风模型[19],在半实物仿真实验的第200 s加入,持续时间15 s。跟踪轨迹结果如表 1和图 7所示。
| 表 1 控制器轨迹跟踪误差 Table 1 Trajectory tracking error of controllers |
|
Download:
|
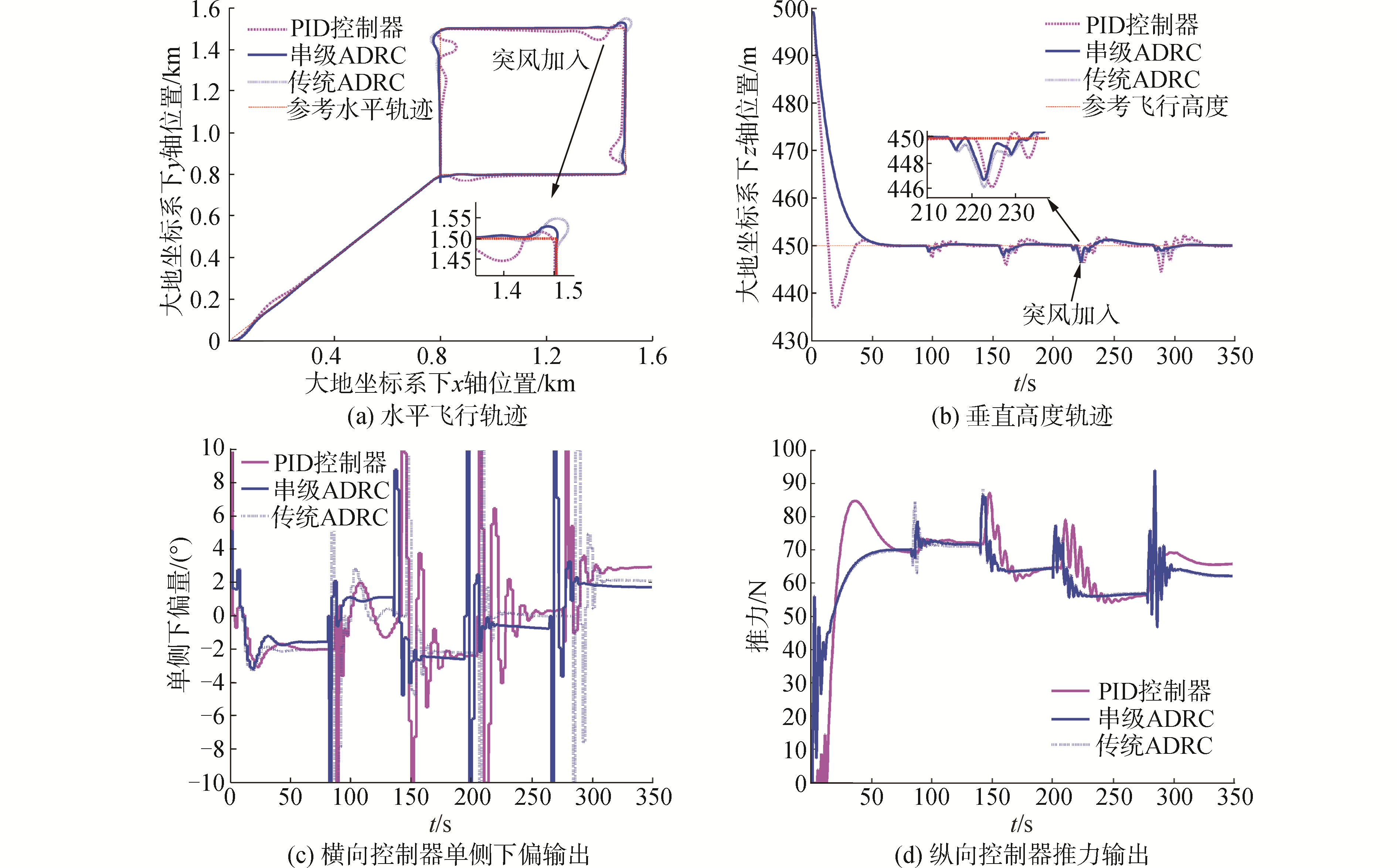
| 图 7 轨迹跟踪控制半实物仿真结果 Fig. 7 Semi-physical simulation results of trajectory tracking control | |
表 1为3种控制器的轨迹跟踪误差对比,图 7为半实物仿真实验结果。通过图 7(a)对比可知,相较于传统ADRC控制器,串级ADRC控制器在跟踪速度和精度上效果更佳,尤其在更换目标点后,能快速靠近目标轨迹并达到稳定状态,距离误差收敛迅速,横向轨迹平均误差为5.06 m,精度较前者提高了0.08 m,最大误差为42.07 m。串级结构对风场和舵机负载转矩扰动的抑制作用更加明显。而PID控制器效果较差,转弯时容易出现超调,系统震荡时间较长,收敛速度慢,横向轨迹平均跟踪误差为10.91 m,最大误差达到58.08 m,并且突风扰动使系统远离目标位置,抗扰性能不如自抗扰控制。从图 7(c)曲线可知,串级ADRC控制器在转弯时控制量很快输出平稳,突风扰动情况下控制量经过短时间震荡后恢复稳定。传统ADRC控制量在扰动下出现小幅震荡,而PID控制量更加严重,舵机动作频繁。从表 1可知,消耗的系统能量s均比串级自抗扰控制器要高。
图 7(b)为高度跟踪结果,由于纵向通道的结构相同,因此2种自抗扰控制器均能够快速无超调的跟踪给定高度,但受横向通道耦合的影响,串级ADRC控制器在扰动和转向时精度损失更小,纵向轨迹平均误差为0.38 m,提高了0.11 m的精度,最大纵向误差也得到了改善。而PID控制器进入目标高度时超调达到12.95 m,系统转弯和双通道间的耦合扰动导致精度损失严重,高度呈现出震荡性收敛,平均误差为1.10 m。在图 7(d)中,串级ADRC控制器的推力输出比传统ADRC控制器更加稳定,整体上比PID控制器较为平滑,突风扰动下推力调节时间更短。
通过分析动力翼伞系统的半实物仿真实验结果,串级自抗扰控制器在跟踪精度,响应速度和抵抗扰动上效果突出,使动力翼伞系统的性能得到了明显提高。
4 结论1) 改进动力翼伞系统8-DOF模型,引入具有负载转矩的直流电机模型,提高了舵机的灵敏度、精度和抗扰能力。
2) 横向通道设计了串级自抗扰控制器,内外环回路分别对负载扰动和风扰进行补偿抑制,使横向控制器做到敏捷控制,提高响应速度。
3) 半实物仿真结果表明,该控制策略实现了对目标轨迹的精确跟踪,提高了系统稳定性和鲁棒性,控制效果优于传统ADRC和PID控制器,在飞行实验中具有重要的指导意义。
下一步工作是在纵向通道上加入推力电机模型,得到转速和推力的关系,将串级自抗扰控制器应用到纵向通道中,并需要在飞行实验中对提出的模型和控制策略进行验证。
| [1] |
YAKIMENKO O A. Precision aerial delivery systems:modeling, dynamics, and control[M]. Reston, VA: AIAA, 2015.
(  0) 0)
|
| [2] |
ZHANG Limin, GAO Haitao, CHEN Zengqiang, et al. Multi-objective global optimal parafoil homing trajectory optimization via Gauss pseudospectral method[J]. Nonlinear dynamics, 2013, 72(1/2): 1-8. DOI:10.1007/s11071-012-0586-9 (  0) 0)
|
| [3] |
LIU Hua, GUO Lei, ZHANG Yumin. An anti-disturbance PD control scheme for attitude control and stabilization of flexible spacecrafts[J]. Nonlinear dynamics, 2012, 67(3): 2081-2088. DOI:10.1007/s11071-011-0130-3 (  0) 0)
|
| [4] |
韩雅慧, 杨春信, 肖华军, 等. 翼伞精确空投系统关键技术和发展趋势[J]. 兵工自动化, 2012, 31(7): 1-7. HAN Yahui, YANG Chunxin, XIAO Huajun, et al. Review on key technology and development of parafoil precise airdrop systems[J]. Ordnance industry automation, 2012, 31(7): 1-7. DOI:10.3969/j.issn.1006-1576.2012.07.001 (  0) 0)
|
| [5] |
ZHU Erlin, SUN Qinglin, TAN Panlong, et al. Modeling of powered parafoil based on Kirchhoff motion equation[J]. Nonlinear dynamics, 2015, 79(1): 617-629. DOI:10.1007/s11071-014-1690-9 (  0) 0)
|
| [6] |
WATANABE M, OCHI Y. Modeling and simulation of nonlinear dynamics of a powered paraglider[C]//Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit. Honolulu, Hawaii: AIAA, 2008: 1-16. DOI: 10.2514/6.2008-7418.
(  0) 0)
|
| [7] |
朱二琳, 张兴会. 翼伞空投系统模糊控制器的设计与实现[J]. 电子测量技术, 2011, 34(4): 46-49, 97. ZHU Erlin, ZHANG Xinghui. Design and application of fuzzy controller in parafoil airdrop system[J]. Electronic measurement technology, 2011, 34(4): 46-49, 97. DOI:10.19651/j.cnki.emt.2011.04.013 (  0) 0)
|
| [8] |
HATTIS P, CAMPBELL D, CARTER D, et al. Providing means for precision airdrop delivery from high altitude[C]//Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit. Keystone, Colorado: AIAA, 2013. DOI: 10.2514/6.2006-6790.
(  0) 0)
|
| [9] |
SLEGERS N, COSTELLO M. Model predictive control of a parafoil and payload system[J]. Journal of guidance, control, and dynamics, 2005, 28(4): 816-821. DOI:10.2514/1.12251 (  0) 0)
|
| [10] |
梁海燕, 任志刚, 许超, 等. 翼伞系统最优归航轨迹设计的敏感度分析方法[J]. 控制理论与应用, 2015, 32(8): 1003-1011. LIANG Haiyan, REN Zhichao, XU Chao, et al. Optimal homing trajectory design for parafoil systems using sensitivity analysis approach[J]. Control theory & applications, 2015, 32(8): 1003-1011. DOI:10.7641/CTA.2015.40855 (  0) 0)
|
| [11] |
谢亚荣.空投任务下翼伞建模与飞行控制研究[D].南京: 南京航空航天大学, 2011. DOI: 10.7666/d.d166701. XIE Yarong. Research on modeling and flight control of parafoil under the airdrop mission[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011. DOI: 10.7666/d.d166701. http://cdmd.cnki.com.cn/Article/CDMD-10287-1011291990.htm (  0) 0)
|
| [12] |
GRIGNION D, CHEN Xiang, KAR N, et al. Estimation of load disturbance torque for DC motor drive systems under robustness and sensitivity consideration[J]. IEEE transactions on industrial electronics, 2014, 61(2): 930-942. DOI:10.1109/tie.2013.2257138 (  0) 0)
|
| [13] |
HAN Jingqing. From PID to active disturbance rejection control[J]. IEEE transactions on industrial electronics, 2009, 56(3): 900-906. DOI:10.1109/TIE.2008.2011621 (  0) 0)
|
| [14] |
XUE Wenchao, BAI Wenyan, YANG Sheng, et al. ADRC With adaptive extended state observer and its application to air-fuel ratio control in gasoline engines[J]. IEEE transactions on industrial electronics, 2015, 62(9): 5847-5857. DOI:10.1109/TIE.2015.2435004 (  0) 0)
|
| [15] |
TAO Jin, SUN Qinglin, TAN Panlong, et al. Active disturbance rejection control (ADRC)-based autonomous homing control of powered parafoils[J]. Nonlinear dynamics, 2016, 86(3): 1461-1476. DOI:10.1007/s11071-016-2972-1 (  0) 0)
|
| [16] |
熊菁.翼伞系统动力学与归航方案研究[D].长沙: 国防科学技术大学, 2005. XIONG Jing. Research on the dynamics and homing project of parafoil system[D]. Changsha: National University of Defense Technology, 2005. http://cdmd.cnki.com.cn/Article/CDMD-90002-2006127563.htm (  0) 0)
|
| [17] |
GAO Zhiqiang. Active disturbance rejection control: A paradigm shift in feedback control system design[C]//2006 American Control Conference. Minneapolis, MN, USA: IEEE, 2006. DOI: 10.1109/ACC.2006.1656579.
(  0) 0)
|
| [18] |
ZHENG Qing, DONG Lili, LEE D H, et al. Active disturbance rejection control for MEMS gyroscopes[J]. IEEE transactions on control systems technology, 2009, 17(6): 1432-1438. DOI:10.1109/TCST.2008.2008638 (  0) 0)
|
| [19] |
ADELFANG S, SMITH O. Gust models for launch vehicle ascent[C]//Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit. Reno, NV, U.S.A: AIAA, 1998. DOI: 10.2514/6.1998-747.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


