2. 安徽理工大学 土木建筑学院, 安徽 淮南 232001
2. School of Civil Engineering and Architecture, Anhui University of Science and Technology, Huainan 232001, China
地应力是导致各种矿山压力显现的力源,也是决定工程煤岩体力学行为的主导因素[1-3]。构造等因素使得深部地应力较为复杂,具体表现为最大主应力方向的差异和两水平侧压系数的复杂化,仅单方面依靠传统经验来设计布置巷道以及进行支护已经不能满足掘进需求。因此,复杂地应力场中深部软岩巷道围岩稳定性规律是学者研究的热点,研究者通过理论分析和数值模拟、实测地应力大小和方向等手段研究了地应力场对巷道围岩稳定性的影响[4-7],并提出相应的预测和控制方法,取得了大量的研究成果[8-13]。
特别随着煤矿开采强度与广度的不断增加, 开采深度越来越大, 地质条件也越来越复杂, 地应力对巷道围岩变形与破坏的影响更加突出。煤矿中的一些灾害, 如顶板冒落、冲击矿压、煤与瓦斯突出及透水等事故, 均与地应力有直接或间接的关系,围岩支护更加困难。然而,对于最大水平主应力与巷道轴线不同夹角下深埋软岩巷道锚杆轴力变化规律以及对应围岩支护设计研究较少。本文以巷道锚固区力学特征作为切入点,研究不同水平主应力方向对巷道锚杆锚固区力学特征响应规律,为巷道支护设计提供理论指导和技术支撑。
1 潘三矿巷道概况和数值模拟模型 1.1 工程背景淮南矿业集团潘三矿二水平东一11-2煤采区岩石回风巷道,掘进区段位于二叠系13-1煤底板以下29~53 m,巷道穿层施工,岩性主要以砂质泥岩为主,设计标高为-735.1~-814.5 m。巷道断面为直墙半圆拱,净宽×净高等于5.2 m×4.1 m,巷道支护采用锚网支护,原支护设计锚杆规格:ϕ22 mm×2 500 mm,间排距:800 mm×800 mm;锚杆材质MG400,锚固剂型号Z2360,采用2支锚固剂,锚固长度1 m左右。
根据巷道所处位置实测地应力成果,最大主应力36.4 MPa,最小主应力15.1 MPa,中间主应力20.3 MPa,其中最大、最小主应力近水平,中间主应力近垂直,最大水平主应力方位112.6°,最小主应力方位204.3°。
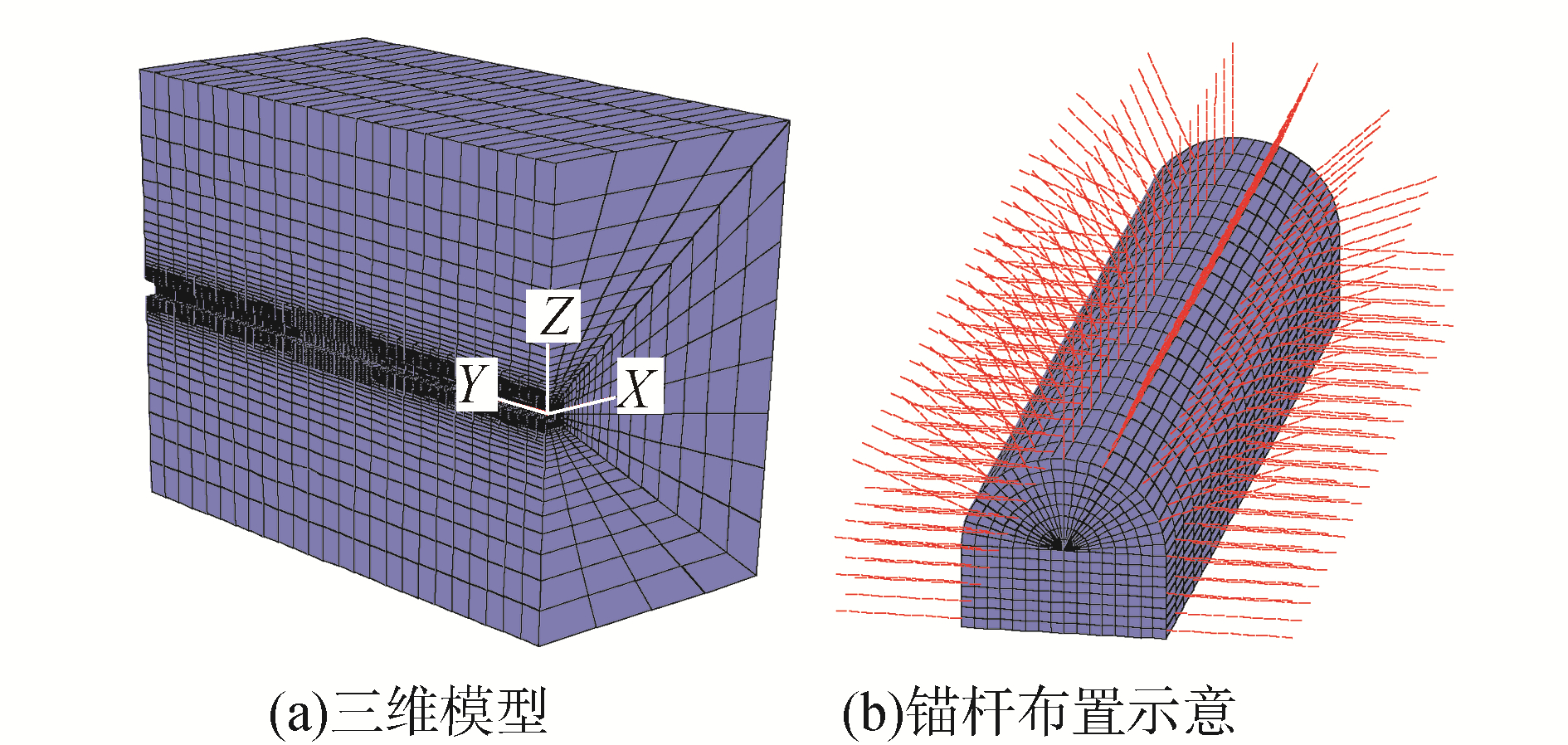
1.2 数值计算模型及方案依据潘三矿二水平东一11-2煤采区岩石回风巷道工程地质条件,选用FLAC3D进行数值计算,建立三维计算模型长、宽、高分别为100 m×100 m×100 m,共有6.3万个单元网格,2 600个锚杆结构单元,模型底面限制垂直移动和水平移动,采用摩尔库伦模型。根据巷道围岩相关力学实验,确定巷道围岩体积模量为4 294 MPa,剪切模量2 702 MPa,摩擦角32°,内聚力1.25 MPa,抗拉强度1.15 MPa,如图 1所示。
|
Download:
|
| 图 1 模型示意 Fig. 1 Schematic diagram of model | |
分别模拟最大水平主应力方向与巷道轴线夹角在0°、10°、20°、30°、40°、50°、60°、70°、80°、90°时的巷道围岩应力分布、锚杆轴力及巷道变形等,巷道锚杆布置如图 2所示。根据最大水平主应力方向与巷道轴线的夹角模型应力边界条件表示为:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{l}} {{p_x}}&{{p_{xy}}}&{{p_{xz}}}\\ {{p_{yx}}}&{{p_y}}&{{p_{yz}}}\\ {{p_{zx}}}&{{p_{zy}}}&{{p_z}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {{{\cos }^2}\alpha \cdot {\sigma _3} + {{\sin }^2}\alpha \cdot {\sigma _1}}&0{}&{ - \frac{1}{2}\sin (2\alpha )\left( {{\sigma _1} - {\sigma _3}} \right)}\\ 0&{{\sigma _2}}&0\\ { - \frac{1}{2}\sin (2\alpha )\left( {{\sigma _1} - {\sigma _3}} \right)}&0&{{{\cos }^2}\alpha \cdot {\sigma _3} + {{\sin }^2}\alpha \cdot {\sigma _1}} \end{array}} \right] \end{array} $ |
在模型中部位置布置2条观测线;一条沿巷中竖向(z方向)布置,自半圆拱圆心从上至下贯通模型;另一条沿巷道横向(x方向)布置,自拱基线自左至右贯通模型。
由图 2可知,最大水平主应力方向与巷道轴线夹角为0°~10°时,顶板岩层水平集中应力峰值趋于平缓,无明显应力集中现象,最大水平主应力方向与巷道轴线夹角为0°~20°时,底板岩层无应力集中现象。随着夹角的增加顶、底板高应力区范围和应力集中程度响应增大,沿竖向顶、底板岩层围岩可分为卸压区、应力增高区和原岩应力区,其中卸压区范围距顶底板0~2 m范围,应力增高区范围2 m~28 m,应力峰值位置分别距顶底板2 m~4 m。不同夹角对应峰值大小、峰值位置及应力集中系数如表 1所示。

|
Download:
|
| 图 2 不同夹角巷道顶底板水平集中应力分布曲线 Fig. 2 Horizontal concentrated stress distribution curve of roof and floor of different angle laneway | |
| 表 1 不同水平主应力夹角下顶底板峰值大小、位置及应力集中系数 Table 1 Peak size, position and stress concentration coefficient of roof and floor under different horizontal principal stress |
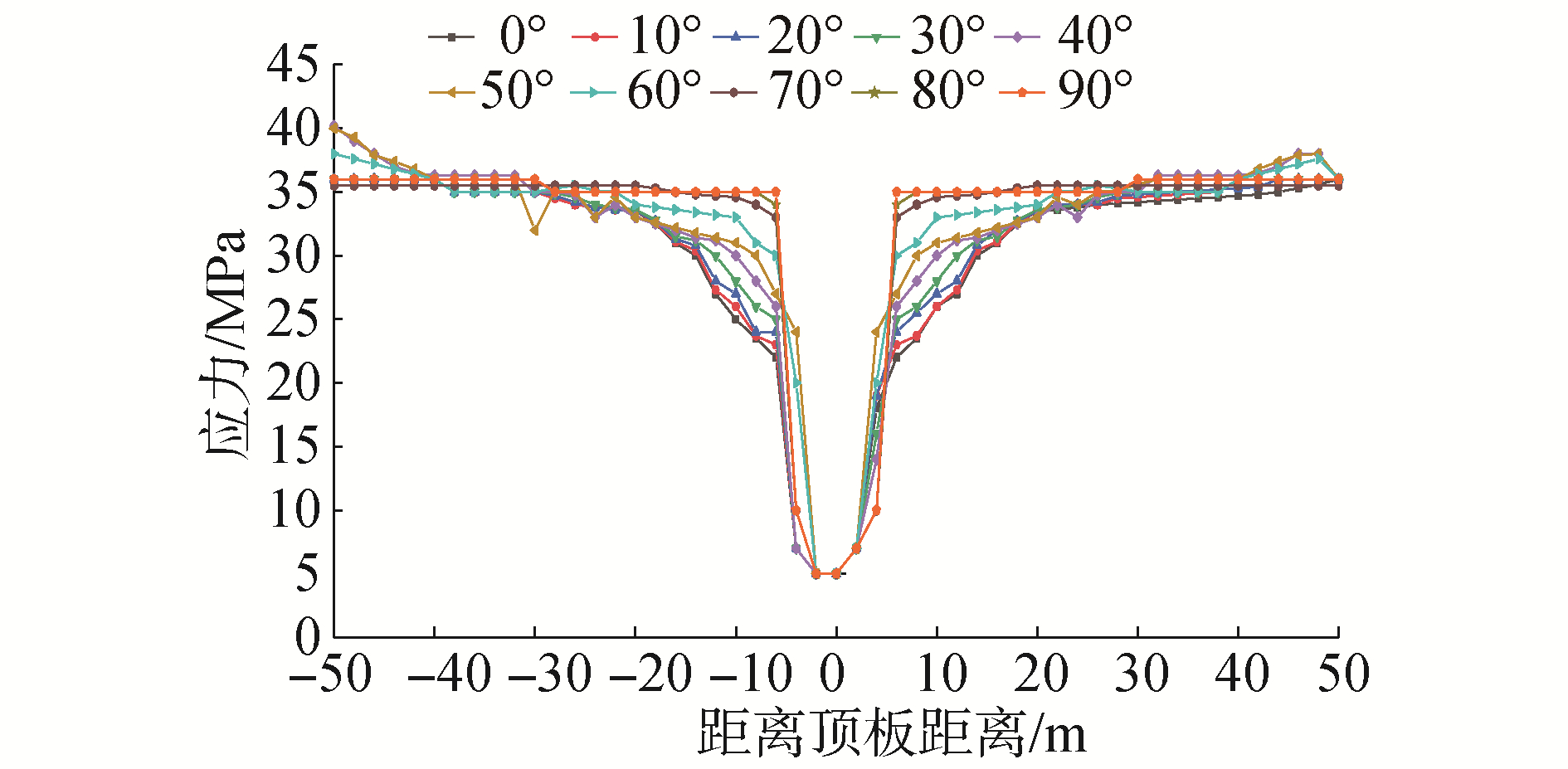
由图 3可知,随着最大水平主应力方向与巷道轴线夹角增大时,巷道两帮岩层卸压范围和卸压幅度响应增大,当夹角为0°时,卸压区范围0~20 m,距巷帮2.5 m处岩层垂直集中应力值为35.5 MPa,当夹角为90°时,卸压区范围2~42 m,距巷帮2.5 m处岩层应力值为22.6 MPa。巷道顶板与帮部围岩应力状态发生变化,锚杆支护状态也随之变化。
|
Download:
|
| 图 3 不同夹角巷道两帮垂直集中应力分布曲线 Fig. 3 Vertical concentrated stress distribution curve of two sides in different angle roadway | |
图 4为最大水平主应力方向与巷道轴线不同夹角情况下围岩最大主应力分布,可以看出巷道开挖后其周边围岩存在一定范围的环状应力降低区,最大水平主应力方向与巷道轴线夹角为30°时,巷道锚固区内围岩应力显著高于夹角为0°时,并且在顶板出现明显应力集中,随着夹角的增大顶底板高应力区范围和应力集中程度相应增大,顶板岩层高应力范围和应力集中程度显著大于底板。

|
Download:
|
| 图 4 最大水平主应力方向巷道围岩应力分布 Fig. 4 Stress distribution of surrounding rock in roadway with different maximum horizontal principal stress | |
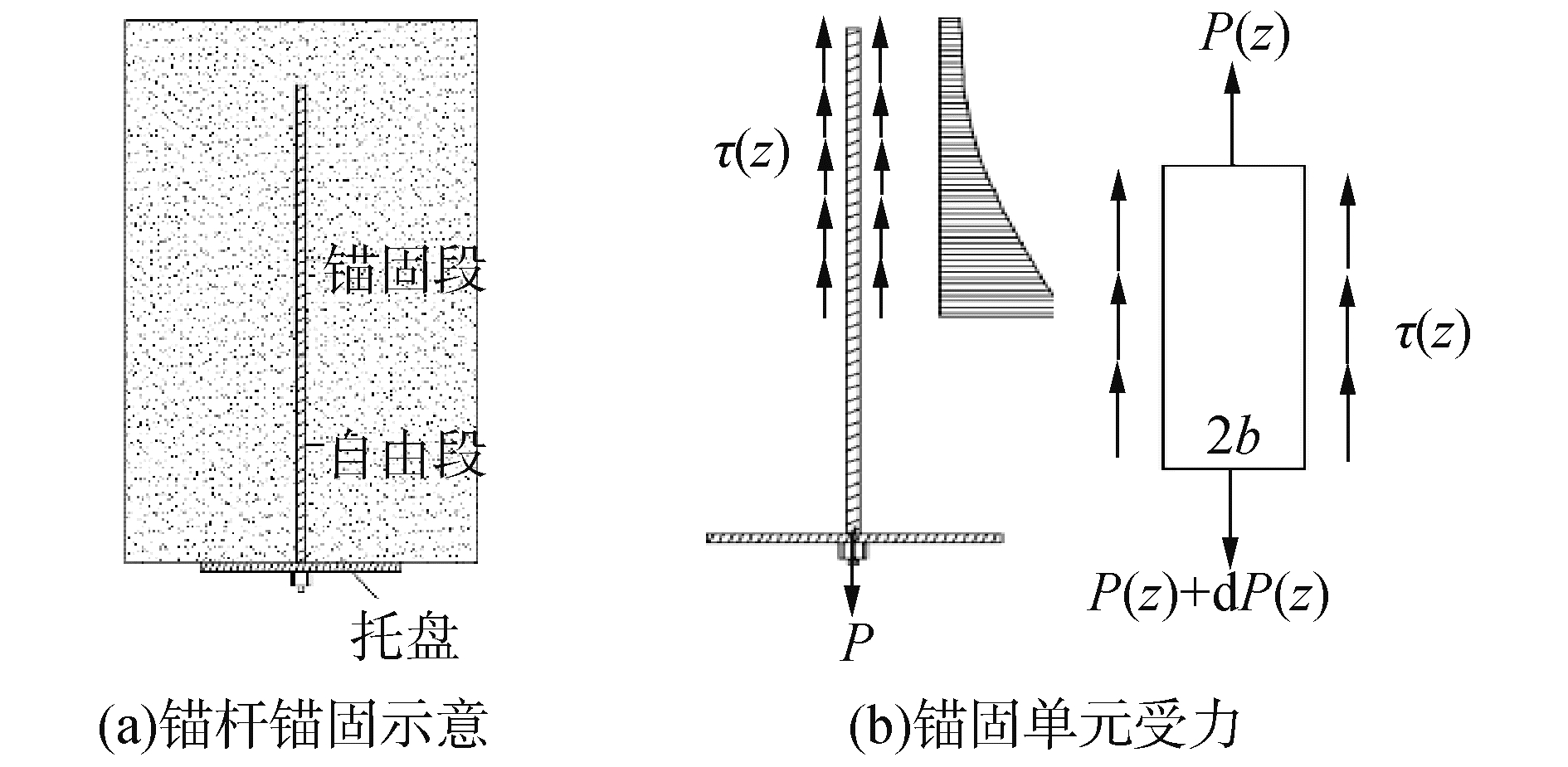
岩石锚杆抑制围岩变形的结果是使其轴力增大,如图 5(a)所示,由于锚杆自由段对锚杆的拉拔作用,使得在锚杆锚固段产生较大的背离巷道洞壁的拉拔剪应力,同时锚杆锚固段处于围岩稳定区,进一步限制围岩变形,锚杆自由段对锚杆锚固段界面外向剪应力拉拔作用的减弱,使得锚杆锚固段界面剪应力迅速衰减直至锚杆终端,如图 5(b)所示。
|
Download:
|
| 图 5 锚杆锚固系统 Fig. 5 Rock bolt and surrounding rock anchor system | |
由文献[9]知,对于锚杆因拉拔而产生的剪应力,假定锚杆锚固段与岩体的变形处于弹性状态,两者变形都满足变形协调条件,设τ(z)为锚固段沿z轴对岩体产生的剪应力,则τ(z)引起锚固外端O点的位移数值上等于锚固段的总伸长量, 由半无限体受集中力作用的Mindlin解可导出锚固段锚杆界面剪应力满足的常微分方程及计算出锚固段端点的轴力:
| $ {\tau ^{\prime \prime }} + rk{\tau ^\prime } + rk\tau = 0 $ | (1) |
| $ k = \frac{{4{\rm{ \mathsf{ π} }}G}}{{(3 - 2\mu ){E_a}A}} $ | (2) |
式中:Ea为锚杆杆体弹性模量;μ为锚固段围岩泊松比。
根据边界条件当r→∞, τ=0, 求解上述方程可得最后可得锚杆所承受的剪应力沿杆体分布:
| $ \tau = \frac{p}{{{\rm{ \mathsf{ π} }}b}}\left( {\frac{1}{2}tx} \right){{\rm{e}}^{\left( { - \frac{1}{2}t\frac{{{E_r}}}{{{E_a}}}{x^2}} \right)}} $ | (3) |
式中:b为锚杆杆体半径;p为锚杆自由端轴力;t表示为:
| $ t = \frac{1}{{(1 - \mu )(3 - 2\mu ){b^2}}} $ | (4) |
式中Er为锚固段围岩等效弹性模量。
由此可得锚杆锚固段轴力为:
| $ p(x) = p - \int_{{x_1}}^x 2 \tau {\rm{ \mathsf{ π} }}b{\rm{d}}x = p{{\rm{e}}^{ - \frac{1}{2}t}}^{\left( {\frac{{{E_r}}}{{{E_a}}}} \right)\left( {x - {x_1}} \right)} $ | (5) |
式中x1为自由端长度。
根据方程(5)可得,锚杆锚固段轴力受到锚杆锚固端围岩等效弹性模量以及锚杆自由段轴力共同作用,等效弹性模量并不是常量,而是关于巷道位置与最大水平主应力作用的函数。围岩锚固段等效弹性模量越大,锚杆锚固段所受轴力越小;巷道掘进方向与水平应力呈30°以下时,巷道围岩整体稳定较好,锚杆自由段轴力相差不多,但巷道帮部和顶板围岩应力集中不同,造成围岩锚固段裂隙发育程度不同,使得围岩等效弹性模量不同,锚杆在锚固段轴力不同;在巷道掘进方向与水平应力呈30°以上时,巷道处于高水平应力,应力由两帮向顶板转移,巷道顶板围岩较易破碎,锚杆自由段轴力较大,锚杆锚固段等效弹性模量小,处于高水平应力下的顶板锚杆相对于处于低水平应力下的顶板锚杆所受到锚杆锚固段轴力大,因此顶板成为支护重点。
通过数值模拟验证,由图 6得最大水平主应力方向与巷道轴线不同夹角情况下模型中部界面(y=50)锚固区锚杆轴力分布,锚杆编号从底脚锚杆自左至右按顺时针编号分别为1~13号。

|
Download:
|
| 图 6 不同水平主应力方向巷道锚杆轴力分布 Fig. 6 Axial force distribution of roadway bolt with different horizontal principal stress | |
由图 7(a)~(d)可知,在锚杆对称布置情况下,锚杆轴力也呈现对称关系,杆体自由段轴力大于锚固段,顶部锚杆轴力随着夹角的增大相应增大,呈现正相关,其中正顶锚杆(7#)轴力增幅最大,向两侧逐渐递减。随着夹角的增大两帮锚杆轴力变化不明显。

|
Download:
|
| 图 7 不同水平主应力方向巷道锚杆分段轴力分布曲线 Fig. 7 Distribution curve of axial force distribution of roadway with different horizontal principal stress | |
图 7为最大水平主应力方向与巷道轴线夹角在0°,10°,…,90°等10种情况下巷道不同位置锚杆轴力分布。
整体上锚杆自由段轴力均大于锚固段,由图 7(a)、(b)可知,当夹角在0°~30°范围内顶板轴力普遍小于两帮锚杆,顶板各位置处锚杆轴力大致相等,即轴力分布曲线呈“凹”状。由图 7(b)可知当夹角为30°时顶板锚杆和帮部锚杆轴力大致相等,即轴力分布曲线呈“口”状。由图 7(b)、(d)可知,当夹角在40~90°顶板锚杆轴力普遍大于两帮锚杆,且随着夹角的增大顶部锚杆轴力显著增大,即轴力分布曲线呈“凸”状,其中拱顶锚杆(7#)增幅最大,当夹角0°时,拱顶锚杆自由端轴力120.7 kN,当夹角90°时,拱顶锚杆自由端轴力249 kN,增幅128 kN;两帮锚杆轴力呈减小趋势。
由上述分析可知,在锚杆对称布置情况下,其轴力分布呈典型的对称性。随着最大水平主应力与巷道轴线夹角的增大,顶部锚杆轴力显著增加,帮部锚杆轴力不增反减,即锚杆轴力分布曲线依次向“凹”、“口”、“凸”状演化。现选取正顶7#锚杆和左帮锚杆3#锚杆为研究对象,更深入的剖析不同夹角下锚杆轴力演化规律。
2.4 不同夹角相同位置处锚杆轴力分布规律图 8为最大水平主应力方向与巷道轴线不同夹角情况下左帮3#锚杆轴力分布曲线,图 8(a)表示沿锚杆长度锚杆轴力分布特点。横轴锚杆长度1.5 m以内为自由段,1.5~2.5 m为锚固段,为更清晰的表示不同水平夹角下,锚杆相同分段长度的锚杆轴力特点,图 8(b)表示不同水平夹角下锚杆在某一位置处轴力变化。

|
Download:
|
| 图 8 3#锚杆轴力分布 Fig. 8 Axial force distribution 3# bolt | |
可知,某一夹角条件下,帮部锚杆自由段轴力大于锚固段,锚杆自由端轴力相等,锚固段轴力呈负指数规律递减。随着夹角增大,锚杆轴力减小,即呈现负相关,自由端轴力从150 kN下降至125 kN,轴力下降了1/6,同时锚固段轴力也相应下降。
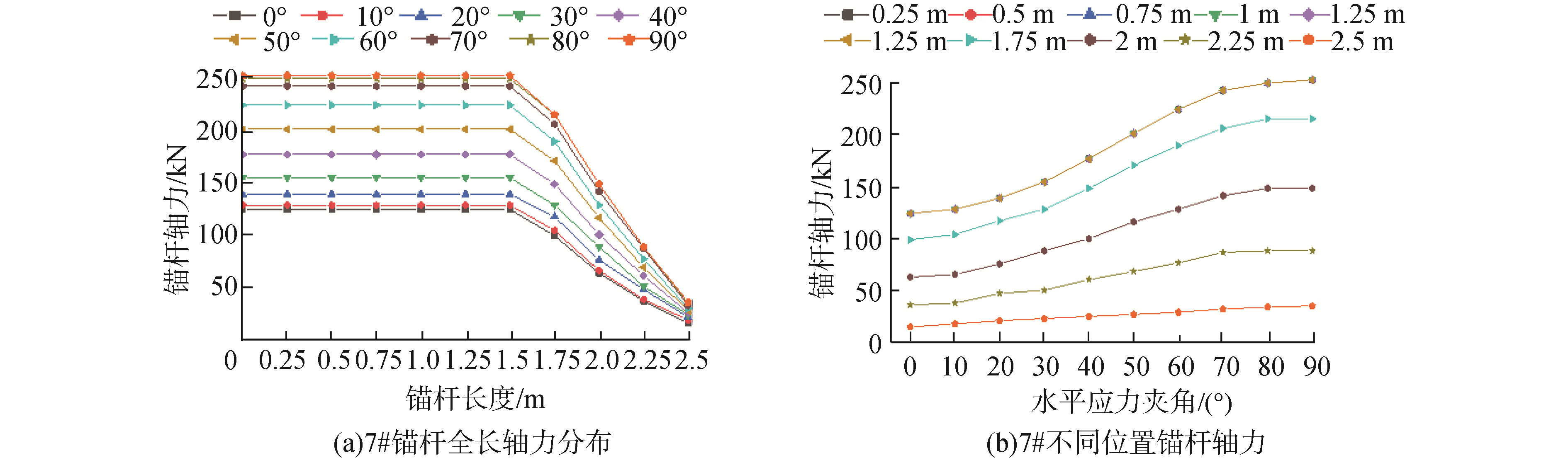
图 9为最大主应力方向与巷道轴线不同夹角情况下正顶7#锚杆轴力分布曲线,图 9(a)、(b)坐标轴及单位与图 8相同。可知,某一夹角条件下,与帮部锚杆类似顶部锚杆自由段轴力大于锚固段,锚杆自由端轴力相等,锚固段轴力呈负指数规律递减。随着夹角增大,锚杆轴力显著增加,即呈现正相关,自由段轴力从125 kN增大至250 kN,轴力增大2倍。同时锚固段轴力也相应增加。在0°~30°、70°~90°范围增加趋势平缓,30°~60°范围增加趋势显著。
|
Download:
|
| 图 9 7#锚杆轴力分布 Fig. 9 Axial force distribution 7# bolt | |
由上述分析可知,端部锚固锚杆沿杆体长度轴力分布可分为2个部分,其中自由段轴力相等,锚固段轴力呈负指数衰减,锚杆整体轴力分布曲线呈“乀”字状。随着最大水平主应力与巷道轴线夹角的增大,顶部锚杆轴力显著增加,与夹角大小呈正相关。帮部锚杆轴力不增反减,与夹角大小呈负相关。
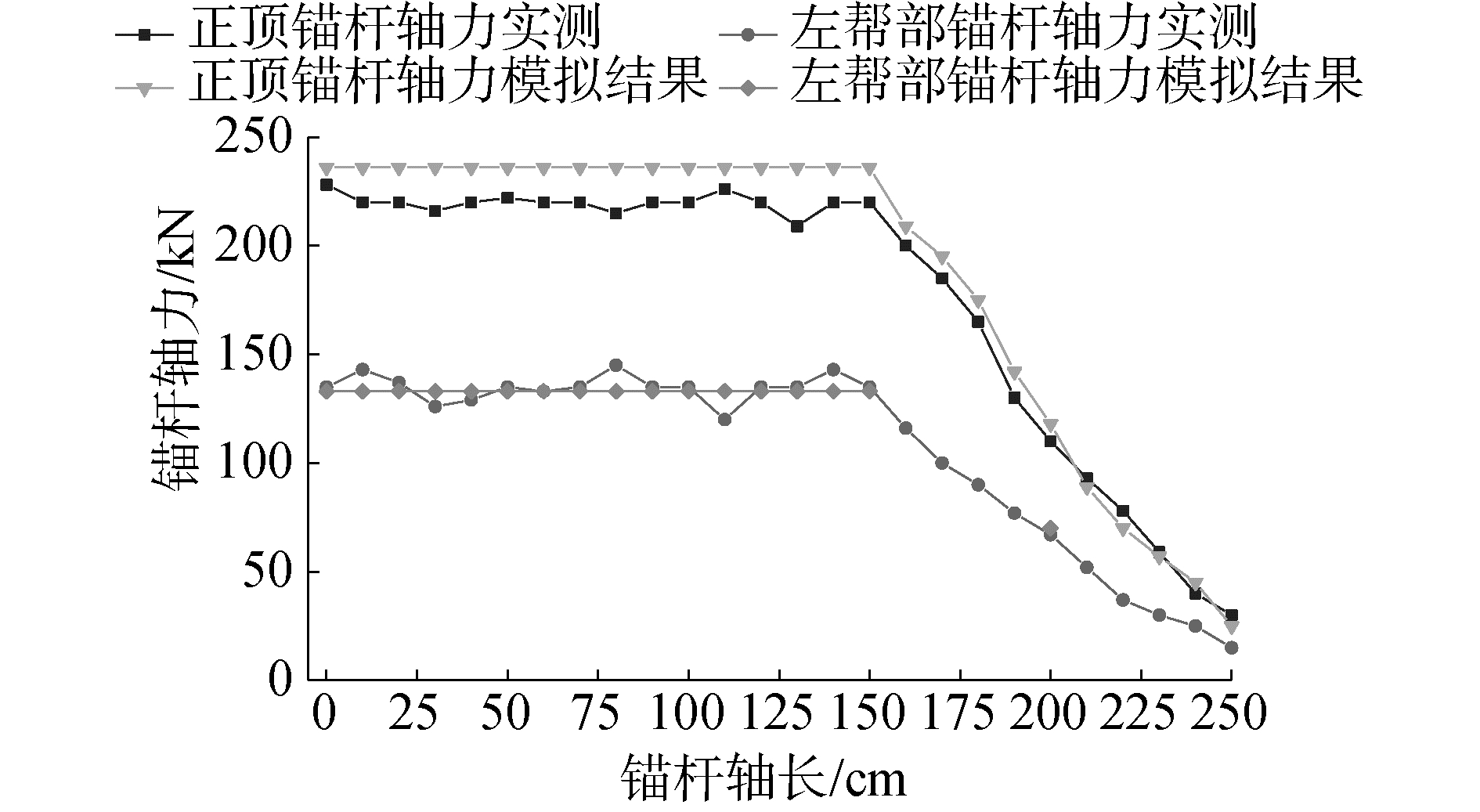
3 锚杆支护优化设计由淮南矿业集团潘三矿二水平东一11-2煤采区岩石回风巷道实测地应力成果,可知该范围最大水平主应力与巷道轴向夹角为77.4°,依据上述不同水平主应力方向巷道锚杆轴力分布图 6(c)、图 6(d),和不同水平主应力方向巷道锚杆轴力分布曲线7(c)、7(d)可知,在该地应力条件下,沿巷道轮廓线轴力分布曲线呈“凸”状,顶板锚杆轴力显著大于帮部锚杆,其中正顶锚杆自由段轴力最大达250 kN,帮部锚杆轴力最大值达150 kN,该类巷道顶板岩层的控制是巷道围岩稳定性控制的重中之重,同时巷道内布置矿压测站监测锚杆轴力及巷道顶板下沉量,监测仪器选用ZMY3.2矿用测力锚杆、顶板离层仪,测得现场锚杆轴力如图 10所示。
|
Download:
|
| 图 10 现场实测锚杆轴力 Fig. 10 Field measurement of anchor force | |
因此对原锚杆支护参数进行优化,帮部锚杆材质选择MG400,加强顶板支护强度,顶板锚杆材质选择MG500,顶板按“3-0-0-3”布置顶板锚索,锚杆间排距、锚杆直径和长度等参数不变。根据数值模拟结果,参照最大主应力方向与巷道轴线不同夹角在80°的情况,正顶锚杆轴力自由段轴力最大值为236 kN,帮部锚杆轴力自由段最大值138 kN,根据对称性,模拟提取数据只提取巷道正顶7#锚杆和左帮部3#锚杆轴力。提取现场正顶锚杆轴力数据和左帮部锚杆轴力数据,由上图可知,顶部和帮部锚杆轴力实测曲线与数值模拟结果形态相差不大,顶部锚杆轴力显著大于帮部锚杆,正顶锚杆轴力最大值接近220 kN,帮部锚杆轴力最大值为135 kN,实测数值与数值计算结果相吻合。
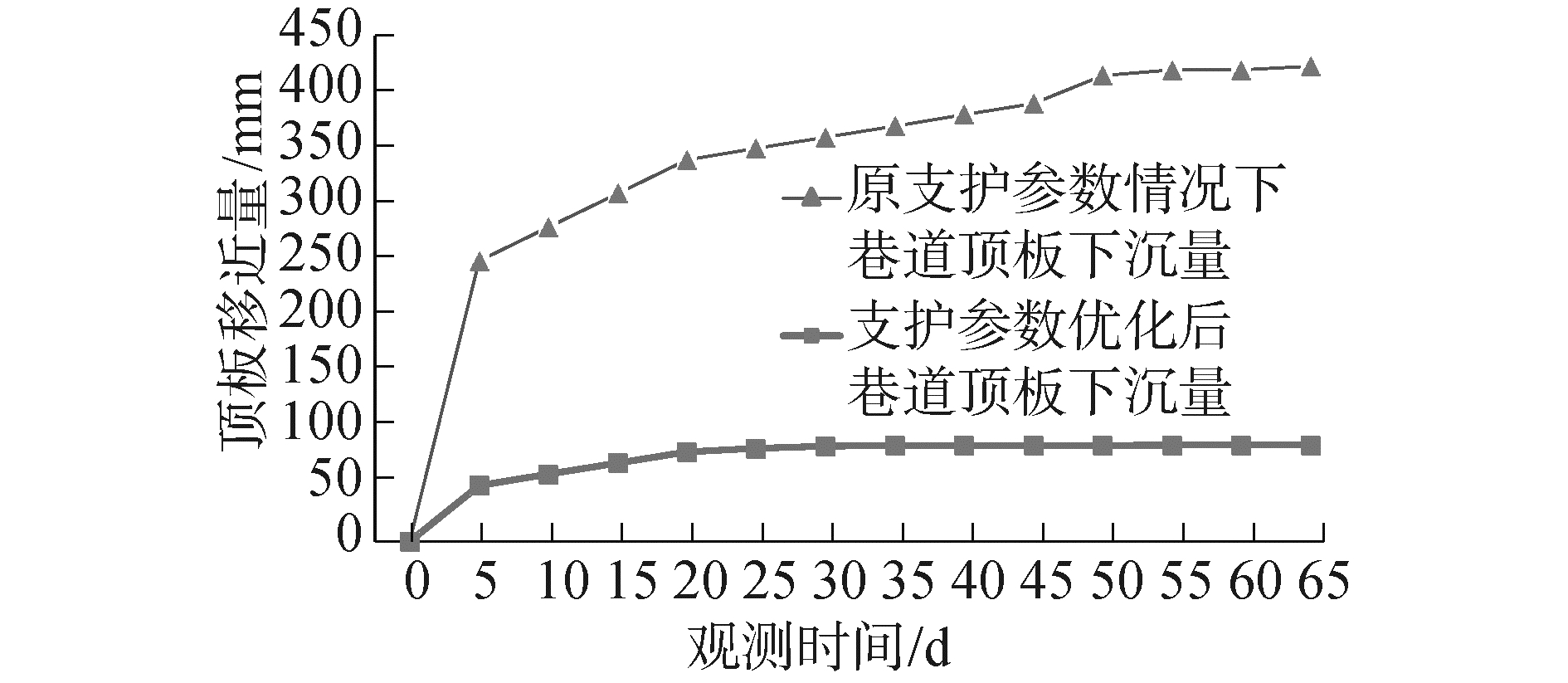
图 11为巷道顶板下沉量统计图,如图所示,在巷道开挖锚杆安装后前5天巷道顶板下沉速度较快,锚杆安装15 d后顶板下沉速度缓和并趋于稳定,按优化设计方案施工后,巷道顶板2个月下沉量为86 mm,下沉量仅为原来的1/5,围岩控制效果较好。
|
Download:
|
| 图 11 巷道顶板下沉量变化曲线 Fig. 11 Roadway roof displacement distribution | |
1) 采用数值模拟得出顶、底板应力分布和应力集中程度及其与最大水平主应力方向变化规律。锚杆轴力与围岩最大水平主应力的方向有相关性,顶部锚杆轴力与夹角呈正相关,而帮部锚杆轴力与夹角呈负相关。
2) 锚杆自由段轴力相等,锚固段轴力沿着围岩内部呈负指数衰减。随着夹角的增大,巷道断面锚杆轴力分布曲线依次向“凹”、“口”、“凸”状演化。
3) 巷道掘进方位与最大水平主应力方向为小夹角的原则进行巷道布置;对于方位与最大水平主应力夹角较大的巷道,顶板与帮部支护参数应进行分类设计。
4) 对于强化顶板支护尤其是加强正顶附近的围岩支护,须加多项措施实现巷道围岩稳定性控制。支护顶板优先选用全长锚固支护方式、提高锚杆预紧力及锚杆杆材强度。
| [1] |
康红普. 煤矿井下应力场类型及相互作用分析[J]. 煤炭学报, 2008, 33(12): 1329-1335. KANG Hongpu. Analysis on types and interaction of stress fields in underground coal mines[J]. Journal of China coal society, 2008, 33(12): 1329-1335. DOI:10.3321/j.issn:0253-9993.2008.12.001 (  0) 0)
|
| [2] |
袁亮, 薛俊华, 刘泉声, 等. 煤矿深部岩巷围岩控制理论与支护技术[J]. 煤炭学报, 2011, 36(4): 535-543. YUAN Liang, XUE Junhua, LIU Quansheng, et al. Surrounding rock stability control theory and support technique in deep rock roadway for coal mine[J]. Journal of China coal society, 2011, 36(4): 535-543. (  0) 0)
|
| [3] |
刘泉声, 刘恺德. 淮南矿区深部地应力场特征研究[J]. 岩土力学, 2012, 33(7): 2089-2096. LIU Quansheng, LIU Kaide. Characteristics of in-situ stress field for deep levels in Huainan coal mine[J]. Rock and soil mechanics, 2012, 33(7): 2089-2096. DOI:10.3969/j.issn.1000-7598.2012.07.026 (  0) 0)
|
| [4] |
陈浩, 任伟中, 李丹, 等. 深埋隧道锚杆支护作用的数值模拟与模型试验研究[J]. 岩土力学, 2011, 32(S1): 719-724, 786. CHEN Hao, REN Weizhong, LI Dan, et al. Numerical simulation and model test study of mechanism of bolt in deep tunnel[J]. Rock and soil mechanics, 2011, 32(S1): 719-724, 786. (  0) 0)
|
| [5] |
李元鑫, 朱哲明, 范君黎. 主应力方向对围岩稳定性的影响[J]. 岩土工程学报, 2014, 36(10): 1908-1914. LI Yuanxin, ZHU Zheming, FAN Junli. Effect of principal stress orientation on stability of surrounding rock of tunnels[J]. Chinese journal of geotechnical engineering, 2014, 36(10): 1908-1914. DOI:10.11779/CJGE201410019 (  0) 0)
|
| [6] |
康红普, 姜鹏飞, 蔡嘉芳. 锚杆支护应力场测试与分析[J]. 煤炭学报, 2014, 39(8): 1521-1529. KANG Hongpu, JIANG Pengfei, CAI Jiafang. Test and analysis on stress fields caused by rock bolting[J]. Journal of China coal society, 2014, 39(8): 1521-1529. (  0) 0)
|
| [7] |
谢广祥, 李传明, 王磊. 巷道围岩应力壳力学特征与工程实践[J]. 煤炭学报, 2016, 41(12): 2986-2992. XIE Guangxiang, LI Chuanming, WANG Lei. Mechanical characteristics and practical application on stress shell of roadway surrounding rock[J]. Journal of China coal society, 2016, 41(12): 2986-2992. (  0) 0)
|
| [8] |
尤春安, 战玉宝. 预应力锚索锚固段的应力分布规律及分析[J]. 岩石力学与工程学报, 2005, 24(6): 925-928. YOU Chunan, ZHAN Yubao. Distributing characters and analysis of stresses in prestressed cables[J]. Chinese journal of rock mechanics and engineering, 2005, 24(6): 925-928. DOI:10.3321/j.issn:1000-6915.2005.06.004 (  0) 0)
|
| [9] |
姚显春, 李宁, 陈蕴生. 隧洞中全长粘结式锚杆的受力分析[J]. 岩石力学与工程学报, 2005, 24(13): 2272-2276. YAO Xianchun, LI Ning, CHEN Yunsheng. Theoretical solution for shear stresses on interface of fully grouted bolt in tunnels[J]. Chinese journal of rock mechanics and engineering, 2005, 24(13): 2272-2276. DOI:10.3321/j.issn:1000-6915.2005.13.012 (  0) 0)
|
| [10] |
文竞舟, 张永兴, 王成. 隧道围岩全长黏结式锚杆界面力学模型研究[J]. 岩土力学, 2013, 34(6): 1645-1651, 1686. WEN Jingzhou, ZHANG Yongxing, WANG Cheng. Study of mechanical model of fully grouted rock bolt's anchorage interface in tunnel surrounding rock[J]. Rock and soil mechanics, 2013, 34(6): 1645-1651, 1686. (  0) 0)
|
| [11] |
鲁岩, 邹喜正, 刘长友, 等. 构造应力场中的巷道布置[J]. 采矿与安全工程学报, 2008, 25(2): 144-149. LU Yan, ZOU Xizheng, LIU Changyou, et al. Roadway layout in tectonic stress field[J]. Journal of mining & safety engineering, 2008, 25(2): 144-149. DOI:10.3969/j.issn.1673-3363.2008.02.004 (  0) 0)
|
| [12] |
孙玉福. 水平应力对巷道围岩稳定性的影响[J]. 煤炭学报, 2010, 35(6): 891-895. SUN Yufu. Affects of in-situ horizontal stress on stability of surrounding rock roadway[J]. Journal of China coal society, 2010, 35(6): 891-895. (  0) 0)
|
| [13] |
梁正召, 龚斌, 吴宪锴, 等. 主应力对洞室围岩失稳破坏行为的影响研究[J]. 岩石力学与工程学报, 2015, 34(S1): 3176-3187. LIANG Zhengzhao, GONG Bin, WU Xiankai, et al. Influence of principal stresses on failure behavior of underground openings[J]. Chinese journal of rock mechanics and engineering, 2015, 34(S1): 3176-3187. (  0) 0)
|
| [14] |
赵一鸣, 张农, 郑西贵, 等. 千米深井厚硬顶板直覆沿空留巷围岩结构优化[J]. 采矿与安全工程学报, 2015, 32(5): 714-720. ZHAO Yiming, ZHANG Nong, ZHENG Xigui, et al. Structural optimization of overlying strata for gob-side entry retaining in 1000 m deep mine with direct thick and hard roof[J]. Journal of mining & safety engineering, 2015, 32(5): 714-720. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


