2. 西南交通大学 土木工程学院, 四川 成都 610031
2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China
季节性冻土区具有较强的地域性,土层结构连续性差,经过寒季、夏季冻融循环作用,路基病害较为严重,给公路的正常运行造成了安全隐患,同时需要花费大量的维修资金对该类路基进行养护[1-2]。如果能够准确掌握季节性冻土类路基随地温变化的变形影响因素,预测其工后融沉值,根据预测结果来制定科学、合理的工程建设方案,可提高路用性能[3]。
当前阶段针对季节性冻土区路基的研究主要为路基的沉降方面,对于路基未来阶段的变形发展趋势预测方面,现有的理论预测模型在实际应用方面存在一定的弊端,主要体现在:单一的预测方法仅适用于一种工况,难以准确拟合受到多种因素影响的路基变形变化规律,导致其最终预测的沉降值偏大或是偏小,预测精度相对较差[4-5]。文献[6]提出的预测模型是采用灰色预测理论对路基未来阶段的变形情况进行预测,对预测结果采用马尔可夫过程进行修正,这种预测模型中参数是基本不变的,不受路基影响因素等变化而变化,但数据量较大时,会影响该模型的预测精度,具有一定的局限性。文献[7]根据路基沉降的变形趋势及其沉降曲线的变化特点,选择具有成长曲线特征的单相预测模型结合支持向量机理论构建组合预测模型。该模型给出的路基变形沉降曲线具有一定的确定性变化规律,但无法因路基沉降观测数据的变化而不断调整,及时将周期性观测数据的变化趋势输入预测模型中,其预测结果仅取决于模型参数的选取,预测的变形量与实际变形量往往偏差较大,应结合季节性冻土区路基变形的实测与模拟结果选取合适的预测模型。
本文针对季节性冻土区路基高边坡热稳定性质的特殊性,依托季节性冻土区路基观测系统,在分析相关监测数据的基础上,对季节性冻土区路基高边坡变形特征及其热稳定性影响因素进行分析;以测试路段的高边坡变形实测数据为训练样本,采用支持向量机算法构建路基变形多因素时变预测模型,并借助该模型对季节性冻土区路基高边坡变形展开预测分析,并进一步完善了季节性冻土区路基高边坡变形的预测理论。
1 季节性冻土区路基高边坡变形特征与影响因素分析季节性冻土区路基变形通常与土体的构造类型、工程地质条件、路基建设质量、道路挖掘以及所处区域所受太阳辐射等条件相关[8]。图 1为路基边坡事故与治理实际拍摄图。

|
Download:
|
| 图 1 边坡治理工程 Fig. 1 Slope treatment project | |
以上图环境为测试区域,设置65个观测断面和4个气象站,监测周期从2016年1月—2017年12月底结束,通过对目标冻土区路基高边坡断面进行长期变形监测、地温监测和气温监测,得到较为全面的路基高边坡变形数据,冻土区路基高边坡变形表现可总结为以下3个特点。
1) 目标冻土区路基在完成一个冻融循环后,路基高边坡变形稳定性较好。
依托于2017年目标冻土区路基变形监测数据,对季节性冻土区路基高边坡变形量进行统计,从观测的监测数据可知变形量低于20 mm,沉降速率小于2 cm/a的路基断面数量可达55个,占整体路基断面的92.2%,在高于20 mm,小于50 mm范围内的路基断面共有5个,这部分占整体比例的7.8%。根据路基设计规范内容:路基设计避免高填深挖,不能避免时,当路基中心填方高度超过20 m或中心挖方深度超过30 m时,宜结合路线方案与桥梁、隧道等构造物或分离式路基进行方案比选;路基设计应控制路基工后沉降量,对软弱地基、路基与桥涵结构物连接处、路基填挖交界处、高路堤、陡坡路堤等,应采取综合措施,防止路基不均匀变形;路基设计应考虑水和冰冻对路基性能的影响,设置完善的防排水系统或防冻害设施,以及必要的路基防护工程等。将其规范要求作为参考,目标冻土区路基变形稳定性较好。
2) 季节性冻土区路基高边坡变形可分为冻胀、融沉2部分,整体表现为融沉冻胀循环。图 2给出目标冻土区路基沉降曲线。其中,横断面A10代表沉降速率小于2 cm/a的路基断面,A23代表沉降速率小于50 mm范围内的路基断面。

|
Download:
|
| 图 2 目标冻土区路基沉降曲线 Fig. 2 Settlement curve of roadbed in target frozen ground | |
分析图 2可以看出,寒季时,目标冻土区活动层温度始终低于0 ℃以下,路基出现冻胀。暖季时,冻土区活动层温度始终上升到0 ℃以上,路基高边坡出现融沉变形,且波动幅度较比寒季时大[9]。在每一个冻融循环内,路基高边坡变形反映为冻胀变形和融沉变形,这两种变形彼此影响,且融沉变形沉降量的波动幅度要明显高于冻胀变形幅度,整体呈现缓慢下沉变形,且随着季节性变化,路基变形速度慢慢降低,但在短时域内不会停止。
3) 目标冻土区阴阳面较为显著的路基高边坡,其相应的截断面上的变形呈现出左右不均。
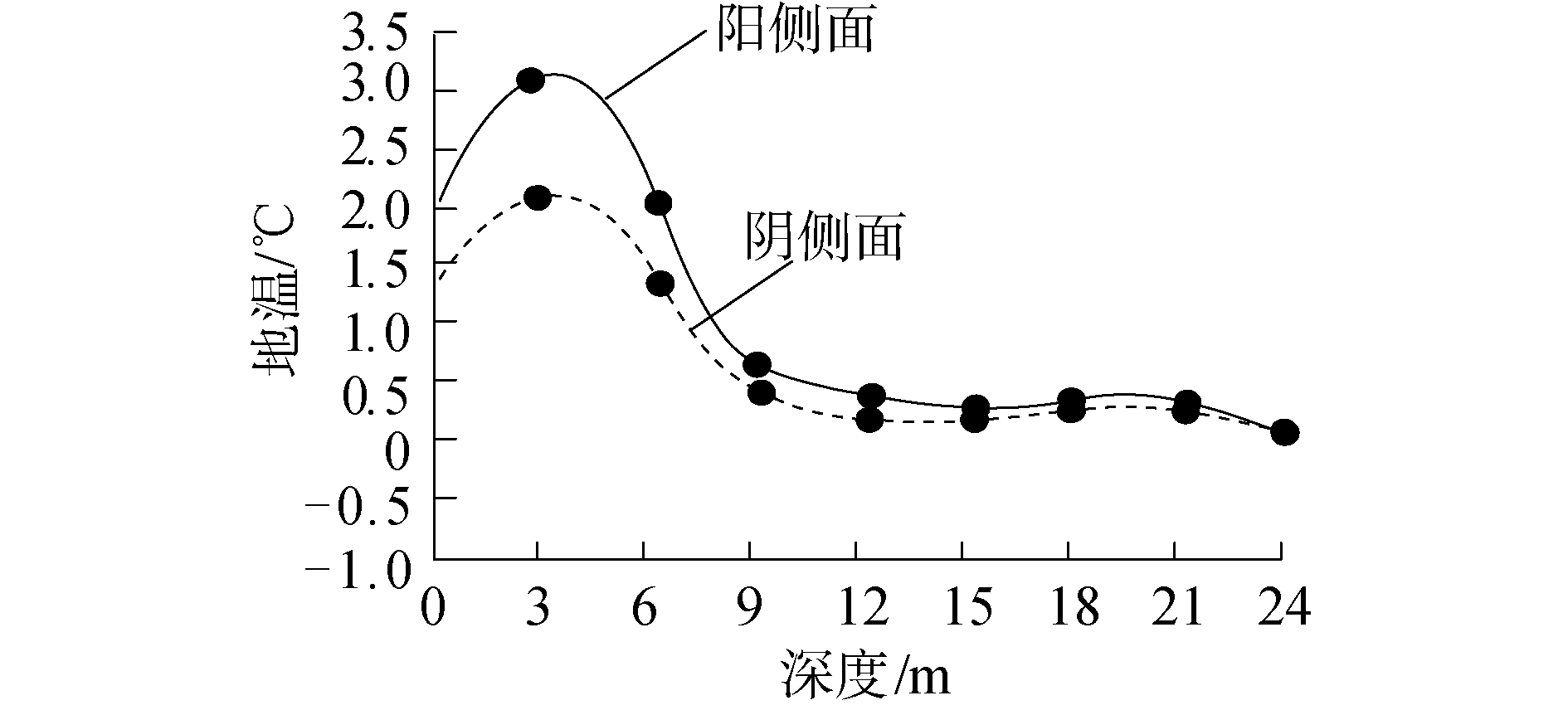
图 3给出了目标冻土区阴阳坡2017年10月平均地温曲线。
|
Download:
|
| 图 3 目标冻土区阴阳坡2017年10月平均地温曲线 Fig. 3 The average ground temperature curve of October 2017 in the target frozen soil area | |
分析图 3可知,所研究的路基高边坡因受到太阳辐射因素的影响,阳坡面地温明显高于阴坡面地温,因温差而导致路基阴阳坡沉降出现差异。引起冻土区路基高边坡发生变形的影响因素有很多,其中导致路基边坡稳定性变差的主要原因有路旁土地开挖、地层温度变化和大气热转换引起路基形变。
以大型有限元分析商业软件ANSYS为分析工具,岩体采用6节点三角形平面单元PLANE2模拟,接触单元采用TARGE169和CONTA172单元。通过单元生死功能模拟开挖施工过程。通过对模型强度参数的折减,使高边坡达到临界破坏状态,根据折减系数的大小得出高边坡的稳定性系数。
道路路旁土地开挖前和开挖后的高边坡的模拟结果,如图 4所示。

|
Download:
|
| 图 4 路旁土地开挖前后不同方向稳定性系数 Fig. 4 Stability coefficients in different directions before and after roadside excavation | |
由图 4可以看出,在路旁土地开挖前,路基的横向、纵向稳定性系数大概为2.77、1.78,而在路基旁道路进行挖掘后,其稳定系数发生了变化,横向、纵向稳定系数分别为2.55、1.78。稳定性的变化主要发生在横向方向,说明土地的开挖影响了路基的横向稳定性,因此路基的抗震性就会明显下降,增加其发生事故的概率。
路基阴阳坡热分布的差异直接影响冻土层温度场的分布,引起路基变形。相关统计结果表明,路基阳坡的沉降变形多数大于路基阴面,说明阳面冻土层的温度场变化幅度更大,也可以视为冻土层高边坡阴阳侧差异与路基变形呈正相关。
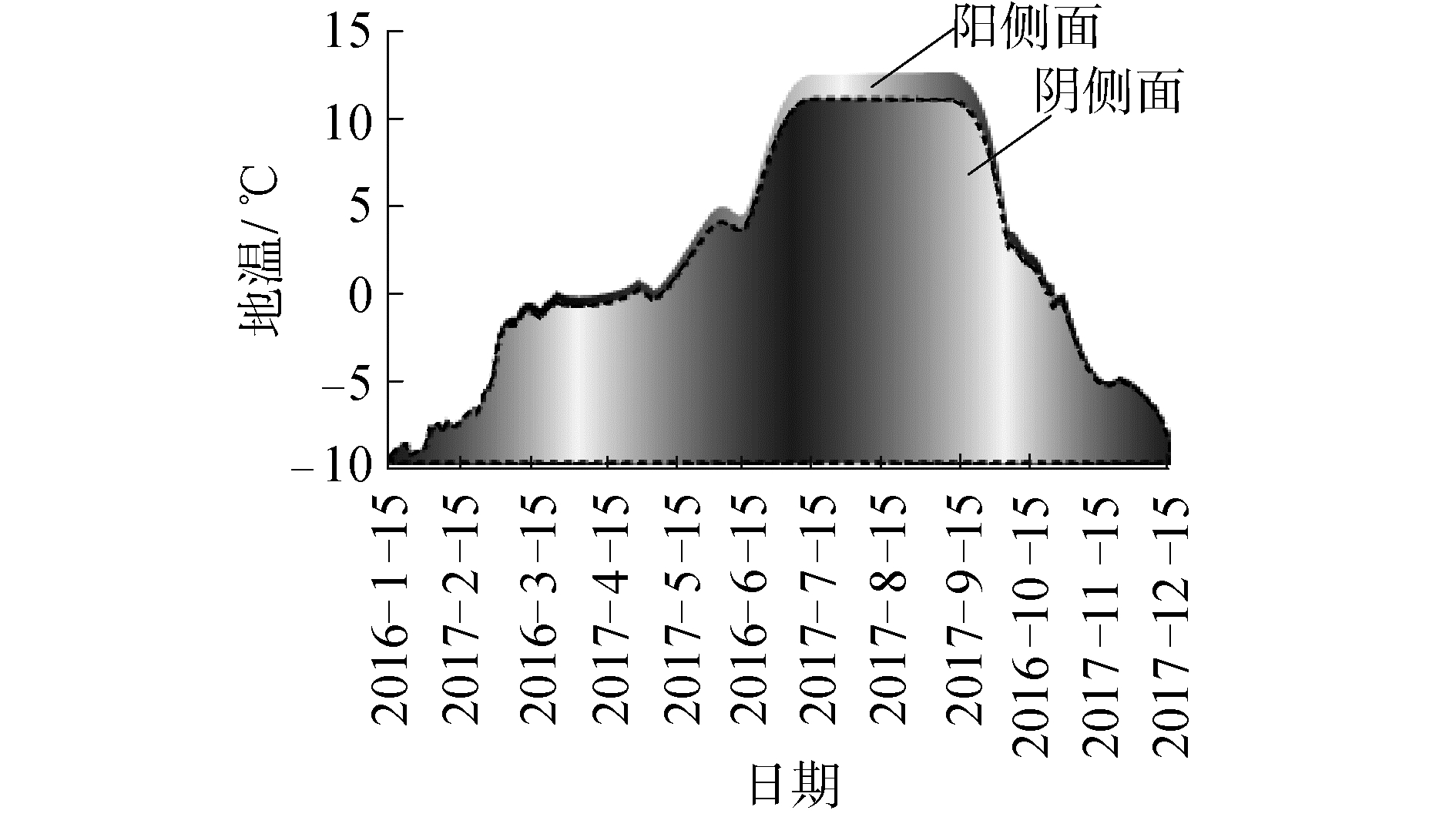
将目标冻土区路基高边坡阴阳侧地温线与路基变形曲线进行对比分析可以看出,目标冻土区路基高边坡阳侧面地温要明显高于阴侧面,路基变形曲线也呈现出路基阳侧面的变形量明显高于阴侧面的情况。依托于2017年目标冻土区路基变形监测数据,对目标路基高边坡横断面2016年—2017年的地温绘制曲线,如图 5所示。
|
Download:
|
| 图 5 目标冻土区路基高边坡断面地温变化过程曲线 Fig. 5 Process curve of ground temperature variation in high slope section of roadbed in permafrost area | |
分析图 5可知,目标冻土区路基高边坡断面地温变化呈现出2种变化规律:1)目标冻土区路基高边坡朝阳侧的地温始终高于背阴侧;2)寒季路基地层温度差异较大,路基阳侧面温度要比阴侧面高。
选取2016年1月—2017年1月的冻土区路基变形监测数据作为一个周期对路基地层温度进行分析,结果如表 1所示。
| 表 1 监测期间路基地层温度统计结果 Table 1 Road base layer temperature statistics during monitoring |
分析表 1可知,目标冻土区路基高边坡阴侧面的冻结指数为阳侧面的2倍多,高边坡阴侧面的融化指数为阳侧面的4/5左右。
依托于2017年目标冻土区路基变形监测数据,分析可得路基变形过程与地温的波动变化关系,如图 6所示。

|
Download:
|
| 图 6 冻土区路基变形过程与地温的年波动变化关系 Fig. 6 Relationship between annual deformation of subgrade deformation and ground temperature in permafrost region | |
分析图 6可知,寒季时,目标冻土区路基地温降低,土体冻结,整体路基形变表现为冻胀变形;夏季时,目标冻土区路基地温逐渐升高,土体融化,路基高边坡变形主要表现为下沉变形;且寒季时目标冻土区路基冻胀变形速度小于融沉变形速度,变形趋势为下沉变形。
从图 6中变形过程可以看出,路基的冻胀变形主要表现在11月份~次年3月之间,路基的沉降变形主要表现在4月~12月份之间,符合所研究地区路基高边坡变形的季节性变化特点。
太阳辐射、目标冻土区路基材料表面与大气的热转换是路基高边坡的主要热源,热量向路基温度场较低的方向传送,目标冻土中冰融化产生融沉现象,导致路基高边坡的变形。
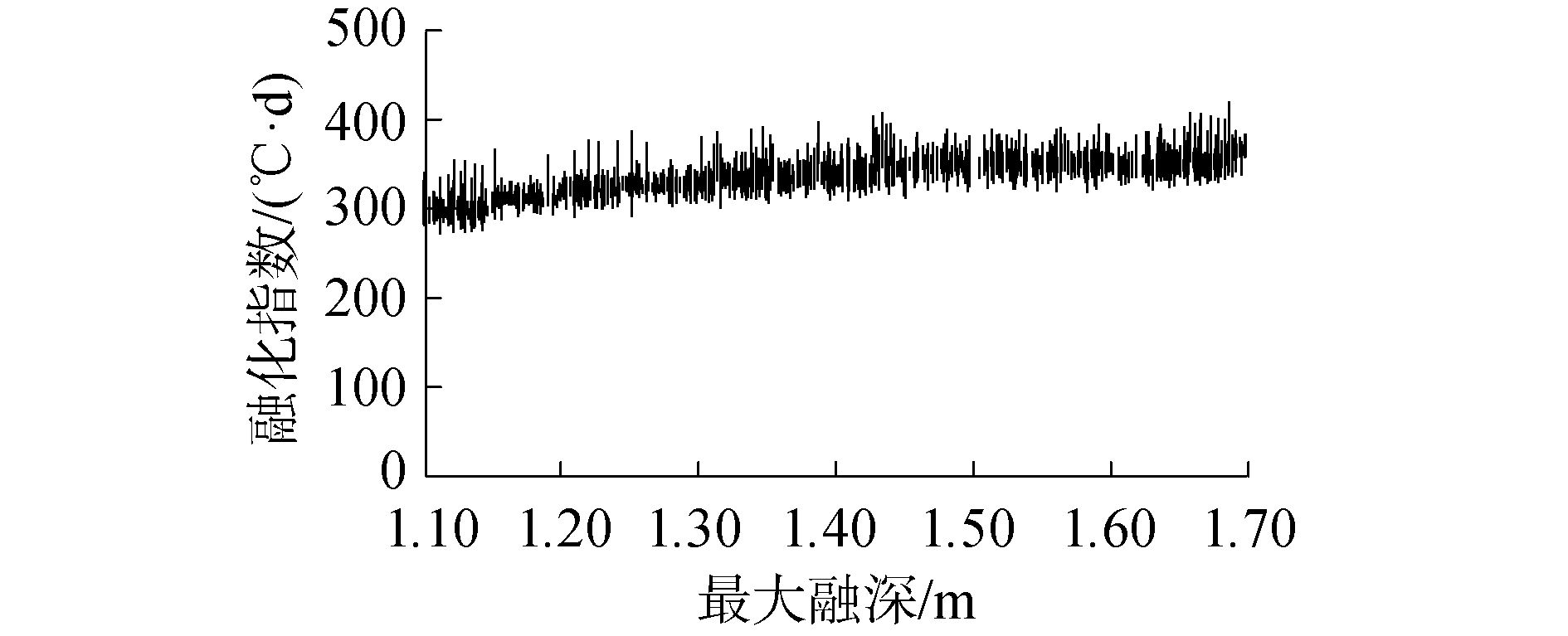
所研究区域路基总积温(融化指数)与其融化深度之间存在较为显著的相关关系,如图 7所示。分析图 7可知,目标冻土区路基最大融深与融化指数表现出正相关,证明底层温度变化以及大气热转换也是影响季节性冻土区路基发生变形的主要影响因素。
|
Download:
|
| 图 7 目标冻土区路基最大融深与融化指数 Fig. 7 Maximum melt depth and melting index of roadbed in target frozen ground | |
以监测路段通车后2年的路基高边坡变形实测数据作为样本,以结构风险最小为原则,通过对样本数据的选择性学习,得到路基高边坡变形各个影响因素之间的内在联系,并通过合理地选取函数子集以及判别函数构建最优函数,以最优函数建立季节性冻土区路基高边坡变形多因素时变预测模型,实现了对季节性冻土区高边坡变形的高精度预测,具体过程如下所述:
在进行季节性冻土区路基高边坡变形预测前,将路基高边坡变形实测数据样本集中的各个样本Di描述为输入向量xi和输出值yi的组合形式,Di=(xi, yi),依据上述描述形式,可将yi与xi之间的映射关系描述为:
| $ {y_i} = g\left( {{\mathit{\boldsymbol{x}}_i}} \right) = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}\left( {{\mathit{\boldsymbol{x}}_i}} \right) + b $ | (1) |
式中:b表示分类阈值;φ表示支持向量机[10]分类面的权值向量;φ(xi)表示向量空间转换的映射函数。对判别函数进行规整化处理,可得到变形实测数据样本点值最优分类面之间的距离δi,即:
| $ {\delta _i} = \frac{1}{{\left\| \mathit{\boldsymbol{\omega }} \right\|}}\left| {g\left( {{\mathit{\boldsymbol{x}}_i}} \right)} \right| $ | (2) |
使δi为最大,则‖ω‖应最小,即最优分类面。对季节性冻土区路基高边坡变形趋势的预测可通过将最优函数的获取转换成存在约束的极值求解问题,即:
| $ \left\{ {\begin{array}{*{20}{l}} {\min J(\mathit{\boldsymbol{\omega }}, \xi ) = \frac{1}{2}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{\omega }} + \frac{1}{2}C{\delta _i}\sum\limits_{i = 1}^n {\xi _i^2} }\\ {{y_i} = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{\omega }}\left( {{\mathit{\boldsymbol{x}}_i}} \right) + b + {\xi _i}} \end{array}} \right. $ | (3) |
式中:J(ω, ξ)用于描述优化函数;ξi表示预测误差;C表示惩罚系数。根据拉格朗日乘法对存在约束的极值进行求解,则有:
| $ \begin{array}{*{20}{c}} {L(\mathit{\boldsymbol{\omega }}, b, \zeta , a) = J(\mathit{\boldsymbol{\omega }}, \xi ) - }\\ {\sum\limits_{i = 1}^n {{a_i}} \left[ {{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\varphi \left( {{\mathit{\boldsymbol{x}}_i}} \right) + b + {\xi _i} - {y_i}} \right]} \end{array} $ | (4) |
式中:ai表示拉格朗日乘子。在获得的解中,不满足ai≠0的向量为支持向量,结合灰色理论以最优函数构建季节性冻土区路基高边坡变形多因素时变预测模型:
| $ Q = \sum\limits_{t = 1}^n L (\mathit{\boldsymbol{\omega }}, b, \zeta , a) $ | (5) |
为了验证季节性冻土区路基高边坡变形多因素时变预测模型的综合有效性,对季节性冻土区路基高边坡变形影响因素进行量化处理,影响边坡稳定的因素有很多,包括地质构造、水平向位移和路基沉降等,其中影响最大的是路基沉降问题,因此实验以路基沉降为研究目标,同时,由于路基高边坡变形实测数据样本中不同影响因素数值间存在明显差异,为了有效减少预测误差,将测试样本数据在[0, 1]内进行规整化处理,将其转换为区间相对值,以下给出其规整化映射函数:
| $ f(x) = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} $ | (6) |
式中x表示测试样本数据。由式(6)转换后,将测试样本中的前5组数据集作为支持向量机学习的训练集,构建季节性冻土区路基高边坡变形多因素时变预测模型。选取季节性冻土区路基高边坡2个断面(K-CA,K-CB)的已监测沉降数据进行分析。
为了对比所提模型、文献[6]模型以及文献[7]模型的精度,引入绝对误差平方和与相对误差平方和作为评价指标:
| $ S = \sum\limits_{t = 1}^n {{{\left( {{S_t} - {y_t}} \right)}^2}} $ | (7) |
| $ E = \sum\limits_{t = 1}^n {{{\left( {\frac{{{S_t} - {y_t}}}{{{y_t}}}} \right)}^2}} $ | (8) |
式中:绝对误差平方S和与相对误差平方和E均为常数。
分别采用所提模型、文献[6]模型以及文献[7]模型计算出的路基高边坡断面(K-CA)变形预测沉降量如表 2所示,模型精度误差如表 3所示。
| 表 2 断面变形沉降实测值与预测值 Table 2 Deformation vertical displacement settlements actual and predicted values |
| 表 3 断面变形沉降预测模型的精度对比 Table 3 Comparison of accuracy of vertical displacement settlement prediction model for section deformation |
分析表 2和表 3可知,对路基高边坡断面(K-CA)的沉降量进行预测,文献[6]模型拟合精度较文献[7]模型好,但拟合值小于实测值,而文献[7]模型拟合值总体趋势大于实测值,相比之下采用支持向量机预测方法获得的预测模型不仅能够有效提高拟合精度,且有效避免了单一预测模型偏大或是偏小的预测趋势。
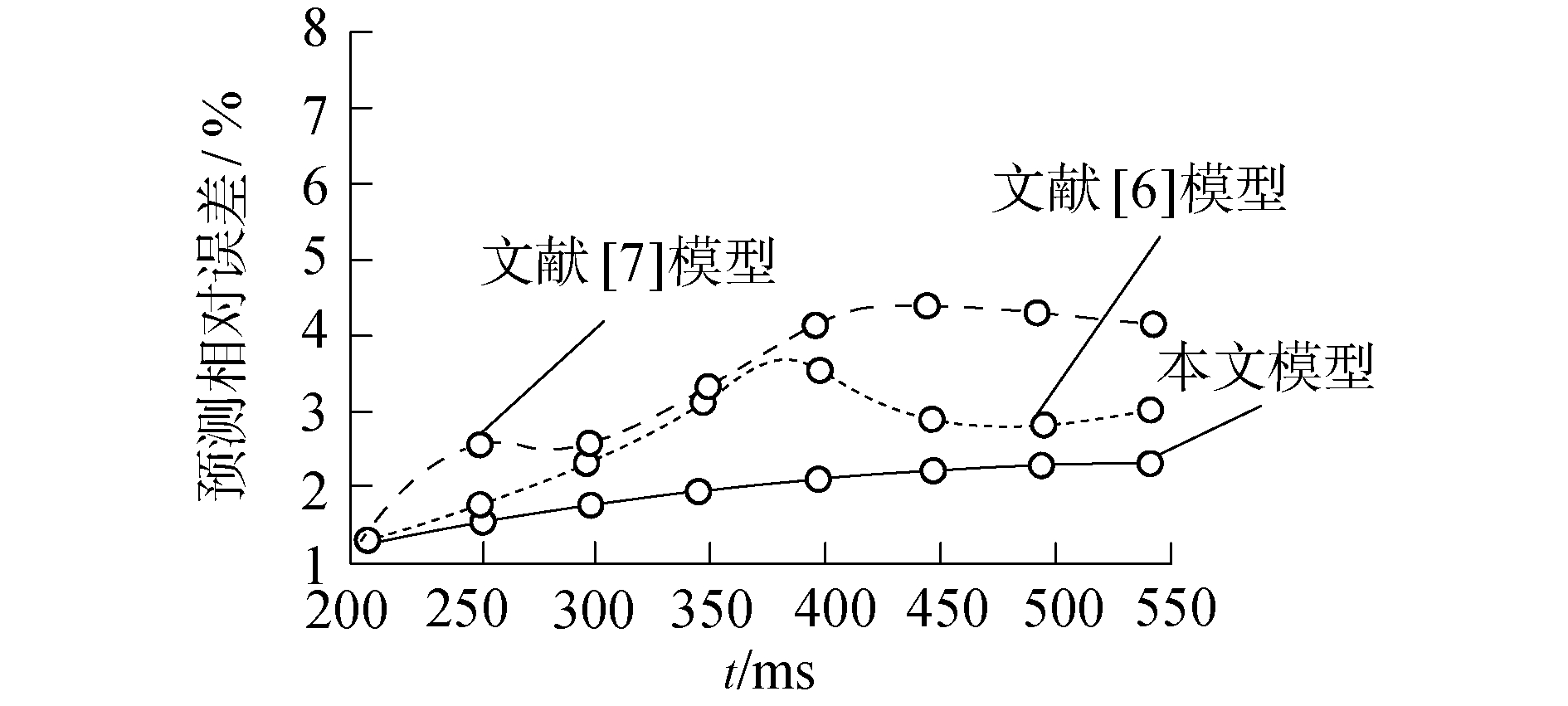
分别采用所提模型、文献[6]模型以及文献[7]模型计算出季节性冻土区路基高边坡断面(K-CB)变形竖向位移预测沉降量与实测值之间的相对误差,如图 8所示。
|
Download:
|
| 图 8 不同模型预测相对误差对比 Fig. 8 Comparison of relative errors in different model predictions | |
分析图 8可知,对于冻土区路基高边坡截面(K-CB)变形预测沉降量与实测值之间的相对误差最终为2%,文献[6]模型相应的相对误差为3%,文献[7]模型相应的相对误差为4%。对于结果说明所提模型预测结果与实测值更为接近。
为了避免路基沉降带来的人力、物力的损失,需要对其进行预报。路基稳定性的评价预报,本文采用以下的2项指标,分别为平均绝对百分比误差MAPE以及均方根误差,以下为其计算公式:
平均绝对百分比误差:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathop{\rm MAPE}\nolimits} = \frac{1}{n}\sum\limits_{k = 1}^n {\frac{{{\varepsilon _i}}}{{\left| {{X^{(0)}}(k)} \right|}}} \times 100\% }\\ {{\varepsilon _i} = \left| {{X^{(0)}}(k) - {{\hat X}^{(0)}}(k)} \right|, {X^{(0)}}(k) \ne 0} \end{array}} \right. $ | (9) |
式中:X(0)(k)表示路基观测值;${{\hat X}^{(0)}}(k)$表示预报值。
均方根误差:
| $ {\rm{RMSE}} = \sqrt {\sum\limits_{i = 1}^n {\varepsilon _i^2/n} } $ | (10) |
式中n为预报个数。
由表 4所给数据可以看出,传统方法预测的数据与实测数据相差较多,且平均绝对百分比误差和均方根误差都偏高,相比之下,本文所提的数据预报方法能够更准确的对冻土路基沉降进行预测,有效提高路基防护效率,同时也说明了所提模型的可靠性和实用性。
| 表 4 不同方法路基沉降数据预报结果 Table 4 Prediction results of subgrade settlement data by different methods |
1) 采用支持向量机预测原理构建一种路基高边坡变形预测模型,通过实测数据验证了所提模型的预测精度较当前预测模型精度有所提高。
2) 为了验证季节性冻土区路基高边坡变形多因素时变预测模型的有效性,进行实验,结果表明采用支持向量机预测方法获得的预测模型不仅能够有效提高拟合精度,有效避免了单一预测模型偏大或是偏小的预测趋势,且具有较高的预测精度,所提预测模型的可靠性和实用性。
但是本文对于季节性冻土区路基高边坡变形影响因素中仅选择了气温指数和冻结指数作为路基变形的理论分析条件,没有将目标路基所处地区的年降水量考虑在内,未来阶段还应当考虑降水量对路基高边坡变形的影响。
| [1] |
靳鹏伟, 何永红. 改进灰色模型高铁隧道路基沉降分析与预测[J]. 铁道科学与工程学报, 2016, 13(12): 2355-2359. JIN Pengwei, HE Yonghong. Settlement analysis and predictation of high-speed rail tunnel subgrade based on the improved Gray model[J]. Journal of railway science and engineering, 2016, 13(12): 2355-2359. DOI:10.3969/j.issn.1672-7029.2016.12.006 (  0) 0)
|
| [2] |
SU Huaizhi, YANG Meng, WEN Zhiping, et al. Deformation-based safety monitoring model for high slope in hydropower project[J]. Journal of civil structural health monitoring, 2016, 6(5): 779-790. DOI:10.1007/s13349-016-0198-z (  0) 0)
|
| [3] |
崔凯, 杨文恒. 软土路基沉降的联合法预测研究[J]. 西南交通大学学报, 2017, 52(5): 926-934. CUI Kai, YANG Wenheng. Prediction soft soil settling using a combination method[J]. Journal of Southwest Jiaotong University, 2017, 52(5): 926-934. DOI:10.3969/j.issn.0258-2724.2017.05.012 (  0) 0)
|
| [4] |
LEUNG A K, NG C W W. Field investigation of deformation characteristics and stress mobilisation of a soil slope[J]. Landslides, 2016, 13(2): 229-240. DOI:10.1007/s10346-015-0561-x (  0) 0)
|
| [5] |
姜献东, 张苏俊, 卢佩霞. 灰色系统模型在软土路基沉降预测中的应用[J]. 施工技术, 2016, 45(5): 81-83. JIANG Xiandong, ZHANG Sujun, LU Peixia. The application of grey system model in settlement prediction of soft soil subgrade[J]. Construction technology, 2016, 45(5): 81-83. (  0) 0)
|
| [6] |
靳鹏伟, 何永红, 陈青海. 马尔可夫残差修正模型的高铁路基变形预测[J]. 测绘科学, 2017, 42(7): 84-88. JIN Pengwei, HE Yonghong, CHEN Qinghai. Deformation prediction of high speed railway subgrade based on Markov besidual error correction model[J]. Science of surveying and mapping, 2017, 42(7): 84-88. (  0) 0)
|
| [7] |
SALOUR F, ERLINGSSON S. Permanent deformation characteristics of silty sand subgrades from multistage RLT tests[J]. International journal of pavement engineering, 2017, 18(3): 236-246. DOI:10.1080/10298436.2015.1065991 (  0) 0)
|
| [8] |
陈良琼. 基于最大Lyapunov指数的公路沉降预测[J]. 信阳师范学院学报(自然科学版), 2017, 30(4): 647-650. CHEN Liangqiong. Forecasting for settlement of highway on Lyapunov exponents[J]. Journal of Xinyang Normal University (natural science edition), 2017, 30(4): 647-650. DOI:10.3969/j.issn.1003-0972.2017.04.029 (  0) 0)
|
| [9] |
周伟杰, 张宏如, 党耀国, 等. 新息优先累加灰色离散模型的构建及应用[J]. 中国管理科学, 2017, 25(8): 140-148. ZHOU Weijie, ZHANG Hongru, DANG Yaoguo, et al. New information priority accumulated grey discrete model and its application[J]. Chinese journal of management science, 2017, 25(8): 140-148. (  0) 0)
|
| [10] |
次旦多杰. 基于冻土特征的青藏公路路基病害分析[J]. 筑路机械与施工机械化, 2017, 34(10): 90-93. CIDAN Duojie. Analysis of subgrade diseases of Qinghai-Tibet highway based on features of permafrost[J]. Road machinery & construction mechanization, 2017, 34(10): 90-93. DOI:10.3969/j.issn.1000-033X.2017.10.013 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


