发射技术是无人机的一个重要研究方向,研究分析发射阶段动力学和影响因素等方面的成果众多。目前对无人机起飞发射的研究主要集中于无人机机体固有的影响因素, 如文献[1-3]对无人机起飞发射系统的外形结构和发射阶段力学和运动学进行了详细地设计分析。在发射过程中不同阶段影响因素的研究侧重点不同,如在火箭发射之初,重点研究无人机的火箭安装参数、机体发射角、闭锁力和火箭离轨速度等影响因素。在火箭发射的过程中,需重点分析无人机气动参数、机身的性能、火箭推力和控制器设计参数对无人机的影响。在控制器设计方面,无人机在起飞发射阶段重点关注无人机纵向、横向姿态的稳定性,由于存在环境风干扰,需要通过设计俯仰角控制参数、滚转角控制参数,以及设计控制律来稳定发射阶段[4-5]。
本文主要分析外界的环境风干扰对特定无人机发射安全的影响。在敏感的发射阶段,无人机始终处于加速状态,空速与姿态角变化剧烈。此时,环境风的干扰会对无人机发射造成不可预估的后果。该无人机在外场飞行试验中,就曾有一次因发射时场地侧风干扰严重,导致发射任务不得不取消。
1 无人机发射运动模型 1.1 特定无人机本文涉及的特定无人机是固定翼无人机项目组研发的一种针对特殊任务的无人机。其最显著的特点是需要兼顾低速和高速飞行性能。从气动布局来说,无人机外形设计应力要求增加升力、减少阻力,但该型无人机速域范围跨度大,低、高速飞行器对气动外形的要求时常会有矛盾。例如为提供足够的升力,低速无人机要求采用较大面积的机翼,这使得零升阻力增加;但零升阻力增加会影响无人机飞行速度的提高,故而高速无人机要求减少机翼面积,二者存在直接冲突。因此该型无人机的气动外形设计具有其特殊性。
为达到设计目的,本文以无人机协同设计系统为基础,参数化设计并调整无人机气动外形,翼身融合优化气动外形,协同设计气动结构、推进装置和控制系统,综合考虑各子系统之间的相互影响产生的协同效应,寻求设计整体最优解,实现各系统所涉及的多学科之间的协调与综合,从而设计出满足任务要求的无人机总体构型方案。利用该设计平台,实验室研制出了本文的研究对象,即一种特殊的气动外形类似于巡飞弹的无人机,其气动性能与飞行稳定性介于飞机与巡航导弹之间。
1.2 无人机的火箭助推零长发射方式零长发射[6]也称零距离发射,是指无人机在一个特制支架上通过火箭助推飞离发射装置,起飞之后扔掉助推火箭,再由机上主发动机完成飞行任务的发射方式。这种方式可使无人机不受起飞距离限制,在短时间内从静止状态迅速达到理想的爬升飞行状态,具有便捷快速,对发射场地无严格要求,适合于野战环境等优点[7-8]。
本文所研究的无人机即采用火箭助推零长发射。该无人机机身尾部装有2台小型涡喷发动机,其后通过推力支架连接一台助推火箭发动机。在助推火箭的作用下,无人机从地面零长发射装置上发射。助推火箭工作几秒后,自动分离。无人机由涡喷发动机完成飞行任务。发射过程具体可分为3个阶段[9]:
1) 将无人机置于发射架上,通过闭锁机构固定,开启发动机并设置为全推力状态。接收到发射命令时,助推火箭点火。火箭推力大于2 800 N时,克服闭锁力,剪断保险销,无人机瞬间离架;
2) 在巨大的火箭推力下,无人机速度急剧增大、高度急剧增加,持续约2 s后,火箭助推结束,火箭与无人机分离,自动脱落;
3) 无人机的推动力只来自于发动机,在控制器作用下需尽快调整飞行姿态:对于纵向系统的姿态,使无人机低头,俯仰角减小;对于横侧向系统的姿态,需保持机体平稳,即机身没有滚转和偏航,然后控制无人机稳定地完成飞行任务。
1.3 运动模型的建立为研究环境风对无人机发射起飞的影响,首先需要建立无人机数学模型。但无人机的运动是复杂的动力学过程,其运动特性受到各种因素影响,例如机体弹性变形、重力加速度随飞行高度的变化、地球的曲率、自转以及大气的运动等。如果把这些因素都包括进去,将会使方程推导和求解过程变得十分复杂,难以处理。因此,在建立数学模型时,对无人机运动做如下假设[10]:
1) 认为无人机是刚体,且质量是常数;
2) 助推火箭对无人机重心影响很小;
3) 假设地面为惯性参照系;
4) 忽略地球曲率,把地面看成平面;
5) 假设重力加速度不随飞行高度变化;
6) 绕质心的旋转运动,机体坐标下,仅考虑X、Y、Z轴的三轴转动惯量的影响。
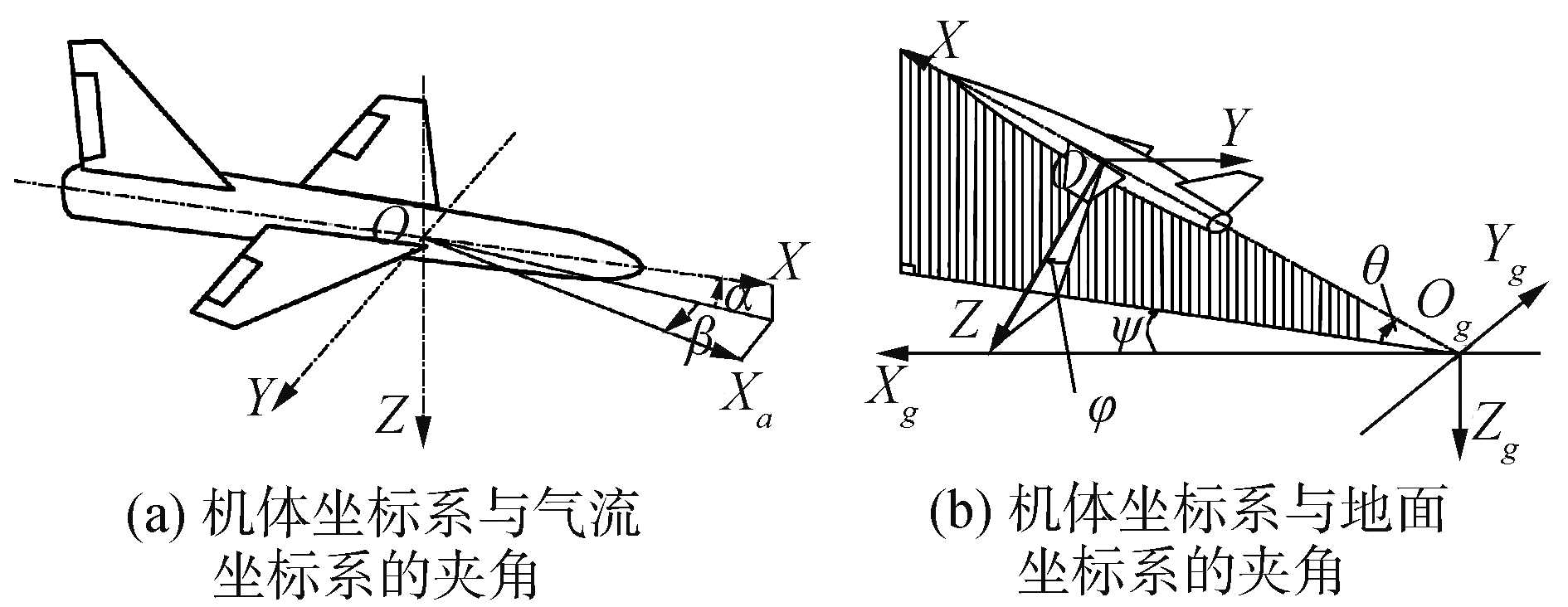
在建立飞行器运动方程时,为了确定相对位置、速度、加速度和外力矢量的分量,必须引入多种坐标系。常用的坐标系有地面坐标系、机体坐标系、气流坐标系、航迹坐标系。图 1为各坐标系之间的夹角示意图。其中图 1(a)为机体坐标系O-XYZ与气流坐标系O-XaYaZa的夹角,α代表攻角,β是侧滑角。图 1(b)机体坐标系O-XYZ与地面坐标系O-XgYgZg的夹角,φ是滚转角,θ代表俯仰角,ψ是偏航角。
|
Download:
|
| 图 1 坐标系之间的夹角示意 Fig. 1 Angles schematic diagram between different coordinate systems | |
描述无人机运动的动力学方程如下:
| $ \left\{ \begin{array}{l} \dot u = vr - wq - g\sin q + {F_x}/m\\ \dot v = wp - ur + g\sin j\cos q + {F_y}/m\\ \dot w = uq - vp + g\cos j\cos q + {F_z}/m \end{array} \right. $ | (1) |
| $ \left\{ {\begin{array}{*{20}{l}} {\dot p = qr\left( {{I_{yy}} - {I_{zz}}} \right)/{I_{xx}} + L/{I_{xx}}}\\ {\dot q = {\mathop{ pr}\nolimits} \left( {{I_{zz}} - {I_{xx}}} \right)/{I_{yy}} + M/{I_{yy}}}\\ {\dot r = pq\left( {{I_{xx}} - {I_{yy}}} \right)/{I_{zz}} + N/{I_{zz}}} \end{array}} \right. $ | (2) |
式中:[u, v, w]为无人机速度向量;[φ, θ, ψ]为无人机欧拉角向量;无人机所受合力向量为[Fx, Fy, Fz];m为无人机质量;g为重力加速度;[p, q, r]为无人机角速度向量;[L, M, N]为无人机所受力矩向量;[Ixx, Iyy, Izz]为无人机转动惯量。
描述无人机运动的运动学方程如下:
| $ \left\{ \begin{array}{l} {{\dot x}_g} = u\cos \theta \cos \psi + v\left( {\sin \varphi \sin \theta \cos \psi - \cos \theta \sin \psi } \right) + \\ \;\;\;\;\;\;\;w\left( {\sin \varphi \sin \psi + \cos \varphi \sin \theta \cos \psi } \right)\\ {{\dot y}_g} = u\cos \theta \sin \psi + v\left( {\sin \varphi \sin \theta \cos \psi + \cos \theta \cos \psi } \right) + \\ \;\;\;\;\;\;\;w\left( { - \sin \varphi \cos \psi + \cos \varphi \sin \theta \sin \psi } \right)\\ {{\dot z}_g} = u\sin \theta - v\sin \varphi \cos \theta - w\cos \varphi \cos \theta \end{array} \right. $ | (3) |
| $ \left\{ \begin{array}{l} \dot \varphi = p + \tan \theta \left( {q\tan \varphi + r\cos \varphi } \right)\\ \dot \theta = q\cos \varphi - r\sin \varphi \\ \dot \psi = \left( {q\sin \varphi + r\cos \varphi } \right)/\cos \theta \end{array} \right. $ | (4) |
式中[xg, yg, zg]是无人机的位置向量。
考虑到无人机在起飞阶段,速度很低,需要描述的时间很短(约2 s左右),舵面的气动效应很小,所以不考虑舵面对飞机稳定性的影响,将舵面偏角设为某一个固定值不变,使无人机保持平飞状态,并在计算过程中忽略它们对气动力的影响。对前述微分方程采用经典的龙格-库塔法(Runge-Kutte)进行求解即可得到无人机的运动状态。
2 无人机发射动力学计算 2.1 空气动力学参数计算作用在飞行器上的外力有重力、推力和气动力。这些外力除重力外,一般不通过飞行器质心,于是会产生绕质心的力矩,即俯仰力矩M、偏航力矩N和滚转力矩L。气动力各分量力可表示:
| $ \left\{ \begin{array}{l} Y = \rho {\mathit{\boldsymbol{V}}^2}S{C_Y}/2\\ D = \rho {\mathit{\boldsymbol{V}}^2}S{C_D}/2\\ C = \rho {\mathit{\boldsymbol{V}}^2}S{C_C}/2 \end{array} \right. $ | (5) |
式中:空气密度为ρ,无人机空速记为V,无人机机翼面积为S时,CY、CD、CC分别为升力系数、阻力系数和侧力系数,其值主要取决于马赫数Ma、雷诺数Re、攻角α、侧滑角β以及飞行器的外形。通常有如下函数关系[11]:
| $ \left\{ \begin{array}{l} {C_Y} = {C_Y}\left( {Ma,\alpha ,{\delta _e};\dot \alpha ,q} \right)\\ {C_D} = {C_D}\left( {Ma,{R_e},\alpha ,{\delta _e},\beta ,{\delta _a},{\delta _r}} \right)\\ {C_C} = {C_C}\left( {Ma,\beta ,{\delta _r};r,\dot \beta } \right) \end{array} \right. $ |
式中:δa、δe、δr、δp分别代表副翼偏角、升降舵偏角、方向舵偏角、油门杆位置。括号中“;”后面的是影响较小的因素,有时可以忽略不计。
气动力矩也可以通过力矩系数表达如下:
| $ \left\{ \begin{array}{l} L = {m_x}\rho {\mathit{\boldsymbol{V}}^2}Sl/2\\ M = {m_y}\rho {\mathit{\boldsymbol{V}}^2}S{c_{\rm{a}}}/2\\ N = {m_z}\rho {\mathit{\boldsymbol{V}}^2}Sl/2 \end{array} \right. $ | (6) |
式中:l是无人机的机翼展长;ca代表机翼的平均气动弦长;[mx, my, mz]分别为滚转力矩系数、俯仰力矩系数、偏航力矩系数。当飞行器外形一定,且质心位置一定时,有如下函数关系:
| $ \left\{ \begin{array}{l} {m_x} = {m_x}\left( {Ma,\beta ,{\delta _a},{\delta _r},p,r,\alpha } \right)\\ {m_y} = {m_y}\left( {Ma,\alpha ,{\delta _e},q,\dot \alpha } \right)\\ {m_z} = {m_z}\left( {Ma,\beta ,{\delta _a},r,p,\alpha ;\dot \beta } \right) \end{array} \right. $ |
本文所研究的无人机飞行时的攻角α较小,根据理论分析,在小攻角范围内,[mx, my, mz]可以看成是攻角α的函数,所以这3个系数所对应的函数是由一系列对应攻角下测得的数据通过二次曲线拟合或者多项式拟合得到。涉及一些静止的状态参量,如α、β等都通过实验的方法得到;而涉及一些动态的参数,如
若无环境风干扰,无人机的地速和空速相等,但在有风的情况下,地速是空速和风速的矢量合成。由于无人机的空速、攻角和侧滑角定义在气流坐标系中,而风干扰向量定义在地面坐标系中,因此需进行坐标转换,将风干扰量对无人机的影响直接体现在侧滑角、攻角和空速上[12]。具体转换过程如下。
首先计算出地面坐标系中环境风干扰向量[Vwx Vwy Vwz],可表示为:
| $ \left\{ \begin{array}{l} {V_{wx}} = {w_v}\cos {w_\theta }\cos {w_\psi }\\ {V_{wy}} = {w_v}\cos {w_\theta }\sin {w_\psi }\\ {V_{wz}} = {w_v}\sin {w_\theta } \end{array} \right. $ | (7) |
[wv wθ wψ]是1×3的矩阵,其中wv是风速的大小;wθ是环境风扰量与xgoyg平面的夹角;wψ是环境风扰量在地面上的投影与xg轴的夹角。
然后通过地面坐标系到机体坐标系的转换矩阵Sθψφ将风干扰项转换到机体系中。风速在机体坐标系中的3个分量[uw, vw, ww]可表示为:
| $ {\left[ {\begin{array}{*{20}{c}} {{u_w}}&{{v_w}}&{{w_w}} \end{array}} \right]^{\rm{T}}} = {\mathit{\boldsymbol{S}}_{\theta \psi \varphi }}{\left[ {\begin{array}{*{20}{c}} {{V_{wx}}}&{{V_{wy}}}&{{V_{wz}}} \end{array}} \right]^{\rm{T}}} $ | (8) |
其中:
| $ {\mathit{\boldsymbol{S}}_{\theta \psi \varphi }} = \left[ {\begin{array}{*{20}{c}} {\cos \theta \cos \psi }&{\cos \theta \sin \psi }&{ - \sin \theta }\\ {\sin \theta \cos \psi \sin \varphi - \sin \psi \cos \varphi }&{\sin \theta \sin \psi \sin \varphi + \cos \psi \cos \varphi }&{ - \cos \theta \sin \varphi }\\ {\sin \theta \cos \psi \cos \varphi + \sin \psi \sin \varphi }&{\sin \theta \sin \psi \cos \varphi - \cos \psi \sin \varphi }&{\cos \theta \cos \varphi } \end{array}} \right] $ |
在机体坐标系中,将转换后的风干扰向量[uw, vw, ww]作为一个外部输入,叠加到空速[u, v, w]上,代入式(1)~(4)得到出风干扰下的攻角和侧滑角,进而求出作用在无人机上的力和力矩,输入到无人机的发射运动模型中进行仿真计算,最终模拟得到无人机的实际飞行情况。
3 无人机发射仿真实验与分析 3.1 仿真实验约束条件在本文中,假定副翼偏角、升降舵偏角、方向舵偏角、油门杆位置处于某一固定位置,即(δa, δe, δr, δp)为固定值,即在飞行过程中不具有对飞行运动姿态的调节作用,完全由外界环境、飞行器初始状态、运动控制方程来决定无人机的运动轨迹与参数。如果这4个参数是可以调节的,则可以实现更加复杂的运动,并且可以提高无人机发射阶段的稳定性[13-14]。
3.2 仿真模型的可行性验证为了尽可能提高实验数据的准确度与合理性,在进行环境风仿真实验之前,首先根据现有的实际试飞数据对无人机的运动模型进行验证校验。
选取不同季节、发射时间与天气的该小型无人机的某8次飞行试验数据作为样本,可以认为该样本受风的影响是随机的。以地速为例,图 2是这8次实际飞行试验的地速测试数据曲线。可以看出,火箭助推零长发射过程中各次试验地速随时间变化的规律是基本相同的;不同飞行试验在同一时刻的地速数值离散幅度很小,变化相对稳定。其他现场试飞发射数据也体现出了类似的性质。

|
Download:
|
| 图 2 8次飞行试验的发射过程UAV地速数据 Fig. 2 UAV ground speed data of eight launch tests | |
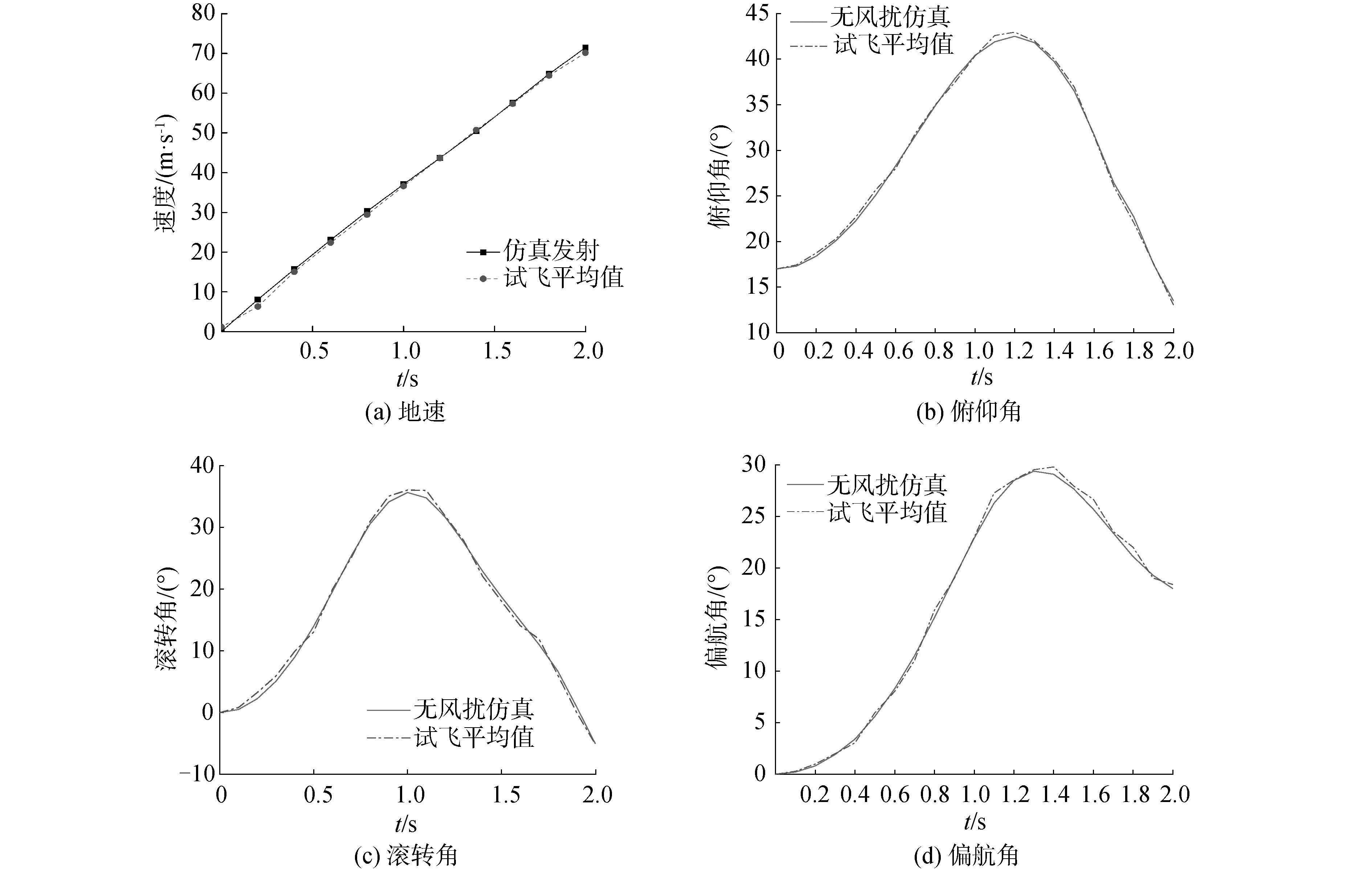
实际飞行试验中,每次风干扰情况各有不同,因而通过对8次试飞数据的算数平均操作来尽可能地消除风的影响。通过对比实际试验的各项平均值与仿真实验中无风状态下获得的计算结果来校验模型,见图 3。结果表明本文建立的UAV运动模型是合理的。
|
Download:
|
| 图 3 发射过程中各项平均试飞参数与仿真实验结果的比较 Fig. 3 Comparison between the mean actual launch and the simulation launch | |
本文设计了3种不同环境风情况下的无人机零长发射仿真实验,通过对发射过程及助推火箭分离时的初始弹道响应进行分析。
1) 对无人机发射过程仿真系统施加逆风,环境风干扰向量中的纵向角、横向角都为0°。
仿真结果显示,无人机发射后的分离高度与风速成正比;地速与风速为反比例关系;空速与风速为正比例关系;而随风速的增加,无人机的攻角和俯仰角呈现上升趋势,见图 4。即逆风时,环境风主要影响火箭脱落时刻无人机爬升的高度,逆风风速越大,高度越高,无人机越安全。

|
Download:
|
| 图 4 逆风时无人机各主要参数与风速的关系 Fig. 4 Relationships between main UAV parameters and wind speed in headwind | |
2) 对无人机发射过程仿真系统施加顺风,环境风干扰向量中的纵向角、横向角都为0°。
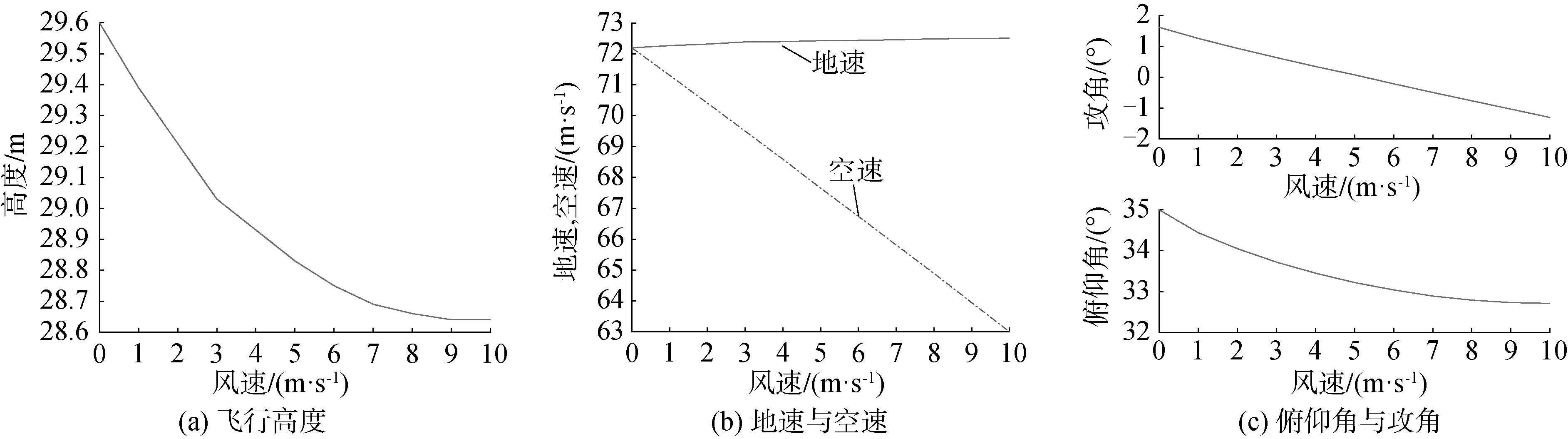
仿真结果显示:此种情况下火箭脱落时刻无人机爬升的高度与风速的大小成反比;地速与风速为正比例关系;空速与风速成反比;随着风速的增加,无人机的攻角和俯仰角呈现下降趋势,见图 5。注意到,当风速大小约为6 m/s时,攻角变为负值,见图 5(c),此时无人机速度方向在机体轴下方,代表无人机处于下滑状态,有坠落的危险。即顺风时,环境风的主要影响仍是无人机火箭脱落时刻爬升的高度,顺风风速越小,高度越高,但对地速影响不大。此外,在实际试飞中,外界环境的顺风风速最好不超过6 m/s,否则存在发射失败的可能。
|
Download:
|
| 图 5 顺风时无人机主要参数与风速的关系 Fig. 5 Relationships between main UAV parameters and wind speed in tailwind | |
3) 对无人机发射过程仿真系统施加正侧风,风干扰向量中的纵向角为0°、横向角为90°。
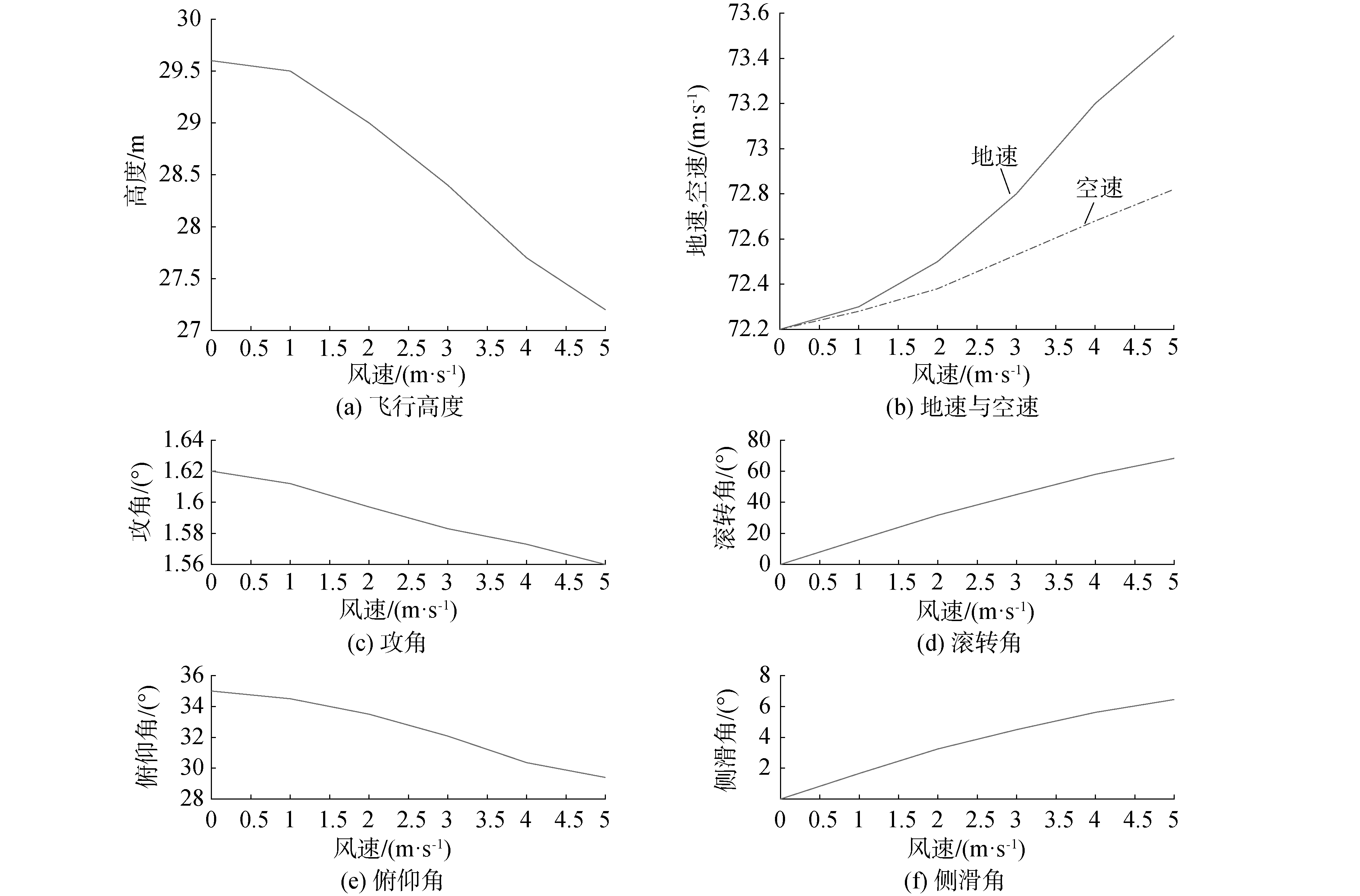
结果显示:火箭脱落时刻无人机爬升的高度与正侧风风速的大小为反比例关系;地速、空速与风速均成正比;而随风速的增加,无人机的攻角和俯仰角呈现下降趋势,但相较于前2种情况,正侧风对这些参数的影响相对较小,见图 6。然而从图 6(f)可见,当正侧风的风速从0变化到5 m/s时,滚转角从0°增加到68.3°,侧滑角从0°增加到6.5°,已经达到控制的边界,无人机处于失控状态。即此时发射过程必须增加横测控制[15]。
|
Download:
|
| 图 6 正侧风时无人机主要参数与风速的关系 Fig. 6 Relationships between main UAV parameters and wind speed in direct crosswind | |
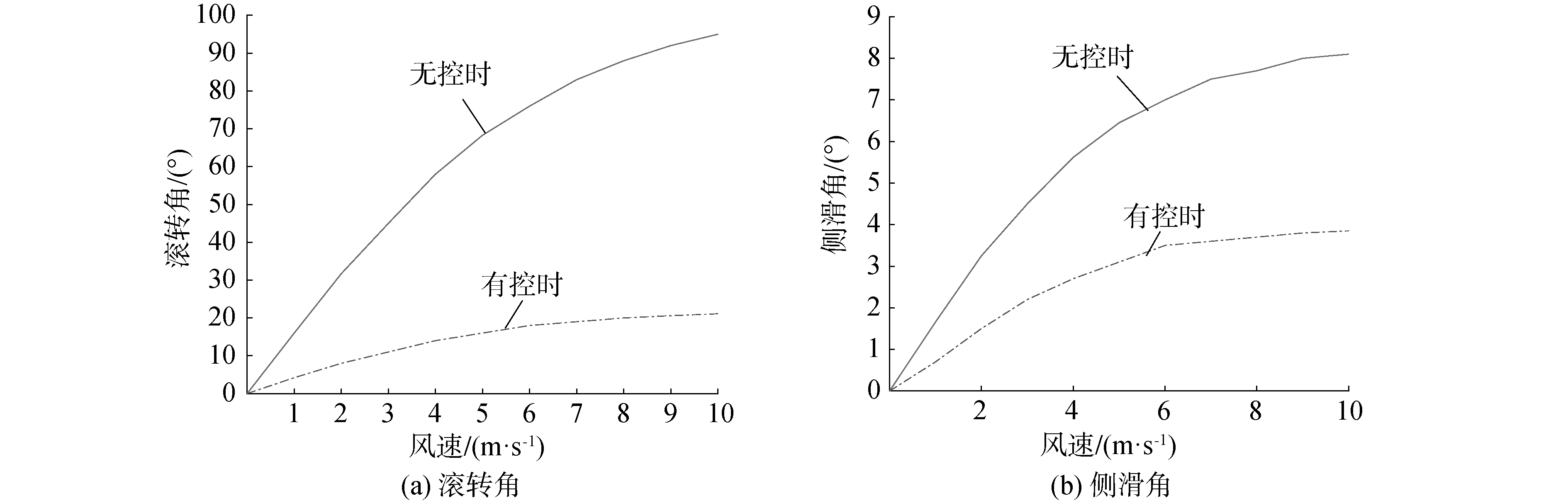
图 7为发射过程加上横测控制前后,风速从0变化到10 m/s时无人机的滚转角和侧滑角变化的对比图。可以看出,加上横测控制以后,无人机的滚转角与侧滑角都大幅缩小。正侧风速小于6 m/s时,滚转角小于20°,侧滑角小于4°,此时无人机起飞是安全的。
|
Download:
|
| 图 7 引入控制前后无人机滚转角与侧滑角的变化 Fig. 7 Changes of UAV roll angle and sideslip angle before and after control | |
1) 仿真实验给出了逆风、顺风和正侧风情况下特定无人机发射过程及助推火箭分离时的初始弹道响应,对仿真结果的分析确定了最佳发射风向以及可容忍的风速大小范围,为保障无人机发射起飞安全建立了定量标准。
2) 结合多次该型无人机实际飞行试验数据,对建立的无人机动力学模型进行了校验和可行性分析,验证了仿真模型的合理性以及最终研究结果的可信性。
3) 在实际飞行试验中,根据本文研究结果,很好的消除了环境风因素对特定无人机发射的干扰,提高了发射的安全性,具有较强的实际应用价值。
| [1] |
石林, 马威, 杨龙军. 基于ADAMS的无人机零长发射动力学仿真及分析[J]. 弹箭与制导学报, 2017, 37(2): 37-39, 43. SHI Lin, MA Wei, YANG Longjun. Simulation and analysis of UAV zero-length launching dynamics based on ADAMS[J]. Journal of projectiles, rockets, missiles and guidance, 2017, 37(2): 37-39, 43. (  0) 0)
|
| [2] |
SILKOV V, ZIRKA A. Calculation of the characteristics of a UAV launch from a ramp[J]. Aviation, 2014, 18(4): 178-184. DOI:10.3846/16487788.2014.985476 (  0) 0)
|
| [3] |
田新锋, 郑成军. 某无人机火箭助推起飞参数计算[J]. 兵工自动化, 2013, 32(5): 25-27. TIAN Xinfeng, ZHENG Chengjun. Launch parameters calculation method for certain type UAV[J]. Ordnance industry automation, 2013, 32(5): 25-27. (  0) 0)
|
| [4] |
杨广, 蒋盼盼, 李泰安, 等. 单发夹角式火箭助推发射起飞仿真技术研究[J]. 飞行力学, 2017, 35(4): 86-88, 93. YANG Guang, JIANG Panpan, LI Taian, et al. Research on simulation technology for single rocket included angle booster launching UAV[J]. Flight dynamics, 2017, 35(4): 86-88, 93. (  0) 0)
|
| [5] |
MARTEL J, DUDLEY J. External pitching moment (EPM) due to turbine engine exhaust impingement on rocket assisted take off (RATO) bottle[C]//Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, US, 2013. https://arc.aiaa.org/doi/abs/10.2514/6.2007-862
(  0) 0)
|
| [6] |
FAHLSTROM P G, GLEASON T J.无人机系统导论[M].郭正, 王鹏, 陈清阳, 等译. 4版.北京: 国防工业出版社, 2015. FAHLSTROM P G, GLEASON T J. Introduction to UAV systems[M]. GUO Zheng, WANG Peng, CHEN Qingyang, et al, trans. 4th ed. Beijing: National Defend Industry Press, 2015. (  0) 0)
|
| [7] |
EYMANN T, MARTEL J. Numerical investigation of launch dynamics for subscale aerial drone with rocket assisted Take-Off (RATO)[C]//Proceedings of 2008 U.S. Air Force T&E Days. Los Angeles, California, 2008. https://www.researchgate.net/publication/269225589_Numerical_Investigation_of_Launch_Dynamics_for_Subscale_Aerial_Drone_with_Rocket_Assisted_Take-Off_RATO
(  0) 0)
|
| [8] |
陶于金. 小型固定翼无人机零长发射参数安全边界研究[J]. 海军航空工程学院学报, 2017, 32(5): 447-451, 468. TAO Yujin. Reasearch on zero-length launch parameters' secure border investigation of small fixed wing UAV[J]. Journal of Naval Aeronautical and Astronautical University, 2017, 32(5): 447-451, 468. (  0) 0)
|
| [9] |
刘付平, 郑耀, 谢芳芳, 等. 助推火箭安装偏差对小型无人机发射安全的影响[J]. 哈尔滨工程大学学报, 2018, 39(8): 1343-1348. LIU Fuping, ZHENG Yao, XIE Fangfang, et al. Effects of a booster rocket installation deviation on the launch safety of a small unmanned aerial vehicle[J]. Journal of Harbin Engineering University, 2018, 39(8): 1343-1348. (  0) 0)
|
| [10] |
YE Z, BHATTACHARYA P, MOHAMADIAN H, et al. Equational dynamic modeling and adaptive control of UAV[C]//Proceedings of 2006 IEEE/SMC International Conference on System of Systems Engineering. Los Angeles, CA, USA, 2006. https://www.researchgate.net/publication/224638582_Equational_dynamic_modeling_and_adaptive_control_of_UAV
(  0) 0)
|
| [11] |
PU Huangzhong, ZHEN Ziyang, WANG Daobo, et al. Improved particle swarm optimization algorithm for intelligently setting UAV attitude controller parameters[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2009, 26(1): 52-57. (  0) 0)
|
| [12] |
夏曼. 螺旋桨无人机火箭助推发射过程控制及影响因素分析研究[J]. 南京:南京航空航天大学, 2016. XIA Man. Research on propeller UAV rocket booster launching control and influential factors[J]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2016. (  0) 0)
|
| [13] |
YANG Zuqiang, FANG Zhou, LI Ping. Bio-inspired collision-free 4D trajectory generation for UAVs using tau strategy[J]. Journal of bionic engineering, 2016, 13(1): 84-97. DOI:10.1016/S1672-6529(14)60162-1 (  0) 0)
|
| [14] |
MUELLER E. Hardware-in-the-loop simulation design for evaluation of unmanned aerial vehicle control systems[C]//AIAA Modeling and Simulation Technologies Conference and Exhibit. Hilton Head, South Carolina, USA, 2007. https://www.aviationsystemsdivision.arc.nasa.gov/publications/modeling/Mueller_E_AIAA_MST_2007_1.pdf
(  0) 0)
|
| [15] |
杨祖强, 方舟, 李平. 基于tau矢量场制导的多无人机协同standoff跟踪方法[J]. 浙江大学学报(工学版), 2016, 50(5): 984-992. YANG Zuqiang, FANG Zhou, LI Ping. Cooperative standoff tracking for multi-UAVs based on tau vector field guidance[J]. Journal of Zhejiang University (engineering science), 2016, 50(5): 984-992. DOI:10.3785/j.issn.1008973X.2016.05.024 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


