2. 中船黄埔文冲船舶有限公司, 广东 广州 510715
2. CSSC Huangpu Wenchong Shipbuilding Company Limited, Guangzhou 510715, China
近年来,浮式海洋结构物由于系泊锚链的损坏而时常发生破坏现象。长时间处于复杂海洋环境中的系泊锚链,在风、浪、流的联合作用下,必定发生损伤,类似腐蚀、磨损等,进而降低锚链的安全性。从载荷作用类型分析,系泊锚链可能受到弯曲、拉伸、扭转等作用。对锚链受拉伸时的性能,众多国内外学者深入研究分析,分析了不同拉伸载荷作用下,锚链的破坏形态与应力变化,以及残余应力对疲劳寿命、锚链应力的改变情况[1-3]。由于锚链所处环境的复杂性,对其受非纯拉伸载荷作用时的情况进一步探究很有必要,尤其是系泊链环所处的导缆孔位置,因为浮式平台的牵连运动,致使其受平面外弯曲载荷的影响而产生破坏现象[4]。因此,在受到平面外弯曲载荷时,系泊锚链链环的应力分布和损伤破坏的分析非常关键。
2002年,几个具有Girassol卸载浮筒,水深1 400 m的系泊线在安装不满8个月的时间就出现故障,上述系泊锚链是根据20 a寿命,参考API-RP-2SK规范中安全因子为3的T-N曲线进行疲劳设计的,事故原因为与浮体结构相连的第4、5个弯曲链环破坏[5]。Vargas等[6-7]根据锚链的失效位置,发现了导致卸载浮筒系泊链失效的原因为平面外弯曲载荷作用,并采用有限元和试验2种方法分析了平面外弯曲应力可能是导致的链环失效破坏的原因。Brake等[8]提出求解了平面外弯曲应力的方法,将平面外弯曲应力表示成以弯曲角度,摩擦系数和拉力作为参数的函数,通过此表达式可求解不同位置处应力。Lassen等[9-10]通过试验的方法验证了系泊锚链平面外弯曲应力与系泊锚链拉力和转动角度之间的关系,并研究了FPSO底部锚链受到平面外弯曲载荷作用时的损伤及改进方式:认为在导缆孔前设置锚链制动器的方法,既能一定程度上缓解平面外弯曲现象,还能改善导缆孔位置的腐蚀现象。Gao等[11]研究了在海洋环境中系泊锚链受时变载荷作用时产生的腐蚀破坏现象,并根据与作用位置有关的腐蚀速率建立了均匀腐蚀概率模型。Melchers等[12]通过对海洋工程所用钢材长时间在海洋环境中腐蚀数据的观测与收集,探究了锚链在海水中的腐蚀速率,认为其腐蚀速率主要受3方面影响:海水温度、海水溶解氧率、水流速度,并得到了求解锚链腐蚀速率的表达式。Arredondo等[13]通过试验分析了R4和R5级锚链在海洋环境中的腐蚀现象,提出了一个基于试验结果的S-N曲线。毛振东等[14]通过试验的方式研究了海洋工程用钢的磨损性能,发现单位面积的磨损量随着磨损时间增加和磨损载荷的增大而增加,磨损表面由磨沟变形变化成犁沟变形。刘金沅[15]通过理论推导的方式发现了定量求解微动磨损的方法,借助有限元模型模拟了系泊锚链在扭转载荷作用下的腐蚀磨损累积损伤。
本文以R4级124 mm直径无档钢链环为对象建立有限元分析模型,对比不同弯曲角度下锚链的应力分布情况和接触特性,然后基于Archard微动磨损理论和均匀腐蚀速率模型,对锚链在不同平面外弯曲角度载荷下的腐蚀和磨损联合作用进行分析。
1 锚链的腐蚀和磨损联合作用 1.1 磨损计算理论工作状态下的锚链,由于外力的作用导致链环间接触面产生相对运动,致使锚链接触面材料逐渐消失,称之为磨损。当链环间接触面之间的相对运动为微米量级往复运动时,导致的磨损称为微动磨损,该种类型的磨损主要由链环的往复运动使其接触面间的微凸体发生粘着磨损和磨粒磨损复合而成[15]。本文采用基于Archard微动磨损理论对锚链的磨损量进行计算[16]。
磨损体积V与滑移距离和环境载荷成正比,与材料接触表面的硬度成反比:
| $ V=k W_{s} / H $ | (1) |
式中:W为载荷;s为滑移距离;H为材料接触表面的硬度,本文取为2.5 GPa;k为材料的磨损系数,通过试验可以确定,本文取为10-6。
实际工作中锚链的接触面是由很多个点组成的,每个点的磨损构成了锚链接触面的磨损,每个点的接触面积假定为A,则接触节点的磨损深度为:
| $ h=\frac{V}{A}=\frac{k}{H} \frac{W s}{A}=\frac{k}{H} \sigma s $ | (2) |
式中:h为节点的磨损深度;σ为节点的接触压应力。
在有限元计算中,式(2)可转换为:
| $ h=\frac{V}{A}=\frac{k}{H} \frac{W_{s}}{A}=\frac{k}{H} \sigma s=\frac{k}{H} \sum\limits_{i=1}^{n} \sigma_{i} s_{i} $ | (3) |
式中:n为载荷步中的载荷子步数;σi对应载荷子步节点的接触压应力;si为对应载荷子步节点滑移距离,即为节点在该时刻垂直于节点所受接触压应力的位移。
受浮式平台的牵连运动,锚链在工作中会遭受到往复载荷的作用,取一定时间做为计算周期,在该周期内各载荷步对应下的磨损深度求得,通过对各个载荷步磨损深度的求和可以得到节点在循环载荷作用周期t0内的累积磨损深度:
| $ h_{0}=\sum\limits_{j=1}^{N} h_{j} $ | (4) |
式中:N为该周期内的载荷步数;hj为对应载荷步中每个节点的磨损深度累积量;h0为对应周期t0内每个节点的磨损深度累积量。
1.2 年腐蚀速率将锚链设计寿命20 a划分成5个计算阶段,结合API规范[17]、DNV规范[18]和Gao等[11]采用的均匀腐蚀概率模型以及Melchers等[12]采用的腐蚀概率模型,计算确定出锚链链环在设计寿命20 a内不同计算阶段的均匀腐蚀速率如表 1所示。
| 表 1 链环不同阶段的腐蚀速率 Table 1 The corrosion ratio of chains at different stage |
基于Archard微动磨损理论和均匀腐蚀计算模型,确定磨损及腐蚀联合作用计算流程如下:
1) 建立锚链链环的有限元分析模型Ⅰ,施加循环周期载荷,可得到接触区域各节点的滑移距离(节点在某时刻的微动磨损滑移距离si为该时刻对应载荷子步下的滑移距离值减去与之相邻的前一载荷子步的滑移距离值)和接触压应力,基于Archard微动磨损理论得到各节点在循环载荷周期t0内的磨损量,进一步即可得到计算周期T0=4 a的总磨损量;
2) 基于表 1的年均匀腐蚀速率,得到计算周期T0=4 a内的总腐蚀量,然后对锚链链环截面尺寸进行削弱建立新的有限元分析模型Ⅱ,用于模拟链环计算周期T0=4 a的总腐蚀;
3) 基于削弱后建立的有限元分析模型Ⅱ,保证削弱前后各节点一一对应的前提下,按照相同的网格划分方法,将步骤1)得到的计算周期T0=4 a各节点磨损量在有限元分析模型Ⅱ中进行反馈更新,通过微调磨损节点位置来对节点的磨损进行模拟,从而得到计算周期T0=4 a考虑了磨损及腐蚀的新有限元模型Ⅲ;
4) 将有限元模型Ⅲ作为下一个计算周期的初始有限元模型,重复步骤1)~3),即可分别得到计算周期T0为8、12、16、20 a同时考虑磨损及腐蚀作用的应力分布。
2 锚链有限元模型 2.1 锚链参数本文选取R4级直径d=124 mm的无档链环作为研究对象,几何尺寸:链环长度为6d,链环宽度为3.35d,链环内缘半径为0.675d;机械性能:屈服强度为600 MPa,抗拉强度为900 MPa,断面伸长率为12%,断面收缩率为50%,弹性模量为2.07×105 MPa,泊松比为0.29。锚链链环的本构关系采用双线性随动硬化模型(BKIN)来模拟,强化段的切线弹性模量为2.73 GPa。
2.2 有限元模型基于ANSYS有限元软件,采用SOLID186单元模拟链环的模型结构。接触设置中,链环间的接触关系采用面面接触模拟,接触对设置中,链环间接触面采用CONTA174单元模拟,采用TARGE170单元模拟目标面。采用非对称接触方式,接触面为左端链环上的接触区域,目标面为右端链环上的接触区域。选用扩增拉格朗日算法作为接触算法,接触摩擦系数为0.3。
采用ICEM对链环进行网格划分,画完网格后的模型如图 1所示,在建立的有限元模型中,节点数量为16 873,单元数量为14 896,接触单元与目标单元数量为4 256个。
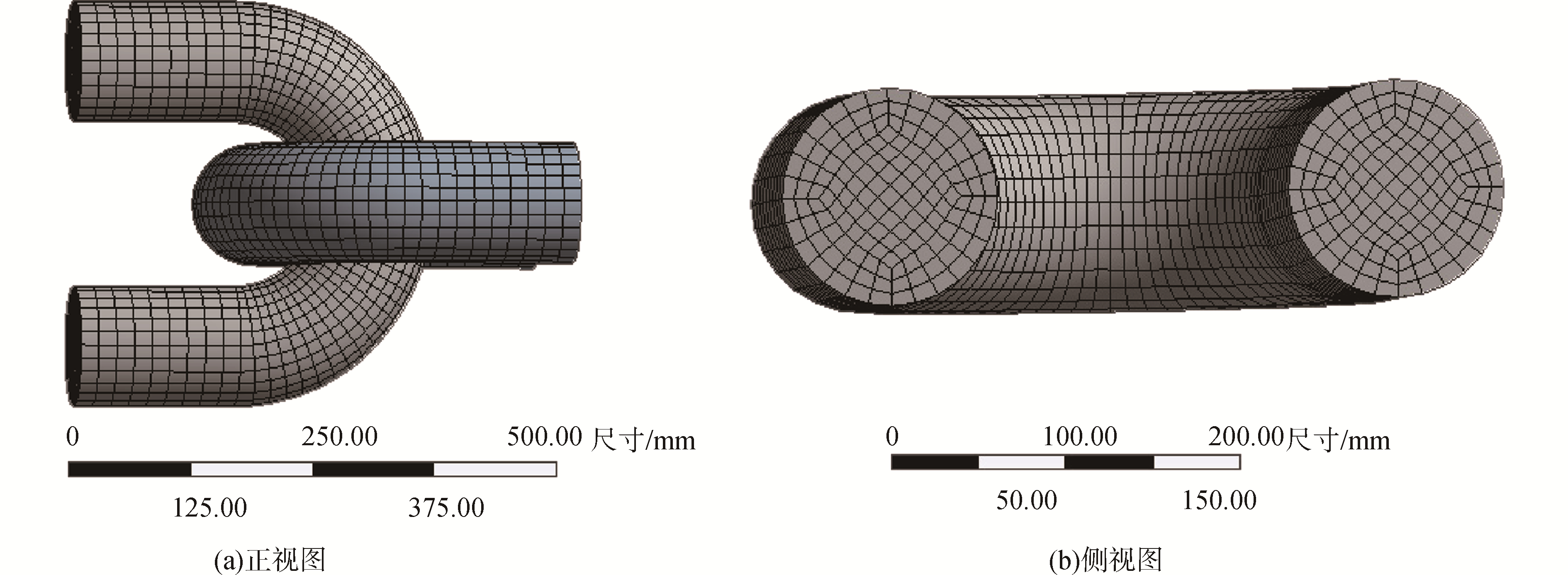
|
Download:
|
| 图 1 有限元模型网格 Fig. 1 Mesh of finite element model | |
链环边界条件施加方式如图 2所示,在横截面处,左端链环为全自由度约束(图中A),在右端链环施加绕Z轴角度约束(图中C,目的是实现平面外弯曲角度的施加,即先对链环施加小的轴向拉力和绕Z轴的旋转角度,当链环满足指定的角度后,再施加下文的工作载荷),在右端链环横截面施加均匀荷载(图中B,载荷方向为沿横截面法线向外)。
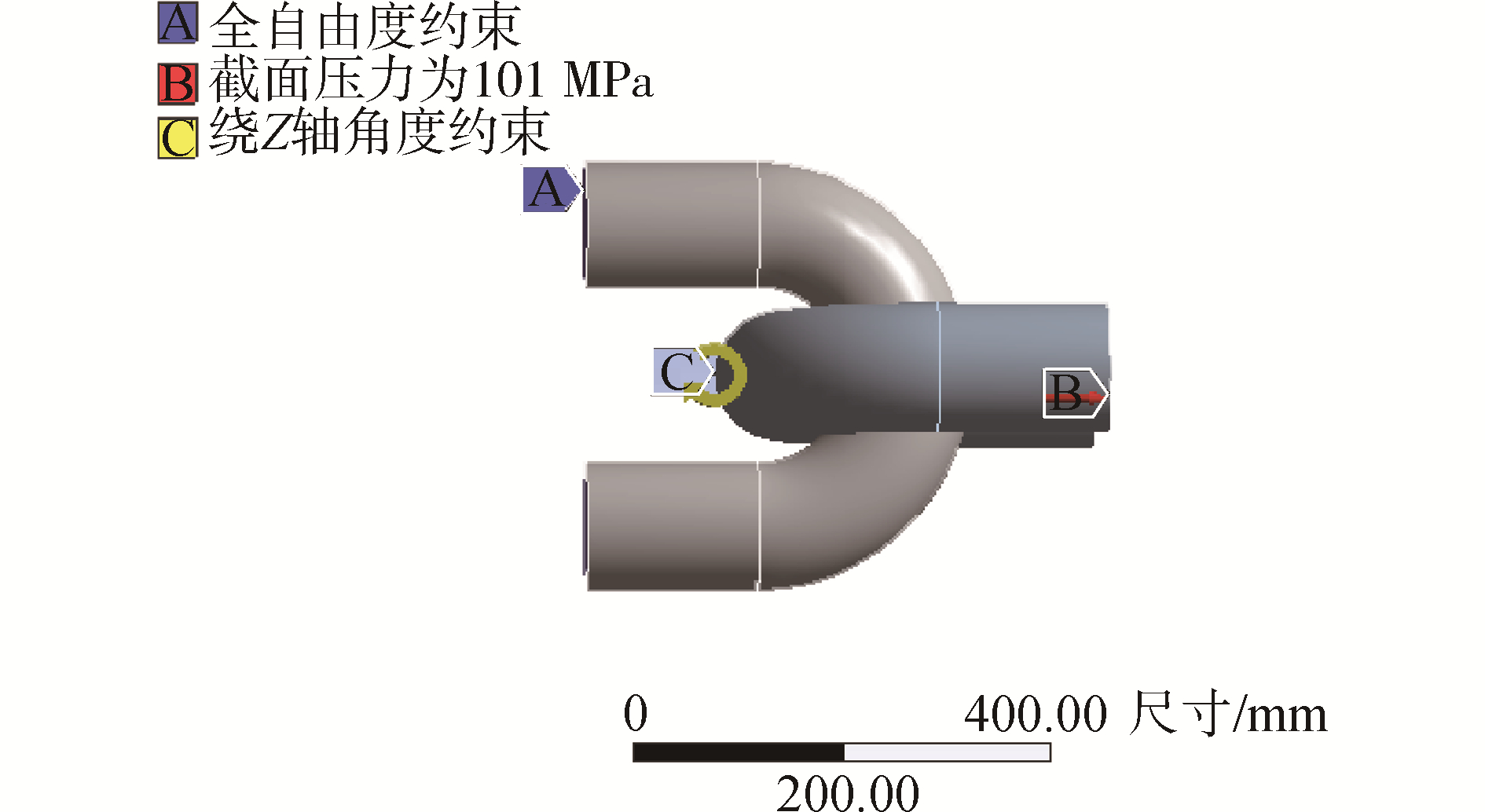
|
Download:
|
| 图 2 有限元模型边界条件 Fig. 2 Boundary condition of finite element model | |
在右端链环横截面处施加均匀分布的工作载荷Fo,用于模拟作业载荷,取值为1/3倍的试验载荷[1],而试验载荷Fp的大小可依据API规范[19]给出的公式计算得到,故由式(5)可计算得到Fo。在考虑链环遭受长期海况的磨损和腐蚀作用时,对链环施加以工作载荷Fo为平均值,动张力变化范围为300 kN,作用周期t0=10 s的循环载荷,与系泊线在典型海况下的动张力响应时程统计值基本保持一致[20]。
| $ F_{\mathrm{o}}=\frac{1}{3} F_{p}=\frac{1}{3} \cdot 0.014 d^{2}(44-0.08 d) $ | (5) |
式中d为链环直径。
3 计算结果及分析锚链链环的平面外弯曲角度一般为2°左右[7],因此,本文选取平面外弯曲角度分别为0°、1°、2°、3°对锚链链环进行有限元模拟。
3.1 不同弯曲角度下的锚链应力基于1.3节的计算流程,暂不考虑腐蚀作用(即取腐蚀年限T0=0),仅沿图 2中B截面施加轴向的工作载荷Fo,本节给出了不同弯曲角度下锚链应力的计算结果。
3.1.1 应力状态分析计算得到锚链链环在不同弯曲角度下的应力分布如图 3所示,接触面的应力分布如图 4所示。

|
Download:
|
| 图 3 不同弯曲角度下应力分布 Fig. 3 Stress distribution of models with different bending angles | |

|
Download:
|
| 图 4 不同弯曲角度下接触面的应力分布 Fig. 4 Stress distribution of contact area with different bending angles | |
由图 3可见,随着弯曲角度的增加,整个模型中应力的最大值分别为648、643、641、641 MPa。其中0°与3°的2种情况的最大应力差别仅为1.08%,可以认为在小角度平面外弯曲范围内,平面外弯曲角度对整个模型中应力的最大值基本没有影响。
将图 4中左侧肩部定义为AA区域,右侧肩部定义为BB区域,将整个接触表面的区域定义为CC区域,整个模型定义为DD区域(图 3中所有区域),得到各区域应力最大值变化趋势如图 5所示。
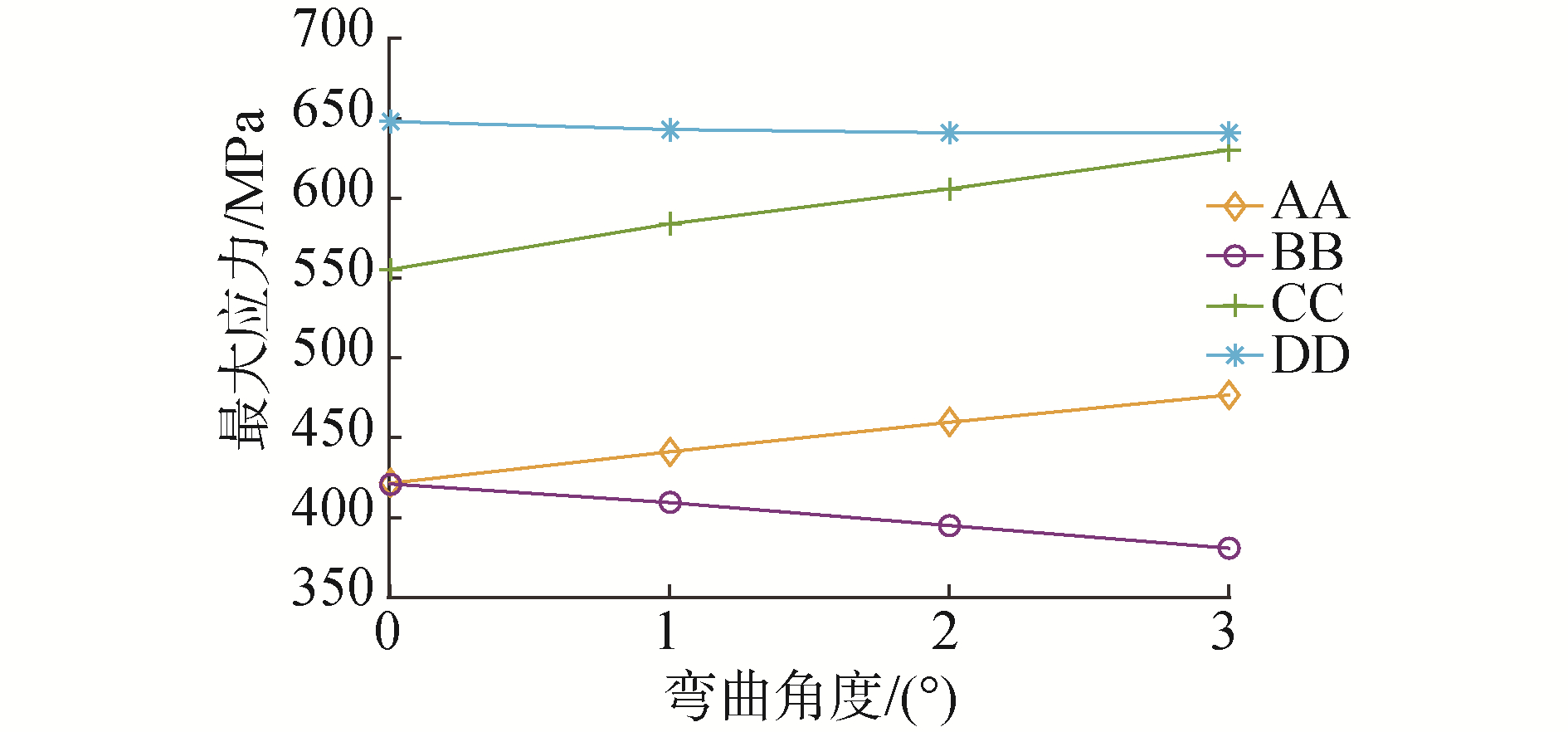
|
Download:
|
| 图 5 不同区域的最大应力 Fig. 5 Maximum stress in different regions | |
由图 5可见,一定的弯曲角度内,锚链接触区域中接触表面应力最大值随弯曲角度的增加,变化显著。此外,链环由直线棒体向接触区域过渡的肩部区域应力分布变化也很明显:由于弯曲角度的存在,相比只施加轴向载荷,AA区域弯矩变大,BB区域弯矩会减小,弯曲角度增加,使得AA区域应力值随之增加,BB区域应力值变小。与实际锚链服役过程中承受平面外弯曲载荷时,AA区域最先发生断裂的情况相符合[7]。对整个模型分析,弯曲角度增加,模型最大应力基本不变(DD曲线),平面外弯曲角度的增加,接触区域的表面应力随之增加(CC曲线)。
3.1.2 接触状态分析由式(1)~(4)可知,链环接触区域的磨损计算与接触区域节点的滑移距离和接触压应力有关。在ANSYS WORKBENCH中的接触分析模块,对链环接触区域进行分析,在不同平面外弯曲角度下,链环的接触状态信息(滑移距离和接触压应力)如图 6、7所示。

|
Download:
|
| 图 6 不同弯曲角度下滑移距离最大值 Fig. 6 Maximum sliding distance with different bending angles | |
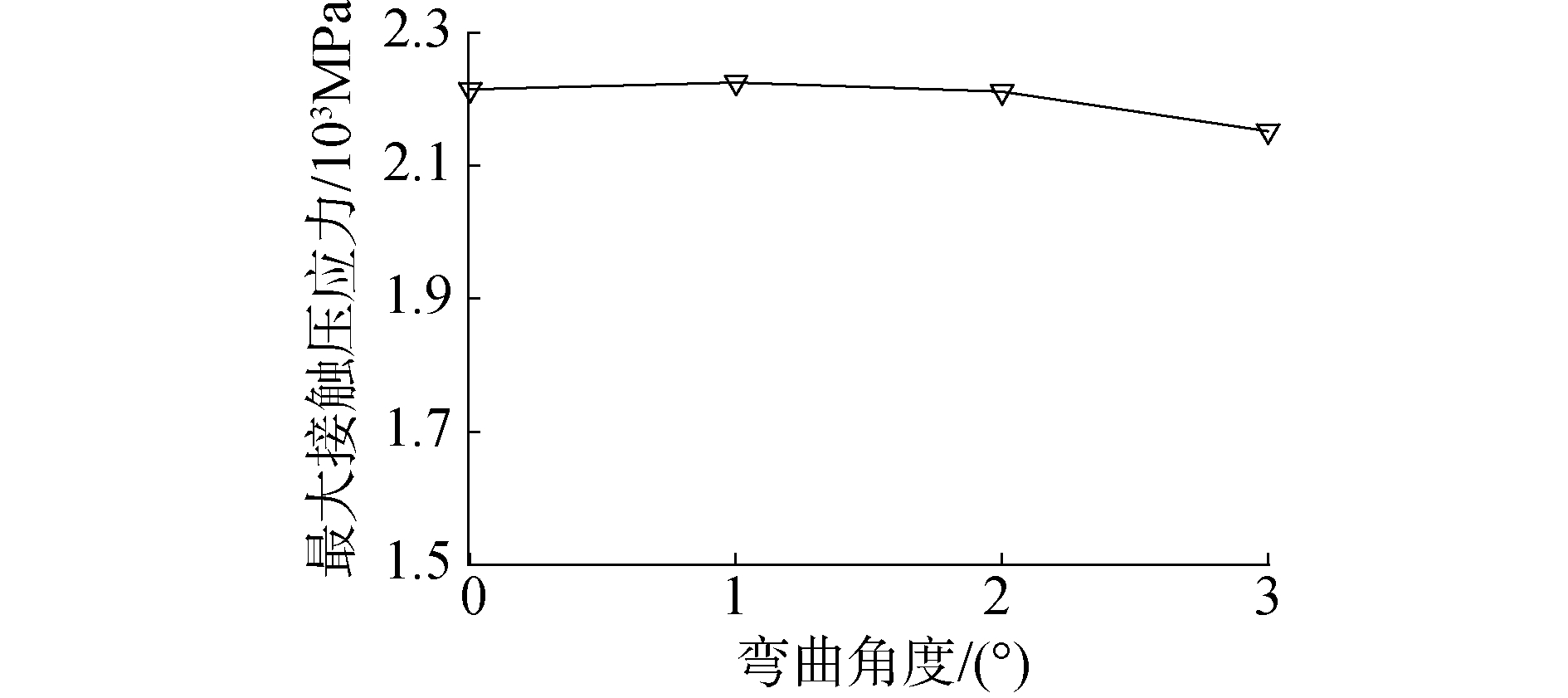
|
Download:
|
| 图 7 不同弯曲角度下接触压应力最大值 Fig. 7 Maximum contact pressure with different bending angles | |
由图 6可见,滑移最大距离随着平面外弯曲角度的增大而迅速增大,尤其是0°和1°的2种情况对比,即纯拉伸载荷与平面外弯曲角度载荷滑移距离最大值相比,有明显的增大。不同平面外弯曲角度时,滑移距离和弯曲角度二者的增大值近似呈线性关系。由图 7可见,接触压应力的值并未随平面外弯曲角度的增加发生改变,最大变化仅为3.28%。因此,接触压应力的值与平面外弯曲角度和及滑移距离的无明显关系,与材料的属性、拉力的大小、摩擦系数有关。在计算接触区域的磨损时,材料属性、滑移距离以及接触压应力均与磨损量有关。因此,计算锚链磨损时,平面外弯曲载荷的存在与否由于对滑移距离和锚链的磨损量均有影响。
3.2 不同腐蚀年限下的锚链应力基于1.3节的计算流程,同时考虑磨损和腐蚀的联合作用,沿着图 2中B截面施加轴向的循环载荷,本节给出了不同弯曲角度和腐蚀计算年限下链环的应力分布变化趋势,具体结果如表 2所示,限于篇幅,仅给出0°和2°的部分结果对比。同时,给出发生磨损4 a后,不同弯曲角度下节点需要进行微调的数量及其节点磨损最大值如表 3所示。
| 表 2 不同腐蚀年限下的应力最大值 Table 2 Maximum stresses with different corrosion years |
| 表 3 节点微调数量及最大磨损值(4 a磨损下) Table 3 Number of wear nodes and maximum wear depths with 4 a wear |
由表 2可见,在不同平面外弯曲角度下,随着腐蚀年限的增加,腐蚀和磨损的联合作用下,链环的应力最大值增加,整体应力水平得到改善,材料应力最大值大于屈服强度,进入塑性变形阶段。但对于0°与2°这2种弯曲角度,相同时间段,应力最大值相差很小,腐蚀年限为20 a时,二者应力最大值变化仅为1.22%,认为二者最大应力近似相等。然而,对于接触部位和由直线棒体向冠部区域过渡的肩部区域的应力,相差较为显著,该区域应力分布如图 8所示。由表 3可见,平面外弯曲角度的增加,节点的最大磨损值随之增加。

|
Download:
|
| 图 8 不同腐蚀年限下接触面的应力分布 Fig. 8 Stress distribution of contact area with different corrosion years | |
在图 8中,弯曲角度为0°时,L-0区域为接触表面左侧肩部区域,R-0区域为接触表面右侧肩部区域,M-0区域为接触表面的中间区域;相对应弯曲角度为2°时的位置分别定义为L-2区域、R-2区域、M-2区域。其各区域应力最大值变化情况如表 4所示。
| 表 4 不同腐蚀年限下各区域的应力最大值 Table 4 Maximum value of stress in different regions with different corrosion years |
由表 4可见,链环的平面外弯曲角度为0°,随腐蚀年限的增加,L-0区域与R-0区域的应力随之增加,但L-0区域和R-0区域的应力水平基本相同;接触区域进入塑性变形的区域随着腐蚀年限增加而增加;整个接触区域的应力最大值始终处于M-0区域,基本不随腐蚀年限的增加而改变。当链环平面外弯曲角度为2°时,随着腐蚀年限的增加,L-2区域和R-2区域的应力随之增加;对于相同的腐蚀年限,L-2区域的应力值远大于L-0区域的应力值,而R-2区域应力值远小于相对应的R-0区域得应力值;接触区域的应力最大值由M-2区域转移到L-2区域。
平面外弯曲角度会导致L-2区域弯矩增加,R-2区域弯矩变小,应力分布也随之改变。在锚链不断遭受磨损和腐蚀联合作用下,由于平面外弯曲角度的存在,会使链环断裂的位置发生改变:在腐蚀年限为20 a时,受平面外弯曲的作用,在接触表面处应力的最大值在L-2区域,而不是接触的M-2区域,链环的应力分布状态发生了改变。因此,在研究链环长期累积损伤时,考虑平面外弯曲载荷的影响十分关键。
4 结论1) 在小角度平面外弯曲范围内,随着弯曲角度的增加,整个模型等效应力最大值几乎不发生变化,接触区域的表面应力增加,链环肩部区域一侧应力值逐渐增加,另一侧应力值逐渐减小。
2) 随着平面外弯曲角度的增加,接触区域的滑移距离最大值迅速增加,而接触压应力值基本未变化,两者叠加后使得平面外弯曲载荷作用下对链环的磨损量有影响。
3) 在不同平面外弯曲角度下,链环在腐蚀和磨损的联合作用下,其应力最大值随着腐蚀年限的增加而增加,链环的整体应力水平提高。
4) 锚链遭受磨损和腐蚀联合作用下,受平面外弯曲角度的影响,可能会使链环的最大应力位置从接触区域转移到肩部区域,从而改变了链环的应力分布状态。
综上,考虑平面外弯曲应力对于系泊钢链环的应力分布变化规律具有重要影响,在设计中应该考虑。今后需进一步考虑施加的荷载条件、残余应力等因素的影响,从而更充分的解释平面外弯曲应力引起的系泊链环失效机理。
| [1] |
PACHECO P M C L, KENEDI P P, JORGE J C F. Elastoplastic analysis of the residual stress in chain links[C]//Proceedings of the 21st International Conference on Offshore Mechanics and Arctic Engineering. Oslo, Norway, 2002. http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleid=1576437
(  0) 0)
|
| [2] |
王文明, 张世联. 流花浮式平台锚链系统安全评估[J]. 造船技术, 2007(4): 25-29, 22. WANG Wenming, ZHANG Shilian. Safety evaluation of Liuhua FPS mooring system[J]. Marine technology, 2007(4): 25-29, 22. DOI:10.3969/j.issn.1000-3878.2007.04.008 (  0) 0)
|
| [3] |
徐伟, 张世联, 王佳颖. 浮式平台损伤锚链的强度评估方法[J]. 中国海洋平台, 2008, 23(2): 34-40. XU Wei, ZHANG Shilian, WANG Jiaying. Strength assessment method of damaged mooring chain for floating production system[J]. China offshore platform, 2008, 23(2): 34-40. DOI:10.3969/j.issn.1001-4500.2008.02.007 (  0) 0)
|
| [4] |
黄佳, 范模, 王忠畅, 等. 南海单点系泊系统故障分析[J]. 船海工程, 2015, 44(5): 88-92. HUANG Jia, FAN Mo, WANG Zhongchang, et al. Failure analysis and improvement of single point mooring systems in South Sea[J]. Ship & ocean engineering, 2015, 44(5): 88-92. DOI:10.3963/j.issn.1671-7953.2015.05.025 (  0) 0)
|
| [5] |
JEAN P, GOESSENS K, HOSTIS D. Failure of chains by bending on deepwater mooring systems[C]//Proceedings of the Offshore Technology Conference. Houston, Texas, USA, 2005. https://www.onepetro.org/conference-paper/OTC-17238-MS
(  0) 0)
|
| [6] |
MELIS C, JEAN P, VARGAS P. Out-of-plane bending testing of chain links[C]//Proceedings of the ASME 200524th International Conference on Offshore Mechanics and Arctic Engineering. Halkidiki, Greece, 2005. https://www.researchgate.net/publication/267603937_Out-of-Plane_Bending_Testing_of_Chain_Links
(  0) 0)
|
| [7] |
VARGAS P, JEAN P. FEA of out-of-plane fatigue mechanism of chain links[C]//Proceedings of the ASME 200524th International Conference on Offshore Mechanics and Arctic Engineering. Halkidiki, Greece, 2005. http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleid=1575699
(  0) 0)
|
| [8] |
TER BRAKE E, VAN DER CAMMEN J, UITTENBOGAARD R. Calculation methodology of out of plane bending of mooring chains[C]//Proceedings of the ASME 200726th International Conference on Offshore Mechanics and Arctic Engineering. San Diego, USA, 2007. http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleid=1593551
(  0) 0)
|
| [9] |
LASSEN T, STORVOLL E, BECH A. Fatigue life prediction of mooring chains subjected to tension and out of plane bending[C]//Proceedings of the ASME 200928th International Conference on Ocean, Offshore and Arctic Engineering. Honolulu, Hawaii, USA, 2009. http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleid=1622627
(  0) 0)
|
| [10] |
LASSEN T, AARSNES J, GLOMNES E. Fatigue design methodology for large mooring chains subjected to out-of-plane bending[C]//Proceedings of the ASME 201433rd International Conference on Ocean, Offshore and Arctic Engineering. San Francisco, California, USA, 2014. http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleid=1911619
(  0) 0)
|
| [11] |
GAO Zhen, MOAN T, HEGGELUND S E. Time variant reliability of mooring system considering corrosion deterioration[C]//Proceedings of the ASME 200524th International Conference on Offshore Mechanics and Arctic Engineering. Halkidiki, Greece, 2005. http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleid=1575401
(  0) 0)
|
| [12] |
MELCHERS R E, MOAN T, GAO Zhen. Corrosion of working chains continuously immersed in seawater[J]. Journal of marine science and technology, 2007, 12(2): 102-110. DOI:10.1007/s00773-006-0227-4 (  0) 0)
|
| [13] |
ARREDONDO A, FERNÁNDEZ J, SILVEIRA E, et al. Corrosion fatigue behavior of mooring chain steel in seawater[C]//Proceedings of the ASME 201635th International Conference on Ocean, Offshore and Arctic Engineering. Busan, South Korea, 2016. http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleid=2570559
(  0) 0)
|
| [14] |
毛振东, 彭昂. 系泊链钢的摩擦磨损研究[J]. 船电技术, 2012, 32(12): 49-51. MAO Zhendong, PENG Ang. Research on frictional wear of mooring chain steel[J]. Marine electric & electronic technology, 2012, 32(12): 49-51. DOI:10.3969/j.issn.1003-4862.2012.12.015 (  0) 0)
|
| [15] |
刘金沅.锚链腐蚀磨损累积损伤评估方法研究[D].大连: 大连理工大学, 2013. LIU Jinyuan. Research on approach for corrosion and wear cumulative damage assessment of chain links[D]. Dalian: Dalian University of Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10141-1013199955.htm (  0) 0)
|
| [16] |
ARCHARD J F. Contact and rubbing of flat surfaces[J]. Journal of applied physics, 1953, 24(8): 981-988. DOI:10.1063/1.1721448 (  0) 0)
|
| [17] |
DNVGL. DNVGL-OS-E301, Position mooring[S]. Norway: DNVGL, 2015.
(  0) 0)
|
| [18] |
API. API RP 2SK, Design and analysis of station keeping systems for floating structures[S]. Washington: API, 2005.
(  0) 0)
|
| [19] |
API. API SPEC 2F. Specification for mooring chain[S]. Washington: API, 2015.
(  0) 0)
|
| [20] |
QIAO Dongsheng, OU Jinping. Global responses analysis of a semi-submersible platform with different mooring models in south china sea[J]. Ships and offshore structures, 2013, 8(5): 441-456. DOI:10.1080/17445302.2012.718971 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


