2. 海洋信息获取与安全工信部重点实验室(哈尔滨工程大学)工业和信息化部, 黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001
2. Key Laboratory of Marine Information Acquisition and Security(Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China;
3. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
被动声呐系统是利用水下目标的辐射噪声来实现目标探测,通常采用传感器阵列获取一定的阵增益、角分辨力。均匀圆阵可获得360°全方位无模糊的方位角信息以及近似相同的角分辨力,被广泛应用于被动声呐系统[1-3]。由于探测距离的增大、水声环境复杂性大,与环境噪声相比,水下目标信号越来越弱,给被动声呐系统带来了新的挑战。尽管增大基阵孔径、阵元数可提高探测能力,但是将导致布放、回收基阵困难。因此,如何在不改变圆阵参数配置的条件下实现对远程目标的被动探测已成为一个急待解决的问题。
目标方位估计是水声信号处理领域的一个重要分支,一般采用阵列信号处理来抑制环境噪声,提高方位估计性能。声矢量传感器可同步共点地拾取声场中某点的声压和振速信息,相比声压传感器可利用更多的声场信息,为水下远程目标的被动探测提供了强有力的支撑。常用的目标方位估计技术有子空间方法和波束形成方法[4]。子空间方法的最大缺点是在低信噪比(signal-to-noise ratio, SNR)下,信源数目估计不准确,其估计性能可能会严重下降[5]。波束形成方法包括常规波束形成方法(conventional beamforming, CBF)和最小方差无畸变响应方法(minimum variance distortionless response, MVDR)等。CBF方法的角分辨力受到瑞利限限制,无法分辨位于一个波束宽度内的多个目标。相比之下,MVDR方法具有较高的角分辨力,在水下目标探测、定位中应用更为广泛。Nehorai等[6]提出了声矢量传感器阵列信号处理方法,即将声矢量传感器的声压和每个振速分量视为独立阵元,从而构建声矢量阵列协方差矩阵。自此之后,以声压振速独立处理理论为基础的CBF、MVDR等方位估计方法被广泛研究[7-10],然而,这些目标方位估计方法不能有效地消除各向同性噪声,在低SNR条件下探测性能有限,不适合远程目标的被动探测。研究发现,在远场声场,有限尺度声源信号的声压和振速是相干的[11];而对于各向同性噪声场,同点测量的噪声的声压和振速是不相关的[11-12]。因此,声压振速联合处理技术具有良好的噪声抑制能力,适合远程目标的检测、估计。文献[13-14]通过湖上实测数据确认了声压振速联合处理技术较声压振速独立处理方法具有更强的噪声抑制能力。杨德森等[15-16]利用相位模态变换原理,将矢量声场分解为一系列相互正交的相位模态,在此基础上将声压振速联合处理理论扩展到声矢量圆阵,提出了声矢量圆阵相位模态域目标方位估计方法。相位模态变换可将圆阵转换成虚拟线阵,从而使空间平滑等解相干算法得以应用于圆阵。但相位模态变换是以空间离散傅里叶变换推导得到的,需要满足Nyquist采样定律,即该变换可激发的最高阶模态数(模态数与信号频率有关)受到阵元数目的限制。如果相位模态变换后的虚拟线阵阵元数大于圆阵阵元数,相位模态域方位估计方法的估计性能将严重下降。文献[17]利用中心对称圆阵的对称特性,提出了空间平均理论,着重研究了非相关目标的方位估计性能。
本文利用中心对称声矢量圆阵的结构特性,将声矢量传感器重新排列,构建了中心对称的阵列形式,并将声压振速联合处理理论和前后向空间平均算法相结合,提出了声矢量圆阵相干双声源方位估计方法。该方法具有较强的噪声抑制能力和较好的方位估计性能。
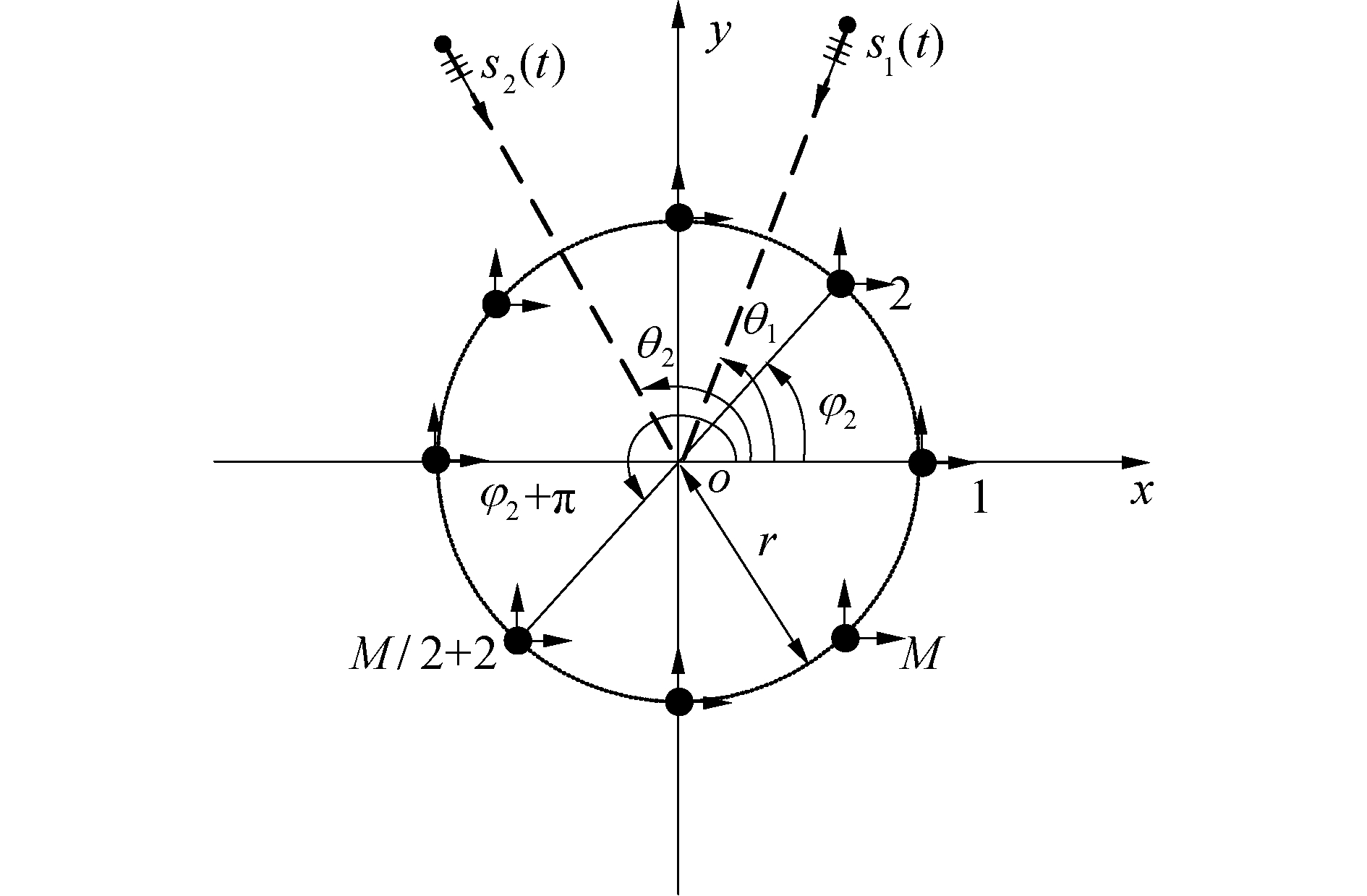
1 声矢量圆阵接收信号模型如图 1所示,由M元(M为偶数)二维声矢量传感器组成的声矢量圆阵位于xy平面,半径为r,圆心与坐标系原点重合,1号声矢量传感器位于x轴,2~M号声矢量传感器依次逆时针布放于圆上,声矢量传感器的2个振速通道方向分别沿着x、y轴的正方向。假设2个窄带相干信号s1(t)、s2(t)从平行于xy平面的方向入射至声矢量圆阵,入射角度分别为θ1、θ2,其中s2(t)=βs1(t),β为复常数。以圆心为参考点,则t时刻声矢量圆阵的接收信号可表示为:
|
Download:
|
| 图 1 声矢量圆阵示意 Fig. 1 Geometry of the uniform circular acoustic vector sensor array | |
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{P}}(t) = {\mathit{\boldsymbol{A}}_p}\mathit{\boldsymbol{S}}(t) + {\mathit{\boldsymbol{N}}_p}(t)}\\ {{\mathit{\boldsymbol{V}}_x}(t) = {\mathit{\boldsymbol{A}}_x}\mathit{\boldsymbol{S}}(t) + {\mathit{\boldsymbol{N}}_x}(t)}\\ {{\mathit{\boldsymbol{V}}_y}(t) = {\mathit{\boldsymbol{A}}_y}\mathit{\boldsymbol{S}}(t) + {\mathit{\boldsymbol{N}}_y}(t)} \end{array}} \right. $ | (1) |
式中:S(t)=[s1(t), s2(t)]T为信号向量;Np(t)、Nx(t)和Ny(t)分别为声压通道和x、y振速通道所接收的噪声向量;P(t)、Vx(t)及Vy(t)分别表示声矢量圆阵接收的声压和x、y振速分量,即:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{P}}(t) = {{\left[ {{P_1}(t),{P_2}(t), \cdots ,{P_M}(t)} \right]}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{V}}_x}(t) = {{\left[ {{V_{x1}}(t),{V_{x2}}(t), \cdots ,{V_{xM}}(t)} \right]}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{V}}_y}(t) = {{\left[ {{V_{y1}}(t),{V_{y2}}(t), \cdots ,{V_{yM}}(t)} \right]}^{\rm{T}}}} \end{array}} \right. $ | (2) |
式中:Pm(t)、Vxm(t)和Vym(t)分别为第m号声矢量传感器所接收的声压和x、y振速分量。Ap、Ax和Ay分别为声矢量圆阵的声压和x、y振速通道的导向矢量矩阵:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{A}}_p} = {{\left[ {{\mathit{\boldsymbol{a}}_{p1}},{\mathit{\boldsymbol{a}}_{p2}}, \cdots ,{\mathit{\boldsymbol{a}}_{pm}}, \cdots ,{\mathit{\boldsymbol{a}}_{pM}}} \right]}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{A}}_x} = {{\left[ {{\mathit{\boldsymbol{a}}_{x1}},{\mathit{\boldsymbol{a}}_{x2}}, \cdots ,{\mathit{\boldsymbol{a}}_{xm}}, \cdots ,{\mathit{\boldsymbol{a}}_{xM}}} \right]}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{A}}_y} = {{\left[ {{\mathit{\boldsymbol{a}}_{y1}},{\mathit{\boldsymbol{a}}_{y2}}, \cdots ,{\mathit{\boldsymbol{a}}_{ym}}, \cdots ,{\mathit{\boldsymbol{a}}_{yM}}} \right]}^{\rm{T}}}} \end{array}} \right. $ | (3) |
其中:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{a}}_{pm}} = \left[ {{a_{pm}}\left( {{\theta _1}} \right),{a_{pm}}\left( {{\theta _2}} \right)} \right]}\\ {{\mathit{\boldsymbol{a}}_{xm}} = \left[ {{a_{pm}}\left( {{\theta _1}} \right)\cos {\theta _1},{a_{pm}}\left( {{\theta _2}} \right)\cos {\theta _2}} \right]}\\ {{\mathit{\boldsymbol{a}}_{ym}} = \left[ {{a_{pm}}\left( {{\theta _1}} \right)\sin {\theta _1},{a_{pm}}\left( {{\theta _2}} \right)\sin {\theta _2}} \right]} \end{array}} \right. $ | (4) |
式中:apm(θh)=ejkrcos(φm-θh)(h=1, 2),φm=2π(m-1)/M为第m号声矢量传感器与x轴正方向的夹角,k=2πf/c为波数,f为信号频率,c为声速。
2 阵元域前后向空间平均理论 2.1 中心对称基阵由偶数元均匀声矢量圆阵的中心对称结构特性可知,第m (m=1, 2, …, M/2)号和第m+M/2号声矢量传感器与x轴夹角有如下关系φM/2+m=π+φm,则:
| $ \left\{\begin{array}{l}{\boldsymbol{a}_{p(M / 2+m)}=\boldsymbol{a}_{p m}^{*}} \\ {\boldsymbol{a}_{x(M / 2+m)}=\boldsymbol{a}_{x m}^{*}} \\ {\boldsymbol{a}_{y(M / 2+m)}=\boldsymbol{a}_{y m}^{*}}\end{array}\right. $ | (5) |
式中:m=1, 2, …, M/2;(·)*表示共轭运算。
将声矢量传感器按[1,2,…,M/2,M,…,M/2+1]重新排序,则重新排列后的声矢量圆阵接收信号可表示为:
| $ \left\{\begin{array}{l}{\tilde{\boldsymbol{P}}(t)=\left[P_{1}(t), \cdots, P_{M / 2}(t), P_{M}(t), \cdots, P_{M / 2+1}(t)\right]^{\mathrm{T}}} \\ {\tilde{\boldsymbol{V}}_{x}(t)=\left[V_{x 1}(t), \cdots, V_{x(M / 2)}(t), V_{x M}(t), \cdots,\right.} \\ \qquad\qquad{V_{x(M / 2+1)}(t) ]^{\mathrm{T}}} \\ {\tilde{\boldsymbol{V}}_{y}(t)=\left[V_{y 1}(t), \cdots, V_{y(M / 2)}(t), V_{y M}(t), \cdots,\right.} \\ \qquad\qquad {V_{y(M / 2+1)}(t) ]^{\mathrm{T}}}\end{array}\right. $ | (6) |
与式(6)相对应的导向矢量矩阵表达式为:
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\tilde A}}}_p} = {\left[ {{\mathit{\boldsymbol{a}}_{p1}}, \cdots ,{\mathit{\boldsymbol{a}}_{pM/2}},{\mathit{\boldsymbol{a}}_{pM}}, \cdots ,{\mathit{\boldsymbol{a}}_{p\left( {M/2 + 1} \right)}}} \right]^{\rm{T}}}\\ {{\mathit{\boldsymbol{\tilde A}}}_x} = {\left[ {{\mathit{\boldsymbol{a}}_{x1}}, \cdots ,{\mathit{\boldsymbol{a}}_{x\left( {M/2} \right)}},{\mathit{\boldsymbol{a}}_{xM}}, \cdots ,{\mathit{\boldsymbol{a}}_{x\left( {M/2 + 1} \right)}}} \right]^{\rm{T}}}\\ {{\mathit{\boldsymbol{\tilde A}}}_y} = {\left[ {{\mathit{\boldsymbol{a}}_{y1}}, \cdots ,{\mathit{\boldsymbol{a}}_{y\left( {M/2} \right)}},{\mathit{\boldsymbol{a}}_{yM}}, \cdots ,{\mathit{\boldsymbol{a}}_{y\left( {M/2 + 1} \right)}}} \right]^{\rm{T}}} \end{array} \right. $ | (7) |
令矩阵J为M×M维置换矩阵,其反对角线元素为1,其余均为0。由式(5)可知,导向矢量矩阵
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\tilde A}}}_p} = \mathit{\boldsymbol{J\tilde A}}_p^ * \\ {{\mathit{\boldsymbol{\tilde A}}}_x} = \mathit{\boldsymbol{J\tilde A}}_x^ * \\ {{\mathit{\boldsymbol{\tilde A}}}_y} = \mathit{\boldsymbol{J\tilde A}}_y^ * \end{array} \right. $ | (8) |
为了提高水下远程目标的探测能力,充分利用声压振速联合处理方法,构建声压与组合振速的互协方差矩阵,在此基础上引入后向互协方差矩阵,通过平均得到前后向空间平均互协方差矩阵,最后以MVDR方法为例得到2个相干源的空间谱。
将式(6)中的2个振速通道信号投影到观测方向ϕc上,得到组合振速:
| $ \begin{array}{l} {\mathit{\boldsymbol{\widetilde V}}_c}(t) = {\mathit{\boldsymbol{\widetilde V}}_x}(t)\cos {\phi _c} + {\mathit{\boldsymbol{\widetilde V}}_y}(t)\sin {\phi _c} = \\ \;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{\widetilde A}}_p}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c}\mathit{\boldsymbol{S}}(t) + {\mathit{\boldsymbol{\widetilde N}}_c}(t) \end{array} $ | (9) |
式中:Φc=diag(cos(ϕc-θ1), cos(ϕc-θ2));
根据平均声能流概念,得到声压与组合振速的互协方差矩阵:
| $ {\mathit{\boldsymbol{R}}_{pv}} = {\rm{E}}\left\{ {\mathit{\boldsymbol{\tilde P}}\left( t \right)\mathit{\boldsymbol{\tilde V}}_c^{\rm{H}}\left( t \right)} \right\} = {\mathit{\boldsymbol{\tilde A}}_p}{\mathit{\boldsymbol{R}}_s}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c}\mathit{\boldsymbol{\tilde A}}_p^{\rm{H}} + {\mathit{\boldsymbol{\rho }}_n} $ | (10) |
其中:
在各向同性噪声场中,同点测得的噪声的声压与振速是互不相关的[9, 11]。假设不同声矢量传感器所接收的噪声的声压、振速也不相关,则:
| $ \left\{ \begin{array}{l} {\rm{E}}\left\{ {{{\mathit{\boldsymbol{\tilde N}}}_{pm}}\left( t \right)\mathit{\boldsymbol{\tilde N}}_{xn}^{\rm{H}}\left( t \right)} \right\} = 0\\ {\rm{E}}\left\{ {{{\mathit{\boldsymbol{\tilde N}}}_{pm}}\left( t \right)\mathit{\boldsymbol{\tilde N}}_{yn}^{\rm{H}}\left( t \right)} \right\} = 0 \end{array} \right. $ | (11) |
式中m, n=1, 2,…, M。
根据式(11)可知,式(10)中的ρn为:
| $ {\mathit{\boldsymbol{\rho }}_n} = \left[ {\begin{array}{*{20}{c}} {{\rho _{11}}}&{{\rho _{12}}}& \cdots &{{\rho _{1M}}}\\ {{\rho _{21}}}&{{\rho _{22}}}& \cdots &{{\rho _{2M}}}\\ \vdots & \vdots & \ddots &{}\\ {{\rho _{M1}}}&{{\rho _{M2}}}& \cdots &{{\rho _{MM}}} \end{array}} \right] = {{\bf{0}}_{M \times M}} $ | (12) |
式中:
将式(12)代入式(10),可得:
| $ {\mathit{\boldsymbol{R}}_{pv}} = {\mathit{\boldsymbol{\tilde A}}_p}{\mathit{\boldsymbol{R'}}_s}\mathit{\boldsymbol{\tilde A}}_p^{\rm{H}} $ | (13) |
式中:R′s=RsΦc。R′s可视为对角矩阵Φc对矩阵Rs中的元素进行加权得到的。
现对R′s进行分析,当入射信号相干时,Rs矩阵为奇异矩阵,即矩阵R′s也为奇异矩阵。为了恢复矩阵R′s的秩,这里加入后向矩阵JRpv*J,得到前后向空间平均的互协方差矩阵,即:
| $ {\mathit{\boldsymbol{R}}_{fb}} = \frac{1}{2}\left( {{\mathit{\boldsymbol{R}}_{pv}} + \mathit{\boldsymbol{JR}}_{pv}^ * \mathit{\boldsymbol{J}}} \right) $ | (14) |
将式(8)、(13)代入式(14),可得:
| $ {\mathit{\boldsymbol{R}}_{fb}} = {\mathit{\boldsymbol{\tilde A}}_p}{\mathop{\rm Re}\nolimits} \left\{ {{{\mathit{\boldsymbol{R'}}}_s}} \right\}\mathit{\boldsymbol{\tilde A}}_p^{\rm{H}} $ | (15) |
式中:Re{R′s}=Re{Rs}Φc,是对角矩阵Φc对Re{Rs}中元素加权得到的。容易看出,矩阵Re{Rs}为满秩矩阵,只要对角矩阵Φc中的元素cos(ϕc-θh)≠0(h=1, 2),Re{R′s}即为满秩矩阵,便可利用互协方差矩阵Rfb来估计相干信号的方位。
值得注意的是,当cos(ϕc-θh) < 0(h=1, 2),互协方差矩阵Rfb的主特征值为负数,在使用MVDR波束形成时,对角加载项可能会使主特征值的绝对值变小,从而导致无法有效地估计目标方位。因此,这里对互协方差矩阵Rfb做修正:
| $ {\mathit{\boldsymbol{\tilde R}}_{fb}} = \mathit{\boldsymbol{U |\boldsymbol{\varLambda}| }}{\mathit{\boldsymbol{U}}^{\rm{H}}} $ | (16) |
式中:U为矩阵Rfb的特征向量,Λ为矩阵Rfb的特征值所构成的对角矩阵;
基于前后向平均的互协方差矩阵
| $ \left\{ \begin{array}{l} \min \;{\mathit{\boldsymbol{w}}^{\rm{H}}}{{\mathit{\boldsymbol{\tilde R}}}_{fb}}\mathit{\boldsymbol{w}}\\ {\rm{subject}}\;{\rm{to}}\;{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{A}}_p}\left( \theta \right) = 1 \end{array} \right. $ | (17) |
式中θ为扫描角度。由此可得MVDR空间谱表达式:
| $ {P_{{\rm{MVDR}}}}\left( {{\theta _n}} \right) = \frac{1}{{\mathit{\boldsymbol{A}}_p^{\rm{H}}\left( {{\theta _n}} \right)\mathit{\boldsymbol{\tilde R}}_{fb}^{ - 1}{\mathit{\boldsymbol{A}}_p}\left( {{\theta _n}} \right)}} $ | (18) |
观测方向ϕc的选择方法有2种:
方法1:根据基于声压阵的常规波束形成方法预估目标方位,若空间谱只有一个主瓣,说明2个相干信号在该主瓣内,则可选择该主瓣所对应的角度作为观测方向;若空间谱有2个主瓣,说明2个主瓣所对应的角度约为2个相干信号的入射方向(设2个主瓣对应的角度分别为ϕ1和ϕ2),则观测方向ϕc可选择2个角度之间的任意角度,或者为了使对角矩阵Φc对Re{Rs}中2个信号的加权值近似相同,观测角度可选择ϕc=(ϕ1+ϕ2)/2。
方法2:任意选择某一观测方向,如果采用本文方法所得的空间谱中只有一个谱峰(设该谱峰对应的角度为ϕ11),说明另一个信号被大大削弱,即对角矩阵Φc对另一信号的加权值约为零;然后,将观测方向指向ϕ11时,通过本文方法估计的空间谱将会出现2个谱峰(设2个谱峰位置对应的角度分别为ϕ21和ϕ22);则观测方向ϕc可选择ϕ21~ϕ22的任意角度,或者为了使对角矩阵Φc对Re{Rs}中2个信号的加权值近似相同,观测方向可选择ϕc=(ϕ21+ϕ22)/2。当任意选择的观测方向所得到的空间谱有2个谱峰(设2个谱峰所对应的角度分别为ϕ1和ϕ2)时,说明对角矩阵Φc=diag(cos(ϕc-θ1), cos(ϕc-θ2))中的元素均不为零,而且说明ϕ1和ϕ2约为2个相干目标的入射方向,则观测方向ϕc可选择ϕ1和ϕ2之间的任意角度,或者为了使对角矩阵Φc对2个信号的加权值近似相同,观测角度可选择ϕc=(ϕ1+ϕ2)/2。
本文研究的是远程目标的方位估计问题,由于方法2利用了声压振速联合处理方法,相比方法1,该方法具有更强的噪声抑制能力,因此本文采用方法2来确定观测方向ϕc。
3 仿真分析仿真采用8元均匀布放的声矢量圆阵,半径r=0.35 m,以圆心为坐标原点,声矢量传感器的2个振速通道分别沿着坐标系x、y轴的正方向,2个相干信号s1(t)、s2(t)分别从远场入射至声矢量圆阵,且s2(t)=βs1(t),其中β=ejπ/3。噪声场各向同性,即每个声矢量传感器接收的噪声的声压、振速是不相关的,同时不同声矢量传感器接收的噪声也是不相关的。以下对比方法都是以前后向空间平均方法为基础进行讨论的。
3.1 声压、声压振速独立和声压振速联合处理对比2个相干源入射角分别为100°、150°,信号频率f=2 kHz,观测方向ϕc=120°,图 2给出了不同SNR条件下的声压、声压振速独立处理以及声压振速联合处理的空间谱图。

|
Download:
|
| 图 2 声压处理、声压振速独立和声压振速联合处理的空间谱仿真结果 Fig. 2 Simulation results of acoustic pressure processing, the independent processing of acoustic pressure and particle velocity, and combined processing of acoustic pressure and particle velocity | |
从图 2中可以看出,声压处理方法在SNR=-5, -10,-15 dB无法有效分辨2个相干目标。声压振速独立处理方法在SNR=-5, -10 dB时可有效分辨2个相干目标,但当SNR下降至-15 dB时该方法已无法有效分辨2个相干信号。相比之下,声压振速联合处理方法在SNR下降到-15 dB时仍可有效分辨2个相干目标。此外,在相同SNR条件下,声压振速联合处理方法较其他2种方法具有较高的空间谱峰和较低的旁瓣。
3.2 阵元域与相位模态域处理方法的空间谱对比2个相干源入射角度分别为100°、150°,观测方向ϕc=120°,SNR=0 dB,图 3分别给出了阵元域声压振速联合处理FB-MVDR和相位模态域声压振速联合处理FB-MVDR的空间谱图,其中对于任意信号频率f,声矢量圆阵所激发的相位模态数为

|
Download:
|
| 图 3 阵元域与相位模态域声压振速联合处理FB-MVDR的空间谱对比分析 Fig. 3 Spatial spectrums of FB-MVDR based on the combined processing of acoustic pressure and particle velocity in element space and mode space | |
从图 3(a)可以看出,当f∈[1 kHz, 1.3 kHz]时,相位模态域虚拟线阵的阵元数为3,由于虚拟阵元数较少,角分辨率较低,相位模态域声压振速联合处理FB-MVDR方法无法分辨2个相干目标;当f∈[1.4 kHz, 2 kHz]和[2.1 kHz, 2.7 kHz]时,虚拟线阵的阵元数分别为5和7,角分辨率较高,该方法可有效估计2个相干目标方位;当f≈2.7 kHz时,该方法估计的目标方位出现偏移;当f>2.7 kHz时,该方法已完全失效。产生这种现象的主要原因是仿真采用的声矢量圆阵可激发的最大相位模态
通过方位估计均方根误差(root mean square error, RMSE)和分辨概率来对比以上方法的方位估计精度及分辨能力。定义方位估计的RMSE为:
| $ {\rm{RMSE}} = \sqrt {\frac{1}{{HN}}\sum\limits_{n = 1}^N {\left\{ {\sum\limits_{h = 1}^H {{{\left( {{{\hat \theta }_{n,h}} - {\theta _h}} \right)}^2}} } \right\}} } $ | (19) |
式中:N=200为独立实验次数;H=2为信源个数;
若某次实验估计的目标方位
| $ \left| {{{\hat \theta }_1} - {\theta _1}} \right| + \left| {{{\hat \theta }_2} - {\theta _2}} \right| < \left| {{{\hat \theta }_1} - {{\hat \theta }_2}} \right| $ | (20) |
则称该次实验中的2个目标被正确分辨,分辨概率是指正确分辨次数占实验总数的百分比[18]。
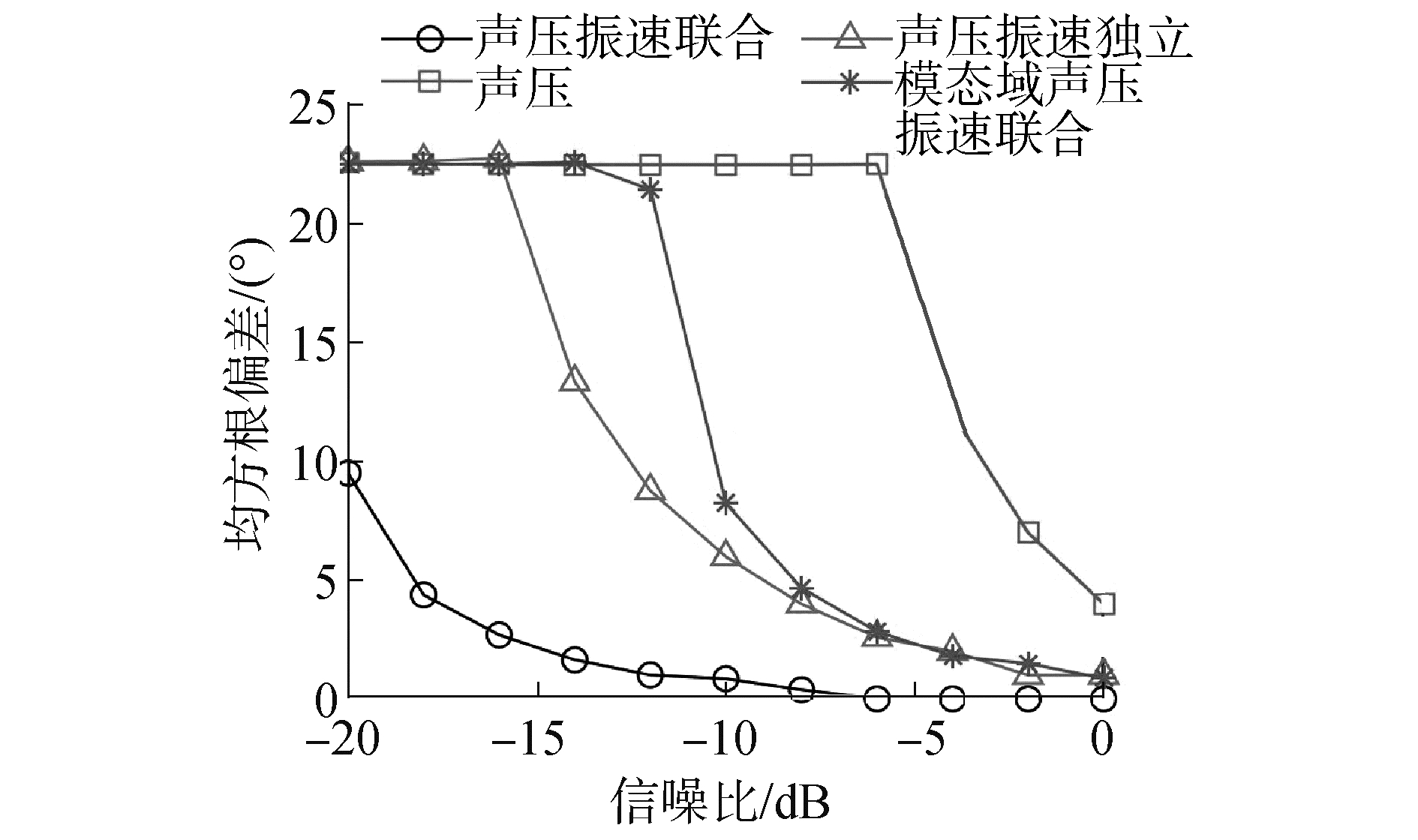
图 4给出了基于阵元域声压处理、声压振速独立处理、声压振速联合处理和相位模态域声压振速联合处理的FB-MVDR在不同SNR条件下的RMSE曲线,其中信号频率f=2 kHz,2个相干信号的入射角度分别为100°、145°,观测方向ϕc=120°。从图 4中可看出,阵元域声压振速联合处理FB-MVDR方法与其他方法相比具有较高的方位估计精度。
|
Download:
|
| 图 4 不同SNR条件下方位估计的均方根误差 Fig. 4 RMSE curves of different methods versus the SNR | |
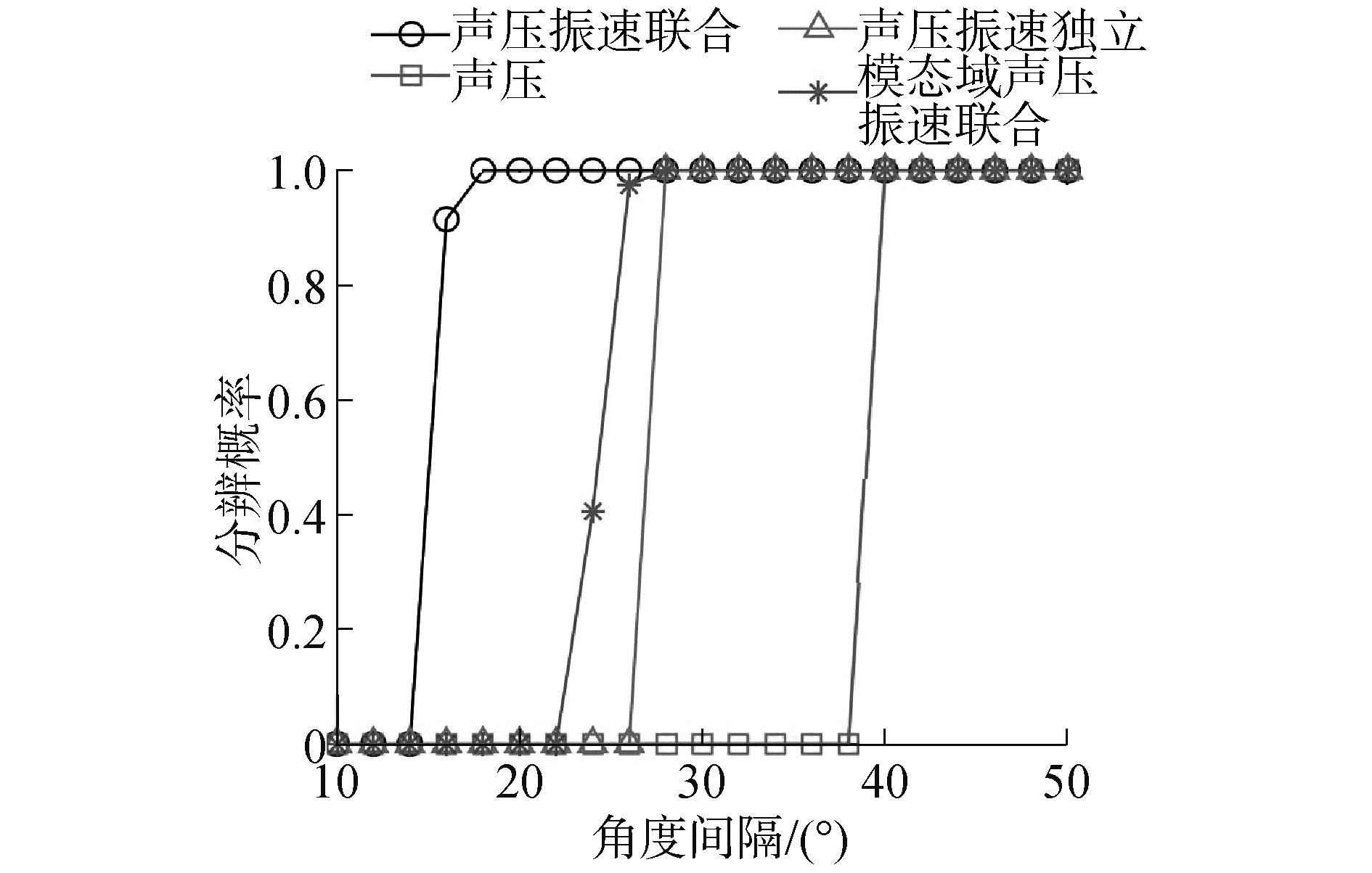
图 5给出了基于阵元域声压处理、声压振速独立处理、声压振速联合处理和相位模态域声压振速联合处理的FB-MVDR的角分辨能力,其中信号频率f=2 kHz,SNR=0 dB,2个相干信号的入射角分别为100°,100°+Δθ,Δθ是以2°为间隔, 从10°变化到50°,观测方向ϕc=121°。从图 5中可以看出,随着2个信号角度间隔的增大,以上方法的分辨能力都有所提高,而且阵元域声压振速联合处理FB-MVDR方法相比其他3种方法具有较高的角分辨能力。
|
Download:
|
| 图 5 不同入射角度间隔条件下各种方法的分辨概率 Fig. 5 Resolution probability curves of different methods versus the angular separation | |
本文利用消声水池实测数据进行声矢量圆阵相干双目标方位估计实验,来验证所提算法的有效性。如图 6所示,该声矢量圆阵由8元声矢量传感器组成,半径为0.35 m。声矢量传感器的2个振速方向分别沿着圆阵的径向和切向布放,然后将其投影到x轴和y轴上得到振速Vx(t)、Vy(t)。2个相干信号是将信号源产生的单频信号输入到2套发射系统(包含功率放大器和发射换能器)发射出去得到的,2个换能器与声矢量圆阵的布放深度均为5 m, 2个换能器相对于声矢量圆阵的入射角度分别为205°和254°。实验过程中采集了背景噪声,通过改变其幅度并将其混入测量的目标信号中来得到不同SNR条件下的声矢量圆阵接收数据。

|
Download:
|
| 图 6 半径0.35 m的8元声矢量圆阵示意 Fig. 6 The geometry of the UCAVSA with 8 acoustic vector sensors and radius is 0.35 m | |
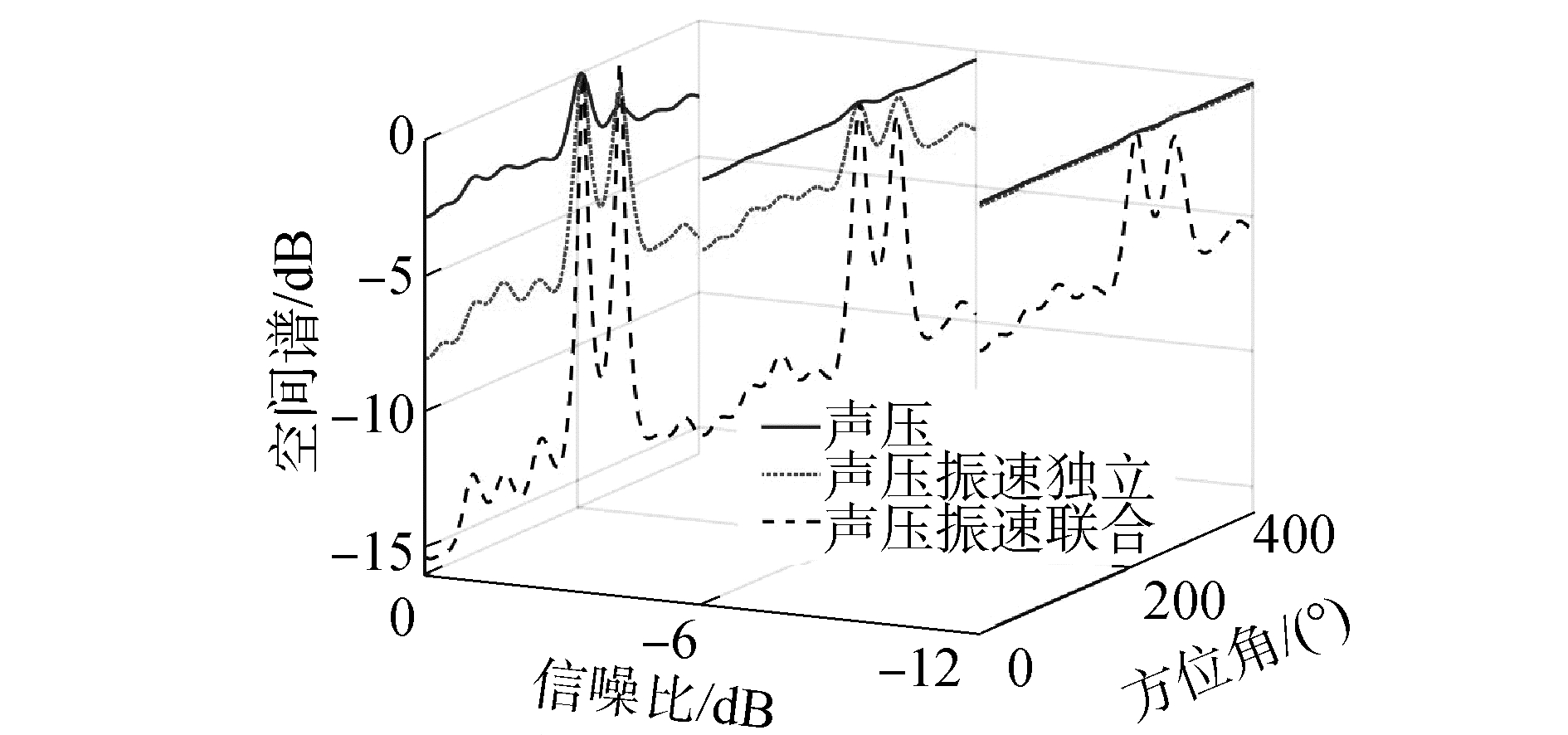
图 7给出了声压处理、声压振速独立处理和声压振速联合处理方法在不同SNR条件下的实验处理结果,其中信号频率为2.5 kHz,观测方向ϕc=230°。
|
Download:
|
| 图 7 声压处理、声压振速独立和声压振速联合处理的实验结果 Fig. 7 Experimental results of acoustic pressure processing, independent processing of the acoustic pressure and particle velocity, combined processing of acoustic pressure and particle velocity | |
从图 7可知,声压处理方法在SNR=0 dB时能估计2个相干目标方位,但其在低信噪(SNR=-6,-12 dB)条件下已不能估计目标方位。声压振速独立处理方法利用了更多的声场信息,在SNR=0,-6 dB条件下可有效估计目标方位,但该方法没有有效地利用声压振速联合处理,抗噪声能力有限,在SNR=-12 dB时已不能估计目标方位。相比之下,声压振速联合处理方法充分利用了各向同性噪声场中声压振速的相关特性,消除了各向同性噪声,在SNR下降至-12 dB时仍可以有效地估计目标方位。
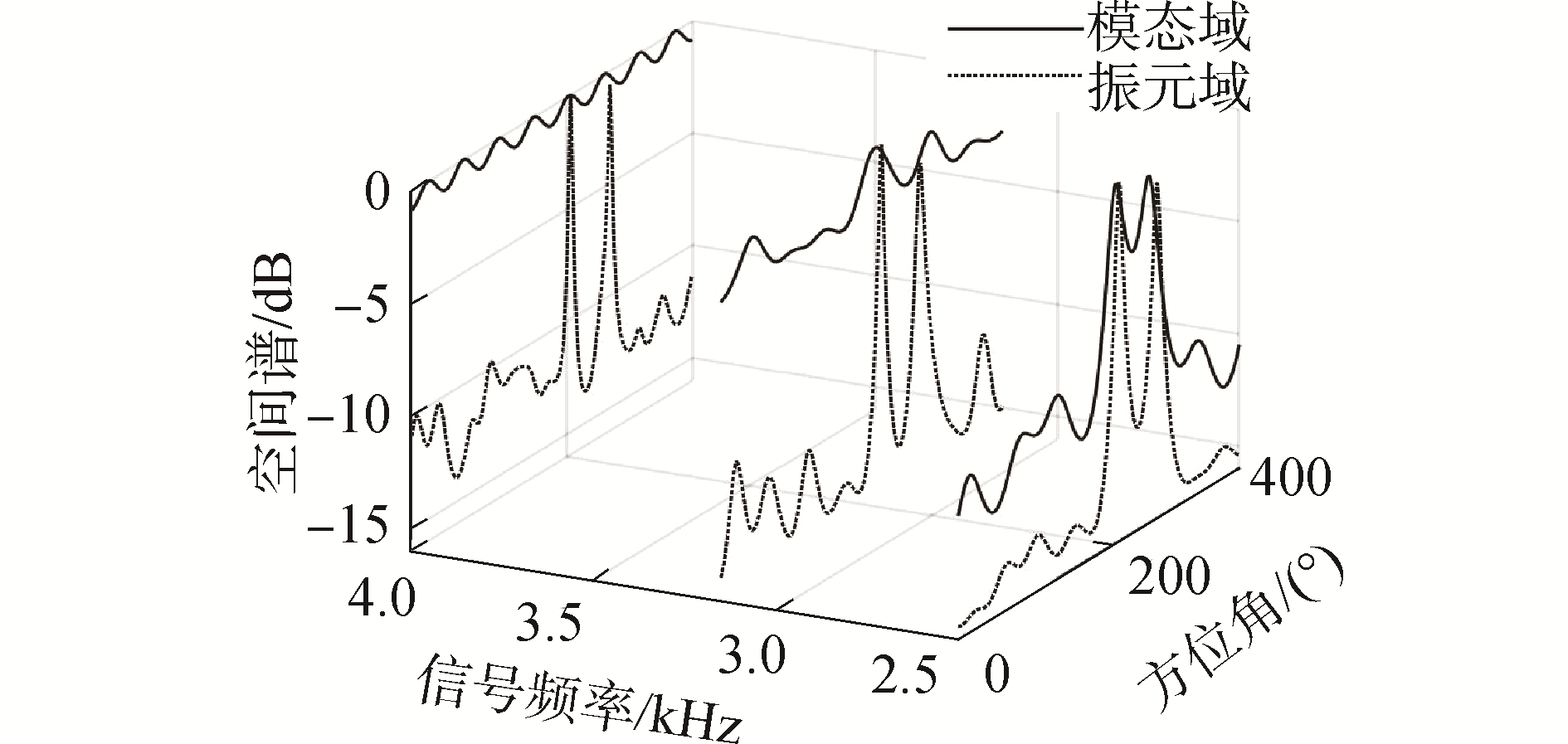
4.2 阵元域与相位模态域处理方法的空间谱对比图 8给出了不同信号频率下的阵元域和相位模态域声压振速联合处理FB-MVDR的空间谱图,其中,SNR=0 dB,信号频率分别为2.5、3.15、4 kHz,观测方向ϕc=230°。从图 8中可以看出,相位模态域声压振速联合处理FB-MVDR方法在信号频率f=2.5 kHz时可有效分辨2个相干目标,但当信号频率f=3.15,4 kHz时(相位模态域虚拟线阵的阵元数大于声矢量圆阵的阵元数),相位模态域声压振速联合处理FB-MVDR方法出现空间混叠,无法有效估计目标方位。相比之下,阵元域声压振速联合处理FB-MVDR方法可有效分辨两相干源目标,且具有较高的空间谱峰和方位估计精度。
|
Download:
|
| 图 8 不同信号频率下相位模态域与阵元域的实验结果 Fig. 8 Experimental results in mode and array-element space under different signal frequencies | |
1) 该方法解决了前后向空间平均方法无法直接应用于声矢量圆阵阵元域的问题。
2) 与相位模态域处理方法相比,该方法具有更好的方位估计性能,并且可处理的信号频率范围更宽。
3) 与声压处理、声压振速独立处理方法相比,该方法具有更强的噪声抑制能力和更好的方位估计性能,明显地提高了水下目标的方位估计性能。
| [1] |
PAVLIDI D, GRIFFIN A, PUIGT M, et al. Real-time multiple sound source localization and counting using a circular microphone array[J]. IEEE transactions on audio, speech, and language processing, 2013, 21(10): 2193-2206. DOI:10.1109/TASL.2013.2272524 (  0) 0)
|
| [2] |
WU Na, QU Zhiyu, SI Weijian, et al. DOA and polarization estimation using an electromagnetic vector sensor uniform circular array based on the ESPRIT algorithm[J]. Sensors, 2016, 16(12): 2109. DOI:10.3390/s16122109 (  0) 0)
|
| [3] |
XUE Bing, FANG Guangyou, JI Yicai. Passive localisation of mixed far-field and near-field sources using uniform circular array[J]. Electronics letters, 2016, 52(20): 1690-1692. DOI:10.1049/el.2016.2091 (  0) 0)
|
| [4] |
NAN TREES H L. Optimum array processing:part iv of detection, estimation, and modulation theory[M]. New York: Wiley Interscience, 2002: 293-303.
(  0) 0)
|
| [5] |
夏麾军, 杨益新, 韩一娜. 改进维纳滤波器及其在目标方位估计中的应用[J]. 声学学报, 2018, 43(4): 646-654. XIA Huijun, YANG Yixin, HAN Yi'na. Modified wiener filter for direction of arrival estimation[J]. Acta acustica, 2018, 43(4): 646-654. (  0) 0)
|
| [6] |
NEHORAI A, PALDI E. Acoustic vector-sensor array processing[J]. IEEE transactions on signal processing, 1994, 42(9): 2481-2491. DOI:10.1109/78.317869 (  0) 0)
|
| [7] |
CHEN H W, ZHAO J W. Wideband MVDR beamforming for acoustic vector sensor linear array[J]. IEE proceedings-radar, sonar and navigation, 2004, 151(3): 158-162. DOI:10.1049/ip-rsn:20040651 (  0) 0)
|
| [8] |
CHEN Huawei, ZHAO Junwei. Coherent signal-subspace processing of acoustic vector sensor array for DOA estimation of wideband sources[J]. Signal processing, 2005, 85(4): 837-847. DOI:10.1016/j.sigpro.2004.07.030 (  0) 0)
|
| [9] |
HAWKES M, NEHORAI A. Acoustic vector-sensor beamforming and Capon direction estimation[J]. IEEE transactions on signal processing, 1998, 46(9): 2291-2304. DOI:10.1109/78.709509 (  0) 0)
|
| [10] |
时洁, 杨德森, 时胜国. 基于矢量阵的运动声源柱面聚焦定位方法试验研究[J]. 物理学报, 2012, 61(12): 124302. SHI Jie, YANG Desen, SHI Shengguo. Experimental research on cylindrical focused beamforming localization method of moving sound sources based on vector sensor array[J]. Acta physica sinica, 2012, 61(12): 124302. DOI:10.7498/aps.61.124302 (  0) 0)
|
| [11] |
惠俊英, 刘宏, 余华兵, 等. 声压振速联合信息处理及其物理基础初探[J]. 声学学报, 2000, 25(4): 303-307. HUI Junying, LIU Hong, YU Huabing, et al. Study on the physical basis of pressure and particle velocity combined processing[J]. Acta acustica, 2000, 25(4): 303-307. DOI:10.3321/j.issn:0371-0025.2000.04.003 (  0) 0)
|
| [12] |
HAWKES M, NEHORAI A. Acoustic vector-sensor correlations in ambient noise[J]. IEEE journal of oceanic engineering, 2001, 26(3): 337-347. DOI:10.1109/48.946508 (  0) 0)
|
| [13] |
白兴宇, 姜煜, 赵春晖. 基于声压振速联合处理的声矢量阵信源数检测与方位估计[J]. 声学学报, 2008, 33(1): 56-61. BAI Xingyu, JIANG Yu, ZHAO Chunhui. Detection of number of sources and direction of arrival estimation based on the combined information processing of pressure and particle velocity using acoustic vector sensor array[J]. Acta acustica, 2008, 33(1): 56-61. DOI:10.3321/j.issn:0371-0025.2008.01.009 (  0) 0)
|
| [14] |
白兴宇, 杨德森, 赵春晖. 基于声压振速联合信息处理的声矢量阵相干信号子空间方法[J]. 声学学报, 2006, 31(5): 410-417. BAI Xingyu, YANG Desen, ZHAO Chunhui. The coherent signal-subspace method based on combined information processing of pressure and particle velocity using the acoustic vector sensor array[J]. Acta acustica, 2006, 31(5): 410-417. DOI:10.3321/j.issn:0371-0025.2006.05.004 (  0) 0)
|
| [15] |
杨德森, 朱中锐, 时胜国, 等. 声矢量圆阵相位模态域目标方位估计[J]. 声学学报, 2014, 39(1): 19-26. YANG Desen, ZHU Zhongrui, SHI Shengguo, et al. Direction-of-arrival estimation based on phase modal space for a uniform circular acoustic vector-sensor array[J]. Acta acustica, 2014, 39(1): 19-26. (  0) 0)
|
| [16] |
杨德森, 朱中锐, 时胜国. 矢量圆阵测向方法[J]. 哈尔滨工程大学学报, 2012, 33(10): 1259-1264. YANG Desen, ZHU Zhongrui, SHI Shengguo. Direction-of-arrival estimation for a circular vector-sensor array[J]. Journal of Harbin Engineering University, 2012, 33(10): 1259-1264. (  0) 0)
|
| [17] |
YE Zhongfu, XIANG Li, XU Xu. DOA estimation with circular array via spatial averaging algorithm[J]. IEEE antennas and wireless propagation letters, 2007, 6(11): 74-76. (  0) 0)
|
| [18] |
GERSHMAN A B. Direction finding using beamspace root estimator banks[J]. IEEE transactions on signal processing, 1998, 46(11): 3131-3135. DOI:10.1109/78.726831 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


